1 Introduction

Since 1980s, interferometry synthetic aperture radar (InSAR) technique has been utilized to monitor the deformation of the Earth’s surface [1] and applied to detecting hazards, e.g., earthquakes [2], ice motion [3], volcanism [4], landslides [5], and groundwater flow [6]. InSAR technique is able to detect motion phenomena on ground surface for large areas and has high accuracy of 3 to 24 cm and spatial resolution (up to 1 m). However, the implementation of InSAR technique is often influenced by three main factors: (1) signal interference due to atmosphere condition; (2) temporal decorrelation due to the changes of the scattering characteristics at different times; and (3) geometric decorrelation due to different imaging geometries arising from the far distances between the satellite repeat orbits. These factors may result in the reduction in the accuracy of deformation monitoring.

To solve these problems, much research work has been devoted to the time series analyses, i.e., the utilization of images collected at different times for the same areas. Furthermore, persistent scatterer interferometry synthetic aperture radar (PSInSAR) approach [7, 8] was developed to conduct the deformation monitoring. These PS points have quite constant scattering properties over time and the reflection dominance within a pixel cell so as to reduce the temporal decorrelation [9, 10] and the geometry decorrelation. In addition, the signal interference can be estimated and removed using the series of images acquired at different times. Later, the small baseline, i.e., the small distances among either the satellite positions or different acquisition times, is introduced to reduce the geometric and temporal decorrelation. This method is also time-series analysis approach and is called the small baseline subset (SBAS) [11, 12].

Recently, many researchers have focused on the improvement of PSInSAR technique, and significant progress has been achieved. In this article, we focus on the past development and the state of the art of this technique. This article is organized as follows: Sects. 2, 3. and 4 review the three steps involved in PSInSAR methods, i.e., PS detection, network formation, and resolution modeling, respectively; in Sect. 5, conclusions are made and outlooks on PSInSAR technique are presented.

2 Persistent scatterer detection

A series of SAR images used in PSInSAR contain billions of image pixels. For such large amount of data, it is necessary to firstly select the most promising scatter locations, i.e., the persistent scatterer candidates (PSCs), to reduce the data in order to ensure the implementation efficiency. The selected PSCs are commonly divided into two classes with different levels. The first level of PSCs is utilized to form a network covering the target area. The second level of PSCs is for the densification of the PS distribution. If PS density is still low over a target area, artificial corner reflectors can be used to provide strong responses in the SAR image so as to achieve a good interferometric phases for the estimation of the deformation and assess the performance of DInSAR and PSI [13–15]. Technical aspects on artificial corner reflectors in DInSAR are described in Ye et al. [16] and Crosetto et al. [17]. This technique has been applied to PSI [18, 19].

The selection of PSCs is based on the amplitude information because of the wrap of original interferometric phases and an amount of phase contributors:

$$\varPhi = \varphi_{\text{flat}} + \varphi_{\text{topo}} + \varphi_{\text{def}} + \varphi_{\text{atm}} + \varphi_{\text{noise}} ,$$
(1)

where \(\varphi_{\text{flat}}\), \(\varphi_{\text{topo}}\), \(\varphi_{\text{def}}\), \(\varphi_{\text{atm}},\) and \(\varphi_{\text{noise}}\) are the phase components about reference surface, topography, deformation, atmospheric delay, and noise, respectively. The detection of PSs depends on the phase stability or coherence of PSs. As the calibrated amplitude stability has a statistical relation to phase stability [8], if a scatterer has a large amplitude so as to dominate the resolution cell, the clutter has little influence on the phase. Based on this phenomenon, pixels with high-phase stability can be selected as PSCs.

Currently, there are three basic methods to detect PSs, i.e., the methods based on normalized amplitude dispersion, phase stability, and correlation. Many attempts have been made to improve these methods [20] or design a hybrid strategy to incorporate three basic methods [21]. In the following part, three typical methods are introduced, respectively.

2.1 Method based on amplitude dispersion

This method is used to detect the PSs according to the analysis of the amplitudes of pixels in time series. The amplitude dispersion \(D_{A}\) can be written as [8]

$$D_{A} = \frac{{\sigma_{A} }}{{m_{A} }} ,$$
(2)

where \(\sigma_{A}\) and \(m_{A}\) are the standard deviation and the mean of the backscattering intensity. In general, the scatterers with low-amplitude dispersions also have low-phase dispersions, while high-amplitude dispersions do not mean high-phase dispersions. Hence, a pixel with the amplitude less than a preset threshold can be regarded as a PS point. In this method, the phase information has been not considered. The method has the merits of high efficiency, easy implementation, and does not need to consider the relationship among adjacent pixels. Thus, it is suitable to the detection of single PS point. Ferretti [8] pointed out that the pixel with the amplitude from 0.25 to 0.4 can be selected as PS. Generally, the minimum number of 25 SAR images is needed in the detection of PS points in order to ensure the statistical significance and the quality of PSs [22].

2.2 Method based on phase stability

As PSs have the characteristic of the stable backscatter in images collected at different times, the phase stability is often considered as a criterion to select PSs. The phase stability can be assessed according to the signal-to-clutter ratio (SCR) [23]. If the average SCR of a pixel is more than a given threshold, the pixel can be regarded as a PS point. The form of SCR can be written as

$$r_{{\text{sc}}} = \frac{{s^{2} }}{{c^{2} }} ,$$
(3)

where s is the amplitude and c represents the clutter. Under the assumption of the equal clutter for a pixel and its surrounding pixels, the SCR for each pixel can be estimated by the phase standard variance \(\sigma_{\phi }\) [8] and the relation among pixels can be written as

$$\sigma_{\phi } = \frac{1}{{\sqrt {2r_{{\text{sc}}} } }}.$$
(4)

If a pixel has the phase standard deviation less than a certain threshold, it can be regarded as a PS. However, if adjacent pixels contain point scatterers [23], the clutter may be overestimated, which may result in the rejection of suitable PSC. In addition, a lot of computation time is needed in the implementation of this method.

2.3 Method based on correlation

If there are N images for a target region, N-1 interferometric pairs can be formed by a master image selected from these images and a slave image. As the backscatter of PSs is almost consistent in the images collected at different times, higher correlation for PSs should be kept in interferometric pairs. If the correlation in a pixel is more than a certain threshold, it can be regarded as PSC. This method can greatly reduce the data in the selection of PSs. In practice, for a pixel, the correlation coefficient \(\gamma\) is estimated by the pixel and its surrounding pixels in a given window size:

$$\gamma\, { = }\,\frac{{\left| {\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {M(i,j)S^{*} (i,j)} } } \right|}}{{\sqrt {\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left| {M(i,j)} \right|^{2} \sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left| {S(i,j)} \right|^{2} } } } } } }} ,$$
(5)

where M and S are the local information sets of pixels on two SAR images of an interferometric pair; \(*\) is the complex conjugation operator.

However, the calculation of the correlation coefficient greatly depends on the selection of the window size. Large size may result in the reliability reduction of PS detection, while small size results in the reliability reduction of the correlation coefficient estimation. In addition, the estimation of the correlation coefficient greatly depends on the quality of master image.

3 PS network construction

After PSC selection, the first-order PSCs are utilized to form a reference network for the full target area. This network is the basic for estimation of the atmospheric and orbital phase screen (APS) and lower-order PSCs can be added to densify this network.

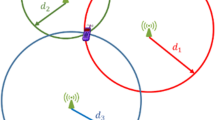
For PS networking, there is a common algorithm based on Delaunay triangulation [24]. Figure 1 shows the examples of the constructed network. In Delaunay network, the PSCs are connected based on the Delaunay triangulation principle. However, the number of arcs in such networks may be low, which results in lower accuracy for the deformation estimation. Furthermore, if an arc is longer than the maximum correlation length of the atmosphere, it will be eliminated, which further reduce the redundancy of the Delaunay network. In order to enhance the redundancy of Delaunay network, Kampes [24] proposed the multi-order networking algorithm. The implementation of this algorithm consists of four steps: (1) setting the minimal number of connecting arcs at each PSC; (2) equally dividing the area around each PSC into sub-areas; (3) selecting the closest PSCs around a PSC in all directions in a circular order; and (4) ignoring the sub-area when the distance between a PSC and its closest PSCs in the direction is too long. This procedure is iteratively implemented until the minimal number of connections at each PSC can be reached. By this algorithm, the PSCs at the outer sides of the crops, rivers, and grassland should be well connected. Once the network is constructed, the differential phase observations at each arc are calculated.

Fig. 1
figure 1

Delaunay triangulation (Liu et al. [25])

Full size image

Later, Liu et al. [25] proposed a freely connected network (FCN) algorithm which is shown in Fig. 2. In this network, if the distance between two PSs is less than a given threshold, they are connected as an arc:

Fig. 2
figure 2

A freely connected network (FCN) (Liu et al. [25])

Full size image
$$S\;(x_{i} ,y_{j} ,x_{i} ,y_{j} ) = \sqrt {f_{r}^{2} \cdot (x_{i} - x_{j} )^{2} + f_{a}^{2} \cdot (y_{i} - y_{j} )^{2} } \le S_{0} ,$$
(6)

where (i, j) are the pixel coordinates in an image; f r and f a are the scaling factors in range and azimuth directions, respectively, which are used to transfer the pixel distance to the geometric distance; and S 0 is a given threshold for the minimal distance. S 0 is determined by the atmospheric gradients. If the atmospheric delay has faster spatial changes, a lower threshold will be selected. FCN can reliably estimate subsidence rates and elevation errors of PSs than the algorithms based on Delaunay triangulation. However, it costs much more computation time.

Zhang et al. [26] developed an algorithm by constructing a local Delaunay triangulation network. In this algorithm, the temporarily coherent point (TCP) which remains reflectivity only for some time spans is used, and the TCPs in a regular patch are connected and some regular patches are placed over the image. This algorithm can ensure the extensive TCP connections without the phase ambiguity. In addition, the constructed network by this algorithm has the connections with small lengths so as to reduce the atmospheric artifact.

4 PSInSAR modeling and solution

DInSAR phase measurements are wrapped in the range of –π to π. Because of the ambiguous nature of the observations, one of the main limitations of PSI is the incapability of measuring ‘‘fast” deformation phenomena. As the ambiguous nature can be eliminated by the network neighborhood differencing, the phase ambiguity can be estimated based on the arc connecting two PSs, instead of two subsequent acquisitions at a single PS. In fact, if the differential deformation phase between two subsequent acquisitions exceeds the range of –π to π, the actual deformation cannot be explicitly retrieved.

After removing the non-deformation phase components, for DInSAR observations, the differential phase of π corresponds to a maximum differential deformation of λ/4 over the revisit interval. For ENVISAT ASAR, TerraSAR-X, Sentinel-1, and ALOS PALSAR, the wavelengths of which are 56, 31, 56, and 236 mm, respectively, and the revisiting time are 35, 11, 12, and 46 days, respectively, the maximum measurable differential deformation rates between two PSs are 147, 257, 426, and 468 mm/year, respectively. Note that these are theoretical values ignoring the phase noises and data processing errors. The noise level of data and the methods adopted to obtain the phase ambiguities greatly influence the actual deformation rates. In addition, the deformation estimation by PSI depends also on the spatial pattern and available PS density of the deformation phenomenon.

If the deformations are greater than the maximum phase ambiguity limit, one effective method for the estimation is SAR offset-tracking (OT) using the amplitude information, i.e., complementing the measurements by tracking very fast deformation. The OT method exploits the SAR amplitude information of at least two SAR images, covering the same area, acquired at different times. The main procedure includes pixel offset estimation, systematic offset removal, and offset field conversion (i.e., from offset in pixel to deformation in m or mm). OT can estimate 2D displacements, the across-track (range) and along-track (azimuth), of a given ground target. The processing utilizes the image matching techniques. Although OT is not affected by the ambiguous nature of the interferometric approaches, it has the disadvantage of low sensitivity to deformation and the coarse accuracy. Theoretically, the accuracy of OT method is 1/10th or 1/20th of the SAR pixel (Fialko et al. [27] and Strozzi et al. [28]). Taking TerraSAR-X as an example, its range pixel spacing and azimuth pixel spacing are around 2.0 m and 1.9 m, respectively, and then the absolute value of the OT measurements accuracy in range and azimuth direction will be in the ranges of [0.1 0.2] m and [0.095 0.19] m, respectively, which is much lower than the measurement accuracies by DInSAR and PSI.

Another key factor of PSI is the deformation model for phase modeling and parameter estimation, and a linear model is often used. If the deformation phenomenon fits well with the linear model, the PSI estimation has desirable accuracy. However, for non-linear deformation phenomenon, the utilization of the linear model may significantly reduce the accuracy of the deformation estimation. Lately, some PSI approaches have been developed by building other deformation models or hybrid models, e.g., polynomial and periodic models. However, all these approaches are under the assumption of the spatial smoothness of the deformation phenomena, which means that all current approaches are limited by the ambiguous nature of the interferometric phases.

For the deformation estimation by PSI, the thermal expansion is also a critical factor [29–31]. Further research on this issue has been extended from single PS to single object, e.g., buildings and bridges. For modeling and estimating thermal expansion, there are three typical approaches. The first one is to extract the thermal expansion from the total observed displacement [31]. However, in this approach, the thermal expansion is not explicitly considered in the modeling such that the estimated deformation is greatly affected by large distortions, especially when there are less SAR images in short periods [32]. In the second approach, the thermal expansion has been explicitly considered as a parameter in the model, e.g., Gernhardt et al. [33], Monserrat et al. [34], Fornaro et al. [35], and Zhang et al. [36]. The third approach aims to extract the thermal expansion coefficient by thermal maps [32, 34].

5 Conclusions and outlook

PSI technique has been widely applied to the measurement of displacements and is able to achieve a high accuracy. Many researchers have focused on this technique and many improvements for PSI have been achieved. In addition, some active SAR missions and the plans have been conducted by agencies to further improve the accuracy and reliability of this technique.

Currently, main tasks on PSI technique include the following aspects:

  1. (1)

    Unbiased estimation of thresholds for cohesive points.

  2. (2)

    In current research on the detection of DS points, typical approaches are the region growing and sample statistical test, e.g., Kolmogorov–Smirnov (KS) test, Anderson–Darling (AD) test, Baumgartner–Weiss–Schindler (BWS) test, and detect the homologous points around the detection center according to the amplitude or intensity. However, as DS consists of its adjacent points with similar scatter characteristics, it is necessary to conduct a further research on the detection of these adjacent points in a clustering manner.

  3. (3)

    For the network construction of PSs, the main problem is how to reduce the possibility of the ambiguity in the arcs in the network. In addition, current methods do not consider the elevation and scatter intensity in the process of the network construction.

  4. (4)

    Current methods reduce the atmosphere delay generally using external data or modeling, while the characteristics of SAR data, e.g., the distribution characteristic, are not used.

  5. (5)

    In the PSI modeling, the estimation of parameters, e.g., for the temperature and atmosphere delay, should be more precise by considering the actual influences of these factors.