1 Introduction

The collection of GPS data from the GPS module in a mobile phone provides the opportunity to analyze the travel behavior of mobile phone holders. Mobile phones are enormously popular, so it is possible to obtain aggregate or disaggregate travel patterns for a whole city or even larger area by this method. The data can be used as a substitute for traditional person trip (PT) surveys and as a data source for activity-based travel demand analysis. GPS data usually includes basic information such as longitude, latitude, and a time stamp, while additional information including speed, acceleration, and signal quality is sometimes available. The basic information can be collected from any GPS module, while the additional information is dependent on modules. Recently, contextual information collected by sensors such as accelerometers, gyroscopes, and rotation vector sensors in smart mobile phones has provided assistance to obtain the transportation mode of mobile phone holders from GPS data [1].

Using this type of data, one of the most significant pre-analysis procedures is to split each continuous trajectory into smaller segments (with a single trip as the smallest unit) whose ends are activities. Stops are taken to be obvious signs of some activity taking place or the trip starting/ending. However, a stop does not necessarily equate to activity. Some stops are followed by a certain activity while others are not. In this paper, two types of stop are defined: activity stops and non-activity stops, respectively. An activity stop is a stop followed immediately by some activity such as work, shopping, recreation, and so on; a non-activity stop is one that is not followed by a particular activity, such as waiting for a green light at an intersection or being stuck in traffic. Identifying stops and distinguishing these two kinds of stop in a trajectory are then essential procedures in the overall analysis of GPS data.

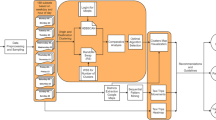
The main contribution of this paper is to advance a method to identify the locations of activity stops using only coordinates and time stamps from a continuous GPS trajectory. This method consists of an improved version of the DBSCAN algorithm (as a first step) and SVMs (as a second step). It has been tested with mobile phone GPS data, with the result that it gives generally better accuracy than other variants of DBSCAN in identifying activity stop locations.

The remainder of this paper is organized as follows: related research is reviewed in the second section. Then Sect. 3 introduces the dataset utilized in this research. The methodology applied in this paper is proposed in the subsequent section, with the constrained density-based spatial clustering of applications with noise (C-DBSCAN) algorithm and support vector machines (SVMs) interpreted in detail. This is followed by the results section. Then a comparison with two other DBSCAN variants is made. Finally, conclusions are drawn.

2 Literature review

A person’s full day can be seen as a series of alternating activities and trips. As a result, to some extent, segmenting continuous GPS data into trips is equivalent to identifying the activity stops in the GPS trajectory. In this subsection, we provide a summary of trip end and activity stop identification in the literature.

Since GPS first came into use as a way to obtain trip features at the beginning of the 21st century, a lot of investigations have paid great attention to trip segmentation or stop location identification. These efforts can be divided into two groups depending on whether the GPS data are continuous or not. Non-continuous GPS data were typically obtained for travel behavior analysis with the first generation of GPS applications, when the GPS devices were installed in vehicles and turned on/off simultaneously with the engine. At that time, “trip segmentation” usually entailed dividing the whole GPS dataset into individual trip-unit segments. On the contrary, continuous GPS data are gathered with the second generation of GPS applications that are portable, extending the collection and analysis of trace data from of the road vehicle mode only to other modes like rail, cycling, and walking. Accordingly, the corresponding research generally mentions “stop location identification.” In this subsection, existing research related to “trip segmentation” and “stop location identification” is summarized in relation to non-continuous GPS data and continuous GSP data, respectively.

2.1 Trip segmentation

Non-continuous GPS data records are obtained when the GPS equipment turns off automatically with the engine or when, as a data collection rule, a portable GPS device is turned off by the subject (the user) at the end of a trip. Gong et al. [2] summarized the GPS data features usually used for trip segmentation in existing research. The time elapsed between two consecutive records is the decisive feature used for trip segmentation, with the premise that the vehicle or subject stops in a certain location. Elapsed time thresholds adopted by researchers include 120 s [3–9], 180 s [10], 300 s [11], and even 600 s [12]. A stop is defined as a speed of 0 m/s [4–11] or less than 0.01 m/s [3] or as a longitude/latitude difference between consecutive records of less than 0.00005° [4–6].

2.2 Stop location identification

Continuous GPS data have been collected since the GPS devices became portable and particularly since smart mobile phones began to feature GPS modules. In this case, the data record the trajectories of a subject during all movement or stops. As a result, trajectories consist of a series of GPS tracking points of definite location and time, perhaps with the addition of speed, acceleration and so on. In methods used to date, these trajectory features have been used directly or indirectly to identify stops and finally to identify activity locations or significant locations for the subject. Some researchers [13–20] have attempted to identify stops for activity in a single step, while others [21–25] have used a two-step procedure: identifying all stops in the first step and refining the identification to isolate activity stops in the second step.

Methods used for identification of stop locations can be generally categorized into the following five groups: centroid-based methods, speed-based methods, duration-based methods, density-based methods, and hybrid methods. A brief review of these is given below.

2.2.1 Centroid-based method

A centroid-based method, specifically, a variant of the k-means clustering algorithm has been applied [15] to obtain the locations that are significant for the subject. The points are divided into k clusters by iteratively calculating the mean of points (or centroid of points) as the new temporary center point within a given radius of the current temporal center point until the center point converges. However, the number of stops, k, has to be known beforehand. It is nearly impossible to know how many stops there are in a trajectory.

2.2.2 Speed-based methods

Agamennoni et al. [13] defined a scoring function involving speeds to reflect the significance of a vehicle’s current location. The scoring function defined the significance of the current location by comparing current speed with two thresholds of speed in a mining environment. Mizuno et al. [22] used speed and change rate of average speed as input features for SVMs to obtain moving and stopping points. Nevertheless, speed-based methods need to know speed, which is not always available to all GPS devices or modules. Besides, some limitations arise in situations such as the subject moving in parking lot or stuck in traffic or in bad weather conditions.

2.2.3 Duration-based methods

Duration-based methods are the most popular method of identifying stop location. Palma et al. [23] and Tran et al. [18] applied a modified DBSCAN algorithm based on a minimum stop duration instead of a minimum number of points in a neighborhood when defining core points. The difference in the two papers is that distance along the trajectory was used for distance calculations by [23], whereas the straight-line distance between two points was used for distance calculations by [18]. Alvares et al. [14] and Xie et al. [19] identified stops by judging stop duration and whether the GPS point intersect with the geometry of a spatial location. The difference is that Ref. [14] used a given threshold stop duration to map the trajectory to possible activities, whereas Ref. [19] utilized a matching table containing minimum and maximum elapsed times for each possible type of activity. One problem of duration-based methods is how to decide on the optimal duration threshold because the result is very sensitive to the setting of this threshold.

2.2.4 Density-based methods

Kami et al. [16] proposed a fast algorithm for probabilistically extracting significant locations from raw GPS data based on data point density. This algorithm eases the difficulty in parameter setting and works well even if there are a variety of noise levels in input data. Zimmermann et al. [25] utilized an interactive density-based clustering algorithm, in which the density was defined on the basis of both the spatial and the temporal properties of a trajectory. Zhou et al. [20] used a simplified mechanism of expanding clusters in DBSCAN. According to the simplified mechanism, any two clusters with shared points can be joined together as one cluster. Density-based methods require data to be collected at more frequent intervals. Moreover, since density-based methods use the concept of spatial point clustering, adjustments are needed when applied to GPS trajectory situations, which are different from those with spatial points with no direction of movement and time stamps.

2.2.5 Hybrid methods

Hybrid methods use two of the variables such as speed, duration, density, etc., together. Andrienko et al. [21] extracted stops with a user-specified minimum duration and a diagonal spacing that is less than a user-specified distance threshold. Leclerc et al. [17] also used duration but with an additional distance criteria for judging whether points are in a stop location or not. Yan et al. [24] used a speed threshold and minimal stop duration to distinguish trajectories into stop episodes and move episodes. The speed threshold is dependent on the moving object and the location of the moving object. Hybrid methods might improve accuracy to some extent, but it is hard to completely avoid the demerits of the other methods mentioned above.

Overall, the centroid-based method is not a good option for identifying stop locations unless the number of clusters (i.e., stops) is known. Due to the limitations of speed-based methods, they can best be utilized as assisting variables to distinguish stops. Duration is a vital variable for identifying stops from trajectories; however, duration thresholds need to be selected very carefully because of their sensitivity. Density-based methods use the spatial reflection of the relationship between activity and point density, and require data with more frequent intervals. Furthermore, density-based methods need to consider trajectory characteristics.

Each of these methods, however, was advanced to suit particular data features. Considering the particular of features of the dataset in this paper, we propose a two-step method which uses a density-based clustering method to identify all types of stops in the first step and then use a supervised machine learning method to distinguish the locations of activity stops and non-activity stops in the second step.

3 Data

The GPS data utilized in the research were collected from 30 volunteers in the Nagoya area of Japan over a period of 5 weeks in 2008. Each volunteer was assigned a mobile phone with GPS module able to record and send GPS information to the server every 10 s. The GPS information sent back includes longitude, latitude, time stamp, signal quality, etc. Sometimes the GPS module returns GPS information with intervals longer than 10 s, such as in the case of communication delay because of tunnels, subways, etc. The signal quality feature of the GPS data is used to identify this kind of signal loss, and points with low signal quality are excluded from the dataset for analysis. Overall, 97.4 % of the GPS communication intervals in the data set are less than 20 s. This interval is adequate for the application of density-based methods to distinguish stop points.

Speed and acceleration are not available in this dataset. On the other hand, volunteers were required to annotate the information by inputting the start, end, mode, and purpose of each trip through an application installed on the smart phones. Additionally, socio-demographic information about each volunteer was collected through a questionnaire, including home and workplace addresses, occupation, yearly income, possession of a driving license, daily primary transportation mode, and so on.

Figure 1 illustrates the basic aggregated statistical analysis of this dataset. Almost all volunteers are in the age group 20–65, the working age in Japan, and almost all have a full time or part time job. This means these volunteers are active trip makers. Automobile, walking, and rail are the main modes of transport; business, returning home, and going to work are the main trip purposes in this dataset.

Fig. 1
figure 1

Aggregated statistical analysis of dataset. Note: One trip may be made by more than one mode so the total number of modes is greater than the total number of purposes

Full size image

The full GPS trip dataset was divided almost equally by time sequence for each subject into two parts: a training dataset for estimating parameters in the C-DBSCAN algorithm and training models in SVMs; and a prediction dataset for validating the C-DBSCAN algorithm and testing the learned SVMs.

4 Methodology

The two-step methodology described above consists of using an improved DBSCAN algorithm in the first step and SVMs in the second step.

4.1 C-DBSCAN algorithm

In this section, key definitions in the original DBSCAN algorithm are introduced first. Then the improved DBSCAN algorithm, named C-DBSCAN, is interpreted.

4.1.1 Original DBSCAN algorithm

We use the same notation as presented by Ester et al. [26]. We apply the key definitions of DBSCAN in the context of GPS tracing points in order to separate the stop points and the moving points from the GPS trajectories.

Definition 1

(Eps-neighborhood of a point) The Eps-neighborhood of a point p, denoted by N Eps(p) , is defined by N Eps(p)  = {q∈D| dist(p,q) ≤ Eps}. Here, N Eps(p) is a set of points in which each point q belongs to database D and has a distance shorter than Eps to point p, and Eps is a given distance threshold.

Definition 2

(Directly density-reachable) A point p is directly density-reachable from a point q w.r.t. Eps, MinPts if.

  1. (1)

    p∈N Eps(q) and

  2. (2)

    |N Eps(q) | ≥ MinPts,

where MinPts is the minimum number of points in the Eps-neighborhood of point q.

Definition 3

(Density-reachable) A point p is density-reachable from a point q w.r.t. Eps and MinPts if there is a chain of points p 1 ,…, p n (where p 1  = q, and p n  = p) such that p i+1 is directly density-reachable from p i .

Definition 4

(Density-connected) A point p is density-connected to a point q w.r.t. Eps and MinPts if there is a point o such that both p and q are density-reachable from o w.r.t. Eps and MinPts.

Definition 5

(Cluster) Let D be a database of points. A cluster C w.r.t. Eps and MinPts is a non-empty subset of D satisfying the following conditions:

  1. (1)

    ∀p, q: if p ∈ C and q is density-reachable from p w.r.t. Eps and MinPts, then q∈ C. (Maximality).

  2. (2)

    ∀p, q ∈ C: p is density-connected to q w.r.t. Eps and MinPts. (Connectivity).

Definition 6

(Noise) Let C 1 ,…, C k be the clusters of database D w.r.t. parameters Eps i and MinPts i , i = 1,…, k. Then we define the noise as the set of points in database D not belonging to any cluster C i , i.e., noise \(= \left\{ {p \in D|\forall i: \, p \notin C_{i} } \right\}.\)

4.1.2 Improvements for application to the context of GPS trajectories

When DBSCAN is applied in the situation of GPS track points, points in a cluster are the equivalent of stop points, which gather together with a higher density; on the other hand, points in the noise are the equivalent of moving points along road or rail network links with a lower density.

The DBSCAN algorithm was developed to solve the spatial point classification problem without consideration of their temporal sequence. Consequently, in a detoured trajectory, one distinguished stop cluster may contain other moving points or points in subsequent clusters sharing the same location. Moreover, due to the definitions and concepts of the original DBSCAN algorithm, points representing movement along a straight road at low speed when the GPS signal transmission frequency is high may be grouped into a single cluster under certain given parameter values. As a result, applying the original DBSCAN algorithm to GPS trajectories may lead to errors. Here, we advance the C-DBSCAN algorithm in which two constraints are added in order to avoid these two potential errors.

The first constraint is all points in a cluster should be temporally sequential. This means the sequential order should increase one by one and no “sudden increase” is allowed in the cluster. If such a “sudden increase” is found, the cluster will be divided into two potential clusters at the point of sudden increase and each one will be tested to see if it satisfies the condition of minimum number of points in one cluster. If not, the points in the potential cluster will be labeled as moving points. Otherwise the points in the potential cluster will be tested by the second constraint.

The second constraint is that the percentage (PCT) of abnormal points in a cluster should not exceed a given threshold named PCT AP . To be specific,

$$PCT \le PCT_{AP}$$
(1)

where \(PCT = \frac{{\left| {AP} \right|}}{\left| C \right|},\;\left| {AP} \right|\) is the number of abnormal points in the cluster and |C| is the total number of points in the same cluster.

Before giving a definition of an abnormal point, the direction and direction change of a point in a cluster need to be explained, as follows. The direction of a point is defined in an imaginary situation in Cartesian coordinates where the point is the origin and the direction is defined as the angle between the negative direction of the vertical axis and the line between the point and the previous point, like α 1 for point P 1 and α2 for point P 2 in Fig. 2. Suppose three points in the cluster are marked sequentially as P 0 , P 1 , and P 2 . The direction change from point to point P 1 is defined as the angle from ray \(\overline{{P_{0} P_{1} }}\) to ray \(\overline{{P_{1} P_{2} }},\) shown as Δα in Fig. 2. Δα is the angular change between α 1 and α 2 , i.e., Δα = α 2 –α 1 . Since we use the cosine value of Δα, it does not matter whether Δα is negative or positive.

Fig. 2
figure 2

Direction of a point and direction change of two points for a second point in different quadrants

Full size image

If a cluster represents a stop location, the points are scattered around the location, and the points should have an even distribution of direction changes. This means that the cosine of direction change (or the direction change coefficient, (DCC)) should nearly always differ from 1. Points with a DCC value close to 1 probably represent movement of the subject along a straight link in the network. In a cluster, the points should have an even distribution of DCC. So abnormal points are those points without an even distribution of DCC, to be specific, a DCC close to 1. Here we use DCC AP denote the approximation to 1.

$$\begin{array}{*{20}c} {Abnormal} & {Po\text{int} = } \\ \end{array} \{ DCC \ge DCC_{AP} |Po\text{int} \in Cluster\} .$$
(2)

4.1.3 C-DBSCAN algorithm

The improved DBSCAN algorithm used in this research, C-DBSCAN, is shown in Fig. 3. First, the DBSCAN algorithm is applied to obtain the cluster points (stop points) and noise points (moving points) in line 2. Then each cluster is tested against constraint 1. Here a new cluster may be split from the older one or the old cluster may be labeled as noise if it does not follow the cluster rule. Finally a cluster satisfying constraint 1 will be tested against constraint 2. Clusters that satisfy both constraints 1 and 2 are marked as stop points; other points are marked as moving points.

Fig. 3
figure 3

C-DBSCAN algorithm

Full size image

4.1.4 Parameter estimation

In the C-DBSCAN algorithm, there are four parameters needing to be estimated. These are Eps, MinPts, DCC AP , and PCT AP . The cumulative frequency method (at least 90 %) is used to estimate these four parameters using the samples in the training dataset. The estimation results of these four parameters are shown in Fig. 4.

Fig. 4
figure 4

Estimation results

Full size image

Figure 4a demonstrates that if MinPts equals four points in the neighborhood, there is 95 % probability a stop point is identified and included in a cluster. Figure 4b shows that with the premise that MinPts equals four points, if an Eps value of less than 25 meters for a cluster candidate means there is a 90 % probability that a stop point is included in a cluster. Figure 4c indicates that there is 90 % probability that a point with DCC value more than 0.8 is a moving point. Figure 4d shows that with the premise that DCC AP is equal to 0.8, a PCT AP value of less than 60 % for a cluster candidate means there is a 93 % probability that the cluster candidate is a stop. Consequently, we obtain the estimated parameters as follows: Eps = 25 m, MinPts = 4, DCC AP  = 0.8, and PCT AP  = 60 %.

Note that demographic information and available modes of transport may influence the thresholds of parameters needing to be estimated. However, in this research, the datasets used for training and testing are obtained from the same group of volunteers using several modes of transport, so we do not verify this influence in detail.

4.2 Support vector machines

SVMs is a supervised machine learning method which can be used for classification or regression analysis. It was developed by Vladimir N. Vapnik, and the current standard incarnation (soft margin) was proposed by Cortes and Vapnik in 1993 and published in 1995 [27].

For application to classification, SVMs divide a training dataset with a hyperplane that maximizes the margin between two classes in the first step. In the second step, the learning from this training dataset is applied to the prediction dataset and the classification is implemented. The hyperplane can be linear or non-linear depending on whether the input data are linear or non-linear. In the non-linear case, SVMs use a kernel function to map the points in the dataset linearly separable in the higher dimensions using a non-linear mapping function \(\phi\) The separating hyperplane in the higher dimensions can be represented by the following formula:

$${\varvec{\omega}}^{\text{T}} \phi ({\varvec{x}}_{{{i}}} ) + b = 0,$$
(3)

where ω is the weight vector normal to the hyperplane, \({\varvec{x}}_{{{i}}} \in R^{{^{{_{n} }} }},\) i = 1,…, l are the n-dimensional vectors used for training or that are to be divided into two classes, and b is the intercept associated with decision boundaries.

Since the instance counts of different labels are not balanced in this dataset, assignment of the same cost value to the two classes would cause skewing of the separating hyperplane towards the minority class as a result of this imbalance. In order to avoid suboptimal SVMs models arising because of the imbalance, two different misclassification costs, C + and C −, are assigned in the SVMs models [28] as the following formulas:

$$\begin{array}{*{20}c} {\mathop {\hbox{min} }\limits_{\omega ,b,\varepsilon } } & \frac{1}{2} \\ \end{array} {\varvec{\omega}}^{{\text{T}}} {\varvec{\omega}} + C^{ + } \sum\limits_{{i|y_{i} = + 1}}^{l} {\xi_{i} } + C^{ - } \sum\limits_{{i|y_{i} = - 1}}^{l} {\xi_{i} } ,$$
(4)
$$\begin{array}{*{20}c} {s.t.} & {y_{i} ({\varvec{\omega}}^{{\text{T}}} \phi ({\varvec{x}}_{{{i}}} ) + b) \ge 1 - \xi } \\ \end{array}_{i} ,$$
(5)
$$\xi_{i} \ge 0,i = 1, \ldots ,l ,$$
(6)

where C + and C − are the misclassification cost (or penalty) for the positive class examples and negative class examples, respectively, \({\varvec{y}} \in R^{l}\) is an indicator vector such that \(y_{i} \in \{ 1, - 1\},\) and \(\xi_{i}\) is the slack variable.

The dual problem of the situation represented by Eqs. (4)–(6) is as follows:

$$\begin{array}{*{20}c} {\mathop {\hbox{min} }\limits_{\omega ,b,\varepsilon } } & \frac{1}{2} \\ \end{array} {\varvec{\alpha}}^{{\text{T}}} {\varvec{Q}}{\varvec{\alpha}} - {\varvec{e}}^{{\text{T}}} {\varvec{\alpha}}.$$
(7)
$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {s.t.} & {0 \le \alpha_{i} \le C^{ + } , \quad if} \\ \end{array} } & {y_{i} = 1;} \\ \end{array}$$
(8)
$$\begin{array}{*{20}c} {0 \le \alpha_{i} \le C^{ - } , \quad if} & {y_{i} = - 1;} \\ \end{array}$$
(9)
$${\varvec{y}}^{{\text{T}}} {\varvec{\alpha}} = 0 ,$$
(10)

where e = [1,….,1]T is the vector of ones, \({\varvec{Q}}\) is an l by l positive semi-definite matrix, \(Q_{ij} \equiv y_{i} y_{j} K({\varvec{x}}_{{{i}}} {\varvec{,x}}_{{{j}}} ),\) and \(K\left( {{\varvec{x}}_{{{i}}} {\varvec{,x}}_{{{j}}} } \right) \equiv \phi \left( {{\varvec{x}}_{{{i}}} } \right)^{\text{T}} \phi \left( {{\varvec{x}}_{{{j}}} } \right)\) is the kernel function.

After problems (7)–(10) are solved, using the primal–dual relationship, the optimal model can be represented as follows:

$${\varvec{\omega}} = \sum\limits_{i = 1}^{l} {y_{i} \alpha_{i} \phi ({\varvec{x}}_{{{i}}} )} ,$$
(11)

and the decision function is expressed as.

$$\text{sgn} \left( {{\varvec{\omega}}^{{\text{T}}} \phi ({\varvec{x}}) + b} \right) = \text{sgn}\left( {\sum\limits_{i = 1}^{l} {y_{i} \alpha_{i} K({\varvec{x}}_{{{i}}} {\varvec{,x}}) + b} } \right).$$
(12)

For the kernel function, \(K({\varvec{x}}_{{{i}}} {\varvec{,x}}_{{{j}}} ),\) a Gaussian kernel is believed to be the most suitable function given our data size and attribute size [29]. The Gaussian kernel function is shown as follows.

$$K({\varvec{x}}_{{{i}}} {\varvec{,x}}_{{{j}}} ) = e^{{ - ||{\varvec{x}}_{{{i}}} - {\varvec{x}}_{{{j}}} ||^{2} /2\sigma^{2} }} ,$$
(13)

where \(\sigma\) is the Gaussian parameter and ||x i -x j || is the Euclidean distance between vectors x i and x j .

To implement this SVMs model, the software LibSVM [28] is utilized. LibSVM applies the SVMs to the training dataset and stores the values of \(y_{i} \alpha_{i} \forall i,b,\) label names, support vectors and other information such as kernel parameters in the trained model file for implementing forecasts on the prediction dataset.

4.2.1 Attribute selection

This section describes the features in GPS trajectories that are selected for implementing SVMs in order to distinguish activity stops and non-activity stops. Stop duration is the first attribute that comes to mind, because no matter what kind of activity takes place, a certain period of time is the basic requirement. The distribution of stop duration for the two kinds of stops in the training data trajectories is illustrated in Fig. 5.

Fig. 5
figure 5

Distribution of stop duration for two kinds of stops

Full size image

This shows that stop duration is an important stop-distinguishing feature of the trajectories. First, a sharp increase in accumulative frequency of activity stop after 300 s, which means almost 80 % of activity stops have a duration more than 300 s, demonstrates that much more activity stops have a much longer duration than non-activity stops. Second, it is found that a threshold can be used to distinguish these two kinds of stops. If 105 s is taken to be the threshold, almost 92.5 % of stops are accurately distinguished. However, this leaves 7.5 % of stops with an erroneous classification. Specifically, almost 7.5 % of activity stops have a stop duration from 30 to 105 s while 7.5 % of non-activity stops have a stop duration from 105 to 170 s. The reasons for these short activity stops may be that subjects incorrectly turn off the GPS function immediately upon arriving home or at the workplace, or particularly efficient deliveries to customers. Non-activity stops with a longer duration may be caused by long waits at major intersections with longer signal cycles. This overlap in stop duration means that other features extracted from the trajectories are also needed as attribute inputs for the SVMs.

Non-activity stops with a longer duration may be caused by long waits at major intersections. It shows in Fig. 5 that longer duration of non-activity stop is more than 105 s and the percentage of more than 180 s is almost zero. It means that non-activity stop in our dataset does not include situation of traffic congestion which usually lasts for a long time. For non-activity stop such as waiting at major intersections, unlike activity stops, it does not involve any local walking, as would be the case with an activity stop at home, a workplace or at a convenience store, post office, and so on. As a result, GPS points collected during non-activity stops are scattered over a very limited area. This area can be measured by taking the average (mean) distance of each of the scattered GPS points to their common centroid. Figure 6 shows the average distance to the centroid for each stop; almost all non-activity stops have an average distance from the centroid of less than 30 meters.

Fig. 6
figure 6

Mean distance from GPS points to the common centroid by stop duration

Full size image

Considering the immediate turning off of GPS functions by some subjects, these short-duration activity stops may be identified by the distance between stop location and the home or workplace. In this research, the shorter of these two distances is used for each stop. This distance is plotted against stop duration in Fig. 7. This demonstrates that activity stops are concentrated within 10 km, whereas non-activity stops are at a greater distance.

Fig. 7
figure 7

Shorter of distances from current location to home and to work place

Full size image

Figure 8 plots stop duration, mean distance of GPS points to the cluster centroid, and the shorter of the distances from the current location to home and to the workplace by activity stop and non-activity stop in three-dimensional space. It can be concluded from this that most stops can be distinguished by the use of the three features. Consequently, these three features are selected and utilized as input features in the SVMs.

Fig. 8
figure 8

Three attributes shown together in three dimensions

Full size image

5 Results

After processing the data for scale, optimal values of the parameters cost, C, and gamma, γ, are calculated by the grid module in LibSVM for different settings of C + and C −. A “grid-search” using cross-validation is implemented. Various pairs of (C, γ) in increasing order are tested exponentially, a method found to be suitably practical to identify good values of parameters by Hsu et al. [29]. The test values of parameters C and γ were as follows: C = 2−30, 2−29,…, 230; γ = 2−30, 2−29,…, 230. These pairs of (C, γ) were tested in five situations: with C +=C, 2C, 3C, 4C, 5C, and C −=C. And a five-fold cross-validation was implemented to avoid the overfitting problem. The results for the tested situations are shown in Table 1. The cross-validation accuracy reaches a peak of 95.65 % when C = 221, γ = 2−3, C +=2C and C −=C.

Table 1 SVM results for different (C, γ) pairs for five situations of C + and C −
Full size table

The learning by the SVMs in situation II is then used to test the dataset, achieving an accuracy of 94.12 %.

This still leaves about 4 %–6 % of stops falsely distinguished as activity stops or non-activity stops. These are the stops with very similar vector values. In future work, these results might be improved by increasing the number of vector dimensions, such as by including the frequency of stops at the same destination, distances to locations on the important address list, GIS information, and so on.

6 Comparison with other methods

6.1 Other methods for comparison

Since the two-step method proposed in this paper is an extension of the DBSCAN algorithm, in this subsection, two variants of the DBSCAN method (one in the duration-based category and the other in the density-based category, respectively) are tested using our dataset in order to compare accuracy. Here we list the primary characteristics of these algorithms. Details can be found in the corresponding papers.

The density-based method is called the DJ-cluster algorithm [20], a simplified version of the DBSCAN algorithm. It uses the same concept of a core point as DBSCAN. However, concerning expansion of the cluster, density-reachability, and density-connectivity are replaced by the concept of density-joinability. To be specific, instead of using core points to expand a cluster, any shared point is used to combine clusters.

The duration-based method is called the TrajDBSCAN algorithm [18]. In contrast with the original DBSCAN algorithm, the key feature of TrajDBSCAN is that it defines a temporal linear neighborhood with a core point determined based on a minimum stop time (not a minimum number of points).

6.2 Accuracy of calculation and results

The aim here is to show differences in accuracy when applying these methods to the identification of activity stop locations in continuous GPS trajectories. We selected the four indexes listed below with which to comprehensively describe accuracy. These indexes were calculated for each stop location, and Table 2 shows the average value of these indexes among all activity stops. Parameter values used in the comparison are the recommended ones or as calculated following the methods in the corresponding papers.

  1. (1)

    Ratio of number of locations identified by method over ground truth. This index is used to evaluate the redundancy of activity stop location candidates. When equal to one, all identified activity stop location candidates are actual activity stop locations. If greater than 1, then activity stop locations have been erroneously determined as candidates by the method. If less than 1, the method has failed to identify some actual activity stop locations.

  2. (2)

    Average distance between center of identified location and ground truth. This index is used to evaluate the geographical accuracy of activity stop location candidates. A shorter distance between the center of an identified location and the ground truth location means higher accuracy has been achieved. Here the center of an activity stop location is calculated as the centroid of the stop points indicating the stop location.

  3. (3)

    Percentage of points in the ground truth correctly identified. This index is used to indicate identification accuracy at the level of GPS points. It shows the percentage of points in the ground truth that are identified by each method. The higher the value of this index, the more actual stop points are correctly identified by the method.

  4. (4)

    Percentage of stop points identified by the method in ground truth. This index is used to show redundancy at the level of GPS points. It shows the percentage of points identified by each method that really exist in the ground truth. The higher the value of this index, the lower the percentage of useless GPS points in the identified stop locations by the method.

The comparative results shown in Table 2 clearly show that the two-step method proposed in this paper gives generally better performance than the other two DBSCAN variants in identifying activity stop locations in the continuous GPS trajectories.

Table 2 Four indexes used to compare the proposed method with other DBSCAN variants
Full size table

7 Summary and conclusions

In this research, a two-step methodology is proposed for identifying activity stops in continuous trajectories utilizing a variation of the DBSCAN algorithm and the SVMs method. In order to adjust DBSCAN to the context of GPS trajectories, two constraints are applied as improvements: a time sequence constraint and a direction change constraint. Three major features are extracted for utilization in the SVMs method: stop duration, mean distance to the centroid of a cluster of points at the stop location, and the shorter of the distances from the current location to home and to the workplace.

Application of this proposed methodology to GPS data collected using mobile phones in the Nagoya area of Japan in 2008 demonstrates that the improved DBSCAN algorithm (C-DBSCAN) achieves an accuracy of 90 % in identifying stop locations and the SVMs method is almost 96 % accurate in distinguishing activity stops from non-activity stops. Therefore, this two-step method may be suitable for identifying activity stops in continuous GPS trajectories with a higher frequency of data points, especially those that lack a speed component for any reason. In comparison with other similar methods, this two-step procedure demonstrates better performance overall.

With the latest GPS-capable devices, the corresponding data collection interval can be as short as one second, and the information collected also covers speed and acceleration. However, the method advanced in this paper can certainly be applied to GPS data with more features than were used in this work. On the other hand, this method also offers the possibility of reducing the number of features required when collecting GPS data, thereby reducing memory requirements.

Since the dataset used in this study has the feature demonstrating the GPS signal quality which was used to exclude the trajectory point with low signal quality caused by the underground or tunnel condition. One future research trend can be trying to include this part of data with the help of supplement data collected by other types of sensors on the mobile phone. We used three features as independent variables in SVMs and there still be improving space. So another direction of future research could be focusing on trying to increase the dimensionality of the vectors utilized in the SVMs for higher accuracy. Our dataset does not include traffic congestion. So for the situations like this, it may be similar to an activity stop and current methods and attributes used in SVMs may not handle it well. But it may also be worthy to try by adding dimensionality of the vectors in the SVMs in the future research.