1 Introduction

The train traffic-induced loads transferred from the rail to the track substructure cause vertical and horizontal deformations (Ahlbeck et al. 1975). These deformations contribute to issues such as track settlement, lateral instability, and track geometry changes. Track settlement increases with the number of train passages (Punetha et al. 2021). The lateral load affects the lateral stability of a railway track and primarily influences significant changes in track geometry (Zakeri et al. 2021). There are two forms of track stability to consider: vertical stability, which pertains to the resistance of vertical forces caused by the train, and lateral stability, which pertains to the resistance of lateral forces caused by the train. The lateral stability then comprises (i) lateral stability in transverse direction, which pertains to the resistance of forces perpendicular to the direction of train passage; and (ii) lateral stability in longitudinal direction, which pertains to the resistance of forces in the direction of train passage. Lateral stability in a track is influenced by different conditions, such as the track orientation, track environment, and train speed. Moreover, lateral track instability becomes a major issue for high-speed trains and trains with heavy axle loads (Esmaeili et al. 2016). This underscores the necessity for developing a simplistic, reliable, and accurate method capable of predicting railway track behaviour, particularly in the lateral direction. Prior research has predominantly addressed track settlement by focusing on vertical loads mainly while ignoring the effect of horizontal loads acting along the transverse and longitudinal directions of the train corridor. These horizontal loads are responsible for inducing lateral instability and geometry changes in railway tracks (Ahlbeck et al. 1975; Choudhury et al. 2008; Zhai et al. 2004; Chen and Zhou 2020). A comprehensive investigation of the influence of lateral loads on the track response is essential to prevent issues such as geometry changes, derailment, track buckling, and lateral instability (Esmaeili et al. 2017).

Several approaches, such as experimental, numerical, and analytical, evaluate the effect of train loads on railway tracks (Punetha et al. 2021). While field or laboratory studies offer valuable insights into track substructure behaviour under train-induced loads, they are often time-consuming and expensive. In contrast, the numerical analyses provides more convenient means of understanding the behaviour of track substructure layers. Past numerical analyses have adopted two-dimensional (Kuo and Huang 2009; Yang et al. 2009; Meena et al. 2020; Sakhare et al. 2023), two and half-dimensional (Alves et al. 2010) and three-dimensional (Banimahd et al. 2013; Sayeed and Shahin 2016; Connolly et al. 2013; Gokuldas et al. 2020; Farooq et al. 2021; Farooq and Nimbalkar 2024) models of ballasted track structures. However, these simulations require substantial computational resources. In contrast to numerical investigations, the analytical approach offers a faster, more economical, and efficient alternative (Knothe and Grassie 1993; Esveld 2001; Connolly et al. 2015). Various analytical models have been developed to predict the response of a track substructure (Punetha et al. 2021, 2020; Choudhury et al. 2008; Knothe and Grassie 1993; Esveld 2001; Zhai and Sun 1994). Ahlbeck et al. (1975) proposed using the beam-on-elastic-foundation (BoEF) approach to predict track layer response, simulating track models with springs and dampers. Their focus primarily lay on vertical response, with lateral response neglected due to its complexity.

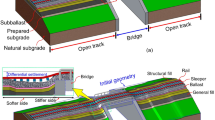
Several researchers have developed analytical models to understand the track substructure behaviour under train-induced loading. These models are primarily based on the beam on elastic foundation (BoEF) approach (Knothe and Grassie 1993) and extend to three-dimensional vehicle-track coupled models (Punetha et al. 2020; Zhai et al. 2009). Typically, these models feature substructure layers represented by springs and/or dashpots (Metrikine and Popp 1999; Takemiya and Bian 2005). Additionally, alternative analytical approaches include lumped mass models, wherein substructure layers are treated as discrete masses connected by rheological elements, such as springs and dashpots (Esmaeili et al. 2016; Choudhury et al. 2008). Punetha et al. (2020) and Punetha et al. (2021) have developed viscoelastic and viscoelastoplastic models based on a rheological framework to predict both vertical recoverable and irrecoverable displacements of the track substructure. Despite the analytical studies evaluating track response primarily in the vertical direction, the comprehensive response of railway tracks should encompass both vertical and lateral deformations (see Fig. 1). Previous analytical studies have largely overlooked lateral track deformations, focusing predominantly on vertical deformations. One straightforward method to calculate lateral track deformations involves utilising Poisson’s ratio. In the subsequent sections of this paper, a comparison of lateral displacements and accelerations obtained using the proposed analytical model, Poisson’s ratio, and previous experimental studies is presented. It is observed that the model predictions employing the current track model align with experimental data, while lateral displacements and accelerations calculated using Poisson’s ratio fail to match the experimental results. This underscores the significance of the proposed analytical model, which adeptly captures track lateral response.

Fig. 1
figure 1

Forces acting on a railway track and the associated deformations

Full size image

This paper introduces a novel methodology for predicting the lateral response of the track substructure layers under train-induced loading. The dynamic nature of lateral forces at the wheel-rail interface can result in gradual lateral deformations over time (Zhai and Sun 1994). In this study, the track lateral response is evaluated using a viscoelastic rheological track model. This model comprises Hooke’s and Newtonian elements arranged sequentially to represent the stiffness (k) and damping (c) characteristics of each track substructure layer. These Hooke’s and Newtonian elements are represented by linear elastic springs and linear viscous dashpots, shown in Fig. 2. To validate the accuracy of the methodology, comparisons are made against published field, laboratory, and analytical investigation data. Following validation, a parametric study is conducted to explore the impact of various train and track parameters on track response. This study aims to offer a straightforward, reliable, and precise methodology for evaluating lateral track deformations induced by train loads.

Fig. 2
figure 2

Viscoelastic model

Full size image

2 Methodology for Prediction of Track Response

Train loads transmitted from rail to track substructure can lead to various issues such as settlement, lateral instability, and changes in track geometry. While the vertical wheel load is responsible mainly for track settlement along with track geometry changes, lateral instability and some track geometry changes also occur due to the lateral/horizontal force component, which has not been given much attention in previous research studies. This lateral instability is affected by the nonuniform and significant lateral displacements, which in turn influence the track geometry. Lateral instability is also a major concern when dealing with heavy axle and/or high-speed trains. Therefore, an investigation of the influence of lateral loads is important to prevent such issues. The proposed method offers straightforward and efficient means for predicting the response of the track substructure. It incorporates a viscoelastic model that specifically evaluates lateral elastic deformation.

In the proposed approach, a viscoelastic rheological model of a ballasted railway track is used, in which the three substructure layers (ballast, capping and subgrade) are represented as lumped masses connected using springs and dashpots. Initially, the load transferred from the sleeper to the substructure layers, through the sleeper-ballast interface (as well as the interface between track superstructure and substructure), is computed, considering both vertical and horizontal components of the load. Subsequently, both the vertical and lateral transient response of the track substructure layers is predicted. A significant innovation of this model is its capability to forecast track lateral deformations, which have often been disregarded in previous studies.

2.1 Prediction of Track Response

The prediction of track response includes a process to assess the overall viscoelastic behaviour of the substructure layers under repeated traffic loads, illustrated in Fig. 3. The analysis requires input data, including train properties and track properties, such as sleeper spacing, density, Young’s modulus, Poisson’s ratio, shear stiffness, shear damping, and thickness of the substructure layers. Once these input parameters are obtained, the effective region of the substructure layers beneath each sleeper is identified, and the vibrating mass, damping coefficient, and stiffness of the track layers are computed. Consequently, the rail seat load-time history is determined at each sleeper location. The stress distribution in the track layers is then estimated for each time instant utilising the method outlined in Sect. 2.2.1. Finally, the total track response is determined for each time instant by solving the dynamic equilibrium equation (denoted in Eqs. 7 and 8). The track response is evaluated at individual sleeper locations, while the deformation profile of the track between sleeper locations can be determined using interpolation techniques.

Fig. 3
figure 3

Flowchart to predict the track response

Full size image

2.2 Load Determination

In a ballasted railway track, the wheel load acting on the superstructure comprises vertical and horizontal components (Knothe and Grassie 1993). These loads act on the rails and get transferred to the sleepers via the rail seats. Theoretically, the load transferred to each rail seat (also known as the rail seat load) depends on the sleeper spacing (s), track modulus (u) and track deflection (δ) (Doyle 1980). The track deflection can be calculated using the following equation (Esveld 2001):

$$\delta \left(x\right)=\frac{{Q}_{\text{w}}}{2uL}{e}^{{~}^{-x}\!\left/ \!{~}_{L}\right.}\left(\text{sin}\frac{x}{L}+\text{cos}\frac{x}{L}\right)$$
(1)

where \(\delta \left(x\right)\) is the track deflection (m) along the length x (m) of the track; \({Q}_{\text{w}}\) is the wheel load (N) equal to 0.5 times the axle load (\({Q}_{\text{a}}\)); L is the characteristic length (m) equal to \({(4EI/u)}^{1/4}\) with E and I as Young’s modulus (N/m2) and moment of inertia (m4) of the rail, respectively. The track deflection computed using Eq. 1 typically spreads over five to nine sleepers from the point of application of the wheel load and is negligible beyond that (Doyle 1980). The track modulus in Eq. 1 is determined using the following equation:

$$\frac{1}{u}= s\left(\frac{1}{{k}_{\text{p}}}+\frac{1}{{k}_{\text{b}}}+\frac{1}{{k}_{\text{c}}}+\frac{1}{{k}_{\text{s}}}\right)$$
(2)

where \({k}_{\text{p}}\) is the spring constant of the rail pad (including the sleeper) (N/m); s is the sleeper spacing (m); and \({k}_{\text{b}}\), \({k}_{\text{c}}\) and \({k}_{\text{s}}\) are the stiffness of ballast, capping and subgrade layers, respectively.

Figure 4 shows an example of rail seat load-time history computed using the above-mentioned approach.

Fig. 4
figure 4

Variation of wheel load and vertical rail seat load with time

Full size image

Alongside the vertical component, the lateral load component can cause significant deformations in the track substructure layers and may lead to lateral track instability. Several empirical equations have been proposed based on field investigations to evaluate the magnitude of this lateral load acting on the track (Doyle 1980). In this study, the lateral load (H) is calculated using the following equation (Zheng et al. 2019):

$$H=0.85\left[15+\frac{{Q}_{\text{w}}}{3}\right]$$
(3)

where \({Q}_{\text{w}}\) is the wheel load in kN.

2.2.1 Stress Distribution

In this study, the modified Boussinesq equations are used to evaluate the stress distribution in the track substructure layers (Frazee 2021). First, the maximum sleeper-ballast contact pressure (Qmax) is calculated using the following equation (Wang et al. 2020).

$${Q}_{\text{max}}= \frac{2{Q}_{\text{r}}}{l\times B}F$$
(4)

where \({Q}_{r}\) is the rail seat load (N) obtained from the axle load; l and B are the length (m) and width (m) of each sleeper; F is the factor of safety. This contact pressure is assumed to act on an infinite strip that extends along the direction of movement of the wheel. The lateral and vertical stresses in the track substructure are then computed using the modified Boussinesq’s formulations (Frazee 2021).

$${Q}_{y}=\frac{{Q}_{max}}{\pi }\left[{\text{tan}}^{-1}\left(\frac{d-y}{z}\right)\right]-{\text{tan}}^{-1}\left(\frac{c-y}{z}\right)+z\left[\frac{d-y}{{\left(d-y\right)}^{2}+{z}^{2}}-\frac{c-y}{{\left(c-y\right)}^{2}+{z}^{2}}\right]$$
(5)
$${Q}_{x}= \left\{\begin{array}{c}\frac{{Q}_{max}}{2}, \text{if} z=0\\ \frac{{Q}_{max}}{\pi }\left[{\text{tan}}^{-1}\left(\frac{p}{z}\right)-\frac{pz}{{p}^{2}+{z}^{2}}\right], \text{otherwise}\end{array}\right.$$
(6)

where p, c and d are empirical track parameters; z is the depth (m); y is the lateral distance along the length of the sleeper (m).

Figure 5 illustrates an example of stress distribution along vertical and lateral directions within the track substructure obtained using Boussinesq’s formulations when the axle load, \({Q}_{\text{a}}\) is 25 t. The wheel load acting on the rail (as shown in Fig. 5) comprises vertical and lateral force components which are used to evaluate vertical and lateral responses of the railway track.

Fig. 5
figure 5

Stress distribution within track substructure

Full size image

2.3 Track Resilient Response

The proposed rheological model for the ballasted railway track consists of three substructure layers: ballast, capping, and subgrade. The response of these layers is predicted by employing springs and dashpots (elastic and viscous elements), as shown in Fig. 6.

Fig. 6
figure 6

Viscoelastic rheological model of a ballasted railway track along: a longitudinal direction b lateral direction

Full size image

2.4 Generalised Dynamic Equation of Motion

The D’Alembert’s principle is applied to the rheological model shown in Fig. 6 to obtain the dynamic equations of motion. For the vertical response, the equilibrium equation is as follows:

$$\left[\begin{array}{ccc}{m}_{\text{s}}& 0& 0\\ 0& {m}_{\text{c}}& 0\\ 0& 0& {m}_{\text{b}}\end{array}\right]\left\{\begin{array}{c}{\ddot{y}}_{\text{s},\text{n}}\left(t\right)\\ {\ddot{y}}_{\text{c},\text{n}}\left(t\right)\\ {\ddot{y}}_{\text{b},\text{n}}\left(t\right)\end{array}\right\}+ \left[\begin{array}{ccc}{c}_{\text{sv}}+{c}_{\text{cv}}+{2c}_{\text{s}}^{s}& {-c}_{\text{cv}}& 0\\ {-c}_{\text{cv}}& {c}_{\text{cv}}+{c}_{\text{bv}}+{2c}_{\text{c}}^{s}& {-c}_{\text{bv}}\\ 0& {-c}_{\text{bv}}& {c}_{\text{bv}}+{2c}_{\text{b}}^{s}\end{array}\right]\left\{\begin{array}{c}{\dot{y}}_{\text{s},\text{n}}\left(t\right)\\ {\dot{y}}_{\text{c},\text{n}}\left(t\right)\\ {\dot{y}}_{\text{b},\text{n}}\left(t\right)\end{array}\right\}+\left[\begin{array}{ccc}{k}_{\text{sv}}+{k}_{\text{cv}}+{2k}_{\text{s}}^{s}& {-k}_{\text{cv}}& 0\\ {-k}_{\text{cv}}& {k}_{\text{cv}}+{k}_{\text{bv}}+{2k}_{\text{c}}^{s}& {-k}_{\text{bv}}\\ 0& {-k}_{\text{bv}}& {k}_{\text{bv}}+{2k}_{\text{b}}^{s}\end{array}\right]\left\{\begin{array}{c}{y}_{\text{s},\text{n}}\left(t\right)\\ {y}_{\text{c},\text{n}}\left(t\right)\\ {y}_{\text{b},\text{n}}\left(t\right)\end{array}\right\}-\left[\begin{array}{ccc}{c}_{\text{s}}^{s}& 0& 0\\ 0& {c}_{\text{c}}^{s}& 0\\ 0& 0& {c}_{\text{b}}^{s}\end{array}\right]\left\{\begin{array}{c}{\dot{y}}_{\text{s},\text{n}+1}\left(t\right)+\\ {\dot{y}}_{\text{c},\text{n}+1}\left(t\right)+\\ {\dot{y}}_{\text{b},\text{n}+1}\left(t\right)+\end{array}\begin{array}{c}{\dot{y}}_{\text{s},\text{n}-1}\left(t\right)\\ {\dot{y}}_{\text{c},\text{n}-1}\left(t\right)\\ {\dot{y}}_{\text{b},\text{n}-1}\left(t\right)\end{array}\right\}-\left[\begin{array}{ccc}{k}_{\text{s}}^{s}& 0& 0\\ 0& {k}_{\text{c}}^{s}& 0\\ 0& 0& {k}_{\text{b}}^{s}\end{array}\right]\left\{\begin{array}{c}{y}_{\text{s},\text{n}+1}\left(t\right)+\\ {y}_{\text{c},\text{n}+1}\left(t\right)+\\ {y}_{\text{b},\text{n}+1}\left(t\right)+\end{array}\begin{array}{c}{y}_{\text{s},\text{n}-1}\left(t\right)\\ {y}_{\text{c},\text{n}-1}\left(t\right)\\ {y}_{\text{b},\text{n}-1}\left(t\right)\end{array}\right\}=\left\{\begin{array}{c}{f}_{\text{sv},\text{n}}\left(t\right)\\ {f}_{\text{cv},\text{n}}\left(t\right)\\ {f}_{\text{bv},\text{n}}\left(t\right)\end{array}\right\}$$
(7)

where subscripts bv, cv, and sv represent ballast, capping and subgrade layers in the vertical direction, respectively; subscripts n, n + 1 and n-1 represent the nth, next and previous to the nth sleeper, respectively; m, c and k are the mass (kg), damping coefficient (Ns/m) and stiffness (N/m), respectively; \(\ddot{y}\left(t\right), \dot{y}(t)\) and \(y(t)\) represent the vertical acceleration (m/s2), velocity (m/s) and displacement (m), respectively; \(f(t)\) denotes the external force (N) acting on a substructure layer; \({c}^{s}\) and \({k}^{s}\) represent the damping (Ns/m) and stiffness (N/m) coefficients, respectively, of the shear dashpots and springs which represent the continuity of track substructure layers along the longitudinal direction (Zhai et al. 2004).

The same principle is applied along the lateral direction, and the corresponding dynamic equation of motion is as follows:

$$\left[\begin{array}{ccc}{m}_{\text{s}}& 0& 0\\ 0& {m}_{\text{c}}& 0\\ 0& 0& {m}_{\text{b}}\end{array}\right]\left\{\begin{array}{c}{\ddot{x}}_{\text{s},\text{n}}(t)\\ {\ddot{x}}_{\text{c},\text{n}}(t)\\ {\ddot{x}}_{\text{b},\text{n}}(t)\end{array}\right\}+\left[\begin{array}{ccc}{c}_{\text{s}}^{s}+{c}_{\text{c}}^{s}& -{c}_{\text{c}}^{s}& 0\\ -{c}_{\text{c}}^{s}& {c}_{\text{c}}^{s}+{c}_{\text{b}}^{s}& -{c}_{\text{b}}^{s}\\ 0& -{c}_{\text{b}}^{s}& {c}_{\text{b}}^{s}\end{array}\right]\left\{\begin{array}{c}{\dot{x}}_{\text{s},\text{n}}\left(t\right)\\ {\dot{x}}_{\text{c},\text{n}}\left(t\right)\\ {\dot{x}}_{\text{b},\text{n}}\left(t\right)\end{array}\right\}+\left[\begin{array}{ccc}{k}_{\text{s}}^{s}+{k}_{\text{c}}^{s}& -{k}_{\text{c}}^{s}& 0\\ -{k}_{\text{c}}^{s}& {k}_{\text{c}}^{s}+{k}_{\text{b}}^{s}& -{k}_{\text{b}}^{s}\\ 0& -{k}_{\text{b}}^{s}& {k}_{\text{b}}^{s}\end{array}\right]\left\{\begin{array}{c}{x}_{\text{s},\text{n}}\left(t\right)\\ {x}_{\text{c},\text{n}}\left(t\right)\\ {x}_{\text{b},\text{n}}\left(t\right)\end{array}\right\}=\left\{\begin{array}{c}{f}_{\text{sh},\text{n}}\left(t\right)\\ {f}_{\text{ch},\text{n}}\left(t\right)\\ {f}_{\text{bh},\text{n}}\left(t\right)\end{array}\right\}$$
(8)

where subscripts bh, ch, and sh represent ballast, capping and subgrade layers in the horizontal direction, respectively; \(\ddot{x}\left(t\right), \dot{x}(t)\) and \(x(t)\) denote the horizontal acceleration (m/s2), velocity (m/s) and displacement (m) and \({f}_{h}(t)\) represents external horizontal force (N). Equations (7) and (8) are solved using Newmark’s β integration method to obtain the transient response for each layer at any time instant, t. Note that 19 sleepers have been considered in this study that are equally spaced at 0.65 m intervals.

2.5 Model Parameters

The input parameters, viz. mass and stiffness for each track substructure layer are determined by considering a trapezoidal distribution of stresses within the substructure (Ahlbeck et al. 1975). The area inside this trapezoid is considered as the effective region for dynamic analysis (Punetha et al. 2020). This load-distribution model does not consider overlapping along the lateral and longitudinal direction. The overlapping along the lateral direction (perpendicular to the direction of movement of train) occurs when the sleeper length is less and the layer thickness and the stress-distribution angles are more, and along the longitudinal direction occurs if the sleeper spacing is less. The mass and stiffness of the substructure layers are thus determined as:

$${m}_{\text{b}}={\rho }_{\text{b}}{h}_{\text{b}}\left[lB+\left(l+B\right){h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+\frac{4}{3}{h}_{b}^{2}{\text{tan}}^{2}{\alpha }_{\text{b}}\right]$$
(9)
$${m}_{\text{c}}={\rho }_{\text{c}}{h}_{\text{c}}\left[lB+\left(l+B\right)\left(2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}\right)+4{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}\left({h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}\right)+\frac{4}{3}{h}_{\text{c}}^{2}{\text{tan}}^{2}{\alpha }_{\text{c}}\right]$$
(10)
$${m}_{\text{s}}={\rho }_{\text{s}}{h}_{\text{s}}\left[lB+\left(l+B\right)\left(2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+2{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}+{h}_{\text{s}}\text{tan}{\alpha }_{\text{s}}\right)+4({h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}})\left({h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}+{h}_{\text{s}}\text{tan}{\alpha }_{\text{s}}\right)+\frac{4}{3}{h}_{\text{s}}^{2}{\text{tan}}^{2}{\alpha }_{\text{s}}\right]$$
(11)
$${k}_{\text{b}}=\frac{2\left(l-B\right)\text{tan}{\alpha }_{\text{b}}}{\text{ln}\left[\frac{l}{B}\times \left(\frac{B+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}}{l+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}}\right)\right]}{E}_{\text{b}}$$
(12)
$${k}_{\text{c}}=\frac{2\left(l-B\right)\text{tan}{\alpha }_{\text{c}}}{\text{ln}\left[\left(\frac{l+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}}{B+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}}\right)\left(\frac{B+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+2{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}}{l+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+2{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}}\right)\right]}{E}_{\text{c}}$$
(13)
$${k}_{\text{s}}=\frac{2\left(l-B\right)\text{tan}{\alpha }_{\text{s}}}{\text{ln}\left[\left(\frac{l+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+2{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}}{B+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+2{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}}\right)\left(\frac{B+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+2{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}+2{h}_{\text{s}}\text{tan}{\alpha }_{\text{s}}}{l+2{h}_{\text{b}}\text{tan}{\alpha }_{\text{b}}+2{h}_{\text{c}}\text{tan}{\alpha }_{\text{c}}+2{h}_{\text{s}}\text{tan}{\alpha }_{\text{s}}}\right)\right]}{E}_{\text{s}}$$
(14)

where the subscripts b, c, and s represent the ballast, capping and subgrade, respectively; h is the layer thickness (m); \(\rho\) is the density (kg/m3); E is the elastic modulus (N/m2). The angle α is the stress distribution angle for each layer and is evaluated using Eq. 15 (Burmister 1958; Giroud and Han 2004):

$$\text{tan}{\alpha }_{\text{b}}=\text{tan}{\alpha }_{\text{b}}^{0}\left[1+0.204\left(\frac{{E}_{\text{b}}}{{E}_{\text{c}}}-1\right)\right]$$
(15a)
$$\text{tan}{\alpha }_{c}=\text{tan}{\alpha }_{\text{c}}^{0}\left[1+0.204\left(\frac{{E}_{c}}{{E}_{\text{s}}}-1\right)\right]$$
(15b)

α0 is the reference stress distribution angle for the considered layer (assumed as 45˚ based on published literature (Zhang et al. 2016)).

The damping coefficient, c, is calculated for each layer (i.e. cb, cc, cs) using the following expressions (Nimbalkar et al. 2012).

$${c}_{\text{b}}=\sqrt{\frac{{E}_{\text{b}}{\rho }_{\text{b}}}{(1+{\nu }_{\text{b}})(1-{\nu }_{\text{b}})}}$$
(16)
$${c}_{\text{c}}=\sqrt{\frac{{E}_{\text{c}}{\rho }_{\text{c}}}{(1+{\nu }_{\text{c}})(1-{\nu }_{\text{c}})}}$$
(17)
$${c}_{\text{s}}=\sqrt{\frac{{E}_{\text{s}}{\rho }_{\text{s}}}{(1+{\nu }_{\text{s}})(1-{\nu }_{\text{s}})}}$$
(18)

where υ represents Poisson’s ratio of each track layer (i.e., υb, υc, υs).

3 Model Validation

The proposed model can be used to evaluate the transient response of track substructure layers under train-induced loading. This response includes displacement, velocity, and acceleration along both vertical and lateral directions. The accuracy of the model is checked by comparing the predicted response with the field, experimental and analytical investigations of Grabe et al. (2005), Priest and Powrie (2009), Mishra et al. (2017), Gu et al. (2022), Xu et al. (2023), Xu et al. (2024) and Punetha et al. (2020). The input data used to obtain the response are listed in Table 1. The shear stiffness and damping coefficients are assumed for each layer. The initial values of shear stiffness and damping coefficients used in the parametric study have been adopted from Zhai et al. (2004), Oscarsson and Dahlberg (1998) and Punetha et al. (2020).

Table 1 Model parameters for validation and parametric study
Full size table

Figure 7 depicts a comparison of the rail seat load obtained from the field investigations by Mishra et al. (2017) along Amtrak’s North-East Corridor in the United States with the predicted values. It can be observed that there is a small difference in the actual and predicted rail seat load-time history, which may be attributed to the fluctuations in the wheel load in the field; however, the trend is in good agreement with the field data.

Fig. 7
figure 7

Comparison of predicted rail seat load against field investigations of Mishra et al. (2017)

Full size image

Priest and Powrie (2009) investigated the track response during the passage of coal wagons for the Broodsnyersplaas-Richards Bay Coal Export Line in South Africa. Low-frequency geophones were used to measure the velocity response beneath a ballasted track, and a video monitoring technique was used to measure sleeper displacement. Table 2 compares the maximum and minimum displacement reported by Priest and Powrie (2009) with the model predictions. It can be observed that the predicted response is in good agreement with the field data.

Table 2 Validation results for displacement obtained in the present study with previous studies by Priest and Powrie (2009) and Punetha et al. (2020)
Full size table

Punetha et al. (2020) performed an analytical study using a ballasted track model in which only vertical displacements were predicted. Table 2 shows the predicted displacement response of the track compared with the analytical formulations of Punetha et al. (2020). It can be observed from Table 2 that the resilient displacement predicted using the present model is similar to the analytical study by Punetha et al. (2020).

Gu et al. (2022) monitored the long-term dynamic response of a full-scale ballasted track model under moving loads by installing velocity sensors on the ballast top to record vibration velocities. Smart rock sensors were also used to capture vertical, lateral and longitudinal ballast accelerations. Figure 8 presents a comparison among the lateral accelerations recorded by Gu et al. (2022), those predicted by the developed track model, and those calculated using Poisson’s ratio, derived from the lateral and axial strains. The lateral accelerations predicted using the developed track model show a reasonable match with the lateral accelerations recorded in the experimental investigations by Gu et al. (2022). However, the lateral acceleration predictions using Poisson’s ratio approach were infinitesimal compared to those recorded by Gu et al. (2022), which suggests that the present study is a better method to capture lateral response in a railway track substructure.

Fig. 8
figure 8

Comparison of predicted lateral ballast acceleration from the present study and calculated using Poisson’s ratio with the experimental results reported by Gu et al. (2022)

Full size image

Xu et al. (2023) checked the lateral stability of ballast in a ballasted railway track by carrying out pullout tests in a laboratory. The experiments were conducted at a scale of 1/5 for the ballasted track model, which was constructed on an aluminium platform to mimic the field conditions. Transducers were attached to both ends of the sleepers to measure vertical and lateral displacements at the ballast top. Figure 9 includes a comparison of lateral displacements obtained in the experimental analysis of Xu et al. (2023) with the lateral displacements of the predicted model and evaluated using Poisson’s ratio. A good match is observed on comparing the lateral displacements of the experimental study with the predicted model results, while the lateral displacements obtained using Poisson’s ratio are much less. The noticeable contrast underscores the close alignment between the predictions made by the current track model and the observed lateral displacements in the experimental study. Conversely, the lateral displacements derived from Poisson’s ratio exhibit significant deviation from the experimental results. This emphasizes the accuracy and applicability of the current track model in forecasting lateral displacements for a ballasted railway track.

Fig. 9
figure 9

Comparison of predicted lateral load-displacements with the experimental results of Xu et al. (2023)

Full size image

Xu et al. (2024) conducted static pull-out tests on a 1/9 scaled model of a ballasted track for a Japanese high-speed train to assess its lateral stability against cyclic lateral forces. These lateral forces were applied using a vibrator on the scaled ballasted track model. Displacement transducers were installed to execute the pull-out tests on the ballasted track, while deflectometers were installed to assess the insufficient lateral resistance against lateral forces. Figure 10 shows a comparison of the lateral displacement obtained in the experimental analysis of Xu et al. (2024) and those predicted by the developed track model. The lateral displacements are also compared with the lateral displacements calculated using Poisson’s ratio. Upon comparison, a significant difference of 199.2% was observed between the lateral displacement values obtained from the experimental study and those predicted by the track model in comparison to those calculated by Poisson’s ratio. This stark difference highlights that the predictions of the present track model closely match the lateral displacements observed in the experimental study, while the lateral displacements calculated using Poisson’s ratio significantly deviate from the experimental results. These findings underscore the suitability of the present track model for accurately predicting the lateral displacements of a ballasted railway track.

Fig. 10
figure 10

Comparison of predicted lateral displacements of the present study and calculated using Poisson’s ratio with the experimental results of Xu et al. (2024)

Full size image

Based on the aforementioned results, it is evident that the predicted track model, a viscoelastic model, can accurately predict the track response to train-induced loads. The superiority of the track model is apparent when comparing it with the lateral response calculated using Poisson’s ratio. Overall, this approach represents a quick and straightforward method for predicting the performance of ballasted railway tracks, particularly in terms of the lateral transient displacement or acceleration of the track substructure.

4 Results and Discussion

A parametric study is conducted to investigate the influence of axle load (Qa), train speed (V) and the thickness of granular layers (hb and hc) on the track substructure behaviour. The track parameters and thickness of each track substructure layer used in the analyses are listed in Table 1. The axle loads considered in this study are 20 to 40 t, which represent the axle load of trains from different countries. For instance, the axle load of trains in Australia is 20–40 t; in the USA, it is 30–36 t; in Europe, it is 20–25 t (Knothe and Grassie 1993); and in China is 21–30 t (Smith and Zhou 2018). Similarly, train speeds ranging from 70 to 200 km/h are considered, representing the spectrum of train speeds adopted globally. For example, train speeds in Europe are 200 to 250 km/h (Knothe and Grassie 1993); in China are 200 to 250 km/h (He et al. 2023); in India are 80 to 200 km/h (Mittal and Chaturvedi 2023). The thickness of granular layers, that is, ballast and capping, was changed to evaluate the influence of each layer on ballast displacement. In this study, the granular layer thickness is varied to check its effect on the transient behaviour of a ballasted railway track. The thickness of the granular layers is varied in two phases. Firstly, the thickness of the ballast layer is increased from 0.1 m to 0.75 m while keeping the capping thickness constant at 0.15 m. Subsequently, the thickness of the ballast is fixed at 0.35 m, and the capping thickness is varied from 0.1 m to 0.7 m. This helped to assess the sensitivity of ballast displacement to the ballast and capping layer thickness. Moreover, a previous study by Punetha et al. (2020) used a similar methodology of changing granular layer thickness between 0.15 to 0.6 m. For each analysis, a single parameter value is varied while the others are kept constant. The nominal values of axle load and train speed are 25 t and 150 km/h, respectively, unless otherwise stated.

4.1 Influence of Axle Load

The influence of axle load on track substructure behaviour is investigated by varying the axle load from 20 to 40 t. Figure 11 illustrates the variation of vertical (Sv) and lateral displacements (Sh) with depth at different axle loads. It is evident from the figure that the lateral displacement increases with increasing axle loads. The Sh increases by 40% and 28.6% when the axle load is increased from 20 to 30 t and 30 to 40 t, respectively. It is also evident from the figure that Sh decreases along the depth of the track. The overall decrease in Sh from the ballast top to the subgrade top is about 34.4%. Towards the bottom of the subgrade, the increase in Sh becomes insignificant and diminishes. The decrease in displacement with depth is due to the stress reduction, which occurs due to the presence of granular layers.

Fig. 11
figure 11

Displacement variation along the depth for different axle loads

Full size image

It is also evident from Fig. 11 that the vertical ballast displacement increases from 4.7 mm to 7.05 mm and 7.05 mm to 9.4 mm when the axle load is increased from 20 to 30 t and 30 to 40 t, respectively. The vertical displacement (Sv) is maximum at the ballast top and decreases along the depth of the track. Moreover, it is apparent from Fig. 11 that both the lateral and vertical (Sh and Sv) displacements decrease nonuniformly along the depth of the track and increases with increasing axle load.

4.2 Influence of Train Speed

The train speed is varied from 70 to 200 km/h to investigate its effect on the behaviour of track substructure layers. Figure 12 shows the variation of vertical (Sv) and lateral displacement (Sh) with depth at different train speeds. It can be observed that the displacement increases on increasing the train speed. The variation of train speed from 70 to 150 km/h results in about a 15% increment in Sh, and increasing the train speed from 70 to 200 km/h, a 26.2% increase is observed. It is also observed that Sv increases on increasing the train speed. On almost doubling the train speed from 70 to 150 km/h, Sv increases by 15%. At the same time, an increment of 26.2% occurs when the speed is increased from 70 to 200 km/h.

Fig. 12
figure 12

Displacement variation along the depth of track substructure at different train speeds

Full size image

In this study, the effect of train speed is considered by employing a dynamic amplification factor (DAF) as a multiplier to the wheel load. On increasing the train speed, DAF increases, affecting the stress and deformation in the substructure layers. The DAF used in the present study is calculated using the following equation (Nimbalkar and Indraratna 2016):

$$DAF=1+i{\left(\frac{V}{D}\right)}^{j}$$
(19)

where V is the train speed (km/h); D is the diameter of the wheel (assumed as 1.019 m in this study); i and j are empirical parameters that depend on axle load and subgrade type, and their values range from 0.0052 to 0.0065 and 0.75 to 1.02, respectively (Nimbalkar and Indraratna 2016).

Figure 13 illustrates the effect of increasing train speed on lateral and vertical ballast acceleration. Increasing the train speed from 70 to 200 km/h increases the ballast lateral and vertical acceleration by 23%. The increase in train speed from 70 to 90 km/h increases the vertical and lateral ballast acceleration by 4%; however, increasing the train speed from 150 to 200 km/h causes an increase in the ballast acceleration by 8%. It is evident that more increments in the train speed will lead to much-increased ballast acceleration.

Fig. 13
figure 13

Variation of ballast acceleration due to increasing train speed

Full size image

4.3 Influence of Granular Layer Thickness

In this study, the granular layer thickness is varied in two phases. Firstly, the thickness of the ballast layer is increased from 0.1 m to 0.75 m while keeping the capping thickness constant at 0.15 m. Subsequently, the thickness of the ballast is fixed at 0.35 m, and the capping thickness is varied from 0.1 m to 0.7 m.

Figure 14 illustrates the lateral and vertical displacement response at the ballast top when the thickness of the granular layers is increased. It can be observed that the ballast top displacement decreases rapidly with increasing granular layer thickness. The maximum vertical ballast top displacement (Sv) is 6.8 mm when the thickness of the ballast layer is 0.1 m. A gradual increase in the ballast thickness from 0.1 to 0.75 m leads to a consistent decrease of Sv. Overall, Sv decreases to 4.7 mm when the ballast thickness is increased to 0.75 m. Meanwhile, the lateral ballast displacement (Sh) reduces up to 4 mm. A smooth decrease of 0.85 mm and 0.27 mm occurs when the ballast thickness varies from 0.1 to 0.3 m and 0.5 to 0.75 mm, respectively. When the capping thickness is increased from 0.1 m to 0.7 m, Sv and Sh decrease by about 1.3 and 1.25 mm, respectively. The overall decrease in Sv and Sh is 26.7% and 30.2%, respectively.

Fig. 14
figure 14

Variation of displacement at the ballast top with granular layer thickness

Full size image

Figure 15 illustrates the variation of Sh and Sv with depth when the ballast thickness is increased, and the capping thickness is kept constant at 0.15 m. On increasing the ballast thickness, both Sh and Sv decrease. The decrease in Sv is 11.4% when the ballast thickness is changed from 0.35 m to 0.55 m and 11.2% when the thickness increases from 0.55 m to 0.75 m. At the same time, Sh decreases by 8.2% and 4.9% when the ballast thickness increases from 0.35 m to 0.55 m and 0.55 m to 0.75 m, respectively.

Fig. 15
figure 15

Displacement variation along the depth of the track at different ballast thickness

Full size image

Figure 16 shows the lateral and vertical response of the track using the second approach of varying the granular layer thickness. In this approach, the capping thickness is varied, and the ballast thickness is kept constant. Similar to the first approach, the lateral and vertical displacements (Sh and Sv) decrease when the capping thickness is increased. The decrease in Sh and Sv occurs by 4–8% on increasing the capping thickness. Along the depth of the track substructure, both Sh and Sv decrease due to an increase in distance from the point of application of load.

Fig. 16
figure 16

Displacement variation along the depth of the track at different capping thickness

Full size image

Figure 17 illustrates the variation of subgrade displacement (Ss) (at the subgrade top) with increasing granular layer thickness; on increasing the granular layer thickness, the vertical and lateral displacement decrease. When the capping thickness is kept constant, the vertical response decreases by 36.9% and the lateral response reduces by 28.5%. While changing the capping thickness and maintaining the ballast thickness constant at 0.35 m, a 26.8% and 30.2% decrease occurs in the vertical and lateral displacements, respectively.

Fig. 17
figure 17

Variation of subgrade displacement due to varying granular layer thickness

Full size image

5 Conclusions

This research presents a novel viscoelastic track model utilising springs and dashpots to predict transient response when subjected to train loads. A significant contribution of this study is the development of a computational technique that can capture lateral response of ballasted railway tracks, an aspect often overlooked in the past research. Additionally, the incorporation of a tri-layered substructure enhances the fidelity of the track representation compared to single or bi-layered models. To validate the proposed methodology, extensive comparisons are made with published analytical, laboratory, and field investigation data. Furthermore, a parametric analysis investigates the impacts of axle load, train velocity, and granular layer thickness on the lateral and vertical responses of track layers. The following conclusions can be drawn from the study:

  • The method offers a straightforward approach involving the solution of governing equations to assess the lateral response of railway tracks. The parametric study clearly demonstrates that the lateral displacement exhibits trends similar to those observed in vertical displacement evaluation.

  • The consistency observed between the predicted responses and the published data confirms the reliability and precision of the approach.

  • The present model predictions demonstrate strong alignment with the experimental data, notably surpassing the accuracy of lateral response evaluations obtained through Poisson’s ratio.

  • The predicted approach proficiently captures nonuniform lateral and vertical displacements along the depth of the track.

  • An increase in axle load significantly amplifies the track displacement. A significant increase from 3.8 to 7.4 mm occurs in the lateral displacement on increasing axle loads from 20 to 40 t. Additionally, the vertical displacement doubles, i.e., changes from 4.7 to 9.4 mm as the axle load is increased from 20 to 40 t.

  • An increase in train speed leads to increased lateral and vertical displacements, although at higher train speeds (i.e., from 150 to 200 km/h), the magnitude of this increase is comparatively less. The lateral displacement increases to 5 mm at a train speed of 200 km/h compared to 3.9 mm at 70 km/h. While, the vertical displacement reaches 6.5 mm at 200 km/h compared to 5 mm at 70 km/h.

  • The variation in granular layer thickness reveals the sensitivity of lateral response to the thickness of the capping layer and vertical response to the thickness of the ballast layer.

The proposed approach is useful to practising railway engineers for assessing the performance of the ballasted railway track along both vertical and lateral directions.