An innovative rheological approach for predicting the behaviour of critical zones in a railway track

Abstract

The poor performance of critical zones along a railway line has long been a subject of concern for rail infrastructure managers. The rapid deterioration of track geometry in these zones is primarily ascribed to limited understanding of the underlying mechanism and scarcity of adequate tools to assess the severity of the potential issue. Therefore, a comprehensive evaluation of their behaviour is paramount to improve the design and ensure adequate service quality. With this objective, a novel methodology is introduced, which can predict the differential plastic deformations at the critical zones and assess the suitability of different countermeasures in improving the track performance. The proposed technique employs a three-dimensional geotechnical rheological track model that considers varied support conditions of the critical zone. The approach is successfully validated with published field data and predictions from finite element analysis. This methodology is then applied to a bridge-open track transition zone, where it is observed that an increase in axle load exacerbates the track geometry degradation problem. The results show that the performance of critical zones with weak subgrade can be improved by increasing the granular layer thickness. Interpretation of the predicted differential settlement for different countermeasures exemplifies the practical significance of the proposed methodology.

1 Introduction

A rapid increase in the demand for heavier freight and high-speed passenger trains has increased concerns regarding the safety and serviceability of the existing railway tracks [5, 47, 55]. The problem is crucial for zones such as transitions between open track and stiff structures (e.g. bridges, culverts or tunnels). These zones (termed critical zones) experience a rapid degradation in track geometry due to inconsistent response on either side of the transition. Consequently, frequent maintenance is required to maintain adequate levels of passenger safety and comfort.

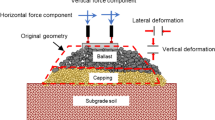
Figure 1a illustrates the critical zones between an embankment and a bridge. The track is founded on multiple soil layers on one side of a critical zone and a concrete slab on the other. Thus, two distinct regions can be identified on each side of the bridge approach, one with a higher track stiffness and the other with a lower track stiffness. When a train passes this transition, the track supported by soil layers inherently deforms more than the track on the bridge. Consequently, differential deformation occurs, which accumulates with multiple train passages and produces an uneven track profile near the bridge approach (see Fig. 1b). This differential track settlement jeopardises the operational safety of the trains and demands expensive maintenance activities to restore the track geometry [54].

Fig. 1

a Open track-bridge transition zone; b transition zone after multiple train passages

Several countermeasures have been proposed to mitigate the track geometry degradation in the critical zones. These techniques employ:

• soft rail pads or resilient mats to reduce the stiffness of the stiffer side [32, 66]

• cellular geoinclusions or ground improvement methods to increase the stiffness of the softer side [8, 49, 57, 90]

• approach slabs or transition wedges to provide a gradual change in track stiffness [11, 58]

• confinement walls, polyurethane geocomposites or gluing materials to reduce track settlements in the softer side [16, 31, 67].

Although previous studies have shown the viability of these countermeasures, the transition zones at several locations still exhibit poor performance [85]. This is due to the site-specific nature of the track deterioration problem and limited understanding of the mechanism of applied countermeasures. An increase in axle load and train speed might exacerbate the problem of differential settlement in these track sections. Thus, a comprehensive evaluation of the behaviour of a transition zone and the effect of various remedial measures is essential to improve the design and optimise the performance. Notably, the problem of predicting the magnitude of track geometry degradation in these zones and the efficacy of various countermeasures still remains an intriguing challenge.

Over the years, several researchers have attempted to gain insight into the complex behaviour of the ballasted tracks in critical zones and the performance of various countermeasures using in situ measurements [e.g. 7, 11, 36, 43, 51, 85] and laboratory testing [e.g. 44, 45]. These investigations highlight the importance of identifying the primary cause of the track geometry deterioration problem before applying an appropriate remedial measure. However, a comprehensive understanding of the performance of a transition requires long-term monitoring of the track response. To record such a vast amount of data through laboratory or field monitoring is quite cumbersome and challenging. Financial constraints, scale effects in experiments, and several influencing variables in field investigations are among the other limitations.

The computational approaches provide an alternative method to understand the track deterioration process and analyse the performance of different remedial measures. Indeed, attempts have been made to study the behaviour of the critical zones using numerical techniques such as finite element (FE) or boundary element (BE) methods, most of which have focused on the transient or short-term response and only considered the elastic behaviour of geomaterials [e.g. 4, 17, 18, 35, 61, 83]. Although the transient response is an essential factor influencing the vehicle–track interaction forces, ride quality and operational safety, an insight into the long-term track performance is inevitable to understand the track geometry degradation mechanism. Researchers have also employed the discrete element method (DEM) to understand the geometry degradation mechanism in the ballasted railway tracks [e.g. 6, 9, 10, 94]. DEM realistically captures the load distribution and particle level interactions in the substructure layers under the train-induced loading [80]. However, it can only be employed to study the behaviour of a small segment of a rail track due to the substantial amount of computational time required to perform DE analyses. In addition, the prediction of the long-term performance of a railway track (i.e. for load cycles in the order of millions) using DEM is impractical owing to the considerable computational effort associated with it.

Prior knowledge of the magnitude of differential settlements accumulated in the substructure layers is the key to the proper design of the critical zones. However, the studies related to the prediction of the differential settlement accumulated in a transition zone over a specified period are somewhat scarce [e.g. 24, 46, 62, 82, 84]. In most studies, the plastic deformation in the soil layers is predicted using empirical expressions. However, uncertainties exist regarding the use of empirical models as they lack general applicability under different loading effects, boundary conditions and soil types [86]. Moreover, such expressions are only applicable to the conditions on which they are based or derived. Clearly, more work is required to establish a theoretically consistent approach to predict the behaviour of the critical zones and analyse the efficacy of various mitigation strategies. Such an approach must employ appropriate constitutive models [e.g. 19, 25, 29, 34, 40, 68, 74, 77] to accurately simulate the accumulation of irrecoverable deformation in the substructure layers.

This paper explains the development of a three-dimensional (3D) mechanistic approach to evaluate the transient and long-term performance of the critical zones. The proposed method employs a simple yet effective geotechnical rheological model to simulate the viscoelastic–plastic behaviour of the substructure layers on both sides of the transition. The technique is validated against the field measurements reported in the literature and the 3D FE predictions. Subsequently, the methodology is applied to an open track–bridge transition and the adequacy of different countermeasures to mitigate the differential track settlements is examined. The essential contribution of this article is the more accurate simulation of the plastic response of geomaterials using slider elements, which are described by appropriate constitutive relationships compared to the existing methods that employ empirical models. The main contribution of practical value is the capability to quickly evaluate the magnitude of the potential problem and assess the suitability of different countermeasures to improve the performance of the critical zones.

2 Methodology

The proposed approach involves two key components:

• A geotechnical rheological track model that considers varied support conditions along the direction of train movement

• Slider elements described by appropriate constitutive relations for geomaterials to capture their plastic response and consequently, predict the differential track settlement in the critical zone

2.1 Geotechnical rheological track model

A typical open track–bridge transition is considered in which the track substructure on the softer side consists of three layers, i.e. ballast, subballast and subgrade, while it comprises a single ballast layer on the stiffer side (see Fig. 2). Because of symmetry along the centreline, only one half of the track is considered. Each substructure layer on both sides of the transition is represented as an array of discrete masses connected via springs, dashpots and slider elements. The bridge and its abutment are simulated as fixed supports due to their negligible deformation compared to the soil layers. The continuity of the track layers along the x-direction (i.e. along the rail length) is represented using shear springs and shear dashpots. The origin of the coordinate system is assumed at the starting point of the stiffer side.

Fig. 2

Rheological model of an open track–bridge transition

The track substructure layers on either side of a transition undergo recoverable and irrecoverable deformation when subjected to train-induced loading [41]. The total vertical displacement of these layers on softer and stiffer sides, at a given time instant, t, can be partitioned into viscoelastic and plastic components, as follows:

$$w_{\text m} = \left\{ {\begin{array}{*{20}c} {w_{\text {g,m}} } \\ {w_{\text {s,m}} } \\ {w_{\text {b,m}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {w_{\text {g,m}}^{{{{ve}}}} + w_{\text {g,m}}^{{{p}}} } \\ {w_{\text {g,m}} + w_{\text {s,m}}^{{{{ve}}}} + w_{\text {s,m}}^{{{p}}} } \\ {w_{\text {s,m}} + w_{\text {b,m}}^{{{{ve}}}} + w_{\text {b,m}}^{{{p}}} } \\ \end{array} } \right\}$$

(1a)

$$w_{\text n} = w_{\text {b,n}}^{ve} + w_{\text {b,n}}^{p}$$

(1b)

where subscripts g, s and b represent the subgrade, subballast and ballast layers, respectively; superscripts ‘p’ and ‘ve’ denote the plastic and viscoelastic components, respectively; subscripts m and n represent the mth and the nth sleepers, respectively; w is the displacement in the vertical direction.

In the present geotechnical rheological model, the viscoelastic component of the response is simulated using spring and dashpots, while a slider element represents the plastic component. Three stages of track response can be identified under train-induced repetitive loading. The first phase is the initial loading stage when the stress state in a track layer is within the yield surface (described by f_g, f_s or f_b for subgrade, subballast and ballast, respectively). In this phase, the springs and dashpots deform, whereas slider elements remain inactive; thus, the track layer behaves in a purely viscoelastic manner. In the second phase, the stress state satisfies the yield criterion (or loading conditions, see Sect. 2.2), thus activating the slider elements, and consequently, the total response is viscoelastic–plastic. The third phase is the unloading phase, in which the springs and dashpots deform, whereas the slider elements get deactivated leading to a viscoelastic response.

The displacement of the slider element is essentially irreversible, and its magnitude is determined by employing appropriate constitutive relationships (Sect. 2.2). The plastic response component, represented by the slip/movement in the slider element, accumulates with repeated train axle passages at a diminishing rate. The softer side usually accumulates greater plastic deformation as compared to the stiffer side, which results in an uneven track profile in the transition zone.

2.1.1 Equations of motion for track substructure

The overall response of the substructure layers is determined by utilising the equations below, which are derived from the dynamic equilibrium condition in the track model (see Fig. 2):

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {m_{{\text{g}}} } & 0 & 0 \\ 0 & {m_{{\text{s}}} } & 0 \\ 0 & 0 & {m_{{\text{b}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\ddot{w}_{{{\text{g}},{\text{m}}}} \left( t \right)} \\ {d\ddot{w}_{{{\text{s}},{\text{m}}}} \left( t \right)} \\ {d\ddot{w}_{{{\text{b}},{\text{m}}}} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{{\text{g}}} + k_{{\text{s}}} + 2k_{{\text{g}}}^{s} } & { - k_{{\text{s}}} } & 0 \\ { - k_{{\text{s}}} } & {k_{{\text{s}}} + k_{{\text{b}}} + 2k_{{\text{s}}}^{s} } & { - k_{{\text{b}}} } \\ 0 & { - k_{{\text{b}}} } & {k_{{\text{b}}} + 2k_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {dw_{{{\text{g}},{\text{m}}}} \left( t \right)} \\ {dw_{{{\text{s}},{\text{m}}}} \left( t \right)} \\ {dw_{{{\text{b}},{\text{m}}}} \left( t \right)} \\ \end{array} } \right\} \hfill \\ + \left[ {\begin{array}{*{20}c} {c_{{\text{g}}} + c_{{\text{s}}} + 2c_{{\text{g}}}^{s} } & { - c_{{\text{s}}} } & 0 \\ { - c_{{\text{s}}} } & {c_{{\text{s}}} + c_{{\text{b}}} + 2c_{{\text{s}}}^{s} } & { - c_{{\text{b}}} } \\ 0 & { - c_{{\text{b}}} } & {c_{{\text{b}}} + 2c_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\dot{w}_{{{\text{g}},{\text{m}}}} \left( t \right)} \\ {d\dot{w}_{{{\text{s}},{\text{m}}}} \left( t \right)} \\ {d\dot{w}_{{{\text{b}},{\text{m}}}} \left( t \right)} \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {c_{{\text{g}}} + 2c_{{\text{g}}}^{s} } & { - c_{{\text{s}}} } & 0 \\ {2c_{{\text{s}}}^{s} } & {c_{{\text{s}}} + 2c_{{\text{s}}}^{s} } & { - c_{{\text{b}}} } \\ {2c_{{\text{b}}}^{s} } & {2c_{{\text{b}}}^{s} } & {c_{{\text{b}}} + 2c_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\dot{w}_{{{\text{g}},{\text{m}}}}^{p} \left( t \right)} \\ {d\dot{w}_{{{\text{s}},{\text{m}}}}^{p} \left( t \right)} \\ {d\dot{w}_{{{\text{b}},{\text{m}}}}^{p} \left( t \right)} \\ \end{array} } \right\} \hfill \\ - \left[ {\begin{array}{*{20}c} {k_{{\text{g}}} + 2k_{{\text{g}}}^{s} } & { - k_{{\text{s}}} } & 0 \\ {2k_{{\text{s}}}^{s} } & {k_{{\text{s}}} + 2k_{{\text{s}}}^{s} } & { - k_{{\text{b}}} } \\ {2k_{{\text{b}}}^{s} } & {2k_{{\text{b}}}^{s} } & {k_{{\text{b}}} + 2k_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {dw_{{{\text{g}},{\text{m}}}}^{p} \left( t \right)} \\ {dw_{{{\text{s}},{\text{m}}}}^{p} \left( t \right)} \\ {dw_{{{\text{b}},{\text{m}}}}^{p} \left( t \right)} \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {c_{{\text{g}}}^{s} } & 0 & 0 \\ 0 & {c_{{\text{s}}}^{s} } & 0 \\ 0 & 0 & {c_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\dot{w}_{{{\text{g}},{\text{m}} - 1}} \left( t \right)} \\ {d\dot{w}_{{{\text{s}},{\text{m}} - 1}} \left( t \right)} \\ {d\dot{w}_{{{\text{b}},{\text{m}} - 1}} \left( t \right)} \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {c_{{\text{g}}}^{s} } & 0 & 0 \\ 0 & {c_{{\text{s}}}^{s} } & 0 \\ 0 & 0 & {c_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\dot{w}_{{{\text{g}},{\text{m}} + 1}} \left( t \right)} \\ {d\dot{w}_{{{\text{s}},{\text{m}} + 1}} \left( t \right)} \\ {d\dot{w}_{{{\text{b}},{\text{m}} + 1}} \left( t \right)} \\ \end{array} } \right\} \hfill \\ - \left[ {\begin{array}{*{20}c} {k_{{\text{g}}}^{s} } & 0 & 0 \\ 0 & {k_{{\text{s}}}^{s} } & 0 \\ 0 & 0 & {k_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {dw_{{{\text{g}},{\text{m}} - 1}} \left( t \right)} \\ {dw_{{{\text{s}},{\text{m}} - 1}} \left( t \right)} \\ {dw_{{{\text{b}},{\text{m}} - 1}} \left( t \right)} \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {k_{{\text{g}}}^{s} } & 0 & 0 \\ 0 & {k_{{\text{s}}}^{s} } & 0 \\ 0 & 0 & {k_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {dw_{{{\text{g}},{\text{m}} + 1}} \left( t \right)} \\ {dw_{{{\text{s}},{\text{m}} + 1}} \left( t \right)} \\ {dw_{{{\text{b}},{\text{m}} + 1}} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {c_{{\text{g}}}^{s} } & 0 & 0 \\ {c_{{\text{s}}}^{s} } & {c_{{\text{s}}}^{s} } & 0 \\ {c_{{\text{b}}}^{s} } & {c_{{\text{b}}}^{s} } & {c_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\dot{w}_{{{\text{g}},{\text{m}} - 1}}^{p} \left( t \right)} \\ {d\dot{w}_{{{\text{s}},{\text{m}} - 1}}^{p} \left( t \right)} \\ {d\dot{w}_{{{\text{b}},{\text{m}} - 1}}^{p} \left( t \right)} \\ \end{array} } \right\} \hfill \\ + \left[ {\begin{array}{*{20}c} {c_{{\text{g}}}^{s} } & 0 & 0 \\ {c_{{\text{s}}}^{s} } & {c_{{\text{s}}}^{s} } & 0 \\ {c_{{\text{b}}}^{s} } & {c_{{\text{b}}}^{s} } & {c_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\dot{w}_{{{\text{g}},{\text{m}} + 1}}^{p} \left( t \right)} \\ {d\dot{w}_{{{\text{s}},{\text{m}} + 1}}^{p} \left( t \right)} \\ {d\dot{w}_{{{\text{b}},{\text{m}} + 1}}^{p} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{{\text{g}}}^{s} } & 0 & 0 \\ {k_{{\text{s}}}^{s} } & {k_{{\text{s}}}^{s} } & 0 \\ {k_{{\text{b}}}^{s} } & {k_{{\text{b}}}^{s} } & {k_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {dw_{{{\text{g}},{\text{m}} - 1}}^{p} \left( t \right)} \\ {dw_{{{\text{s}},{\text{m}} - 1}}^{p} \left( t \right)} \\ {dw_{{{\text{b}},{\text{m}} - 1}}^{p} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{{\text{g}}}^{s} } & 0 & 0 \\ {k_{{\text{s}}}^{s} } & {k_{{\text{s}}}^{s} } & 0 \\ {k_{{\text{b}}}^{s} } & {k_{{\text{b}}}^{s} } & {k_{{\text{b}}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {dw_{{{\text{g}},{\text{m}} + 1}}^{p} \left( t \right)} \\ {dw_{{{\text{s}},{\text{m}} + 1}}^{p} \left( t \right)} \\ {dw_{{{\text{b}},{\text{m}} + 1}}^{p} \left( t \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {dF_{{{\text{g}},{\text{m}}}} \left( t \right)} \\ {dF_{{{\text{s}},{\text{m}}}} \left( t \right)} \\ {dF_{{{\text{b}},{\text{m}}}} \left( t \right)} \\ \end{array} } \right\} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \end{gathered}$$

(2a)

$$\begin{gathered} m_{\text b}^{r} d\ddot{w}_{\text {b,n}} \left( t \right) + k_{\text b}^{r} \left[ {dw_{\text {b,n}} \left( t \right) - dw_{\text {b,n}}^{p} \left( t \right)} \right] + c_{\text b}^{r} \left[ {d\dot{w}_{\text {b,n}} \left( t \right) - d\dot{w}_{\text {b,n}}^{p} \left( t \right)} \right] \hfill \\ + c_{\text b}^{s,r} \left\{2\left[ {d\dot{w}_{\text {b,n}} \left( t \right) - d\dot{w}_{\text {b,n}}^{p} \left( t \right)} \right] - \left[ {d\dot{w}_{\text {b,n - 1}} \left( t \right) - d\dot{w}_{\text {b,n - 1}}^{p} \left( t \right)} \right] - \left[ {d\dot{w}_{\text {b,n + 1}} \left( t \right) - d\dot{w}_{\text {b,n + 1}}^{p} \left( t \right)} \right]\right\} \hfill \\ + k_{\text b}^{s,r} \left\{2\left[ {dw_{\text {b,n}} \left( t \right) - dw_{\text {b,n}}^{p} \left( t \right)} \right] - \left[ {dw_{\text {b,n - 1}} \left( t \right) - dw_{\text {b,n - 1}}^{p} \left( t \right)} \right] - \left[ {dw_{\text {b,n + 1}} \left( t \right) - dw_{\text {b,n + 1}}^{p} \left( t \right)} \right]\right\} = dF_{\text {b,n}}^{r} \left( t \right) \hfill \\ \end{gathered}$$

(2b)

where m, c and k denote the vibrating mass, damping coefficient and stiffness, respectively; k^s and c^s are the shear stiffness and shear damping coefficient, respectively; superscript ‘r’ represents the stiffer zone; subscripts m, m + 1 and m-1 denote the mth, next and previous to the mth sleeper in the softer zone, respectively; subscript n denotes the nth sleeper in the stiffer zone; dF is the force increment; $\dot{w}$ and $\ddot{w}$ represent velocity and acceleration, respectively. The force increments dF_g,m and dF_s,m are taken as 0 while increments dF_b,m and $d{F}_{\text{b,n}}^{r}$ are equal to the rail-seat load increment calculated using a procedure described in Sect. 2.3.

Equations (2a) and (2b) represent the response of the track layers in the softer and stiffer side of the transition zone, respectively. These equations are solved using Newmark’s beta numerical integration method at each time instant, t, to calculate the overall response of the track substructure layers below each sleeper location.

2.1.2 Vibrating mass, springs and dashpots

To solve Eqs. (2a) and (2b), the parameters such as vibrating mass, spring stiffness and damping coefficient for the ballast, subballast and subgrade layers are required. The mass and spring stiffness for the track layers can be determined analytically based on the geometry of their effective acting region, which is assumed to coincide with a pyramidal-shaped load distribution zone within these layers [1, 92, 93].

It is plausible that the load-distribution pyramids below adjoining sleepers may overlap along both transverse (along sleeper length) and longitudinal (along rail length) directions in case of thick substructure layers, small sleeper length and spacing, and large load distribution angles. Figures 3a and 3b show the effective acting region of the track layers below individual sleeper location in the softer and stiffer side of the transition zone, respectively. The effective region is a truncated pyramid whose geometry varies depending on the extent of overlapping within the track layers.

Fig. 3

Effective acting region of track layers considered in the analysis at a softer side; b stiffer side

The vibrating mass for each substructure layer is computed by multiplying the volume of the effective portion with the density. The spring stiffness is calculated by considering the analogy between the effective acting region and an axially loaded bar having a non-uniform cross-section. The expressions to compute the mass, stiffness and damping coefficients are provided in Appendix A.

It can be noted that the present technique involves the use of classical springs, dashpots, and slider elements to simulate the behaviour of track substructure layers. These elements can also be replaced by advanced elements such as fractional dashpots (or spring-pots) to simulate viscoelastic behaviour and plastic slider elements employing fractional constitutive models to capture the material plasticity [70, 71, 74,75,76] (see Appendix B for more details). The advantage of employing fractional elements is that they can capture the complex constitutive behaviour of geomaterials, which typically involves features such as memory-intensive or path-dependent response and state-dependent non-associated stress-dilatancy relationship [73, 77,78,79].

2.2 Plastic slider elements

The slider elements simulate the plastic component of the response of the substructure layers. A yield criterion, f, characterises these elements and the loading–unloading conditions govern their activation or deactivation. These elements remain deactivated until the stress state in a track layer satisfies the yield criterion, f. From this state, the element may either start moving or remain deactivated, depending on whether the yield criterion remains satisfied. The slider element undergoes continuous movement/slip if the yield criterion remains satisfied, which can be expressed by Prager’s consistency condition, i.e. $\dot{f}=0$. If the consistency condition is satisfied, the plastic strain increments, ${d{\bf \varepsilon}}_{\text{ij}}^{p}$, are derived from the flow rule as follows:

$$d{\bf \varepsilon}_{\text {ij}}^{p} = \lambda \frac{\partial g}{{\partial {\bf \sigma}_{\text {ij}} }}$$

(3)

where σ_ij is the stress tensor; λ is the plastic multiplier; g is the potential function. λ and f must satisfy the following loading–unloading (Kuhn-Tucker) conditions [64] to differentiate between the activation and deactivation of the slider element:

$$\lambda \ge 0;\;f \le 0;\;\lambda f = 0$$

(4)

This equation suggests that for the activation of the slider element, λ must be greater than zero, the stresses must be admissible, and the yield criterion must remain satisfied. The element deactivates when the stresses are admissible, but the yield criterion is not fulfilled. The deactivation may also occur if the yield criterion is satisfied but λ is zero.

The formulation in Eqs. (2a) and (2b) requires the magnitude of vertical plastic displacement; therefore, the plastic strain increment, ${d\varepsilon }_{\text {z}}^{p}$, calculated using Eq. (3), is translated into the plastic displacement by multiplying it with the thickness of the substructure layer.

$$dw_{{\bigsqcup}}^{p} \left( t \right) = h_{{\bigsqcup}} d\varepsilon_{\text z,\bigsqcup}^{p} \left( t \right)$$

(5)

where symbol ${\bigsqcup }$ denotes any of the substructure layers and it can be b, s or g; h is the thickness of substructure layer.

Subsequently, the rate of plastic displacement increment, $d{\dot{w}}_{\bigsqcup }^{p}\left(t\right)$, is evaluated by differentiating $d{{w}}_{\bigsqcup }^{p}$ with respect to time. $d{{w}}_{\bigsqcup }^{p}$ and $d{\dot{{w}}}_{\bigsqcup }^{p}$ are used as inputs in Eqs. (2a) and (2b), which are solved to calculate the total response of the track layers in the critical zone.

The evaluation of plastic displacement or slip in the slider elements requires appropriate constitutive relationships for the geomaterials. The constitutive relationships chosen for the granular layers (i.e. subballast and ballast) and subgrade are described below. These models are simple and typically require 6–7 parameters to reproduce the behaviour of geomaterials with reasonable accuracy [29, 38, 40]. In addition, most of the parameters have a clear physical meaning and can be derived easily.

The yield function, flow and hardening rules for ballast and subballast layers follow the Nor-sand model developed by Jefferies and co-workers [28, 30]. Table 1 provides the main aspects of the model formulation. This model can simulate the behaviour of geomaterials under general (3D) loading for a broad range of density and loading conditions. The model has been used previously to simulate the behaviour of geomaterials such as clean or silty sands, mine tailings, ballast and subballast [20, 27, 29, 56].

Table 1 Model summary for slider elements for ballast and subballast [26, 29]

The constitutive parameters for the slider element for the granular layers are the altitude of the critical state line (CSL) at p = 1 kPa (Γ), the slope of CSL (λ_c), critical stress ratio for triaxial compression (M_tc), volumetric coupling parameter (N_v), state-dilatancy parameter (χ_tc), cyclic hardening parameter (a_c), and plastic hardening parameter (H). The parameters Γ and λ_c can be derived using the data from multiple undrained and drained triaxial tests on samples at different densities [30]. M_tc and N_v are determined by drawing a best-fit line through the triaxial test data plotted in the stress-dilatancy form [peak stress ratio (η_max) against maximum dilatancy (D_p,max)]. The slope and intercept of this line yields (1 – N_v) and M_tc, respectively. χ_tc is derived by drawing a best-fit line (passing along the origin) through the triaxial test data plotted in the state-dilatancy form [D_p,max versus state parameter (ψ) at maximum dilatancy] [29]. The value of H can be determined using iterative forward modelling of drained triaxial test data [27]. The parameter a_c is calibrated against multiple cyclic triaxial test data. The typical values of Γ, λ_c, M_tc, N_v, χ_tc and H for different geomaterials can be found in [29].

For the subgrade, the yield function, flow and hardening rules are based on the model developed by Ma et al. [40] to reproduce the response of geomaterials subjected to three-dimensional repeated loading conditions. The progressive increment of plastic strain with the number of load repetitions is accounted for by employing the concept of subloading surfaces [22] (see Appendix C). Table 2 provides a summary of the main aspects of the model formulation.

Table 2 Model summary for slider elements for subgrade [38,39,40]

The constitutive parameters for the slider element for the subgrade are λ_c, the slope of swelling line (κ), critical state friction angle under triaxial compression (φ_c), characteristic stress parameter (ξ), spacing parameter (A) and cyclic hardening parameter (a_c). The parameters λ_c and κ can be determined using the isotropic compression and swelling test data. φ_c is derived from multiple triaxial compression test data. ξ and A are computed using the expressions provided in Table 2, which involve the use of critical state friction angle under triaxial extension (φ_e) that can be derived from multiple triaxial extension test data. a_c is calibrated against multiple cyclic triaxial test data. The typical values of λ_c, κ, φ_c, ξ, and A for different soil types can be found in [38,39,40].

2.3 Determination of train-induced load at each sleeper location

As shown in Fig. 2, the train-induced vertical rail-seat load excites the geotechnical rheological model at each sleeper position. This load is transmitted from the superstructure (comprising rail, rail pads, fasteners and sleepers) to the substructure layers through the sleeper-ballast contact. Its magnitude can either be assumed or determined theoretically using the beam on an elastic foundation (BoEF) approach [3, 14, 88]. In this study, the BoEF technique is employed to compute the rail-seat load-time history at each sleeper position considered. As per the BoEF method, the rail-seat load, Q_r can be computed using the following expression [14]:

$$Q_{\text {r,m}} \left( t \right) = kS\mathop \sum \limits_{i = 1}^{{n_{\text t} }} \delta \left( {x_{\text m}^{i} ,t} \right)$$

(6)

where Q_r,m (t) is the vertical rail-seat load (N) acting on the mth sleeper at time instant, t; k is the track modulus (Pa); S is the sleeper spacing (m); δ is the vertical track deflection (m); $x_{\text {m}}^{i}$ is the distance between mth sleeper and the ith wheel; n_t is the total number of wheels considered in the analysis. A detailed procedure for evaluating the rail-seat load is provided in Appendix D.

To account for the dynamic effects due to moving loads, a dynamic amplification factor (DAF) has been used in this study, which is a multiplier to the wheel load. This DAF is calculated as [47]:

$${\text{DAF}} = 1 + i_{1} \left( {\frac{V}{{D_{{\text{w}}} }}} \right)^{{i_{2} }}$$

(7)

where V and D_w are the train speed (km/h) and wheel diameter (m), respectively; i₁ and i₂ are empirical parameters whose values depend on the wheel load and subgrade type, and typically lie in the range of 0.0052–0.0065 and 0.75–1.02, respectively. This equation was developed using the data collected from field investigations and accounts for the stress amplification due to various effects such as dynamic vehicle–track interaction and sleeper passing frequency [15, 47].

2.3.1 Determination of stress state for slider elements

The constitutive models for the slider elements require continuum stress variables (for instance, q and p) as the input. Therefore, the vertical rail-seat load is translated to these stress variables using the modified Boussinesq solutions [53, 87] (see Appendix E). Since three substructure layers are considered in the softer side, the theory of equivalent thickness is employed to convert multiple layers into an equivalent thickness of a single-layered material [50, 52]. This method of determining the stress variables for slider elements from the boundary forces is similar to other existing approaches [e.g. 13]. It must be noted that all the stresses are taken as effective.

2.4 Application of the methodology

The proposed approach can be employed in the following sequence: first, the varied track structure composition along the longitudinal direction is identified. Then, the effective portion of the substructure layers below individual sleeper location is determined, and the model parameters such as vibrating mass, spring stiffness and damping coefficients are computed (Sect. 2.1.2). Subsequently, the magnitude of load transferred from the superstructure to the substructure layers is determined for each zone (stiffer and softer), and the stress state for the plastic slider elements is derived using the modified Boussinesq solutions (Sects. 2.3 and 2.3.1). For each time step, the loading–unloading conditions for the slider elements are inspected. If the slider is active, the magnitude of plastic displacement in the slider element is calculated (Sect. 2.2). Finally, Eqs. (2a) and (2b) are solved to determine the total response of the track transition zone.

3 Model validation

3.1 Comparison with 3D finite element model results

3.1.1 Model development

Figure 4 shows the 3D FE model of the bridge-open track transition zone developed using ABAQUS [12]. The transition zone geometry is based on a section of railway track along the Amtrak’s northeast corridor in the USA, which comprises three regions: open track, near bridge (approach zone) and the bridge [7]. The track consists of rails supported by sleepers placed at a spacing of 0.61 m. A 0.305 m thick ballast layer is provided below the sleepers along the entire length of the track. A multilayered system underlies the ballast layer at the open track and the near bridge zones (see Fig. 4). The ballast layer at the bridge is supported by the concrete deck slab, which is simulated by restricting the vertical displacement of the bottom nodes of the ballast layer.

Fig. 4

3D finite element model of the bridge-open track transition zone

The total thickness of the substructure at the open track and near bridge region is 20 m. The model dimension along the track transverse direction (i.e. y-direction) is taken as 20 m to ensure sufficient distance between the analysis segment and model boundaries. The vertical boundaries at the sides are connected to dashpots in horizontal and vertical directions to prevent the spurious reflections of stress waves. The nodes at the bottom boundary are assumed to be fixed, i.e. their movement is restricted in both vertical and horizontal directions. Only one half of the track is modelled owing to symmetry along the track centreline.

The superstructure and the substructure layers are discretised using eight-noded 3D brick elements of type C3D8R, and the entire FE model comprises 301,176 elements. A fine mesh is used near the track region, and its coarseness is increased progressively with an increase in distance from the track [63]. Other details are provided in Appendix F.

3.1.2 Comparison of track response

Table 3 lists the material properties used in the model predictions for both open track and near bridge locations (adopted from [7]). The rheological model considers the soil layers beneath the subballast layer as a single equivalent layer. Figure 5a shows the variation of vertical displacement at the ballast top along the length of the track predicted using the proposed method and the FE analysis.

Table 3 Model parameters for evaluation of track response

Fig. 5

Comparison of results predicted using the proposed method and FEM: a variation of vertical displacement at ballast top with distance along the track; b variation of vertical deformation with time for ballast, subballast and subgrade

Figure 5b shows the variation of transient vertical deformation in the track substructure layers with time during the passage of two bogies from adjacent wagons. A good agreement between the results predicted using the present method and that obtained from FEM can be observed.

The main advantage of the proposed technique is its significantly higher computational efficiency over the FE analysis. For the present case, the proposed approach took 1080 s, and FEM took about 355,615 s on a high-performance computing facility using thirty 2.5 GHz processors running in parallel.

3.2 Comparison of results with data from field tests

The accuracy of the proposed methodology is investigated by comparing the predicted results with the field data reported by Paixão et al. [51] for an underpass-embankment transition zone in Portugal. The transition zone comprised of two wedge-shaped engineered fills between the underpass and the embankment that were constructed using unbound granular material (UGM) and cement bound mixtures (CBM). Table 3 lists the parameters employed in the analysis. Figure 6 presents a comparison of the vertical track displacement predicted using the present method with the field data recorded during one passage of the Portuguese Alfa pendular passenger tilting train at sections S3 and S4 (located at 8.4 m and 1.8 m from the underpass, respectively). It can be observed that the predicted results are in an acceptable agreement with the field measurements. The predicted results somewhat underestimate the vertical displacement at both the sections. This underestimation might be attributed to the fact that the present method ignores the variation of the damping coefficient and elastic modulus with strain [2]. The accuracy of the present approach can be improved further by considering the strain dependency of the damping coefficient and elastic modulus. Nevertheless, the predicted average value of the peaks in the displacement–time history varies by 18 and 12% from the corresponding field values in sections S3 and S4, respectively.

Fig. 6

Comparison of predicted transient vertical displacement at sections S3 and S4 with the field data reported by Paixão et al. [51]

Mishra et al. [43] recorded the vertical deformation in the track substructure layers near three bridge approaches along Amtrak’s north-east corridor in the USA. Figure 7 presents a comparison of the accumulation of inelastic deformation in the ballast (layer 1), subballast (layer 2) and subgrade layers (layers 3–5 approximated to a single equivalent layer) predicted using the present method with the field data. Tables 3, 4 and 5 list the parameters used in the model predictions. It can be observed that the predicted results are in an acceptable agreement with the field data. The model can accurately predict the accumulation of settlement in the substructure layers under train-induced repeated loading at a diminishing rate. The discrepancy in the trends for the ballast and subballast layers may be attributed to factors such as the use of an associated flow rule for simulating the behaviour of granular materials, particle degradation effects [81] or principal stress rotation effects [21]. This discrepancy can be reduced by employing advanced approaches, such as fractional plasticity-based models [70, 71, 74, 75], that can simulate the response of granular materials (particularly the volumetric strains) more accurately. Indeed, particle degradation (especially ballast breakage) adversely affects the track performance by intensifying the accumulation of irrecoverable deformations [47]. This feature can be incorporated in the constitutive models for slider elements by modifying the stress–dilatancy relationship or the plastic flow rule to include the energy dissipation from particle breakage [25, 79, 81]. Nevertheless, this aspect shall be dealt with in future investigations to improve the accuracy of the predicted results.

Fig. 7

Comparison of predicted settlement in substructure layers with the field data reported by Mishra et al. [43]

Table 4 Constitutive parameters for granular layers

Table 5 Constitutive parameters for subgrade

Thus, it is apparent that the proposed methodology can accurately simulate the behaviour of the railway tracks in the transition zones. The technique can reproduce the observed transient behaviour in addition to the accumulation of settlement in the substructure layers at a diminishing rate with reasonable accuracy.

4 Results and discussion

4.1 Performance under increased axle load

The validated methodology is used to investigate the performance of an open track–bridge transition (shown in Fig. 2) subjected to an increase in axle load. Tables 3, 4 and 5 list the parameters employed in the parametric analysis. The values of the constitutive parameters were derived from the cyclic triaxial tests on ballast, subballast and subgrade soil conducted by Suiker et al. [69] and Wichtmann [89]. The ballast considered in this analysis is crushed basalt, which is classified as uniformly graded gravel. The subballast is well-graded sand with gravel while, the subgrade soil is quartz sand. The axle load is varied between 20 and 30 t to investigate its influence on the behaviour of the transition zone.

Figure 8a shows the variation of cumulative settlement along the track length for three different axle loads. It can be observed that the differential settlement between the softer and stiffer side of the transition increases with an increase in the axle load. It increases by 25 and 26% as the axle load increases from 20 to 25 t and from 25 to 30 t, respectively, after a cumulative tonnage of 25 million gross tonnes (MGT). The differential settlement also increases with an increase in tonnage. For 25 t axle load, the differential settlement increases from 16.2 mm at 0.1 MGT to 27 mm at 25 MGT.

Fig. 8

Variation of settlement at different axle loads with a distance; b tonnage at different locations

Figure 8b shows the variation of settlement of the track substructure with tonnage for the three axle loads at three different locations. The settlement at 7 m from the bridge increases by 25 and 58% with an increase in axle load from 20 to 25 t and 30 t, respectively. Similarly, the settlement at 0.3 m from the bridge and 4 m on the bridge increases by 51 and 47%, respectively, with an increase in axle load from 20 to 30 t.

It must be noted that the contribution of ballast breakage to the track settlement is ignored in this study. The ballast breakage typically increases with an increase in axle load, which is expected to enhance the track settlement further [72]. Nevertheless, the influence of particle breakage on the performance of transitions at increased axle loads shall be explored in future investigations by modifying the constitutive relationships for the slider elements.

Thus, an increase in axle load increases the differential settlement in the transition zone, exacerbating the track geometry degradation problem. Therefore, the application of remedial measures becomes more necessary with an increase in the axle loads.

4.2 Performance under increased granular layer thickness

In the previous section, the axle load increased the differential settlement in the transition zone. A plausible technique for reducing this differential settlement is to increase the thickness of the granular layers (ballast or subballast). This section investigates the efficacy of increased granular layer thickness in decreasing the differential settlement. Two cases are studied: in the first case, the ballast thickness, h_b, is increased from 0.3 to 0.9 m, while the subballast thickness, h_s, is kept constant at 0.15 m. In the second case, h_s is increased from 0.15 to 0.6 m, while h_b is assigned a constant value of 0.3 m. An axle load of 25 t is considered in both cases.

4.2.1 Influence of ballast thickness

Figure 9 shows the influence of h_b on the response of the transition zone. It can be observed that the differential settlement decreases with an increase in h_b. The possible reason for such behaviour is that the subgrade soil is the weakest material involved in this critical zone, and its contribution towards the total settlement is maximum (about 90% for h_b = 0.3 m). On increasing h_b, the stress transferred to the subgrade soil decreases. This happens due to a higher stress spreading ability of the thicker ballast layer. The validity of this conjecture is investigated by comparing the stress distribution in the subballast and subgrade layers with depth for different h_b (shown in Fig. 10). It is observed that the stress decreases with an increase in h_b. At the subgrade top, the vertical stress decreases by 23.7, 20.4, 18.5 and 16% on increasing the ballast thickness from 0.3 to 0.45, 0.6, 0.75 and 0.9 m, respectively. This stress reduction leads to a decrease in the settlement on the softer side (a reduction of 48% with an increase in h_b from 0.3 to 0.9 m). Consequently, the differential settlement between the stiffer and softer side of the transition decreases with an increase in h_b.

Fig. 9

Variation of settlement with distance at different ballast layer thickness

Fig. 10

Distribution of vertical stress with depth at 3.5 m from the bridge for different ballast layer thickness

4.2.2 Influence of subballast thickness

Figure 11 shows the influence of h_s on the behaviour of the bridge-open track transition zone. It can be observed that the differential settlement decreases with an increase in h_s. The reason being the reduction in the subgrade stress on increasing h_s. As shown in Fig. 12, the stress at the subgrade top decreases by 23.1, 20.2 and 17.5% on increasing h_s from 0.15 to 0.3, 0.45 and 0.6 m, respectively. Therefore, the settlement on the softer side and, consequently, the differential settlement decreases with an increase in subballast thickness.

Fig. 11

Variation of settlement with distance at different subballast layer thickness

Fig. 12

Distribution of vertical stress with depth at 3.5 m from the bridge for different subballast layer thickness

It is apparent that increasing the thickness of the granular layers can improve the performance of the railway track transition zone. Because the differential settlement in this case was primarily caused by the subgrade soil on the softer side, this technique worked rather effectively. Thus, it is crucial to correctly identify the root cause of the track geometry degradation problem in the transition zone before selecting an appropriate remedial measure.

5 Practical relevance and potential applications

The proposed methodology provides a convenient means to assess the performance of different countermeasures in mitigating the differential settlement at a critical zone. To demonstrate this capability, the performance of two different mitigation strategies is compared. As discussed in Sect. 4, large plastic deformation in the subgrade is the primary cause of differential settlement in this study. Therefore, two different remedial strategies are employed: (a) decreasing the stress transferred to the subgrade; (b) strengthening the subgrade. The magnitude of subgrade stress can be reduced by either increasing the thickness (discussed in Sects. 4.2.1 and 4.2.2) or stiffness of the granular layers (e.g. by using cellular geoinclusions) [37]. The subgrade soil can be strengthened by using ground improvement techniques.

Figure 13 shows the influence of increasing the ballast stiffness near the bridge approach (improved zone) on the differential settlement. The elastic modulus of the ballast layer in the improved zone is increased by 1.5–3 times the nominal value to represent the improvement. It can be observed that the performance of the transition zones can be improved by increasing the stiffness of the ballast layer. The differential settlement between the track on the stiffer and the softer side is reduced by 13% on increasing the ballast modulus from 200 to 600 MPa.

Fig. 13

Variation of settlement with distance when ballast modulus in the improved zone is increased from 200 to 600 MPa

Figure 14 shows the influence of increasing the subballast stiffness near the bridge approach on the differential settlement. The elastic modulus of the subballast layer in the improved zone is increased by 1.5–3 times the nominal value to represent the stiffness increase provided by the remedial measure. It can be observed that the performance of the transition zone can be improved by increasing the subballast layer stiffness. The differential settlement between the track on the stiffer and the softer side, accumulated after a tonnage of 25 MGT, decreases by 5% on increasing the subballast modulus from 115 to 345 MPa. Although the differential settlement decreases with an increase in the stiffness of the granular layers, the reduction is very small. This observation can be attributed to a combination of two counteracting effects. First, an increase in granular layer stiffness increases the track modulus (hence the rail seat load), which amplifies the stresses in substructure layers [37]. Second, a stiffer granular layer distributes the load to a wider area, thereby reducing the magnitude of stresses. Due to these two counteracting effects, the overall reduction in the stresses transmitted to the subgrade soil is small. Consequently, the plastic deformation in the subgrade reduces by a small amount and a minor reduction in the differential settlement is observed.

Fig. 14

Variation of settlement with distance when subballast modulus in the improved zone is increased from 115 to 345 MPa

Figure 15 shows the influence of improving the subgrade strength near the bridge approach on the track response. The friction angle of the subgrade layer in the improved zone is increased to represent the strength increment provided by the countermeasures. It can be observed that the performance of the transition zone is significantly improved by increasing the subgrade strength. The differential settlement between the track on the stiffer and the softer side decreases by 39% on increasing the subgrade friction angle from 31° to 40°. Thus, it is evident that the remedies intended to strengthen the subgrade soil are more effective in mitigating the track geometry degradation in this study than those intended to increase the stiffness of the granular layers.

Fig. 15

Variation of settlement with distance when subgrade friction angle in the improved zone is increased from 31° to 40°

6 Concluding remarks

This paper introduces a novel methodology for predicting the transient and long-term behaviour of the ballasted railway tracks in the critical zones. The main features of the proposed technique include:

• Simplified yet effective approach to simulate the behaviour of the tracks with varied support conditions along the longitudinal direction, including the enhanced capability to predict the differential settlements, which are major concerns for transition zones.

• Rational method that considers material plasticity through the use of slider elements, which are described by appropriate constitutive relationships as opposed to existing methods employing empirical settlement models to capture material plasticity.

• Quick and straightforward technique that does not require any commercial FE-based software in contrast to existing approaches that rely on these software.

• Convenient method to assess the performance of different remedial measures in mitigating the differential settlement at the critical zone.

A good agreement of the predicted results with those recorded in the field and computed using FE simulations prove that the novel approach can accurately predict the response of the critical track zones. The validated approach is then applied to an open track-bridge transition, and the main findings are as follows:

• An increase in axle load exacerbates the track geometry degradation problem. Therefore, it is essential to provide remedial strategies in the critical zones on which heavier trains are expected in future.

• The use of thicker granular layers reduced the differential settlement at the open track-bridge transition considered in this study. This technique worked well because the subgrade layer was the major contributor to the differential settlement, and a thicker granular layer reduced the subgrade settlement.

• The techniques intended to increase the strength of the subgrade may be more effective than the strategies aimed at improving the stiffness of granular layers for transition zones with weak/soft subgrade. However, this strategy (subgrade strength increment) may be inappropriate for the transitions where the granular layers are primary contributors to the differential settlement [see for e.g. 36]. Thus, it is crucial to correctly identify the primary cause of the differential settlement problem before selecting an appropriate countermeasure.

The outcomes of this study have huge potential to influence the real-world design implications of track critical zones. The approach is original, simple yet elegant, and it can enhance, if not fully replace, present complex track modelling procedures for anticipating the behaviour of critical zones and adopting appropriate mitigation strategies.

Nevertheless, there are a few limitations associated with the proposed technique:

• No-slip condition is assumed for the interfaces formed between different substructure layers. However, there could be relative horizontal movement at these interfaces under train-induced loading. This interface shear behaviour can be simulated by employing interaction springs and dashpots between the substructure layers in the horizontal direction [33, 42].

• The effects of vehicle–track interaction are incorporated by using a simplified approach that employs a dynamic amplification factor.

• The strain dependency of elastic modulus and damping coefficients has been neglected.

• The effects of particle degradation, principal stress rotation and moisture fluctuations on the behaviour of track materials have been ignored.

• The change in material properties due to cumulative plastic deformation under repeated loading is neglected.

The future investigations shall address these shortcomings to improve the accuracy of the proposed methodology.

Appendices

Appendix A. Determination of mass, stiffness and damping coefficient

The vibrating mass and stiffness of the track layers for the non-overlapped case can be determined using the following equations:

$$m_{{{\text b}}} = \rho_{{{\text b}}} h_{{\text{b}}} \left[ {b_{{{\text{sl}}}} l_{{\text{e}}} + \left( {b_{{{\text{sl}}}} + l_{{\text{e}}} } \right)h_{{{\text b}}} \tan \alpha + \frac{4}{3}h_{{{\text b}}}^{2} \tan^{2} \alpha } \right]$$

(8)

$$m_{{\text{s}}} = \rho_{{{\text s}}} h_{{{\text s}}} \left[ {b_{{{\text{sl}}}} l_{{\text{e}}} + \left( {b_{{{\text{sl}}}} + l_{{{e}}} } \right)\left( {2h_{{\text{b}}} \tan \alpha + h_{{\text{s}}} \tan \beta } \right) + 4h_{{\text{b}}} \tan \alpha \left( {h_{{\text{b}}} \tan \alpha + h_{{\text{s}}} \tan \beta } \right) + \frac{4}{3}h_{{\text{s}}}^{2} \tan^{2} \beta } \right]$$

(9)

$$m_{{\text{g}}} = \rho_{{\text{g}}} h_{{\text{g}}} \left[ {b_{{{\text{sl}}}} l_{{\text{e}}} + \left( {b_{{{\text{sl}}}} + l_{{\text{e}}} } \right)\left( {2h_{{\text{b}}} \tan \alpha + 2h_{{\text{s}}} \tan \beta + h_{{\text{g}}} \tan \gamma } \right) + 4\left( {h_{{\text{b}}} \tan \alpha + h_{{\text{s}}} \tan \beta } \right)\left( {h_{{\text{b}}} \tan \alpha + h_{{\text{s}}} \tan \beta + h_{{\text{g}}} \tan \gamma } \right) + \frac{4}{3}h_{{\text{g}}}^{2} \tan^{2} \gamma } \right]$$

(10)

$$m_{{\text{b}}}^{r} = \rho_{{\text{b}}}^{r} h_{{\text{b}}}^{r} \left[ {b_{{{\text{sl}}}} l_{{\text{e}}} + \left( {b_{{{\text{sl}}}} + l_{{\text{e}}} } \right)h_{{\text{b}}}^{r} \tan \alpha^{r} + \frac{4}{3}\left( {h_{{\text{b}}}^{r} } \right)^{2} \tan^{2} \alpha^{r} } \right]$$

(11)

$$k_{{\text{b}}} = E_{{\text{b}}} \frac{{2\left( {l_{{\text{e}}} - b_{{{\text{sl}}}} } \right)\tan \alpha }}{{\ln \left[ {\frac{{l_{{\text{e}}} }}{{b_{{{\text{sl}}}} }}\left( {\frac{{b_{{{\text{sl}}}} + 2h_{{\text{b}}} \tan \alpha }}{{l_{{\text{e}}} + 2h_{{\text{b}}} \tan \alpha }}} \right)} \right]}}$$

(12)

$$k_{{\text{s}}} = E_{{\text{s}}} \frac{{2\left( {l_{{\text{e}}} - b_{{{\text{sl}}}} } \right)\tan \beta }}{{\ln \left[ {\left( {\frac{{l_{{\text{e}}} + 2h_{{\text{b}}} \tan \alpha }}{{b_{{{\text{sl}}}} + 2h_{{\text{b}}} \tan \alpha }}} \right)\left( {\frac{{b_{{{\text{sl}}}} + 2h_{{\text{b}}} \tan \alpha + 2h_{{\text{s}}} \tan \beta }}{{l_{{\text{e}}} + 2h_{{\text{b}}} \tan \alpha + 2h_{{\text{s}}} \tan \beta }}} \right)} \right]}}$$

(13)

$$k_{{\text{g}}} = E_{{\text{g}}} \frac{{2\left( {l_{{\text{e}}} - b_{{{\text{sl}}}} } \right)\tan \gamma }}{{\ln \left[ {\left( {\frac{{l_{{\text{e}}} + 2h_{{\text{b}}} \tan \alpha + 2h_{{\text{s}}} \tan \beta }}{{b_{{{\text{sl}}}} + 2h_{{\text{b}}} \tan \alpha + 2h_{{\text{s}}} \tan \beta }}} \right)\left( {\frac{{b_{{{\text{sl}}}} + 2h_{{\text{b}}} \tan \alpha + 2h_{{\text{s}}} \tan \beta + 2h_{{\text{g}}} \tan \gamma }}{{l_{{\text{e}}} + 2h_{{\text{b}}} \tan \alpha + 2h_{{\text{s}}} \tan \beta + 2h_{{\text{g}}} \tan \gamma }}} \right)} \right]}}$$

(14)

$$k_{{\text{b}}}^{r} = E_{{\text{b}}}^{r} \frac{{2\left( {l_{{\text{e}}} - b_{{{\text{sl}}}} } \right)\tan \alpha^{r} }}{{\ln \left[ {\frac{{l_{{\text{e}}} }}{{b_{{{\text{sl}}}} }}\left( {\frac{{b_{{{\text{sl}}}} + 2h_{{\text{b}}}^{r} \tan \alpha^{r} }}{{l_{{\text{e}}} + 2h_{{\text{b}}}^{r} \tan \alpha^{r} }}} \right)} \right]}}$$

(15)

where superscript ‘r’ represents the stiffer side; ρ, h and E represent the density (kg/m³), thickness (m) and elastic modulus (Pa) of the substructure layers, respectively; b_sl and l_e are the width (m) and effective length (m) of sleeper, respectively; γ, β and α are the load distribution angles (°) of subgrade, subballast and ballast layers, respectively. A similar approach can be followed to derive these parameters for the overlapped case.

The load distribution angles for the track layers in softer and stiffer sides are calculated as follows:

$$\alpha = \tan^{ - 1} \left\{ {\frac{a}{{h_{{\text{b}}} }}\left[ {\sqrt {\frac{{\sigma_{{{\text{slb}}}} }}{{\sigma_{{{\text{bs}}}} }}} - 1} \right]} \right\}$$

(16)

$$\beta = \tan^{ - 1} \left\{ {\frac{{\left( {a + h_{{\text{b}}} \tan \alpha } \right)}}{{h_{{\text{s}}} }}\left[ {\sqrt {\frac{{\sigma_{{{\text{bs}}}} }}{{\sigma_{{{\text{sg}}}} }}} - 1} \right]} \right\}$$

(17)

$$\gamma = \tan^{ - 1} \left\{ {\frac{{\left( {a + h_{{\text{b}}} \tan \alpha + h_{{\text{s}}} \tan \beta } \right)}}{{h_{{\text{g}}} }}\left[ {\sqrt {\frac{{\sigma_{{{\text{sg}}}} }}{{\sigma_{{{\text{gb}}}} }}} - 1} \right]} \right\}$$

(18)

$$\alpha^{r} = \tan^{ - 1} \left\{ {\frac{{a^{r} }}{{h_{{\text{b}}}^{r} }}\left[ {\sqrt {\frac{{\sigma_{{{\text{slb}}}}^{r} }}{{\sigma_{{{\text{bb}}}}^{r} }}} - 1} \right]} \right\}$$

(19)

where superscript r represents the stiffer zone; a is the radius of the sleeper-ballast contact area (m); σ_bs, σ_sg and σ_slb are the vertical stresses (Pa) at the ballast-subballast, subballast-subgrade and sleeper-ballast interfaces, respectively; σ_gb and ${\sigma }_{\mathrm{bb}}^{r}$ are the vertical stresses (Pa) at the bottom of the substructure layers in the softer side and stiffer side of the transition, respectively.

The damping coefficient for the substructure layers per unit area is computed using [48]:

$$c_{{\bigsqcup}} = \sqrt {\frac{{\rho_{{\bigsqcup}} E_{{\bigsqcup}} }}{{\left( {1 - \nu_{{\bigsqcup}} } \right)\left( {1 + \nu_{{\bigsqcup}} } \right)}}}$$

(20)

where symbol ${\bigsqcup }$ denotes any of the substructure layers and can be g, s or b; $\nu$ represents the Poisson’s ratio.

Appendix B. Use of fractional elements in the rheological model

Figure 

Fig. 16

Rheological model of a bridge-embankment transition zone involving fractional elements

16 shows the geotechnical rheological track model in which each substructure layer is represented as an array of discrete masses connected via fractional dashpots (spring-pots) and slider elements. The equations of motion for this model are as follows:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {m_{\text g} } & 0 & 0 \\ 0 & {m_{\text s} } & 0 \\ 0 & 0 & {m_{\text b} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{w}_{\text {g,m}} \left( t \right)} \\ {\ddot{w}_{\text {s,m}} \left( t \right)} \\ {\ddot{w}_{\text {b,m}} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\overline{c}_{\text g} + \overline{c}_{\text s} + 2\overline{c}_{\text g}^{s} } & { - \overline{c}_{\text s} } & 0 \\ { - \overline{c}_{\text s} } & {\overline{c}_{\text s} + \overline{c}_{\text b} + 2\overline{c}_{\text s}^{s} } & { - \overline{c}_{\text b} } \\ 0 & { - \overline{c}_{\text b} } & {\overline{c}_{\text b} + 2\overline{c}_{\text b}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {D^{{\alpha_{\text g} }} w_{\text {g,m}} \left( t \right)} \\ {D^{{\alpha_{\text s} }} w_{\text {s,m}} \left( t \right)} \\ {D^{{\alpha_{\text b} }} w_{\text {b,m}} \left( t \right)} \\ \end{array} } \right\} \hfill \\ - \left[ {\begin{array}{*{20}c} {\overline{c}_{\text g} + 2\overline{c}_{\text g}^{s} } & { - \overline{c}_{\text s} } & 0 \\ {2\overline{c}_{\text s}^{s} } & {\overline{c}_{\text s} + 2\overline{c}_{\text s}^{s} } & { - \overline{c}_{\text b} } \\ {2\overline{c}_{\text b}^{s} } & {2\overline{c}_{\text b}^{s} } & {\overline{c}_{\text b} + 2\overline{c}_{\text b}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {D^{{\alpha_{\text g} }} w_{\text {g,m}}^{p} \left( t \right)} \\ {D^{{\alpha_{\text s} }} w_{\text {s,m}}^{p} \left( t \right)} \\ {D^{{\alpha_{\text b} }} w_{\text {b,m}}^{p} \left( t \right)} \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {\overline{c}_{\text g}^{s} } & 0 & 0 \\ 0 & {\overline{c}_{\text s}^{s} } & 0 \\ 0 & 0 & {\overline{c}_{\text b}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {D^{{\alpha_{\text g} }} w_{\text {g,m - 1}} \left( t \right)} \\ {D^{{\alpha_{\text s} }} w_{\text {s,m - 1}} \left( t \right)} \\ {D^{{\alpha_{\text b} }} w_{\text {b,m - 1}} \left( t \right)} \\ \end{array} } \right\} \hfill \\ - \left[ {\begin{array}{*{20}c} {\overline{c}_{\text g}^{s} } & 0 & 0 \\ 0 & {\overline{c}_{\text s}^{s} } & 0 \\ 0 & 0 & {\overline{c}_{\text b}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {D^{{\alpha_{\text g} }} w_{\text {g,m + 1}} \left( t \right)} \\ {D^{{\alpha_{\text s} }} w_{\text {s,m + 1}} \left( t \right)} \\ {D^{{\alpha_{\text b} }} w_{\text {b,m + 1}} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\overline{c}_{\text g}^{s} } & 0 & 0 \\ {\overline{c}_{\text s}^{s} } & {\overline{c}_{\text s}^{s} } & 0 \\ {\overline{c}_{\text b}^{s} } & {\overline{c}_{\text b}^{s} } & {\overline{c}_{\text b}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {D^{{\alpha_{\text g} }} w_{\text {g,m - 1}}^{p} \left( t \right)} \\ {D^{{\alpha_{\text s} }} w_{\text {s,m - 1}}^{p} \left( t \right)} \\ {D^{{\alpha_{\text b} }} w_{\text {b,m - 1}}^{p} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\overline{c}_{\text g}^{s} } & 0 & 0 \\ {\overline{c}_{\text s}^{s} } & {\overline{c}_{\text s}^{s} } & 0 \\ {\overline{c}_{\text b}^{s} } & {\overline{c}_{\text b}^{s} } & {\overline{c}_{\text b}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {D^{{\alpha_{\text g} }} w_{\text {g,m + 1}}^{p} \left( t \right)} \\ {D^{{\alpha_{\text s} }} w_{\text {s,m + 1}}^{p} \left( t \right)} \\ {D^{{\alpha_{\text b} }} w_{\text {b,m + 1}}^{p} \left( t \right)} \\ \end{array} } \right\} \hfill \\ = \left\{ {\begin{array}{*{20}c} {F_{\text {g,m}} \left( t \right)} \\ {F_{\text {s,m}} \left( t \right)} \\ {F_{\text {b,m}} \left( t \right)} \\ \end{array} } \right\} \hfill \\ \end{gathered}$$

(21a)

$$m_{\text b}^{r} \ddot{w}_{\text {b,n}} \left( t \right) + \overline{c}_{\text b}^{r} \left[ {D^{{\alpha_{\text b}^{r} }} w_{\text {b,n}} \left( t \right) - D^{{\alpha_{\text b}^{r} }} w_{\text {b,n}}^{p} \left( t \right)} \right] + \overline{c}_{\text b}^{s,r} \left\{2\left[ {D^{{\alpha_{\text b}^{r} }} w_{\text {b,n}} \left( t \right) - D^{{\alpha_{\text b}^{r} }} w_{\text {b,n}}^{p} \left( t \right)} \right] - \left[ {D^{{\alpha_{\text b}^{r} }} w_{\text {b,n - 1}} \left( t \right) - D^{{\alpha_{\text b}^{r} }} w_{\text {b,n - 1}}^{p} \left( t \right)} \right] - \left[ {D^{{\alpha_{\text b}^{r} }} w_{\text {b,n + 1}} \left( t \right) - D^{{\alpha_{\text b}^{r} }} w_{\text {b,n + 1}}^{p} \left( t \right)} \right]\right\} = F_{\text {b,n}}^{r} \left( t \right)$$

(21b)

where D^α represents the fractional derivative operator (D^α  = d^α/dt^α); $\overline{c}$ is the equivalent coefficient of the spring-pot; α_b, α_s and α_g are the fractional derivative order of ballast, subballast and subgrade, respectively; superscript r represents the stiffer zone. These equations can be solved using the modified Newmark’s beta numerical integration method [65] at each time instant, to calculate the overall response of the track substructure layers.

Appendix C. Prediction of plastic strain accumulation using the concept of subloading surface

In this study, three subloading surfaces are used: current (f_c), reference (f_r) and transitional (f_t) (see Table 2). The surface f_c passes through the current stress state during both activation and deactivation stages of the slider element [that are governed by Eq. (4) (taking f = f_c)], surface f_r hardens isotropically by virtue of the accumulated plastic strains, and f_t evolves according to the current state of the slider (whether activated or deactivated). It must be noted that both f_r and f_t retain geometrical similarity to the surface f_c during their evolution.

At the commencement of the first activation stage, f_c, f_r and f_t are coincident and the value of parameter R_g, (which controls the magnitude of plastic strain increment) (see Table 2) is 1. During this activation stage, the surfaces f_c and f_r expand simultaneously, whereas f_t remains fixed at its initial position. The value of R_g during this stage remains unity, and the magnitude of plastic strain increment is computed using Eq. (3). On deactivation of the slider, the surface f_t hardens and becomes coincident with f_c, and R_g becomes zero. During the deactivated stage, both f_c and f_t soften simultaneously, whereas f_r remains in the position acquired at the end of the active stage. During this stage, R_g = 0 and no plastic strains are generated.

As the slider is reactivated, both f_c and f_r harden simultaneously, while the surface f_t retains the position acquired at the end of the deactivated stage. Since the magnitude of R_g remains below unity during reactivated stage (as f_c and f_r are not coincident), the magnitude of plastic strain accumulated during this stage is smaller than the first activated stage.

This procedure is repeated for the remaining load cycles or activation-deactivation stages of the slider element to compute the progressive accumulation of plastic strain (at a diminishing rate) with an increase in the number of load repetitions.

Appendix D. Determination of rail-seat load

As per the BoEF method, the rail-seat load is simply the product of track modulus, sleeper spacing and track deflection (i.e. k × S × δ). The track modulus may either be evaluated from the field measurements on a railroad track [59] or can be estimated theoretically as [14]:

$$\frac{1}{k} = S\left( {\frac{1}{{k_{{\text{p}}} }} + \frac{1}{{k_{{\text{b}}} }} + \frac{1}{{k_{{\text{s}}} }} + \frac{1}{{k_{{\text{g}}} }}} \right)$$

(22)

where k_p, k_b, k_s and k_g are the stiffness of the rail-pad, ballast, subballast and subgrade layers, respectively. For the stiffer zone of the track, Eq. (22) reduces to:

$$\frac{1}{{k^{r} }} = S\left( {\frac{1}{{k_{{\text{p}}}^{r} }} + \frac{1}{{k_{{\text{b}}}^{r} }}} \right)$$

(23)

where the superscript r represents the stiffer zone.

The vertical track deflection is obtained from [15]:

$$\delta \left( x \right) = \frac{{Q_{{\text{w}}} }}{2kL}e^{{ - \frac{x}{L}}} \left[ {\cos \left( \frac{x}{L} \right) + \sin \left( \frac{x}{L} \right)} \right]$$

(24)

where Q_w is the static wheel load (N); x is the distance along the rail length (m); L is the characteristic length (m), which is a function of k, Young’s modulus, E_r, and moment of inertia, I_r, of the rail:

$$L = \left( {\frac{{4E_{{\text{r}}} I_{{\text{r}}} }}{k}} \right)^{\frac{1}{4}}$$

(25)

According to Eq. (24), the wheel load causes a downward track deflection up to a distance of 3πL/4 on both sides from the application point. Therefore, the vertical rail-seat load at each time instant, t, due to one wheel can be computed for every sleeper located inside this zone. Since the train comprises multiple wheels, the influence of other wheels is incorporated by using the superposition principle [see Eq. (6)].

Figure 

Fig. 17

a Train configuration; track response at time instant b t₁; c t₂; d t₃; variation of rail-seat load with time at e mth sleeper; f nth sleeper during one complete train passage

17 demonstrates the evaluation of rail-seat load and its variation with time at mth and nth sleeper locations during the passage of Acela Express passenger train. Figure 17a shows the train configuration. The train is assumed to be travelling from the softer to the stiffer side of the transition. Figure 17b shows the vertical track deflection at time instant t₁ calculated using Eq. (24) for wheels Q₁ and Q₂. It is apparent that only the leading wheel Q₁ contributes to the track deflection at the mth sleeper. The deflection at the nth sleeper, which lies in the stiffer zone, is zero since it is far from the influence of wheels Q₁ and Q₂ at time instant t₁.

At time instant t₂, the total vertical track deflection at the mth sleeper is the sum of contributions from both Q₁ and Q₂ (see Fig. 17c). In contrast, the deflection at the nth sleeper is still zero since it is far away from the influence of wheels Q₁ and Q₂. Figure 17d shows the vertical track deflection at time instant t₃ for wheels Q₁, Q₂, Q₃ and Q₄. It can be seen that the wheels Q₃ and Q₁ contribute to the track deflection at the mth and nth sleepers, respectively. Since the stiffness of the stiffer zone is much higher, it follows that the magnitude of track deflection is lower at the nth sleeper than the mth sleeper. Using a similar procedure, the vertical track deflection at other sleeper locations is calculated. Finally, the variation of rail-seat load with time is computed using Eq. (6) for all the sleeper positions considered in the analysis.

Figures 17e and 17f show the variation of vertical rail-seat load with time for mth and nth sleepers, respectively, computed for one passage of the train at a speed of 150 km/h. It can be seen that the magnitude of rail-seat load is much higher at the stiffer side of the track (see Fig. 17f) as compared to the softer side (see Fig. 17e). This increment in rail-seat load is plausible since the track modulus of stiffer side is much higher than the softer side.

Appendix E. Stress distribution

Figure 

Fig. 18

Wheel load transfer from the superstructure to the substructure layers

18 shows the transmission of the train-induced vertical load from the superstructure to the substructure layers. At a particular time instant, the load from an individual wheel is distributed to multiple sleepers through the rail seats, with the maximum load on the sleeper below the wheel. The load on each rail seat, termed as the rail-seat load, is applied to the ballast surface over a circular area (termed sleeper-ballast contact area) whose size depends on the width, b_sl, and effective length, l_e, of the sleeper. Subsequently, the stress state for the slider elements for the substructure layers is evaluated by considering the sleeper-ballast contact pressure to be uniformly distributed over this area [60].

First, the multiple substructure layers are translated to an equivalent single layer. The equivalent thickness of granular layers are determined as [23]:

$$h_{{\text{b}}}^{e} = \left\{ {\begin{array}{*{20}c} {h_{{\text{b}}} \left[ {\frac{{\left( {1 - \nu_{{\text{g}}}^{2} } \right)E_{{\text{b}}} }}{{\left( {1 - \nu_{{\text{b}}}^{2} } \right)E_{{\text{g}}} }}} \right]^{\frac{1}{3}} , E_{{\text{b}}} > E_{{\text{g}}} } \\ {h_{{\text{b}}} \left\{0.75 + 0.25\left[ {\frac{{\left( {1 - \nu_{{\text{g}}}^{2} } \right)E_{{\text{b}}} }}{{\left( {1 - \nu_{{\text{b}}}^{2} } \right)E_{{\text{g}}} }}} \right]^{\frac{1}{3}}\right\} , E_{{\text{b}}} < E_{{\text{g}}} } \\ \end{array} } \right.$$

(26)

$$h_{{\text{s}}}^{e} = \left\{ {\begin{array}{*{20}c} {h_{{\text{s}}} \left[ {\frac{{\left( {1 - \nu_{{\text{g}}}^{2} } \right)E_{{\text{s}}} }}{{\left( {1 - \nu_{{\text{s}}}^{2} } \right)E_{{\text{g}}} }}} \right]^{\frac{1}{3}} , E_{{\text{s}}} > E_{{\text{g}}} } \\ {h_{{\text{s}}} \left\{0.75 + 0.25\left[ {\frac{{\left( {1 - \nu_{{\text{g}}}^{2} } \right)E_{{\text{s}}} }}{{\left( {1 - \nu_{{\text{s}}}^{2} } \right)E_{{\text{g}}} }}} \right]^{\frac{1}{3}}\right\} , E_{{\text{s}}} < E_{{\text{g}}} } \\ \end{array} } \right.$$

(27)

where the superscript e represents equivalent thickness. After translating multiple layers into an equivalent single layer, the stress state for the slider elements is determined by employing the Boussinesq solutions for a uniformly loaded circular area. Subsequently, the estimated distribution is used to derive the stress parameters (e.g. p and q) for the slider elements.

Appendix F. Vehicle and wheel-rail contact modelling

In the FE model, the vehicle is modelled as a multi-body system consisting of two bogies from adjacent wagons, and four wheels in this analysis (see Fig. 4). Two levels of suspensions are considered: one between the bogie and the wheel (primary suspension) and the other between the car body and bogie (secondary suspension). The car body, bogie and wheels are simulated as rigid bodies, while the suspensions are modelled using springs and dashpots. The vertical stiffness of primary and secondary suspensions are considered as 1400 and 450 kN/m, respectively. The damping coefficient of the primary and secondary suspensions are taken as 120 and 40 kNs/m, respectively. The wheel-rail contact is simulated using the Hertzian non-linear contact theory, following Zhai et al. [91].