Introduction

Gastric cancer is one of the most common causes of cancer-related mortality and is the fifth most common cause of all cancers worldwide [1]. It is thought that the incidence of gastric cancer varies with age, with people aged 60 and above being at greatest risk [2].

In the UK, standard first-line therapy for inoperable advanced gastric cancer (AGC) is capecitabine in combination with platinum-based chemotherapy [3]. Response to this first-line chemotherapy is limited, and it is estimated that more than 50% of patients do not respond (or the duration of response is short). Consequently, for most patients, a second-line therapy is frequently necessary. Whilst AGC remains a difficult condition to cure, there are many interventions licenced for second-line treatment of gastric cancer, however no current standard of care exists. AGC can have a detrimental effect on the patient’s quality of life, with a range of symptoms and complications experienced, particularly as the disease progresses (for example, pathologic peritoneal and pleural effusions, hematemesis, or bleeding in the stomach). Therefore, it is important to explore the relative efficacy between comparators, particularly for reimbursement agencies where budget constraints rely upon selecting cost-effective interventions.

Typically, evidence synthesis of time-to-event data [for example, overall survival (OS)] is commonly by way of hazard ratios (HR) and is reliant upon the assumption of proportion hazards between interventions. This assumption is often violated when survival curves of different interventions cross, implying that the HR over time is in fact, not constant over time. This strong assumption of proportional hazards has implications, particularly when evidence synthesis results are utilised in cost-effectiveness (CE) models required for drug reimbursement.

Alternative methods have been proposed to avoid the proportional hazards assumption in meta-analyses; Jansen [4] presents the application of fractional polynomials to synthesise data for treatment of non-small cell lung carcinoma and Ouwens [5] applies a Weibull model within a network meta-analysis (NMA), comparing interventions for treatment of multiple myeloma. Cope [6] extended methods proposed by Ouwens [5], fitting a series of parametric models within an NMA for second-line treatment of advanced breast cancer. Ladyzynski [7] also utilises fractional polynomials to analyse time-to-event outcomes for treatment of chronic lymphocytic leukaemia.

A systematic literature review (SLR) and NMA was performed by Badiani [2] evaluating second-line interventions for treatment of AGC; the difference in median OS was the measure of relative efficacy. However, synthesis of median OS is an unreliable choice of outcome measure to estimate relative efficacy (compared with HRs) as median survival does not account for time-to-event and censoring information, and no information is captured regarding the follow-up times [8, 9] Median survival relies upon data at a single time point, resulting in inaccurate estimations of treatment effects and loss of statistical power [10].

This paper attempts to synthesise recreated data from all studies identified by Badiani [2] to estimate comparative efficacy between second-line interventions for AGC, avoiding the synthesis of HRs and differences in median OS and instead, relying on more recently-published sophisticated statistical methods; fitting a series of parametric survival curves within an NMA to obtain pooled survival estimates for all identified treatments. The results published by Badiani [2] provide a basis upon which results from a parametric survival modelling approach to NMA may be compared with those obtained when adopting conventional NMA methods. A more complex multi-dimensional approach may yield more informative and flexible output, which can subsequently be incorporated in a cost-effectiveness model.

Methods

Literature Search

An SLR was conducted by Badiani [2] and is summarised as follows: searches were conducted of electronic databases PubMed and Scopus, identifying evidence for the effectiveness of interventions for second-line AGC. A date restriction was applied, identifying published literature between 1990 and 2015. Less than 400 citations were retrieved through PubMed. A single search term of “advanced gastric cancer” was used and “randomized controlled trials” was applied as a filter.

Inclusion Criteria

All citations were screened either by abstract or full text. The evidence base was limited to randomised controlled trials (RCT). Additional inclusion criteria were (1) metastatic or non-resectable, locally advance gastric or gastro-oesophageal junction adenocarcinoma, (2) adult population with an age range of 18–75, (3) adequate organ function (including bone marrow function, liver function, kidney function), (4) Eastern Cooperative Oncology Group (ECOG) performance status of 0, 1 or 2 and (5) first-line chemotherapy with fluoropyrimidine plus platinum with or without anthracycline.

Quality Assessment

Two reviewers assessed the quality of the evidence base identified in the SLR using the Cochrane Collaboration’s tool [11], evaluating the risk of bias across six domains (random sequence generation, concealment of allocation, blinding of participants, incomplete data, selective outcome reporting and other sources of bias). Further details regarding the SLR methodology may be found in the original publication reported by Badiani [2].

Statistical Analysis

Data Extraction Process

All studies identified in the SLR were assessed for appropriate statistical content; papers which reported a Kaplan–Meier curve for OS were included in the analysis. Kaplan–Meier curves were digitized using GetData Graph Digitizer software [12] and individual patient data (IPD) was recreated using an algorithm in R proposed by Guyot [13]. The pseudo-IPD for each trial were then partitioned into three-monthly intervals over the entire follow-up period. The number of patients at risk of an event and total number of observed events at the beginning of each interval were captured, accounting for the presence of censoring in the observed time-to-event data. A binomial likelihood function for the number of deaths in an interval [t, t + 3] was used such that:

$$r_{jkt} \sim {\text{Bin}}\left( {p_{jkt} , n_{jkt} } \right),$$

where r jkt and n jkt represent the number of observed deaths within each three-month interval and the number of patients at risk at the start of the time interval, respectively, for study j in arm k. The p jkt represents the cumulative incidence of death within each three-month interval. Further details of the methodology of estimating interval data is presented by Jansen [4] and Ouwens [5]. Data arising from three-arm trials were split into individual two-arm studies. The correlation between arms was not accounted for, instead, the number of patients in the baseline treatment was split evenly between the two studies; an approach used by Ladyzynski [7], as described in the Cochrane Handbook [14]. Data from each trial was then amalgamated to form the synthesis dataset.

Synthesis of Evidence

A Bayesian NMA utilising Markov chain Monte Carlo (MCMC) methods was performed adopting methodology proposed by Jansen [4] and Ouwens [5]. Such approach relies upon the use of prior distributions (which should reflect prior beliefs regarding the plausibility of possible values for the parameters of interest) in combination with a likelihood function, which yields the posterior distribution upon which to base summary estimates. Ouwens [5] reported results from a specific first-order polynomial corresponding to a Weibull distribution, which yields scale (μ 1jA ) and shape (μ 2jA ) parameters for the baseline treatment for the anchor treatment, \(A\) in study \(j\), along with two sets of relative treatment effects (i.e., differences in scale \((d_{1Ak} )\) and shape \((d_{2Ak} )\) parameters for each remaining treatment \(k\)). The posterior means of μ 1jA and μ 2jA (when combined with the relative treatment effects) were used to calculate the scale and shape parameters of all treatments. The approach used by Ouwens [5] was extended, and, as such, a series of parametric models (exponential, Weibull, Gompertz, log-logistic and log-normal) were fitted to the data to estimate long-term survival prognosis for each intervention for the treatment of AGC, in line with methodology adopted by Cope [6].

Analyses were performed using statistical software R (version 3.2.3) [15] and JAGS [16]. Analyses were based on 10,000 samples which were retained after a burn-in of 60,000 iterations were discarded, after which point convergence was observed. The length of the burn-in period was determined based on assessment of the Brooks-Gelman-Rubin statistic [17] for two chains with varying initial values. A thinning interval of ten was chosen to reduce the autocorrelation between samples and to ensure the chain was mixing well and was representative of the posterior distribution. Both fixed-effect and random-effects models were fitted to the data. Vague prior distributions were assigned to all stochastic parameters (the study-specific effects, μ ijA and the treatment effects, d iAk ). In the random-effects models, a Wishart prior distribution was used for the between-study variance for all parameters.

Presentation of Results

Recreated Kaplan–Meier curves for all studies included in the analysis are presented (digitized IPD), and are grouped by intervention to inspect the variation in survival prognosis. The parameter estimates for each of the survival distributions obtained from the NMA are presented at their median value, along with their respective 95% credible intervals (CrI). These parameter estimates represent the baseline scale and shape estimates for the anchor treatment along with the relative treatment effects. Model fit is also summarised according to the Deviance Information Criterion (DIC). The pooled survival curves are presented for each of the survival distributions along with the expected mean survival based on full extrapolation (up to 60 months) of each of the curves. The probability of each treatment being the best, along with expected mean survival are also presented for each of the parametric models.

Compliance with Ethics Guidelines

This article is based on previously conducted studies and does not involve any new studies of human or animal subjects performed by any of the authors.

Results

Search Results

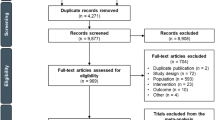
In total, 355 and 612 articles were identified in PubMed and Scopus, respectively. Twelve articles were assessed at full text level. Of these, seven trials met the inclusion criteria, including a total of 2298 patients. A PRISMA chart is presented in Fig. 1 and is adapted from that presented by Badiani [2].

Fig. 1
figure 1

PRISMA chart. Figure adapted from Badiani [2]

Full size image

Study Characteristics and Quality Assessment

Key characteristics of the identified studies are presented in Table 1, as reported by Badiani [2]. The number of patients included across the studies ranged from 40 to 675. The mean age was comparable across studies (ranging from 56 to 65). Race was particularly varied, including Asian, black, and white patients. According to Badiani [2], all RCTs showed a low risk of bias, with the only source of potential bias arising from the open-label design of three of the trials, however all other items assessed were deemed low risk of bias.

Table 1 Trial baseline characteristics
Full size table

Data Analysis

All seven studies [18,19,20,21,22,23,24] included in the analysis performed by Badiani [2] reported Kaplan–Meier curves for OS, which were subsequently digitized to obtain IPD. In total, seven interventions were in included; best supportive care (BSC), docetaxel, everolimus, irinotecan; paclitaxel, ramucirumab and ramucirumab plus paclitaxel. The network of evidence is presented in Fig. 2. BSC is the most commonly compared treatment in the network (five studies) followed by irinotecan (three studies). Docetaxel and paclitaxel were included within two studies and everolimus, ramucirumab and ramucirumab plus paclitaxel were each included in one study. For all comparators, data were extremely mature, as shown by the recreated Kaplan–Meier curves (Fig. 3), with maximum follow-up times across studies ranging from 9.3 months (Thuss-Patience [18]) to 33.0 months (Hironaka [19]). BSC was selected as the anchor treatment due its positioning within the network of evidence as well as the frequency of occurrence within the identified evidence base.

Fig. 2
figure 2

Network of evidence. Solid lines represent two-arm trials (n = 6); dashed lines represent three-arm trials (n = 1); node size is proportional to the number of patients treated with intervention

Full size image
Fig. 3
figure 3

Kaplan–Meier curves by treatment as observed in the trials

Full size image

Random-effects model results are presented in the main text, with fixed-effect results presented in the supplementary material (Table S1). For each parametric model, the DIC showed a negligible difference in fit between the fixed and random-effects models. Adopting a random-effects approach may be considered preferable as it allows for the presence of between-study heterogeneity. Table 2 shows a summary of the NMA estimates for each parametric model (represented by median values) along with their respective 95% CrIs. The parameter estimates for the anchor treatment, BSC, are presented along with the absolute effects for all remaining interventions (estimated as the sum of the baseline estimate and the relative differences versus BSC). The log-logistic distribution provided the best fit to the data (corresponding to the lowest DIC value), with the exponential distribution providing the worst fit (highest DIC value). The baseline shape and scale parameters (BSC) and the relative treatment effects may be combined in order to estimate the survival probabilities over time for each of the survival functions, as shown in Fig. 4. A time horizon of 60 months was used for extrapolation, by which time all survival functions estimated zero probability of remaining alive. This is a plausible time frame upon inspection of the Kaplan–Meier survival curves, and expected poor prognosis of AGC patients [25]. The shape of the curves varies dependent on the parametric model selected, however ramucirumab plus paclitaxel typically shows the greatest probability of survival over time across all the distributions explored (at least up to 18 months’ post-randomisation). An important observation further supporting deviation away from the synthesis of HRs is that the survival curves cross for some of the treatments; docetaxel shows greater survival prognosis versus ramucirumab plus paclitaxel from around 19 months onwards (Gompertz distribution), suggesting that the proportional hazard may not be valid in this instance and some of the within-study cumulative hazard plots [presented in Figure S1 (Supplementary Material)] also do not particularly support the proportional hazards assumption.

Table 2 NMA parameter estimates (random-effects models)
Full size table
Fig. 4
figure 4

Extrapolated parametric survival curves based on NMA estimates

Full size image

Table 3 shows a summary of expected mean survival times (based on extrapolation of up to 60 months) calculated as the area under the curve, which may be derived from the shape and scale parameters. The log-logistic model estimates the greatest mean survival for each of the treatments; ramucirumab plus paclitaxel gains around 6 months’ additional survival benefit versus BSC. The trend across distributions is consistent, with ramucirumab plus paclitaxel always showing the greatest expected OS, followed by paclitaxel, irinotecan, docetaxel and ramucirumab, everolimus and BSC. Expected OS times varied somewhat across distributions for the same treatment; the greatest difference in mean OS was for ramucirumab, where expected OS was 6.37 (exponential distribution) versus 9.07 (log-logistic distribution), showing a difference in mean OS of around 2.3 months. This shows the results may be sensitive to the choice of distribution, and may be more pronounced when a smaller number of patients are included in the analysis. Figure 5 shows the probability of being the best treatment for each of the parametric curves over the full extrapolation period. The trend observed clearly shows that ramucirumab plus paclitaxel has a substantially higher probability of being ranked as the best treatment over all other treatments included in the network up until around 24–36 months. Noting that there was less data available as the follow-up time increases, less weight should be attributed to the latter part of the curves; from around 30 months, all curves have less than 30% chance of being ranked as the best treatment, i.e.,it becomes increasingly difficult to select the best intervention over time.

Table 3 Expected overall survival (random-effects models)
Full size table
Fig. 5
figure 5

Probability of being the best treatment over time

Full size image

Badiani [2] reports all pairwise treatment comparisons (represented by difference in median OS). They conclude that two of the interventions (paclitaxel and ramucirumab plus paclitaxel) are statistically significantly superior to BSC and in addition, ramucirumab plus paclitaxel is statistically significantly superior to irinotecan, docetaxel, paclitaxel and everolimus. They found that ramucirumab plus paclitaxel and paclitaxel were the best two treatments which gained a mean OS improvement of 6.6 and 3.6 months over BSC, respectively. Ramucirumab plus paclitaxel gained a mean improvement 5.6 months over both docetaxel and ramucirumab and 5.5, 4.0 and 3.0 months over everolimus, irinotecan and paclitaxel, respectively. The mean differences reported by Badiani [2] are comparable to the differences in expected mean survival estimates (Table 3). These findings support the reliability of employing a more complex approach to evidence synthesis, yielding more flexible output over differences in median OS, and estimates a more complex form of relative treatment effects, which may be more informative and reliable for subsequent inclusion in CE models.

Treatment ranking histograms are also presented by Badiani [2], which show the probability of each treatment attaining each possible rank and are frequently reported when presenting output from an NMA. They show that ramucirumab plus paclitaxel has a 98% chance of being ranked as the best treatment (out of all seven interventions). Using a parametric modelling approach and selecting the best fitting model (according to the DIC), ramucirumab plus paclitaxel has a 40% chance of being the best treatment (over a 60-month follow-up period). All other interventions are expected to have between 0.2% (BSC) and 20% (ramucirumab) chance of being the best. The ranking probability trends are consistent across both methodologies (those reported by Badiani [2] and those presented in this paper) and the order of treatments is almost identical, with ramucirumab plus paclitaxel expected to yield the most optimistic survival prospects, followed by paclitaxel, irinotecan, ramucirumab, docetaxel, everolimus and BSC.

Discussion

The NMA results using a more intricate approach are in agreement with those reported by Badiani [2] and show that ramucirumab plus paclitaxel is likely to be the most effective intervention (out of the seven comparators included in the analysis) for second-line treatment of AGC, however survival prospects are particularly poor for this population, with expected survival of around 12 months on treatment with ramucirumab plus paclitaxel, with extremely low probability of survival beyond three years post-commencement of any of the second-line treatments under observation. Differences in mean survival show a similar trend in treatment rankings as that reported by Badiani [2]; ramucirumab plus paclitaxel is shown to be the best intervention, followed by paclitaxel and irinotecan, with docetaxel, everolimus, ramucirumab yielding comparatively similar efficacy, and BSC expected to be the worst treatment. The ordering of treatments was consistent across distributions, however, the exponential, log-logistic and log-normal models showed slightly more optimistic longer term survival prospects compared with the Weibull and Gompertz models. Whilst not all treatments included in the NMA are approved by NICE for this indication, inclusion of all comparators enabled a like-for-like comparison with NMA results presented by Badiani [2], which helped to explore the robustness of results and provided a mechanism of assessing external validity.

The results presented in “Results” show the potential advantages of adopting a multi-dimensional approach to evidence synthesis. Utilising a more complex and sophisticated approach yields more flexible output, which may subsequently be used in a CE model submitted for drug reimbursement, without the need for assuming proportional hazards, or reliance on a single summary statistic (e.g., median survival). A common approach to evidence synthesis of time to event data relies on HRs as the selected summary statistic, and this may lead to inaccurate extrapolations, and; therefore, the relative treatment effects may either be under or over estimated. Analysis of median survival is also shown to be extremely limited. A more complex approach such as parametric survival modelling or fractional polynomials makes use of all available data, and reconstruction of IPD from published literature enables data synthesis to incorporate information regarding the shape of the observed Kaplan–Meier data. Ouwens [5] and Cope [6] both employ a similar approach when estimating comparative efficacy in an oncology setting. A comparison between different NMA approaches is presented in Table 4, which identifies key advantages and disadvantages of commonly used approaches to synthesis of time-to-event data. Whilst synthesis of median survival and HRs is often performed for simplicity and transparency reasons, relative efficacy is limited to a single point estimate and is therefore not as informative for inclusion in subsequent economic modelling. An NMA using parametric modelling enables extrapolation and long-term predictions to be made whilst not limited to the proportional hazards assumption underpinning HRs.

Table 4 Comparison of NMA methods used in oncology
Full size table

The approach adopted within this paper is performed within a Bayesian framework, which lends itself to natural inclusion within economic models; the exact posterior distribution may be incorporated directly into the model, avoiding assumptions regarding specification of distributions, preserving correlation and capturing the uncertainty in model parameters, which may be propagated through the economic model.

However, a more complex approach to evidence synthesis is not without its limitations; similar to a conventional NMA, this method also relies on the presence of a connected network of interventions. In addition, it is difficult to explain the statistical heterogeneity between trials and adjust for any imbalances that may be present in the data. Ouwens [5] proposes incorporating a treatment by a covariate interaction term, which may adjust for such treatment-effect modifiers. More recently, matching-adjusted indirect comparison methodology proposed by Signorovitch [26] has been applied to account and adjust for observed differences in trial populations. The general principle of this approach is based on reweighting IPD from an index trial along to ‘match’ published comparator data. This method is particularly advantageous when there is a disconnected network of evidence and provides a way of estimating relative efficacy whilst attempting to balance trial populations. However, a multi-dimensional approach, whilst being data-intensive, can incorporate multiple sources of data and capture all pairwise relative effects within a uniform analysis.

This approach is reliant on Kaplan–Meier curves (along with the number at risk) or IPD being available. Where follow-up is particularly short (immature data), this will introduce additional uncertainty into the extrapolation. Moreover, the tails of the survival curves may vary substantially across distributions, and the clinical plausibility of the extrapolation as well as model fit should be taken into consideration. The choice of fixed versus random effects models should also be considered. Inconsistency between direct and indirect evidence was not assessed, but could be explored as part of further research.

Conclusions

The results presented in this paper support the overall findings and trends as reported by Badiani [2]; however, the multi-dimensional approach adopted for evidence synthesis yields more informative output, which may be pivotal when incorporating within a CE model for subsequent submissions to health technology agencies. Reliance upon the proportional hazards assumption is no longer required when estimating relative efficacy between interventions. Whilst parametric modelling and fractional polynomials approaches are data-intensive, such sophisticated statistical methods may provide more reliable and robust estimates of comparative efficacy, which may result in more informative decision-making for drug reimbursement.