1 Introduction

The milling process is one of the conventional methods of advanced manufacturing processes. Production of various workpieces with complex shapes is the main benefit of the milling process. However, self-excited vibration, a.k.a. chatter, is present in almost every machining process, and it may cause adverse effects, such as tool damage, poor surface quality, and excessive noise. Regeneration and mode coupling are two main mechanisms that cause the chatter phenomenon in the machining [1, 2] and the regeneration is more prevalent in the milling process. The regeneration occurs when the cut produced at time t leaves a wavy surface on the material regenerated during subsequent cut [3]. Hence, the dynamics of the milling process can be represented as two-dimensional delay differential equations (DDE) caused by the regeneration effects.

One of the challenges in the manufacturing community is investigating how to reduce the chatter effects in the machining process, and many studies have been done to suppress chatter in milling processes. Such suppression can be categorized into two main types; active control method and passive control method. Model predictive control [4], robust control strategies [5], and robust optimal approach [6] have been studied as the active control methods for the milling chatter suppression. Chatter control using \(\mu \)-synthesis is used for the high-speed milling process [7]. Using equipment, including absorbers, or adjusting the stiffness and damping coefficients of the system, can be categorized as a passive control that increases the stability region. Moreover, optimal passive vibration control [8] and chatter prevention by acoustic signal feedback [9] have been used as passive control strategies.

Active control is a highly efficient method based on actuators and feedback control, which can be categorized into two classes: active workpiece holder and active spindle system based on the position of the actuators. For the first class, Sallese et al. proposed an active fixture using a novel control strategy for the mitigation of chatter instability in the milling [10]. Rashid and Nicolescu designed a palletized work-holding system via piezo-actuators for active vibration control of the milling process [11]. Because of the system uncertainty and in order to apply a non-conservative control input for different parameters, it is more desirable to synthesize a (computationally inexpensive) active control to the milling process. However, the existing methods do not provide a stable controller that is optimal yet for different uncertainties.

In the manufacturing community, it is crucial to provide guidance to select different parameters, such as axial depth of cut or spindle speed, that lead to stable system behavior. Stability lobe diagram (SLD) analysis is one of the methods for the prediction of the stable region in varying the axial depth of cut and spindle speed. The SLD illustrates graphical instructions for the stable region, for parameter selection in spindle speed and axial cutting depth. Altintas et al. introduced an analytical method for the prediction of the stability lobes in milling [12]. Insperger et al. [13] presented a new method for determining the stability condition of the high-speed milling process as a delayed differential equation. Moreover, the semi-discretization method (SDM) [14, 15] and full-discretization method [16] have been used for the prediction of the milling stability. The Rung–Kutta-based complete discretization method also is used for the prediction of chatter stability in the milling process [17].

Various two-dimensional linear and nonlinear models are proposed for the milling process and cutting forces [18, 19]. Warminski et al. [20] proposed an approximate analytical solution in the nonlinear milling process. Li et al. [21] presented a predictive time domain for the modelling and simulation of the chatter in the milling process. Moreover, Altintas suggested a three-dimensional milling model considering the axial vibration mode [22].

An effective strategy for the stability analysis and controller design for a time-delay system (TDS) is the Lyapunov-based method. There are two main Lyapunov methods to control TDSs: the Krasovskii method of Lyapunov functional [23] and the Razumikhin of Lyapunov functions [24]. The two Lyapunov methods for linear TDSs result in Linear Matrix Inequalities (LMIs) conditions. In this paper, we focus on the delay-independent Lyapunov–Krasovskii method because the Lyapunov–Razumikhin approach generally leads to more conservative results than those based on the Lyapunov–Krasovskii theorem [25]. Furthermore, Razumikhin’s approach is useful for time-varying delays [26].

Providing a stabilizing controller that can easily take into account the different uncertainties is important in the milling process. Moreover, this controller must not yield too much chatter in the transition mode. In this paper, we aim at providing an optimal stabilizing controller for the milling process (that can be applied to any time-delay system) that is computationally inexpensive and also takes parametric uncertainties into consideration. The dynamic model of the milling process is considered a two-dimensional delayed differential equation in both linear and nonlinear dynamics. A Lyapunov–Krasovskii-based strategy will be extracted for the linear TDS in the presence of parametric uncertainty. Then we optimize a cost function based on the controller gain to achieve the optimal closed-loop behaviour. We apply the robust controller to the nonlinear TDS. The SLDs illustrate the improvement of the stable region via the controller in both nominal and uncertain plants using SDM. Moreover, it will be shown that the controller can improve the adverse effects of the bifurcation behavior of the system.

One of the main challenges that is solved by this paper, was establishing an inexpensive optimization problem that results in the lowest transient chatter (by applying minimum controller gain) while satisfying the robust stability. The contribution of the present work is designing a delay-independent optimal robust controller for time-delay systems based on the Lyapunov–Krasovskii method. To compare our work with the literature, in [27], the authors have proposed the use of PD and fuzzy control to achieve an active feedback control where the optimality can achieve indirectly by the fuzzy control, which causes more computational efforts than our work. Moreover, the stability (under uncertainty) of such a controller is challenging to be guaranteed. While, for instance, the authors in [28] have proposed a Lyapunov-based stabilizing control for the milling process, however, it overlooks the optimality and the method does not result in a unique solution necessarily. Furthermore, [29] suggests a similar idea based on LMI. Linear quadratic Gaussian (LQG) has been proposed in [30] to provide an optimal stabilizing controller, however, the time-delay dynamics need to be approximated by linear dynamics, and applying time-delay dynamics directly is very challenging.

The rest of the paper is structured as follows. Section 2 provides a 2-DOF linear and nonlinear dynamic model of the milling process. Section 3 details the designing of an optimal robust controller for TDS. Section 4 illustrates the simulation results, including the time response, control signals, SLD, bifurcation, etc. Finally, Sect. 5 delivers a conclusion.

2 Dynamic modeling of the milling process

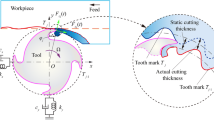
As shown in Fig. 1, the milling process can be considered as dynamics in two degrees of freedom in the x-y plane [21, 31]. The immersion angle \(\phi _j,\, j=0,1,\ldots ,N-1\) measures the clock-wise angle from the direction \(-y\) to the tooth \((j+1)\)th, and N is the number of total teeth. For a straight tool, the immersion angle \(\phi _j(t)\) in \([\textrm{rad}]\) can be expressed as follows:

$$\begin{aligned} \phi _j(t)=\frac{2\pi }{60} \Omega t+\frac{2\pi }{N}j, \quad j=0,1,\ldots ,N-1 \end{aligned}$$
(1)

where \(\Omega \) is the spindle speed in \([\mathrm {rev/min}]\).

Fig. 1
figure 1

(Left) The 2-DOF milling model. (Right) The regeneration mechanism

Full size image

Dynamic chip thickness \(h(\phi _j)\) in the regenerative chatter can be expressed as:

$$\begin{aligned} h(\phi _j)&=\left( \left[ x(t)-x(t-\tau )\right] \sin {\phi _j}+\left[ y(t)-y(t-\tau )\right] \right. \nonumber \\&\quad \times \left. \cos {\phi _j}\right) g(\phi _j) \end{aligned}$$
(2)

where \(\tau ={60}/{(N \Omega )}\) is the time delay in \([\textrm{sec}]\), x and y are the displacements in two directions. Indeed, \(\tau \) is the time difference between two neighbor teeth. Function \(g(\phi _j)\) is a step function that determines the effective range of the chip thickness function, and is represented as follows:

$$\begin{aligned} g(\phi _j)= \left\{ \begin{matrix} 1 &{} \phi _{\textrm{st}} \le \phi _j \le \phi _{\textrm{ex}}\\ 0 &{} \textrm{otherwise} \end{matrix}\right. \end{aligned}$$
(3)

where \(\phi _{\textrm{st}}\) is the start immersion angle and \(\phi _{\textrm{ex}}\) is the exit immersion angle.

In the linear modelling, the tangential \(F^l_{\textrm{tj}}\) and radial \(F^l_{\textrm{tj}}\) cutting forces are acting on the tooth j are proportional to the chip thickness h and the axial depth of cut b, as follows:

$$\begin{aligned} F^{l}_{\textrm{tj}}=K_{\textrm{tc}} b h(\phi _j) \end{aligned}$$
(4a)
$$\begin{aligned} F^l_{\textrm{rj}}=K_{\textrm{rc}} b h(\phi _j) \end{aligned}$$
(4b)

where \(K_{\textrm{tc}}\) and \(K_{\textrm{rc}}\) are the constant cutting coefficients. By projection of the forces \(F^l_{\textrm{tj}}\) and \(F^l_{\textrm{rj}}\) on the x and y directions and summing the forces in all teeth, dynamic milling forces \(F^l_x\) and \(F^l_y\) on the x and y directions are evaluated using Eqs. (2) and (4) as follows:

$$\begin{aligned}&F^l(\Delta x, \Delta y)=\left[ \begin{matrix} F^l_x \\ F^l_y \end{matrix}\right] \nonumber \\&\quad =\sum _{j=0}^{N-1} \left[ \begin{matrix} \cos (\phi _j) &{} \sin (\phi _j)\\ -\sin (\phi _j) &{} \cos (\phi _j) \end{matrix}\right] \left[ \begin{matrix} F^l_{\textrm{tj}} \\ F^l_{\textrm{rj}} \end{matrix}\right] =b\sum _{j=0}^{N-1} H_j \left[ \begin{matrix} \Delta x \\ \Delta y \end{matrix}\right] \end{aligned}$$
(5)

where

$$\begin{aligned} \Delta x&=x(t-\tau )-x(t) \end{aligned}$$
(6a)
$$\begin{aligned} \Delta y&=y(t-\tau )-y(t) \end{aligned}$$
(6b)

and

$$\begin{aligned} H_j&= \left[ \begin{matrix} H_{xx,j} &{} H_{xy,j}\\ H_{yx,j} &{} H_{yy,j} \end{matrix}\right] \end{aligned}$$
(7a)
$$\begin{aligned} H_{xx,j}&= \left[ K_{\textrm{tc}} \cos (\phi _j)+K_{\textrm{rc}}\sin {\phi _j}\right] \sin {\phi _j}g(\phi _j) \end{aligned}$$
(7b)
$$\begin{aligned} H_{xy,j}&= \left[ K_{\textrm{tc}} \cos (\phi _j)+K_{\textrm{rc}}\sin {\phi _j}\right] \cos {\phi _j}g(\phi _j) \end{aligned}$$
(7c)
$$\begin{aligned} H_{yx,j}&= \left[ -K_{\textrm{tc}} \sin (\phi _j)+K_{\textrm{rc}}\cos {\phi _j}\right] \sin {\phi _j}g(\phi _j) \end{aligned}$$
(7d)
$$\begin{aligned} H_{yy,j}&= \left[ -K_{\textrm{tc}} \sin (\phi _j)+K_{\textrm{rc}}\cos {\phi _j}\right] \cos {\phi _j}g(\phi _j) \end{aligned}$$
(7e)

Since Eq. (5) expresses time-varying dynamics; for the sake of simplification, the average component of the Fourier series expansion is considered [32]. This assumption is quite common in the literature and is valid for the scope of the current research. Summing \(H_j\) and averaging, yields:

$$\begin{aligned} {{\bar{H}}}=\frac{1}{\tau } \int _0^\tau \sum _{j=0}^{N-1} H_j(\phi _j) \textrm{d}t \end{aligned}$$
(8)

A half immersion up-milling is a milling process when \(\phi _{\textrm{st}}=0\), \(\phi _{\textrm{ex}}=\pi /2\). For the half immersion up-milling with \(N=4\), the matrix \({{\bar{H}}}\) reads:

$$\begin{aligned} {{\bar{H}}}=\left[ \begin{matrix} {K_{\textrm{tc}}}/{\pi }+{K_{\textrm{rc}}}/{2} &{} {K_{\textrm{tc}}}/{2}+{K_{\textrm{rc}}}/{\pi }\\ -{K_{\textrm{tc}}}/{2}+{K_{\textrm{rc}}}/{\pi } &{} -{K_{\textrm{tc}}}/{\pi }+{K_{\textrm{rc}}}/{2} \end{matrix}\right] \end{aligned}$$
(9)

Then Eq. (5) is rewritten as follows:

$$\begin{aligned} F^l(\Delta x, \Delta y) =b {{\bar{H}}} \left[ \begin{matrix} x(t-\tau )-x(t) \\ y(t-\tau )-y(t) \end{matrix}\right] \end{aligned}$$
(10)

Hence, the dynamic equation of the two-dimensional milling process can be expressed as follows (see Fig. 1):

$$\begin{aligned} M{\ddot{X}}+C{\dot{X}}+KX&=F^l(\Delta x, \Delta y)+u\nonumber \\&=b{\bar{H}}(X(t-\tau )-X(t))+u \end{aligned}$$
(11)

where \(X:=[x,y]^\top \) and \(u:=[u_x,u_y]^\top \) are the displacement and control-input vectors, respectively. Matrices \(M:=\textrm{diag}(m_x,m_y)\), \(C:=\textrm{diag}(c_x,c_y)\), \(K:=\textrm{diag}(k_x,k_y)\) are the mass, damping, and stiffness matrices, respectively.

2.1 Nonlinear modeling

A nonlinear model of the milling process can describe dynamical behaviors more accurately and can express some nonlinear phenomena such as bifurcation, jump, and chaos [33]. In this case, the cutting forces are considered as third-degree polynomial functions of thickness, i.e.:

$$\begin{aligned} F^{nl}_{\textrm{tj}}&=b(\xi _1 h^3+\xi _2 h^2+\xi _3 h+ \xi _4) \end{aligned}$$
(12a)
$$\begin{aligned} F^{nl}_{\textrm{rj}}&=b(\eta _1 h^3+\eta _2 h^2+\eta _3 h+ \eta _4) \end{aligned}$$
(12b)

where \(F^{nl}_{\textrm{tj}}\) and \(F^{nl}_{\textrm{rj}}\) are nonlinear tangential and radial cutting forces, respectively, and \(\eta _i, \xi _i, i=1,\ldots ,4 \) are the coefficients of the nonlinear cutting forces. Similar to the linear model, by the projection of these forces on the x and y axis and averaging, it yields:

$$\begin{aligned}&F^{nl}(\Delta x, \Delta y)=\nonumber \\ {}&\qquad b {{\bar{G}}} [\Delta x^3,\Delta y^3,\Delta x^2,\Delta y^2,\nonumber \\&\Delta x,\Delta y,\Delta x^2\Delta y,\Delta x\Delta y^2,\Delta x\Delta y]^\top +b {{\bar{G}}}_0 \end{aligned}$$
(13)

where \({{\bar{G}}}_0=[-2(\xi _4+\eta _4)/\pi , 2(\xi _4-\eta _4)/\pi ]^\top \) and \({{\bar{G}}}=[{{\bar{g}}}_{ij}]\in {\mathbb {R}}^{9\times 9}\) is obtained as follows:

$$\begin{aligned} \begin{matrix} {{\bar{g}}}_{11}=-\frac{\xi _1}{2\pi }-\frac{3\eta _1}{8} &{} {{\bar{g}}}_{12}=-\frac{\eta _1}{2\pi }-\frac{3\xi _1}{8} &{} {{\bar{g}}}_{13}=-\frac{2\xi _2}{3\pi }-\frac{4\eta _2}{3\pi }\\ {{\bar{g}}}_{14}=-\frac{2\eta _2}{3\pi }-\frac{4\xi _2}{3\pi } &{} \bar{g}_{15}=-\frac{\xi _3}{\pi }-\frac{\eta _3}{2} &{} {{\bar{g}}}_{16}=-\frac{\eta _3}{\pi }-\frac{\xi _3}{2} \\ {{\bar{g}}}_{17}=-\frac{\xi _1}{2\pi }-\frac{3\eta _1}{8} &{} \bar{g}_{18}=-\frac{\eta _1}{2\pi }-\frac{3\xi _1}{8} &{} \bar{g}_{19}=-\frac{2\eta _2}{3\pi }-\frac{4\xi _2}{3\pi } \end{matrix} \end{aligned}$$
(14)

and the second row of the matrix \({{\bar{G}}}\) is obtained by converting \(\xi _i\rightarrow \eta _i\) and \(\eta _i\rightarrow -\xi _i\) corresponding to the first row. Finally, the two-dimensional nonlinear model of the milling is obtained as follows:

$$\begin{aligned} M{\ddot{X}}+C{\dot{X}}+KX=F^{nl}(\Delta x, \Delta y)+u \end{aligned}$$
(15)

In the next section, we detail the stability analysis and controller design for TDSs.

3 Lyapunov-based robust optimal control

In this section, we detail the stability analysis of TDS and propose a memoryless stabilizing controller. We will guarantee the asymptotic stability of the closed-loop system in the presence of different parametric uncertainty and optimize the controller gain. Finally, the implementation of the proposed controller for the nonlinear dynamics will be discussed.

A general time-delay system or TDS can be written as the following functional differential equation [34]:

$$\begin{aligned} \dot{\varvec{\textrm{x}}}(t)=\varvec{\textrm{f}}(t,\varvec{\textrm{x}}_t) \end{aligned}$$
(16)

where \(\varvec{\textrm{x}}\in {\mathbb {R}}^n\) is the state, \(t\in [t_0,\infty )\) is the physical time, \(\varvec{\textrm{f}}:{\mathbb {R}}\times C[-\tau ,0]\rightarrow {\mathbb {R}}^n\) is a continuous and locally Lipschitz function, representing the dynamics, C is the Banach space of continuous function, \(\tau >0\) is the time-delay of the system and \(\varvec{\textrm{x}}_t\) is defined as follows:

$$\begin{aligned} \varvec{\textrm{x}}_t(\theta )=\varvec{\textrm{x}}(t+\theta ),\quad -\tau \le \theta \le 0 \end{aligned}$$
(17)

and the initial condition function is \(\Psi (\theta )\), i.e:

$$\begin{aligned} \varvec{\textrm{x}}(t_0+\theta )=\varvec{\mathrm {\Psi }}(\theta ), \quad -\tau \le \theta \le 0 \end{aligned}$$
(18)

The next theorem provides sufficient conditions to guarantee the stability of TDS (16).

Theorem 1

(Lyapunov–Krasovskii Theorem [35]) Suppose \(u,v,w: {\mathbb {R}}^+\rightarrow {\mathbb {R}}^{+}\) are continuous non-decreasing functions, u(s) and v(s) are positive for \(s > 0\), and \(u(0)=v(0)=0\). If there is a continuous functional \(V: {\mathbb {R}} \times C[-\tau ,0]\rightarrow {\mathbb {R}}^+\) such that:

$$\begin{aligned} u(\Vert \varvec{\textrm{x}}(t)\Vert )\le V(t,\varvec{\textrm{x}}_t)&\le v(\Vert \varvec{\textrm{x}}(t)\Vert _c) \end{aligned}$$
(19a)
$$\begin{aligned} {\dot{V}}(t,\varvec{\textrm{x}}_t)&\le -w(\Vert \varvec{\textrm{x}}(t)\Vert ) \end{aligned}$$
(19b)

where

$$\begin{aligned} {\dot{V}}(t,\varvec{\textrm{x}}_t)\overset{\Delta }{=}\ {}&\lim _{r\rightarrow 0^+} \sup \frac{1}{r}\left( V(t+r,\varvec{\textrm{x}}_{t+r})-V(t,x_t)\right) \end{aligned}$$
(20a)
$$\begin{aligned} \Vert \varvec{\textrm{x}}(t)\Vert _c\overset{\Delta }{=}\ {}&\sup _{-\tau \le \theta \le 0}\Vert \varvec{\textrm{x}}(t+\theta )\Vert \end{aligned}$$
(20b)

and \(\Vert \varvec{\textrm{x}}(t)\Vert \) refers to the Euclidean vector norm. Then, the solution \(\varvec{\textrm{x}}(t)\) of Eq. (16) is uniformly stable. If \(w(s)>0\) for \(s>0\), then it is uniformly asymptotically stable. If \(u(s)\rightarrow \infty \) as \(s\rightarrow \infty \), then it is globally uniformly asymptotically stable.

Proof

See [34]. \(\square \)

In practice, it is quite a challenging task to find the function V that satisfies the conditions of the Theorem 1 when f is a general nonlinear function. Hence, we discuss the stability of linear dynamics. Moreover, a robust controller can be applied to the nonlinear dynamics with reasonable close behaviour with its linearized dynamics. A Linear, single-delay TDS can be written as follows:

$$\begin{aligned} \dot{\varvec{\textrm{x}}}(t)=A\varvec{\textrm{x}}(t)+A_1\varvec{\textrm{x}}(t-\tau ) \end{aligned}$$
(21)

where \(A,A_1\in {\mathbb {R}}^{n\times n}\) are constant matrices. The next theorem discusses the stability of linear time-delay dynamics.

Theorem 2

[34] System (21) is asymptotically stable if there exist matrices \(P>0\), and \(P_1>0\) such that

$$\begin{aligned} \left[ \begin{matrix} PA+A^\top P+P_1 &{} PA_1\\ A_1^\top P &{} -P_1 \end{matrix} \right] <0 \end{aligned}$$
(22)

Proof

See Theorem 2.5 in [34]. \(\square \)

Therefore, a sufficient condition to ensure the stability of a linear TDS is to find positive matrices P and \(P_1\), which satisfy (22).

3.1 Memoryless stabilizing controller

In this section, we discuss stabilizing and memoryless controllers for the linear TDS. The aim of designing a memoryless controller is finding a matrix \(\kappa \in {\mathbb {R}}^{m\times n}\), independent of \(\tau \), such that the following controlled TDS:

$$\begin{aligned} \dot{\varvec{\textrm{x}}}(t)=A\varvec{\textrm{x}}(t)+A_1\varvec{\textrm{x}}(t-\tau )+B\varvec{\textrm{u}}(t) \end{aligned}$$
(23)

is asymptotically stable with the following control law:

$$\begin{aligned} \varvec{\textrm{u}}(t)=\kappa \varvec{\textrm{x}}(t) \end{aligned}$$
(24)

where \(B\in {\mathbb {R}}^{n\times m}\) is a constant matrix and \(\varvec{\textrm{u}}\in {\mathbb {R}}^m\) is the control signal. Note that one can represent (11) in the form of (23) using the following matrices:

$$\begin{aligned} A&=\begin{bmatrix} 0 &{} I_{2\times 2}\\ -M^{-1}(K+b{{\bar{H}}}) &{} -M^{-1}C \end{bmatrix} \end{aligned}$$
(25a)
$$\begin{aligned} A_1&=\begin{bmatrix} 0_{2\times 2} &{} 0_{2\times 2} \\ bM^{-1}{{\bar{H}}} &{} 0_{2\times 2} \end{bmatrix} \end{aligned}$$
(25b)
$$\begin{aligned} B&=\begin{bmatrix} 0_{2\times 2}\\ M^{-1} \end{bmatrix} \end{aligned}$$
(25c)

The next theorem presents a method based on the Linear Matrix Inequality (LMI) problem to obtain a feedback and memoryless controller.

Theorem 3

The closed-loop system described by Eq. (23) with state feedback control \(\varvec{\textrm{u}}(t)=\kappa \varvec{\textrm{x}}(t)\) is asymptotically stable, if there exist matrices \(Q>0\), \(Q_1>0\) and Y such that:

$$\begin{aligned} \left[ \begin{matrix} AQ+QA^\top +BY+Y^\top B^\top +Q_1 &{} A_1 Q \\ Q A_1^\top &{} -Q_1 \end{matrix} \right] <0 \end{aligned}$$
(26)

then the control law is \(\kappa =YQ^{-1}\).

Proof

Substitution \(\varvec{\textrm{u}}(t)=\kappa \varvec{\textrm{x}}(t)\) in (23), yields:

$$\begin{aligned} \dot{\varvec{\textrm{x}}}(t)=(A+B\kappa )\varvec{\textrm{x}}(t)+A_1\varvec{\textrm{x}}(t-\tau ) \end{aligned}$$
(27)

by conversion \(A\rightarrow A+B\kappa \), Eq. (22) can be written as:

$$\begin{aligned} \left[ \begin{matrix} P(A+B\kappa )+(A+B\kappa )^\top P+P_1 &{} PA_1 \\ A_1^\top &{} -P_1 \end{matrix} \right] <0 \end{aligned}$$
(28)

Or equivalently:

$$\begin{aligned}&P^{-1}\left[ \begin{matrix} P(A+B\kappa )+(A+B\kappa )^\top P+P_1 &{} PA_1 \\ A_1^\top &{} -P_1 \end{matrix} \right] P^{-1}=\nonumber \\ {}&\qquad \left[ \begin{matrix} AQ+QA^\top +BY+Y^\top B^\top +Q_1 &{} A_1 Q \\ Q A_1^\top &{} -Q_1 \end{matrix} \right] <0 \end{aligned}$$
(29)

where we have used \(Q=P^{-1},Q_1=P^{-1} P_1 P^{-1},\) and \(Y=\kappa P^{-1}\). Then:

(30)

and

$$\begin{aligned} P>0, P_1>0 \Rightarrow Q>0, Q_1>0 \end{aligned}$$
(31)

\(\square \)

Note that the control law in (30) is independent of the time-delay \(\tau \) and consequently independent of the spindle speed \(\Omega \). It is obvious that by considering other Lyapunov functions, the obtained controller may depend on the time delay. Therefore, in that case, it must be adjusted for the different spindle speeds.

3.2 Robustness guarantee

Another challenging issue is considering the robustness conditions for the control law in the presence of parametric uncertainties. Since the value of the axial depth of cut b can vary in the interval \([b_{\textrm{min}},b_{\textrm{max}}]\) by the user or model uncertainty, the control strategy must be robust in this interval. The next theorem provides a useful procedure to guarantee robustness.

Theorem 4

The system described by Eq. (23) is asymptotically stable with the control law \(u(t)=\kappa x(t)\) for any \(b\in [b_{\textrm{min}},b_{\textrm{max}}]\), if there exist matrices \(S>0\), \(S_1>0\) and Y such that:

$$\begin{aligned}&\Gamma (b_i):=\nonumber \\&\left[ \begin{matrix} A(b_i)S\!+\!SA(b_i)^\top \!+\!BY\!+\!Y^\top B^\top +S_1 &{} A_1(b_i)^\top S \\ S A_1(b_i)^\top &{} -S_1 \end{matrix} \right] <0, \end{aligned}$$
(32)

for \(b_i\in \{b_{\textrm{min}},b_{\textrm{max}}\}\), where \(A(b_{\textrm{min}})\) and \(A(b_{\textrm{max}})\) is the matrix A evaluated at \(b_{\textrm{min}}\) and \(b_{\textrm{max}}\), respectively. The same statement holds for \(A_1\). The robust controller gain is obtained from \(\kappa =YS^{-1}\).

Proof

For any \(b\in [b_{\textrm{min}},b_{\textrm{max}}]\) there exists a unique \(m\in [0,1]\) such that

$$\begin{aligned} b=m b_{\textrm{min}} +(1-m)b_{\textrm{max}} \end{aligned}$$
(33)

then from (32):

$$\begin{aligned}&\Gamma (b)=m \Gamma (b_{\textrm{min}}) +(1-m)\Gamma (b_{\textrm{max}})<0,\quad \nonumber \\&\forall b\in [b_{\textrm{min}},b_{\textrm{max}}] \end{aligned}$$
(34)

Note that we have used the fact that A and \(A_1\) depend on b linearly (see Eq. (25)). Similar to the previous discussion, \(K=YS^{-1}\) is the controller gain. \(\square \)

From Theorem 4, one can observe that in order to guarantee the robustness of the proposed controller for the other model parameters that linearly appear in matrices A and \(A_1\) (i.e., stiffness \(k_x, k_y\) and damping \(c_x, c_y\)), we need to find \(S_1, S>0\) and Y, such that:

$$\begin{aligned}&\Gamma (b_i,k_{x,i},k_{y,i},c_{x,i},c_{y,i}):=\nonumber \\&\left[ \begin{matrix} A^iS+S(A^i)^\top +BY+Y^\top B^\top +S_1 &{} (A^i_1)^\top S \\ S (A^i_1)^\top &{} -S_1 \end{matrix} \right] <0,\nonumber \\&\qquad \qquad b_i\in \{b_{\textrm{min}},b_{\textrm{max}}\}, k_{x,i}\in \{k_{x,\textrm{min}},k_{x,\textrm{max}}\},\nonumber \\&k_{y,i}\in \{k_{y,\textrm{min}},k_{y,\textrm{max}}\},\nonumber \\&\qquad \qquad \qquad c_{x,i}\in \{c_{x,\textrm{min}},c_{x,\textrm{max}}\}, c_{y,i}\in \{c_{y,\textrm{min}},c_{y,\textrm{max}}\} \end{aligned}$$
(35)

where

$$\begin{aligned} A^i=A(b_i,k_{x,i},k_{y,i},c_{x,i},c_{y,i}), \quad \nonumber \\ A_1^i=A_1(b_i,k_{x,i},k_{y,i},c_{x,i},c_{y,i}) \end{aligned}$$
(36)

then the controller gain \(\kappa =YS^{-1}\) is stabilizing for every \(b_i\in [b_{\textrm{min}},b_{\textrm{max}}]\), \( k_{x,i}\in [k_{x,\textrm{min}},k_{x,\textrm{max}}]\), \( k_{y,i}\in [k_{y,\textrm{min}},k_{y,\textrm{max}}]\), \( c_{x,i}\in [c_{x,\textrm{min}},c_{x,\textrm{max}}]\), \( c_{y,i}\in [c_{y,\textrm{min}},c_{y,\textrm{max}}]\). Indeed, to guarantee the robustness of the system, only we need to guarantee the negative definiteness of matrix \(\Gamma (b_i,k_{x,i},k_{y,i},c_{x,i},c_{y,i})\) at the bounds and Eq. (35) can be interpreted as an extension of Theorem 4.

3.3 Optimal control design

Each feasible solution of the LMI in Eq. (32), yields a different controller gain \(\kappa \). Indeed, (32) provides a set of feasible solutions for the controller gain. Although the robust controllers, obtained from the previous section, guarantee the stability of the closed-loop system, the vibrations of the transition can still be destructive if it has a significant amplitude. This phenomenon happens when the control inputs have large amplitudes. Then it will be worth defining a cost function to reach a unique solution and provide the best performance of the system behavior by minimizing the cost function. In most industrial control problems, such as the milling process, the control gain needs to be as small as possible in the norm-2 sense, so that the control input and the closed-loop trajectories will remain within a reasonable range. Indeed, norm-2 can be one of the essential indicators in designing the controller, and minimizing it is directly related to optimizing control inputs. On the other hand, given the nonlinearity of the control gain relative to the Y and S (\(K=YS^{-1}\)), the nonlinear matrix optimization problem with LMI constraints is a challenging problem due to the high dimensionality and nonlinearity of \(\Vert \kappa \Vert _2\). Then the objective function must be simplified. Using the Schur complement [36], the following inequalities can be written:

$$\begin{aligned} Y^\top Y< L_{Y}I&\Leftrightarrow 0<L_{Y}I-Y^\top Y \Leftrightarrow 0<\left[ \begin{matrix} L_{Y}I &{} Y^\top \\ Y &{} I \end{matrix}\right] \end{aligned}$$
(37a)
$$\begin{aligned} S^{-1}< L_S I&\Leftrightarrow 0<L_S I-S^{-1} \Leftrightarrow 0<\left[ \begin{matrix} L_{S}I &{} I \\ I &{} S \end{matrix}\right] \end{aligned}$$
(37b)

where \(L_Y\) and \(L_S\) are positive scalars which determine an upper bound for Y and \(S^{-1}\) respectively. Then, the controller K can be bounded by the following:

$$\begin{aligned} \kappa ^\top \kappa =S^{-1}Y^\top Y S^{-1}< L_{Y} S^{-1} S^{-1}<L_YL_S^2 I \end{aligned}$$
(38)

and

$$\begin{aligned} \Vert \kappa \Vert _2=\sqrt{\lambda _{\textrm{max}}(\kappa ^\top \kappa )}<L_S\sqrt{L_Y} \end{aligned}$$
(39)

In summary, the following Nonlinear Programming (NLP) with the LMI constraints should be solved:

$$\begin{aligned} \min _{L_S,L_Y, S,S_1,Y}&\qquad L_S \sqrt{L_Y} \end{aligned}$$
(40a)
$$\begin{aligned} \mathrm {s.t.} \qquad&\qquad 0<\left[ \begin{matrix} L_{Y}I &{} Y^\top \\ Y &{} I \end{matrix}\right] , 0<\left[ \begin{matrix} L_{S}I &{} I \\ I &{} S \end{matrix}\right] \end{aligned}$$
(40b)
$$\begin{aligned}&\qquad \Gamma (b_i,k_{x,j},k_{y,k},c_{x,l},c_{y,m}) <0,\,\,\nonumber \\&\quad \forall i,j,k,l,m \in \{\textrm{min},\textrm{max}\} \end{aligned}$$
(40c)
$$\begin{aligned}&\qquad L_S>0,\,\, L_Y>0,\,\, S>0,\,\, S_1>0 \end{aligned}$$
(40d)

The objective of the problem is a nonlinear function with two scalar variables. If the solution exists, this objective implies the minimum controller gain and the constraints guarantee the robust stability of the closed-loop system. In order to solve (40), we first define a feasible set as follows:

$$\begin{aligned}&\text {feasible set}=\{(L_S,L_Y)\in {\mathbb {R}}^2\,|\,L_S>0,\,L_Y>0\,\nonumber \\&\quad \text {and}\,\exists S,S_1,Y : (40b), (40c), (40d)\} \end{aligned}$$
(41)

Then by plotting the contours of \(L_S \sqrt{L_Y}\), the optimal point is the first cross point of the contours with the feasible set. Figure 2 shows the schematic of the procedure.

Fig. 2
figure 2

Solving NLP (40)

Full size image

3.4 Applying the controller to the nonlinear dynamics

In this section, we discuss briefly the practical aspects of implementing the proposed controller to the nonlinear dynamics.

The nonlinear dynamics of the milling process have attracted attention because of its exciting phenomena, e.g., bifurcation, jump, limit cycle, etc. In order to implement the designed linear control to nonlinear dynamics, we first compare the nonlinear trajectory and linear trajectory. Then we obtain an upper bound for its equivalent parametric uncertainty. Finally, using the robust procedure discussed in the previous section, we implement the controller to the nonlinear system.

One can observe that the nonlinear system resulting from (15) is a perturbed version of the linear dynamics resulting from (11) with some additional perturbation term as a function of \(\Delta x\) and \(\Delta y\). Since for a stabilizing controller for the linear system \(\Delta x\rightarrow 0\) and \(\Delta y\rightarrow 0\) as \(t\rightarrow \infty \), then these perturbations will vanish as \(t\rightarrow \infty \). It has been shown in [37], for a perturbed system with some additional mild assumption on the smoothness of the dynamics and boundness of the perturbation term, the stabilizing controller for the nominal system (here, the linear system) is also stabilizing for the perturbed system (here, the nonlinear system).

One of the fascinating phenomena in the chattering context is predicting or evaluating Stability Lobes Diagram (SLD). The SDP is a plot of the axial depth of cut b versus the spindle speed \(\Omega \), which shows the region of the stability of the system. We use the semi-discretization method (SDM) to predict the stability of lobes. In this method, the delayed term is approximated as a weighted sum of the two neighboring discrete delayed state values. Finally, the Floquet transition \(\Phi \) matrix will be determined over a single period. The location of the eigenvalues of \(\Phi \) determines the stability of the system. for the sake of brevity, we do not discuss the mathematical details of SDM in this paper. Interested readers can have a look at [15].

Bifurcation and limit cycles are other interesting phenomena in the implementation of the controller for nonlinear dynamics. The bifurcation occurs when changing a parameter (in this paper, axial depth of cut b) changes the stability behavior of the system. The position of exiting of the eigenvalues of the Floquet matrix \(\Phi \) from the unit circle determines the type of bifurcation, e.g., Hopf, Flip, etc.

4 Simulation

In this section, we provide the simulation results of the proposed method. The parameters of the linear and nonlinear models are used from [38], where Moradi et al. presented a modal experimental procedure to determine these values (Table 1). Figure 3 compares the time response of linear and nonlinear dynamics for the open-loop milling system.

Table 1 Values of model parameters [38]
Full size table
Fig. 3
figure 3

Comparison of Linear (red) and Nonlinear (blue) dynamics. (Color figure online)

Full size image

4.1 Closed-loop behaviour

First, we design a stabilizing controller at \(b=2\)mm using Theorem 3. It implies the following control gain:

$$\begin{aligned} \kappa =\left[ \begin{matrix} -2.3108\times 10^5 &{} -1.9201\times 10^5 &{} -7.4160 &{} 1.5822\\ 1.2215\times 10^5 &{} -1.5913\times 10^4 &{} -1.6926 &{} -7.0255 \end{matrix} \right] \end{aligned}$$
(42)

The time response of the uncontrolled (open-loop system) and closed-loop system are shown in Figs. 4 and 5 for the nonlinear and linear plants, respectively. As can be seen, the open-loop system is unstable, while the closed-loop is asymptotically stable in both linear and nonlinear cases. The control forces (control inputs) for the nonlinear and linear processes are shown in Fig. 6.

Fig. 4
figure 4

Time response for the nonlinear system with controller (blue) and without the controller (red) at \(\Omega =3000\) rpm and b = 2 mm. (Color figure online)

Full size image
Fig. 5
figure 5

Time response for the linear system with controller (blue) and without the controller (red) at \(\Omega =3000\) rpm and b = 2 mm. (Color figure online)

Full size image
Fig. 6
figure 6

Controller forces \(u_x\) and \(u_y\) for the linear (blue) and nonlinear (red) system. (Color figure online)

Full size image

4.2 Stability lobes

The SLD of the process without (blue) and with control (red) are shown in Fig. 7. This figure is obtained from SDM for the linear system (solid lines) and manual trial-and-error for the nonlinear system (dots). In the manual trial-and-error method, at a fixed spindle speed, we increase the axial depth of cut b to obtain a stability boundary. Then we do this procedure in a loop for different spindle speeds. It is noticeable that the controller has caused a significant increase in the stability area. Note that the linear and nonlinear behaviours are closer for the lower axial depth of cut b as expected.

Fig. 7
figure 7

Stability lobes with controller (red) and without the controller (blue) for linear (solid lines) suing SDM and the nonlinear (dots) using manual trial-and-error. (Color figure online)

Full size image

For the high-speed milling with increasing the stability area, the design of the controller is needed to guarantee a larger stable area. To this end, we resolve the optimization problem with robustness for \(b_{\textrm{max}}=5\,\textrm{mm}\) and obtain the following result for the control gain:

$$\begin{aligned} \kappa =\left[ \begin{matrix} -3.9078\times 10^6 &{} -2.5988\times 10^6 &{} -23.4332 &{} 5.4984\\ -1.9101\times 10^6 &{} -2.3296\times 10^6 &{} -22.671 &{} -24.173 \end{matrix} \right] \end{aligned}$$
(43)

Figure 8 shows the stability lobes for high-speed milling (\(\Omega =\) 5000–70000 rpm) with this controller (red) and without controller (blue).

Fig. 8
figure 8

The high-speed milling stability lobes with controller (red) and without the controller (blue). (Color figure online)

Full size image

4.3 Bifurcation control

In the milling process, the system’s behavior switches from the stable to the unstable condition as the axial depth of cut increases in each spindle speed. Indeed, for every spindle speed, there is an axial depth of cut for which the bifurcation occurs. Figure 9 shows the (Hopf) bifurcation at the speed \(\Omega =\) 4500 rpm. In this case, the bifurcation occurs at \(b=1.65\,\textrm{mm}\).

Fig. 9
figure 9

The Hopf bifurcation. a Changing the axial depth of cut \(b=\) 1.5–1.8 mm at \(\Omega =4500\) rpm. b Exiting of the eigenvalues of the Floquet matrix \(\Phi \) from the unit circle

Full size image

In the high-speed milling, another type of bifurcation, so-called Flip bifurcation, is observed (Fig. 10). For instance, at \(\Omega =\) 55,000 rpm, by increasing the axial depth of cut, the eigenvalues of the Floquet matrix exit from the negative axis of the real axis.

Fig. 10
figure 10

The Flip bifurcation for the high-speed milling. a Changing the axial depth of cut b = 3–4 mm at \(\Omega =\) 55,000 rpm. b Exiting of the eigenvalues of the Floquet matrix \(\Phi \) from the unit circle

Full size image

Figures 11 and 12 illustrate the effect of the controller on the bifurcation and limit cycles at the spindle speeds of 3500 rpm and 5500 rpm, respectively. In addition to postponing the limit cycles to the higher depths of cut (about 1 mm in each case), it has reduced the vibration amplitudes.

Fig. 11
figure 11

Effect of the controller on the limit cycle at \(\Omega \) = 3500 rpm; without controller (red) at \(b=1.39\) mm; with the controller (blue) at \(b=2.31\) mm. (Color figure online)

Full size image
Fig. 12
figure 12

Effect of the controller on limit cycle at \(\Omega =5500\) rpm; without controller (red) at \(b=1.46\) mm; with the controller (blue) at \(b=2.45\) mm. (Color figure online)

Full size image

Figure 13 shows the phase portrait for the controlled system at \(\Omega =\) 5500 rpm and \(b = 4\) mm. As it is shown, the system has asymptotic steady behavior. By comparison with Fig. 10, we realize that the controller has changed the type of the flip bifurcation to the asymptotically stable behaviour. In fact, changing the type of bifurcation can be the goal of bifurcation control.

Fig. 13
figure 13

Phase portrait in the high-speed milling with the controller at \(\Omega =\) 55,000 rpm and \(b=4\) mm

Full size image

4.4 Robustness

In order to obtain a robust controller in presence of parametric uncertainty in \(k_x\), \(k_y\), \(c_x\), and \(c_y\), we use (32) with \(10\%\) uncertainty in \(k_x\) and \(c_x\), and \(20\%\) uncertainty in \(k_y\) and \(c_y\). It implies the following controller gain:

$$\begin{aligned} \kappa =\left[ \begin{matrix} -3.54\times 10^5 &{} -2.86\times 10^5 &{} -9.66 &{} 2.59\\ 1.41\times 10^5 &{} -2.32\times 10^4 &{} -2.31 &{} -8.29 \end{matrix} \right] \end{aligned}$$
(44)

The SLD with this controller (red) and without controller (green) for the minimum, maximum and nominal values in each of the four parameters \(k_x\), \(k_y\), \(c_x\) and \(c_y\) ( \(3^4=81\) totally) are shown in Fig. 14. The nominal plant with the controller and without it, is denoted in black. This diagram indicates that the controller can increase the stable region in the presence of parametric uncertainties corresponding to the stiffness and damping coefficients.

Fig. 14
figure 14

The SLDs with uncertainty in the stiffness and damping coefficients. With controller (red), without controller (green), and the nominal plant (black). (Color figure online)

Full size image

For the parameters such as the mass \(m_x, m_y\) that appears nonlinearly in matrices A and \( A_1\), we first plot the SLD for the process (without controller) in the presence of parametric uncertainty. Then, by choosing a proper value for \(b_{\textrm{max}}\) as the nominal case, control gain is designed. That is, the amount of \(b_{\textrm{max}}\) must be large enough to cover all of the SLD with uncertainty and be on top of them. Figure 15 shows the SLD for the process with \(20\%\) parametric uncertainty for \(m_y\) and \(10\%\) for \(m_x\). It provides five modes for \(m_y\) (\(m_y=\{0.8,0.9,1,1.1,1.2\}\times {\bar{m}}_y\)) as well as five modes for \(m_x\) (\(m_x=\{0.9,0.95,1,1.05,1.1\}\times {\bar{m}}_x\)) in total \(5^2=25\) different graphs.

Fig. 15
figure 15

The SLDs with uncertainty in the mass. With controller (red), without controller (green), and the nominal plant (black). (Color figure online)

Full size image

Time response of the process with an arbitrary set of uncertain parameters in the nonlinear and the linear cases are shown in Figs. 16 and 17, respectively. For this simulation, the parameters have been selected as \(m_x=1.1{\bar{m}}_x\), \(m_y=0.8{\bar{m}}_y\), \(k_x=1.1{\bar{k}}_x\), \(k_y=0.8{\bar{k}}_y\), \(c_x=0.9{\bar{c}}_x\), \(c_y=1.2{\bar{c}}_y\), \(\Omega =3000\,\textrm{rpm}\), \(b=2\,\textrm{mm}\). Figure 18 shows the input forces (control efforts), which are higher than those of the nominal plant forces (compare with Fig. 6).

Fig. 16
figure 16

Time response for the uncertain nonlinear system with controller (blue) and without the controller (red) at \(\Omega =3000\) rpm and \(b=2\) mm. (Color figure online)

Full size image
Fig. 17
figure 17

Time response for the uncertain linear system with controller (blue) and without the controller (red) at \(\Omega =3000\) rpm and \(b=2\) mm. (Color figure online)

Full size image
Fig. 18
figure 18

Controller forces \(u_x\) and \(u_y\) for the linear (blue) and nonlinear (red) uncertain system. (Color figure online)

Full size image

4.5 Comparison with an intelligent controller

In order to illustrate the efficiency of the proposed controller, we compare the Lyapunov–Krasovskii-based controller with a Learning-based intelligent controller presented in [39]. Figure 19 shows the time response of the process for \(\Omega = 4000\, \textrm{rpm}\) and \(b = 2.1\, \textrm{mm}\). As is shown, the proposed controller has lower transitions and lower settling times (higher speed) as well as a lower amplitude of the trajectories.

Fig. 19
figure 19

Time response for the nonlinear system with proposed controller (red) and the learning-based intelligent controller (blue) at \(\Omega =4000\) rpm and b = 2.1 mm. (Color figure online)

Full size image

Finally, in order to compare the performances of the two controllers, the Integral Absolute Error (IAE) index is defined as follows:

$$\begin{aligned} \textrm{IAE}&:=\int _{0}^\infty (|x(t)|+|y(t)|)\textrm{d}t \end{aligned}$$
(45)

Indeed, a lower value for the IAE corresponds to a better controller. By evaluating the IAE index (see Fig 19), it can be seen that the index for the intelligent controller is about 3.65 times higher than the proposed optimal control. Therefore, the proposed controller has improved IAE by about 3.65 times.

We ought to stress here that the presented method, among the active control methods, needs relatively less computational effort. For instance, unlike the MPC method [4], in which the optimization must be solved at every time step, in the presented methods, we solve an optimization only once that preserves stability and uncertainty simultaneously.

5 Conclusions

In this paper, a delay-independent optimal robust controller is developed for TDSs based on Lyapunov–Krasovskii and implemented for the milling process in the presence of parametric uncertainties. An inexpensive nonlinear optimization problem with LMI constraints is solved to determine the optimal stabilizing controller gain for the different parametric uncertainty. The objective function of the optimization is corresponding to the norm-2 of controller gain, while the IMI constraints guarantee stability and robustness. SLDs are obtained from the SDM, and they illustrated the increment of the stable regions via the proposed controller in both nominal and uncertain plants. Improving the adverse effects of the Hopf and Flip bifurcation was another advantage of the controller. We showed that the proposed controller almost doubled the stability area and approximately halved the radius of the limit cycles by postponing the stability margin to the higher axial depth. Moreover, it has improved the IAE index by about 3.65 times compared with an intelligent controller.

Designing a controller for nonlinear time-varying dynamics of the milling process and considering external stochastic disturbance in the system can be the future research directions. Moreover, applying the proposed method to more complex and high-dimensional dynamics and investigating in the real system, and getting experiment results are other potential research.