Fractional order mathematical model for B.1.1.529 SARS-Cov-2 Omicron variant with quarantine and vaccination

Abstract

In this paper, a fractional order nonlinear model for Omicron, known as B.1.1.529 SARS-Cov-2 variant, is proposed. The COVID-19 vaccine and quarantine are inserted to ensure the safety of host population in the model. The fundamentals of positivity and boundedness of the model solution are simulated. The reproduction number is estimated to determine whether or not the epidemic will spread further in Tamilnadu, India. Real Omicron variant pandemic data from Tamilnadu, India, are validated. The fractional-order generalization of the proposed model, along with real data-based numerical simulations, is the novelty of this study.

1 Introduction

As of November 24, 2021, Omicron has been found in several nations and was still the dominant variety everywhere. Omicron infection results in a less serious illness than infection with the earlier forms. Omicron may cause a milder form of disease, according to preliminary research, but some people who acquire this variant’s infection still run the risk of developing serious illness, needing hospitalization, and even passing away. One should take precautions even if only a tiny portion of those with Omicron infection require hospitalization because the high incidence of cases could collapse the healthcare system. The Omicron variation, also known as B.1.1.5 29 SARS-Cov-2 Variant, was less contagious than the original COVID-19 virus and the Delta variant. People who have the Omicron variant infection may exhibit symptoms that are similar to those of earlier forms. For an individual, experienced a prior infection, received a COVID-19 vaccination, and the existence of other health issues can all affect the presence and intensity of symptoms. The most effective public health measure for preventing COVID-19 and reducing the possibility of new variations arising is still COVID-19 vaccination. This covers the initial course, booster shots, and any necessary subsequent doses. It is anticipated that the current vaccines will guard against the serious sickness, hospital stays, and fatalities brought on by Omicron variant infection. Breakthrough infections in vaccinated people are also likely.

Several mathematical models have been developed in a wide range of manners to describe how diseases spread in sub-population compartments. In [1], the authors proposed a nonlinear model for the co-dynamics of tuberculosis and COVID-19. In [2], the authors modeled the spatial distribution of a COVID-19 with vaccination using a diffusion equation. In [3], the researchers proposed a novel delay-type model of COVID-19 with a convex incidence rate. The authors in [4] simulated the impact of quarantine and hospitalization on the transmission of COVID-19. In Peter et al. [5], proposed a novel model of COVID-19 using real data from Pakistan. In [6], the authors proposed a nonlinear model of COVID-19 for studying the outbreaks in Nigeria with optimal controls. The Omicron variant is challenging mathematicians to rethink models that have aided India’s comprehension of COVID-19 and response to the outbreak. With the next wave of the pandemic, everyone from those who get tested to whom most likely to get the virus has altered, providing new hurdles for those who model its impact. The vaccine class has been considered in the models, which allows appropriate antibodies to be supplied to the recovered and powerless persons in the host population when a wiped out individual recovers from an illness [7,8,9]. Asymptotic strong characteristics move from the infection free consistent state to the endemic consistent state. Because there are no known numerical approaches for developing Lyapunov capabilities for epidemic models, investigating the global aspects of a pestilence model framework is difficult [10, 11].

Many mathematical models have been constructed for COVID-19 without the vaccination and Quarantine compartment [12,13,14,15]. In this study, we combined the results of papers [16,17,18,19,20] to create an Omicron variant model with a variable population size.

The fractional derivatives have been utilized in the mathematical modeling of biological phenomena throughout the last few decades. This is due to the fact that fractional calculus can more precisely explain and process the retention and heritage characteristics of different materials than integer order models. As a result, many approaches have been used to examine the aforementioned field, including qualitative theory and numerical analysis. Therefore, using various mathematical methodologies, researchers enlarged the classical calculus to the fractional order. Considering mathematical models with fractional derivatives are effective instruments for researching infectious diseases [21,22,23]. The researchers looked at COVID-19 mathematical models using fractional order derivatives, and the findings were excellent [24,25,26,27,28,29,30].

We have constructed a fractional Omicron mathematical model in this research. The existence, uniqueness, and positivity of the solution are also deduced for the proposed Caputo-type fractional Omicron mathematical model by referring [31,32,33,34,35]. The paper is formulated as follows: In Sect. 2, we propose the fractional-order model by using Caputo fractional derivatives. In Sect. 3, we perform the qualitative analyses of the model containing the proofs of positivity and boundedness of the solution, existence of steady-state solutions, and the existence and uniqueness of the model solution. Computational simulations are done in Sect. 4 to validate and reinforce our theoretical findings for Omicron B.1.1.529 SARS-Cov-2. We conclude our findings in Sect. 5.

2 Model formulation

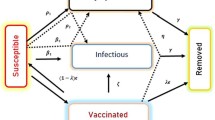
Firstly, we establish an integer-order model based on nonlinear ordinary differential equations. The total population denoted by N(t) is divided into state equations representing susceptible individuals S(t), exposed individuals E(t), infected individuals I(t), quarantined individuals Q(t), confirmed individuals $I_c(t)$, recovered individuals R(t), vaccinated individuals V(t), and the reservoir compartment W(t).

In the model development, there are associated concerns that (i) the birth and death rates are specific. (ii) People who are susceptible get contaminated if they come into contact with an infectious person who is not vaccinated. (iii) Vaccines lose their effectiveness over time, causing people to lose their immunity. (iv) A person who has been infected recovers after therapy. (v) No long-term recovery is possible. (vi) The population has a homogeneous combination. (vii) For Omicron, the COVID-19 vaccinations are indicated. (viii) Vaccine can be given to isolated people. (ix) Individuals who have been separated may pass out as a result of their isolation.

In the model, we are going to use the following notations given in Table 1.

Table 1 Parameters and their descriptions

Considering the given aspects, the integer-order mathematical model is derived as follows:

$$\begin{aligned} \frac{{\textrm{d}}S}{{\textrm{d}}t}= & {} \Lambda - \delta _n S - \mu _s SI + \rho _r R + \rho _v V, \nonumber \\ \frac{{\textrm{d}}E}{{\textrm{d}}t}= & {} \mu _s SI -(\delta _n + k + \gamma _i + \delta _c)E, \nonumber \\ \frac{{\textrm{d}}I}{{\textrm{d}}t}= & {} \gamma _i E-(\delta _n + \delta _e + \nu _r+\tau +\omega _c)I, \nonumber \\ \frac{{\textrm{d}}Q}{{\textrm{d}}t}= & {} kE + \tau I + \zeta _q I_c - (\gamma _r + \eta _v + \delta _n) Q, \nonumber \\ \frac{{\textrm{d}}I_c}{{\textrm{d}}t}= & {} \delta _c E-(\zeta _q +\gamma _c + \zeta _w +\delta _n)I_c, \nonumber \\ \frac{{\textrm{d}}R}{{\textrm{d}}t}= & {} \nu _r I+\gamma _r Q+\gamma _c I_c - (\delta _n + \rho _r + \alpha _v)R, \nonumber \\ \frac{{\textrm{d}}V}{{\textrm{d}}t}= & {} \eta _v Q+\alpha _v R - (\delta _n + \rho _v)V, \nonumber \\ \frac{{\textrm{d}}W}{{\textrm{d}}t}= & {} \omega _c I+\zeta _w I_c -\delta _n W, \end{aligned}$$

(1)

with the initial conditions $S(0) = S_0$, $E(0) = E_{0}$, $I(0) = I_{0}$, $Q(0)=Q_{0}$, $I_c(0) = I_{c_0}$, $R(0) = R_0$, $V(0) = V_0$, $W(0) = W_0$.

2.1 Fractional-order model formulation

In the integer-order systems, the fading memory crossover effects and some others, like a random walk, cannot be captured. It means the classical systems do not contain memory because classical derivative operators are local and cannot express the physical nature of the model efficiently. To overcome these drawbacks in our case, we consider a fractional-order model in this section.

Firstly, we recall the following definitions from fractional calculus.

Definition 1

Let $\Psi$ be a continuous function on [0, T]. The Caputo fractional derivative is given by [36]

$$\begin{aligned} ^CD^\delta \Psi (t)=\frac{1}{\Gamma (n-\delta )}\int _{0}^{t} (t-\alpha )^{n-\delta -1} \frac{{\textrm{d}}^n}{{\textrm{d}}\alpha ^n}\Psi (t)(\alpha ){\textrm{d}}\alpha , \end{aligned}$$

(2)

where $n = [\delta ]+1$ and $[\delta ]$ represents the integer part function.

Definition 2

The Riemann–Liouville fractional integral is given by [36]

$$\begin{aligned} {\mathcal {I}}^\delta \Psi (t)=\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} \Psi (\alpha ){\textrm{d}}\alpha . \end{aligned}$$

(3)

We have mentioned that the classical models do not contain memory because memory effects can only be better captured by using fractional-order derivatives. Therefore, the corresponding model of fractional-order differential equations in the Caputo sense is written as follows:

$$\begin{aligned} ^CD^\delta S= & {} \Lambda ^\delta - \delta _n^{\delta }S - \mu _s^{\delta } SI + \rho _r^{\delta }R + \rho _v^{\delta }V, \nonumber \\ ^CD^\delta E= & {} \mu _s^{\delta } SI -(\xi _1)E, \nonumber \\ ^CD^\delta I= & {} \gamma _i^{\delta }E-(\xi _2)I, \nonumber \\ ^CD^\delta Q= & {} k^\delta E + \tau ^{\delta } I + \zeta _q^{\delta }I_c - (\xi _3) Q, \nonumber \\ ^CD^\delta I_c= & {} \delta _c^{\delta }E-(\xi _4)I_c, \nonumber \\ ^CD^\delta R= & {} \nu _r^{\delta } I+\gamma _r^{\delta } Q+\gamma _c^{\delta }I_c - (\xi _5)R, \nonumber \\ ^CD^\delta V= & {} \eta _v^{\delta } Q +\alpha _v^{\delta }R - (\xi _6)V, \nonumber \\ ^CD^\delta W= & {} \omega _c^{\delta }I+\zeta _w^{\delta }I_c -\delta _n^{\delta }W, \end{aligned}$$

(4)

where $\xi _1 = \delta _n^{\delta } + k^\delta + \gamma _i^{\delta } +\delta _c^{\delta }$, $\xi _2=\delta _n^{\delta } + \delta _e^{\delta } +\nu _r^{\delta }+\tau ^{\delta } +\omega _c^{\delta }$, $\xi _3=\gamma _r^{\delta } + \eta _v^{\delta } + \delta _n^{\delta }$, $\xi _4 = \zeta _q^{\delta } +\gamma _c^{\delta } +\zeta _w^{\delta }+\delta _n^{\delta }$, $\xi _5 = \delta _n^{\delta } +\rho _r^{\delta } + \alpha _v^{\delta }$ and $\xi _6 = \delta _n^{\delta } + \rho _v^{\delta }$. The notation $^CD^\delta$ denotes the Caputo derivative operator with order $\delta$. The model is defined subject to the initial conditions $S(0) = S_0, E(0) = E_{0}, I(0) = I_{0}, Q(0)=Q_{0}, I_c(0) = I_{c_0}, R(0) = R_0, V(0) = V_0, W(0) = W_0$ (Fig. 1).

Fig. 1

Network of the model

3 Qualitative analyses

Here we derive some important analyses to explore the characteristics of the proposed Caputo-type fractional order model.

3.1 Positivity and boundedness of the model

To check the non-negativity of the solution, we define $R_{+}^{8}=\left\{ {\mathcal {U}} \in R^{8} \mid {\mathcal {U}} \ge 0\right\}$ and ${\mathcal {U}}(t)=(S(t), E(t), I(t), Q(t)$, $I_c(t), R(t), V(t), W(t))^{T}$

We recall the generalized mean values theorem.

Lemma 1

Let ${\mathcal {U}}({t}) \in {C}[{a}, {b}]$ and ${ }^{C} D_{t}^{\delta } {\mathcal {U}}({t}) \in ({a}, {b}]$, then ${\mathcal {U}}(t)={\mathcal {U}}(a)+\frac{1}{\Gamma (\beta )}\left( { }^{C} D_{t}^{\delta } {\mathcal {U}}\right) (\zeta )(t-a)^{\delta }$ with $a \le \zeta \le t, \forall t \in (a, b]$.

Corollary 2

Let ${\mathcal {U}}({t}) \in C[{a}, {b}]$ and ${ }^{\delta } D_{t}^{C} {\mathcal {U}}({t}) \in ({a}, {b}]$ where $\delta \in (0,1]$. Then, it is clear from Lemma 1 that if ${ }^{\delta } D_{t}^{C} {\mathcal {U}}({t}) \ge 0, \forall {t} \in ({a}, {b}]$, then the function ${\mathcal {U}}({t})$ is non-decreasing, and if ${ }^{\delta } D_{t}^{C} {\mathcal {U}}({t}) \le 0, \forall {t} \in ({a}, {b}]$, then the function ${\mathcal {U}}({t})$ is non-increasing for all $t \in [a, b]$.

To justify the non-negativity of the solution, it is necessary to show that the solution on every hyperplane bounding the positive orthant, the vector field points to $R_{+}^{8}$.

Theorem 3

If S(0), E(0), I(0), Q(0), $I_c(0)$, R(0), V(0), and W(0) are positive and bounded in $R+^8$, then S(t), E(t), I(t), Q(t), $I_c(t)$, R(t), V(t), and W(t) are also positive and bounded in $R+^8$ for all $t > 0$.

Proof

From model (4), we get

$$\begin{aligned}&{}^{C} D_{t}^{\delta } S(t)_{S=0} =\rho _r^{\delta }R + \rho _v^{\delta }V \ge 0, \\&{}^{C} D_{t}^{\delta } E(t)_{E=0}= \mu _s^{\delta } SI \ge 0, \\&{}^{C} D_{t}^{\delta } I(t)_{I=0}=\gamma _i^{\delta }E \ge 0, \\&{}^{C} D_{t}^{\delta } Q(t)_{Q=0} =k^\delta E + \tau ^{\delta } I + \zeta _q^{\delta }I_c \ge 0, \\&{}^{C} D_{t}^{\delta } I_c(t)_{I_c=0}= \delta _c^{\delta }E \ge 0, \\&{}^{C} D_{t}^{\delta } R(t)_{R=0} =\nu _r^{\delta } I+\gamma _r^{\delta } Q+\gamma _c^{\delta }I_c \ge 0, \\&{}^{C} D_{t}^{\delta } V(t)_{V=0} =\eta _v^{\delta } Q+\alpha _v^{\delta }R \ge 0, \\&{}^{C} D_{t}^{\delta } W(t)_{W=0} =\omega _c^{\delta }I+\zeta _w^{\delta }I_c \ge 0, \end{aligned}$$

Therefore, applying Corollary 2, we get that our solution is nonnegative and will lie in the defined feasible region.

By adding the equations of the model (4), we get

$$\begin{aligned} ^CD_t^\delta N= \Lambda ^\delta -(S+E+I+Q+I_c+R+V+W) \delta _n^{\delta }-\delta _e^{\delta } I, \end{aligned}$$

(5)

which gives ${^CD_t^\delta N} \le \Lambda ^\delta -N\delta _n^{\delta }$. Thus, by taking Laplace transform we get

$$\begin{aligned} N(s) \le \frac{\Lambda ^\delta }{s\big (s^\delta +\delta _n^{\delta }\big )} +N(0) \frac{s^{(\delta -1)}}{s^\delta +\delta _n^{\delta }}. \end{aligned}$$

(6)

By taking inverse Laplace transform and solving, we get

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } N(t) \le \frac{\Lambda ^\delta }{\delta _n^{\delta }} . \end{aligned}$$

(7)

Then it follows the positivity and boundedness of (4) for all t>0. $\square$

3.2 Existence of steady state solutions

The model (4) is static, i.e., the time independent solutions exist. The steady state solution in the infection-free state, when $I=0$, is derived by

$$\begin{aligned} E_q^0&= \big (S^0,E^0,I^0,Q^0,I_c^0,R^0,V^0,W^0\big )\nonumber \\&=\left( \frac{\Lambda ^\delta }{\delta _n^{\delta }}, 0, 0, 0, 0, 0, 0, 0 \right) . \end{aligned}$$

(8)

In the presence of infection, i.e., $I \ne 0$, the steady state solution is derived by

$$\begin{aligned} E_q^1 = \big (S^1,E^1,I^1,Q^1,I_c^1,R^1,V^1,W^1\big ), \end{aligned}$$

(9)

where

$$\begin{aligned} S^1= & {} \frac{\xi _2}{\gamma _i^{\delta }} \left( \frac{\Lambda ^\delta \mu _s^{\delta }\gamma _i^{\delta } -\delta _n^{\delta }\xi _1\xi _2}{\mu _s^{\delta } \big (\xi _1\xi _2-\rho _v^{\delta }\gamma _i^{\delta }J-\gamma _i^{\delta }G\big )}\right) ,\\ E^1= & {} \frac{\xi _1\xi _2}{\mu _s^{\delta }\gamma _i^{\delta }} \left( \frac{\Lambda ^\delta \mu _s^{\delta }\gamma _i^{\delta } -\delta _n^{\delta }\xi _1\xi _2}{\mu _s^{\delta } (\xi _1\xi _2-\rho _v^{\delta }\gamma _i^{\delta }J -\gamma _i^{\delta }G)}\right) , \\ I^1= & {} \frac{\Lambda ^\delta \mu _s^{\delta }\gamma _i^{\delta } -\delta _n^{\delta }\xi _1\xi _2}{\mu _s^{\delta } \big (\xi _1\xi _2-\rho _v^{\delta }\gamma _i^{\delta }J-\gamma _i^{\delta }G\big )}, \\ Q^1= & {} \frac{\xi _2\xi _4+\tau ^{\delta }\xi _4\gamma _i^{\delta } +\zeta _q^{\delta }\delta _c^{\delta }\xi _2}{\xi _3\xi _4 \gamma _i^{\delta }}\left( \frac{\Lambda ^\delta \mu _s^{\delta } \gamma _i^{\delta }-\delta _n^{\delta }\xi _1\xi _2}{\mu _s^{\delta }\big (\xi _1\xi _2-\rho _v^{\delta } \gamma _i^{\delta }J-\gamma _i^{\delta }G\big )}\right) , \\ I_c^1= & {} \frac{\delta _c^{\delta }\xi _2}{\xi _4\gamma _i^{\delta }} \left( \frac{\Lambda ^\delta \mu _s^{\delta }\gamma _i^{\delta } -\delta _n^{\delta }\xi _1\xi _2}{\mu _s^{\delta } \big (\xi _1\xi _2-\rho _v^{\delta }\gamma _i^{\delta }J -\gamma _i^{\delta }G\big )}\right) , \\ R^1= & {} \frac{\nu _r^{\delta }\gamma _i^{\delta } \xi _3\xi _4+\gamma _r^{\delta }\big (\xi _2\xi _4 +\tau ^{\delta }\xi _4\gamma _i^{\delta } +\zeta _q^{\delta }\delta _c^{\delta }\xi _2\big ) +\gamma _i^{\delta }\delta _c^{\delta }\xi _2\xi _3}{\gamma _i^{\delta }\xi _3\xi _4\xi _5}\\{} & {} \left( \frac{\Lambda ^\delta \mu _s^{\delta } \gamma _i^{\delta }-\delta _n^{\delta }\xi _1\xi _2}{\mu _s^{\delta } \big (\xi _1\xi _2-\rho _v^{\delta }\gamma _i^{\delta }J -\gamma _i^{\delta }G\big )}\right) , \\ V^1= & {} \frac{\eta _v^{\delta }\gamma _i^{\delta } \xi _5\big (\xi _2\xi _4+\tau ^{\delta }\xi _4\gamma _i^{\delta } +\zeta _q^{\delta }\delta _c^{\delta }\xi _2\big )}{\xi _3\xi _4 \gamma _i^{\delta }\xi _5} \\{} & {} +\frac{\alpha _v^{\delta }[\nu _r^{\delta } \gamma _i^{\delta }\xi _3\xi _4+\gamma _r^{\delta } \big (\xi _2\xi _4+\tau ^{\delta }\xi _4\gamma _i^{\delta } +\zeta _q^{\delta }\delta _c^{\delta }\xi _2\big ) +\gamma _i^{\delta }\delta _c^{\delta }\xi _2\xi _3]}{\xi _3\xi _4\gamma _i^{\delta }\xi _5}\\{} & {} \left( \frac{\Lambda ^\delta \mu _s^{\delta } \gamma _i^{\delta }-\delta _n^{\delta }\xi _1\xi _2}{\mu _s^{\delta } \big (\xi _1\xi _2-\rho _v^{\delta } \gamma _i^{\delta }J-\gamma _i^{\delta }G\big )}\right) , \\ W^1= & {} \frac{\gamma _i^{\delta }\omega _c^{\delta }\xi _4 +\zeta _w^{\delta }\delta _c^{\delta }\xi _2}{\delta _n^{\delta } \gamma _i^{\delta }\xi _4}\left( \frac{\Lambda ^\delta \mu _s^{\delta }\gamma _i^{\delta }-\delta _n^{\delta } \xi _1\xi _2}{\mu _s^{\delta }\big (\xi _1\xi _2-\rho _v^{\delta } \gamma _i^{\delta }J-\gamma _i^{\delta }G\big )}\right) , \end{aligned}$$

with

$$\begin{aligned} J= & {} \frac{\nu _r^{\delta }\gamma _i^{\delta }\xi _3\xi _4 +\gamma _r^{\delta }\big (\xi _2\xi _4+\tau ^{\delta }\xi _4 \gamma _i^{\delta }+\zeta _q^{\delta }\delta _c^{\delta }\xi _2\big ) +\gamma _i^{\delta }\delta _c^{\delta }\xi _2\xi _3}{\gamma _i^{\delta }\xi _3\xi _4\xi _5}, \\ G= & {} \frac{\eta _v^{\delta }\gamma _i^{\delta }\xi _5 \big (\xi _2\xi _4+\tau ^{\delta }\xi _4\gamma _i^{\delta } +\zeta _q^{\delta }\delta _c^{\delta }\xi _2\big )}{\xi _3\xi _4\gamma _i^{\delta }\xi _5} \\{} & {} +\frac{\alpha _v^{\delta }\big [\nu _r^{\delta } \gamma _i^{\delta }\xi _3\xi _4+\gamma _r^{\delta } \big (\xi _2\xi _4+\tau ^{\delta }\xi _4\gamma _i^{\delta } +\zeta _q^{\delta }\delta _c^{\delta }\xi _2\big ) +\gamma _i^{\delta }\delta _c^{\delta }\xi _2\xi _3\big ]}{\xi _3\xi _4\gamma _i^{\delta }\xi _5}. \end{aligned}$$

The fundamental reproduction number $R_0$ is calculated by next generation matrix method [37, 38]. Hence, $R_0$ is given by

$$\begin{aligned}&R_0(GV^{-1})\nonumber \\ {}&= \frac{\Lambda ^\delta \mu _s^{\delta } \gamma _i^{\delta }}{\delta _n^{\delta }\big (\delta _n^{\delta } + k^\delta + \gamma _i^{\delta } + \delta _c^{\delta }\big ) \big (\delta _n^{\delta } + \delta _e^{\delta } + \nu _r^{\delta } +\tau ^{\delta } +\omega _c^{\delta }\big )}. \end{aligned}$$

(10)

When $R_0 < 1$, contaminations are disappearing from the host population. However, if $R_0>1$, the contaminations harm and become endemic, likely to require appropriate clinical treatments to halt the disease’s spread.

Theorem 4

The disease-free equilibrium $E_{0}$ of the proposed model (4) is stable if $R_{0}<1$ and unstable if $R_{0}>1$.

Proof

To derive the stability analysis of the disease-free equilibrium points, we consider the linearization of the given model at any equilibrium point $(S^0,E^0,I^0,Q^0,I_c^0,R^0,V^0,$$W^0)$ as follows:

$$\begin{aligned} ^CD^\delta S= & {} \Lambda ^\delta - \delta _n^{\delta }S -\mu _s^{\delta } S^*I - \mu _s^{\delta } SI^* + \rho _r^{\delta }R +\rho _v^{\delta }V, \nonumber \\ ^CD^\delta E= & {} \mu _s^{\delta } S^*I + \mu _s^{\delta } SI^* -(\xi _1)E, \nonumber \\ ^CD^\delta I= & {} \gamma _i^{\delta }E-(\xi _2)I, \nonumber \\ ^CD^\delta Q= & {} k^\delta E + \tau ^{\delta } I +\zeta _q^{\delta }I_c - (\xi _3) Q, \nonumber \\ ^CD^\delta I_c= & {} \delta _c^{\delta }E-(\xi _4)I_c, \nonumber \\ ^CD^\delta R= & {} \nu _r^{\delta } I+\gamma _r^{\delta } Q +\gamma _c^{\delta }I_c - (\xi _5)R, \nonumber \\ ^CD^\delta V= & {} \eta _v^{\delta } Q +\alpha _v^{\delta }R - (\xi _6)V, \nonumber \\ ^CD^\delta W= & {} \omega _c^{\delta }I +\zeta _w^{\delta }I_c -\delta _n^{\delta }W. \end{aligned}$$

(11)

Using the Laplace transformation on both sides of above system provides

$$\begin{aligned} s^{\delta } {\mathscr {C}}[S(s)]-s^{\delta -1} S(0)= & {} \Lambda ^\delta -\delta _n^{\delta }{\mathscr {C}}[S(s)] - \mu _s^{\delta } I^*{\mathscr {C}}[S(s)] - \mu _s^{\delta } S^*{\mathscr {C}}[I(s)] \nonumber \\{} & {} + \rho _r^{\delta }{\mathscr {C}}[R(s)] +\rho _v^{\delta }{\mathscr {C}}[V(s)], \nonumber \\ s^{\delta } {\mathscr {C}}[E(s)]-s^{\delta -1} E(0)= & {} \mu _s^{\delta } I^*{\mathscr {C}}[S(s)] + \mu _s^{\delta } S^*{\mathscr {C}}[I(s)] -(\xi _1){\mathscr {C}}[E(s)], \nonumber \\ s^{\delta } {\mathscr {C}}[I(s)]-s^{\delta -1} I(0)= & {} \gamma _i^{\delta }{\mathscr {C}}[E(s)]-(\xi _2) {\mathscr {C}}[I(s)], \nonumber \\ s^{\delta } {\mathscr {C}}[Q(s)]-s^{\delta -1} Q(0)= & {} k^\delta {\mathscr {C}}[E(s)] + \tau ^{\delta } {\mathscr {C}}[I(s)] + \zeta _q^{\delta }{\mathscr {C}}[I_c(s)] - (\xi _3) {\mathscr {C}}[Q(s)], \nonumber \\ s^{\delta } {\mathscr {C}}[I_q(s)]-s^{\delta -1} I_q(0)= & {} \delta _c^{\delta }{\mathscr {C}}[E(s)]-(\xi _4){\mathscr {C}}[I_c(s)],\nonumber \\ s^{\delta } {\mathscr {C}}[R(s)]-s^{\delta -1} R(0)= & {} \nu _r^{\delta } {\mathscr {C}}[I(s)]+\gamma _r^{\delta } {\mathscr {C}}[Q(s)]+\gamma _c^{\delta }{\mathscr {C}}[I_c(s)] -(\xi _5){\mathscr {C}}[R(s)], \nonumber \\ s^{\delta } {\mathscr {C}}[V(s)]-s^{\delta -1} V(0)= & {} \eta _v^{\delta } {\mathscr {C}}[Q(s)]+\alpha _v^{\delta }{\mathscr {C}}[R(s)] -(\xi _6){\mathscr {C}}[V(s)], \nonumber \\ s^{\delta } {\mathscr {C}}[W(s)]-s^{\delta -1} W(0)= & {} \omega _c^{\delta }{\mathscr {C}}[I(s)]+\zeta _w^{\delta }{\mathscr {C}}[I_c(s)] -\delta _n^{\delta }{\mathscr {C}}[W(s)], \end{aligned}$$

(12)

where ${\mathscr {C}}[S(s)], {\mathscr {C}}[E(s)], {\mathscr {C}}[I(s)], {\mathscr {C}}[Q(s)], {\mathscr {C}}[I_(s)],$${\mathscr {C}}[R(s)], {\mathscr {C}}[V(s)]$, and ${\mathscr {C}}[W(s)]$ are the Laplace transformations of $S(t), E(t), I(t), Q(t), I_c(t), R(t), V(t)$, and W(t). The proposed system (12) can be rewritten by

$$\begin{aligned}&\Delta (s) \cdot [L[S(s)] L[E(s)]L[I(s)] L[Q(s)]\nonumber \\ {}&\quad [L[I_c(s)]L[R(s)]L[V(s)]L[W(s)]] \\&\quad =\left[ \nu _1(s) \nu _2(s)\nu _3(s) \nu _4(s)\nu _5(s)\nu _6(s)\nu _7(s)\nu _8(s)\right] , \end{aligned}$$

where

$$\begin{aligned}{} & {} \left( \begin{array}{l} \nu _1(s)=s^{\delta -1} S(0), \\ \nu _2(s)=s^{\delta -1} E(0), \\ \nu _3(s)=s^{\delta -1} I(0), \\ \nu _4(s)=s^{\delta -1} Q(0), \\ \nu _5(s)=s^{\delta -1} I_c(0), \\ \nu _6(s)=s^{\delta -1} R(0), \\ \nu _7(s)=s^{\delta -1} V(0), \\ \nu _8(s)=s^{\delta -1} W(0), \end{array}\right. \end{aligned}$$

$$\begin{aligned}{} & {} \Delta (s)=\left[ \begin{array}{cccccccc} s^{\delta }+\delta _n^{\delta }+\mu _s^{\delta } I^* &{} 0 &{} \mu _s^{\delta }S^* &{} 0 &{} 0 &{} -\rho _r^{\delta } &{} -\rho _v^{\delta } &{} 0 \\ -\mu _s^{\delta } I^* &{} s^{\delta }+\xi _1 &{} -\mu _s^{\delta }S^* &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -\gamma _i^{\delta } &{} s^{\delta }+\xi _2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -k &{} -\tau ^{\delta } &{} s^{\delta }+\xi _3 &{} -\zeta _q^{\delta } &{} 0 &{} 0 &{} 0 \\ 0 &{} -\delta _c^{\delta } &{} 0 &{} 0 &{} s^{\delta }+\xi _4 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -\nu _r^{\delta } &{} -\gamma _r^{\delta } &{} -\gamma _c^{\delta } &{} s^{\delta }+\xi _5 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\eta _v^{\delta } &{} 0 &{} -\alpha _v^{\delta } &{} s^{\delta }+\xi _6 &{} 0 \\ 0 &{} 0 &{} -\omega _c^{\delta } &{} 0 &{} -\zeta _w^{\delta } &{} 0 &{} 0 &{} s^{\delta }+\delta _n^{\delta } \\ \end{array}\right] , \end{aligned}$$

which is a characteristic matrix of system (12). Now, the characteristic matrix of the given system at disease-free equilibrium (DFE) $E_q^0 =\big (\frac{\Lambda ^\delta }{\delta _n^{\delta }},0, 0, 0, 0, 0, 0, 0 \big )$ is given by

$$\begin{aligned} \Delta (s)=\left[ \begin{array}{cccccccc} s^{\delta }+\delta _n^{\delta } &{} 0 &{} \mu _s^{\delta }S^* &{} 0 &{} 0 &{} -\rho _r^{\delta } &{} -\rho _v^{\delta } &{} 0 \\ 0 &{} s^{\delta }+\xi _1 &{} -\mu _s^{\delta }S^* &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -\gamma _i^{\delta } &{} s^{\delta }+\xi _2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -k^\delta &{} -\tau ^{\delta } &{} s^{\delta }+\xi _3 &{} -\zeta _q^{\delta } &{} 0 &{} 0 &{} 0 \\ 0 &{} -\delta _c^{\delta } &{} 0 &{} 0 &{} s^{\delta }+\xi _4 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -\nu _r^{\delta } &{} -\gamma _r^{\delta } &{} -\gamma _c^{\delta } &{} s^{\delta }+\xi _5 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\eta _v^{\delta } &{} 0 &{} -\alpha _v^{\delta } &{} s^{\delta }+\xi _6 &{} 0 \\ 0 &{} 0 &{} -\omega _c^{\delta } &{} 0 &{} -\zeta _w^{\delta } &{} 0 &{} 0 &{} s^{\delta }+\delta _n^{\delta } \\ \end{array}\right] . \end{aligned}$$

The eigenvalues are $-\delta _n^{\delta }$, $-\delta _n^{\delta }$, $\frac{1}{2}\big (-\xi _1-\xi _2-$ $\sqrt{\xi _1^2+4\mu _s^{\delta }S^* \gamma _i^{\delta }-2\xi _1\xi _2+\xi _2^2}\big )$, $\frac{1}{2}\big (-\xi _1-\xi _2+$ $\sqrt{\xi _1^2+4\mu _s^{\delta }S^* \gamma _i^{\delta }-2\xi _1\xi _2+\xi _2^2}\big )$, $-\xi _3$, $-\xi _4$, $-\xi _5$, $-\xi _6$. The given system (4) is stable when $-\xi _1-\xi _2+\sqrt{\xi _1^2+4\mu _s^{\delta }S^* \gamma _i^{\delta }-2\xi _1\xi _2+\xi _2^2}<0$ or $\sqrt{\xi _1^2+4\mu _s^{\delta }S^*\gamma _i^{\delta } -2\xi _1\xi _2+\xi _2^2}<(\xi _1+\xi _2)$ or $\xi _1^2+4 \mu _s^{\delta }S^*\gamma _i^{\delta }-2\xi _1\xi _2+\xi _2^2<(\xi _1+\xi _2)^2$ or $\mu _s^{\delta }S^*\gamma _i^{\delta }<\xi _1\xi _2$, i.e., $\frac{\mu _s^{\delta }S^*\gamma _i^{\delta }}{\xi _1\xi _2}< 1$. That is $R_0 < 1$. Clearly, infection free steady state $E^0$ is locally asymptotically stable if $R_0 < 1$ and unstable if $R_0 >1$. $\square$

3.3 Existence and uniqueness

The system (4) can be written in the form:

$$\begin{aligned} {}^{C}{D}^{\delta } U({t})= & {} {\mathcal {H}}({t}, {\mathcal {U}}({t})), \quad 0<\delta \le 1, \nonumber \\ U(0)= & {} U_{0}. \end{aligned}$$

(13)

To find the existence of solution, a Banach space is defined as ${{\mathcal {B}}}={B}_{1} \times {B}_{2} \times {B}_{3} \times {B}_{4} \times {B}_{5}\times {B}_{6} \times {B}_{7} \times {B}_{8}$, where ${B}_{i}=C([0, T])$, $(i=1,2, \ldots , 8)$ under the norm $\Vert {\mathcal {U}}\Vert$ = $\Vert \left( {S}, {E}, {I}, {Q}, I_c, {R}, V, W\right) \Vert$ = $\max _{t\in [0,t]}[\vert S(t) \vert ,\vert E(t) \vert$, $\vert I(t) \vert , \vert Q(t) \vert , \vert I_c(t) \vert , \vert R(t) \vert , \vert V(t) \vert , \vert W(t) \vert ]$.

Let ${{\mathcal {Z}}}: {A} \rightarrow {A}$ be an operator defined as follows:

$$\begin{aligned} {{\mathcal {Z}}}({\mathcal {U}})({t})=Z_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{{t}}({t}-{\alpha })^{\delta -1} {{\mathcal {H}}}(\alpha , {\mathcal {U}}(\alpha )) {{\textrm{d}}\alpha }. \end{aligned}$$

Using the Riemann Liouville type integral, Eq. (13) solved as follows: ${\mathcal {U}}({t})={\mathcal {U}}_{0} +\frac{1}{\Gamma (\theta )} \int _{0}^{{t}}({t}-{\alpha })^{\delta -1} {{\mathcal {H}}}({\alpha }, {\mathcal {U}}({\alpha })) {{\textrm{d}}\alpha }$ where

$$\begin{aligned} \left\{ \begin{array}{l} S(t)=S_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , S) {\textrm{d}}\alpha , \\ E(t)=E_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , E) {\textrm{d}}\alpha , \\ I(t)=I_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , I) {\textrm{d}}\alpha , \\ Q(t)=Q_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , Q) {\textrm{d}}\alpha , \\ I_c(t)={I-c}_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , I_c) {\textrm{d}}\alpha , \\ R(t)=R_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , R) {\textrm{d}}\alpha , \\ V(t)=V_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , V) {\textrm{d}}\alpha , \\ W(t)=W_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , W) {\textrm{d}}\alpha , \end{array}\right. \end{aligned}$$

(14)

with

$$\begin{aligned} \left\{ \begin{array}{l} {\mathcal {H}}(t, S)= \Lambda ^\delta - \delta _n^{\delta }S - \mu _s^{\delta } SI + \rho _r^{\delta }R + \rho _v^{\delta }V, \\ {\mathcal {H}}(t, E) = \mu _s^{\delta } SI -(\xi _1)E, \\ {\mathcal {H}}(t, I) = \gamma _i^{\delta }E-(\xi _2)I, \\ {\mathcal {H}}(t, Q) = k^\delta E + \tau ^{\delta } I + \zeta _q^{\delta }I_c - (\xi _3) Q, \\ {\mathcal {H}}(t, I_c) = \delta _c^{\delta }E-(\xi _4)I_c, \\ {\mathcal {H}}(t, R) = \nu _r^{\delta } I+\gamma _r^{\delta } Q+\gamma _c^{\delta }I_c - (\xi _5)R, \\ {\mathcal {H}}(t, V) = \eta _v^{\delta } Q+\alpha _v^{\delta }R - (\xi _6)V, \\ {\mathcal {H}}(t, W) = \omega _c^{\delta }I+\zeta _w^{\delta }I_c -\delta _n^{\delta }W. \end{array}\right. \end{aligned}$$

(15)

The following theorems show the existence of a solution.

Theorem 5

Let $S(t), E(t), I(t), Q(t), I_c(t), R(t), V(t)$ and W(t) be nonnegative bounded functions. Then the system (15) satisfies Lipschitz condition are contraction mappings, if the following condition holds, $0 \le N = \max \{ {\mathcal {F}}_{{\mathcal {H}}_1}$, ${\mathcal {F}}_{{\mathcal {H}}_2}$, ${\mathcal {F}}_{{\mathcal {H}}_3}$, ${\mathcal {F}}_{{\mathcal {H}}_4}$, ${\mathcal {F}}_{{\mathcal {H}}_5}$, ${\mathcal {F}}_{{\mathcal {H}}_6}$, ${\mathcal {F}}_{{\mathcal {H}}_7}$, ${\mathcal {F}}_{{\mathcal {H}}_8} \} < 1$, the functions are contractions.

Proof

Assume that $S(t), E(t), I(t), Q(t), I_c(t), R(t), V(t)$ and W(t) are nonnegative bounded functions. That is, there are some positive constants $\beta _{1}, \beta _{2}, \beta _{3}, \beta _{4}, \beta _{5}, \beta _{6}, \beta _{7}, \beta _{8}$, such that $\Vert S(t)\Vert \le \beta _{1}, \Vert E(t)\Vert \le \beta _{2}, \Vert I(t)\Vert \le \beta _{3}, \Vert Q(t)\Vert \le \beta _{4}, \Vert I_c(t)\Vert \le \beta _{5}, \Vert R(t)\Vert \le \beta _{6}, \Vert V(t)\Vert \le \beta _{7}, \Vert W(t)\Vert \le \beta _{8}$.

Considering the function ${\mathcal {H}}(\alpha , S)$, for any S and $S_1$, we can get

$$\begin{aligned} \left\| {\mathcal {H}}(\alpha , S)-{\mathcal {H}}(\alpha , S_1)\right\|&=\left\| \delta _n^{\delta }\left( S-S_1\right) +\mu _s^{\delta }I \left( S-S_1\right) \right\| \nonumber \\&\le \left\| \delta _n^{\delta }\left( S-S_1\right) \right\| +\left\| \mu _s^{\delta }I\left( S-S_1\right) \right\| \nonumber \\&\le \left( \delta _n^{\delta }+\mu _s^{\delta }\Vert I(t)\Vert \right) \left\| S-S_1\right\| \nonumber \\&\le \left( \delta _n^{\delta }+\mu _s^{\delta }\beta _{3}\right) \left\| S-S_{1}\right\| \nonumber \\&\le {\mathcal {F}}_{{\mathcal {H}}_1}\left\| S-S_{1}\right\| . \end{aligned}$$

(16)

where ${\mathcal {F}}_{{\mathcal {H}}_1}=\delta _n^{\delta } +\mu _s^{\delta }\beta _{3}$. Hence, ${\mathcal {H}}(\alpha , S)$ satisfies the Lipschitz condition. Similarly, we can find ${\mathcal {F}}_{{\mathcal {H}}_i}$, for $i= 2$,3,4,5,6,7,8 so that ${\mathcal {H}}(\alpha , S)$, ${\mathcal {H}}(\alpha , E)$, ${\mathcal {H}}(\alpha , I)$, ${\mathcal {H}}(\alpha , Q)$, ${\mathcal {H}}(\alpha , I_c)$, ${\mathcal {H}}(\alpha , R)$, ${\mathcal {H}}(\alpha , V)$, and ${\mathcal {H}}(\alpha , W)$ satisfy the Lipschitz’s conditions.

Also, when the condition $0 \le N = \max \{{\mathcal {F}}_{{\mathcal {H}}_1}$, ${\mathcal {F}}_{{\mathcal {H}}_2}$, ${\mathcal {F}}_{{\mathcal {H}}_3}$, ${\mathcal {F}}_{{\mathcal {H}}_4}$, ${\mathcal {F}}_{{\mathcal {H}}_5}$, ${\mathcal {F}}_{{\mathcal {H}}_6}$, ${\mathcal {F}}_{{\mathcal {H}}_7}$, ${\mathcal {F}}_{{\mathcal {H}}_8} \} < 1$ holds, the functions are contractions. $\square$

Equation (14) can be formulated as follows:

$$\begin{aligned} U_n(t) = \left\{ \begin{array}{l} S_n(t)=S_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , S_{n-1}) {\textrm{d}}\alpha , \\ E_n(t)=E_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , E_{n-1}) {\textrm{d}}\alpha , \\ I_n(t)=I_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , I_{n-1}) {\textrm{d}}\alpha , \\ Q_n(t)=Q_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , Q_{n-1}) {\textrm{d}}\alpha , \\ I_{c_n}(t)={I-c}_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , I_{c_{n-1}}) {\textrm{d}}\alpha , \\ R_n(t)=R_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , R_{n-1}) {\textrm{d}}\alpha , \\ V_n(t)=V_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , V_{n-1}) {\textrm{d}}\alpha , \\ W_n(t)=W_{0}+\frac{1}{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , W_{n-1}) {\textrm{d}}\alpha . \end{array}\right. \end{aligned}$$

The provided initial conditions establish the first elements of the given equations. The contrast between two terms is expressed by

$$\begin{aligned} \Psi _{1_n}(t)&=S_{n}(t)-S_{n-1}(t) \\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , S_{n-1})-{\mathcal {H}} (\alpha , S_{n-2})\right] {\textrm{d}}\alpha , \\ \Psi _{2_n}(t)&=E_{n}(t)-E_{n-1}(t) \\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , E_{n-1})-{\mathcal {H}} (\alpha , E_{n-2})\right] {\textrm{d}}\alpha , \\ \Psi _{3_n}(t)&=I_{n}(t)-I_{n-1}(t) \\&= \frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , S_{n-1})-{\mathcal {H}} (\alpha , S_{n-2})\right] {\textrm{d}}\alpha , \\ \Psi _{4_n}(t)&=Q_{n}(t)-Q_{n-1}(t) \\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , Q_{n-1})-{\mathcal {H}} (\alpha , Q_{n-2})\right] {\textrm{d}}\alpha , \\ \Psi _{5_n}(t)&=I_{c_{n}}(t)-I_{c_{n-1}}(t)\\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , I_{c_{n-1}})-{\mathcal {H}} (\alpha , I_{c_{n-2}})\right] {\textrm{d}}\alpha , \\ \Psi _{6_n}(t)&=R_{n}(t)-R_{n-1}(t) \\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , R_{n-1})-{\mathcal {H}} (\alpha , R_{n-2})\right] {\textrm{d}}\alpha , \\ \Psi _{7_n}(t)&=V_{n}(t)-V_{n-1}(t) \\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , V_{n-1})-{\mathcal {H}} (\alpha , V_{n-2})\right] {\textrm{d}}\alpha , \\ \Psi _{8_n}(t)&=W_{n}(t)-W_{n-1}(t) \\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , W_{n-1})-{\mathcal {H}} (\alpha , W_{n-2})\right] {\textrm{d}}\alpha , \end{aligned}$$

where

$$\begin{aligned} U_n(t) = {\left\{ \begin{array}{ll} S_{n}(t)=\sum _{i=0}^{n} \Psi _{1_i}(t), &{} E_{n}(t)=\sum _{i=0}^{n} \Psi _{2_i}(t), \\ I_{n}(t)=\sum _{i=0}^{n} \Psi _{3_i}(t), &{} Q_{n}(t)=\sum _{i=0}^{n} \Psi _{4_i}(t), \\ I_{c_n}(t)=\sum _{i=0}^{n} \Psi _{5_i}(t), &{} R_{n}(t)=\sum _{i=0}^{n} \Psi _{6_i}(t), \\ V_{n}(t)=\sum _{i=0}^{n} \Psi _{7_i}(t), &{} W_{n}(t)=\sum _{i=0}^{n} \Psi _{8_i}(t). \end{array}\right. } \end{aligned}$$

(17)

Consider

$$\begin{aligned} \left\| \Psi _{1_n}(t)\right\|&=\left\| S_{n}(t)-S_{n-1}(t)\right\| \\&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}} (\alpha , S_{n-1})-{\mathcal {H}}(\alpha , S_{n-1})\right] {\textrm{d}}\alpha \\&=\frac{\beta _{1}}{\Gamma (\delta )} \int _{0}^{t}\left\| S_{n-1} -S_{n-2}\right\| {\textrm{d}}\alpha \\&=\frac{\beta _{1}}{\Gamma (\delta )} \int _{0}^{t} \left\| \Psi _{1_{n-1}}(t)\right\| {\textrm{d}}\alpha . \end{aligned}$$

Hence, we can get

$$\begin{aligned} \left\| \Psi _{i_n}(t)\right\| =\frac{\beta _{i}}{\Gamma (\delta )} \int _{0}^{t}\left\| \Psi _{i_{n-1}}(t)\right\| {\textrm{d}}\alpha \ {\textrm{for}} \ i = 1,2,\ldots 8. \end{aligned}$$

(18)

The system (17) exists and smooth.

For, we have that the functions S(t), E(t), I(t), Q(t), $I_c(t)$, R(t), V(t) and W(t) are bounded and all kernels ${\mathcal {H}}(t,S)$, ${\mathcal {H}}(t,E)$, ${\mathcal {H}}(t,I)$, ${\mathcal {H}}(t,Q)$, ${\mathcal {H}}(t,I_c)$, ${\mathcal {H}}(t,R)$, ${\mathcal {H}}(t,V)$ and ${\mathcal {H}}(t,W)$ fulfill Lipschitz’s conditions; thus, we get the following relations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \left\| \Psi _{1_n}(t)\right\| \le \Vert S(0)\Vert \left\| \frac{\beta _{1}}{\Gamma (\delta )} t\right\| ^{n}, &{} \left\| \Psi _{2_n}(t)\right\| \le \Vert E(0)\Vert \left\| \frac{\beta _{2}}{\Gamma (\delta )} t\right\| ^{n}, \\ \left\| \Psi _{3_n}(t)\right\| \le \Vert I(0)\Vert \left\| \frac{\beta _{3}}{\Gamma (\delta )} t\right\| ^{n}, &{} \left\| \Psi _{4_n}(t)\right\| \le \Vert Q(0)\Vert \left\| \frac{\beta _{4}}{\Gamma (\delta )} t\right\| ^{n}, \\ \left\| \Psi _{5_n}(t)\right\| \le \Vert I_c(0)\Vert \left\| \frac{\beta _{5}}{\Gamma (\delta )} t\right\| ^{n}, &{} \left\| \Psi _{6_n}(t)\right\| \le \Vert R(0)\Vert \left\| \frac{\beta _{6}}{\Gamma (\delta )} t\right\| ^{n}, \\ \left\| \Psi _{7_n}(t)\right\| \le \Vert V(0)\Vert \left\| \frac{\beta _{7}}{\Gamma (\delta )} t\right\| ^{n}, &{} \left\| \Psi _{8_n}(t)\right\| \le \Vert W(0)\Vert \left\| \frac{\beta _{8}}{\Gamma (\delta )} t\right\| ^{n}. \end{array}\right. } \end{aligned}$$

(19)

The system (19) shows the existence and smoothness of the function defined in (17).

Theorem 6

Let ${{\mathcal {Z}}}: {{\mathcal {A}}} \rightarrow {{\mathcal {A}}}$ be completely continuous and let ${\mathcal {H}}:[0, T] \times {{\mathcal {A}}} \rightarrow {\mathbb {R}}$ be continuous and there exists a constant ${\mathcal {F}}_{{\mathcal {H}}}>0$ such that for ${U}, {U_1} \in {\mathcal {A}}$,

$$\begin{aligned} \vert {\mathcal {H}}(t, U)-{\mathcal {H}}(t, U_1)\vert \le {\mathcal {F}}_{{\mathcal {H}}}\vert U-U_1\vert \end{aligned}$$

is hold. Then there is at least one solution for the considered system (4).

Proof

To prove the operator, ${\mathcal {Z}}$ is completely continuous. The sequence $\left\{ U_{n}\right\}$ converges to $U \in {\mathcal {A}}$. After n-iterations define the remainder terms as $D_{1_n}(t)$, $D_{2_n}(t)$, $D_{3_n}(t)$, $D_{4_n}(t)$, $D_{5_n}(t)$, $D_{6_n}(t)$, $D_{7_n}(t)$, $D_{8_n}(t)$, such that

$$\begin{aligned} S(t)-S(0)= & {} S_{n}(t)-D_{1_n}(t), \ E(t)-E(0) = E_{n}(t)-D_{2_n}(t) \\ I(t)-I(0)= & {} I_{n}(t)-D_{3_n}(t), \ Q(t)-Q(0) = Q_{n}(t)-D_{4_n}(t), \\ I_c(t)-I_c(0)= & {} I_{c_n}(t)-D_{5_n}(t), \ R(t)-R(0) = R_{n}(t)-D_{6_n}(t), \\ V(t)-V(0)= & {} V_{n}(t)-D_{7_n}(t), \ W(t)-W(0) =W_{n}(t)-D_{8_n}(t). \end{aligned}$$

Using triangle inequality along with the Lipschitz condition of ${\mathcal {H}}(t, S)$, we obtain:

$$\begin{aligned} \left\| D_{1_n}(t)\right\|&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , S)-{\mathcal {H}} (\alpha , S_{n-1})\right] {\textrm{d}}\alpha \\&\le \frac{\beta _{1}}{\Gamma (\delta )} \left\| S-S_{n-1}\right\| t . \end{aligned}$$

Using the above process recursively, we get

$$\begin{aligned} \left\| D_{1_n}(t)\right\| \le \left\| \frac{C_{1}}{\Gamma (\delta )} t\right\| ^{n+1} \beta _{1}. \end{aligned}$$

Then, at $t_{0}>1$

$$\begin{aligned} \left\| D_{n}(t)\right\| \le \left\| \frac{C_{1}}{\Gamma (\delta )} t_{0}\right\| ^{n+1} \beta _{1}. \end{aligned}$$

Taking limit as n tends to infinity, we get

$$\begin{aligned} \lim _{n \rightarrow \infty }\left\| D_{1_n}(t)\right\| \le \lim _{n \rightarrow \infty } \left\| \frac{C_{1}}{\Gamma (\delta )} t_{0}\right\| ^{n+1} \beta _{1}. \end{aligned}$$

(20)

For $\frac{C_{i}}{\Gamma (\delta )} t_{0}<1$, Eq. (20) becomes $\lim _{n \rightarrow \infty }\left\| D_{1_n}(t)\right\| =0$ Similarly, as n tends to infinity, we can get $\left\| D_{i_n}(t)\right\| \rightarrow 0$.

Hence, for $t \in [0, T]$, we have $S_{n}(t) \rightarrow S(t) \ as \ n\rightarrow \infty$, and therefore,

$$\begin{aligned} \left\| {\mathcal {Z}}(S_{n})-{\mathcal {Z}}(S)\right\|&\le \frac{1}{\Gamma (\delta )} \max _{t \in [0, T]}\\&\quad \int _{0}^{t}(t-\alpha )^{\delta -1}\vert {\mathcal {H}} (\alpha , S_{n}(\alpha ))-{\mathcal {H}}(\alpha , S(\alpha ))\vert {\textrm{d}}\alpha , \\&\le \frac{{\mathcal {F}}_{{\mathcal {H}}}}{\Gamma (\delta )} \Vert S_{n}-S\Vert _{t \rightarrow [0, T]} \\&\quad \int _{0}^{t}(t-\alpha )^{\delta -1} {\textrm{d}}\alpha \le \frac{T^{\delta } {\mathcal {F}}_{{\mathcal {H}}}}{\Gamma (\delta +1)}\left\| S_{n}-S\right\| . \end{aligned}$$

Fig. 2

Exposed E(t) and infected I(t) people against time t in the data of Tamilnadu

Fig. 3

Isolated Q(t) and recovered R(t) people against time t in the data of Tamilnadu

Fig. 4

The infected I(t) against time t for the districts Chennai and Chengalpattu of Tamilnadu

Fig. 5

The infected I(t) against time t for the districts Coimbatore and Vellore of Tamilnadu

Fig. 6

Exposed E(t) and confirmed $I_c(t)$ people against time t

Fig. 7

Vaccinated V(t) and reservoir W(t) people against time t

Fig. 8

Stability of the given Omicron system against time t in the four districts Coimbatore, Chennai, Chengalpattu and Vellore of Tamilnadu

Since $S_{n} \rightarrow S$, $\Vert {\mathcal {Z}}\left( S_{n}\right) -{\mathcal {Z}}(S)\Vert \rightarrow 0$ as $n \rightarrow \infty$ and hence $\Vert {\mathcal {Z}}\left( U_{n}\right) -{\mathcal {Z}}(U)\Vert \rightarrow 0$ as $n \rightarrow \infty$. Thus, ${\mathcal {Z}}$ is continues. Let a bounded set ${\mathcal {M}} \subset {\mathcal {A}}$. Then by definition of ${\mathcal {A}}$, $\vert {\mathcal {H}}({t}, {\mathcal {U}}(t))\vert \le {\mathcal {L}}_{{\mathcal {H}}}, {\mathcal {L}}_{{\mathcal {H}}}>0, \forall U \in {\mathcal {M}}$. Then for each $U \in {\mathcal {M}}$, we can obtain

$$\begin{aligned} \Vert {\mathcal {Z}}(U)\Vert&\le \frac{1}{\Gamma (\delta )} \max _{t \rightarrow [0, T]} \int _{0}^{t}(t-\alpha )^{\delta -1} \vert {\mathcal {H}}(\alpha , Z(\alpha ))\vert {\textrm{d}}\alpha \\&\le \frac{{\mathcal {L}}_{{\mathcal {H}}}}{\Gamma (\delta )} \max _{t \rightarrow [0, T]} \int _{0}^{t}(t-\alpha )^{\delta -1} {\textrm{d}}\alpha \le \frac{T^\delta {\mathcal {L}}_{{\mathcal {H}}}}{\Gamma (\delta +1)}. \end{aligned}$$

Thus, ${{\mathcal {Z}}}$ is uniformly bounded. Further, suppose $0 \le t_2 \le t_1 \le T$. Then

$$\begin{aligned}&\Vert {\mathcal {Z}}(U)(t_{1})-{\mathcal {Z}}(U)(t_{2})\Vert \\&\quad \le \frac{{\mathcal {L}}_{{\mathcal {H}}}}{\Gamma (\delta )} \max _{t \rightarrow [0, T]}\left| \int _{0}^{t_{1}} (t_{1} - \alpha )^{\delta -1} {\textrm{d}}\alpha - \int _{0}^{t_{2}} ({t}_{2}-\alpha )^{\delta -1} {\textrm{d}}\alpha \right| , \\&\quad \le \frac{{\mathcal {L}}_{{\mathcal {H}}}}{\Gamma (\delta +1)} \max _{t \rightarrow [0, T]}\vert t_{1}^{\delta }-t_{2}^{\delta } \vert \rightarrow 0 \ {\textrm{as}} \ t_{1} \rightarrow t_{2}. \end{aligned}$$

Table 2 Omicron status across the districts of Tamilnadu as on March 11, 2022

Fig. 9

Infected, isolated and recovered individuals against time t in Tamilnadu

Fig. 10

Stability condition of the Tamilnadu against time t with various $\delta$

Fig. 11

Recovered range about various reproduction numbers 0.66, 0.92, 0.63 and 0.06 in Chennai and Coimbatore districts

Fig. 12

Recovered range about various reproduction numbers 0.66, 0.92, 0.63 and 0.06 in Chengalpattu and Vellore districts

Fig. 13

Isolated, confirmed, recovered and vaccinated people of four districts for the given data when $\delta =1$

Thus, ${\mathcal {Z}}$ is equicontinuous. ${\mathcal {Z}}$ is compact, and hence, it is completely continuous because of the continuousness and boundedness, it. Let $\Psi =\{U \in {\mathcal {A}}: U=\rho {\mathcal {Z}}(U), \rho \in [0,1]\}$, we need to confirm that $\Psi$ is bounded. Suppose $U \in \Psi$, say S, then for $t \in [0$, T], we have:

$$\begin{aligned} \Vert S\Vert&=\max _{t \rightarrow [0, T]}\left\{ \frac{\rho }{\Gamma (\delta )} \int _{0}^{t}(t-\alpha )^{\delta -1} {\mathcal {H}}(\alpha , S(\alpha )) {\textrm{d}}\alpha \right\} \\&\le \frac{{\mathcal {L}}_{{\mathcal {H}}}}{\Gamma (\delta )} \max _{T \rightarrow [0, T]} \int _{0}^{t}(t-\alpha )^{\delta -1} {\textrm{d}}\alpha \le \frac{T^{\delta } {\mathcal {L}}_{{\mathcal {H}}}}{\Gamma (\delta +1)} . \end{aligned}$$

Thus, the operator is completely continuous. The set $\Psi$ is also bounded. Therefore, ${\mathcal {Z}}$ has at least one fixed point [39]. So, the considered system (4) has the same number of solutions. $\square$

Theorem 7

If $\frac{\beta _{i}}{\Gamma (\delta )} t<1$, for $i=1,2, \ldots , 8$, then the system (4) has a unique solution.

Proof

Assume that $\{S_{\nu }(t), E_{\nu }(t), I_{\nu }(t)$, $Q_{1}(t), I_{c_\nu }(t), R_{\nu }(t), V_{\nu }(t), W_{\nu }(t)\}$ is another set of solutions of the system (4); then,

$$\begin{aligned} \left\| S(t)-S_{\nu }(t)\right\|&=\frac{1}{\Gamma (\delta )} \int _{0}^{t}\left[ {\mathcal {H}}(\alpha , S)-{\mathcal {H}} (\alpha , S_{\nu })\right] {\textrm{d}}\alpha \\&=\frac{\beta _{1}}{\Gamma (\delta )}t \Vert S(t)-S_{\nu }(t)\Vert . \end{aligned}$$

Thus,

$$\begin{aligned} \left( 1-\frac{\beta _{1}}{\Gamma (\delta )} t\right) \Vert S(t)-S_{1}(t)\Vert \le 0. \end{aligned}$$

(21)

Since $\frac{\beta _{i}}{\Gamma (\delta )} t<1$ for $i = 1$, (21) becomes $\left\| S(t)-S_{\nu }(t)\right\| =0.$

Hence, $S(t)=S_{\nu }(t)$. Similarly, for $i=2,3, \ldots , 8$, we can get $E(t)=E_{\nu }(t); \ I(t)=I_{\nu }(t); \ Q(t)=Q_{\nu }(t); \ I_{c_\nu }(t)=I_{c_\nu }(t); R(t)=R_{\nu }(t); \ V(t)=V_{\nu }(t)$; $W(t)=W_{\nu }(t)$. Hence, the system (4) has a unique solution. $\square$

4 Numerical analysis

In the second wave of the corona virus, India experienced a high infection rate. We have gathered data from Tamilnadu, India for our study [40]. The first case of the Omicron strain of SARS-CoV-2 by a traveler from another nation was reported in Tamil Nadu on Wednesday, December 15th. Tamil Nadu has been infected with the highly transmissible and fast-spreading form of SARS-CoV-2 just three weeks after the first confirmed Omicron case was reported.

On December 29, when 739 people tested positive, the number of daily cases began to rise, quickly reaching over 10,000 on January 8. In the initial wave, it took 58 days for the daily count in the state to rise from 1000 to nearly 7000 cases. It took 26 days for the cases in the second wave to rise from 1000 to over 7000. The number of cases reached 36,000 after another 38 days. The daily instances, on the other hand, have only taken 7 days to increase from 1000 to 7000. Chennai has quickly become a hotspot, fueling the growth. Due to the high caseload, Chengalpattu, Coimbatore and Vellore are the other areas of concern. Whole genome sequencing revealed that 99.9% of the samples were of the Delta variant in the last three months. Earlier, it was 65% Omicron and 35% Delta due to the fast changing situation. According to a statement released by the Tamil Nadu public health department, the BA.2 sub variation of Omicron was found in 18.4% of the samples sequenced in the state from January to March 2022. On March 11th, the state of Tamilnadu achieves a safe position against the propagation of Omicron viruses and a death rate of zero [40,41,42,43]. Mathematica is used to calculate the numerical solution using Adams–Bashforth–Moulton scheme. The values of the variables and parameters are listed in Tables 1 and 2.

Table 3 Values of the variables

The solution for (4) demonstrates that it is unstable locally and will never become stable when $R_0>1$, as shown in the figures. The steady state solution becomes stable when the contact rate is controlled and the vaccination class is increased when $R_0<1$. We conclude from all of the data that if the number of isolated, recovered, and vaccinated people increases, the host community will be safe from the Omicron variant. We also discovered that if the intercessions are strictly followed, the spread of the second wave of SARS Cov-2 Omicron variant is reduced.

Figures 2 and 3 describe the visualization of the impact of Omicron variant in the susceptible individual, infected individual, isolated individual and recovered individual against time t in the overall state of Tamilnadu.

Figures 4 and 5 illustrate the infected individuals against time t in Tamilnadu’s four districts. Because the government increased the number of quarantine and vaccination facilities, the number of infected people has decreased significantly.

Figures 6 and 7 describe the exposed, confirmed, vaccinated and the reservoir rates of the host of human population, respectively, against the time t in the state of Tamilnadu. Figs. 2 and 6 show how persons in Tamilnadu were infected and confirmed with the Omicron variant in the beginning and recovered by the end of March 11th, 2022. It is obvious from Figs. 2 and 6 that once the exposed population increases, all other compartments increase as well. Due to the loss of immunity, we see a newfound availability of susceptible individuals after nearly 50 days in our model. In addition, if there is an increase in isolated and vaccinated classes, a disease-free field will exist after 80 days when $\delta =0.97$.

The stability of the Omicron mathematical model for the four districts of Chennai, Coimbatore, Chengalpattu and Vellore is depicted in Fig. 8. During the Omicron period, which runs from December 25th to March 11th, 2022, the people of these four districts have a high rate of illness. When people were vaccinated according to government instructions, the infection rate progressively decreased to a low level. From the fractional-order simulations, we notice that according to the various fractional-order cases, the infection can take more time to disappear from the population compared to integer-order observations. The biological reason for such delay in disease control can be not following the quarantine, not taking the vaccine, or not using basic protective controls. Integer-order derivatives can’t capture such effects.

According to Table 2, as of March 11, the number of infected people in these four districts has decreased to 42, 13, 12 and 4 in the districts of Chennai, Coimbatore, Chengalpattu and Vellore, respectively, based on RT PCR sample tests 3233, 1233, 1286 and 1017, with no death.

Figure 9 describes the relation between the rates of infected, isolated and recovered people in the infection period of Omicron in Tamilnadu state.

Figure 10 demonstrates the stability graph representation of the constructed model in the host population in Tamilnadu with various order of $\delta$. Figure 10 shows that when the Omicron variant was first discovered, its spread was rapid, and when the government implemented quarantine and vaccination at a high rate, the variant’s spread was reduced to a safe level. On March 11, 2022, the state of Tamilnadu discovered that no one had caused the death of Omicron. COVID-19 vaccinations helped people avoid infection with the SARS CoV-2 Omicron variant.

Figures 11 and 12 describe the recovered rate of the four districts Chennai, Coimbatore, Chengalpattu and Vellore according to the corresponding reproduction numbers 0.66, 0.92, 0.63 and 0.06.

Figure 13 describes the isolated, confirmed, recovered and vaccinated individuals rates of the four districts Chennai, Coimbatore, Chengalpattu and Vellore.

We can observe from Fig. 13 and Table 3 that the infected rate decreases and the recovered rate increased after a rapid spread over a short time with the reproduction number $R_0 < 1$. As a result, the system in the four districts, as well as the entire state of Tamilnadu, is stable.

5 Conclusions

In this research, a novel epidemic fractional-order mathematical model for Omicron B.1.1.529 SARS-Cov-2 Variant was developed with eight compartments and important parameters. The data acquired from Tamil Nadu and several of its districts, together with our mathematical model, suggest that the Omicron variant infection has stabilized after a few months. This model outperforms other mathematical models by taking into account the nonlinear force of quarantine, vaccine, infection and care, as well as the right inclusion of valuable parameters. The principles of reproduction number calculated with this model are an outbreak threshold that determined whether or not the disease would go further in Tamilnadu where $R_0<1$. The fundamentals of positivity, boundedness and the existence of unique solutions have been examined and validated. There are infection-free steady-state solutions that are asymptotically stable when $R_0<1$. Finally, the current Omicron variant pandemic data of Tamilnadu, India, are validated. In the fractional-order simulations, we have observed the possibility of delay in the decrement of Omicron cases. The biological reason for such delay in disease control can be not following the quarantine, not taking the vaccine, or not using basic protective controls. Such effects could not be captured by using integer-order derivatives.

In the future, the proposed model can be considered to forecast disease outbreaks for any other real data. Also, the same model can be generalized by using several other fractional derivatives.