1 Introduction

Heinrich Wilhelm Gottfried von Waldeyer-Hartz, a German scientist, is credited with coining the term “neuron” in 1891. Neurons are nerve cells that send and receive messages from the brain. The neuron is made up of a cell body, or soma, with branching dendrites that act as signal receivers and an axon that carries nerve signals. The axon terminals send the electrochemical signal across a synapse at the opposite end of the axon (the space between the axon terminal and the receiving cell).

Neuron dynamics have been described using a variety of models. A set of first-order ordinary differential equations has been used to describe the dynamic behavior that a neuron model exhibits. The Hodgkin–Huxley (HH) model [1], which takes into account the ionic process and current on the surface of the cell membrane, is the most well-known dynamical model of the biological neuron. It represents the behavior of the membrane action potential of the giant squid axon. The authors of [2] proposed the Leaky Integrate and Fire neuron (LIF), which is generally used in experiments on large networks. In [3], a silicon hardware implementation of neurons considered in neuromorphic circuits was explored. The accuracy of the LIF neuron was not good because of its unrealistic simplicity, so it did not match with experimental outputs. In ref. [4], an optimized realization of the Morris-Lecar neuromorphic model was introduced. In ref. [5], the Hindmarsh–Rose neuron model was considered to take memristors to imitate the connection between the magnetic flux and membrane potential of the electromagnetic field. Several neuron models [6,7,8] have been introduced to analyze the electrical behaviors of neuron and the outcomes are used to produce similar phases and modes such as spiking, quiescent, bursting, and even chaotic states.

Fractional calculus, one of the most useful areas of research in applied mathematics, contains various types of differential and integral operators [9,10,11,12]. Fractional-order operators have been successfully implemented to describe a number of real-world problems. The authors in [13] introduced a fractional mathematical model for the huanglongbing transmission within a citrus tree. In [14], a study on the structure of the alkali-silica chemical reaction model using the Caputo fractional derivatives has been proposed. A Caputo-type corneal shape mathematical model with novel observations has been given in [15]. In [16], the optimal controls on the transmission of the bovine schistosomiasis epidemic model have been derived using fractional derivatives. The authors in [17] have introduced a fractal-fractional model of the AH1N1/09 virus. In [18], some novel analyses of a non-autonomous cardiac conduction model have been performed. In [19], the dynamics of a linear triatomic molecule have been defined using fractional derivatives.

The fractional derivatives have been implemented to analyze the models of neuron. In [20], the authors have proposed a fractional model with synchronization of electrically coupled neuron systems. In [21], a fractional leaky integrate and fire model has been given, considering neuronal spike timing adaptation. In [22], the fractional Izhikevich and Fitzhugh–Nagumo neuron modeling was introduced. In [23], the spiking and bursting behaviors of the fractional Izhikevich model were discussed. In [24], the authors have discussed low-voltage low-power integrable CMOS circuit application of integer- and fractional-order Fitzhugh–Nagumo neuron model. In [25], the structure of a neuron considering integer- and fractional-order discontinuous external magnetic flux has been given. In [26], a study on the fractional Izhikevich neuron model with synchronization and FPGA realization has been given. In [27], the authors proposed the synchronization of the fractional neuron model considering noise. In [28], an FPGA realization of a fractional-order neuron was discussed. In [29], the chimera state in the network of fractional Fitzhugh–Nagumo neurons has been investigated. In [30], a survey on the dynamics and implementation methods of fractional neuron models has been given. In [31], some novel analyses of the numerical approximations of fractional spiking neuron models have been given. In [32], a fractional-order Fitzhugh–Nagumo neuron model has been analyzed.

In this study, we propose a fractional-order neuron model, revising the previously published integer-order model [33] using the following generalized Caputo fractional derivative:

Definition 1

[34] The generalized Caputo-type fractional derivative, \(D^{\gamma , \rho }_{d_+},\) of order \(\gamma >0\) is defined by

$$\begin{aligned}{} & {} (D^{\gamma , \rho }_{d_+} u)(t) =\dfrac{\rho ^{\gamma - n+ 1}}{\Gamma (n- \gamma ) }\nonumber \\{} & {} \quad \int ^t_d{s^{\rho - 1}{(t^\rho - s^\rho )}^{n- \gamma - 1}\bigg ({s^{1- \rho }\dfrac{\textrm{d}}{\textrm{d}s}}\bigg )^n u(s)\textrm{d}s},~~ t> d, \end{aligned}$$
(1)

where \( \rho > 0, d \ge 0,~ and~ n- 1< \gamma \le n.\)

We apply fractional derivatives because the fractional-order model contains memory in the system, and the parameters with fractional order can enrich the model performance, providing one degree of freedom. The paper is organized in the following sections: In Sect. 2, the description of the proposed fractional-order model is given with the results of the existence of a unique solution. In Sect. 3, the numerical solution of the proposed model is derived using a modified version of the Euler method along with the stability and error estimation of the scheme. In Sect. 4, the graphical simulations are given. In Sect. 5, the results are concluded.

Fig. 1
figure 1

Parameter values: \(k_1= 1.0, I_1= 6.0, f_1= 0.06, I_2= 6.0, f_2= 0.06, \lambda _H= 0.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 0.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image

2 Model description

The proposed revised form of an integer-order neuron model [33] using the generalized Caputo fractional derivative is given by

$$\begin{aligned} \begin{aligned}&^C_0D_t^{\gamma , \rho }v= -\bigg (\frac{v^3}{3}-k_1v\bigg )-i + I_{ext}+ \lambda _H(\alpha +3 \beta w^2)v,\\&^C_0D_t^{\gamma , \rho }i= v-k_2 i- \lambda _E(a+ bq^2)i,\\&^C_0D_t^{\gamma , \rho }q= k_3i,\\&^C_0D_t^{\gamma , \rho }w= -k_4v, \end{aligned} \end{aligned}$$
(2)

where \(I_{ext}= I_1 \sin (\pi f_1 t) + I_2 \cos (\pi f_2 t)\) defines external forcing current with different frequencies \(f_1, f_2\) and currents \(I_1, I_2\). \(^C_0D_t^{\gamma , \rho }\) denotes the generalized Caputo derivative with order \(\gamma \) along with extra parameter \(\rho \). Moreover v, i, q, and w define the voltage, current, charge, and magnetic flux in the case of dimensionless parameters, respectively. \(\lambda _H\) and \(\lambda _E\) are the switching factors of the magnetic and electric field. Other parameters are \(k_1, k_2, k_3, k_4\) and \(\alpha , \beta , a, b\) are described briefly in ref. [33]. The reason for showing an interest in the given model is the proposed model contains multiple factors, namely, electromagnetic field effects, various frequency brands of external forcing current, and the amplitude and frequency of the external magnetic radiation, to capture the variations in the membrane potential. Also, incorporating an extra parameter \(\rho \) along with fractional-order \(\gamma \) adding one more degree of freedom, makes the proposed methodology advanced to the general Caputo case.

Fig. 2
figure 2

Parameter values: \(k_1= 1.0, I_1= 6.0, f_1= 0.06, I_2= 6.0, f_2= 6.66, \lambda _H= 0.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 0.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image

For further investigations, let us define

$$\begin{aligned} \left\{ \begin{array}{ll} x_1(t, v, i, q, w)= -\bigg (\frac{v^3}{3}-k_1v\bigg )-i \\ \qquad \qquad \qquad + I_{ext}+ \lambda _H(\alpha +3 \beta w^2)v,\\ x_2(t, v, i, q, w)= v-k_2 i- \lambda _E(a+ bq^2)i,\\ x_3(t, v, i, q, w)= k_3i,\\ x_4(t, v, i, q, w)= -k_4v.\\ \end{array}\right. \end{aligned}$$
(3)

and

$$\begin{aligned}&u(t)=\left\{ \begin{aligned}&v(t)\\ {}&i(t)\\ {}&q(t)\\ {}&w(t) \end{aligned} \right. , \ \ \ u_0(t)=\left\{ \begin{aligned}&v_0(t)\\ {}&i_0(t)\\ {}&q_0(t)\\ {}&w_0(t) \end{aligned} \right. , \nonumber \\&x(t, u(t))=\left\{ \begin{aligned}&x_1(t, v, i, q, w)\\ {}&x_2(t, v, i, q, w)\\ {}&x_3(t, v, i, q, w)\\ {}&x_4(t, v, i, q, w) \end{aligned} \right. . \end{aligned}$$
(4)

Then, the proposed model (2) can be expressed in terms of the following initial value problem (IVP) for the given function u(t) with singular kernel x(t, u) on the time interval [0, T]:

$$\begin{aligned} ^C_0D_t^{\gamma , \rho } u(t)&= x(t, u(t)),\ t\in [0, T], \ 0<\gamma \le 1,\end{aligned}$$
(5a)
$$\begin{aligned} u(0)&= u_0, \end{aligned}$$
(5b)

The related Volterra integral equation (VIE) of the IVP (5a)–(5b) is given by [34]

$$\begin{aligned} u(t)= u(0)+ \dfrac{{\rho }^{1- \gamma }}{\Gamma (\gamma )}\int _{0}^{t}{s^{\rho - 1}{(t^\rho - s^\rho )}^{\gamma - 1}x(s, u)\textrm{d}s}. \end{aligned}$$
(6)

Firstly, we recall the results regarding the existence of unique solution for the above given IVP (5a) and (5b) using following theorems.

Theorem 1

(Existence) [35]. For \( 0< \gamma \le 1,~ u_0 \in \mathbb {R},~ T^*> 0,~ J> 0,\) consider the set \( \zeta := \{(t, u):~ t \in [0, T^*],~ | u- u_0 | \le J\}\) and define the continuous function \(x: \zeta \rightarrow \mathbb {R}\). Let \(M:= \sup _{(t, u)\in \zeta } |x(t, u)|\) and

$$\begin{aligned} T= \left\{ \begin{array}{ll} T^*,&{}\qquad if M= 0,\\ min \{T^*, {\bigg (\dfrac{J\Gamma (\gamma +1)\rho ^\gamma }{M}\bigg )}^{\dfrac{1}{\gamma }}\}&{}\qquad otherwise. \end{array}\right. \end{aligned}$$
(7)

Then, a function \( u\in \mathcal {C}[0, T]\) exists and it satisfies the IVP (5a) and (5b).

Theorem 2

(Uniqueness) [35]. Let \(u(0)\in \mathbb {R},~ J> 0,~ T^* > 0,\) and the set \(\zeta \) given in Theorem 1. Consider the continuous function \(x: \zeta \rightarrow \mathbb {R}\) satisfying the Lipschitz condition for variable u, i.e.,

$$\begin{aligned} |x(t, u_1) - x(t, u_2)| \le V|u_1 - u_2|, \end{aligned}$$

where \(V > 0\) is a constant independent to \(t, u_1,~ and ~u_2.\) Then a unique solution \( u\in \mathcal {C}[0, T]\) for the IVP (5a) and (5b) exists.

Theorem 3

The solution of model (2) is uniformly stable on [0, T] for some \(T>0.\)

Proof

On the contrary, we assume that there exists two solutions u(t) and v(t) of model (2) with initial conditions u(0) and v(0),  such that

$$\begin{aligned} u(t)&= u(0)+\frac{\rho ^{1-\gamma }}{\Gamma {(\gamma )}}\int _{0}^{t}s^{\rho -1}\left( t^{\rho } -s^{\rho }\right) ^{\gamma -1}x(s,u)\textrm{d}s\end{aligned}$$
(8)
$$\begin{aligned} v(t)&= v(0)+\frac{\rho ^{1-\gamma }}{\Gamma {(\gamma )}}\int _{0}^{t}s^{\rho -1}\left( t^{\rho } -s^{\rho }\right) ^{\gamma -1}y(s,v)\textrm{d}s \end{aligned}$$
(9)

It follows that

$$\begin{aligned} \Vert u-v\Vert\le & {} \sup _{t}\left( \frac{\rho ^{1-\gamma }}{\Gamma {(\gamma )}}\int _{0}^{t}s^{\rho -1}\left( t^{\rho } -s^{\rho }\right) ^{\gamma -1}|x(s,u)\right. \nonumber \\{} & {} \left. -y(s,v)|\textrm{d}s\right) \nonumber \\\le & {} \sup _{t}\left( \frac{\rho ^{1-\gamma }}{\Gamma {(\gamma )}}\int _{0}^{t}s^{\rho -1}\left( t^{\rho } -s^{\rho }\right) ^{\gamma -1}\textrm{d}s\right) \Vert x-y\Vert \nonumber \\\le & {} \frac{1}{\rho ^{\gamma }\Gamma (\gamma +1)}h^{\gamma } \Vert x-y\Vert , \end{aligned}$$
(10)

where \(h= \sup _{t} t^\rho \). We choose \(\Vert x-y\Vert <\frac{\rho ^{\gamma }\Gamma (\gamma +1)}{h^\gamma }\epsilon .\) Then from (10), we conclude that

$$\begin{aligned} \Vert u-v\Vert <\epsilon . \end{aligned}$$

This implies that the solution of model (2) is uniformly stable on [0, T]. \(\square \)

3 Numerical solution using generalized Euler method

Several numerical methods have been derived to solve fractional-order systems in the last few years. In [36], a finite-difference predictor–corrector scheme was introduced for fractional differential equations. In [37], the authors have derived a short and efficient method to solve generalized Caputo-type differential equations. In [38], a modified predictor–corrector method has been introduced to solve generalized Caputo-type differential equations with delay. In [39], the authors have derived the generalized differential transform method to simulate impulsive fractional differential equations. In [40], the authors proposed a generalized Lucas polynomial sequence approach for fractional differential equations. In [41], a novel operation matrix scheme for solving generalized Caputo-type fractal–fractional differential equations has been derived. The author in [42] proposed an orthonormal ultraspherical operational matrix algorithm for generalized Caputo-type fractal–fractional Riccati equation.

Fig. 3
figure 3

Parameter values: \(k_1= 1.0, I_1= 6.0, f_1= 0.06, I_2= 6.0, f_2= 0.06, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image
Fig. 4
figure 4

Parameter values: \(k_1= 1.0, I_1= 6.0, f_1= 0.06, I_2= 6.0, f_2= 6.66, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image

In this section, we use the generalized Euler method given in [43] and using a non-uniform grid, to numerically solve the proposed IVP (5a) and (5b) (or model (2)). The time range [a, T] is taken as a discrete set of points

$$\begin{aligned} {\left\{ \begin{array}{ll} t_0= a,\\ t_{j+1}= {(t^\rho _j+ h)}^{1/ \rho },~~~ j= 0, 1,\ldots ,N- 1, \end{array}\right. } \end{aligned}$$
(11)

where \(h = \dfrac{T^\rho - t_0^\rho }{N}\). The solution is derived as approximations using a sequence \(u_{j},~ j = 0, 1,\ldots ,N,\) such that \(u_{k} \approx u(t_k) (k = 1, 2,\ldots , j).\) The following Volterra integral equation can represent the exact solution of the given IVP:

$$\begin{aligned} u(t)= u(t_0)+ \dfrac{{\rho }^{1- \gamma }}{\Gamma (\gamma )}\int _{t_0}^{t}{s^{\rho - 1}{(t^\rho - s^\rho )}^{\gamma - 1}x(s, u)\textrm{d}s}. \end{aligned}$$
(12)

As a consequences, we can write

$$\begin{aligned}{} & {} u(t_{j+1})= u(t_0)+ \dfrac{{\rho }^{1- \gamma }}{\Gamma (\gamma )}\sum \limits _{k=0}^{j}\nonumber \\{} & {} \quad \int _{t_k^\rho }^{t_{k+1}^\rho }{s^{\rho - 1}{(t_{j+1}^\rho - s^\rho )}^{\gamma - 1}x(s, u(s))}\textrm{d}s. \end{aligned}$$
(13)

Taking \(z = s^\rho \), we get

$$\begin{aligned}{} & {} u(t_{j+1})= u(t_0)+ \dfrac{{\rho }^{- \gamma }}{\Gamma (\gamma )}\sum \limits _{k=0}^{j}\nonumber \\{} & {} \quad \int _{t_k^\rho }^{t_{k+1}^\rho }{(t_{j+1}^\rho - z)}^{\gamma - 1}x(z^{1/\rho }, u(z^{1/\rho }))\textrm{d}z. \end{aligned}$$
(14)

In each of the subintervals, using composite rectangle rule, we define the approximation

$$\begin{aligned} \begin{aligned}&\dfrac{{\rho }^{- \gamma }}{\Gamma (\gamma )}\sum \limits _{k=0}^{j}\int _{t_k^\rho }^{t_{k+1}^\rho }{(t_{j+1}^\rho - z)}^{\gamma - 1}x(t_k, u(t_k))\textrm{d}z\\&\quad = \dfrac{{\rho }^{- \gamma }}{\Gamma (\gamma )}\sum \limits _{k=0}^{j}x(t_k, u(t_k))\int _{t_k^\rho }^{t_{k+1}^\rho }{(t_{j+1}^\rho - z)}^{\gamma - 1}\textrm{d}z\\&\quad = \dfrac{{\rho }^{- \gamma }}{\Gamma (\gamma )}\sum \limits _{k=0}^{j}x(t_k, u(t_k))\bigg [\dfrac{-1}{\gamma }{(t_{j+1}^\rho - z)}^{\gamma }|^{t_{k+1}^\rho }_{t_{k}^\rho }\bigg ]\\&\quad = \dfrac{{\rho }^{- \gamma }}{\Gamma (\gamma +1)}\sum \limits _{k=0}^{j}x(t_k, u(t_k))\bigg [{(t_{j+1}^\rho - t_k^\rho )}^{\gamma }- {(t_{j+1}^\rho - t_{k+1}^\rho )}^{\gamma }\bigg ].\\ \end{aligned} \end{aligned}$$
(15)

The above approximation (15) gives the following explicit formula

$$\begin{aligned} u_{k+1}= u_0+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}x(t_j, u_j), \end{aligned}$$
(16)

where

$$\begin{aligned} b_{j, k+1}= {(k+1- j)}^{\gamma }-{(k- j)}^\gamma . \end{aligned}$$
(17)

Therefore, the algorithm of the numerical solution of the proposed system (2) is derived as follows:

$$\begin{aligned} \begin{aligned} v_{k+1}&= v_0+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}\bigg [-\bigg (\frac{v_j^3}{3}-k_1v_j\bigg )\\&\quad \quad -i_j + I_{ext}+ \lambda _H(\alpha +3 \beta w_j^2)v_j\bigg ],\\&i_{k+1}= i_0+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}\big [v_j-k_2 i_j\\&\quad \quad \quad - \lambda _E(a+ bq_j^2)i_j \big ],\\&q_{k+1}= q_0+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}\big [k_3i_j \big ],\\&w_{k+1}= w_0+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}\big [-k_4v_j \big ]. \end{aligned} \end{aligned}$$
(18)
Fig. 5
figure 5

Parameter values: \(k_1= 1.0, I_1= 6.0, f_1= 0.06, I_2= 6.0, f_2= 0.006, \lambda _H= 1.0, \alpha = 0.01, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image
Fig. 6
figure 6

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.02, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image

3.1 Stability analysis

Lemma 1

[44] If \(0< \beta < 1\) and b is a nonnegative integer, then there exist two positive quantities \(\mathcal {C}_{\beta , 1}\) and \(\mathcal {C}_{\beta , 2}\) which depend on \(\beta ,\) such that

$$\begin{aligned} (b + 1)^{\beta }- b^{\beta } \le \mathcal {C}_{\beta , 1}(b + 1)^{\beta - 1}, \end{aligned}$$

and

$$\begin{aligned} (b + 2)^{\beta + 1} - 2(b + 1)^{\beta + 1} + b^{\beta + 1} \le \mathcal {C}_{\beta , 2}(b + 1)^{\beta - 1}. \end{aligned}$$

Lemma 2

[44] Let \(d_{p, s} = (s - p )^{\beta - 1} (p = 1, 2,\ldots , s - 1)\) and \( d_{p, s}= 0\) for \(p \ge s, rh\le T, \beta , h, M, T> 0\) and r is a positive integer. Also, let \(\sum _{p= r}^{p= s}d_{p, s}|e_p|= 0\) for \(b> s \ge 1.\) If

$$\begin{aligned} |e_s|\le Mh^{\beta } \sum \limits _{p=1}^{s-1}d_{p,s}|e_p| + |\gamma _0|,~~~s= 1,2,\ldots ,r, \end{aligned}$$

then

$$\begin{aligned} |e_r|\le \mathcal {C}|\gamma _0|,~~~r= 1,2,\ldots \end{aligned}$$

where \(\mathcal {C}\) is a positive constant independent to h and r.

Theorem 4

Let the kernel x(t, u) satisfy the Lipschitz condition and \( u_{m}~ (m = 1,\ldots , k + 1)\) be the solution of Eqn. (16). Then, the proposed numerical method is conditionally stable.

Proof

Let \(\tilde{u_{0}},\) and \(\tilde{u_{m}}~(m= 0,\ldots , k+1)\) are the perturbations of \( u_{0},\) and \(u_{m}\), simultaneously. Then, the following approximation expression is obtained from Eq. (16)

$$\begin{aligned}{} & {} u_{k+1}+ \tilde{u}_{{k+1}}= u_0+ \tilde{u_{0}}+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\nonumber \\{} & {} \quad \sum \limits _{k=0}^{j}b_{k, j+1}x(t_k, u_k+ \tilde{u_{k}}), \end{aligned}$$
(19)

where \( b_{k, j+1}= [{(j+1- k)}^{\gamma }-{(j- k)}^\gamma ].\)

Fig. 7
figure 7

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image

Combining Eqs. (16) and (19), we obtain

$$\begin{aligned} |\tilde{u}_{{k+1}}|{} & {} = |\tilde{u_{0}}+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{k=0}^{j}b_{k, j+1}(x(t_k, u_k+ \tilde{u_{k}})\nonumber \\{} & {} \quad - x(t_k, u_k))|. \end{aligned}$$
(20)

From the triangle inequality and Lipschitz condition, we have

$$\begin{aligned} |\tilde{u}_{{k+1}}|\le \zeta _0+ \dfrac{\rho ^{- \gamma }h^\gamma m_1 \mathcal {C}_{\gamma }}{\Gamma (\gamma +2)}\bigg (\sum \limits _{k=1}^{j} b_{k, j+1}|\tilde{u_{k}}|\bigg ), \end{aligned}$$
(21)

where \(\zeta _0= \max _{0\le k\le N}\{|\tilde{u_{0}}|+ \dfrac{\rho ^{-\gamma }h^\gamma m_1 b_{k,0}}{\Gamma (\gamma +2)}|\tilde{u_{0}}|\}\). Here, \(C_{\gamma }\) is a positive constant dependent to \(\gamma \) (Lemma 1) and h is possibly small. From Lemma 2, we get \( |\tilde{u}_{{k+1}}|\le \mathcal {C} \zeta _0,\) where \(\mathcal {C}\) is a positive constant independent to k and h. This gives the required result. \(\square \)

3.2 Error analysis

Fig. 8
figure 8

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.8, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image

Lemma 3

[43] Let u(t) be the solution of (12), and x(t, u) be continuous and satisfies the Lipschitz condition with respect to u for a sufficiently small h. Then, we have

$$\begin{aligned}{} & {} |\int _{0}^{t^\rho _{n+ 1}}s^{\rho - 1} (t^\rho _{n+ 1}- s^\rho )^{\gamma - 1} x(s, u(t))\textrm{d}s\\{} & {} \quad - \frac{\rho ^{-\gamma }h^\gamma }{\gamma }\sum \limits _{m=0}^{n}b_{m, n+1}x(t_m, u(t_m)) | \le C_2h^{\sigma (\gamma )}. \end{aligned}$$

Theorem 5

For the proposed scheme (16), we have

$$\begin{aligned} |u(t_{k+ 1})- u_{k+ 1}|\le Ch^\gamma ,~ k= 0,\ldots ,N- 1, \end{aligned}$$
(22)

where C is a positive constant independent to h and k.

Proof

Let \(u(t_0)= u_0,\) and \(e_k= u(t_k)-u_k.\) Using the Volterra Eq. (6) and applying Eq. (16), we define the error expression as follows:

$$\begin{aligned} u(t_{k+ 1})- u_{k+ 1}{} & {} = \dfrac{{\rho }^{1- \gamma }}{\Gamma (\gamma )}\int _{0}^{t}{s^{\rho - 1}{(t^\rho - s^\rho )}^{\gamma - 1}x(s, u)\textrm{d}s}\\{} & {} \quad - \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}x(t_j, u_j). \end{aligned}$$

Therefore,

$$\begin{aligned} |u(t_{k+ 1})- u_{k+ 1}| =&|\dfrac{{\rho }^{1- \gamma }}{\Gamma (\gamma )}\int _{0}^{t}{s^{\rho - 1}{(t^\rho - s^\rho )}^{\gamma - 1}x(s, u)\textrm{d}s}\nonumber \\&- \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}x(t_j, u_j)|\nonumber \\ \le&|\dfrac{{\rho }^{1- \gamma }}{\Gamma (\gamma )}\int _{0}^{t}{s^{\rho - 1}{(t^\rho - s^\rho )}^{\gamma - 1}x(s, u)\textrm{d}s}\nonumber \\&- \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=0}^{k}b_{j, k+1}x(t_j, u{(t_j)}|\nonumber \\&+ \dfrac{\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\nonumber \\&\sum \limits _{j=1}^{k}b_{j, k+1}|x(t_j, u_{(t_j)}- x(t_j, u_j) |\nonumber \\ \le&\dfrac{\mathcal {C}_2}{\Gamma (\gamma )}h^{\sigma (\gamma )}+ \dfrac{L\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\sum \limits _{j=1}^{k}b_{j, k+1} |e_j|\nonumber \\ \le&\dfrac{\mathcal {C}_2}{\Gamma (\gamma )}h^{\sigma (\gamma )}+ \dfrac{L \mathcal {C}_{\gamma , 1}\rho ^{-\gamma }h^\gamma }{\Gamma (\gamma +1)}\nonumber \\&\sum \limits _{j=1}^{k}(k+1-j)^{\gamma -1} |e_j|, \end{aligned}$$
(23)

where we used Lemmas 3, 1, and the Lipschitz property. Using Lemma 2, we get the required results. \(\square \)

Fig. 9
figure 9

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 1.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\)

Full size image

4 Graphical simulations

Now we derive the numerical solution of the model (2) using the above-mentioned generalized Euler algorithm (18). The step size is fixed as \(h=0.01\) and extra parameter \(\rho = 0.98\), which generates a non-uniform grid Eq. (11). The initial values are fixed as \((v_0, i_0, q_0, w_0) = (0.2, 0.01, 0.2, 0.01)\). We fix the parameters \(k_1 = 1.0, k_2 = 1.0, k_3 = 1.0, k_4 = 0.01.\)

Fig. 10
figure 10

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01, V_{th}= 1.0, A_0= 0.01, A_1= 0.1, B_1= 0.1, A_2= 0.1, B_2= 0.1\)

Full size image
Fig. 11
figure 11

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01, V_{th}= 1.0, A_0= 0.01, A_1= 1.1, B_1= 0.1, A_2= 0.1, B_2= 0.1\)

Full size image
Fig. 12
figure 12

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01, V_{th}= 1.0, A_0= 0.01, A_1= 3.1, B_1= 0.1, A_2= 0.1, B_2= 0.1\)

Full size image

For the parameter values \(a = 0.2, b = 0.1, \alpha = 1.0, \beta = 0.02,\) the charge- and magnetic flux-controlled memristor can represent nonlinear electrical bustling. In Fig. 1, the phase plots of membrane potential v(t) versus current i(t) are plotted for the given parameter values at fractional orders \(\gamma = 0.85, 1\) (Fig. 1a) and \(\gamma = 0.75, 0.95\) (Fig. 1b), respectively. Here, we notice that the phase portraits are nearly the same at each of the fractional-order values.

We know that the behavior of the plots is incumbent on the frequency of the external forcing current factor \(I_{ext}\) because the exciting state can be disposed of by the external forcing. Therefore, to check the mode dependency of electrical bustling on external excitation, we plotted Fig. 2 by changing \(f_2= 0.06\) to \(f_2= 6.66\) (other parameter values are the same as for Fig. 1). Here, we see that the phase diagrams Fig. 2a, b differ from the plots of Fig. 1 which justifies that the multiple modes can be generated in the electrical bustling.

In the previous two cases, the electromagnetic field was not incorporated as \(\lambda _E = \lambda _H = 0\). In Fig. 3, we consider the electromagnetic field changing with time taking \(\lambda _E = 1.0, \lambda _H = 1.0\). Also, the electrical movements of an isolated neuron are explored with \(I_1 = I_2 = 6.0, f_1 = 0.06, f_2= 0.06\).

In Fig. 4, we take \(f_2= 6.66\) (other parameter values are same as for Fig. 3). Here, we see that Fig. 4a, b shows that the phase portraits become dense and periodic phases are converted into chaotic phases. In particular, we can see that the phase portraits obtained at fractional orders \(\gamma = 0.85, 0.75\) are denser compared to the nearest values of \(\gamma = 1\). This justifies that fractional-order cases generate more varieties in the phase portraits between v(t) and i(t).

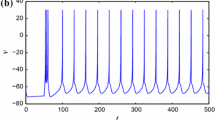
In Fig. 5, the firing patterns of neural activities are plotted for the parameter values \(k_1= 1.0, I_1= 6.0, f_1= 0.06, I_2= 6.0, f_2= 0.006, \lambda _H= 1.0, \alpha = 0.01, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01\) at the given fractional-order values. Here, we notice that in each fractional-order case, the dynamics of the plots is same.

Using the external forcing current, we can adjust the excitability which results in the various firing patterns. Now we consider the various value of \(I_{ext}\) by changing the values of frequency \(f_2\), whereas the frequency \(f_1\) is fixed at zero. From the group of Figs. 6, 7, 8, and 9, we can see that the electrical movements can be controlled to produce periodic oscillations when \(I_{ext}\) is incorporated with various frequencies. From Fig. 9, we notice that at fractional order values \(\gamma = 0.75, 0.85\), the patterns of membrane potential are more uniform compared to the nearest values of fractional order \(\gamma =1\).

Fig. 13
figure 13

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01, V_{th}= 1.0, A_0= 0.01, A_1= 0.1, B_1= 0.05, A_2= 0.1, B_2= 0.1\)

Full size image
Fig. 14
figure 14

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01, V_{th}= 1.0, A_0= 0.01, A_1= 0.1, B_1= 0.01, A_2= 0.1, B_2= 0.1\)

Full size image
Fig. 15
figure 15

At parameters: \(k_1= 1.0, I_1= 0.0, f_1= 0.0, I_2= 6.0, f_2= 0.2, \lambda _H= 1.0, \alpha = 1.0, \beta = 0.02, k_2= 1.0, \lambda _E= 1.0, a= 0.2, b= 0.1, k_3= 1.0, k_4= 0.01, V_{th}= 1.0, A_0= 0.01, A_1= 0.1, B_1= 0.001, A_2= 0.1, B_2= 0.1\)

Full size image

As experimented in ref. [33], the magnetic excitation was incorporated by a circular induction coil on the neural circuit when external electromagnetic radiation was imposed. In this case, the new revised model is given as follows:

$$\begin{aligned} ^C_0D_t^{\gamma , \rho }v{} & {} = -\bigg (\frac{v^3}{3}-k_1v\bigg )-i \nonumber \\{} & {} \qquad + I_{ext}+ \lambda _H(\alpha +3 \beta w^2)v,\nonumber \\ ^C_0D_t^{\gamma , \rho }i{} & {} = v-k_2 i- \lambda _E(a+ bq^2)i,\nonumber \\ ^C_0D_t^{\gamma , \rho }q{} & {} = k_3i,\nonumber \\ ^C_0D_t^{\gamma , \rho }w{} & {} = -k_4v+ V_{th} \exp {(-A_0t)}[A_1\cos (B_1t)\nonumber \\{} & {} \qquad + A_2 \sin (B_2t)], \end{aligned}$$
(24)

where the term \(V_{th} \exp {(-A_0t)}[A_1\cos (B_1t)+ A_2 \sin (B_2t)]\) defines the external electromagnetic radiation incorporated by a stimulator coil and \(V_{th}\) is the induction potential threshold. \(A_0, A_1, A_2\), and \(B_1, B_2\) are the damping ratio, amplitudes, and angular frequencies of source of radiation, simultaneously. The meaning of occurrence of large diversity in \(B_1, B_2\) is the both low- and high-frequency signals are interpolated on the neuron, respectively.

Now we plot the numerical solution of this new revised model (24) using the aforementioned generalized Euler algorithm (18). In the cluster of Figs. 10, 11, 12, 13, 14, and 15, we plotted the time-series graphs of membrane potential in an isolate neuron changing the amplitude \(A_1\) or frequency \(B_1\) in the external magnetic radiation when \(V_{th} = 1.0, A_0 = 0.01\).

In Figs. 10, 11, and 12, the frequency \(B_1\) is fixed at \(B_1= 0.1\) where the amplitude \(A_1\) is taken as \(A_1= 0.1\) (Fig. 10a, b), \(A_1= 1.1\) (Fig. 11a, b), \(A_1= 3.1\) (Fig. 12a, b). It is noticed in Fig. 11 that near to the fractional order \(\gamma =1, 0.95, 0.85\), the periodic solutions are disturbed but at fractional order \(\gamma =0.75\), the periodic solutions nearly to be exists. This justifies the possibility of the existence of various solutions in the case of fractional derivatives.

In Figs. 13, 14, and 15, the amplitude \(A_1\) is fixed at \(A_1= 0.1\) where the frequency \(B_1\) is taken as \(B_1= 0.05\) (Fig. 13a, b), \(B_1= 0.01\) (Fig. 14a, b), \(B_1= 0.001\) (Fig. 15a, b). It is noticed in Figs. 14 and 15 that near to the fractional order \(\gamma =1, 0.95\), the solutions are not perfectly periodic but at fractional order \(\gamma =0.85, 0.75\), the periodic solution exists.

From the graphical observations, we notice that fractional orders may change the behavior of the solution because of memory effects. The simulations are performed in Mathematica. The suggested methodology is not just restricted to simulating the proposed types of neuron models. This scheme can be used in modern control systems such as optimal deep learning control for modernized microgrids [45], fuzzy control for current sharing and voltage balancing in microgrids [46], etc.

5 Conclusions

In this study, we have investigated the dynamics of a fractional-order neuron model using generalized Caputo fractional derivatives. We have given proof of the existence of a unique solution for the proposed model. A new version of the Euler method has been used to derive the numerical solution of the model. The stability and error estimation have been proved for the proposed numerical scheme. In the graphical simulations, the influences of model parameters have been explored, and the results are explained briefly. From the performed analysis, we conclude that the fractional-order values provide more degree of freedom in the solutions and justify most of the possible cases of the proposed neuron model outputs. In the future, the given neuron model can be redefined using any other fractional derivative, or the same model can be revisited after a new circuit experiment. Moreover, some theoretical simulations of the stability and bifurcation of the system can be performed.