1 Introduction

Diabetes mellitus, commonly referred to simply as diabetes, is a chronic disease that occurs when the human body either doesn’t make enough insulin or can’t use it as well as it should. In the digestive process, that is, in the process of separating the foods we eat into their sources, when we consume carbohydrates such as bread and pasta, our body decomposes carbohydrates into sugar. Sugar reaches the cells of the body until it is eliminated from the body and uses insulin, which is a key for transfer. Insulin is a hormone produced by the pancreas and acts as a key to the cell wall. When the body isn’t able to take glucose (sugar) in its cells and use it for energy, this results in a build-up of extra sugar in the bloodstream. Thus, diabetes is caused by the pancreas not producing insulin or not producing enough insulin, or if it produces enough insulin, the cell does not respond to it or cannot use it enough. Without ongoing, controlled management and treatment, diabetes causes high levels of sugar to accumulate in the blood. This leads to dangerous complications and damage to organs, such as coronary artery disease (individuals with diabetes are four times more likely to have a stroke than individuals without the disease), loss of consciousness, visual disturbances which can lead to blindness, and risk of infections. Additionally, someone with diabetes is the most vulnerable to infection, high blood pressure, narrowing of the arteries, neuropathy (nerve damage), nephropathy (kidney damage), hearing loss, and depression [24].

In the treatment of diabetes, it is important to gain healthy eating habits to keep the blood sugar level within normal limits as well as blood pressure and cholesterol levels, and by achieving a healthy body weight. The most important basis of the most important treatment of the disease is a healthy diet; in addition to an effective diet, oral medications or injections in the treatment of diabetes are recommended by doctors during the treatment process. According to data from the World Health Organization, approximately 442 million people have diabetes, and diabetes-related deaths reach 1.5 million each year. It has been predicted that the prevalence of diabetes mellitus will reach up to 642 million by the year 2040 globally [33]. Diabetes is an insidious disease and is usually noticed after it settles in the body. As said before, the disease can be fatal in the long term, as it destroys the vessels and organs. For this reason, many researchers have frequently studied the illness.

Nowadays, mathematical modeling is considered an effective and important tool for describing the cause and transmission dynamics of many common infectious diseases such as the HIV/AIDS [29, 30], COVID-19 [27, 31, 48], tuberculosis (TB) [3, 37], Lassa fever [4], Ebola, syphilis [9] cancer cells [36], polio [21] and many others which are classified in [4]. In recent years, a fractional-order derivative which is being regarded as an extension of the integer-order derivative has gained a lot of scholars’ attention due to its nonlocal properties and memory effects [22, 41]. The fractional-order derivatives depend not only on the current state but on all of its historical states and thus have memory properties [41]. Based on these special properties of fractional differentiation and integration, many scholars have applied the concept of fractional differentiation and integration to model several nonlinear phenomena in medicine, engineering, physics, and applied sciences. For instance, Diethelm [12] used the fraction calculus idea to study dengue dynamics and confirmed in his work that the proposed fractional-order model better agrees with the real data of the dengue disease with an integer-order case. In a similar development, Naik et al [29, 31] through fractional differentiation proposed fractional order models for the transmission of the HIV/AID and COVID-19 diseases and showed that their models predict the better dynamics of the disease in fractional-order cases over the standard order scenarios.

A new concept of differentiation that involves the derivatives of bi-order has been suggested in recent years; the first is termed fractional-order, while the second case is known as fractal dimension. This type of integral and differential equation is still poorly reported in the literature. Hence, the present paper is considering the modeling and analysis of the fractal-fractional diabetes mellitus model using the derivative with a power law kernel, which is generally believed to have a similar physical interpretation to the classical or integer order derivative. The concept of fractal-fractional operators has been applied in engineering, physics, biology, and biomedical processes to successfully model a range of real-world problems [8, 14, 19, 28, 34,35,36, 53]. Owing to the successful application of this derivative to model a range of real-life scenarios, we are motivated in this work by applying the concept of fractal-fractional operators of orders \((\zeta , \epsilon )\) to model the diabetes mellitus differential equations in the sense of the Caputo operator and demonstrate the influence of the fractal and fractional orders on the behavior of each of the subclasses in the population. As far as we are concerned, we are not aware of any formulation of the diabetes mellitus model with fractal-fractional derivatives.

The remainder part of this work is organized into sections as follows. A quick tour of some useful definitions of fractal-fractional operators is given in Sect. 2. The dynamics of the diabetes mellitus model of integer and non-integer order cases are introduced in Sect. 3, linear stability analysis as well as the existence and uniqueness of solutions via fractal-fractional operators are also examined. In Sect. 4, a novel numerical approximation technique for the solution of the proposed model described by the Caputo-fractal-fractional derivatives is presented. Numerical experiments which depict the behavior of dynamics under investigation are reported for different instances of orders \(\zeta ,\epsilon \in (0, 1]\) which are reported in Sect. 5. The conclusion is finally given.

2 Preliminaries

In this segment, a quick tour of some properties and useful definitions of fractional and fractal-fractional Riemann–Liouville–Caputo operators are reported. In terms of mathematics, the models of fractional derivatives have used power law memory kernel to define the fractional derivative so that the system can better characterize memory and global correlation.

In Caputo sense, the fractional derivative of order \(\alpha \) is formulated as

$$\begin{aligned}{} & {} ^C_0 D_y^\alpha (f(y))=\frac{1}{\Gamma (n-\alpha )}\int _{0}^{y}(y-s)^{n-\alpha -1}\frac{d^nf(s)}{ds^n}ds,\;\;\nonumber \\{} & {} \qquad \qquad \qquad \qquad n-1<\alpha \le n. \end{aligned}$$
(2.1)

Similarly, in Riemann–Liouville sense, the fractional derivative of order \(\alpha \) is defined as

$$\begin{aligned}{} & {} ^R_0 D_y^\alpha (f(y))=\frac{1}{\Gamma (n-\alpha )}\frac{d^n}{dy^n}\int _{0}^{y}(y-s)^{n-\alpha -1}f(s)ds,\;\;\nonumber \\{} & {} \qquad \qquad \qquad \qquad n-1<\alpha \le n. \end{aligned}$$
(2.2)

Let f(t) be a function, the generalized fractional integral \(I^{\alpha ,\beta }_{a+}\) of order \(\alpha >0\) is defined as [32]

$$\begin{aligned} I^{\alpha ,\beta }_{a+} f(t)=\frac{\beta ^{1-\alpha }}{\Gamma (\alpha )}\int _{a}^{t} s^{\beta -1}(t^\beta -s^\beta )^{\alpha -1}f(s)ds \end{aligned}$$
(2.3)

where \(\beta >0\) and \(t>a\). The corresponding Riemann-type fractional derivative of order \(\alpha >0\) is defined as:

$$\begin{aligned}{} & {} ^RD^{\alpha ,\beta }_{a+} f(t)=\frac{\beta ^{\alpha -n+1}}{\Gamma (n-\alpha )}\left( t^{1-\beta }\frac{d}{dt}\right) ^n\int _{a}^{t} s^{\beta -1}(t^\beta \nonumber \\{} & {} \qquad \qquad \qquad \qquad -s^\beta )^{n-\alpha -1}f(s)ds, \;\;t>a \end{aligned}$$
(2.4)

where \(\beta >0\), \(a\ge 0\) and \(n=\lceil \alpha \rceil \).

The generalized Caputo fractional operator of order \(\alpha >0\) is formulated as [32]:

$$\begin{aligned}{} & {} ^CD^{\alpha ,\beta }_{a+} f(t)=\frac{\beta ^{\alpha -n+1}}{\Gamma (n-\alpha )}\int _{a}^{t}s^{\beta -1} (t^\beta \nonumber \\{} & {} \qquad \qquad \qquad \qquad -s^\beta )^{n-\alpha -1} \left( s^{1-\beta }\frac{d}{ds}\right) ^n f(s)ds, \;\; t>a\nonumber \\ \end{aligned}$$
(2.5)

where \(\beta >0\), \(a\ge 0\), \(n-1<\alpha <n\), \(n=\lceil \alpha \rceil \), and \(f(t)\in C^n[a,b]\). In addition, the above Caputo derivative satisfies the following property

$$\begin{aligned} ^CD^{\alpha ,\beta }_{a+} \Theta =0, \;\;\;\Theta \;\; \text {is a constant}. \end{aligned}$$
(2.6)

Definition 2.1

(Fractal Fractional derivative in Riemann–Liouville sense with power law kernel [8]): Let \(f\left( t\right) \) is a continuous and differentiable function in the interval \(\left( t_{1},t_{2}\right) \) and its fractional order is \(\epsilon ,\) with \(\zeta \) order of Riemann–Liouville sense derivative involving power law (PL) kernel is given as:

$$\begin{aligned} _{0}^{FFP}D_{t}^{\zeta ,\epsilon }f\left( t\right) =\frac{1}{\Gamma \left( m-\zeta \right) }\frac{d}{dt^{\epsilon }}\int \limits _{0}^{t}\left( t-s\right) ^{m-\zeta -1}f\left( s\right) ds \end{aligned}$$

with \(p-1<\zeta ,\epsilon \le p\) where p is any natural number and \( \frac{df\left( s\right) }{ds^{\epsilon }}=\lim \limits _{t\rightarrow s} \frac{f\left( t\right) -f\left( s\right) }{t^{\epsilon }-s^{\epsilon }}.\)

Definition 2.2

(Fractal Fractional integral with power law kernel [8]): Let \(\epsilon \)-order differentiable function \(f\left( t\right) \) is continuousin \(\left( t_{1},t_{2}\right) ,\) the fractal fractional integral of \(f\left( t\right) \) with \(\zeta -\)order fractal fractional with power law (PL) kernel is given as:

$$\begin{aligned} ^{FFP}I^{\zeta ,\epsilon }f\left( t\right) =\frac{\zeta }{\Gamma \left( \epsilon \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}f\left( s\right) ds \end{aligned}$$

3 The diabetes mellitus model

Mathematical modeling and analysis are interested in the abundance of literature. The right way to predict the dynamics and components of diabetes is depend on the development of mathematical models. Especially the epistemology of diabetes, the question of what we know and how much we know, reforms into a source of information through the exploring of many exciting different models. The effect of many factors on diabetes and the cruising and behavior of the disease has been studied, such as cold weather, viruses, obesity or being overweight, impaired glucose tolerance, ethnic background, sedentary lifestyle, polycystic ovary syndrome, age, etc. In some of the work that has been done in recent years, Awad et al. [5] have been able to absorb the effects of diabetes on tuberculosis and have predictions about the rates between 2020–2050. In this study, the authors have used an age-structured TB-DM dynamic mathematical model. Ying et al. [58] have modeled and analyzed the hypoglycemia effect of diabetic women in their newborns. In [28], Mollah et al have studied the effect of the awareness program on diabetes through Homotopy analysis and defined the model with fractional derivative. The study on the size of the diabetes population and the rate of diabetes patients with complications have also been examined using the fractional variation method and the fractional Homotopy perturbation method in [43]. Rashid analyzed the SDC model, which takes into account the behavior of diabetes, using fractional derivative with non-singular kernel. Omame et al. [39] have evaluated the model which examines common interactions between COVID-19 and the genetic characteristics of diabetes with the Atangana-Belanau derivative. In this model, they assessed the spread of COVID-19 and vaccines available the COVID-19 vaccine and how much it could help to reduce its infection along with diabetes. Toriba et al. [52] have analyzed the model which examined the relationship between glucose and insulin. In addition to the studies mentioned above, Wang et al. [55] have studied obesity, parents’ diabetes story, and the effects of genes on Type 2 diabetes. Purnami et al. [45] have examined the diabetes model in relation to lifestyle and genetic effects. Aye et al [6] have developed a mathematical model for diabetes mellitus dynamics and complications and analyzed by Homotopy Perturbation Method. Rosado [46] have extended the model of Ackerman given in [7], analyzing a mathematical model that determines diabetes in patients based on the glucose test. The size of diabetes with or without complications has been investigated by Boutayeb [10]. Side [51] have examined the diabetes mellitus without genetic factors, seeking the solution of the model with Runge method. Pinto et al. [40] have proposed, analyzed and presented numerical results a model on clinical implications of diabetes mellitus in the dynamics of TB transmission. Xie [56] has addressed the local existence and uniqueness of solution of the model. Awad et al. [1] have investigated the impact of intervention strategies for controlling TB among people with diabetes mellitus. Theoretical and numerical investigation of the bio-medical glucose-insulin model has been discussed on a fractional-order model been Caputo-Fabrizio by Saleem et al. [47]. In [49], the authors have considered type II diabetes and presented a model for obtaining time courses to health and disease and sought the effects on these time courses of altering the CHO and lipid content of the diet. In [2], Al-Hussein et al. [2] have proposed a mathematical model for endocrine glucose-insulin metabolic regulatory feedback system and presented its numerical investigation. Analysis of a mathematical model of diabetes mellitus during pregnancy is investigated by Daud et al. [11]. Srivastava et al. [50] have focused on a fractional-order model of diabetes and they considered model with its complications. For more knowledge about diabetes and related studies, see in [16, 17, 20, 54, 58]

The profound and wistful effects of diabetes on human life due to complications have been the motivation of this study. Thus, in order to improve our understanding of the mechanisms underlying diabetes, and to make predictions about the behavior of the illness, examining and analyzing models of diabetes are the best strategy. For this reason, in this study, we are going to consider the diabetes mellitus model without genetic factors with treatment as follows:

$$\begin{aligned} \frac{dq\left( t\right) }{dt}&=\kappa -\mu q\left( t\right) -\beta q\left( t\right) y\left( t\right) , \nonumber \\ \frac{dy\left( t\right) }{dt}&=\beta q\left( t\right) y\left( t\right) -\left( \mu +1\right) y\left( t\right) , \nonumber \\ \frac{dz\left( t\right) }{dt}&=\alpha \gamma y\left( t\right) -\left( \mu +\delta \right) z\left( t\right) , \nonumber \\ \frac{dp\left( t\right) }{dt}&=\left( 1-\alpha \gamma \right) y\left( t\right) -\left( \mu +\sigma \right) p\left( t\right) ,\nonumber \\ x\left( t\right)&=q\left( t\right) +y\left( t\right) +z\left( t\right) +p\left( t\right) , \end{aligned}$$
(3.1)

subject to initial conditions of the form

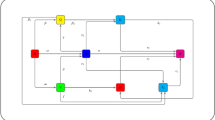
$$\begin{aligned} q(0)=q_0, y(0)=y_0, z(0)=z_0, p(0)=p_0, x(0)=x_0, \end{aligned}$$

where \(x\left( t\right) \) states the total number of people living in any country or region. In epidemiological patterns, it represents a clear sample rather than the whole of society. \(q\left( t\right) \) is a class of sensitive people, which is a class of population members who risk being infected by a disease. \(y\left( t\right) ,\)refers to the dynamics of the class of individuals exposed to or without symptoms. \(z\left( t\right) \) represents the class of individuals who have the disease but cannot access the treatment, and finally \(p\left( t\right) \) represents the class of individuals who have the disease but have reached treatment. Before explaining the other parameters in the above system, the fifth equation of the system can be written as follows

$$\begin{aligned} \frac{dx\left( t\right) }{dt}=\frac{dq\left( t\right) }{dt}+\frac{dy\left( t\right) }{dt}+\frac{dz\left( t\right) }{dt}+\frac{dp\left( t\right) }{dt}. \end{aligned}$$

if the first four equations add up side by side, it yields

$$\begin{aligned} \frac{dx\left( t\right) }{dt}= & {} \kappa -\mu \left( q\left( t\right) +y\left( t\right) +z\left( t\right) +p\left( t\right) \right) \nonumber \\{} & {} -\left( \delta +\sigma \right) p\left( t\right) . \end{aligned}$$

This allows us to achieve a simpler version of the system as described in diagram 1, and the resulting dynamical model becomes

Fig. 1
figure 1

Diagrammatic flowchart for the diabetes mellitus model

Full size image
$$\begin{aligned}&\frac{dx\left( t\right) }{dt}=\kappa -\mu x\left( t\right) -\delta z\left( t\right) -\sigma p\left( t\right) ,\nonumber \\&\frac{dy\left( t\right) }{dt}=\beta \left( x\left( t\right) {-}y\left( t\right) {-}z\left( t\right) {-}p\left( t\right) \right) y{-}\left( \mu +1\right) y\left( t\right) , \nonumber \\&\frac{dz\left( t\right) }{dt}=\alpha \gamma y\left( t\right) -\left( \mu +\delta \right) z\left( t\right) , \nonumber \\&\frac{dp\left( t\right) }{dt}=\left( 1-\alpha \gamma \right) y\left( t\right) -\left( \mu +\sigma \right) p\left( t\right) , \end{aligned}$$
(3.2)

where

$$\begin{aligned}&\kappa :\text {the number of individuals born in the population at a }\\&\qquad \text {specific time range} \\&\mu :\text { the number of death occurs in the population in a }\\&\qquad \text {specific time range} \\&\delta :\text {the rate of individuals who have been infected with a }\\&\qquad \text {particular disease } \\&\qquad \text {and eventually died of it (case fatality rate)}\\&\sigma :\text {the rate of death from disease with the treatment} \\&\alpha \gamma :\text {rate of transfer of disease from latent individuals to }\\&\qquad \text {sick individuals without treatment} \\&\beta :\text { the rate of transfer of infectious disease from hidden}\\&\qquad \text { individuals to sensitive individuals.} \end{aligned}$$

3.1 Fractal-fractional diabetes mellitus model

The concept of fractal was first formally introduced to the physical sciences more than 20 years ago by Beniot Mandelbrot. Mandelbort constructed the foundations of the concept by formally introducing his monograph to the physical world, which brought together mathematical, experimental, and physical arguments that undermined the conventional picture of the physical world. Mandelbrot, while evaluating the phenomenological formations, drew his attention to the challenges of explaining the process in physical processes such as blood coagulation, ice melting, and phase transitions with physics equations. In order to overcome this bottleneck, alternative and competitive methodologies have been presented. The idea of fractal-fractional was developed as a new idea by Atangana on fractional calculus. The defined operator in this new idea involves two orders. One of them represents the order of the fractional derivative, and the other represents the fractal dimension. Thus, fractal dimension can be examined simultaneously, as well as the fractal order.

The fact that the fractal fractional derivative provides the opportunity to examine the fractal dimension while evaluating the real phenomena in terms of fractional has enabled many researchers to concentrate on this subject. Many studies valuable papers, books, and scientific reports have been carried out with the concepts of fractional and fractal derivatives and they can be found there and in the references therein [15, 18, 25, 38, 57].

Now, let us redefine the diabetes mellitus model under fractal-fractional derivative in Caputo sense as follows:

$$\begin{aligned} \begin{array}{l} ^{FFP}D^{\zeta ,\epsilon }x\left( t\right) =\kappa -\mu x\left( t\right) -\delta z\left( t\right) -\sigma p\left( t\right) , \\ ^{FFP}D^{\zeta ,\epsilon }y\left( t\right) =\beta \left( x\left( t\right) -y\left( t\right) -z\left( t\right) -p\left( t\right) \right) y\\ \qquad \qquad \qquad \qquad -\left( \mu +1\right) y\left( t\right) , \\ ^{FFP}D^{\zeta ,\epsilon }z\left( t\right) =\alpha \gamma y\left( t\right) -\left( \mu +\delta \right) z\left( t\right) , \\ ^{FFP}D^{\zeta ,\epsilon }p\left( t\right) =\left( 1-\alpha \gamma \right) y\left( t\right) -\left( \mu +\sigma \right) p\left( t\right) . \end{array}\nonumber \\ \end{aligned}$$
(3.3)

During the analysis of the model given in (3.3) following ways are going to be followed: In the first section, we are going to present the required definitions. Equilibrium points and stability of the model are going to be lied in the second section and in the third section, the existence and uniqueness of the mentioned model are going to be investigated. Then, numerical results, simulations, and conclusion are going to take place in the advanced sections. The main idea of this study is to consider the model under fractal-fractional derivative.

3.2 Analysis of the diabetes mellitus model

Let us consider the diabetes mellitus model without genetic factors under fractal fractional order derivative as follows

$$\begin{aligned} \begin{array}{l} ^{FFP}D^{\zeta ,\epsilon }x\left( t\right) =\kappa -\mu x\left( t\right) -\delta z\left( t\right) -\sigma p\left( t\right) , \\ ^{FFP}D^{\zeta ,\epsilon }y\left( t\right) =\beta \left( x\left( t\right) -y\left( t\right) -z\left( t\right) -p\left( t\right) \right) y\\ \quad -\left( \mu +1\right) y\left( t\right) , \\ ^{FFP}D^{\zeta ,\epsilon }z\left( t\right) =\alpha \gamma y\left( t\right) -\left( \mu +\delta \right) z\left( t\right) , \\ ^{FFP}D^{\zeta ,\epsilon }p\left( t\right) =\left( 1-\alpha \gamma \right) y\left( t\right) -\left( \mu +\sigma \right) p\left( t\right) . \end{array} \end{aligned}$$
(3.4)

Since the integral is differentiable, we can rewrite the system (3.4) as follows

$$\begin{aligned} \begin{array}{l} ^{RL}D^{\zeta }x\left( t\right) =\epsilon t^{\epsilon -1}\left( \kappa -\mu x\left( t\right) -\delta z\left( t\right) -\sigma p\left( t\right) \right) \\ ^{RL}D^{\zeta }y\left( t\right) =\epsilon t^{\epsilon -1}\left( \beta \left( x\left( t\right) -y\left( t\right) -z\left( t\right) -p\left( t\right) \right) y\right. \\ \quad \left. -\left( \mu +1\right) y\left( t\right) \right) , \\ ^{RL}D^{\zeta }z\left( t\right) =\epsilon t^{\epsilon -1}\left( \alpha \gamma y\left( t\right) -\left( \mu +\delta \right) z\left( t\right) \right) , \\ ^{RL}D^{\zeta }p\left( t\right) =\epsilon t^{\epsilon -1}\left( \left( 1-\alpha \gamma \right) y\left( t\right) -\left( \mu +\sigma \right) p\left( t\right) \right) . \end{array} \end{aligned}$$
(3.5)

Now, when we replace the derivative \(^{RL}D\) by \(^{C}D,\) applying fractional integral, we get the solution as follows

$$\begin{aligned} \circledast \left( t\right) =\circledast \left( 0\right) +\frac{\epsilon }{\Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\Im \left( \circledast \left( s\right) ,s\right) ds\nonumber \\ \end{aligned}$$
(3.6)

where

$$\begin{aligned}{} & {} \circledast \left( t\right) =\left\{ \begin{array}{c} x\left( t\right) \\ y\left( t\right) \\ z\left( t\right) \\ p\left( t\right) \end{array} \right. \nonumber \\{} & {} \circledast \left( 0\right) =\left\{ \begin{array}{c} x_{0} \\ y_{0} \\ z_{0} \\ p_{0} \end{array} \right. \nonumber \\{} & {} \Im \left( \circledast \left( t\right) ,t\right) \nonumber \\{} & {} \qquad =\left\{ \begin{array}{l} \ell _{1}\left( x,y,z,p,t\right) =\kappa -\mu x\left( t\right) -\delta z\left( t\right) -\sigma p\left( t\right) \\ \ell _{2}\left( x,y,z,p,t\right) =\beta \left( x\left( t\right) -y\left( t\right) -z\left( t\right) \right. \\ \left. \qquad \qquad \qquad \qquad -p\left( t\right) \right) y-\left( \mu +1\right) y\left( t\right) \\ \ell _{3}\left( x,y,z,p,t\right) =\alpha \gamma y\left( t\right) -\left( \mu +\delta \right) z\left( t\right) \\ \ell _{4}\left( x,y,z,p,t\right) {=}\left( 1{-}\alpha \gamma \right) y\left( t\right) {-}\left( \mu +\sigma \right) p\left( t\right) . \end{array} \right. \nonumber \\ \end{aligned}$$
(3.7)

3.2.1 Critical (equilibrium) points

Finding critical points, that is, equilibrium points of a system is a process that analyzes how the actual solutions behave in the neighborhood of the equilibrium points without solving the system. In this section, we will carry out the equilibrium points and stability conditions of the system given in (3.4) by setting the derivatives to zero, then solving the system simultaneously.

The disease-free equilibrium is can be defined as the point at which there is not a disease in the population. Thus, the disease-free equilibrium lies at the point \(E_{0}=\left( \frac{\kappa }{\alpha },0,0,0\right) \) and the unique endemic equilibrium point is \(E_{1}=\left( x^{*},y^{*},z^{*},p^{*}\right) \) can be obtained as follows

$$\begin{aligned} x^{*}= & {} \frac{\alpha \beta ^2 \kappa (\mu +\sigma )+\beta (\delta \kappa (-\alpha \gamma +\mu +\sigma +1)+\kappa \mu (-\alpha \gamma +\mu +\sigma +1)+\alpha \delta (\mu +1) (\mu +\sigma ))+(\mu +1) \sigma (1-\alpha \gamma ) (\delta +\mu )}{\beta (\delta +\mu ) (\mu +\sigma ) (\alpha (\beta -\gamma )+\mu +1)}\\ y^{*}= & {} \frac{\beta \kappa -\mu \left( 1+\mu \right) }{\beta \left( 1+\alpha \left( \beta -\gamma \right) +\mu \right) },\quad z^{*}=\frac{\alpha \beta }{\left( \delta +\mu \right) }y^{*},\quad p^{*}=-\frac{\alpha \gamma -1}{\mu +\delta }y^{*}. \end{aligned}$$

The basic reproduction number given by \(R_{0}=\gamma \kappa /\left( \alpha +\alpha ^{2}\right) \). Now, in order to investigate stability, the eigenvalues of Jacobian matrix of (3.4) will consider;

$$\begin{aligned} J{=}\left[ \begin{array}{cccc} -\mu &{} 0 &{} -\delta &{} -\sigma \\ \beta y &{} \gamma \left( x-2y-z-p\right) -\left( \mu +1\right) &{} -\beta y &{} -\beta y \\ 0 &{} \alpha \gamma &{} -\left( \mu +\delta \right) &{} 0 \\ 0 &{} 1-\alpha \gamma &{} 0 &{} -\left( \mu +\sigma \right) \end{array} \right] \nonumber \\ \end{aligned}$$
(3.8)

When we evaluate Jacobian at the endemic equilibrium point \(E_{0}=\left( \frac{\kappa }{\alpha },0,0,0\right) ,\) we get;

$$\begin{aligned} J_{0}=\left[ \begin{array}{cccc} -\mu &{} 0 &{} -\delta &{} -\sigma \\ 0 &{} \frac{\beta \kappa }{\mu }-\left( \mu +1\right) &{} 0 &{} 0 \\ 0 &{} \alpha \gamma &{} -\left( \mu +\delta \right) &{} 0 \\ 0 &{} 1-\alpha \gamma &{} 0 &{} -\left( \mu +\sigma \right) \end{array} \right] \end{aligned}$$
(3.9)

An equilibrium point \(E_{0}=\left( \frac{\kappa }{\alpha },0,0,0\right) \) of the system (3.4) is stable if all the eigenvalues (\( \lambda \)) of \(J_{0},\) the Jacobian evaluated at \(E_{0},\) have negative real parts. Thus, the characteristic equation of (3.9) is obtained as

$$\begin{aligned}{} & {} \left( \frac{\beta \kappa }{\mu }-\mu -1-\lambda \right) \left( \lambda ^{2}+\lambda \delta +2\lambda \mu +\delta \mu +\mu ^{2}\right) \\{} & {} \quad \left( -\mu -\sigma -\lambda \right) =0 \end{aligned}$$

and related eigenvalues are

$$\begin{aligned} \begin{array}{l} \lambda _{1}=-\mu \\ \lambda _{2}=-\delta -\mu \\ \lambda _{3}=-\mu -\sigma \\ \lambda _{4}=\frac{\beta \kappa -\mu -\mu ^{2}}{\mu } \end{array} \end{aligned}$$

Because all the parameters used are positive, then for \(R_{0}<1,\) \(E_{0}\) is stable.

3.2.2 Existence and uniqueness

In this section, we are going to establish sufficient conditions on the existence of a unique solution of (3.5) using Banach fixed point theorem.

Let \(B_{nch}=C\times C\times C\times C\) is a Banach space under thenorm

$$\begin{aligned} \left\| \circledast \left( t\right) \right\| =\max \limits _{t\in I}\left\| x\left( t\right) +y(t)+z(t)+p(t)\right\| \end{aligned}$$

and

$$\begin{aligned} I=\left( t_{0}-\omega ,t_{0}+\omega \right) \end{aligned}$$

is a finite time interval. Now, we are going to show existence theorems by proving that T is a contraction mapping, So that

$$\begin{aligned} \begin{array}{l} T:B_{nch}\rightarrow B_{nch} \\ \\ \quad \circledast \left( t\right) \rightarrow T\left( \circledast \left( t\right) \right) \\ \qquad =\circledast \left( 0\right) +\frac{\epsilon }{ \Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\Im \left( \circledast \left( s\right) ,s\right) ds \end{array} \end{aligned}$$
(3.10)

Let \(\circledast _{0}\)is any point in \(B_{nch};\)

$$\begin{aligned} \begin{array}{l} \left\| \circledast \left( t\right) -\circledast _{0}\right\| \\ \quad {=}\left\| \circledast \left( 0\right) +\frac{\epsilon }{\Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t{-}s\right) ^{\zeta {-}1}s^{\epsilon {-}1}\Im \left( \circledast \left( s\right) ,s\right) ds-\circledast _{0}\right\| \\ \quad =\left\| \frac{\epsilon }{\Gamma \left( \zeta \right) } \int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\Im \left( \circledast \left( s\right) ,s\right) ds\right\| \\ \quad \le \frac{\epsilon T_{\max }^{\zeta +\epsilon -1}}{ \Gamma \left( \zeta \right) }\left\| \Im \left( \circledast \left( t\right) ,t\right) \right\| =\frac{\epsilon T_{\max }^{\zeta +\epsilon -1}}{\Gamma \left( \zeta \right) }\Psi \end{array} \nonumber \\ \end{aligned}$$
(3.11)

then there exists a unique fixed point \(\circledast _{0}\in B_{nch}.\)

Now, we need the condition that if \(\circledast _{1}\left( t\right) -\circledast _{2}\left( t\right) \) is small than \(\Im \left( \circledast _{1}\left( t\right) ,t\right) -\Im \left( \circledast _{2}\left( t\right) ,t\right) \) should be small, too. For (3.6);

$$\begin{aligned} \begin{array}{l} \left\| \Im \left( \circledast _{1}\left( t\right) ,t\right) -\Im \left( \circledast _{2}\left( t\right) ,t\right) \right\| \\ \quad =\left\| \circledast _{1}\left( 0\right) +\frac{\epsilon }{\Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\Im \left( \circledast _{1}\left( s\right) ,s\right) ds\right. \\ \qquad \left. -\circledast _{2}\left( 0\right) -\frac{\epsilon }{ \Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\Im \left( \circledast _{2}\left( s\right) ,s\right) ds\right\| \\ \quad \le \left\| \circledast _{1}\left( 0\right) -\circledast _{2}\left( 0\right) \right\| +\frac{\epsilon }{\Gamma \left( \zeta \right) }\\ \qquad \left\| \int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \Im \left( \circledast _{1}\left( s\right) ,s\right) -\Im \left( \circledast _{2}\left( s\right) ,s\right) \right) ds\right\| \\ \quad \le \left\| \circledast _{1}\left( 0\right) -\circledast _{2}\left( 0\right) \right\| \\ \qquad \quad +\frac{\epsilon T_{\max }^{\zeta +\epsilon -1}}{\Gamma \left( \zeta \right) }\left\| \left( \Im \left( \circledast _{1}\left( t\right) ,t\right) -\Im \left( \circledast _{2}\left( t\right) ,t\right) \right) \right\| \\ \quad \le \left\| \circledast _{1}\left( 0\right) -\circledast _{2}\left( 0\right) \right\| +\frac{\epsilon T_{\max }^{\zeta +\epsilon -1}}{\Gamma \left( \zeta \right) }\Psi \le \Theta . \end{array} \end{aligned}$$

4 Numerical scheme for the fractal-fractional diabetes mellitus model without genetic factors

In this section, we are going to establish a numerical scheme for diabetes mellitus model in order to present the numerical behavior of the model under fractal fractional derivative. For this purpose, let recall the model given in (3.5)

$$\begin{aligned} \begin{array}{l} ^{C}D^{\zeta }x\left( t\right) =\epsilon t^{\epsilon -1}\left( \kappa -\mu x\left( t\right) -\delta z\left( t\right) -\sigma p\left( t\right) \right) \\ ^{C}D^{\zeta }y\left( t\right) =\epsilon t^{\epsilon -1}\left( \beta \left( x\left( t\right) -y\left( t\right) -z\left( t\right) -p\left( t\right) \right) y\right. \\ \quad \left. -\left( \mu +1\right) y\left( t\right) \right) , \\ ^{C}D^{\zeta }z\left( t\right) =\epsilon t^{\epsilon -1}\left( \alpha \gamma y\left( t\right) -\left( \mu +\delta \right) z\left( t\right) \right) , \\ ^{C}D^{\zeta }p\left( t\right) =\epsilon t^{\epsilon -1}\left( \left( 1-\alpha \gamma \right) y\left( t\right) -\left( \mu +\sigma \right) p\left( t\right) \right) . \end{array} \end{aligned}$$
(4.1)

Using the approximation of the integrals on the right-hand side of above system, we get

$$\begin{aligned} \begin{array}{l} x\left( t\right) =x\left( 0\right) +\frac{\epsilon }{\Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \kappa -\mu x\left( s\right) -\delta z\left( s\right) \right. \\ \quad \quad \left. -\sigma p\left( s\right) \right) ds \\ y\left( t\right) =y\left( 0\right) +\frac{\epsilon }{\Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \beta \left( x\left( s\right) -y\left( s\right) \right. \right. \\ \quad \quad \left. \left. -z\left( s\right) -p\left( s\right) \right) y-\left( \mu +1\right) y\left( s\right) \right) ds \\ z\left( t\right) =z\left( 0\right) +\frac{\epsilon }{\Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \alpha \gamma y\left( s\right) \right. \\ \quad \quad \left. -\left( \mu +\delta \right) z\left( s\right) \right) ds \\ p\left( t\right) =p\left( 0\right) +\frac{\epsilon }{\Gamma \left( \zeta \right) }\int \limits _{0}^{t}\left( t-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \left( 1-\alpha \gamma \right) y\left( s\right) \right. \\ \quad \quad \left. -\left( \mu +\sigma \right) p\left( s\right) \right) ds. \end{array} \end{aligned}$$
(4.2)

Thus, at time \(t=t_{n+1}\)

$$\begin{aligned} x^{n+1}&=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \int \limits _{0}^{t_{n+1}}\left( t_{n+1}-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \kappa -\mu x\left( s\right) \right. \nonumber \\&\quad \left. -\delta z\left( s\right) -\sigma p\left( s\right) \right) ds\nonumber \\ y^{n+1}&=y^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \int \limits _{0}^{t_{n+1}}\left( t_{n+1}-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \beta \left( x\left( s\right) -y\left( s\right) \right. \right. \nonumber \\&\quad \left. \left. -z\left( s\right) -p\left( s\right) \right) y-\left( \mu +1\right) y\left( s\right) \right) ds \nonumber \\ z^{n+1}&=z^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \int \limits _{0}^{t_{n+1}}\left( t_{n+1}-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \alpha \gamma y\left( s\right) \right. \nonumber \\&\quad \left. -\left( \mu +\delta \right) z\left( s\right) \right) ds \nonumber \\ p^{n+1}&=p^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \int \limits _{0}^{t_{n+1}}\left( t_{n+1}-s\right) ^{\zeta -1}s^{\epsilon -1}\left( \left( 1-\alpha \gamma \right) y\left( s\right) \right. \nonumber \\&\quad \left. -\left( \mu +\sigma \right) p\left( s\right) \right) ds. \end{aligned}$$
(4.3)

Now, we are going to apply an approximation to functions \(s^{\epsilon -1}\left( \kappa -\mu x\left( s\right) -\delta z\left( s\right) -\sigma p\left( s\right) \right) ,\) \(s^{\epsilon -1}\Big ( \beta \Big ( x\left( s\right) -y\left( s\right) -z\left( s\right) -p\left( s\right) \Big ) y-\left( \mu +1\right) y\left( s\right) \Big ),\) \(s^{\epsilon -1}\Big ( \alpha \gamma y\left( s\right) -\left( \mu +\delta \right) z\left( s\right) \Big ) \) and \(s^{\epsilon -1}\left( \left( 1-\alpha \gamma \right) y\left( s\right) -\left( \mu +\sigma \right) p\left( s\right) \right) \). For convince; the functions seen in (4.3) are called with \(\ell _{i}\left( x,y,z,p\right) ,i=1,2,3,4\) as previous section. Therefore,

$$\begin{aligned}&P_{j}\left( s\right) \approx s^{\epsilon -1}\ell _{i}\left( x,y,z,p,s\right) =\frac{s-t_{j-1}}{t_{j}-t_{j-1}}t_{j}^{\epsilon -1}\ell _{i}\nonumber \\&\qquad \times \left( x,y,z,p,t_{j}\right) -\frac{s-t_{j}}{t_{j}-t_{j-1}}t_{j-1}^{\epsilon -1}\ell _{i}\left( x,y,z,p,t_{j-1}\right) \nonumber \\&\quad i=1,2,3,4 \end{aligned}$$
(4.4)

When we use the approximation (4.4) in (4.3), respectively, we get

$$\begin{aligned} x^{n+1}&=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \sum \limits _{j=0}^{n}\int \limits _{t_{j}}^{t_{j+1}}\left( t_{n+1}\right. \nonumber \\&\quad \left. -s\right) ^{\zeta -1}s^{\epsilon -1}\ell _{1}\left( x,y,z,p,s\right) ds\nonumber \\&=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) }\sum \limits _{j=0}^{n}\int \limits _{t_{j}}^{t_{j+1}}\left( t_{n+1}-s\right) ^{\zeta -1}\nonumber \\&\quad \times \left[ \frac{s-t_{j-1}}{t_{j}-t_{j-1}}t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z\right. \right. \nonumber \\&\quad \left. \left. ,p,t_{j}\right) -\frac{s-t_{j}}{t_{j}-t_{j-1}} t_{j-1}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j-1}\right) \right] ds\nonumber \\&=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) }\sum \limits _{j=0}^{n}\int \limits _{t_{j}}^{t_{j+1}}\left( t_{n+1}-s\right) ^{\zeta -1}\nonumber \\&\quad \left[ \frac{s-t_{j-1}}{t_{j}-t_{j-1}}t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z\right. \right. \left. \left. ,p,t_{j}\right) \right] ds \nonumber \\&\quad -\frac{\epsilon }{\Gamma \left( \zeta \right) }\sum \limits _{j=0}^{n}\int \limits _{t_{j}}^{t_{j+1}}\left( t_{n+1}-s\right) ^{\zeta -1}\nonumber \\&\quad \left[ \frac{ s-t_{j}}{t_{j}-t_{j-1}}t_{j-1}^{\epsilon -1}\ell _{1}\left( x,y,z\right. \right. \left. \left. ,p,t_{j-1}\right) \right] ds \end{aligned}$$
(4.5)

and after some arrangement, we can write

$$\begin{aligned} x^{n+1}&=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \sum \limits _{j=0}^{n}\int \limits _{t_{j}}^{t_{j+1}}\frac{\left( t_{n+1}-s\right) ^{\zeta -1}\left( s-t_{j-1}\right) }{t_{j}-t_{j-1}}\nonumber \\&\qquad \times \Bigg [t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \Bigg ] ds \nonumber \\&=-\frac{\epsilon }{\Gamma \left( \zeta \right) }\sum \limits _{j=0}^{n}\int \limits _{t_{j}}^{t_{j+1}}\frac{\left( t_{n+1}-s\right) ^{\zeta -1}\left( s-t_{j}\right) }{t_{j}-t_{j-1}}\nonumber \\&\qquad \times \left[ t_{j-1}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j-1}\right) \right] ds \end{aligned}$$
(4.6)

and

$$\begin{aligned} x^{n+1}=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \sum \limits _{j=0}^{n}I_{1}-\frac{\epsilon }{\Gamma \left( \zeta \right) } \sum \limits _{j=0}^{n}I_{2} \end{aligned}$$
(4.7)

where

$$\begin{aligned} I_{1}&=\int \limits _{t_{j}}^{t_{j+1}}\frac{\left( t_{n+1}-s\right) ^{\zeta -1}\left( s-t_{j-1}\right) }{t_{j}-t_{j-1}}\left[ t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \right] ds\nonumber \\ I_{2}&=\int \limits _{t_{j}}^{t_{j+1}}\frac{\left( t_{n+1}-s\right) ^{\zeta -1}\left( s-t_{j}\right) }{t_{j}-t_{j-1}}\left[ t_{j-1}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j-1}\right) \right] ds. \end{aligned}$$
(4.8)

Now, our aim is to calculate the integrals \(I_{1}\) and \(I_{2},\) so using the transformation \(y=t_{n+1}-s,\) we obtain following integral equation

$$\begin{aligned} I_{1}&=\int \limits _{t_{j}}^{t_{j+1}}\frac{\left( t_{n+1}-s\right) ^{\zeta -1}\left( s-t_{j-1}\right) }{t_{j}-t_{j-1}}\left[ t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \right] ds \nonumber \\&=-\int \limits _{t_{n+1}-t_{j}}^{t_{n+1}-t_{j+1}}\frac{y^{\zeta -1}\left( t_{n+1}-y-t_{j-1}\right) }{t_{j}-t_{j-1}}\nonumber \\&\quad \times \left[ t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \right] dy \nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \int \limits _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}\nonumber \\&\quad \times \frac{y^{\zeta -1}\left( t_{n+1}-y-t_{j-1}\right) }{t_{j}-t_{j-1}}dy\nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \frac{1}{\Delta t }\int \limits _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}y^{\zeta -1}\left( \left( n+1\right) \Delta t\right. \nonumber \\&\qquad \left. -\left( j-1\right) \Delta t-y\right) dy \nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \frac{1}{\Delta t }\int \limits _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}\nonumber \\&\quad \times \left[ \Delta t\left( n-j-2\right) y^{\zeta -1}-y^{\zeta }\right] dy \nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \frac{1}{\Delta t }\nonumber \\&\quad \times \left\{ \frac{\Delta t\left( n-j-2\right) y^{\zeta }}{\zeta }-\frac{ y^{\zeta +1}}{\zeta +1}\right\} _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}\nonumber \\&=\frac{t_{j}^{\epsilon -1}}{\zeta \left( \zeta +1\right) }\ell _{1}\left( x,y,z,p,t_{j}\right) \nonumber \\&\quad \times \left\{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \right. \nonumber \\&\qquad \left. -\left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \right\} \end{aligned}$$
(4.9)
Table 1 Numerical solution showing the performance of scheme (4.11) for various \(\zeta \) with \(\epsilon =0.99\) and \(t=10\). Other parameters are given in Fig. 2
Full size table
Fig. 2
figure 2

Simulation results for fractal-fractional diabetes mellitus in the sense of Caputo with varying orders. Other parameters are set as \(\kappa =1, \mu =0.13869, \delta =0.06654, \sigma =0.09281, \beta =0.0009, \alpha \gamma =0.88187\). Simulation runs for time \(t=80\)

Full size image
Fig. 3
figure 3

numerical results with \(\kappa =1, \beta =0.009\) for different instances of \(\zeta \) and \(\epsilon \). Other parameters are given in Fig. 2 caption

Full size image

and

$$\begin{aligned} I_{2}&=\int \limits _{t_{j}}^{t_{j+1}}\frac{\left( t_{n+1}-s\right) ^{\zeta -1}\left( s-t_{j}\right) }{t_{j}-t_{j-1}}\left[ t_{j-1}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j-1}\right) \right] ds\nonumber \\&=\int \limits _{t_{n+1}-t_{j}}^{t_{n+1}-t_{j+1}}\frac{y^{\zeta -1}\left( t_{n+1}-y-t_{j}\right) }{t_{j}-t_{j-1}}\left[ t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \right] dy\nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \int \limits _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}\frac{y^{\zeta -1}\left( t_{n+1}-y-t_{j}\right) }{t_{j}-t_{j-1}}dy \nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \frac{1}{\Delta t }\int \limits _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}y^{\zeta -1}\left( \left( n+1-j\right) \Delta t\right. \nonumber \\&\quad \left. -y\right) dy \nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \frac{1}{\Delta t }\int \limits _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}\left[ \Delta t\left( n+1-j\right) y^{\zeta -1}\right. \nonumber \\&\left. -y^{\zeta }\right] dy \nonumber \\&=t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \frac{1}{\Delta t }\nonumber \\&\quad \times \left\{ \frac{\Delta t\left( n+1-j\right) y^{\zeta }}{\zeta }-\frac{ y^{\zeta +1}}{\zeta +1}\right\} _{t_{n+1}-t_{j+1}}^{t_{n+1}-t_{j}}\nonumber \\&=\frac{t_{j}^{\epsilon -1}}{\zeta \left( \zeta +1\right) }\ell _{1}\left( x,y,z,p,t_{j}\right) \left\{ \left( n-j+1\right) ^{\zeta +1}-\left( n\right. \right. \nonumber \\&\quad \left. \left. -j\right) ^{\zeta }\left( \zeta +n-j+1\right) \right\} . \end{aligned}$$
(4.10)

Using \(I_{1\text { }}\) and \(I_{2\text { }}\)in (4.7), we get

$$\begin{aligned} x^{n+1}&=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta \right) } \sum \limits _{j=0}^{n}t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \left\{ \left( n-j\right. \right. \\&\quad \left. \left. +1\right) ^{\zeta }\left( \zeta +n-j+2\right) -\left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \right\} \\&\quad -\frac{\epsilon }{\Gamma \left( \zeta \right) }\sum \limits _{j=0}^{n}t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \nonumber \\&\quad \times \left\{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j\right. \right. \\&\left. \left. +2\right) -\left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \right\} . \end{aligned}$$

So, the system given in (4.3) transform following algebraic equation system as follows

Fig. 4
figure 4

numerical results with \(\kappa =0.02, \beta =0.009\) for different instances of \(\zeta \) and \(\epsilon \). Other parameters are given in Fig. 2 caption

Full size image
Fig. 5
figure 5

Numerical results showing the effect of \(\kappa =0.50\) for different instances of \(\zeta \) and \(\epsilon \). Other parameters are given in Fig. 2 caption

Full size image
Fig. 6
figure 6

The presence of attractors show that the entire population coexist and permanents regardless of time (days) and fractal-fractional orders. Parameters are given in Fig. 2 caption

Full size image
Fig. 7
figure 7

The presence of attractors showing the effect of \(\beta =0.02(0.02)0.08\). The fractal-fractional parameters are given as \(\zeta =0.98\) and \(\epsilon =0.99\)

Full size image
Fig. 8
figure 8

Numerical results showing effects of \(\beta \) with fixed values of \(\zeta =0.98\) and \(\epsilon =0.99\). Other parameters remain as defined in Fig. 2 caption

Full size image
$$\begin{aligned} x^{n+1}&=x^{0}+\frac{\epsilon }{\Gamma \left( \zeta +2\right) } \sum \limits _{j=0}^{n}t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \nonumber \\&\quad \times \Bigg \{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \nonumber \\&\qquad -\left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \Bigg \} \nonumber \\&\qquad -\frac{\epsilon }{\Gamma \left( \zeta +2\right) }\sum \limits _{j=0}^{n} t_{j}^{\epsilon -1}\ell _{1}\left( x,y,z,p,t_{j}\right) \nonumber \\&\qquad \times \Bigg \{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \nonumber \\&\qquad -\left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \Bigg \}\nonumber \\ y^{n+1}&=y^{0}+\frac{\epsilon }{\Gamma \left( \zeta +2\right) }\sum \limits _{j=0}^{n} t_{j}^{\epsilon -1}\ell _{2}\left( x,y,z,p,t_{j}\right) \nonumber \\&\qquad \times \Bigg \{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \nonumber \\&\qquad -\left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \Bigg \}\nonumber \\&\qquad - \frac{\epsilon }{\Gamma \left( \zeta +2\right) }\sum \limits _{j=0}^{n}t_{j}^{\epsilon -1} \ell _{2}\left( x,y,z,p,t_{j}\right) \nonumber \\&\quad \Bigg \{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \nonumber \\&\qquad -\left( n-j\right) ^{\zeta } \left( 2\zeta +n-j+2\right) \Bigg \}\nonumber \\ z^{n+1}&=z^{0}+\frac{\epsilon }{\Gamma \left( \zeta +2\right) }\sum \limits _{j=0}^{n} t_{j}^{\epsilon -1}\ell _{3}\left( x,y,z,p,t_{j}\right) \nonumber \\&\qquad \times \Bigg \{ \left( n -j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \nonumber \\&\qquad - \left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \Bigg \}\nonumber \\&\quad -\frac{\epsilon }{ \Gamma \left( \zeta +2\right) }\sum \limits _{j=0}^{n}t_{j}^{\epsilon -1}\ell _{3}\left( x,y,z,p,t_{j}\right) \nonumber \\&\qquad \times \Bigg \{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \nonumber \\&\qquad -\left( n-j\right) ^{\zeta }\left( 2\zeta +n-j+2\right) \Bigg \}\nonumber \\ p^{n+1}&=p^{0}+\frac{\epsilon }{\Gamma \left( \zeta +2\right) } \sum \limits _{j=0}^{n}t_{j}^{\epsilon -1}\ell _{4}\left( x,y,z,p,t_{j}\right) \nonumber \\&\qquad \times \Bigg \{ \left( n-j+1\right) ^{\zeta }\left( \zeta +n-j+2\right) \nonumber \\&\qquad -\left( n-j\right) ^{\zeta } \left( 2\zeta +n-j+2\right) \Bigg \}-\frac{\epsilon }{\Gamma \left( \zeta +2\right) }\nonumber \\&\qquad \sum \limits _{j=0}^{n}t_{j}^{\epsilon -1}\ell _{4}\left( x,y,z,p,t_{j}\right) \left\{ \left( n-j+1\right) ^{\zeta }(\zeta +n\right. \nonumber \\&\quad \left. -j+2)-\left( n-j\right) ^{\zeta } \left( 2\zeta +n-j+2\right) \right\} . \end{aligned}$$
(4.11)

It should be noted that we do not have analytical solution to model (3.3); we follow the idea suggested in [23] check the performance of the Caputo fractal-fractional diabetes mellitus scheme by setting the step-size \(h=0.001\) as the reference solution. Numerical results for various step sizes and fractal-fractional parameters are tabulated in Table 1.

Table 2 Initial conditions for diabetes mellitus model
Full size table

5 Numerical experiments and results

In this section, our attention will be devoted to numerical solution of the fractal-fractional diabetes mellitus model without the genetic factors (3.4). The resulting numerical approximation for the fractal-fractional diabetes mellitus model as given by equation (4.11) is advanced in time by suing the MATLAB ODE15s code. All simulations are carried out with the aid of MATLAB 2021a package on a digital ALIENWARE computer, Core i7, 9th generation, with 32GB RAM, 512GB SSD, and 8GB Nvidia gtx1070 graphics card.

In addition, we are going to present the treatment of patients with diabetes mellitus without genetic factors under the fractional-fractal order derivatives in the sense of the Caputo operator. First, let’s redefine the variables to be determined in the model. \(x\left( t\right) \) is the number of susceptible individuals in the population, and the number of individuals exposed to diabetes and asymptomatic is symbolized by \(y\left( t\right) \). The number of individuals with diabetes but not treated is defined by \(z\left( t\right) \), and the number of individuals with diabetes and access to treatment is shown by \(p\left( t\right) \). The initial conditions used in the simulation experiments are given in Table 2 with time-step \(h=0.01\).

Considering the parameters observed in the system for a total simulation time \(t=80\)/days are given as follows; the birth rate in the population is \(\kappa =1;\) the value of natural death rate is \(\mu =0.13869;\) death rate of untreated patients with diabetes \(\delta =0,06654;\) death rate of treated patients with diabetes \(\sigma =0,09281;\) the rate of infective contact of susceptible individuals to latent individuals \(\beta =0.0009;\) and the latent rate of movement of the individual becomes infected \(\alpha \gamma =0.88187.\) First of all, the values of variables are given in Table 3 at different time levels and the behavior of \(x\left( t\right) ,y\left( t\right) ,z\left( t\right) \) and \(p\left( t\right) \) are presented in Figs. 2-6 for \(h=0.01\), and at different instances of fractional order \(\epsilon \in (0, 1]\), and fractal dimension \(\zeta \in (0, 1]\).

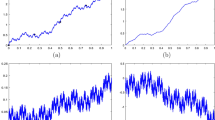
Table 3 The values of variables at various times
Full size table

Numerical experiments are conducted for different values of parameters to mimic the dynamic behavior of the fractal-fractional diabetes mellitus model as displayed in Figs. 2-8. To start with, we observed the numerical scheme (4.11) with fixed parameters as given above, and allow the fractal-fractional values \((\zeta , \epsilon )\) to vary by assuming that both the fractal dimension and the fractional derivative orders are equal, that is \(\zeta =\epsilon \). Figure 2 shows the behaviors of susceptible people x(t), exposed people y(t), infected population z(t), and recovered people due to the availability of treatment p(t) versus time t in days with variation in the memory index \(\zeta \) and \(\epsilon \) at different values as given in the figure captions. Figure 2 shows the dynamic effects for different values of \(\zeta \) and \(\epsilon \), as we can see when \(\zeta =\epsilon =0.75\), the susceptible and infected population are also increasing, but decreased drastically as both \(\zeta \rightarrow 1\) and \(\epsilon \rightarrow 1\). This means that decrease in parameters \(\zeta ,\epsilon \) result in an increase in the susceptible and infected populations.

Next, we are considering the behavior of individual subclass with respect to parameter perturbation with \(\beta \) which represents the rate of infectious contact of susceptible individuals to the latent population as shown in Fig. 3 for different fractal-fractional order values. It is obvious that the behavior of sub-population y(t), z(t) and p(t) follow a similar trend as the values \(\zeta ,\epsilon \rightarrow 1\), that is, with \(\zeta =\epsilon =0.80(0.05)1.00\). With \(\kappa =0.02\), and retained value \(\beta =0.009\), one obtained the dynamic response in Fig. 4, it was discovered that the lower the values of \(\zeta \) and \(\epsilon \), the higher the number of people living with the diabetes mellitus. To keep the affected class down, both \(\zeta \) and \(\epsilon \) must tends to unity. In Fig. 5, we utilized parameters \(\kappa =0.50\) subject to when \(\zeta \ne \epsilon \). Various numerical results for alternating values of fractal dimension \(\zeta \) and fractional order \(\epsilon \) are displayed for various sub-population classes.

In the previous section, it was shown that the proposed model’s solution exists and is unique. In the same vein, we shall justify through numerical experiments that the solution of the diabetes mellitus model described by the fractal-fractional derivative in the sense of the Caputo operator exists. To achieve this, we let \(\zeta =\epsilon \in (0, 1]\), with parameters \(\kappa =1, \mu =0.13869, \delta =0,06654, \sigma =0,09281, \gamma =0.88187\), and \(\beta =0.0009\) to obtain a 3D attractors in Fig. 6 which correspond to \(\zeta =\epsilon =0.78 (blue), \zeta =\epsilon =0.85 (black), \zeta =\epsilon =0.95 (red)\) and \(\zeta =\epsilon =1.00 \) (green), respectively. The presence of attractors of various sub-population shows that all classes will coexist within a given population over a period of time t, regardless of the choice of \(\zeta \) and \(\beta \) or any other parameters. For instance, and to justify this assertion, we set \(\beta =(0.02, 0.04, 0.06, 0.08)\) which corresponds to black, red, green, and blue lines, respectively, to obtain the dynamic behavior in Fig. 7. The corresponding time solutions for each of the sub-population are given in Fig. 8. Hence, the key parameters which play a major role in the simulation experiment of the diabetes mellitus model in this work are the fractal dimension \(\zeta \) and fractional order \(\epsilon \)

6 Conclusion

Diabetes is tagged as a chronic, metabolic disease signalized by elevated levels of blood glucose (or blood sugar), which results over time in serious damage to the heart, blood vessels, eyes, kidneys, and nerves in the body. The most common is type-II diabetes, usually in adults, which occurs when the body is resistant to insulin or does not produce enough insulin. In the past three decades, the prevalence of type-II diabetes has risen dramatically in countries of all income levels. Type-I diabetes, once called juvenile diabetes or insulin-dependent diabetes is a chronic condition in which the pancreas produces little or no insulin by itself. Therefore, for people living with this deadly disease, access to affordable treatment, including insulin, is critical to their survival. In this paper, a four compartmental model describing the diabetes mellitus disease without genetic factors is investigated in the sense of the Caputo fractal-fractional operator. At first, we uncovered the critical points to identify the stability analysis of the model being considered, then successfully demonstrated the existence and uniqueness conditions of the solution using Picard Lindelof theorem when defined by the fractal fractional derivative of the model without genetic factors. A viable numerical approximation technique was formulated to discretize the proposed model. The resulting system of fractal-fractional differential equations was advanced in time with the novel inbuilt ODE15s MATLAB R2021a package. Numerical results for different instances of fractal dimension and fractional-order parameters are reported for each of the sub-classes. It was observed via simulation experiments that whenever the values of \(\zeta ,\epsilon \) is decreasing, says tend to 0, the number of people living with diabetes witness an upsurge, but when \(\zeta ,\epsilon \rightarrow 1\), the population of individuals living with diabetes will be reducing. To have a population free of diabetes, both \(\zeta \) and \(\epsilon \) must tend to unity. Also in Table 1, the utmost solutions were recorded with \((\zeta ,\epsilon )\rightarrow 1\). Extension of the fractal-fractional operator to model more complex scenarios in engineering and biomedical processes is left for future work.