Skip to main content
SpringerLink
Log in

Periodic cutting motions in a vibration-assisted, regenerative, nonlinear Orthogonal turning system

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

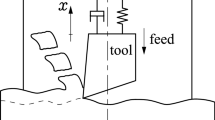
In this paper, a mathematical model of 2-degrees-of-freedom (2-DOF), vibration-assisted, regenerative, nonlinear orthogonal turning system is developed. The period-1 motions of such a system are predicted through the discrete mapping method. The discrete mapping is constructed by discretization of equations of motion of the machine-tool system. The periodic motions of such a machine tool system are determined through the mapping structures, and the stability and bifurcation conditions of the period-1 motions are determined by eigenvalue analysis. The variation of period-1 motions with respect to active excitation from a servo unit is presented from the bifurcation diagram of periodic nodes. Numerical simulations are carried out for small-amplitude and large-amplitude machine-tool vibration. The machine tool chatter occurs once the horizontal and vertical displacement of the machine-tool are out-of-phase. Such a relation could be used for the chatter detection of vibration-assisted machining.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Tobias SA (1965) Machine-tool Vibration. (trans: Burton AH). New York: John Wiley & Sons

  2. Brehl DE, Dow TA (2008) Review of vibration-assisted machining. Precis Eng 32:153–172

    Article  Google Scholar 

  3. Zhang SJ, To S, Zhang GQ, Zhu ZW (2015) A review of machine-tool vibration and its influence upon surface generation in ultra-precision machining. Int J Mach Tool Manuf 91:34–42

    Article  Google Scholar 

  4. Arnold RN (1946) Mechanism of tool vibration in cutting of steel. In: Proceedings Institution of Mechanical Engineers 154: 261-284

  5. Tobias SA, Fishwick W (1958) Theory of regenerative machine tool chatter. Engineer 205(7):199–203

    Google Scholar 

  6. Tlusty J, Polacek M (1963) The stability of machine tools against self-excited vibration in machining. In: Processing of the ASME International Research in Production Engineering, Pittsburgh, PA: 465-474

  7. Koenigsberger F, Tlusty J (1970) Machine tool structures, vol 1. Pergamon Press, New York

    Google Scholar 

  8. Hooke JC, Tobias SA (1964) Finite amplitude instability – a new type of chatter. In: Proceeding of 4th MTDR: 97–100

  9. Wiercigroch M, Budak E (2001) Sources of nonlinearities, chatter generation and suppression in metal cutting. Philos Trans R Soc A 359(1781):663–693

    Article  Google Scholar 

  10. Hanna NH, Tobias SA (1974) A theory of nonlinear regenerative chatter. J Eng Ind 96(1):247–255

    Article  Google Scholar 

  11. Tlusty J, Ismail F (1982) Basic nonlinearity in machining chatter. CIRP Ann 30:229–304

    Google Scholar 

  12. Shi HM, Tobias SA (1984) Theory of finite amplitude machine tool instability. Int J Mach Tool Des Res 24(1):45–69

    Article  Google Scholar 

  13. Garbec I (1986) Chaos generated by the cutting process. Phys Lett A 117:394–386

    Article  MathSciNet  Google Scholar 

  14. Garbec I (1988) Chaotic dynamics of the cutting process. Int J Mach Tools Manuf 28:19–32

    Article  Google Scholar 

  15. Moon FC, Kalmar-Nagy T (2001) Nonlinear models for complex dynamics in cutting materials. Philos Trans R Soc A 359:695–711

    Article  Google Scholar 

  16. Insperger T, Stephan G, Turi J (2006) State-dependent delay in regenerative turning processes. Nonlinear Dyn 47:275–283

    Article  Google Scholar 

  17. Gegg BC, Suh CS, Luo ACJ (2011) Machine tool vibration and cutting dynamics. Springer, New York

    Book  Google Scholar 

  18. Lehotzky D, Insperger T, Stepan G (2015) State-dependent, non-smooth model of chatter vibrations in turning. In: Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, Massachusetts, USA

  19. Liu MK, Suh CS (2012) On controlling milling instability and chatter at high speed. J Appl Nonlinear Dyn 1(1):59–72

    Article  Google Scholar 

  20. Liu MK, Suh CS (2014) Simultaneous time-frequency control of friction induced instability. J Appl Nonlinear Dyn 3(3):227–244

    Article  Google Scholar 

  21. Halfmann EC, Suh CS, Hung WNP (2017) Dynamics of turning operation Part I: experimental analysis using instantaneous frequency. J Vib Test Syst Dyn 1:15–33

    Google Scholar 

  22. Halfmann EC, Suh CS, Hung WNP (2017) Dynamics of turning operation Part II: model validation and stability at high speed. J Vib Test Syst Dyn 1:35–52

    Google Scholar 

  23. Halfmann EC, Suh CS (2017) On the temporal and spectral characteristics of micro-milling dynamics. J Vib Test Syst Dyn 1:177–193

    Google Scholar 

  24. Dassanayake AV, Suh CS (2017) Impact of tool geometry and tool feed on machining stability. J Vib Test Syst Dyn 1:295–317

    Google Scholar 

  25. Luo ACJ (2015) Discretization and implicit mapping dynamics. HEP/Springer, Beijing/Dordrecht

    Book  Google Scholar 

  26. Luo ACJ, Guo Y (2015) A semi-analytical prediction of periodic motions in Duffing oscillator through mapping structures. Discontin Nonlinearity Complex 4(2):121–150

    Article  Google Scholar 

  27. Xing SY, Luo ACJ (2019) On a global sequential scenario of bifurcation trees to chaos in a first-order, periodically excited, time-delayed system. Int J Bifurc Chaos 29(10):1950141

    Article  MathSciNet  Google Scholar 

  28. Xing SY, Luo ACJ (2017) Towards infinite bifurcation trees of period-1 motions to chaos in a time-delayed, twin-well Duffing oscillator. J Vib Test Syst Dyn 1(4):353–392

    MathSciNet  Google Scholar 

  29. Xu YY, Chen ZB, Luo ACJ (2019) On bifurcation trees of period-1 to period-2 motions in a nonlinear Jeffcott rotor system. Int J Mech Sci 160:429–450

    Article  Google Scholar 

  30. Luo ACJ, Guo C (2019) A period-1 motion to chaos in a periodically forced, damped, double-pendulum. J Vib Test Syst Dyn 3(3):259–280

    Google Scholar 

  31. Guo Y, Luo ACJ (2017) Complete bifurcation trees of a parametrically driven pendulum. J Vib Test Syst Dyn 1(2):93–134

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, California Polytechnic State University, San Luis Obispo, CA, 93401, USA

    Siyuan Xing

  2. Department of Mechanical and Industrial Engineering, Southern Illinois University Edwardsville, Edwardsville, IL, 62026-1805, USA

    Albert C. J. Luo

Authors
  1. Siyuan Xing
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Albert C. J. Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Albert C. J. Luo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xing, S., Luo, A.C.J. Periodic cutting motions in a vibration-assisted, regenerative, nonlinear Orthogonal turning system. Int. J. Dynam. Control 10, 1–12 (2022). https://doi.org/10.1007/s40435-021-00779-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-021-00779-3

Keywords

Search

Navigation