Time delays in numerical modeling of frontal thoracic blast pressure wave responses

Abstract

In this work a lumped mass mechanical model of a thorax subject to a blast pressure wave is taken into consideration. A thorax spring-dashpot model developed by Lobdell is implemented in numerical modeling of dynamics of the multibody system. The five degrees of freedom mechanical model of a chest adjacent to the elastic backrest is subject to an impulse loading generated by the blast pressure wave released by an explosion. The so-called coupling of the pressure wave to the thorax is reconsidered. With respect to the evident existence of inherent time delays of displacements, the system of coupled bodies is described by a time delay differential equations that are derived from the large-scale systems approach. Numerical solutions present interesting dynamical behavior of the bio-inspired system resulting from inherent time delays and a time of arrival of the blast pressure wave. There is pointed out that the inherent state time delays change dynamical response of the multibody system. Proper time of deployment of the foam-based armor plate reduces relative compression of the thorax, which is to be protected by a bullet-proof waistcoat.

1 Introduction

Intrinsic delays in states of physical quantities characterize many dynamical systems in physics, material engineering, ballistics, biology and chemistry [1–5]. Natural or artificial control systems have delays from the sensing of a variable and the initiation of appropriate response. Mathematics of systems with time delays pose basic mathematical challenges. They can be described mathematically by delay differential equations, which belong to the class of functional differential equations [6]. The effect of a delay influences dynamical responses of investigated systems, and is strongly visible in behavior of multibody systems. The time delay terms of differential equations produce an infinite number of roots of the characteristic equation, making the corresponding dynamical behavior difficult to analyze. One solves such problems indirectly by applying some approximations, but a limitation in accuracy that leads to the instability of systems can occur [7]. More effective methods based on an analytic approach to obtain the complete solution of systems represented by the delay differential equations based on the concept of Lambert W function was developed in [8].

From the other side, numerical methods can be used to aid any mathematical modeling.

Numerical methods are today popular in biodynamics and, in particular, in dynamical analysis of primary blast lung injuries caused by the pressure wave released by an explosion [9]. Rapid motion of the human’s chest wall creates a pressure wave in the lung material [10]. A concept to protect the chest is to use a layer foam material behind a massive armor plate worn over the chest. Coupling of the blast wave to the thorax causes that soft tissues like lungs placed in the contents of the thorax can sustain large stress and strain rate [11]. To investigate the mechanical responses of the internal organs, a complex modeling is required. Homogeneous and linear elasticity material properties are assigned to each part of the model, whereas the human cartilages and bones may have different material properties. Such conditions are taken into consideration by Lobdell’s model which has been reconsidered in this work to perform numerical solutions of a large-scale time-delay system.

In this paper the problem of modeling of a multibody biomechanical system of thorax is considered. On the basis of the theory of large-scale continuous-time systems an uncertain model of thorax has been written in the representation allowing to define its parametric uncertainties and complex interactions between its subsystems. The parametric uncertainties make the discontinuous system more difficult to solve, but it is compensated by more accurate numerical solution and evident possibility of inclusion of time delays in the impulse responses.

The fact is that, if we consider an exponential decaying response that takes about 0.2 ms, then the time delay superposed on each body of the system play an important role.

A large-scale dynamical system can be characterized by a large number of state variables, system parametric uncertainties, and a complex interaction between sub-systems [12, 13]. In view of reliability and practical implementation, time delays have to be incorporated into the numerical modeling of the large-scale physical systems due to the real transport of mass, propagation of vibrations and computation times.

2 Variation of the air-blast over-pressure wave

Explosions in air create intense shock waves capable of transferring large transient pressures and impulses to the objects they intercept [14]. The free-field pressure time response from an explosion in air is described by known Friedlander’s waveform

$$\begin{aligned} p(x,t)=p_0e^{(x-v_0t)/(v_0t_i)}, \end{aligned}$$

(1)

where $p(x,t)$ is the pressure at a point $x$ and time $t$, $p_0$ is the blast over-pressure (maximum amplitude), $t_i$ is the wave decaying time and $v_0$ is the sound speed in air. A blast wave propagates outward from an explosion. It consists of a shock front, which precedes a phase of positive pressure and can be followed by a negative pressure phase, which is not taken into the analysis.

For the numerical experiment carried out in this work one assumes that the wave has arrived after the explosion in time $t_\mathrm{arr}$ at the buffer mass $m_1$ placed at $x=0$ in front of the investigated multibody system (see Fig. 2). Therefore, the simplified time-dependent characteristics of the pressure wave [9] is given

$$\begin{aligned} p(t)=p_0e^{-t/t_i}. \end{aligned}$$

(2)

It will be more useful in numerical computations to represent the pressure wave as the effective impact force $u_b(t)$ per an effective area $a$ of the chest subject to the air shock. Temporal variation of the blast wave that reaches the armor plate is estimated using the following conditions:

• (C1) The most harmful positive phase of the blast wave profile is assumed [15].

• (C2) Maximum amplitude $p_0=1\,\hbox {MPa}$ due to a 10 kg TNT explosion at 2.2 m standoff.

• (C3) Wave decay time $t_i=1.66\,\hbox {ms}$ causes a decrease of $p_0$ to zero within $t_r=1.2\,\hbox {ms}$, such that the impulse $I=0.4\,\hbox {kPa}\, \hbox {s}$ impinges onto the armor buffer plate.

• (C4) The effective area $a=1.825\times 10^{-2}\,\hbox {m}^2$ of the PUR-foam plate and the chest.

• (C5) Maximum amplitude of the effective impact force $u_0=18.25\,\hbox {kN}$ (see Fig. 1).

• (C6) Impact force $u(t)$ decreases after time $t_i$ to $u_0/e$.

• (C7) Arrival time of blast wave after detonation $t_{\text {arr}}=1\,\hbox {ms}$.

• (C8) Mass of the buffer plate $m_1=0.365\,\hbox {kg}$ for the foam’s density $\rho _f=20\,\hbox {kg/m}^2$.

• (C9) Reaction force of the armor plate worn over the chest to the blast wave during buffer deployment depends on the foam’s unloading properties (see $\sigma _u(\varepsilon )$ in Table 1).

• (C10) Buffer deployment time for an active mitigation concept depends on $\sigma _u(\varepsilon )$ as well.

• (C11) Maximum incident over-pressure cannot exceed 13 kN, which is determined from the lung damage threshold on Bowen curve [16], and for duration of positive incident over-pressure equal to 1 ms.

Fig. 1

Blast load with $u_0$ peak pressure and $t_i$ decay coefficient. A time history of positive phase of the blast over-pressure wave arrived after $t_a$ at the buffer mass

Table 1 Foam model parameters for estimation of $\sigma (\varepsilon )$ curve with hysteresis

If a sensor capable of detecting the electromagnetic emission [17] created at the instant of detonation affords a time delay, $t_a$, between detonation and the arrival of the blast wave then a buffer deploys by using a high-speed actuator, such as a propellant. The force exerted on the buffer as it deploys must assure that the reaction pressure exerted on the protected chest does not exceed 0.3 MPa. For detonations of high explosives the peak over-pressure can cause injury to the thorax.

In the study, the foam deploys with a lower peak over-pressure determined by $\sigma _u(\varepsilon )$ (see Table 1), and the impact time-response dynamics is assessed for a model problem consisting of 10 kg of a high explosion TNT at 2.2 m standoff. The relevant ConWep [16] computations of peak pressure $p_0$ over the atmospheric pressure, impulse $I$ and arrival time $t_\mathrm{arr}$ as a function of range are found in [14]. Finally, we can write

$$\begin{aligned} u_b(t)=u_0e^{-t/t_i}. \end{aligned}$$

(3)

Corresponding time history of positive phase of the blast wave is depicted in Fig. 1.

3 The foam-based armor with buffer plate

Foam materials have the ability to deform at low stress level while absorbing mechanical energy. Foam is used in applications of impact protection, to absorb the kinetic energy of an impact, and reduce the maximum stress on the protected object [9]. The foam material reduces peak acceleration while increasing the duration of the impact.

Pressure waves released by explosions cause the so-called primary blast injuries. They significantly affect the air-containing organs of human body [18], and in particular, lungs. A lung injury caused by the pressure wave occurs after rapid motion of the chest wall, which creates a following pressure wave in the lung structure. This is referred to as coupling of the blast wave to the thorax. A concept to protect lungs against primary blast injury is to use a layer of foam material behind a massive armor plate worn over the chest [9].

Capability of energy absorbing is the basic feature of foams. They are deformed and absorb the impact energy [19] while keeping the stress acting on the armor plate loaded with the blast wave. One of the common features of energy absorption foam materials is that there is a discernible plateau in their compression stress–strain curves. It means, that the foam materials can absorb energy by deformation, but keep the stress almost constant [19, 20].

The typical shape of the stress–strain curve for solid foams has been presented in [21], and including hysteresis, in [22]. The model proposed by Goog encompasses few parameters dependent on relative density, because Young modulus and plateau stress usually increase and densification strain decreases with increasing foam density.

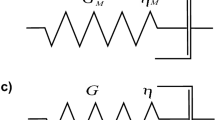
In this work the assumed foam model is a little modification of Goog’s model that is completed with a hysteresis. It consist of three systems in parallel, (see in Fig. 2):

• (G1) The Maxwell arm, containing a spring (linear stiffness $k_{16}$) and dashpot (viscosity $c_{62}$) in series. First component describes the first and second region of foam compression and deformation, if the plateau stress is constant.

• (G2) Linear spring $k_p$. The second stiffness represents a shape of the plateau. It is integrated to describe the increasing or decreasing part of the plateau.

• (G3) Nonlinear spring $k_D$. The third stiffness is responsible for densification part. It is given by the formula

  $$\begin{aligned}&k_D(\varepsilon )=\gamma (1-e^\varepsilon )^n,\end{aligned}$$

  (4a)
  $$\begin{aligned}&\varepsilon =\frac{x_1-x_2}{h_f}, \end{aligned}$$

  (4b)

  where $\gamma$ and $n$ are the model parameters, $\varepsilon$ is the strain and $h_f$ is a thickness of the foam.

Each element of the spring-dashpot model will produce the following components of reaction force:

$$\begin{aligned} F_p&= a\sigma _p=ak_p\varepsilon =\frac{a}{h_f}k_p(x_1-x_2),\end{aligned}$$

(5a)

$$\begin{aligned} F_D&= a\sigma _D=ak_D\varepsilon =\frac{a}{h_f}\gamma (1-e^\varepsilon )^n(x_1-x_2),\end{aligned}$$

(5b)

$$\begin{aligned} F_c&= a\sigma _c=ac_{62}\dot{\varepsilon }_c=\frac{a}{h_f}c_{62}(\dot{x}_2-\dot{x}_6),\end{aligned}$$

(5c)

$$\begin{aligned} F_k&= a\sigma _k=ak_{16}\varepsilon _k=\frac{a}{h_f}k_{16}(x_1-x_6), \end{aligned}$$

(5d)

where $k_p,\, \gamma ,\, c_{62},\, k_{16}$ are stresses in MPa.

Polymeric open-cell foams exhibit complex nonlinear behavior [22]. As it was mentioned, the stress–strain curve for uniaxial compression shows three well distinguishable regimes (G1–G3). The same three regimes are present during unloading of the foam but the response exhibits a hysteresis loop. For the numerical experiment, loading $\sigma (\varepsilon )|_{\dot{\varepsilon }>0}$ and unloading $\sigma (\varepsilon )|_{\dot{\varepsilon }\le 0}$ curves are estimated, respectively, for the model parameters of foam densities $\rho _l=50\,\hbox {kg/m}^3$ and $\rho _u=40\,\hbox {kg/m}^{3}$ (divided by two) listed in Table 1 (compare with [21]).

4 Mechanical model of the idealized thorax supported from behind

The problem of time-varying position- and velocity-dependent system parameters is reflected in the modeling by many factors, i.e. Maxwell elements. Skeletal deflection of the thorax was determined by the difference between displacements of its anterior and posterior walls. The parameter discontinuity observed in connections between the directly coupled lumped masses of the mechanical idealization appear in four cases:

• (U1) If a relative displacement $x_{21}(t)-x_{31}(t)<0$ measured between the front and back walls of the thorax exceeds $d=3.8\,\hbox {cm}$, then a bi-linear spring stiffness $k_{23}$ doubles its value that satisfies the Kroell corridors at large deflection. Stiffness of contents of the thorax changes due to the nonlinear material behavior of the rib cage.

• (U2) If a velocity of relative displacement of front and back wall of the thorax becomes negative, i.e. $x_{22}(t)$ $-x_{32}(t)<0$, then a parameter $c_{23}$ of viscous damping doubles its value. A different damping coefficient responsible for elongation and compression is assumed in order to satisfy the descending part of the Kroell corridors.

• (U3) If a foam material is compressed (in loading state) or relaxed (in unloading state), then two different phenomenological solid foam models, which are nonlinear according to (G1–G3) are assumed (see $\sigma _l(\varepsilon )$ and $\sigma _u(\varepsilon )$ in Table 1).

• (U4) If the foam is fully deployed and there is not compressing force acting on it, then its modeling is changed from the full nonlinear viscoelastic foam model (G1–G3) to a reduced one, which is modeled by a spring connection of elasticity $k_p$ between the proof mass $m_1$ and the front wall’s mass $m_2$ of the thorax (see $\sigma _d(\varepsilon )$ in Table 1).

• (U5) If the foam achieves a state of full deployment, then the proof mass $m_1$ (the armor plate) starts to pull the posterior wall of the chest via the waistcoat. In consequence, the spring-dashpot model is being activated, so $k_{13}$ and $c_{13}$ become different from zero. It is because a deployable foam-based armor plate is assumed in the experiment to be integrated on an outer side of the bullet-proof waistcoat, which is worn over the chest.

In general, discontinuity sources (U1–U5) in the system’s stiffness and damping produce coexisting time-varying uncertainties. Modeling of the investigated system dynamics is quite complicated, but the large-scale system’s representation does make it easier.

An idealized biomechanical model of a thorax supported from behind has been depicted in Fig. 2. Extended models of a sitting human are analyzed in [23]. The concept of the thorax model bases on Lobdell’s approach that was developed by General Motors to study the response of the human thorax in automobile crashes [24]. An application of the model has been presented in [9], where the model was consisted of a configuration of springs and dashpot elements. Injury which results from the pressure wave released by an explosion is referred to as primary blast injury [14]. Primary blast injury most significantly affects the air-containing organs of the body [18].

Fig. 2

The biomechanical model of a thorax subject to frontal blast over-pressure wave ($m_1$—proof mass of the armor plate, $m_2,\, m_3$—masses of posterior and anterior wall of the chest, respectively, $m_4$—mass of the backrest)

The Lobdell’s model was developed through measuring the thoracic response of a human subject to an impact load. Use of the Lobdell model has been extended by researchers to the field of protection against blast, to predict the thoracic response to a blast wave [25].

In this paper, the model and some associated concepts of limiting injuries caused by air blasts mentioned above are reconsidered in one system and supplemented too. The following ones are incorporated:

• (a) a support attached to the thorax from behind,

• (b) basic approximation of air pressure wave given in Friedlander’s form [26],

• (c) a phenomenological model for solid foams introduced in [21],

• (d) a deployable waistcoat with integrated (initially compressed) foam-based armor plate.

An idealized air-blast pressure wave reaches an effective area of the foam-based armor plate, which is represented by the body of mass $m_1$, which is by the assumed foam model attached elastically to the second body of mass $m_2$ (front wall of the thorax, see Fig. 3).

Fig. 3

Particular view of the lumped mass mechanical model of a thorax subject to the frontal blast pressure wave ($m_1$—proof mass, $m_4$—mass of the support, $k_{13}$ and $c_{13}$—spring-dashpot model of a bullet-proof waistcoat)

4.1 Formulation of the large-scale problem

Let us take into consideration a class of uncertain conti-nuous-time system composed of $N$-coupled sub-systems as follows

$$\begin{aligned} \frac{d\bar{x}_i(t)}{dt}&= \,\bigl ( \mathbf A_i+\varDelta \mathbf A_{ii}(t) \bigr ) \bar{x}_i(t)\nonumber \\&\quad +\sum {}_{j\ne i}^N\bigl ( \mathbf A_{ij}+\varDelta \mathbf A_{ij}(t) \bigr ) \bar{x}_j(t'_j)\nonumber \\&\quad +\bigl ( \mathbf B_i+\varDelta \mathbf B_i(t) \bigr ) \bar{u}(t)\;,\end{aligned}$$

(6a)

$$\begin{aligned} \bar{y}_i(t)&= \;\mathbf C_i\bar{x}_i(t)+\mathbf D_i\bar{u}(t),\quad i=1,\dots ,N\;, \end{aligned}$$

(6b)

where $\bar{x}_i(t)\in \mathbb R^{n_i\times 2},\, \bar{u}(t)\in \mathbb R^{m_i}$, and $\bar{y}_i(t)\in \mathbb R^{l_i}$ denote, respectively: vectors of system states, control inputs, and system outputs, $t'_j=t-\tau _j$.

The dynamical system (6) of $i$ coupled sub-systems is described by the internal behavior time-independent state matrices $\mathbf A_i^{n_i\times n_i}$, while the control inputs matrix $\mathbf B_i^{n_i\times m_i}$, the system output matrix $\mathbf C_i^{l_i\times n_i}$ and the control inputs transition matrix $\mathbf D^{l_i\times m_i}$ represent connections between the external world and the system, $\tau _j$ is the time delay of $j$th coupled system. In current investigations, control inputs do not directly influence the system outputs, therefore matrix $\mathbf D_i^{l_i\times m_i}$ is zero. For the purpose of solution of the proposed problem there are introduced in Eq. (6) time-dependent matrices $\varDelta \mathbf A_{ii}^{n_i\times n_i}$ $\varDelta \mathbf A_{ji}^{n_i\times n_i}$ and $\varDelta \mathbf B_i^{n_i\times m_i}$ that define, respectively: the system’s state and control input uncertainties. It allows for a more or less precise inclusion of the system’s parameters disturbances (U1–U5) given in a form of known time-dependent function or in a quite different form of a dynamically dependent function on the internal system state (time- or state-varying properties are allowed to be modeled as well). Matrices $\varDelta \mathbf A_{ji}^{n_i\times n_i}$ represent all possibilities of connections between interconnected sub-systems of the entire system.

Particular view of the biomechanical model of a thorax subject to frontal blast pressure wave has been shown in Fig. 3. From the left side: effective foam armor’s mass $m_1$ under the pressure impact, front body of mass $m_2$ in anterior surface of the chest wall, rear body of mass $m_3$ in posterior surface of the chest wall, $m_4$ – mass of the support.

Equations (6) can be expanded to the following form

$$\begin{aligned} \dot{\bar{x}}_1(t)&= (\mathbf A_{11}+\varDelta \mathbf A_{11})\bar{x}_1(t)+(\mathbf A_{12}+\varDelta \mathbf A_{12})\bar{x}_2(t'_2)\nonumber \\&+\varDelta \mathbf A_{13}\bar{x}_3(t'_3) + \varDelta \mathbf A_{16}\bar{x}_6(t'_6) + \mathbf B_1\bar{u}(t),\end{aligned}$$

(7a)

$$\begin{aligned} \dot{\bar{x}}_2(t)&= (\mathbf A_{22}+\varDelta \mathbf A_{22})\bar{x}_2(t)+(\mathbf A_{21}+\varDelta \mathbf A_{21})\bar{x}_1(t'_1)\nonumber \\&+(\mathbf A_{23}+\varDelta \mathbf A_{23})\bar{x}_3(t'_3)+\mathbf A_{25}\bar{x}_5(t'_5)\nonumber \\&+\varDelta \mathbf A_{26}\bar{x}_6(t'_6)\end{aligned}$$

(7b)

$$\begin{aligned} \dot{\bar{x}}_3(t)&= (\mathbf A_{33}+\varDelta \mathbf A_{33})\bar{x}_3(t)+(\mathbf A_{32}+\varDelta \mathbf A_{32})\bar{x}_2(t'_2)\nonumber \\&+\varDelta \mathbf A_{31}\bar{x}_1(t'_3)+\mathbf A_{34}\bar{x}_4(t'_4) + \mathbf A_{35}\bar{x}_5(t'_5)\nonumber \\&+\mathbf B_3\bar{u}(t),\end{aligned}$$

(7c)

$$\begin{aligned} \dot{\bar{x}}_4(t)&= \mathbf A_{44}\bar{x}_4(t)+\mathbf A_{43}\bar{x}_3(t'_3),\end{aligned}$$

(7d)

$$\begin{aligned} \dot{\bar{x}}_5(t)&= \mathbf A_{55}\bar{x}_5(t)+\mathbf A_{52}\bar{x}_2(t'_2)+\mathbf A_{53}\bar{x}_3(t'_3),\end{aligned}$$

(7e)

$$\begin{aligned} \dot{\bar{x}}_6(t)&= \varDelta \mathbf A_{66}\bar{x}_6(t) + \varDelta \mathbf A_{61}\bar{x}_1(t'_1) + \mathbf A_{62}\bar{x}_2(t'_2),\end{aligned}$$

(7f)

$$\begin{aligned} y(t)&= \begin{bmatrix} 0&1&-1&0\\0&0&0&0 \end{bmatrix}\bar{x}_i, \end{aligned}$$

(7g)

where $\bar{x}_i=\begin{bmatrix} x_{i1},\, x_{i2} \end{bmatrix}^T$, $\dot{\bar{x}}_i=\begin{bmatrix} \dot{x}_{i1},\, \dot{x}_{i2} \end{bmatrix}^T$, $\bar{u}=\begin{bmatrix} u_b,u_s \end{bmatrix}^T$, impact force of blast pressure wave $u_b(t)$ is given by Eq. (3), and a reaction force of the support

$$\begin{aligned} u_s(t)=-k_sx_{41}(t)-c_sx_{42}(t). \end{aligned}$$

(8)

Note, displacements $x_5$ and $x_6$ marked in Fig. 3 of massless points in Maxwell elements are expressed in Eq. (7e) by $x_{51}$ and in Eq. (7f) by $x_{61}$, while corresponding velocities are obtained directly from a two-point method for approximating the derivative of displacements

$$\begin{aligned} \dot{x}_{i2}=\frac{x_{i1}(t+h)-x_{i1}(t-h)}{2h},\quad i=5,6. \end{aligned}$$

Non-zero state-space matrices are as follows:

$$\begin{aligned} \mathbf A_{11}&= \begin{bmatrix} 0&1\\ \frac{-k_p}{m_1}&0 \end{bmatrix}, \mathbf A_{12}=\begin{bmatrix} 0&0\\ \frac{k_p}{m_1}&0 \end{bmatrix},\\ \mathbf A_{22}&= \begin{bmatrix} 0&1\\ \frac{-k_{23}-k_{23}'-k_p}{m_2}&\frac{-c_{23}}{m_2} \end{bmatrix}, \mathbf A_{21}=\begin{bmatrix} 0&0\\ \frac{k_p}{m_2}&0 \end{bmatrix},\\ \mathbf A_{23}&= \begin{bmatrix} 0&0\\\frac{k_{23}}{m_2}&\frac{c_{23}}{m_2} \end{bmatrix}, \mathbf A_{25}=\begin{bmatrix} 0&0\\ \frac{k_{23}'}{m_2}&0 \end{bmatrix},\\ \mathbf A_{33}&= \begin{bmatrix} 0&1\\ \frac{-k_{23}-k_{34}}{m_3}&\frac{-c_{23}-c_{23}'-c_{34}}{m_3} \end{bmatrix}, \mathbf A_{32}=\begin{bmatrix} 0&0\\\frac{k_{23}}{m_3}&\frac{c_{23}}{m_3} \end{bmatrix},\\ \mathbf A_{34}&= \begin{bmatrix} 0&0\\ \frac{k_{34}}{m_3}&\frac{c_{34}}{m_3} \end{bmatrix}, \mathbf A_{35}=\begin{bmatrix} 0&0\\ 0&\frac{c_{23}'}{m_3} \end{bmatrix},\\ \mathbf A_{44}&= \begin{bmatrix} 0&1\\ \frac{-k_{34}}{m_4}&\frac{-c_{34}}{m_4} \end{bmatrix}, \mathbf A_{43}=\begin{bmatrix} 0&0\\ \frac{k_{34}}{m_4}&\frac{c_{34}}{m_4} \end{bmatrix},\\ \mathbf A_{55}&= \begin{bmatrix} -\frac{k_{23}'}{c_{23}'}&0\\ 0&0 \end{bmatrix}, \mathbf A_{52}=\begin{bmatrix} \frac{k_{23}'}{c_{23}'}&0\\ 0&0 \end{bmatrix}, \mathbf A_{53}=\begin{bmatrix} 0&1\\0&0 \end{bmatrix},\\ \mathbf A_{62}&= \begin{bmatrix} 0&1\\ 0&0 \end{bmatrix}, \mathbf B_1=\begin{bmatrix} 0&0\\ \frac{1}{m_1}&0 \end{bmatrix}, \mathbf B_4=\begin{bmatrix} 0&0\\ 0&\frac{1}{m_4} \end{bmatrix},\\ \varDelta \mathbf A_{11}&= \begin{bmatrix} 0&0 \\ -\frac{k_{\text {d}}(t)-k_{16}(t)-k_{13}(t)}{m_1}&-\frac{c_{13}(t)}{m_1} \end{bmatrix},\\ \varDelta \mathbf A_{12}&= \begin{bmatrix} 0&0 \\ \frac{k_{\text {d}}(t)}{m_1}&0 \end{bmatrix}, \varDelta \mathbf A_{16}=\begin{bmatrix} 0&0 \\ \frac{k_{16}(t)}{m_1}&0 \end{bmatrix},\\ \varDelta \mathbf A_{13}&= \begin{bmatrix} 0&0 \\ -\frac{k_{13}(t)}{m_1}&\frac{c_{13}(t)}{m_1} \end{bmatrix},\\ \varDelta \mathbf A_{22}&= \begin{bmatrix} 0&0\\\frac{-k_{23}(t)-k_{\text {d}}(t)}{m_2}&\frac{-c_{23}(t)-c_{62}(t)}{m_2} \end{bmatrix},\\ \varDelta \mathbf A_{21}&= \begin{bmatrix} 0&0\\\frac{k_{\text {d}}(t)}{m_2}&0 \end{bmatrix}, \varDelta \mathbf A_{23}=\begin{bmatrix} 0&0\\ \frac{k_{23}(t)}{m_2}&\frac{c_{23}(t)}{m_2} \end{bmatrix},\\ \varDelta \mathbf A_{26}&= \begin{bmatrix} 0&0\\ 0&\frac{c_{62}(t)}{m_2} \end{bmatrix},\\ \varDelta \mathbf A_{33}&= \begin{bmatrix} 0&0\\\frac{-k_{23}(t)-k_{13}(t)}{m_3}&\frac{-c_{23}(t)-c_{13}(t)}{m_3} \end{bmatrix},\\ \varDelta \mathbf A_{32}&= \begin{bmatrix} 0&0\\ \frac{k_{23}(t)}{m_3}&\frac{c_{23}(t)}{m_3} \end{bmatrix}, \varDelta \mathbf A_{31}=\begin{bmatrix} 0&0\\ \frac{k_{13}(t)}{m_3}&\frac{c_{13}(t)}{m_3} \end{bmatrix},\\ \varDelta \mathbf A_{66}&= \begin{bmatrix} \frac{-k_{16}(t)}{c_{16}(t)}&0\\ 0&0 \end{bmatrix}, \varDelta \mathbf A_{61}=\begin{bmatrix} \frac{ k_{16}(t)}{c_{16}(t)}&0\\ 0&0 \end{bmatrix}, \end{aligned}$$

In (7g), a difference $x_{21}(t)-x_{31}(t)$ in displacements of bodies denoted by $m_2$ and $m_3$ will be the observed system output. In Eq. (7) zero matrices are neglected.

4.2 Uncertainties and the switching matrices

The problem definition uncovers some new features of the investigated bio-inspired system shown in Fig. 3. The problem of time-varying parameters that introduce to the model some uncertainties have been solved numerically by definition of multivalued matrices switched in accordance to cases (U1–U5). Stiffness of chest cave interior with organs increases at condition (U1) about two times to appropriately approximate the real chest’s compression. It obviously means, that stiffness of the rheological coupling increases discontinuously with regard to a greater than $d$ compression of the thorax $x_r$, and that damping ability of the coupling varies in time as the thorax is subject to a suitable compression or relaxation. Such discontinuity in the sub-system’s stiffness and damping produces parameter uncertainties dependent on state variable.

4.2.1 Uncertainties (U1–U2)

One can encounter in Eqs. (7b) and (7c) four $\varDelta \mathbf A_{ij}(t)$ parameter uncertainties of the analyzed dynamical system:

$$\begin{aligned}&\begin{array}{l} \varDelta \mathbf A_{ij}(t)=\begin{bmatrix} 0&{}0\\ \frac{\sigma (i,j)k_{23}(t)}{m_i}&{}\frac{\sigma (i,j)c_{23}(t)}{m_i} \end{bmatrix}\\ =\mathbf D_{i}\mathbf F(t)\mathbf E_{ij}\;, \end{array} \end{aligned}$$

(9a)

$$\begin{aligned}&\begin{array}{l} \sigma (i,j)=-\text {sgn}\bigl ( (-1)^{i+j} \bigr ) \;, \end{array} \end{aligned}$$

(9b)

where $i,j=2,3$.

Distribution of entries in $\varDelta \mathbf A_{ij}(t)$ does not change over their all possibilities. Therefore, the unknown time-varying real-valued matrix $F(t)$ is assumed to be defined in the same way, but $\mathbf F^T(t)\mathbf F(t)\le \mathbf I$ must hold for $t\in \mathbb R^+,\, \mathbf I$ is the identity matrix. The introduced decomposition $\mathbf D\mathbf F\mathbf E$ includes some known constant real-valued matrices $\mathbf D_i$ and $\mathbf E_{ij}$ of appropriate dimensions that need to be estimated to use them, for instance, in a solution of LMI problems [12, 27].

Dependently on $x_r(t)$ and $v_r(t)$ the following forms of the uncertainty matrix $\varDelta \mathbf A_{22}(t)=\varDelta \mathbf A^{(k)}_{22}$ in Eq. (7b) are possible:

$$\begin{aligned} \varDelta \mathbf A^{(k)}_{22}={\left\{ \begin{array}{ll}\begin{bmatrix} 0&{}0\\ 0&{}0 \end{bmatrix} &{} \text {if}\;s_1\; \text {then}\;k=1\;,\\ \begin{bmatrix} 0&{}0\\ \frac{-k_{23}}{m_2}&{}0 \end{bmatrix} &{} \text {if}\;s_2\; \text {then}\;k=2\;,\\ \begin{bmatrix} 0&{}0\\ 0&{}\frac{-c_{23}}{m_2} \end{bmatrix} &{} \text {if}\;s_3\; \text {then}\;k=3\;,\\ \begin{bmatrix} 0&{}0\\ \frac{-k_{23}}{m_2}&{} \frac{-c_{23}}{m_2} \end{bmatrix} &{} \text {if}\;s_4\; \text {then}\;k=4\;,\end{array}\right. } \end{aligned}$$

(10)

where the remaining $\varDelta \mathbf A_{ij}(t)$, for $i,j=2,3$ are to be defined in a similar way, $s_k=\{x_r(t),v_r(t): x_r(t)<d \wedge v_r(t)>0;\, x_r(t)\ge d \wedge v_r(t)>0;\, x_r(t)<d \wedge v_r(t)\le 0;\, x_r(t)\ge d \wedge v_r(t)\le 0\}$ defines rheological properties of the biomechanical system. Switching conditions $s_i$ will select only one of $k$ possibilities $\varDelta \mathbf A^{(k)}_{ij}$ for $k=1\dots 4$ dependently on values of pairs $(x_r(t),v_r(t))$ creating the discontinuous time history of uncertainties $\varDelta \mathbf A_{ij}(t)$ of the state matrices of coupled two degrees-of-freedom neighboring subsystems.

To find better description of the existing switching nature it is now required to choice $\mathbf D_i$ and $\mathbf E_{ij}$ matrices of a decomposition. For instance, an exemplary decomposition of $\varDelta \mathbf A^{(k)}_{22}$, for $k=3$ could be made accordingly to the scheme presented in [28].

Perturbation matrix $\mathbf F(t)$ will depend on $k$ cases that have been delivered in the case statement (10). Therefore, with regard to $\mathbf F^T(t)\mathbf F(t)\le \mathbf I$ and using Eq. (9) the following formula reads

$$\begin{aligned} \begin{aligned} \varDelta \mathbf A^{(k)}_{i,j}&=\mathbf D_i \mathbf F^{(k)}\mathbf E_{ij}\\&=\begin{bmatrix} 0&0\\0&\delta _{4i} \end{bmatrix} F^{(k)} \begin{bmatrix} \frac{\sigma (i,j)\beta _1}{\gamma }&0 \\ 0&\frac{\sigma (i,j)\beta _4}{\gamma } \end{bmatrix},\\ k&=1\dots 4\;, \end{aligned} \end{aligned}$$

(11)

where $i,j=2,3,\, \sigma (i,j)$ is given in Eq. (9b), and $\mathbf F(t)$ will switch between

$$\begin{aligned} \mathbf F^{(k)}={\left\{ \begin{array}{ll}\begin{bmatrix} 0&{}0\\ 0&{}0 \end{bmatrix} &{} \text {if}\;s_1\; \text {then}\;k=1\;,\\ \begin{bmatrix} 0&{}\pm \gamma \\ \pm \gamma &{}0 \end{bmatrix} &{} \text {if}\;s_2\; \text {then}\;k=2\;,\\ \begin{bmatrix} \pm \gamma &{}0\\ 0&{}\pm \gamma \end{bmatrix} &{} \text {if}\;s_3\; \text {then}\;k=3\;,\\ \begin{bmatrix} 0&{}\pm \gamma \\ \pm \gamma &{} \pm \gamma \end{bmatrix} &{} \text {if}\;s_4\; \text {then}\;k=4\;.\end{array}\right. } \end{aligned}$$

(12)

The case statement (12) captures switching properties of $\varDelta \mathbf A_{ij}(t)$ described in comments to (10). As it was expected, $\mathbf F(t)$ is defined in the same way for four uncertainties of the model, matrices $\mathbf D_i$ and $\mathbf E_{ij}$ are constant and their entries will depend on the sub-system that they are related to.

To check correctness of the previously made estimations let the following parameters be assigned for the uncertainties: $\delta _{42}=1/m_2,\, \delta _{43}=1/m_3,\, \beta _1=k_{23},\, \beta _4=c_{23},\, \gamma \ne 0$. For example, $\varDelta A^{(4)}_{2,2}=D_2\bar{F}^{(4)}E_{22}=[[0,0],[0,1/m_2]]\cdot [[0,\gamma ],[\gamma ,\gamma ]]\cdot [[-k_{23}/\gamma ,0],[0,-c_{23}/\gamma ]]=[[0,0],[-k_{23}/m_2,-c_{23}/m_2]]$ what is in agreement with the fourth case of Eq. (10). Parameter $\gamma =0.618033$ was estimated numerically [28].

4.2.2 Uncertainties (U3–U4)

While a foam material is compressed (in loading state) or relaxed (in unloading state), two different phenomenological solid foam models $\sigma _l(\varepsilon )$ and $\sigma _u(\varepsilon )$, which are nonlinear according to (G1–G3) are assumed (see in Table 1). If the foam is fully deployed and there is not compressing force acting on it, then its modeling is changed from full nonlinear viscoelastic foam model (G1–G3) to a reduced one $\sigma _d(\varepsilon )$, which states a spring connection of elasticity $k_p$ between the proof mass $m_1$ and the front wall’s mass $m_2$ of the chest (see in Table 1).

$$\begin{aligned} \sigma ={\left\{ \begin{array}{ll}\sigma _l(\varepsilon ) &{} \text {if}\;\varepsilon >0\quad \text {and}\;\dot{\varepsilon }> 0\;,\\ \sigma _u(\varepsilon ), &{} \text {if}\;\varepsilon >0\quad \text {and}\;\dot{\varepsilon }\le 0\;,\\ \sigma _d(\varepsilon ), &{} \text {if}\;\varepsilon \le 0 \end{array}\right. } \end{aligned}$$

(13)

4.2.3 Uncertainty (U5)

While the foam achieves a state of full deployment, the proof mass $m_1$ (the armor plate) starts to pull the posterior part of the thorax via the waistcoat. The spring-dashpot model is being activated, $k_{13}$ and $c_{13}$ become different from zero. It is because in the experiment a deployable foam-based armor plate is integrated on an outer side of the bullet-proof waistcoat, which is worn over the chest.

$$\begin{aligned} F_{13}(t)={\left\{ \begin{array}{ll}-k_{13}(x_{11}-x_{31}) - c_{13}(x_{12}-x_{32}),&{} \text {if}\;\varepsilon \le 0,\\ 0, &{} \text {if}\;\varepsilon >0,\\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(14)

Numerical integration of 12 differential equations of first order is a bit conditioned, but it better approximates complex dynamics of the biomechanical model of the chest subject to an impulsive loading. It is equipped with additional bodies like armor plate and backrest of a seat which have an influence on behavior of the investigated multibody system.

5 Numerical experiments

Two sources of variability are applied in the numerical simulation to investigate responses of the analyzed multibody system:

• (1) Various arrival times of impact force $u_b(t)$ at foam-based armor plate.

• (2) Various inherent time delays $\tau _i$ of each subsystem of the thorax.

Parameters of the simulation:

• 1. $m_1 = 0.365,\, m_2 = 0.45,\, m_3=27,\, m_4=10\,\hbox {kg}$;

• 2. $k_{13} = 10^5,\, k_{23} = 0.263\times 10^5,\, k_{23}' = 0.132\times 10^5,\, k_{34} = 0.05\times 10^5,\, k_\mathrm{s} = 0.1\times 10^5\,\hbox {N/m}$;

• 3. $c_{13} = 0.02\times 10^3,\, c_{23} = 0.52\times 10^3,\, c_{23}' = 0.18\times 10^3,\, c_{34} = 0.1\times 10^3,\, c_\mathrm{s} = 0.1\times 10^3\,\hbox {N/m}$;

• 4. foam thickness $h_f=0.1\,\hbox {m}$;

• 5. number of iterations $N = 5\times 10^4$;

• 6. step time of numerical integration $h=2\times 10^{-6}$;

• 7. time delays used: $t'_{1i}=t'_{2i}=t'_{3i}=ih\, (i=1\dots 5)$;

• 8. all initial conditions of state variables are zero except $x_{11}(0)=0.7h_f$ (compressed foam thickness equals 3 cm);

• 9. the remaining conditions are provided in (C1–C11), (G1–G3), (U1–U5) and Table 1.

Stress $F_{\text {ch}}$ in the thorax’s model is calculated according to the formula

$$\begin{aligned} F_\mathrm{ch}&=k_{23}(x_{21}-x_{31})+c_{23}(x_{22}-x_{32}), \end{aligned}$$

(15)

where $k_{23},\bar{x}_{2}, \bar{x}_{3}$ are time-dependent.

Deployment of the foam initiates all the numerical experiments presented below.

5.1 Influence of blast wave time arrivals

Figures 4 and 5 exhibit significant differences in the system’s dynamical behavior. The time histories were computed for a few time delays of arrival (ranging from 2.5 ms to 0) of the air-blast pressure wave that reaches the foam-based armor plate. It is seen that for $t_a$ equal about 0.5 ms the relative deformation is about 4 cm. If the foam’s deployment delay is greater, then the strain in the thorax rises comparing with the non-delayed counterpart. The results prove that even small time delay affects the dynamics, but in this particular case, both the deformation (Fig. 7) and maximum stress (Fig. 8) decrease.

Fig. 4

Time histories of displacements $x_{11}(t),\, x_{21}(t)$ and $x_{31}(t)$ as a function of $t_a$

Fig. 5

Time histories (a, b) of a relative displacement $x_{21}-x_{31}$ and the corresponding stress–strain curve (c) as a function of blast wave time arrivals

5.2 Influence of inherent time delays

Figures 6 and 7 exhibit significant differences in behavior of the dynamical system.

Fig. 6

Time histories of displacements $x_{11}(t)$, $x_{21}(t)$ and $x_{31}(t)$ as a function of inherent time delay $\tau _i$

Fig. 7

Time history of the relative displacement $x_{21}(t)-x_{31}(t)$ as a function of inherent time delay $\tau _i$

The time histories were computed at very small time delays (ranging from $5h$ to $h=2\times 10^{-6}$) and compared with the non-delayed counterpart. The results prove that even small time delay affects the dynamics, but in this particular case, both the deformation (Fig. 7) and maximum stress (Fig. 8) decrease, as well as a side effect in a form of small amplitude vibrations of higher frequency appears.

Fig. 8

Stress–strain curve as a function of $\tau _i$

Figure 8 presents a comparison of stress–strain characteristics of the chest’s model deformation estimated for a non-delayed (for $\tau _6$) and the delayed displacements of bodies $m_i,\, i=1,2,3$. One could observe, that even small time delays of about a few time steps of numerical integration play significant role in the blast pressure wave response. Inherent time delays in modeling of the chest are important. Condition (C11) will be satisfied if the time delay $\tau =5h$ (see Fig. 8).

5.3 Animation of motion

The six degrees of freedom dynamical system has been numerically solved using dedicated procedures coded in Python. Numpy and matplotlib libraries served as the tools for manipulation on multidimensional tables, plotting of frames and saving them in png files. A set of 1000 frames has been generated and joined to make an animation. Exemplary frame is shown in Fig. 9.

Fig. 9

A frame taken from animation of motion of the investigated multibody system

6 Conclusions

Importance of time delays in numerical solution of the analyzed multibody system is confirmed. Modeling of response of the thorax when energized by air-blast over-pressure has gained new quality. There were mentioned in the literature overview some attempts regarded to the study, but significance of time delays have not been sufficiently emphasized. Therefore, this work sheds new light on mathematical description and modeling of the phenomenon. The system under investigation has received a new useful representation by application of the large-scale systems approach. It allowed to include many uncertainties of parameters and time-delay dependencies of state variables making the modeling more flexible and ready for future improvements.

Interesting dynamical behavior of the bio-inspired system is solved numerically. There is pointed out that the inherent state time delays change dynamical response of the multibody system. Proper time of deployment (initiated about 0.6 ms before an impact of the blast wave) of the foam-based armor plate reduces (at some conditions of the experiment) relative compression of the thorax.