1 Introduction

The synchronization of two identical chaotic dynamical systems was extensively investigated since Pecora and Carroll [1] discussed such a topic in 1990. In 1995, Rulkov et al. [2] discussed a generalized synchronization of chaos in directionally coupled chaotic systems. In 1999, Mainieri and Rehacek [3] proposed the projective synchronization of the Lorenz systems with the scaling factors. In 2006, Yan et al. [4] discussed the adaptive synchronization control for chaotic symmetric gyroscopes from an adaptive sliding mode control. In 2007, Li [5] discussed the modified projective synchronization of the drive-response systems with a scaling matrix. In 2008, Hu et al. [6] extended the idea of projective synchronization to hybrid projective synchronization, and the different state variables can be synchronized with different scaling factors. A sliding mode control was used to investigate the generalized projective synchronization of two chaotic gyroscopes with dead-zone input by Hung et al. [7]. In 2010, Chen et al. [8] studied the adaptive generalized synchronization between Chen system and a multi-scroll with uncertain parameters. In 2011, Yu and Li [9] discussed the full state hybrid projective synchronization between different chaotic systems with fully unknown parameters. Wu et al. [10] investigated the generalized function projective synchronization of two hyperchaotic Chen systems for the secure communication schemes. In 2012, Li [11] used the tracking control to investigate the generalized projective synchronization of hyperchaotic systems with unknown parameter and disturbance. Wang [12] utilized the state observer to study a generalized projective synchronization of hyperchaotic systems. Niu et al. [13] investigated the adaptive projective synchronization of different chaotic systems with nonlinearity inputs. In those studies, the Lyapunov method was explored to determine the stability for error systems. The control laws designed are often complicated, and the implementation becomes much difficult in practical engineering. In 2009, Luo [14] developed a different theory for synchronization of dynamical systems under specific constraints from the theory of discontinuous dynamical systems. The G-functions were introduced to determine the switchability of a flow from one domain to another in discontinuous dynamical systems. The gyroscope system has a wide spectrum of applications in navigation, aeronautics and space engineering. Min and Luo [15] used such a theory to investigate the chaotic synchronization of two nonlinear gyroscope systems, and Min [16] applied such a new theory to the generalized projective synchronization of a chaotic gyroscope with a periodic gyroscope, and the analytical conditions of synchronization were developed. The noised gyroscope systems should be synchronized with the expected gyroscope systems. In 2013, Min and Luo [17] discussed the parameter characteristics of projective synchronization of two different motion states of the gyroscope system. For security, function synchronization of two dynamical systems should be considered. Thus, the projective function synchronization of two gyroscope systems with different motions under sinusoidal constraints will be of great interest. The investigation objective is to make a current system to synchronize with the expected behaviors in design.

In this paper, from the theory of discontinuous dynamical systems, the necessary and sufficient conditions for the projective function synchronization of two gyroscope systems with different dynamical behaviors will be derived. From the analytical conditions, the invariant domain for the partial and full, projective function synchronizations will be achieved. Finally, numerical illustrations for projective function synchronization of two chaotic gyroscope systems under sinusoidal constraints will be performed.

2 Problem description

Consider a gyroscope system as

$$\begin{aligned} {\dot{x}}_{1}&= x_{2}, \nonumber \\ {\dot{x}}_{2}&= h(x_{1})-c_{1} x_{2}-c_{2} x_{2}^{3} +(\beta +f_{1} \sin \omega t)\sin x_{1}, \end{aligned}$$
(1)

where \(x_1\) is rotation angle, \(x_2\) is angular velocity, \(f_1 \sin \omega t\) is a parametric excitation, and a nonlinear function \(h(x_1)\) is

$$\begin{aligned} h(x_1)=-\alpha ^{2}\frac{(1-\cos x_1)^{2}}{\sin ^{3}x_1}. \end{aligned}$$
(2)

The gyroscope system in Eq. (1) is regarded as the master system, and a second controlled gyroscope system is considered as a slave system, i.e.,

$$\begin{aligned} \!\!\left\{ \begin{array}{l} \dot{y}_1 =y_2-u_1 (t), \\ \dot{y}_2 =h(y_1)-c_1 y_2-c_2 y_2^3 +(\beta +f_2 \sin \omega t)\sin y_1-u_2 (t), \\ \end{array}\right. \end{aligned}$$
(3)

with

$$\begin{aligned} h(y_1)=-\frac{\alpha ^{2}(1-\cos y_1)^{2}}{\sin ^{3}y_1}. \end{aligned}$$
(4)

If parameter \(f_2\) in Eq. (3) without control is different from \(f_1\) in Eq. (1), then the master and slave systems have different dynamical behaviors. Consider control laws for the projective functional synchronization with sinusoidal constraint as

$$\begin{aligned} \begin{array}{ll} u_1 &{}= k_1 \hbox {sgn}(y_1-p_1 \sin x_1), \\ u_2 &{}= k_2 \hbox {sgn}(y_2-p_2 x_2 \cos x_1) \end{array} \end{aligned}$$
(5)

where \(k_1\) and \(k_2\) are controller parameters, \(p_1\) and \(p_2\) are scaling factors. Thus the projective function synchronization of the slave system with the master system can be achieved under the sinusoidal constrains. The control laws in Eq. (5) can be designed any forms of functions.

From the foregoing equations, the state variables for the master and slave systems are

$$\begin{aligned} \mathbf{x}=(x_1,x_2)^\mathrm{T} \quad \hbox {and}\quad \mathbf{y}=(y_1,y_2)^\mathrm{T}, \end{aligned}$$
(6)

and components for the corresponding vector fields are

$$\begin{aligned}&{\fancyscript{F}}_1 (\mathbf{x},t) = x_2 \quad \hbox {and}\quad {\fancyscript{F}}_2 (\mathbf{x},t)=h(x_1)-c_1 x_2-c_2 x_2^3\nonumber \\&\quad +(\beta +f_1 \sin \omega t)\sin x_1, \nonumber \\&\tilde{F}_1 (\mathbf{y},t) = y_2 \quad \hbox {and}\quad \tilde{F}_2 (\mathbf{y},t)=h(y_1)-c_1 y_2-c_2 y_2^3 \nonumber \\&\quad +(\beta +f_2 \sin \omega t)\sin y_1.\nonumber \\ \end{aligned}$$
(7)

The controlled slave system becomes

$$\begin{aligned} \dot{\mathbf{y}}=\tilde{\mathbf{F}}(\mathbf{y},t)-\mathbf{u}(\mathbf{x},\mathbf{y},t)=\mathbf{F}(\mathbf{y},t), \end{aligned}$$
(8)

where the vector field \(\mathbf{F}(\mathbf{y},t)=(F_1 (\mathbf{y},t),F_2 (\mathbf{y},t))^\mathrm{T}\).

With the control law in Eq. (5), the controlled gyroscope system will become discontinuous. There are four domains and four boundaries with different vector fields. The four domains \(\Omega _\alpha \) (\(\alpha =1,2,3,4)\) for the controlled slave system are

$$\begin{aligned} \Omega _1&= \left\{ \left. {(y_1,y_2)} \right| y_1-p_1 \sin (x_1 (t))>0, y_2 \right. \nonumber \\&\quad \left. -p_2 x_2 (t)\cos (x_1 (t))>0\right\} , \nonumber \\ \Omega _2&= \left\{ \left. {(y_1,y_2)} \right| y_1-p_1 \sin (x_1 (t))>0, y_2 \right. \nonumber \\&\quad \left. -p_2 x_2 (t)\cos (x_1 (t))<0\right\} , \nonumber \\ \Omega _3&= \left\{ \left. {(y_1,y_2)} \right| y_1-p_1 \sin (x_1 (t))<0, y_2 \right. \\&\quad \left. -p_2 x_2 (t)\cos (x_1 (t))<0\right\} , \nonumber \\ \Omega _4&= \left\{ \left. {(y_1,y_2)} \right| y_1-p_1 \sin (x_1 (t))<0, y_2 \right. \nonumber \\&\quad \left. -p_2 x_2 (t)\cos (x_1 (t))>0\right\} .\nonumber \end{aligned}$$
(9)

The boundaries \(\partial \Omega _{\alpha \beta }\) (\(\alpha ,\beta =1,2,3,4;\alpha \ne \beta )\) of four domains are

$$\begin{aligned} \partial \Omega _{12}&= \left\{ \left. {(y_1,y_2)} \right| \varphi _{12} =y_2-p_2 x_2 (t)\cos (x_1 (t))=0, \right. \nonumber \\&\quad \left. y_1 -p_1 \sin (x_1 (t))>0 \right\} , \nonumber \\ \partial \Omega _{23}&= \left\{ \left. {(y_1,y_2)} \right| \varphi _{23} =y_1-p_1 \sin (x_1 (t))=0, \right. \nonumber \\&\quad \left. y_2-p_2 x_2 (t)\cos (x_1 (t))<0 \right\} , \nonumber \\ \partial \Omega _{34}&= \left\{ \left. {(y_1,y_2)} \right| \varphi _{34} =y_2-p_2 x_2 (t)\cos (x_1 (t))=0, \right. \nonumber \\&\quad \left. y_1 -p_1 \sin (x_1 (t))<0 \right\} , \nonumber \\ \partial \Omega _{41}&= \left\{ \left. {(y_1,y_2)} \right| \varphi _{41} =y_1-p_1 \sin (x_1 (t))=0, \right. \nonumber \\&\quad \left. y_2-p_2 x_2 (t)\cos (x_1 (t))>0 \right\} . \end{aligned}$$
(10)

where the subscript \((\cdot )_{\alpha \beta }\) denotes the boundary from \(\Omega _\alpha \) to \(\Omega _\beta \). The intersection point of four boundaries \(\partial \Omega _{\alpha \beta }\) (\(\alpha ,\beta =1,2,3,4;\alpha \ne \beta )\) is

$$\begin{aligned} \angle \partial \Omega _{\alpha \beta }&= \displaystyle \mathop {\bigcap }\limits _{\alpha =1}^4 \mathop {\bigcap }\limits _{\beta =1}^4 \partial \Omega _{\alpha \beta }\nonumber \\&= \left\{ \left. {(y_1,y_2)} \right| \varphi _{23} =y_1 -p_1 \sin (x_1 (t))=0,\right. \nonumber \\&\left. y_2 -p_2 x_2 (t)\cos (x_1 (t))=0 \right\} . \end{aligned}$$
(11)

On the domain \(\Omega _\alpha \), the controlled gyroscope is

$$\begin{aligned} \dot{\mathbf{y}}^{(\alpha )}=\mathbf{F}^{(\alpha )}(\mathbf{y}^{(\alpha )},t) \end{aligned}$$
(12)

where

$$\begin{aligned} \mathbf{F}^{(\alpha )}(\mathbf{y}^{(\alpha )},t)&= (F_1^{(\alpha )},F_2^{(\alpha )})^\mathrm{T}, \nonumber \\ F_1^{(\alpha )} (\mathbf{y}^{(\alpha )},t)&= y_2^{(\alpha )}-k_1 \,\hbox {for}\, \alpha =1,2; \nonumber \\ F_1^{(\alpha )} (\mathbf{y}^{(\alpha )},t)&= y_2^{(\alpha )} +k_1 \,\hbox {for}\, \alpha =3,4; \nonumber \\ F_2^{(\alpha )} (\mathbf{y}^{(\alpha )},t)&= h(y_1^{(\alpha )})-c_1 y_2^{(\alpha )}-c_2 (y_2^{(\alpha )})^{3}\nonumber \\&\quad +(\beta +f_2 \sin \omega t)\sin y_1^{(\alpha )}\nonumber \\&\quad -k_2 \,\hbox {for}\, \alpha =1,4; \nonumber \\ F_2^{(\alpha )} (\mathbf{y}^{(\alpha )},t)&= h (y_1^{(\alpha )})-c_1 y_2^{(\alpha )}-c_2 (y_2^{(\alpha )})^{3} \nonumber \\&\quad +(\beta +f_2 \sin \omega t)\sin y_1^{(\alpha )}\nonumber \\&\quad +\,k_2 \,\hbox {for}\, \alpha =2,3. \end{aligned}$$
(13)

and

$$\begin{aligned} h (y_1^{(\alpha )})=-\alpha ^{2} (1-\cos y_1^{(\alpha )} )^{2}/\sin ^{3} (y_1^{(\alpha )}). \end{aligned}$$
(14)

The dynamical systems on the boundaries \(\partial \Omega _{\alpha \beta }\) are

$$\begin{aligned}&\dot{\mathbf{y}}^{(\alpha \beta )}=\mathbf{F}^{(\alpha \beta )}(\mathbf{y}^{(\alpha \beta )},\mathbf{x}(t),t); \nonumber \\&\dot{\mathbf{x}}=\fancyscript{F}(\mathbf{x},t) \end{aligned}$$
(15)

where

$$\begin{aligned}&\mathbf{F}^{(\alpha \beta )}=(F_1^{(\alpha \beta )},F_2^{(\alpha \beta )})^\mathrm{T}, \nonumber \\&F_1^{(\alpha \beta )} (\mathbf{y}^{(\alpha \beta )},t)=y_2 -p_1 x_2 \cos x_1, \nonumber \\&F_2^{(\alpha \beta )} (\mathbf{y}^{(\alpha \beta )},t)=p_2 (\dot{x}_2 \cos x_1-x_2^2 \sin x_1). \end{aligned}$$
(16)

and

$$\begin{aligned} \begin{array}{ll} &{}y_1^{(\alpha \beta )} = p_1 \sin x_1 \,\hbox {and}\, y_2^{(\alpha \beta )} =p_2 x_2 \cos x_1\\ &{}\hbox {on}\,\,\partial \Omega _{\alpha \beta }\,\hbox {for}\,(\alpha ,\beta )=\{(2,3),(4,1)\}; \\ &{}y_1^{(\alpha \beta )} = p_1 \sin x_1+ C \hbox {and}\, y_2^{(\alpha \beta )} =p_2 x_2 \cos x_1+ C \\ &{}\hbox {on}\,\, \partial \Omega _{\alpha \beta } \,\hbox {for}\, (\alpha ,\beta )=\{(1,2),(3,4)\}. \end{array} \end{aligned}$$
(17)

From the above equations, the boundaries and corner for the controlled gyroscope system are dependent on time in absolute coordinate. For simplicity, relative coordinates are introduced as

$$\begin{aligned} z_1 =y_1-p_1 \sin x_1 \,\hbox {and}\, z_2 =y_2-p_2 x_2 \cos x_1 \end{aligned}$$
(18)

The corresponding domains, boundaries and synchronization corner in the relative frame can be expressed by

$$\begin{aligned} \begin{array}{lll} \Omega _1 (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| z_1 >0,z_2 >0 \right\} \!, \\ \Omega _2 (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| z_1 >0,z_2 <0 \right\} \!, \\ \Omega _3 (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| z_1 <0,z_2 <0 \right\} \!, \\ \Omega _4 (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| z_1 <0,z_2 >0 \right\} \!. \end{array} \end{aligned}$$
(19)
$$\begin{aligned} \begin{array}{lll} \partial \Omega _{12} (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| \varphi _{12} =z_2 =0,z_1 >0 \right\} \!, \\ \partial \Omega _{23} (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| \varphi _{23} =z_1 =0,z_2 <0 \right\} \!, \\ \partial \Omega _{34} (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| \varphi _{34} =z_2 =0,z_1 <0 \right\} \!, \\ \partial \Omega _{41} (t)&{}=&{}\left\{ \left. (z_1,z_2) \right| \varphi _{41} =z_1 =0,z_2 >0 \right\} \!. \end{array} \end{aligned}$$
(20)

and

$$\begin{aligned} \angle \partial \Omega _{\alpha \beta } =\mathop {\bigcap }\limits _{\alpha =1}^{4} \mathop {\bigcap }\limits _{\beta =1}^{4} \partial \Omega _{\alpha \beta } =\left\{ \left. {(z_1,z_2)} \right| z_1 =0,z_2 =0 \right\} . \end{aligned}$$
(21)

The partition of the phase plane in the relative frame is depicted in Fig. 1. The boundaries in the relative coordinates are independent of time. For such domains, boundaries and vertex, the analytical conditions for projective function synchronization of the controlled slave system and master system can be developed from the theory for discontinuous dynamical systems. The controlled gyroscope system in the relative coordinates becomes

$$\begin{aligned} \dot{\mathbf{z}}^{(\alpha )}=\mathbf{g}^{(\alpha )}(\mathbf{z}^{(\alpha )},\mathbf{x},t) \quad \hbox {with}\,\, \dot{\mathbf{x}}={\fancyscript{F}}(\mathbf{x},t) \end{aligned}$$
(22)

where

$$\begin{aligned} \mathbf{g}^{(\alpha )}(\mathbf{z}^{(\alpha )},\mathbf{x},t)&= (g_1^{(\alpha )},g_2^{(\alpha )})^\mathrm{T}; \nonumber \\ g_1^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)&= z_2^{(\alpha )} +(p_2-p_1)x_2 \cos x_1) \nonumber \\&\quad -k_1, \hbox {for }\alpha =1,2;\nonumber \\ g_1^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)&= z_2^{(\alpha )} +(p_2-p_1)x_2 \cos x_1) \\&\quad +k_1, \hbox {for }\alpha =3,4;\nonumber \\ g_2^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)&= \Psi (\mathbf{z}^{(\alpha )},\mathbf{x},t)-k_2, \hbox { for }\alpha =1,4; \nonumber \\ g_2^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)&= \Psi (\mathbf{z}^{(\alpha )},\mathbf{x},t)+k_2, \hbox {for }\alpha =2,3.\nonumber \end{aligned}$$
(23)

with

Fig. 1
figure 1

Phase plane partitions and boundaries in the relative coordinate. a relative velocity boundary, b relative displacement boundary

Full size image
$$\begin{aligned} \Psi (\mathbf{z}^{(\alpha )},\mathbf{x},t)&= h(z_1^{(\alpha )} +p_1 \sin x_1)-p_2 h(x_1)\cos x_1 \nonumber \\&\quad -c_2 \left[ (z_2^{(\alpha )} +p_2 x_2 \cos x_1)^{3}-p_2 x_2^3 \cos x_1\right] \nonumber \\&\quad +\,x_2^2 \sin x_1-c_1 z_2^{(\alpha )} +\beta \left[ \sin (z_1^{(\alpha )} +p_1 \sin x_1)\right. \nonumber \\&\quad -0.5p_2 \sin 2x_1\Big ] +\left[ f_2 \sin (z_1^{(\alpha )} +p_1 \sin x_1)\right. \nonumber \\&\quad -0.5\,f_1 p_2 \sin 2x_1\Big ] \times \sin \omega t, \end{aligned}$$
(24)

The equations of motion on the boundary in the relative coordinates become

$$\begin{aligned} \dot{\mathbf{z}}^{(\alpha \beta )}=\mathbf{g}^{(\alpha \beta )}(\mathbf{z}^{(\alpha \beta )},\mathbf{x},t) \quad \hbox {with}\,\, \dot{\mathbf{x}}={\fancyscript{F}}(\mathbf{x},t); \end{aligned}$$
(25)

where

$$\begin{aligned}&\!\!\! \mathbf{g}^{(\alpha \beta )}(\mathbf{z}^{(\alpha \beta )},\mathbf{x},t)=(g_1^{(\alpha \beta )},g_2^{(\alpha \beta )})^\mathrm{T}; \nonumber \\&\!\!\! g_1^{(\alpha \beta )} (\mathbf{z}^{(\alpha \beta )},\mathbf{x},t)=z_2 =0 \quad \hbox {and }\, g_2^{(\alpha \beta )} (\mathbf{z}^{(\alpha \beta )},\mathbf{x},t)=0,\nonumber \\ \end{aligned}$$
(26)

with

$$\begin{aligned}&z_1^{(\alpha \beta )} = 0 \quad \hbox {and}\, z_2^{(\alpha \beta )} =0\nonumber \\&\hbox {on}\, \partial \Omega _{\alpha \beta } \,\hbox {for}\, (\alpha ,\beta )=\{(2,3),(4,1)\}; \!\!\!\!\nonumber \\&z_1^{(\alpha \beta )} = C \quad \hbox {and z}_2^{(\alpha \beta )} =0\nonumber \\&\hbox {on}\, \partial \Omega _{\alpha \beta } \,\hbox {for}\, (\alpha ,\beta )=\{(1,2),(3,4)\}. \!\!\!\! \end{aligned}$$
(27)

3 Function synchronization

From the theory of discontinuous dynamical system in Luo [14, 18–20], the analytical conditions for function synchronization of two gyroscope systems can be developed. The G-functions in the relative coordinates are introduced for \(z_m \in \partial \Omega _{ij}\) at \(t=t_m\) are introduced as

$$\begin{aligned}&G_{\partial \Omega _{ij}}^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm })\nonumber \\&\quad =\mathbf{n}_{\partial \Omega _{ij}}^\mathrm{T}\cdot \left[ \mathbf{g}^{(\alpha )}(\mathbf{z}_m,\mathbf{x},t_{m\pm })-\mathbf{g}^{(ij)}(\mathbf{z}_m,\mathbf{x},t_{m\pm })\right] , \end{aligned}$$
(28)
$$\begin{aligned}&G_{\partial \Omega _{ij}}^{(1,\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm })\nonumber \\&\quad =\mathbf{n}_{\partial \Omega _{ij}}^\mathrm{T}\cdot \left[ D\mathbf{g}^{(\alpha )}(\mathbf{z}_m,\mathbf{x},t_{m\pm })-D\mathbf{g}^{(ij)}(\mathbf{z}_m,\mathbf{x},t_{m\pm })\right] \!.\quad \end{aligned}$$
(29)

where \(G_{\partial \Omega _{ij}}^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm })\) and \(G_{\partial \Omega _{ij}}^{(1,\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm })\) are the zero-order and first-order G-functions of the flow in \(\Omega _\alpha \,(\alpha \in \{i,j\})\) at the boundary \(\partial \Omega _{ij}\,(i,j=1,2,3,4)\). The switching \(t_m\) represents the time of the motion on the boundary and the switching time \(t_{m\pm } =t_m \pm 0\) means motions in domains very close to the boundary rather than on the boundary. The normal vectors of the relative boundaries in Eq. (20) are

$$\begin{aligned} \mathbf{n}_{\partial \Omega _{12}} =\mathbf{n}_{\partial \Omega _{34}} =(0,1)^\mathrm{T} \quad \hbox {and}\,\, \mathbf{n}_{\partial \Omega _{23}} =\mathbf{n}_{\partial \Omega _{14}}=(1,0)^\mathrm{T}.\nonumber \\ \end{aligned}$$
(30)

The corresponding G-functions at boundary \(\partial \Omega _{ij}\) \((i,j=1,2,3,4)\) from Eqs. (22)–(24) are for domain \(\Omega _\alpha (\alpha \in \{1,2,3,4\})\)

$$\begin{aligned}&\!\!\! G_{\partial \Omega _{12}}^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }){=}G_{\partial \Omega _{34}}^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }){=}g_2^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }), \nonumber \\&\!\!\! G_{\partial \Omega _{23}}^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }){=}G_{\partial \Omega _{14}}^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }){=}g_1^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }); \nonumber \\&\!\!\! G_{\partial \Omega _{12}}^{(1,\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }){=}G_{\partial \Omega _{34}}^{(1,\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }){=}Dg_2^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }), \nonumber \\&\!\!\! G_{\partial \Omega _{23}}^{(1,\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm })\!{=}\!G_{\partial \Omega _{14}}^{(1,\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }){=}Dg_1^{(\alpha )} (\mathbf{z}_m,\mathbf{x},t_{m\pm }); \nonumber \\ \end{aligned}$$
(31)

where

$$\begin{aligned}&Dg_1^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)\nonumber \\&\quad =h(z_1^{(\alpha )} +p_1 \sin x_1)-p_1 h(x_1)\cos x_1 \nonumber \\&\qquad -c_1 \left[ z_2^{(\alpha )} +(p_2-p_1)x_2 \cos x_1 \right] \nonumber \\&\qquad -c_2 \left[ (z_2^{(\alpha )} +p_2 x_2 \cos x_1)^{3}-p_1 x_2^3 \cos x_1 \right] \nonumber \\&\qquad +(\beta +f_2 \sin \omega t)\sin (z_1^{(\alpha )} +p_1 \sin x_1) \nonumber \\&\qquad -\frac{1}{2}p_1 (\beta +f_1 \sin \omega t)\sin 2x_1 +p_1 x_2 \sin x_1, \nonumber \\&Dg_2^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)\nonumber \\&\quad = \left[ h_1 (z_1^{(\alpha )} \!+\!p_1 \sin x_1)\!+\!(\beta +f_2 \sin \omega t) \right. \nonumber \\&\qquad \left. \times \cos (z_1^{(\alpha )} +p_1 \sin x_1)\right] F_1 (\mathbf{z}^{(\alpha )}+\mathbf{x},t) \nonumber \\&\qquad - \left[ c_1 +3c_2 (z_2^{(\alpha )} +p_2 x_2 \cos x_1)^{2}\right] \nonumber \\&\qquad \times F_2 (\mathbf{z}^{(\alpha )}+\mathbf{x},t)+ \left[ f_2 \sin (z_1^{(\alpha )} +p_1 \sin x_1)\right. \nonumber \\&\qquad \left. -\frac{1}{2}p_2 f_1 \sin 2x_1 \right] \nonumber \\&\qquad \times \omega \cos \omega t -p_2 \left[ h_1 (x_1)\cos x_1\right. \nonumber \\&\qquad \left. +(\beta +f_1 \sin \omega t)\cos ^{2}x_1\right] \nonumber \\&\qquad \times F_1 (\mathbf{x},t) +p_2 \big (c_1 \cos x_1 \nonumber \\&\qquad +3c_2 x_2^2 \cos x_1 +3x_2 \sin x_1\big )\nonumber \\&\qquad \times F_2 (\mathbf{x},t); \end{aligned}$$
(32)

with

$$\begin{aligned} \begin{aligned} h_1 (z_1^{(\alpha )} +p_1 \sin x_1)&=\alpha ^{2}(\cos ^{3}(z_1^{(\alpha )} +p_1 \sin x_1) \\&-\,4\cos ^{2}(z_1^{(\alpha )} +p_1 \sin x_1) \\&+5\cos (z_1^{(\alpha )} +p_1 \sin x_1)-2)/\\&\sin ^{4}(z_1^{(\alpha )} +p_1 \sin x_1) \\ h_1 (x_1)&= {\alpha }^{2}(\cos ^{3}x_1-4\cos ^{2}x_1 \\&\quad +5\cos x_1-2)/\sin ^{4}x_1. \end{aligned} \end{aligned}$$
(33)

for \({\alpha }=1,2,3,4\).

The G-functions in domains \(\Omega _{\alpha }\,(\alpha \in \{1,2,3,4\})\) with respect to the boundary are

$$\begin{aligned}&G_{\partial \Omega _{12}}^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=G_{\partial \Omega _{34}}^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=g_2^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t), \nonumber \\&G_{\partial \Omega _{23}}^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=G_{\partial \Omega _{14}}^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=g_1^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t); \nonumber \\&G_{\partial \Omega _{12}}^{(1,\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=G_{\partial \Omega _{34}}^{(1,\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=Dg_2^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t), \nonumber \\&G_{\partial \Omega _{23}}^{(1,\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=G_{\partial \Omega _{14}}^{(1,\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)=Dg_1^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t). \nonumber \\ \end{aligned}$$
(34)

From the theory for discontinuous dynamical systems [19, 20], the switchability of a flow to the boundary \(\partial \Omega _{{\alpha } \beta }\) for \(({\alpha },\beta )=\{(1,2),(2,3),(3,4),(1,4)\}\). The sliding flow of the controlled gyroscope system on the separation boundary, the conditions for projective function synchronization of the two gyroscope systems at the intersection point are

$$\begin{aligned} \begin{array}{lll} &{}&{} \left. \begin{array}{l} G_{\partial \Omega _{14}}^{(1)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_1^{(1)} (\mathbf{z}_m,\mathbf{x},t_{m-})<0, \\ G_{\partial \Omega _{12}}^{(1)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_2^{(1)} (\mathbf{z}_m,\mathbf{x},t_{m-})<0, \\ \end{array}\right\} \\ &{}&{}\qquad \hbox {for } \mathbf{z}_m \in \partial \Omega _{12} \cap \partial \Omega _{14} \hbox { on } \Omega _1; \\ &{}&{} \left. \begin{array}{l} G_{\partial \Omega _{12}}^{(2)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_2^{(2)} (\mathbf{z}_m,\mathbf{x},t_{m-})>0, \\ G_{\partial \Omega _{23}}^{(2)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_1^{(2)} (\mathbf{z}_m,\mathbf{x},t_{m-})<0, \\ \end{array} \right\} \\ &{}&{}\qquad \hbox {for }\mathbf{z}_m \in \partial \Omega _{12} \cap \partial \Omega _{23} \hbox { on } \Omega _2; \\ &{}&{} \left. \begin{array}{l} G_{\partial \Omega _{23}}^{(3)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_1^{(3)} (\mathbf{z}_m,\mathbf{x},t_{m-})>0, \\ G_{\partial \Omega _{34}}^{(3)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_2^{(3)} (\mathbf{z}_m,\mathbf{x},t_{m-})>0, \\ \end{array} \right\} \\ &{}&{}\qquad \hbox {for }\mathbf{z}_m \in \partial \Omega _{23} \cap \partial \Omega _{34} \hbox { on } \Omega _3;\\ &{}&{} \left. \begin{array}{l} G_{\partial \Omega _{34}}^{(4)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_2^{(4)} (\mathbf{z}_m,\mathbf{x},t_{m-})<0, \\ G_{\partial \Omega _{14}}^{(4)} (\mathbf{z}_m,\mathbf{x},t_{m-})=g_1^{(4)} (\mathbf{z}_m,\mathbf{x},t_{m-})>0, \\ \end{array} \right\} \\ &{}&{}\qquad \hbox {for } \mathbf{z}_m \in \partial \Omega _{34} \cap \partial \Omega _{14} \hbox { on } \Omega _4. \end{array} \end{aligned}$$
(35)

From Eq. (23), the following functions are defined as

$$\begin{aligned}&g_1 (\mathbf{z}^{(\alpha )},\mathbf{x},t)\equiv g_1^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)\nonumber \\&\quad =z_2^{(\alpha )} +(p_2-p_1)x_2 \cos x_1 -k_1\nonumber \\&\quad \hbox { in } \Omega _\alpha \hbox { for } \alpha =1,2;\nonumber \\&g_2 (\mathbf{z}^{(\alpha )},\mathbf{x},t)\equiv g_1^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)\nonumber \\&\quad =z_2^{(\alpha )} +(p_2-p_1)x_2 \cos x_1 +k_1\nonumber \\&\quad \hbox { in } \Omega _\alpha \hbox { for } \alpha =3,4;\nonumber \\&g_3 (\mathbf{z}^{(\alpha )},\mathbf{x},t)\equiv g_2^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)\nonumber \\&\quad =\psi (\mathbf{z}^{(\alpha )},\mathbf{x},t)-k_2\nonumber \\&\quad \hbox { in } \Omega _\alpha \hbox { for } \alpha =1,4;\nonumber \\&g_4 (\mathbf{z}^{(\alpha )},\mathbf{x},t)\equiv g_2^{(\alpha )} (\mathbf{z}^{(\alpha )},\mathbf{x},t)\nonumber \\&\quad =\psi (\mathbf{z}^{(\alpha )},\mathbf{x},t) +k_2\nonumber \\&\quad \hbox { in } \Omega _\alpha \hbox { for } \alpha =2,3. \end{aligned}$$
(36)

Therefore, the synchronization conditions in Eqs. (35) become

$$\begin{aligned} \begin{array}{lll} &{}&{} g_1 (\mathbf{z}_m,\mathbf{x},t_{m-})=z_{2m} +(p_2-p_1)x_2 \cos x_1-k_1 <0, \\ &{}&{} g_2 (\mathbf{z}_m,\mathbf{x},t_{m-})=z_{2m} {+}(p_2-p_1)x_2 \cos x_1 {+}k_1 >0,\\ &{}&{} g_3 (\mathbf{z}_m,\mathbf{x},t_{m-})=\psi (\mathbf{z}_m,\mathbf{x},t_{m-})-k_2 <0, \\ &{}&{} g_4 (\mathbf{z}_m,\mathbf{x},t_{m-})=\psi (\mathbf{z}_m,\mathbf{x},t_{m-})+k_2 >0. \end{array} \end{aligned}$$
(37)

Setting \({\mathbf{z}}_{m} ={\mathbf{0}}\), the analytical conditions of projective function synchronization for the controlled gyroscope with the expected chaotic gyroscope system are

$$\begin{aligned} \begin{array}{lll} &{}&{} g_1 (\mathbf{z}_m,\mathbf{x},t_{m-})=(p_2-p_1)x_2 \cos x_1-k_1 <0, \\ &{}&{} g_2 (\mathbf{z}_m,\mathbf{x},t_{m-})=(p_2-p_1)x_2 \cos x_1 +k_1 >0, \\ &{}&{} g_3 (\mathbf{z}_m,\mathbf{x},t_{m-})=\psi (\mathbf{x},t_{m-})-k_2 <0, \\ &{}&{} g_4 (\mathbf{z}_m,\mathbf{x},t_{m-})=\psi (\mathbf{x},t_{m-})+k_2 >0. \end{array} \end{aligned}$$
(38)

where

$$\begin{aligned}&\psi (\mathbf{x},t_{m-})\nonumber \\&\quad =x_2^2 \sin x_1 +h(p_1 \sin x_1)-p_2 h(x_1)\cos x_1 \nonumber \\&\qquad -\,c_2 [(p_2 x_2 \cos x_1)^{3}-p_2 x_2^3 \cos x_1] \nonumber \\&\qquad +\,\beta [\sin (p_1 \sin x_1)-0.5p_2 \sin 2x_1] \nonumber \\&\qquad +\,[f_2 \sin (p_1 \sin x_1)-0.5\,f_1 p_2 \sin 2x_1]\sin \omega t_{m-}, \nonumber \\ \end{aligned}$$
(39)

and the synchronization invariant domain is

$$\begin{aligned}&-k_1 <(p_2-p_1)x_2 \cos x_1 \,{<}\,k_1\nonumber \\&-k_2 \,{<}\,\Psi (\mathbf{x},t_{m-})\,{<}\,k_2, \end{aligned}$$
(40)

from which the synchronization invariant domain depends on the master system, control parameters \(k_1, k_2\), and scaling factors \(p_1, p_2\). From Luo [19, 20], if the projective function synchronization for two gyroscope systems disappears, the vanishing conditions for projective function synchronization on \(\partial \Omega _{\alpha \beta }\) for \((\alpha ,\beta )=\{(1,4),(2,3)\}\) are

$$\begin{aligned}&\left. \begin{array}{l} g_1 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\mp })=z_{2m}^{(\alpha )}-k_1 =0, \\ Dg_1 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\mp })={\fancyscript{G}}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\mp })>0, \\ g_2 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m-})=z_{2m}^{(\beta )} +k_1 >0, \\ \end{array} \right\} \nonumber \\&\hbox {for } z_{m+\varepsilon } =y_1-p_1 \sin x_1 >0,\hbox {and} \nonumber \\&\left. \begin{array}{l} g_1 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m-})=z_{2m}^{(\alpha )}-k_1 <0, \\ g_2 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\mp })=z_{2m}^{(\beta )} +k_1 =0, \\ Dg_2 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\mp })={\fancyscript{G}}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\mp })<0, \\ \end{array} \right\} \nonumber \\&\hbox { for } z_{m+\varepsilon } =y_1-p_1 \sin x_1 <0. \end{aligned}$$
(41)

and the vanishing conditions of projective function synchronization on another boundary \(\partial \Omega _{\alpha \beta }\) for \((\alpha ,\beta )\in \{(1,2),(4,3)\}\) are

$$\begin{aligned}&\left. \begin{array}{l} g_3 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\mp })=\fancyscript{G}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\mp })-k_2 =0, \\ Dg_3 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\mp })=D\fancyscript{G}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\mp })>0, \\ g_4 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m-})=\fancyscript{G}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m-})+k_2 >0, \\ \end{array} \right\} \nonumber \\&\hbox {for }\dot{z}_{m+\varepsilon } =y_2-p_2 x_2 \cos x_1 >0,\hbox {and} \nonumber \\&\left. \begin{array}{l} g_3 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m-})=\fancyscript{G}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m-})-k_2 <0, \\ g_4 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\mp })=\fancyscript{G}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\mp })+k_2 =0, \\ D g_4 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\mp })=D\fancyscript{G}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\mp })<0, \\ \end{array} \right\} \nonumber \\&\hbox {for }\dot{z}_{m+\varepsilon } =y_2-p_2 x_2 \cos x_1 < 0. \end{aligned}$$
(42)

From Luo [19, 20], the onset conditions of projective function synchronization on \(\partial \Omega _{\alpha \beta }\) for \((\alpha ,\beta )\in \{(1,4),(2,3)\}\) are

$$\begin{aligned}&\left. \begin{array}{l} g_1 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\pm })=z_{2m}^{(\alpha )}-k_1 =0, \\ Dg_1 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\pm })=\fancyscript{G}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\pm })>0, \\ g_2 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m-})=z_{2m}^{(\beta )} +k_1 >0; \\ \end{array} \right\} \nonumber \\&\!\!\! \hbox {for } z_{m-\varepsilon } =y_1-p_1 \sin x_1 >0,\hbox {and} \nonumber \\&\!\!\! \left. \begin{array}{l} g_1 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m-})=z_{2m}^{(\alpha )}-k_1 <0; \\ g_2 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\pm })=z_{2m}^{(\beta )} +k_1 =0, \\ Dg_2 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\pm })=\fancyscript{G}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\pm })<0 \\ \end{array} \right\} \\&\!\!\! \hbox {for }z_{m-\varepsilon } =y_1-p_1 \sin x_1 >0.\nonumber \end{aligned}$$
(43)

and the onset conditions of projective function synchronization on another boundary \(\partial \Omega _{\alpha \beta } \)for \((\alpha ,\beta )\!=\!\{(1,2),(4,3)\}\) are

$$\begin{aligned}&\!\!\! \left. \begin{array}{l} g_3 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\pm })=\fancyscript{G}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\pm })-k_2 =0, \\ Dg_3 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\pm })=D\fancyscript{G}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m\pm })>0; \\ g_4 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m-})=\fancyscript{G}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m-})+k_2 >0 \\ \end{array} \right\} \nonumber \\&\!\!\! \hbox {for } \dot{z}_{m-\varepsilon } =y_2-p_2 x_2 \hbox {cos} x_1 >0,\hbox {and} \nonumber \\&\!\!\! \left. \begin{array}{l} g_3 (\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m-})=\fancyscript{G}(\mathbf{z}_m^{(\alpha )},\mathbf{x},t_{m-})-k_2 <0; \\ g_4 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\pm })=\fancyscript{G}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\pm })+k_2 =0, \\ Dg_4 (\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\pm })=D\fancyscript{G}(\mathbf{z}_m^{(\beta )},\mathbf{x},t_{m\pm })<0 \\ \end{array} \right\} \\&\!\!\! \hbox {for }\dot{z}_{m-\varepsilon } =y_2-p_2 x_2 \hbox {cos} x_1 <0.\nonumber \end{aligned}$$
(44)

4 Numerical illustrations

Numerical results will be presented to make a better understanding of the projective function synchronization of two gyroscope systems with different dynamical behaviors. The parameters of nonlinear gyroscope systems are considered as

$$\begin{aligned} \begin{aligned}&\quad \displaystyle \alpha ^{2}=100,\beta =1,c_1 =0.5,c_2 =0.05,\omega =2, \\&\quad \displaystyle f_1=38.0,f_2 =35.9,p_1 =0.5,p_2 =1.2 \\&\quad \displaystyle (x_1,x_2)=(0.17391, 1.36406)\,\,\mathrm{and}\\&\quad \displaystyle (y_1,y_2) =(0.32878,0.67165). \end{aligned} \end{aligned}$$
(45)

With the above parameters and initial conditions, the master system possesses chaotic motion but the slave system without control possesses a period-4 motion.

From the analytical conditions for synchronization of two gyroscope systems, the synchronization switching scenario of the controlled gyroscope system varying with control parameter \(k_2\) is plotted in Fig. 2 with \(k_1 =5\). At switching points, \(y_{1k} =p_1 \sin x_{1k}\) and \(y_{2k} =p_2 x_{2k} \cos x_{1k}\). Thus, only switching points are presented in the synchronization scenario. The switching displacement and phases versus parameter \(k_2\) for synchronization of the controlled periodic gyroscope with the chaotic gyroscope are illustrated in Fig. 2a, b. The distributions of appearance and disappearance of projective function synchronization for the master and slave systems in phase plane are presented in Fig. 2c, d, respectively. For the synchronization scenario at \(k_1 =5\), the partial projective function synchronization of two gyroscopes exists in \(k_2 \in (0.09,16.75)\). If \(k_2 \in (0,0.09),\) the projective function synchronization of chaotic motions for two systems cannot be obtained. If \(k_2 \in (16.75,\infty )\), the full, projective function synchronization of chaotic motions for such two systems is achieved. The switching scenarios are chaotic because the motion of master system is chaotic. For a global view of projective function synchronization, the parameter map \((k_1,k_2)\) is presented in Fig. 3. Non-synchronization, partial synchronization and full synchronization are labeled by the corresponding acronyms “NS”, “PS” and “FS”, respectively. For \(k_1 >1.2\) and \(k_2 >16.75\), the projective function synchronization of the two systems exists. However, only the partial, projective function synchronization exist for \(0<k_1 <1.2\) and \(k_2 >16.75\). For small \(k_2\), the non-synchronization area is given herein.

Fig. 2
figure 2

The projective function synchronization scenario for the switching points against the control parameter \(k_2\). Master system: a switching velocity, b switching phase, c switching points in phase. Slave system: d switching points in phase space (FS full synchronization, PS partial synchronization, NS non-synchronization, A synchronization appearance, D synchronization disappearance)

Full size image
Fig. 3
figure 3

The parameter map \((k_1,k_2)\) for projective function synchronicity of the controlled periodic gyroscope with the chaotic gyroscope system (FS full synchronization, PS partial synchronization, NS non-synchronization)

Full size image

To guarantee the projective function synchronization of two gyroscope systems, the invariant domain of the slave system in Fig. 4a is generated from the conditions in Eq. (40) for the control parameters \(k_1 =5\) and \(k_2 =9\). The shaded regions are for non-synchronization, and the other areas are for synchronization. The boundaries are the maximum and minimum values for the onset and vanishing of function synchronization. For the controlled gyroscope system to synchronize with the chaotic gyroscope, the portion for the projective function synchronization of the trajectories of two gyroscope systems should be in the synchronization invariant domain. Otherwise, the projective function synchronization for the two gyroscope systems cannot be formed. From the parameter map \((k_1,k_2)\), the partial projective function synchronization of two gyroscope systems exists for \(k_1 =5\) and \(k_2 =9\). In Fig. 4b, c, displacement and velocity responses for the master and slave gyroscope systems are partially synchronized. Hollow and filled circular symbols represent switching points for appearance and disappearance, respectively. The big gray symbols are initial conditions. In phase plane, the invariant domains of function synchronization are embedded. The projective function synchronization of trajectories lie in the invariant domain. To observe the partial function synchronization of two gyroscopes with different behaviors, the velocity \(y_2\) versus \(x_2 \cos x_1\) is plotted in Fig. 4d. The time histories of displacements and G-functions are depicted in Fig. 4e, f. The symbols “N” and “S” represent “non-synchronization” and “synchronization”. The non-shaded regions are for non-synchronization, and the G-functions for non-synchronization are presented by dashed curve. The shaded areas are for synchronization, and the corresponding G-functions satisfy the synchronization conditions in Eq. (38), i.e. \(g_1 <0, g_2 >0, g_3 <0\) and \(g_4 >0.\)

Fig. 4
figure 4

The partial function synchronization for the periodic motion with the chaotic attractor of gyroscope dynamical systems: a function synchronization invariant domain, b trajectories of master system, c trajectories of slave system, and d velocity \(y_2\) versus \(x_2 \cos x_1\), e displacement responses, f G-function responses. (S synchronization, N non-synchronization. Hollow circular symbols synchronization appearance, filled circular symbols synchronization disappearance)

Full size image

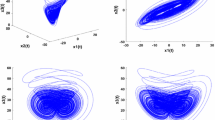
From the parameter map, for \(k_1 =5\) and \(k_2 =16\), the full, projective function synchronization for the controlled periodic gyroscope with the chaotic gyroscope takes place, as shown in Figs. 5 and 6. The G-function distributions along the displacement are plotted in Fig. 5a, b. The analytical conditions for projective function synchronization in Eq. (38) is satisfied, which means the controlled periodic gyroscope is synchronized fully with the chaotic gyroscope. The phase trajectories of the master and slave systems are presented in Fig. 5c, d, and the invariant domains are also embedded. All the trajectories of two systems lie in the synchronization invariant domain. Compared to the identical synchronization, the projective function synchronization of chaotic motions cannot be observed directly because the synchronization is based on a sinusoidal function. Thus, the relationship of state variables between master and slave systems should be presented. In Fig. 6a, b, the displacement \(x_1\) versus \(y_1\) and the velocity \(x_2\) versus \(y_2\) are depicted, respectively. In addition, the displacement \(y_1\) versus \(\sin x_1\) and the velocity \(y_2\) versus \(x_2 \cos x_1\) are also shown in Fig. 6c, d. The state variables of two coupled gyroscopes are satisfied \(y_1 =0.5\sin x_1\) and \(y_2 =1.2x_2 \cos x_1\).

Fig. 5
figure 5

The full generalized synchronization in the invariant domain: a G-function \(g_i (i=1,2)\) distribution, b G-function \(g_i (i=3,4)\) distribution, c trajectories of master system, d trajectories of slave system. S synchronization, NS non-synchronization. Hollow circular symbols synchronization appearance, filled circular symbols synchronization disappearance)

Full size image
Fig. 6
figure 6

The relationship of state variables of two coupled gyroscopes with full function synchronization: a the displacement \(x_1\) versus \(y_1\), b the velocity \(x_2\) versus \(y_2\), c the displacement \(y_1 \)versus \(\sin x_1\), and d the velocity \(y_2\) versus \(x_2 \cos x_1\). (Hollow circular symbols are synchronization appearance, gray symbols denote the initial conditions)

Full size image

5 Conclusions

The projective function synchronization of two gyroscopes with different motions was investigated under sinusoidal constraints. From the theory of discontinuous dynamical systems, the analytical conditions of such projective function synchronization were developed, which gives the function synchronization mechanism of two gyroscope systems. With special parameters, the partial and full projective function synchronizations were numerically simulated to illustrate analytical conditions. The corresponding invariant domains for the projective function synchronization were also obtained. This investigation provides a better understanding of the projective function synchronization dynamics of two gyroscope systems.