Study on hydro-magnetic capillary instability with mass transfer through porous media

Abstract

The linear analysis of hydro-magnetic capillary instability of a cylindrical interface between two viscous and magnetic fluids in a fully saturated porous medium has been carried out, when the fluids are subjected to a constant axial magnetic field and, when there is heat and mass transfer across the interface. The viscous potential flow theory has been used for the investigation. Viscosity enters through normal stress balance in the viscous potential flow theory and tangential stresses are not considered. A dispersion relation that accounts for the growth of axisymmetric waves is derived and stability is discussed theoretically as well as numerically. Stability criterion is given by critical value of applied magnetic field as well as critical wave number. Various graphs have been drawn to show the effect of various physical parameters such as magnetic field strength, heat transfer capillary number, vapour fraction, permeability and porosity on the stability of the system. It has been observed that heat transfer and magnetic field both have stabilizing effect while porosity has destabilizing effect on the stability of the system.

1 Introduction

The viscous stresses in a flow field can be divided into two parts; tangential and normal stresses. If the flow is irrotational, the viscous term in the Navier–Stokes equation is zero but the viscous stresses are not zero. The irrotational theory which includes the effect of normal viscous stresses at the interface is called viscous potential flow (VPF) theory. In this theory, the velocity can be expressed as gradient of potential function. Therefore, the viscous term i.e. $\mu \nabla ^{2}$ u in the Navier–Stokes equation is identically zero but the viscosity is not zero, where $\mu$ denotes the viscosity and ${{\varvec{u}}}$ denotes the velocity of the fluid flow. To study the capillary instability of a viscous fluid cylinder surrounded by another viscous fluid, Funada and Joseph [1] have applied the VPF theory and observed that the VPF theory gives good agreement with the experimental results. Funada and Joseph [2] have also applied the VPF theory to study the capillary instability of viscoelastic fluid of Maxwell type surrounded by a viscous fluid and found that the elastic property of the fluid enhances the instability.

The heat and mass transfer phenomenon is encountered in a wide variety of engineering applications such as boiling heat transfer and geophysical problems. The increase of these applications in the past decades has urged scientists and engineers to provide a mathematical model to study the effect of heat transfer across the interface. The very first study available in the literature related to heat and mass transfer in the interfacial stability was made by Hsieh [3]. He has used the potential flow theory to solve the governing equations but the study was restricted to the inviscid fluids. Nayak and Chakraborty [4] have solved the problem of Kelvin–Helmholtz instability but they have taken this problem in the cylindrical geometry. Awasthi and Agrawal [5] have studied the similar problem as taken by Hsieh [3] but they have considered both fluids as viscous. The effect of heat and mass transfer on the Kelvin–Helmholtz instability was studied by Asthana and Agrawal [6] when both fluids are miscible and viscous. Kim et al. [7] extended the work of Funada and Joseph [1] including the effect of interfacial heat and mass transfer. They have found that the interfacial heat and mass transfer phenomenon resists the growth of disturbance waves. Awasthi and Agrawal [8] studied the nonlinear effects on the capillary instability when the fluids are miscible and viscous and found that the nonlinearity reduces the region of stability.

The flow through porous media has been of considerable interest in recent years due to its importance in various fields such as in the fields of agriculture engineering to study the underground water resources, seepage of water in river beds and in petroleum technology. The effect of medium porosity on Kelvin–Helmholtz instability of two viscous fluids has been studied by Asthana et al. [9]. They have used potential flow theory and found that porosity of the medium plays stabilizing role. The Kelvin–Helmholtz and Rayleigh–Taylor instability at the plane interface with heat and mass transfer through porous media using VPF theory was considered by Allah [10]. He found that the Kelvin–Helmholtz instability grows in porous medium as compared to viscous medium. Awasthi and Asthana [11] have investigated the effect of heat and mass transfer on the capillary instability when the medium is porous and found that heat and mass transfer completely stabilize the system.

The study of the interaction between magnetic fields and electrically conducting fluids is known as Magnetohydrodynamics. The effect of magnetic field on the stability of various types of fluid flows is an important domain of study. The magnetohydrodynamic interfacial instability with heat and mass transfer is of fundamental importance in number of applications such as design of many types of contacting equipment, e.g., boilers, condensers, reactors, and others in industrial and environmental processes. The capillary instability with heat and mass transfer in a magnetic field occurs in many practical applications such as electronic magnetic ink jet printer and fluid jet amplifier. Elhefnawy and Radwan [12] studied the stability of magnetic inviscid fluids in cylindrical geometry with heat and mass transfer across the interface. Elhefnawy [13] analyzed the stability of the magnetic fluids of cylindrical interface with heat and mass transfer and periodic radial field. Bubble formation in superposed magnetic fluids in the presence of heat and mass transfer has been studied by Gill et al. [14]. Lee [15] considered the nonlinear stability of magnetic fluids with heat and mass transfer and showed that nonlinearity increases the region of stability with heat and mass transfer.

Recently, Awasthi et al. [16] have studied the effect of tangential magnetic field on the Kelvin–Helmholtz instability at the plane interface when there is heat and mass transfer across the interface and concluded that the tangential magnetic field has stabilizing effect on the stability of the system.

The objective of the present work is to study the effect of axial magnetic field on the capillary instability of cylindrical interface separating two fluids in a porous medium using viscous potential flow theory, when there is heat and mass transfer across the interface. Both the fluids are taken as incompressible, viscous and magnetic with different kinematic viscosities, magnetic permeability’s, which have not been considered earlier. The effect of gravity and free surface charges at the interface is neglected. The Brinkman model has been used for the investigation and a dispersion relation that accounts for the growth of axisymmetric waves is derived. Stability is discussed theoretically as well as numerically. A critical value of the magnetic field as well as the critical wave number is obtained. The effect of ratio of permeability of fluids on stability of the system is also studied and shown graphically. Various neutral curves have been drawn to show the effect of various physical parameters such as magnetic field, heat transfer capillary number, on the stability of the system.

2 Problem formulation

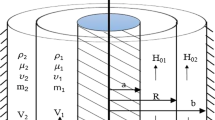
A system of two incompressible, magnetic and viscous fluids, separated by a cylindrical interface, is considered in an annular porous medium with constant porosity $\varepsilon$ and constant permeability $k_1$ as shown in Fig. 1. A cylindrical system of coordinates $(r,\theta ,z)$ is assumed so that in the equilibrium state z-axis is the axis of symmetry of the system. The undisturbed cylindrical interface is taken at radius $R$. In the formulation the superscripts 1 and 2 denote the variables associated with the fluid inside and outside the interface, respectively. In undisturbed state, viscous fluid layer of thickness $h_1$, density $\rho ^{(1)}$, viscosity $\mu ^{(1)}$ and magnetic permeability $\mu _m^{(1)}$ occupies the inner region $r_1 <r<R$ and viscous fluid layer of thickness $h_2$, density $\rho ^{(2)}$, viscosity $\mu ^{(2)}$ and magnetic permeability $\mu _m^{(2)}$ occupies the outer region $R<r<r_2$ where $h_1 =R-r_1$ and $h_2 =r_2 -R$. Surface tension at the interface is taken as $\sigma$. The bounding surfaces $r=r_1$ and $r=r_2$ are considered to be rigid. The only resistance term taken is $-\frac{\mu }{k_1 }v$ where $\mu$ denotes to the fluid viscosity, $k_1$ represents the medium permeability and $v$ is the Darcian velocity. The temperatures at $r=r_1 , r=R$ and $r=r_2$ are $T_1 , T_0$ and $T_2$ respectively. Both fluids are assumed to be incompressible and irrotational. In the basic state, thermodynamics equilibrium is assumed and the interface temperature $T_0$ is set equal to the saturation temperature.

Fig. 1

Equilibrium configuration of the system

Assuming that Darcy’s law is valid, we obtain the following momentum and continuity equations:

$$\begin{aligned} \rho \frac{dv}{dt}&= -\nabla p-\frac{\mu }{k_1 }v\end{aligned}$$

(1)

$$\begin{aligned} \nabla \cdot v&= 0 \end{aligned}$$

(2)

Here $p$ represents pressure, $\mu$ denotes fluid viscosity, $k_1$ is the medium permeability and $v$ is the Darcian (filter) velocity. Taking an average of the fluid velocity over a volume V we get the intrinsic average velocity v, which is related to $v$ by the Dupuit–Forchheimer relationship $v=\varepsilon \text{ v }$. where $\varepsilon$ represents the porosity of the medium which is defined as the fraction of the total volume of the medium that is occupied by void space.

Small axisymmetric disturbances are superimposed on the basic rest state. After disturbance, the interface is given by

$$\begin{aligned} F(r,z,t)=r-R-\eta \left( {z,t} \right) =0, \end{aligned}$$

(3)

where $\eta$, the perturbation in the radius of the interface from the equilibrium value $R$, and for which the outward unit normal vector is given by

$$\begin{aligned} {{\varvec{n}}} =\frac{\nabla F}{\left| {\nabla F} \right| }= \left\{ {\left. {1+\left( {\frac{\partial \eta }{\partial z}} \right) ^{2}} \right\} ^{-1/2}} \right. \left( {{{\varvec{e}}}_{{\varvec{r}}} -\frac{\partial \eta }{\partial z}{{\varvec{e}}}_{{\varvec{z}}} } \right) , \end{aligned}$$

(4)

where ${{\varvec{e}}}_{{\varvec{r}}}$ and ${{\varvec{e}}}_{{\varvec{z}}}$ are unit vectors along $r$ and $z$ directions, respectively.

In each fluid layer velocity can be expressed as the gradient of the potential function $\phi (r,z,t)$ and the potential functions satisfy the Laplace’s equation i.e.

$$\begin{aligned} \nabla ^{2}\phi ^{(j)}=0,\quad j=1,2 \end{aligned}$$

(5)

where $\nabla ^{2}=\frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{\partial ^{2}}{\partial z^{2}}$.

The two fluids are subjected to an external magnetic field $H_0$, acting along $z$-axis i.e. ${{\varvec{H}}}=H_0 \mathbf{e}_z$.

It is assumed that the quasi-static approximation is valid for the problem, hence the magnetic field can be derived from magnetic scalar potential function $\psi _m (r,z,t)$ such that

$$\begin{aligned} {{\varvec{H}}}_j =H_0 \mathbf{e}_z -\nabla \psi _m^{(j)} ,\quad (j=1,2). \end{aligned}$$

(6)

Gauss’s law requires that the electric potentials also satisfy Laplace’s equation i.e.

$$\begin{aligned} \nabla ^{2}\psi _m^{(j)} =0,\quad (j=1,2). \end{aligned}$$

(7)

The boundary conditions at the rigid cylindrical surfaces $r=r_1$ and $r=r_2$ are given by

$$\begin{aligned} \frac{\partial \phi ^{(j)}}{\partial r}&= 0\quad \text{ at }\quad r=r_j ,\quad (j=1,2),\end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial \psi _m^{(j)} }{\partial z}&= 0\quad \text{ at }\quad r=r_j, \quad (j=1,2). \end{aligned}$$

(9)

The tangential component of the magnetic field must be continuous across the interface i.e.

$$\begin{aligned} \left[ {H_t } \right] =0, \end{aligned}$$

(10)

where $H_t (=\left| {\mathbf{n}\times {{\varvec{H}}}} \right| )$ is the tangential component of the magnetic field and $\left[ x \right]$ represents the difference in a quantity across the interface, it is defined as $\left[ x \right] =x^{(2)}-x^{(1)}$.

There is discontinuity in the normal current across the interface; charge accumulation within a material element is balanced by conduction from bulk fluid on either side of the surface. The boundary condition, corresponding to normal component of the magnetic induction, at the interface is given by

$$\begin{aligned} \left[ {\mu _m H_n } \right] =0, \end{aligned}$$

(11)

where $H_n (=\mathbf{n}\cdot {{\varvec{H}}})$ is the normal component of the magnetic field.

It is assumed that phase-change takes place locally in such a way that the net phase-change rate at the interface is equal to zero. The interfacial condition, which expresses the conservation of mass across the interface, can be written as

$$\begin{aligned} \left[ {\rho \left( {\frac{\partial F}{\partial t}+\nabla \phi \cdot \nabla F} \right) } \right] =0\quad \text{ at }\quad r=R+\eta \end{aligned}$$

(12)

The interfacial condition for energy transfer proposed by Hsieh [3] is expressed as

$$\begin{aligned} L\rho ^{(1)}\left( {\frac{\partial F}{\partial t}\!+\!\nabla \varphi ^{(1)}\cdot \nabla F} \right) =S\left( \eta \right) \quad \text{ at }\quad r=R\!+\!\eta \end{aligned}$$

(13)

where $L$ is the latent heat released during phase transformation and $S\left( \eta \right)$ denotes the net heat flux from the interface. In deriving Eq. (13), we have assumed that the amount of latent heat released depends mainly on the instantaneous position of the interface.

In the equilibrium state, the heat fluxes in positive $r$-direction in the fluid phases 1 and 2 are ${-K_1 \left( {T_1 -T_0 } \right) }/R \ln \left( {{R_1 }/R} \right)$ and ${-K_2 \left( {T_0 -T_2 } \right) }/R \ln \left( {R/{R_2 }} \right)$ respectively where $K_{1}$ and $K_2$ denote the heat conductivities of the two fluids. The net heat flux $S\left( \eta \right)$ is expressed as (Nayak and Chakraborty [4])

$$\begin{aligned} S\left( \eta \right)&= \frac{K_2 \left( {T_0 -T_2 } \right) }{\left( {R+\eta } \right) \left( {\ln r_2 -\ln \left( {R+\eta } \right) } \right) }\nonumber \\&-\,\frac{K_1 \left( {T_1 -T_0 } \right) }{\left( {R+\eta } \right) \left( {\ln \left( {R+\eta } \right) -\ln r_1 } \right) }. \end{aligned}$$

(14)

On expanding $S\left( \eta \right)$ about $r=R$ i.e. at $\eta =0$,

$$\begin{aligned} S\left( \eta \right) \!=\! S\left( 0 \right) +\eta {S}^{\prime }\left( 0 \right) +\!\frac{1}{2}\eta ^{2}{S}^{\prime \prime }\left( 0 \right) +\!\frac{1}{6}\eta ^{3}{S}^{\prime \prime \prime }\left( 0 \right) \!+\!\cdots \quad \end{aligned}$$

(15)

Since $S\left( 0 \right) =0$, from Eq. (12) we get

$$\begin{aligned} \frac{K_2 \left( {T_0 - T_2 } \right) }{R\ln \left( {{r_2 }/R} \right) }=\frac{K_1 \left( {T_1 - T_0 } \right) }{R\ln \left( {R/{r_1 }} \right) }=G, \text{ where } \text{ G } \text{ is } \text{ a } \text{ constant. }\nonumber \\ \end{aligned}$$

(16)

Hence in the equilibrium state, heat fluxes across the interfaces are equal.

The interfacial condition for conservation of momentum is given by;

$$\begin{aligned}&\rho ^{(1)}\left( {\nabla \phi ^{(1)}\cdot \nabla F} \right) \left( {\frac{\partial F}{\partial t}+\nabla \phi ^{(1)}\cdot \nabla F} \right) \nonumber \\&\qquad =\rho ^{(2)}\left( {\nabla \phi ^{(2)}\cdot \nabla F} \right) \left( {\frac{\partial F}{\partial t}+\nabla \phi ^{(2)}\cdot \nabla F} \right) \nonumber \\&\qquad \quad +\left( p_2 \!-\!p_1 \!-\!2\mu ^{(2)}\frac{\partial \text{ v }_2 }{\partial r}+2\mu ^{(1)}\frac{\partial \text{ v }_1 }{\partial r}\right. \nonumber \\&\qquad \quad \left. -\frac{1}{2}\left[ {\mu _m \left( {H_n^2 \!-\!H_t^2 } \right) } \right] \!+\!\sigma \nabla \cdot \mathbf{n} \right) \left| {\nabla F} \right| ^{2}\quad \text{ at }\;r \!=\! R\!+\!\eta \nonumber \\ \end{aligned}$$

(17)

where $p$ represents the pressure and $\sigma$ denotes the surface tension. Surface tension has been assumed to be a constant, neglecting its dependence on temperature. Pressure can be obtained using Bernoulli’s equation.

3 Linearized equations

It has been observed that the asymmetric disturbances are always stable for capillary instability. A long cylinder of liquid is unstable to the axisymmetric disturbances with wavelengths greater than $2\pi R$, where $R$ is the radius of the cylinder. Hence, we have considered only axisymmetric disturbances in this analysis. Now, axisymmetric disturbances are imposed on the Eqs. (10–13) and (17) and retaining the linear terms we can get the following equations.

$$\begin{aligned}&\left[ {\frac{\partial \psi _m }{\partial z}} \right] =0\end{aligned}$$

(18)

$$\begin{aligned}&\left[ {\mu _m \left( {\frac{\partial \psi _m }{\partial r}+H_0 \frac{\partial \eta }{\partial z}} \right) } \right] =0,\end{aligned}$$

(19)

$$\begin{aligned}&\left[ {\rho \left( {\frac{\partial \phi }{\partial r}-\frac{\partial \eta }{\partial t}} \right) } \right] =0,\end{aligned}$$

(20)

$$\begin{aligned}&\rho ^{(1)}\left( {\frac{\partial \phi ^{(1)}}{\partial r}-\frac{\partial \eta }{\partial t}} \right) =\alpha \eta ,\end{aligned}$$

(21)

$$\begin{aligned}&\left[ {\rho \left( \frac{1}{\varepsilon }\frac{\partial \phi }{\partial t}+\frac{1}{\rho }\frac{\mu }{k_1 }\phi \right) +\frac{2\mu }{\varepsilon }\frac{\partial ^{2}\phi }{\partial r^{2}}+\mu _m H_0 \frac{\partial \psi _m }{\partial z}} \right] \nonumber \\&\qquad =-\sigma \left( \frac{\partial ^{2}\eta }{\partial z^{2}}+\frac{\eta }{R^{2}}\right) \end{aligned}$$

(22)

where $\alpha =\frac{G}{LR}\frac{\ln (r_2 /r_1 )}{\ln (r_2 /R)\ln (R/r_1 )}$

For the linearization of Eq. (17), we have followed the approach adopted by Awasthi and Asthana [11]. In Eq. (17) the velocity $\text{ v }_j (j=1,2)$ represent the intrinsic average velocity. Using the Dupuit–Forchheimer relationship $\text{ v }=\frac{v}{\varepsilon }$ where $v$ is the Darcian velocity and $\varepsilon$ represents the porosity of the medium. Putting this value in Eq. (17) and retaining the linear terms, we can get Eq. (22).

Now the normal mode technique is used to find the solution of the governing equations. Letting the interface elevation be represented by

$$\begin{aligned} \eta =A \exp \left( {i\left( {kz-\omega t} \right) } \right) + c. c., \end{aligned}$$

(23)

where $A$ represents the amplitude of the surface wave, $k$ denotes the real wave number, $\omega$ is the growth rate and $c. c.$ refers the complex conjugate of the preceding term.

On solving Eqs. (5) and (7) with the help of boundary conditions (18–21), we get

$$\begin{aligned} \phi ^{(1)}&= \frac{1}{k}\left( {\frac{\alpha }{\rho ^{(1)}}-i\omega } \right) E^{(1)}(kr)A\exp \left( {i\left( {kz-\omega t} \right) } \right) +c. c.\nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} \phi ^{(2)}&= \frac{1}{k}\left( {\frac{\alpha }{\rho ^{(2)}}-i\omega } \right) E^{(2)}(kr)A\exp \left( {i\left( {kz-\omega t} \right) } \right) +c. c.\nonumber \\ \end{aligned}$$

(25)

$$\begin{aligned} \psi _m^{(1)}&= \frac{i \left( {\mu _m^{(2)} -\mu _m^{(1)} } \right) H_0 g_2 (k) }{\mu _m^{(1)} g_2 (k) G_1 (k)-\mu _m^{(2)} g_1 (k) G_2 (k)}\nonumber \\&\times \left( {I_0 (k r_1 )K_0 (k r)-I_0 (k r_1 )K_0 (k r)} \right) \nonumber \\&\times A\exp \left( {i\left( {kz-\omega t} \right) } \right) +c. c.\end{aligned}$$

(26)

$$\begin{aligned} \psi _m^{(2)}&= \frac{i \left( {\mu _m^{(2)} -\mu _m^{(1)} } \right) H_0 g_1 (k) }{\mu _m^{(1)} g_2 (k) G_1 (k)-\mu _m^{(2)} g_1 (k) G_2 (k)}\nonumber \\&\times \left( {I_0 (kr)K_0 (kr_{ 2} )-I_0 (kr_{ 2} )K_0 (kr)} \right) \nonumber \\&\times A\exp \left( {i\left( {kz-\omega t} \right) } \right) +c. c. \end{aligned}$$

(27)

where

$$\begin{aligned}&E^{(j)}(kR)=\frac{I_0 (kr)K_1 (kr_j )+I_1 (kr_j )K_0 (kr)}{I_1 (kR)K_1 (kr_j )-I_1 (kr_j )K_1 (kR)},\\&g_j (k)=I_0 (k r_j )K_0 (k R)-I_0 (k R)K_0 (k r_j ),\\&G_j (k)=I_1 (k R)K_0 (k r_j )-I_0 (k r_j )K_1 (k R),\quad (j=1,2) \end{aligned}$$

and symbols $I_n$ and $K_n$ are modified Bessel’s functions of first and second kind of order $n(=0,1)$ respectively.

4 Dispersion relation

Substituting the values of $\eta ,\phi ^{(1)}, \phi ^{(2)}, \psi _m^{(1)}$ and $\psi _m^{(2)}$ in Eq. (22) we get the dispersion relation

$$\begin{aligned} D(\omega ,k)=a_0 \omega ^{2}+ia_1 \omega -a_2 =0 \end{aligned}$$

(28)

where

$$\begin{aligned}&a_0 =\frac{\rho ^{(1)}}{\varepsilon }E^{(1)}(kR)-\frac{\rho ^{(2)}}{\varepsilon }E^{(2)}(kR)\\&a_1 =\frac{\alpha }{\varepsilon }\left( {E^{(1)}(kR)-E^{(2)}(kR)} \right) \\&\qquad +\frac{2k^{2}}{\varepsilon }\left( {\mu ^{(1)}F^{(1)}(kR)-\mu ^{(2)}F^{(2)}(kR)} \right) \\&\qquad +\frac{1}{k_1 }\left( {\mu ^{(1)}E^{(1)}(kR)-\mu ^{(1)}E^{(2)}(kR)} \right) \\&a_2 =\frac{\alpha }{k_1 }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}E^{(1)}(kR)-\frac{\mu ^{(2)}}{\rho ^{(2)}}E^{(2)}(kR)} \right) \\&\qquad +\frac{2k^{2}\alpha }{\varepsilon }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}F^{(1)}(kR)-\frac{\mu ^{(2)}}{\rho ^{(2)}}F^{(2)}(kR)} \right) \\&\qquad +\,\sigma k(k^{2}-\frac{1}{R^{2}})-\frac{k^{2}H_0^2 g_1 (k)g_2 (k)\left( {\mu _m^{(2)} -\mu _m^{(1)} } \right) ^{2}}{\mu _m^{(1)} g_2 (k) G_1 (k)-\mu _m^{(2)} g_1 (k) G_2 (k)} \\&F^{(1)}(kR)\!=\!E^{(1)}(kR)\!-\!\frac{1}{kR}, \quad F^{(2)}(kR)\!=\!E^{(2)}(kR)\!-\!\frac{1}{kR} \end{aligned}$$

After using the transformation $\omega =i\omega _0$, the dispersion relation is obtained in growth rate $\omega _0$ i.e.

$$\begin{aligned} a_0 \omega _0 ^{2}+ a_1 \omega _0 +a_2 =0. \end{aligned}$$

(29)

On application of the Routh–Hurwitz criteria in the Eq. (29) the stability condition is $a_0 >0,a_1 >0,a_2 >0$.

Using the properties of modified Bessel functions, we have $a_0 >0$ trivially and since $\mu ^{(1)}$ and $\mu ^{(2)}$ are positive so $a_1 >0$.

Hence the condition of stability gives rise to $a_2 >0$,

$$\begin{aligned} \left( {\begin{array}{l} \frac{\alpha }{k_1 }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}E^{(1)}(k_c R)-\frac{\mu ^{(2)}}{\rho ^{(2)}}E^{(2)}(k_c R)} \right) \\ \quad +\,\frac{2k^{2}\alpha }{\varepsilon }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}F^{(1)}(k_c R)-\frac{\mu ^{(2)}}{\rho ^{(2)}}F^{(2)}(k_c R)} \right) \\ \quad +\,\sigma k_c \left( k_c^2-\frac{1}{R^{2}}\right) \\ \displaystyle \quad -\frac{k_c^2 (H_0 )_c^2 g_1 (k_c )g_2 (k_c )\left( {\mu _m^{(2)} \!-\!\mu _m^{(1)} } \right) ^{2}}{\mu _m^{(1)} g_1 (k_c ) G_2 (k_c )-\mu _m^{(2)} g_2 (k_c ) G_1 (k_c )}\\ \end{array}} \right) >0 \end{aligned}$$

(30)

Hence we conclude that the system is stable for $k\ge k_c$ and unstable $k<k_c$, where $k_c$ is the critical value of the wave number.

Equation (30) can also be written as

$$\begin{aligned}&\frac{k_c^2 (H_0 )_c^2 g_1 (k_c )g_2 (k_c )\left( {\mu _m^{(2)} -\mu _m^{(1)} } \right) ^{2}}{\mu _m^{(1)} g_1 (k_c ) G_2 (k_c )-\mu _m^{(2)} g_2 (k_c ) G_1 (k_c )}\nonumber \\&\quad <\left( {\begin{array}{l} \frac{\alpha }{k_1 }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}E^{(1)}(k_c R)-\frac{\mu ^{(2)}}{\rho ^{(2)}}E^{(2)}(k_c R)} \right) +\sigma k_c \left( k_c^2 -\frac{1}{R^{2}}\right) \\ +\,\frac{2k^{2}\alpha }{\varepsilon }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}F^{(1)}(k_c R)-\frac{\mu ^{(2)}}{\rho ^{(2)}}F^{(2)}(k_c R)} \right) \\ \end{array}} \right) \nonumber \\ \end{aligned}$$

(31)

It is also concluded that the system is stable for $H\le H_c$ and unstable for $H>H_c$, where $H_c$ is the critical value of the magnetic field.

The condition for neutral stability is given by

$$\begin{aligned}&\frac{\alpha }{k_1 }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}E^{(1)}(k_c R)-\frac{\mu ^{(2)}}{\rho ^{(2)}}E^{(2)}(k_c R)} \right) \nonumber \\&\qquad +\,\frac{2k^{2}\alpha }{\varepsilon }\left( {\frac{\mu ^{(1)}}{\rho ^{(1)}}F^{(1)}(k_c R)-\frac{\mu ^{(2)}}{\rho ^{(2)}}F^{(2)}(k_c R)} \right) \nonumber \\&\qquad +\,\sigma k_c (k_c^2 -\frac{1}{R^{2}})\nonumber \\&\quad =\frac{k_c^2 (H_0 )_c^2 g_1 (k_c )g_2 (k_c )\left( {\mu _m^{(2)} -\mu _m^{(1)} } \right) ^{2}}{\mu _m^{(1)} g_1 (k_c ) G_2 (k_c )-\mu _m^{(2)} g_2 (k_c ) G_1 (k_c )} \end{aligned}$$

(32)

For $H_0 =0$, Eq. (32) is reduced to dispersion relation as obtained by Awasthi and Asthana [11]. In Eq. (32) putting $H_0 =0,\varepsilon =1,k_1 \rightarrow \infty$ we get the dispersion relation as obtained by Kim et al. [7]. Choosing $\mu _1 =0, \mu _2 =0, \alpha =0, r_1 \rightarrow 0, r_2 \rightarrow \infty \text{ and } H_0 =0$, the dispersion relation (32) reduces to form $\omega _{^{0}}^2 =\frac{T(1-x^{2})}{R^{3}}\left[ {\frac{xI_1 (x)K_1 (x)}{\rho ^{(1)}I_0 (x)K_1 (x)+\rho ^{(2)}I_1 (x)K_0 (x)}} \right] ,$ using the results ${I}^{\prime }_0 (x)=I_1 (x), {K}^{\prime }_0 (x)=-K_1 (x), x=kR, \mathop {\lim }\nolimits _{r_1 \rightarrow 0} {K}^{\prime }_0 (kr_1 )\rightarrow \infty , \quad \mathop {\lim }\nolimits _{r_2 \rightarrow \infty } {I}^{\prime }_0 (kr_2 )\rightarrow \infty$. Here the condition for stability is $x>1$, which is well known Rayleigh criteria for a cylindrical jet.

5 Dimensionless form of dispersion relation

Considering the dimensionless variables

$$\begin{aligned} \hat{{r}}&= r/h, \hat{{z}}=z/h, \hat{{\eta }}=\eta /h,\hat{{t}}=t/\tau , \hat{{\omega }}=\omega \tau , \hat{{k}}=kh,\\&\hat{{h}}=h_1 /h=\varphi ,\hat{{R}}=\hat{{r}}_1 +\varphi , \end{aligned}$$

where the length scale $h$ and time scale $\tau$ are defined as $h=r_2 -r_1 ,\tau =\sqrt{{\rho ^{(2)}h^{3}}/\sigma }$.

Also $\begin{array}{l} \hat{{\rho }}\!=\!\frac{\rho ^{(1)}}{\rho ^{(2)}},\quad \hat{{\mu }} \!=\!\frac{\mu ^{(1)}}{\mu ^{(2)}},\quad Oh\!=\!\frac{\sqrt{\rho ^{(2)}\sigma h}}{\mu ^{(2)}}, \quad \hat{{\alpha }}\!=\!\frac{\alpha }{{\rho ^{(2)}}/\tau }, \quad \Lambda \!=\!\frac{2\hat{{\alpha }}}{Oh},\\ \kappa =\frac{\hat{{\mu }}}{\hat{{\rho }}},\quad \hat{{p}}_1 =\frac{h^{2}}{k_1 },\quad \hat{{\mu }}_m =\frac{\mu _m^{(1)} }{\mu _m^{(2)} },\quad \hat{{H}}^{2}=\frac{\mu _m^{(2)} H_0^2 h}{\sigma } \\ \end{array}$

where $Oh$ denotes the Ohnesorge number and it is defined as the ratio of the surface tension force to the inertia force, $\hat{{\alpha }}$ represents the heat transfer capillary number, $\varphi$ denotes the inner fluid fraction, $\kappa$ represents the kinematic viscosity ratio and $\Lambda$ denotes the alternative heat transfer capillary number.

The dimensionless form of Eq. (28) can be written as

$$\begin{aligned} D(\hat{{\omega }},\hat{{k}})=\hat{{a}}_0 \hat{{\omega }}^{2}+i\hat{{a}}_1 \hat{{\omega }}-\hat{{a}}_2 =0 \end{aligned}$$

(33)

$$\begin{aligned} \hat{{a}}_0&= \frac{1}{\varepsilon }\left( {\hat{{\rho }}E^{(1)}(\hat{{k}}\hat{{R}})-E^{(2)}(\hat{{k}}\hat{{R}})} \right) \\ \hat{{a}}_1&= \frac{\hat{{\alpha }}}{\varepsilon }\left( {E^{(1)}(\hat{{k}}\hat{{R}})-E^{(2)}(\hat{{k}}\hat{{R}})} \right) \\&+\frac{2\hat{{k}}^{2}}{oh}\left( {\hat{{\mu }}\frac{1}{\varepsilon }F^{(1)}(\hat{{k}}\hat{{R}})-\frac{1}{\varepsilon }F^{(2)}(\hat{{k}}\hat{{R}})} \right) \\&\quad +\frac{\hat{{p}}_1 }{oh}\left( {\hat{{\mu }}E^{(1)}(\hat{{k}}\hat{{R}})-E^{(2)}(\hat{{k}}\hat{{R}})} \right) \\ \hat{{a}}_2&= \frac{\hat{{\alpha }}}{oh}\frac{\hat{{p}}_1 }{\varepsilon }\left( {\frac{\hat{{\mu }}}{\hat{{\rho }}}E^{(1)}(\hat{{k}}\hat{{R}})-E^{(2)}(\hat{{k}}\hat{{R}})} \right) \\&+\frac{2\hat{{k}}^{2}\hat{{\alpha }}}{oh}\left( {\frac{\hat{{\mu }}}{\hat{{\rho }}}\frac{1}{\varepsilon }F^{(1)}(\hat{{k}}\hat{{R}})-\frac{1}{\varepsilon }F^{(2)}(\hat{{k}}\hat{{R}})} \right) \\&+\,\hat{{k}}\left( \hat{{k}}^{2}-\frac{1}{\hat{{R}}^{2}}\right) -\frac{\hat{{k}}^{2}\hat{{H}}^{2}g_1 (\hat{{k}})g_2 (\hat{{k}})(1-\hat{{\mu }}_m )^{2}}{\hat{{\mu }}_m g_2 (\hat{{k}}) G_1 (\hat{{k}})-g_1 (\hat{{k}}) G_2 (\hat{{k}})} \end{aligned}$$

and non-dimensional form of Eq. (32) is given by:

$$\begin{aligned} \left( {\begin{array}{l} \frac{\Lambda }{2}\frac{\hat{{p}}_1 }{\varepsilon }\left( {\kappa E^{(1)}(\hat{{k}}_c \hat{{R}})-E^{(2)}(\hat{{k}}_c \hat{{R}})} \right) \\ \quad +\frac{\Lambda \hat{{k}}_c^2 }{\varepsilon }\left( {\kappa F^{(1)}\left( \hat{{k}}_c \hat{{R}}\right) -F^{(2)}(\hat{{k}}_c \hat{{R}})} \right) \\ \quad \displaystyle +\, \hat{{k}}_c \left( \hat{{k}}_c^2 -\frac{1}{\hat{{R}}^{2}}\right) \\ \displaystyle \quad -\frac{\hat{{k}}_c^2 \hat{{H}}^{2}g_1 (\hat{{k}}_c )g_2 (\hat{{k}}_c )(1-\hat{{\mu }}_m )^{2}}{\hat{{\mu }}_m g_2 (\hat{{k}}_c ) G_1 (\hat{{k}}_c )-g_1 (\hat{{k}}_c ) G_2 (\hat{{k}}_c )} \\ \end{array}} \right) =0 \end{aligned}$$

(34)

6 Results and discussions

In this section, the numerical computation has been carried out using the expressions presented in the previous section for a film boiling condition. We have taken steam and water as working fluids identified with phase 1 and phase 2, respectively, such that $T_1 >T_0 >T_2$. We are treating steam as incompressible since the Mach number is expected to be small. In film boiling, the water-steam interface is in saturation condition and the temperature $T_0$ is equal to the saturation temperature. Following parametric values have been taken:

$$\begin{aligned}&\rho ^{(1)}= 0.001\,{\text{ g/cm }}^{3},\quad \rho ^{(2)}=1.0\,{\text{ g/cm }}^{3},\\&\mu ^{(1)}=0.00001\,{\text{ poise }},\quad \mu ^{(2)}=0.01\,{\text{ poise }},\\&\sigma =72.3\,{\text{ dyne/cm }} \end{aligned}$$

The diameters of the inner and outer cylinders are taken as 1 and 2 cm, respectively. The ratio of magnetic permeability $\hat{{\mu }}_m$ is taken as 0.5 for numerical calculations. At the interface, phase change is taking place. Neutral curves for wave number divide the plane into a stable region above the curve and an unstable region below the curve while neutral curves for the magnetic field divide the plane into a stable region below the curve and an unstable region above the curve. In the following the effect of various physical parameters on the onset of instability is interpreted through various figures.

The effect of alternative heat-transfer capillary dimensionless group $\Lambda$ on the neutral curves for critical wave number have been shown in Fig. 2 when the magnetic field strength $\hat{{H}}=2$. Here we have found that if we take $\Lambda$ constant and increase $\kappa$, the critical wave number $k_c$ reduces for fixed value of vapour fraction $\varphi$; hence the VPF theory predicts longer stable waves. As alternative heat-transfer capillary dimensionless group $\Lambda$ increases, the stable region also increases. Since $\Lambda$ is directly proportional to the heat flux and inversely proportional to the surface tension. Therefore, surface tension has destabilizing effect on the stability of the system while heat flux has stabilizing effect. This is the similar result as one obtained by Awasthi and Asthana [11] for the capillary instability with heat and mass transfer through porous media in the absence of magnetic field. Therefore, it has been concluded that the behaviour of heat transfer across the interface does not affected by the presence of magnetic field. The effect of heat and mass transfer on the stability of the system can be explained in terms of local evaporation and condensation at the interface. At a perturbed interface, crests are warmer because they are closer to the hotter boundary on the vapour side, thus local evaporation takes place, whereas troughs are cooler and thus condensation takes place. The liquid is protruding to a hotter region and the evaporation will diminish the growth of disturbance waves.

Fig. 2

Neutral curves for critical wave number when $\hat{{H}}=2,\varphi =0.05,\varepsilon =0.3, \hat{{p}}_1 =1/0.0004$, for the different values of heat transfer capillary number $\Lambda$

The effect of magnetic field strength $\hat{{H}}$ on the neutral curves for the critical wave number $k_c$ has been studied in Fig. 3. It has been observed that for a fixed value of $\kappa$ and $\Lambda$, the critical wave number $k_c$ decreases on increasing magnetic field strength $\hat{{H}}$. Therefore, it is concluded that $\hat{{H}}$ has stabilizing effect. If magnetic field is present in the analysis, the term contributed from the applied magnetic field added in the right hand side of the Eq. (34) and so that critical value of wave number decreases and system will become more stable. For a fixed value of vapour thickness $\varphi$, on increasing $\kappa$, the critical wave number $k_c$ decreases and finally vanishes at threshold $\kappa$.

Fig. 3

Neutral curves for critical wave number when $\Lambda =10^{-6},\varphi =0.05,\varepsilon =0.3, \hat{{p}}_1 =1/0.0004,$ for the different values of magnetic field strength $\hat{{H}}$

The effect of permeability of medium on the stability of the system has been considered in Fig. 4. We have observed that as $\hat{{p}}_1$ increases the stable region increases and since the non-dimensional number $\hat{{p}}_1$ is inversely proportional to the medium permeability $k_1$, so the medium permeability $k_1$ has destabilizing effect on the stability of the system. The variation of growth rate curves for different values of medium porosity has been shown in Fig. 5. The porosity of the medium plays a destabilizing effect on the stability of the system as observed from Fig. 5.

Fig. 4

Neutral curves for critical magnetic field when $\Lambda =10^{-6},\varphi =0.05,\varepsilon =0.4$ for the different values of $\hat{{p}}_1$

Fig. 5

Growth rate curves when $\hat{{H}}=2,\hat{{\rho }}=0.001,\hat{{\mu }}=0.001,\varphi =0.05,\hat{{\alpha }}=10^{-6}, Oh=100,\hat{{p}}_1 =1/0.0004$ for the different values of porosity $\varepsilon$

The variation of growth rate $\hat{{\omega }}_0$ for different values of magnetic permeability ratio of two fluids $\hat{{\mu }}_m$ has been shown in Fig. 6 when $\hat{{H}}=2$ and $\varphi =0.05$. The figure shows that as the ratio of the magnetic permeability of the two fluids increases, the growth of disturbance waves first increases and after that decreases. It concludes that $\hat{{\mu }}_m$ shows dual nature in the stability analysis i.e. destabilizing as well as stabilizing effect. At the constant value of the magnetic field, the most unstable case was found when both the fluids have same permittivity i.e. $\hat{{\mu }}_m =1$. This happens because at $\hat{{\mu }}_m =1$, the effect of magnetic field vanishes.

Fig. 6

Growth rate curves when $\Lambda =10^{-6},\varphi =0.05,\hat{{p}}_1 =1/0.0004$ for the different values of magnetic permeability ratio of two fluids $\hat{{\mu }}_m$

Figure 7 shows the effect of vapour fraction on the neutral curves of critical value of magnetic field. As vapour fraction increases, the stable region decreases at the constant value of heat flux and this concludes that the vapour fraction has destabilizing effect on the stability of the system. On increasing the vapour fraction, more heat is supplied to the interface and so the interface becomes unstable. Vapour fraction also plays destabilizing role in the nonlinear analysis of capillary instability in viscous media when there is heat and mass transfer across the interface as observed by Awasthi and Agrawal [8].

Fig. 7

Neutral curves for critical magnetic field when $\Lambda =10^{-6},\varepsilon =0.4, \hat{{p}}_1 =1/0.0004$ for the different values of vapour fraction $\varphi$

7 Conclusion

We have studied the effect of axial magnetic field on the capillary instability, when there is heat and mass transfer across the interface and, when the medium is porous of constant porosity and permeability. The VPF theory has been used for investigation and a dispersion relation is obtained which is a quadratic equation in growth rate. The stability condition is obtained by applying Routh–Hurwitz criterion. A critical value of magnetic field as well as critical wave number is obtained. The system is unstable when the magnetic field is greater than the critical value of magnetic field, otherwise it is stable. It is observed that the heat and mass transfer has stabilizing effect on the stability of the system and this effect is enhanced in the presence of magnetic field. The heat and mass transfer completely stabilizes the interface against capillary effects even in the presence of magnetic field. It is also observed that the axial magnetic field increases the stability of the system. The ratio of magnetic permeability has dual effect while vapour fraction destabilizes the system. The heat and mass transfer, for inviscid fluids, has no effect on the stability of the system, while it has stabilizing effect on the stability for viscous fluids. Medium Porosity and permeability both have destabilizing effect on the stability of the system.