1 Introduction

The harmonic balance (HB) method can be used to determine analytical approximate solutions to nonlinear oscillatory systems for which the nonlinear terms are “not small”, i.e., no perturbation parameter requires to exist [1–3]. However, it is very difficult to construct analytical approximations of high accuracy using such an approach because it requires solving of a set of complicated nonlinear algebraic equations.

In recent years, some improved HB methods have been developed. An analytical approximate technique for large amplitude oscillations of a class of conservative single degree-of-freedom systems with odd nonlinearity was proposed [4]. The method incorporates salient features of both Newton’s method and the HB method. Unlike the classical harmonic balance method, accurate analytical approximate solutions are possible because linearization of the governing differential equation by Newton’s method is conducted prior to harmonic balancing. The approach yields simple linear algebraic equations instead of nonlinear algebraic equations which are without an analytical solution. Only a few iterations are required to yield very accurate analytical approximate solutions for the whole range of oscillation amplitude beyond the domain of solution by the HB method. In general, the success of this method for conservative systems requires that the nonlinear restoring force is an odd function of the displacement measured from the stable equilibrium position. If this condition is not satisfied, the methods mentioned above lead to inconsistencies [5]. To overcome this deficiency, an approach [6] was proposed to construct accurate analytical approximate period and periodic solution to general strong nonlinear conservative single degree-of-freedom oscillators. Based on the original general nonlinear oscillator, two new oscillators with odd nonlinearity are first addressed [7]. Based on the analytical approximate solutions to odd nonlinear oscillators developed [4], analytical approximate solutions to the original general nonlinear oscillator was achieved by combining the approximate solutions corresponding to, respectively, the two new oscillators introduced. The interesting features of the proposed approach are the simplicity and excellent accuracy of the period and corresponding periodic solution for small as well as large oscillation amplitudes. The proposed methods [4, 6, 7] have been applied and generalized to various types of nonlinear vibration problems in mechanics and physics, for examples, the readers are referred to references [8–15]. Especially, approximate frequency-amplitude relations and periodic solutions to an oscillating charge in the electric field of a ring [16] were constructed [11, 17], but the nonlinear restoring force was only an odd function of displacement.

This paper is focused on the nonlinear oscillations of a charge placed on a finite conducting wire along the axis of two charged spheres. For the oscillator, the nonlinear restoring force is a rational function of the displacement measured from the stable equilibrium position, yet it is not an odd function of displacement. To solve the nonlinear differential equation, a change of variable is first introduced and the differential equation is then expressed in a form that the Fourier series can be obtained. Based on the previous approaches [4, 6, 7], analytical approximations to the oscillation frequency and periodic solutions for the oscillator are constructed. The approximate frequency and periodic solutions obtained are valid for a wide range of oscillation amplitude.

2 Formulation

Two small charged spheres are fixed with distance 2l apart is illustrated in Fig. 1. A charge is placed on a finite conducting wire along the axis of the two charged spheres and it is free to slide along the axis [18]. The left sphere has a charge \(Q_1\) and the right one has a charge \(Q_2\), whereas the intermediate charge \(Q_0\) has mass\(M\).

Fig. 1
figure 1

A charge in the electric field of two charged spheres

Full size image

It is easy to know that the movable charge \(Q_0\) has a stable static equilibrium position between two outside spheres, if and only if the charges \(Q_0, Q_1\) and \(Q_2\) are of the same sign. Without loss of generality, we consider the positive charge cases and assume \(Q_1 \ge Q_2\). In dimensionless form, the equation of motion for the intermediate charge is [18]

$$\begin{aligned} \begin{aligned}&\frac{dx^{2}}{dt^{2}}+\frac{\alpha ^{2}}{(1-x)^{2}}- \frac{1}{(1+x)^{2}}=0,x(0)=x_0,\\&\frac{dx}{dt}(0)=0\,(0<\alpha \le 1) \end{aligned} \end{aligned}$$
(1)

where \(x=\frac{\tilde{x}}{l}, \, t=\frac{\tilde{t}}{\omega _0}, \omega _0^2 = \frac{Q_0 Q_1}{4\pi \varepsilon _0 Ml^{3}}, \alpha ^{2}= \frac{Q_2}{Q_1}, x_0 \equiv {\tilde{x}_0}/l<1, \tilde{x}_0\) is the initial value of \(\tilde{x}\) and \(\varepsilon _0\) is permittivity. It is an example of a general nonlinear oscillatory system having a rational form for the restoring force which is not an odd function of displacement. The corresponding potential energy of this system is

$$\begin{aligned} \hat{{V}}(x)=\frac{\alpha ^{2}}{1-x}+\frac{1}{1+x} \end{aligned}$$
(2)

For \(\left| x\right| <1\), the system has one stable equilibrium point \(x_1 =\frac{1-\alpha }{1+\alpha }\). Hence, oscillation may occur about the stable equilibrium point \(x_1\) and it is either symmetric \((\alpha =1)\) or asymmetric \((\alpha <1)\) about this point.

It is the interest of this paper to construct analytical approximate periodic solution to Eq. (1). Although a method for constructing approximate solutions to general strong nonlinear oscillators has been proposed [6], for this present problem, the restoring force \(f(x)=\frac{\alpha ^{2}}{(1-x)^{2}}-\frac{1}{(1+x)^{2}}\) is a rational function of \(x\), and coefficients for the corresponding Fourier series are difficult to be determined. In this paper, the previous methods [4, 6, 7] are to be generalized to construct analytical approximations to oscillations of this system. The procedure yields rapid convergence with respect to exact solution and the results are valid for a wide range of oscillation amplitudes.

3 Solution methodology

A change of variable is first made so that the equilibrium point of the oscillatory system is transformed to the origin in the new coordinate system. Let

$$\begin{aligned} u=x-\frac{1-\alpha }{1+\alpha } \end{aligned}$$
(3)

Substituting Eq. (3) into Eq. (1) leads to

$$\begin{aligned} \ddot{u}\!+\!\frac{\alpha ^{2}}{(\alpha \beta -u)^{2}}-\frac{1}{(\beta +u)^{2}}\!=\!0,\quad u(0)=A, \dot{u}(0)=0.\qquad \end{aligned}$$
(4)

where a dot denotes differentiation with respect to \(t\), and \(\beta =\frac{2}{1+\alpha }, A=x_0 -\frac{1-\alpha }{1+\alpha }< \frac{2\alpha }{1+\alpha }\). The corresponding potential energy function for Eq. (4) is

$$\begin{aligned} V(u)=\frac{\alpha ^{2}}{\alpha \beta -u}+\frac{1}{\beta +u} \end{aligned}$$
(5)

and it reaches its minimum at \(u=0\). Thus, the system oscillates between asymmetric limits \(\left[ {-B,A}\right] \) where both \(-B\left( {B>0}\right) \) and \(A\) have the same energy level, i.e., \(V\left( {-B}\right) =V\left( A\right) \), and

$$\begin{aligned} B=\frac{\alpha \beta A}{(\alpha -1)A+\alpha \beta } \end{aligned}$$
(6)

Once \(u\) in Eq. (4) is solved, \(x\) can be determined by using Eq. (3). Hence, attention will be focused on Eq. (4) only.

Introducing a new independent variable \(\tau =\omega t\), Eq. (4) can be expressed as

$$\begin{aligned}&\Omega (\alpha \beta -u)^{2}(\beta +u)^{2}{u}^{\prime \prime }+4\alpha u+(\alpha ^{2}-1)u^{2}=0,\nonumber \\&\quad u(0)=A,\quad {u}^{\prime }(0)=0. \end{aligned}$$
(7)

where \(\Omega = \omega ^{2}\) and a prime denotes differentiation with respect to \(\tau \). The new independent variable is chosen in a way such that the solution of Eq. (7) is a periodic function of \(\tau \) of period \(2\pi \). The corresponding period of nonlinear oscillation is given by \(T={2\pi }/{\sqrt{\Omega }}\). Here, both periodic solution \(u(\tau )\) and period \(T\) depend on \(A\).

Similar to the previous approach [7, 14], two new nonlinear oscillating systems which oscillate between the symmetric bounds \([-H,H]\) are introduced

$$\begin{aligned} \Omega \mathrm{K}(u,\lambda ){u}^{\prime \prime }+\Phi (u,\lambda )=0,\quad u(0)=H,\quad {u}^{\prime }(0)=0 \end{aligned}$$
(8a)

where

$$\begin{aligned} \mathrm{K}(u,\lambda )&= \left\{ {\begin{array}{l} (\alpha \beta -\lambda u)^{2}(\beta +\lambda u)^{2}\;\quad \text{ if }\;u\ge 0, \\ (\alpha \beta +\lambda u)^{2}(\beta -\lambda u)^{2}\;\quad \text{ if }\;u<0, \\ \end{array}}\right. \end{aligned}$$
(8b)
$$\begin{aligned} \Phi (u,\lambda )&= \left\{ {\begin{array}{l} 4\alpha u+(\alpha ^{2}-1)\lambda u^{2}\;\quad \text{ if }\;u\ge 0, \\ 4\alpha u-(\alpha ^{2}-1)\lambda u^{2}\;\quad \text{ if }\;u<0. \\ \end{array}} \right. \end{aligned}$$
(8c)

and \(\lambda =\pm 1\). Here, \(H=A\) for \(\lambda =+1\), and \(H=B\) for \(\lambda =-1\), respectively are set. In order to construct an analytical approximation to Eq. (7), the two newly introduced odd systems in Eq. (8a) are studied by using the method in Wu et al. [4].

Following the single term HB approximation, let

$$\begin{aligned} u_1^\lambda (\tau )=H\cos \tau \end{aligned}$$
(9)

which satisfies the initial conditions in Eq. (8a). Substituting Eq. (9) into Eq. (8a) and setting the coefficient of the resulting \(\cos \tau \) to zero yield

$$\begin{aligned}&\Omega _1^\lambda \left( H\right) \nonumber \\&\quad =\frac{160\left( {3\pi \alpha +2\lambda H\alpha _2}\right) }{75\pi H^{4}-512\lambda H^{3}\beta \alpha _1 +90\pi H^{2}\beta ^{2}\alpha _3 +640\lambda H\alpha \beta ^{3} \alpha _1 +120\pi \alpha ^{2}\beta ^{4}} \nonumber \\ \end{aligned}$$
(10)

where \(\alpha _1 =\alpha -1, \alpha _2 = \alpha ^{2}-1, \alpha _3 =1-4\alpha + \alpha ^{2}\). Therefore, the first approximate periodic solution is

$$\begin{aligned} \begin{array}{rl} T_1^\lambda &{}={2\pi }/{\sqrt{\Omega _1^\lambda \left( H\right) }} \\ u_1^\lambda \left( \tau \right) &{}=H\cos \tau \\ \tau &{}=\sqrt{\Omega _1^\lambda \left( H\right) }\,t \\ \end{array} \end{aligned}$$
(11)

Using \(u_1^\lambda (\tau )\) and \(\Omega _1^\lambda (A)\) as initial approximations to the solution of Eq. (8a), Newton’s method and the HB method are jointly applied to solve Eq. (8a). The first step is the Newton procedure. The periodic solution and the square of frequency of Eq. (8a) can be expressed as

$$\begin{aligned} \begin{array}{rl} u^{\lambda }&{}=u_1^\lambda +\Delta u_1^\lambda \\ \Omega ^{\lambda }&{}=\Omega _1^\lambda +\Delta \Omega _1^\lambda \\ \end{array} \end{aligned}$$
(12)

Substituting Eq. (12) into Eq. (8a) and linearing with respect to the correction terms \(\Delta u_1^\lambda \) and \(\Delta \Omega _1^\lambda \) lead to

$$\begin{aligned} \begin{aligned}&[\mathrm{K}(u_1^\lambda ,\lambda )+\mathrm{K}_u (u_1^\lambda , \lambda ) \Delta u_1^\lambda ]\Omega _1^\lambda (u_1^\lambda )^{\prime \prime } +[\Omega _1^\lambda (\Delta u_1^\lambda )^{\prime \prime }\\&\quad +\Delta \Omega _1^\lambda (u_1^\lambda )^{\prime \prime }]\mathrm{K}(u_1^\lambda , \lambda )\!+\!\Phi (u_1^\lambda , \lambda )\!+\! \Phi _u (u_1^\lambda , \lambda )\Delta u_1^\lambda \!=\!0\\&\Delta u_1^\lambda (0)=0\\&(\Delta u_1^\lambda )^{\prime }(0)=0 \end{aligned} \end{aligned}$$
(13)

where subscript \(u\) denotes derivative with respect to \(u\). The resulting linearized equation in \(\Delta u_1^\lambda \) and \(\Delta \Omega _1^\lambda \) in Eq. (13) will be solved by the harmonic balance method. The approximate solution to Eq. (13) can be developed by setting \(\Delta u_1^\lambda \) as

$$\begin{aligned} \Delta u_1^\lambda (\tau )=x_1^\lambda (\cos \tau -\cos 3\tau ) \end{aligned}$$
(14)

which satisfies the initial condition in Eq. (13) at the outset. Substituting Eqs. (9–10) and (14) into Eq. (13), expanding the resulting expression in a trigonometric series and setting the coefficients of \(\cos \tau \) and \(\cos 3\tau \) to zeros, respectively, yield two linear equations in unknowns \(x_1^\lambda \) and \(\Delta \Omega _1^\lambda \). Solving these equations results in

$$\begin{aligned} \begin{aligned} \Delta \Omega _1^\lambda (H)&=L_1 (H,\lambda )\Gamma (H,\lambda ) \\ x_1^\lambda (H)&=14HL_2 (H,\lambda )\Gamma (H,\lambda ) \\ \end{aligned} \end{aligned}$$
(15)

where

$$\begin{aligned} \begin{array}{rl} \Gamma (H,\lambda )&{}=H{[896\lambda \alpha _2 -L_3 (H,\lambda ) \Omega _1^\lambda ]}/\left[ HL_3 (H, \lambda )L_1 (H,\lambda )\right. \\ &{}\qquad \left. -\,14L_2 (H,\lambda )L_4 (H,\lambda )\right] , \\ L_1 (H,\lambda )&{}\equiv 448(15\alpha \pi +16\lambda H\alpha _2) +(1575\pi H^{4}+840\pi H^{2}\alpha _3 \beta ^{2} \\ &{}\qquad -\,1680\pi \alpha ^{2}\beta ^{4}-8192\lambda H^{3}\alpha _1 \beta ) \Omega _1^\lambda , \\ L_2 (H,\lambda )&{}\equiv 75\pi H^{4}+90\pi H^{2}\alpha _3 \beta ^{2} +120\pi \alpha ^{2}\beta ^{4}\\ &{}\qquad -\,512\lambda H^{3}\alpha _1 \beta +640 \lambda H\alpha _1 \beta ,\\ L_3 (H,\lambda )&{}\equiv 525\pi H^{3}+420\pi H\alpha _3 \beta ^{2} -3072\lambda H^{2}\alpha _1 \beta \\ &{}\qquad +\,1792\lambda \alpha _1 \alpha \beta ^{3}, \\ L_4 (H,\lambda )&{}\equiv -320(21\pi \alpha +16\lambda H\alpha _2) +(5565\pi H^{4}\\ &{}\qquad +\,7980\pi H^{2}\alpha _3 \beta ^{2}+15120\pi \alpha ^{2}\beta ^{4}\\ &{}\qquad -\,40960\lambda H^{3}\alpha _1 \beta +65536\lambda H\alpha _1 \alpha \beta ^{3})\Omega _1^\lambda .\\ \end{array} \end{aligned}$$

Therefore, the second approximations to the period and periodic solution of the nonlinear oscillator are

$$\begin{aligned} \begin{array}{rl} T_2^\lambda \left( H\right) &{}=\sqrt{{2\pi }/{\Omega _2^\lambda \left( H\right) }} \\ \Omega _2^\lambda \left( H\right) &{}=\Omega _1^\lambda \left( H\right) + \Delta \Omega _1^\lambda \left( H\right) \\ u_2^\lambda \left( t\right) &{}=u_1^\lambda \left( t\right) + \Delta u_1^\lambda \left( t\right) =[H+x_1^\lambda (H)]\cos \tau \\ &{}\qquad -x_1^\lambda \left( H\right) \cos 3\tau \\ \tau &{}=\sqrt{\Omega _2^\lambda \left( H\right) }\;t \\ \end{array} \end{aligned}$$
(16)

Here, derivation of higher-order analytical approximation can be conducted in a similar procedure and it is omitted for simplicity. By setting \(\lambda =+1,H=A\) and \(\lambda =-1,H=B\), respectively, in Eqs. (11) and (16), the corresponding first and second analytical approximate periods and the periodic solutions \(T_n^{\mathrm{+1}} \left( A\right) , u_n^{\mathrm{+1}} \left( t\right) \) and \(T_n^{-1} \left( B\right) , u_n^{-1} \left( t\right) (n=1,2)\) to the two newly introduced odd oscillating systems in Eqs. (8a–c), respectively, can be obtained. From these analytical approximate solutions, the corresponding \(n\;\text{ th }\;(n=1,2)\) analytical approximate period and periodic solution for Eq. (4) can be constructed as follows [7]

$$\begin{aligned} T_n \left( A\right) =\frac{T_n^{\mathrm{+1}} \left( A\right) }{2}+ \frac{T_n^{-1} \left( B\right) }{2} \end{aligned}$$
(17)

and

$$\begin{aligned} u_n \left( t\right) = \left\{ {\begin{array}{l} u_n^{+1} \left( t\right) \qquad \qquad \qquad \qquad \qquad \qquad \text{ for }\;0\le t\le \frac{T_n^{\mathrm{+1}} \left( A\right) }{4}\\ u_n^{-1} \left( {t-\frac{T_n^{\mathrm{+1}} \left( A\right) }{4} +\frac{T_n^{-1} \left( B\right) }{4}}\right) \quad \text{ for }\; \frac{T_n^{\text{+1 }}\left( A\right) }{4}\le t\le \frac{T_n^{\mathrm{+1}} \left( A\right) }{4}+\frac{T_n^{-1} \left( B\right) }{2}\\ u_n^{\mathrm{+1}} \left( {t+\frac{T_n^{\mathrm{+1}} \left( A\right) }{2} -\frac{T_n^{-1} \left( B \right) }{2}}\right) \quad \text{ for }\; \frac{T_n^{\text{+1 }} \left( A\right) }{4} +\frac{T_n^{-1} \left( B\right) }{2}\le t\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \le \frac{T_n^{\mathrm{+1}} \left( A\right) }{2}+\frac{T_n^{-1} \left( B\right) }{2} \\ \end{array}}\right. \!\!\!\!\nonumber \\ \end{aligned}$$
(18)

4 Comparison of solutions

The Lindstedt–Poincaré (L–P) perturbation method [1, 3] is applied to Eq. (4). By expanding \(f(u)=\frac{\alpha ^{2}}{(\alpha \beta -u)^{2}}-\frac{1}{(\beta +u)^{2}}\) in Eq. (4) into a Taylor series about \(u=0\) and keeping the first three terms only, the resulting equation is

$$\begin{aligned} \begin{aligned} \ddot{u}+\alpha _1 u+\alpha _2 u^{2}+\alpha _3 u^{3}&=0\\ u(0)&=A\\ \dot{u}(0)&=0 \end{aligned} \end{aligned}$$
(19)

where \(\alpha _1 =\frac{2}{\beta ^{3}}\left( {1+\frac{1}{\alpha }}\right) , \alpha _2 =-\frac{3}{\beta ^{4}}\left( {1-\frac{1}{\alpha ^{2}}}\right) , \alpha _3 =\frac{4}{\beta ^{5}}\left( {1+\frac{1}{\alpha ^{3}}}\right) \).

Applying the L–P perturbation method [3] to Eq. (19) gives the second-order analytical approximate solution as follows

$$\begin{aligned} T_{\mathrm{LP}} (A)&= 2\pi \left[ {\sqrt{\alpha _1}+\frac{A^{2}(9\alpha _1 \alpha _3 -10\alpha _2^2)}{24\alpha _1^{3/2}}}\right] ^{-1} \nonumber \\ u_{\mathrm{LP}} (t)&= -\frac{\alpha _2 A^{2}}{2\alpha _1} +A\left( {1+\frac{\alpha _2 A}{3\alpha _1}}\right) \cos \frac{2\pi t}{T_{\mathrm{LP}} (A)}\\&\quad \quad +\,\frac{\alpha _2 A^{2}}{6\alpha _1}\cos \frac{4\pi t}{T_{\mathrm{LP}} (A)} \nonumber \end{aligned}$$
(20)

On the other hand, direct integration yields the exact period \(T_e \left( A\right) \) as

$$\begin{aligned} T_{\mathrm{e}} (A)&= \int _0^{\pi /2} {2\sqrt{A}\cos \left( {\frac{t}{2}}\right) }\nonumber \\&\times {\left[ {\frac{\alpha ^{2}}{(\alpha \beta -A)(\alpha \beta -A\cos t)}- \frac{1}{(\beta +A)(\beta +A\cos t)}}\right] ^{-1/2}} dt\nonumber \\&+ \int _0^{\pi /2} {2\sqrt{B}\cos \left( {\frac{t}{2}}\right) }\nonumber \\&\times {\left[ {\frac{1}{(\beta -B)(\beta -B\cos t)}-\frac{\alpha ^{2}}{(\alpha \beta +B)(\alpha \beta +B\cos t)}}\right] ^{-1/2}} dt \nonumber \\ \end{aligned}$$
(21)

where \(B\) is given by Eq. (6).

For \(\alpha =1/3, \alpha =1/2\) and \(\alpha =1\), the exact period \(T_e \left( A\right) \) obtained by integrating Eq. (21) and the ratios of the approximate periods \(T_1, T_2, T_{\mathrm{LP}}\) in Eqs. (17) and (20), respectively, to the exact period are listed in Table 1. Note that for \(\alpha \le 1\), the oscillation amplitude should be restricted to \(A<\frac{2\alpha }{1+\alpha }\). Table 1 indicates that the second approximate period \(T_2\) computed by using Eq. (17) is excellent for entire range of oscillation amplitudes. In generally, the first approximate period \(T_1\) computed by Eq. (17) is acceptable.

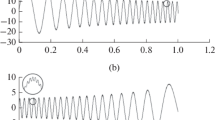
Table 1 Comparison of approximate periods with exact period
Full size table

For \(\alpha =1/3, A=0.2, A=0.41;\;\alpha =1/2, A=0.3, A=0.54\) and \(\alpha =1, A=0.4, A=0.7\), the exact periodic solution \(u_e \left( t\right) \) obtained by directly integrating Eq. (4) and the approximate analytical periodic solutions \(u_1 (t), u_2 \left( t\right) \) and \(u_{\mathrm{LP}} (t)\), computed by using Eqs. (18) and (20), respectively, are plotted in Figs. 2, 3, 4, 5, 6 and 7.

Fig. 2
figure 2

Comparison of approximate and exact periodic solutions for \(\alpha =1/3, A=0.2\)

Full size image
Fig. 3
figure 3

Comparison of approximate and exact periodic solutions for \(\alpha =1/3, A=0.41\)

Full size image
Fig. 4
figure 4

Comparison of approximate and exact periodic solutions for \(\alpha =1/2, A=0.3\)

Full size image
Fig. 5
figure 5

Comparison of approximate and exact periodic solutions for \(\alpha =1/2, A=0.54\)

Full size image
Fig. 6
figure 6

Comparison of approximate and exact periodic solutions for \(\alpha =1, A=0.4\)

Full size image
Fig. 7
figure 7

Comparison of approximate and exact periodic solutions for \(\alpha =1, A=0.7\)

Full size image

These figures show that the second approximate analytical periodic solutions as derived in Eq. (18) provides the most excellent solution with respect to the exact periodic solution for all oscillation amplitude within the range investigated.

5 Conclusions

In summary, based on the linearized HB method, analytical approximations to the period and periodic solution for oscillation of a charge placed on a finite conducting wire along the axis of two charged spheres have been derived and some accurate numerical solutions are presented. It is concluded that the second analytical approximation shows excellent agreement with numerical solutions obtained from the exact integral expressions. In addition, the approximate analytical solutions are valid for a wide range of geometrically permitted amplitude of oscillation. The approximate but accurate expressions enable further studies on the effects of various geometric and material parameters on large nonlinear oscillations of the system.