1 Introduction

Stochastic phenomena can arise in various physical and engineering processes [25] such as cosmic physics [10], communication systems [22], traffic control [11], etc. They can change the behavior of systems and lead them to instability. Thus, investigating the stability of stochastic differential equations (SDEs) and modeling such systems are of a great importance. In many engineering applications, they can be modeled as wide band random processes with certain properties or approximately as white Gaussian noise processes that excite dynamical systems. During the recent decades, techniques for analysis and control of stochastic differential equations have been developed. Some background regarding the theory of stochastic systems can be found in Meditch [17] and Ibrahim [9].

Similar to the theory of SDEs, time-delayed dynamical systems and delay-differential equations (DDEs) in particular, due to of the vast variety of applications in science and engineering they can be relevant to, have attracted increasing attention due to the instability and poor performance that a time delay can cause. There have been a number of studies focusing on stability analysis of stochastic delay differential equations (SDDEs) in the literature [2, 5, 8, 9, 11, 13–17, 19, 20, 22]. Stochastic stability of the equilibrium solution of SDDEs can be studied from different notions of stability including asymptotic stability [5, 15], exponential stability [16, 20], moment stability [14, 19], etc. Two methods that are used to prove stability in the framework of Lyapunov’s direct method include the Lyapunov–Krasovskii functional and the Lyapunov-Razmukhin function. Examples of stability analysis of SDDEs using the Lyapunov–Krasovskii functional can be found in Chen et al. [2] and He et al. [8], while examples of the Lyapunov-Razmukhin function are found in Mackey and Nechaeva [13].

Stability conditions for DDEs can be distinguished either in a delay-independent condition which is applicable to all values of delay, or in a delay-dependent condition which corresponds to some specific values of delay. The first type of stability condition is comprehensive but conservative, while the second type is more selective and less conservative. Some examples of investigations considering delay-dependent stability conditions of DDEs and SDDEs include but not limited to [5, 23, 24], while both delay-independent and delay-dependent conditions are found in Mackey and Nechaeva [13]. The stability criteria are often expressed in terms of a Linear Matrix Inequality (LMI) or Riccati equation in the literature. Less often than for DDEs, the stability region of SDDEs have been shown. Some examples of stability criteria in terms of LMIs include [6, 12, 20] and those in terms of Ricatti equations include [4, 26]. It is important to note that these LMI-based approaches cannot produce analytical stability criteria in terms of system parameters and thus stability regions must be obtained numerically.

Motivated by the analysis in Mackey and Nechaeva [13], in this paper analytical stability conditions of scalar linear and nonlinear stochastic systems with discrete time delay are obtained and analyzed in the parameter space by using Lyapunov-based approaches consisting of both Lyapunov–Razumikhin and Lyapunov–Krasovskii methods. To compare, we also obtain frequency-based and Lyapunov-based stability results for the deterministic linear time-delay system for which the frequency-based approach gives the well-known exact stability domain [18, 21]. We then compare both frequency and Lyapunov-based approaches for the deterministic time-delay system with the resulting stability conditions for linear and nonlinear stochastic time-delayed systems in which both additive and multiplicative stochastic Brownian motion excitations in the Ito form are considered. Choosing a suitable Lyapunov function and manipulating it correctly is crucial since it can directly determine the conservativeness of the resulting stability condition in the parameter space. We further show that using Lyapunov–Razumikhin and Lyapunov–Krasovskii methods may lead to the same stability domains. In addition, it is shown that the proposed approach yields a less conservative region in comparison with other LMI-based Lyapunov approaches in the literature.

For the linear stochastic time-delay system, we first represent the SDDE in Ito’s form which is more suitable for stability analysis. Then, in contrast to [13] in which the stochastic systems were distinguished by additive or multiplicative noise processes, this paper considers a more general form in which both additive and multiplicative noise processes are represented simultaneously. Based on the equation of the system in the Ito form, by applying the Lyapunov–Razumikhin functions and Lyapunov–Krasovskii functionals the asymptotic stability in the mean square sense is investigated and the least conservative stability region is derived and shown in the parameter space. Then, a numerical stability analysis for the SDDE is conducted using a stochastic extension of the semidiscretization method and criteria for first and second moment stability to compare with the Lyapunov-based results. Finaly, an extension to the case of nonlinear stochastic DDEs is shown by employing a Lipschitz condition to treat nonlinear functions of the current and delayed states.

2 Mean square stochastic stability and Lyapunov analysis

In this section, we discuss techniques that are necessary to study the stability of a class of scalar stochastic time-delay systems. Solutions for SDDEs are well-defined by using stochastic calculus, along with some concepts of time-delay systems, see e.g. [1].

The most general class of scalar autonomous SDDEs in the Ito form can be expressed in differential form as

$$\begin{aligned}&dx(t) = (ax(t) + bx(t - \tau ))dt + (\bar{\sigma }_{0} + \bar{\sigma }_{1} x(t) \nonumber \\&\qquad \qquad \,\, +\, \bar{\sigma }_{2} x(t - \tau ))d\beta (t),\quad {t \ge 0} \nonumber \\&x(\theta ) = \phi (\theta ),\quad {- \tau \le \theta \le 0,} \end{aligned}$$
(1)

where \( x(t) \in \mathcal R , \tau \) is the positive constant discrete time delay, \(x_t(\theta )=x(t+\theta )\in \mathcal C [-\tau ,0]\) for \(-\tau \le \theta \le 0\) is the infinite dimensional state residing in the Banach space of continuous functions on the interval of length \(\tau \), the parameters \( a,b,\bar{\sigma }_0,\bar{\sigma }_1\) and \(\bar{\sigma }_2 \) are deterministic constant scalars, and \( \beta (t) \in \mathcal R \) is a stochastic Brownian motion process for which it and the corresponding increment \(d\beta (t)\) satisfy [9]

$$\begin{aligned}&\beta (0) = 0,\quad E\{ \beta (t)\} = 0,\quad E\{ \beta ^{2} (t)\} = \sigma ^{2} t\quad \nonumber \\&E\{ d\beta (t)\} = 0,\quad E\{ d\beta ^{2} (t)\} = \sigma ^{2} dt, \end{aligned}$$
(2)

where \(\sigma ^2\) is the variance parameter of the Brownian motion process. The \(\phi (\theta )\) in Eq. (1) is the initial function on the interval \([-\tau ,0]\) and may be deterministic or stochastic. If \(d\beta (t)=0\) in Eq. (1), then it results in a scalar deterministic time-delayed system which can be expressed in the conventional form \(\dot{x}=ax(t)+bx(t-\tau )\). Note that the stochastic term involving \(\bar{\sigma }_0\) is a nonhomogeneous term representing additive stochastic excitation, while the terms involving \(\bar{\sigma }_1\) and \(\bar{\sigma }_2\) represent multiplicative stochastic excitation. It is worth mentioning that Eq. (1) is more general than that studied in Mackey and Nechaeva [13].

As with any stochastic differential equation, the differential form in Eq. (1) can also be interpreted in the equivalent integral form

$$\begin{aligned} x(t)&= x(0)+\int \limits _0^t {[ax(s)+bx(s-\tau )]ds} \nonumber \\&+ \int \limits _0^t{[\bar{\sigma }_0+\bar{\sigma }_1x(s)+\bar{\sigma }_2x(s-\tau )]d\beta (s)}. \end{aligned}$$
(3)

The terms in the second integral which involves \(\bar{\sigma }_1\) (and \(\bar{\sigma }_2\) if \(\phi (\theta )\) is stochastic ) result in the Ito stochastic integrals. More details on the stochastic calculus are given in Ibrahim [9].

We now define the type of stochastic stability that will be employed when discussing the stability properties of Eq. (1).

Definition 1

The trivial solution of Eq. (1) is stable in the mean square sense if for each \(\epsilon >0\), there exists \(\delta (\epsilon ,\phi )>0\) such that

$$\begin{aligned} {\mathop {{\sup E\{\phi ^2 (\theta )}\}}\limits _ {-\tau \le \theta \le 0}}<\delta \Rightarrow E\{x^2(t;\phi )\}< \epsilon \quad \text{ for }\,\text{ all }\quad t\ge 0. \end{aligned}$$
(4)

where \(E\{\}\) represents the expectation operator. The trivial solution is said to be asymptotically stable in the mean square if it is stable and

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } E\{x^2 (t;\phi )\}= 0 \quad t \ge 0. \end{aligned}$$
(5)

These two concepts can be changed to the uniform stability and uniform asymptotic stability in the mean square if the function \(\delta \) is independent of the initial function \(\phi (\theta )\), i.e., \(\delta (\epsilon )\).

Note that determining the stability of Eq. (1) by using Definition 1 is a challenging task. To analyze the stability of such systems in the time domain, Lyapunov-based methods such as Lyapunov–Razumikhin or Lyapunov–Krasovskii methods, which extend the standard Lyapunov stability method to DDEs, are employed. The following lemmas provide the sufficient conditions for the stability of Eq. (1).

Lemma 1

(Lyapunov–Razumikhin) Assume a scalar Lyapunov function candidate \(V(x(t))\) satisfies

$$\begin{aligned} u(|x(t)|)\le V(x(t)) \le v(|x(t)|), \end{aligned}$$
(6)

where \(|.|\) is the absolute value on \(\mathcal R \), and \(u, v\) belongs to the class \(\mathcal K \) functions defined as

$$\begin{aligned} \mathcal K :&= \left\{ \chi :\mathcal R \rightarrow \mathcal R |\,\chi \, a\,continuous\,and\,\right. \nonumber \\&\left. strictly\,increasing\,function,\, \chi (0)=0\right\} . \end{aligned}$$

If the differential of \(V(x(t))\) along the trajectories of Eq. (1), which can be calculated by using Ito’s differential rule as

$$\begin{aligned} dV(x(t))&= \left[ \frac{\partial V}{\partial x} (ax(t)+bx(t-\tau ))+\frac{1}{2}(\sigma _0+\sigma _1x(t) \right. \nonumber \\&+\left. \sigma _2x(t-\tau ))^2\frac{\partial ^2 V}{\partial x^2}\right] dt+\frac{\partial V}{\partial x}(\bar{\sigma }_0+\bar{\sigma }_1x(t) \nonumber \\&+\bar{\sigma }_2x(t-\tau ))d\beta (t), \end{aligned}$$
(7)

satisfies

$$\begin{aligned}&E\{dV(x(t))\}\le -E\{w(|x(t)|)\}dt, \end{aligned}$$
(8)

where \(\sigma _0=\sigma ^2\bar{\sigma }_0, \sigma _1=\sigma ^2\bar{\sigma }_1, \sigma _2=\sigma ^2\bar{\sigma }_2\), and \(w(s)>0\) for all \(s>0\), and if there exists a continuous and nondecreasing function \(p(s)>s\) for all \(s>0\) such that

$$\begin{aligned} E\{V(x_t(\theta ))\} \le E\{p(V(x(t)))\}\quad {\text{ for } \text{ all }} -\tau \le \theta \le 0, \end{aligned}$$

then, the trivial solution of Eq. (1) is asymptotically stable in the mean square and the Lyapunov–Razumikhin sense. In this paper, we will set \(w(s)=\gamma s^2\) for some \(\gamma >0\), and \(p(s)=\rho s\) for some \(\rho >0\).

Lemma 2

(Lyapunov–Krasovskii) The trivial solution of Eq. (1) is asymptotically stable in the mean square if there exists a functional candidate \(V(t,x_t(\theta ))\) such that

$$\begin{aligned} u(|x(t)|)\le V(t,x_t(\theta )) \le v(|x_t(\theta )|_s), \end{aligned}$$

where \(|x_t(\theta )|_s=sup\{|x_t(\theta )|\}\), and

$$\begin{aligned} {\textit{dE}}\{V(t,x_t(\theta )\}\le -E\{w(|x(t)|)\}dt. \end{aligned}$$
(9)

More details on the proof of these two lemmas can be found in [6]. It should be also noted that if the system is deterministic, then Ito’s differential rule changes to the normal differential rule, and as a result the second and last term in Eq. (7) vanish. The purpose of the following sections is to establish the analytical region of stability in the parameter space in which a scalar linear deterministic time-delay system is asymptotically stable, and the stochastic system is asymptotically stable in the mean square sense.

3 Scalar deterministic time-delay system

In this section, we briefly review the application of Lemmas 1 and 2 to scalar deterministic time-delay systems and compare the results to the well-known exact stability conditions obtained using frequency domain criteria. This will motivate the application of the Lemmas to the full SDDE in the following section and produce deterministic stability boundaries with which to compare the stochastic stability boundaries. By setting \(\bar{\sigma }_0=\bar{\sigma }_1=\bar{\sigma }_2=0\) in Eq. (1) and dividing by \(dt\), we obtain the equivalent system

$$\begin{aligned} \dot{x}=ax(t)+bx(t-\tau ),\quad x(\theta )=\phi (\theta ),\quad -\tau \le \theta \le 0, \nonumber \\ \end{aligned}$$
(10)

For fixed values of \(\tau \) we obtain the stability boundaries in two-dimensional parameter space, i.e., \(Oab\).

Fig. 1
figure 1

Stability region of \(\dot{x}(t)=ax(t)+bx(t-\tau )\) using the frequency domain approach for \(\tau =1(sec)\)

Full size image

The following frequency domain stability result for the deterministic case is well-known and has been discussed in several places, see e.g.[6, 18, 21].

Theorem 1

The trivial solution of Eq. (10) is delay-dependent asymptotically stable if

$$\begin{aligned} \tau < \tau _{max} = \frac{{ \cos ^{ - 1} ( - a/b)}}{{\sqrt{b^2 - a^2 } }},\quad a + b<0, \end{aligned}$$
(11)

where \(\tau _{max}\) is the maximum value of the time-delay that the system can tolerate without going to the unstable region, and is delay-independent asymptotically stable if

$$\begin{aligned} a < - \left| b \right| . \end{aligned}$$
(12)

Since the above result is well-established, we omit the proof here and refer the reader to [6, 18, 21] for further details.

The stability region of Eq. (10) for \(\tau _{max}=1\) (sec) is shown in Fig. 1. Delay-independent and delay-dependent stability regions resulting from Theorem 1 are plotted in Fig. 1a, b, respectively, and the combined stability region for the solution of Eq. (10) is shown in Fig. 1c, d. Note that the system without time-delay, i.e., \(b=0\), is unstable if \(a\) is positive, but the addition of the time-delay term makes the resulting system asymptotically stable for \(a<1\) and for some range of \(b\). This can be seen in Fig. 1d.

We now address the stability analysis of Eq. (10) using Lyapunov-based methods. The benefit of using Lyapunov-based methods is that the stability conditions can be determined without knowing the exact solution. The following theorem expresses a delay-independent sufficient condition for the stability of Eq. (10).

Theorem 2

The solution of the linear deterministic time-delay system of Eq. (10) is delay-independent uniformly asymptotically stable if Eq. (12) holds.

Proof

Define a Lyapunov–Razumikhin function candidate \( V (x(t)) \) on \( \mathcal R \) as

$$\begin{aligned} V(x(t))=\frac{1}{2}x^2(t). \end{aligned}$$
(13)

The time derivative of the above Lyapunov function along its trajectories can be written as

$$\begin{aligned} \dot{V}(x(t))=x\dot{x}. \end{aligned}$$
(14)

The solution of Eq. (10) becomes asymptotically stable when \(\dot{V}(x(t))<0\) and satisfies \( V(x_t(\theta ))<\rho V(x(t))\) for some \( \rho >1 \) and \(-\tau \le \theta \le 0\). As a result, by choosing \(\theta =-\tau \) we can obtain

$$\begin{aligned}&{x^2(t-\tau )}< \rho {x^2}(t) \nonumber \\&\quad \Rightarrow \left| {x(t-\tau )} \right| < \sqrt{\rho }\left| {x(t)} \right| . \end{aligned}$$
(15)

Substituting Eq. (10) into Eq. (14) and using the above inequality, yields

$$\begin{aligned} \dot{V}(x(t))&= x(t)(ax(t) + bx(t-\tau )) \nonumber \\&\le ax^2(t) + \left| b \right| \left| {x(t)} \right| \left| x(t-\tau )\right| \nonumber \\&\le ax^2(t) + \sqrt{\rho }\left| b \right| x^2(t)\nonumber \\&= (a + \sqrt{\rho }\left| b \right| ){x^2}(t) \le -\gamma x^2(t), \end{aligned}$$
(16)

where \(\gamma >0\). Therefore, if \( (a +\sqrt{\rho }\left| {b}\right| ) < -\gamma \), it guarantees the negativeness of Eq. (16) and implies that Eq. (10) is asymptotically stable. Note that, for some sufficiently small \( \gamma ,\epsilon > 0 \), by setting \( \rho = 1+\epsilon \) , the stability region in the \(a-b\) plane can be expanded to the maximum area, \(\left| b \right| < - a\), and the condition of the Theorem 2 can be achieved. The Lyapunov–Krasovskii method is another method of obtaining this condition.We will now show how we can obtain the same stability condition as in Lyapunov–Razumikhin method by using a suitable Lyapunov–Krasovskii functional.

Define a Lyapunov–Krasovskii functional candidate \(V (x_t(\theta ))\) on \(\mathcal C [-\tau ,0]\) as

$$\begin{aligned} V(x_t(\theta )) = \frac{1}{2}{x^2(t)} + \frac{1}{2}\left| b \right| \int \limits _{t - \tau }^t {{x^2}} (s)ds, \end{aligned}$$
(17)

which is once differentiable with respect to \( t \) and twice differentiable with respect to \( x \). The time derivative of the above Lyapunov functional along its trajectories can be written as

$$\begin{aligned} \dot{V}(x_t(\theta ))=x\dot{x}+\frac{1}{2}\left| b \right| x^2(t)-\frac{1}{2}\left| b \right| x^2(t-\tau ). \end{aligned}$$
(18)

Substituting Eq. (10) into Eq. (18), implies

$$\begin{aligned}&\dot{V}(x_t(\theta ))=ax^2(t)+bx(t)x(t-\tau )+\frac{1}{2}\left| b \right| x^2(t) \nonumber \\&\qquad \qquad \qquad -\frac{1}{2}\left| b \right| x^2(t-\tau ). \end{aligned}$$
(19)

The second and fourth terms on the right hand side of Eq. (19) can be rewritten as quadratic forms:

$$\begin{aligned}&bx(t)x(t - \tau ) - \frac{1}{2}\left| b \right| {x^2}(t - \tau ) \nonumber \\&\quad = -\frac{1}{2}\left| b \right| {(sgn(b)x(t) - x(t - \tau ))^2}+\,\frac{1}{2}\left| b \right| {x^2}(t), \end{aligned}$$
(20)

where \(sgn(.)\) represents the sign function. Substituting Eq. (20) into Eq. (19) yields

$$\begin{aligned}&\dot{V}(x_t(\theta ))=(a\!+\!\left| b \right| )x^2(t)\!-\! \frac{1}{2}\left| b \right| {(sgn(b)x(t) \!-\! x(t \!-\! \tau ))^2} \nonumber \\&\le (a + \left| b \right| ){x^2}(t). \end{aligned}$$
(21)

The right hand side of Eq. (21) should be negative so we can write

$$\begin{aligned} \dot{V}(x_t(\theta ))\le (a + \left| b \right| ){x^2}(t)\le -\gamma x^2(t), \end{aligned}$$
(22)

where \(\gamma >0\). If \( a + \left| b \right| <-\gamma \), then the condition of Lemma 2 is satisfied, and the maximum bound of the stability region is obtained by setting \(\gamma =0\). Consequently the delay-independent stability condition is obtained.\(\square \)

In the last theorem, we developed a condition for delay-independent stability. We can now turn our attention to the delay-dependent stability criteria. To do this, the Newton-Leibniz formula

$$\begin{aligned} x(t) - x(t - \tau ) = \int \limits _{t - \tau }^t {\dot{x}(s)ds}, \end{aligned}$$
(23)

is used to transform Eq. (10) into the model

$$\begin{aligned} \dot{x}(t) = (a + b)x(t) - b\int \limits _{t - \tau }^t {\dot{x}(s)ds}. \end{aligned}$$
(24)

Substituting Eq. (10) into Eq. (24) yields

$$\begin{aligned} \dot{x}(t)&= (a + b)x(t) - b\int \limits _{t - \tau } ^t {ax(s)ds} - b\int \limits _{t - \tau }^t {bx(s - \tau )ds} \nonumber \\&= (a + b)x(t) - ab\int \limits _{t - \tau }^t {x(s)ds} - {b^2}\int \limits _{t - 2\tau }^{t - \tau } {x(s)ds}. \nonumber \\ \end{aligned}$$
(25)

The following theorem gives a delay-dependent sufficient condition for the stability region of Eq. (10) in the parameter space.

Theorem 3

The solution of the linear deterministic time-delay system of Eq. (10) is delay-dependent uniformly asymptotically stable if

$$\begin{aligned} \tau < {\tau _{_{max}}} \equiv \frac{{ - (a + b)}}{{ \left| {ab} \right| + {b^2}}},\quad a + b < 0. \end{aligned}$$
(26)

Proof

Define the Lyapunov–Razumikhin function candidate \( V (x(t)) \) on \( \mathcal R \) as in Eq. (13) The time derivative of the above Lyapunov function along its trajectories can be written as \(\dot{V}(x(t))=x\dot{x}\), whenever \( x_t(\theta ) \) satisfies \( V(x_t(\theta ))<\rho V(x(t))\) for some \( \rho >1 \) and \(-\tau \le \theta \le 0\). This implies that \(|x_t(\theta )|<\sqrt{\rho }|x(t)|\). Integrating both sides with respect to \(\theta \), over intervals \([-\tau ,0]\) and \([-2\tau ,-\tau ]\) and defining the variable \(s=t+\theta \) implies

$$\begin{aligned} \int \limits _{t - \tau }^t {\left| {x(s)} \right| ds }&= \int \limits _{-\tau }^0 {\left| {x_t(\theta )} \right| d \theta }< \sqrt{\rho }\int \limits _{-\tau }^0 {\left| {x(t)} \right| d\theta } \nonumber \\&= \sqrt{\rho }\tau \left| x(t) \right| \nonumber \\ \int \limits _{t - 2\tau }^{t - \tau } {\left| {x(s)} \right| ds}&= \int \limits _{- 2\tau }^{- \tau } {\left| {x_t(\theta )} \right| d \theta } <\sqrt{\rho }\int \limits _{- 2\tau }^{- \tau } {\left| {x(t)} \right| d\theta }\nonumber \\&= \sqrt{\rho }\tau \left| x(t) \right| . \end{aligned}$$
(27)

On the other hand substituting Eq. (25) into \(\dot{V}(x(t))\) yields

$$\begin{aligned} \dot{V}(x(t))&\!=\!x(t)\left[ \!(a \!+\! b)x(t) \!-\!ab \int \limits _{t \!-\! \tau }^t {{x(s)} ds }\!-\!{b^2}\int \limits _{t \!-\! 2\tau } ^{t \!-\! \tau } {{x(s)}ds}\!\right] \nonumber \\&\le (a + b)x^2(t) + \left| {x(t)} \right| \left| {ab} \right| \int \limits _{t - \tau }^t {\left| {x(s)} \right| ds }\nonumber \\&+{b^2}\left| x(t)\right| \int \limits _{t - 2\tau }^{t - \tau } {\left| {x(s)}\right| ds}\nonumber \\&\le (a + b + \sqrt{\rho }\tau \left| {ab} \right| + \sqrt{\rho }\tau {b^2}){x^2}(t) \nonumber \\&\le -\gamma x^2(t). \end{aligned}$$
(28)

which implies that the region of asymptotic stability of Eq. (10) in the parameter space is \((a + b + \sqrt{\rho }\tau \left| {ab} \right| + \sqrt{\rho }\tau {b^2})<-\gamma \). For some sufficiently small \(\gamma , \epsilon > 0 , \rho = 1+\epsilon \), we can derive the maximum region as in Eq. (26).

We can also derive this condition based on the Lyapunov–Krasovskii method. The system model (10) still needs be represented in a form which is appropriate to derive the stability condition in terms of the delay \( \tau \). For this purpose, by using Eq. (23), Eq. (10) can be represented as

$$\begin{aligned} \frac{d}{{dt}}(x+ b\int \limits _{t - \tau }^t {x(s)ds} ) = (a+b)x(t). \end{aligned}$$
(29)

The advantages of expressing the system in this form is that there are no delay terms on the right hand side of Eq. (29). Define a Lyapunov–Krasovskii functional candidate \( V (x_t(\theta )) \) on \(\mathcal C [-\tau ,0]\) as

$$\begin{aligned} V(x_t(\theta ))&= {(x(t) + b\int \limits _{t - \tau }^t {x(s)ds} )^2} \nonumber \\&+\left| (a + b) b \right| \int \limits _{t - \tau }^t ( \int \limits _\eta ^t {x^2(s)ds)d\eta }. \end{aligned}$$
(30)

Taking the time derivative of the above Lyapunov–Krasovskii functional along the solutions of Eq. (29) yields

$$\begin{aligned} \dot{V}(x_t(\theta ))&= 2[(x(t) + b\int \limits _{t - \tau }^t {x(s)ds} ](a + b)x(t) \nonumber \\&+\left| {(a + b)b} \right| \int \limits _{t - \tau }^t {\left[ x^2(t)-{x^2}(\eta )\right] } d\eta , \end{aligned}$$

or after some simplification

$$\begin{aligned} \dot{V}(x_t(\theta ))&= 2{x^2}(t)(a + b)+2(a + b)b\int \limits _{t - \tau }^t {{x}(t)x(s )ds} \nonumber \\&-\left| {(a + b)b} \right| \int \limits _{t - \tau }^t {{x^2}(\eta )} d\eta +\tau \left| {(a + b)b} \right| {x^2}(t). \nonumber \\ \end{aligned}$$
(31)

Now by using Holer’s inequality for integrals [7]

$$\begin{aligned}&\int \limits _{t-\tau }^{t}{x(t)x(s)ds}\le \left( \int \limits _{t-\tau }^{t}{(x(t))^2ds}\right) ^{\frac{1}{2}}\left( \int \limits _{t-\tau }^{t}{(x(s))^2ds}\right) ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(32)

and the fact that scalars \(u,v\) always satisfy \(2uv \le {u^2} + {v^2}\), the second term on the right hand side of Eq. (31) can be expressed as

$$\begin{aligned}&2(a + b)b\int \limits _{t - \tau }^t {x(t)x(s)ds} \le 2\left| {(a + b)b} \right| \nonumber \\&{\sqrt{\int \limits _{t - \tau }^t {{x^2}(t)ds}}}{\sqrt{\int \limits _{t - \tau }^t {{x^2}(s )ds }}} \nonumber \\&\le \tau \left| {(a + b)b} \right| {x^2}(t) + \left| {(a + b)b} \right| \int \limits _{t - \tau }^t {{x^2(s)}ds }. \end{aligned}$$
(33)

Substituting Eq. (33) into Eq. (31) yields

$$\begin{aligned} \dot{V}(x_t(\theta ))&\le 2{x^2}(t)(a + b) + \tau \left| {(a + b)b} \right| {x^2}(t) \nonumber \\&+\left| {(a + b)b} \right| \int \limits _{t - \tau }^t {{x^2}(s )ds }- \left| {(a + b)b} \right| \int \limits _{t - \tau }^t {{x^2}(s )} ds\nonumber \\&+ \tau \left| {(a + b)b} \right| {x^2}(t)\le -\gamma x^2(t), \end{aligned}$$
(34)
Fig. 2
figure 2

Stability region of \(\dot{x}(t)=ax(t)+bx(t-\tau )\) using the Lyapunov approach for \(\tau =1(sec)\) (gray region) in comparison with the stability domain of the frequency domain approach (yellow region) and the stability domain of Eq. (38) for \(d=6.6667\) (red dashed boundary in (a). (Color figure online)

Full size image

and thus

$$\begin{aligned} \dot{V}(x_t(\theta ))&\le 2{x^2}(t)(a + b) + 2\tau \left| {(a + b)b} \right| x^2(t) \nonumber \\&= 2{x^2}(t)(a + b + \tau \left| {ab+ b^2} \right| )\nonumber \\&\le 2{x^2}(t)(a + b + \tau ( \left| {ab} \right| +b^2))\le - \gamma x^2(t), \nonumber \\ \end{aligned}$$
(35)

if \( a + b + \tau ( \left| {ab} \right| +b^2)<-\gamma \). This implies the condition of Theorem 3, if \(\gamma \) goes to zero to obtain the maximum stability region. Note that in the stability criterion of Theorem 3, the value of the time-delay is always positive so the extra condition \(a+b<0\) needs to be added to guarantee the positiveness of \(\tau \).\(\square \)

The resulting stability conditions presented in Theorems 2 and 3 in the parameter space by using either the Lyapunov–Razumikhin method or the Lyapunov–Krasovskii method for the corresponding delay-independent case and the delay-dependent case are the same. These stability conditions are shown in Fig. 2. The delay-independent and the delay-dependent regions are shown in Fig. 2a, b, respectively, and Fig. 2c, d present the whole resulting stability region of Eq. (10) by using the Lyapunov approach. The yellow regions with dashed boundaries in all parts of Fig. 2 represent the stability conditions of Eq. (10) by using the frequency domain approach.

Remark 1

A comparison between the stability region derived by using the frequency domain approach and the Lyapunov based methods via the time-domain approach for different values of the time-delay parameter \(\tau \) are illustrated in Fig. 3. The frequency domain approach gives the precise stability domain since the exact imaginary roots of the corresponding characteristic equation are considered as the maximum bound of the stability region, while the time domain analysis provides a conservative estimate of the stability region. This is due to the fact that Lyapunov methods are based on sufficient conditions so they have a degree of conservativeness. It can be also seen from this figure that for small values of \(\tau \), the Lyapunov analysis gives a more conservative region than the frequency domain approach. However, by increasing the value of the time-delay, the stability area of the resulting Lyapunov analysis moves toward the frequency domain stability area and finally overlays with that quite well.

Fig. 3
figure 3

The entire stability region of \(\dot{x}(t)=ax(t)+bx(t-\tau )\) using the Lyapunov approach (gray region) and frequency domain approach (yellow region) for nine different values of the delay. (Color figure online)

Full size image

Remark 2

It should be noted that choosing different Lyapunov functions or manipulating them differently than in Theorems 2 and 3 may lead to more conservative regions of stability. For example in Gu et al. [6], the delay-independent stability condition of Eq. (10) obtained by using the following Lyapunov–Krasovskii functional

$$\begin{aligned} V(x_t(\theta )) =\frac{1}{2}p{x^2(t)}+\frac{1}{2}q \int \limits _{t - \tau }^t {{x^2}} (s)ds, \end{aligned}$$
(36)

for unknown positive scalars \(p\) and \(q\) has been derived in terms of the matrix inequality \(X(t)^TAX(t)<0\) where \(X(t)=[x(t)~x(t-\tau )]^T\) and

$$\begin{aligned} A=\left[ {\begin{array}{*{20}{c}} {2pa + q} &{}\quad {p{b}} \\ {bp} &{}\quad { - q} \\ \end{array}} \right] < 0. \end{aligned}$$
(37)

Solving the above yields

$$\begin{aligned} a<\frac{-pb^2}{2q}-\frac{q}{2p}=\frac{-b^2}{2d}-\frac{d}{2}, \end{aligned}$$
(38)

where \(d=\frac{q}{p}\). As is seen in Eq. (17), \(V(x_t(\theta ))\) can be expressed in terms of the parameter \(d\) where the maximum area of delay-independent asymptotic stability for Eq. (10), which is \(a<-|b|\), will be obtained when \(d=|b|\). It can be seen that choosing different values of \(p\) and \(q\) lead to more conservative regions of stability. For example, for finding the maximum area of delay-independent asymptotic stability of Eq. (10) numerically for constant \(d\), we can define an optimization problem for the interval \(-10\le a\le 0\) in the parameter space \(Oab\) by choosing a cost function as a summation of the area under the curves (38) and (12). Solving this optimization problem, we can obtain the optimal constant \(d=6.6667\). The region of delay-independent asymptotic stability of Eq. (10) for this Lyapunov–Krasovskii functional is plotted in Fig. 2a with the dashed boundary. As we can see in this figure, this region is more conservative than the one obtained by choosing \(d=|b|\).

4 Scalar stochastic time-delay systems

In the following, we will develop the stability criteria for Eq. (1) for both delay-independent and delay dependent cases which is more general than that studied in [13]. Note that all lemmas and definitions in the previous sections can be applied to the corresponding linear stochastic time-delay system governed by Eq. (1).

4.1 Delay-independent stability criteria

In this subsection, we will address the delay-independent stability criterion of Eq. (1), and derive a sufficient condition for the stochastic stability of the system by using Lyapunov-based methods in the time domain. It should be noted that the stability conditions are expressed in terms of system parameters, and is independent of the delay value. The following theorem establishes the mean square stability criterion for Eq. (1).

Theorem 4

Letting \(\lambda ={\mathop {\sup E\{| {\phi (\theta )}|\}}\limits _{-\tau \le \theta \le 0}}\), the solution of the linear stochastic time-delay system of Eq. (1) is delay-independent uniformly asymptotically stable in the mean square if

$$\begin{aligned} a < - \left| b \right| -\frac{1}{2}(\sigma _1+ \sigma _2)^2- \frac{2{|\sigma _0|(|\sigma _1|+| \sigma _2|)}\lambda +{\sigma _0^2}}{{2\lambda ^2}}. \nonumber \\ \end{aligned}$$
(39)

Proof

We first use the the Lyapunov–Razumikhin based method to give a proof for the theorem. The Lyapunov–Razumikhin function candidate \( V (x(t)) \) on \( \mathcal R \) can be defined as \(V(x(t))=\frac{1}{2}x^2(t)\). Using Eq. (7), the time derivative of the above Lyapunov function along its trajectories in Ito’s sense can be written in the form

$$\begin{aligned} dV(x(t))&= \left[ x(t)(ax(t) + bx(t - \tau )) \right. \nonumber \\&+\,\left. \frac{1}{2}(\sigma _0+\sigma _1x(t)+\sigma _2x(t-\tau ))^2\right] dt \nonumber \\&+\,x(t)\left[ \bar{\sigma }_0+\bar{\sigma }_1x(t)+\bar{\sigma }_2x(t-\tau )\right] d\beta (t). \end{aligned}$$
(40)

Inserting Eq. (15) into Eq. (40) and taking the expected value from the resulting equation yields

$$\begin{aligned} {\textit{dE}}\{V(x(t))\}&\le [(a+\sqrt{\rho }\left| b \right| +\frac{1}{2}\sigma _1^2+\frac{1}{2}\rho \sigma _2^2\nonumber \\&+\sqrt{\rho }|\sigma _1||\sigma _2|)E\{x^2 (t)\}+(|\sigma _0||\sigma _1|\nonumber \\&+\sqrt{\rho }|\sigma _0|| \sigma _2|)E\{|x(t)|\}+\frac{1}{2}\sigma _0^2]dt. \end{aligned}$$
(41)

Note that based on Lemma 1, we can conclude that Eq. (1) is asymptotically stable in the mean square if \({\textit{dE}}\{V(x(t)\})\) is strictly decreasing and satisfies

$$\begin{aligned} {\textit{dE}}\{V(x(t)\})&\le -E\{w(|x(t)|)\}dt \nonumber \\&\le [AE\{x^2 (t)\}+{\textit{BE}}\{|x(t)|\}+ \frac{1}{2} \sigma _0^2]dt \nonumber \\&\le -\gamma E\{x^2(t)\}dt\nonumber \\&\Rightarrow [(A+\gamma )E\{x^2 (t)\}+{\textit{BE}}\{|x(t)|\}\nonumber \\&+\frac{1}{2}\sigma _0^2]dt \le 0, \end{aligned}$$
(42)

where \(A=(a+\sqrt{\rho }\left| b \right| +\frac{1}{2}\sigma _1^2+\frac{1}{2}\rho \sigma _2^2+\sqrt{\rho }|\sigma _1||\sigma _2|)\), and \(B=|\sigma _0||\sigma _1|+\sqrt{\rho }|\sigma _0||\sigma _2|\). Therefore, the asymptotic stability of the system in the mean square is fulfilled if we rewrite Eq. (42) as

$$\begin{aligned} 0 \le E\{x^2(t)\} \le - \frac{{\frac{1}{2}\sigma _0 ^2+{\textit{BE}}\{|x(t)|\} }}{A+\gamma }, \end{aligned}$$
(43)

assuming that \(A +\gamma <0\) or equivalently \( a < -\sqrt{\rho }\left| b\right| -\frac{1}{2}\sigma ^2_1-\frac{1}{2}\rho \sigma _2^2-\sqrt{\rho }|\sigma _1||\sigma _2|-\gamma \). It is also important to realize that the stability criterion derived in Eq. (43) implies that the trivial solution of Eq. (1) is asymptotically stable in the mean square in the set \(G=\{x\in \mathcal R |\,\ E\{x^2(t)\} \le - \frac{{\frac{1}{2}\sigma _0 ^2+BE\{|x(t)|\} }}{A+\gamma },A+\gamma <0\}\), which depends on \(x(t)\). For the purpose of the stability analysis in the parameter space, we need to define a set that is independent of the value of \(E\{x^2(t)\}\). Hence, if the global maximum or upper bound of \( E\{V(x(t))\}=\frac{1}{2}E\{x^2(t)\}\) satisfies Eq. (43), all the other values of \( E\{V(x(t))\}=\frac{1}{2}E\{x^2(t)\},~0\le t\le \infty \) can still satisfy this inequality. Fortunately, we found that \(dE\{V(x(t))\}\) is a strictly decreasing function under the condition of Eq. (42), so that the upper bound of \(E\{x^2(t)\}\) can be easily derived as follows:

$$\begin{aligned}&{\textit{dE}}\{ V(x(t))\}\le E\{(-w|x(t)|)\}, \quad t\in [0,\infty ]\nonumber \\&\quad \Rightarrow E\{V(x(t))\}-E\{V(0)\}\le -\gamma E\{x^2(t)\}\nonumber \\&\quad \Rightarrow E\{x^2(t)\}-E\{x^2(0)\}\le -2\gamma E\{x^2(t)\}\nonumber \\&\quad \Rightarrow E\{x^2(t)\} \le \frac{1}{1+2\gamma } E\{x^2(0)\}. \end{aligned}$$
(44)

On the other hand, the expected value of the initial function \(\phi (\theta )\) is also known, and its upper bound can be defined as \(\sup E\{|\phi (\theta )|\}\). Thus we can show that \( E\{x^2(0)\}\le \sup E\{{\phi ^2 (\theta )}\}\). Therefore, Eq. (44) can be expressed as

$$\begin{aligned} E\{x^2(t)\}\le \frac{1}{1+2\gamma }\mathop {\sup E\{{\phi ^2(\theta )}\}}\limits _{-\tau \le \theta \le 0} \quad t\in [0,\infty ], \end{aligned}$$
(45)

or

$$\begin{aligned} E\{|x(t)|\}\le \sqrt{\frac{1}{1+2\gamma }}\mathop {\sup E\{| {\phi (\theta )} |\}}\limits _{-\tau \le \theta \le 0} \quad t\in [0,\infty ]. \end{aligned}$$
(46)

This inequality can guarantee the exponential stability of Eq. (1). According to the above discussion, we can substitute Eqs. (45–46) into the condition (43) to get the following stability condition.

$$\begin{aligned}&a \le - \sqrt{\rho }\left| b \right| -\frac{1}{2}\sigma _1^2-\frac{1}{2}\rho \sigma _2^2 -\sqrt{\rho }|\sigma _1||\sigma _2|-\gamma \nonumber \\&\quad -\frac{\frac{2| \sigma _0|(|\sigma _1|+\sqrt{\rho }|\sigma _2|)}{\sqrt{1+2\gamma }} \lambda +\sigma _0^2}{\frac{2\lambda ^2}{1+2\gamma }}, \end{aligned}$$
(47)

where \(\lambda ={\mathop {\sup E\{| {\phi (\theta )}|\}}\limits _{-\tau \le \theta \le 0}}\). This condition gives a region in the parameter space where Eq. (1) is asymptotically stable in the mean square sense. We wish to determine the maximum bound of this region to get a less conservative criterion. This maximum bound is the curve that divides stable and unstable regions. The system is only stable in the mean square in that area, and can be obtained according to the definition of \(\gamma \) and \(\rho \) in Lemma 1, when \(\gamma \rightarrow 0\) and \(\rho \rightarrow 1\) as

$$\begin{aligned}&\lim _{{\gamma \rightarrow 0},{\rho \rightarrow 1}}\left\{ a = - \sqrt{\rho }\left| b \right| -\frac{1}{2}\sigma _1^2-\frac{1}{2}\sqrt{\rho }\sigma _2^2- \sqrt{\rho }|\sigma _1||\sigma _2|\right. \nonumber \\&\qquad \qquad \quad -\gamma - \left. \frac{\frac{2|\sigma _0|(| \sigma _1|+\sqrt{\rho }|\sigma _2|)}{\sqrt{1+2\gamma }}\lambda + \sigma _0^2}{\frac{2\lambda ^2}{1+2\gamma }}\right\} ,\nonumber \\ \Rightarrow a&= - \left| b \right| -\frac{1}{2}(\sigma _1+ \sigma _2)^2- \frac{2{|\sigma _0|(|\sigma _1|+|\sigma _2|)}\lambda +{ \sigma _0^2}}{{2\lambda ^2}}. \nonumber \\ \end{aligned}$$
(48)

Therefore for the asymptotic stability in the parameter space, we can conclude that Eq. (39) holds.

For the Lyapunov–Krasovskii method, we choose to simplify Eq. (1) by removing the multiplicative stochastic excitation \(\bar{\sigma }_2x(t-\tau )d\beta (t)\) by setting \(\bar{\sigma }_2=0\) in Eq. (1). The Lyapunov–Krasovskii functional candidate \( V (x_t(\theta )) \) on \(\mathcal C [-\tau ,0]\) can be chosen as in Eq. (17). The differential of this scalar Lyapunov–Krasovskii functional along the trajectories of Eq. (1) obtained by using the Ito’s differential rule from Eq. (7) is as follows:

$$\begin{aligned} dV(x_t(\theta ))&= \{x(t)(ax(t)+bx(t-\tau ))+ \frac{1}{2}\left| b \right| x^2(t) \nonumber \\&-\,\frac{1}{2}\left| b \right| x^2(t-\tau )+\frac{1}{2}(\sigma _0+\sigma _1x(t))^2\}dt\nonumber \\&+x(t)(\sigma _0+ \sigma _1x(t)) \beta (t). \nonumber \\ \end{aligned}$$
(49)

The terms on the right hand side of Eq. (49) which consist of delay can be written as quadratic forms

$$\begin{aligned}&bx(t)x(t - \tau )dt -\frac{1}{2}\left| b \right| {x^2}(t - \tau )dt \nonumber \\&= -\frac{1}{2}\left| b \right| {(sgn(b)x(t) -x(t - \tau ))^2}dt+\frac{1}{2}\left| b \right| {x^2}(t)dt. \nonumber \\ \end{aligned}$$
(50)

Substituting Eq. (50) into Eq. (49) and taking expected value of the resulting equation yields

$$\begin{aligned}&{\textit{dE}}\{V(x_t(\theta ))\}=\left[ (a+\left| b \right| +\frac{1}{2}\sigma _1^2)E\{x^2(t)\}\right. \nonumber \\&\quad -\frac{1}{2}\left. \left| b \right| {\left( sgn(b)E \{x(t)\}-E\{x(t - \tau )\}\right) ^2}\right. \nonumber \\&\quad +\left. \sigma _0\sigma _1E\{x(t)\}+ \frac{1}{2}\sigma _0^2\right] dt. \end{aligned}$$
(51)

We can observe that in Eq. (51), the term \(-\left| b \right| (sgn(b)E\{x(t)\} - E\{x(t - \tau )\})^2\) is already negative, therefore we only need to consider the other remaining terms to fulfill Lemma 2, i.e., \({\textit{dE}}\{V(x_t(\theta ))\}<E\{-w|x(t)|\}\). Equation (51) implies

$$\begin{aligned} {\textit{dE}}\{V(x_t(\theta ))\}&\le \left[ (a+\left| b \right| +\frac{1}{2}\sigma _1^2)E\{x^2(t)\}\right. \nonumber \\&\left. +\sigma _0 \sigma _1E\{x(t)\}+\frac{1}{2}\sigma _0^2\right] \nonumber \\&\le -\gamma E\{x^2(t)\}. \end{aligned}$$
(52)

Therefore the asymptotic stability condition of the system is given as

$$\begin{aligned} 0 \le E\{x^2(t)\} \le \left| \frac{{-\frac{1}{2} \sigma _0 ^2-\sigma _0\sigma _1E\{x(t)\} }}{a+|b|+ \frac{1}{2}\sigma _1^2+\gamma }\right| . \end{aligned}$$
(53)

Alternatively, by using the absolute value, we can write

$$\begin{aligned}&0 \le E\{x^2(t)\} \le - \frac{{\frac{1}{2}\sigma _0 ^2+|\sigma _0\sigma _1|E\{|x(t)|\} }}{a+|b|+\frac{1}{2}\sigma _1^2+\gamma },\nonumber \\&a < -|b|-\frac{1}{2}\sigma _1^2-\gamma . \end{aligned}$$
(54)

Following the similar strategy as in the previous part of the proof, (i.e., the Lyapunov–Razumikhin based method), we can show that Eq. (39) holds for \(\sigma _2=0\).\(\square \)

Note that the case of having additive noise in a linear stochastic time-delay system corresponds to (1) with \(\sigma _1=\sigma _2=0\). In this case the stochastic stability from Theorem 4 is defined as \(a\le -|b|-\frac{\sigma _0^2}{2\lambda ^2}\). Furthermore, setting \(\sigma _2=\sigma _0=0\) leads to the stochastic time-delay system with multiplicative noise whose stability region can be defined as \( a \le - \left| b \right| -\frac{1}{2}\sigma _1^2\). Both of these results, which are less general than Eq. (39), were obtained in Mackey and Nechaeva [13].

4.2 Delay-dependent stability criteria

Unlike the delay-independent stability criteria, delay-dependent conditions depend on the magnitude of the delay. In this section, we will investigate sufficient conditions for the delay-dependent stability of the system described by Eq. (1) in the time domain. Before proceeding, however, we need to modify our system equation to make it suitable for the stability analysis. By using the Newton–Leibniz formula in Eq. (23), the system model in Eq. (1) can be transformed to the following form

$$\begin{aligned} dx(t)&= \left[ ax(t)+b\left( x(t)-\int \limits _{t - \tau }^t dx(s)\right) \right] dt \nonumber \\&+(\bar{\sigma }_0+\bar{\sigma }_1x(t)+\bar{\sigma }_2x(t-\tau ))d\beta (t) \nonumber \\&= \left[ (a+b)x(t)-ab\int \limits _{t - \tau }^t {x(s)} ds -b^2\int \limits _{t - 2\tau }^{t-\tau } {x(s)} ds\right. \nonumber \\&\left. -b\int \limits _{t - \tau }^t {(\bar{\sigma }_0+\bar{\sigma }_1x(s)+ \bar{\sigma }_2x(s-\tau ))d\beta (s)}\right] dt \nonumber \\&+(\bar{\sigma }_0+\bar{\sigma }_1x(t)+\bar{\sigma }_2x(t-\tau )) d\beta (t),\quad \nonumber \\ x(\theta )&= \phi (\theta ) - \tau \le \theta \le 0. \end{aligned}$$
(55)

Note that we used the fact that \(\int \limits _{t-\tau }^{t}x(s-\tau )ds=\int \limits _{t-2\tau }^{t-\tau }x(s)ds\). The following theorem represents the delay-dependent stability condition for Eq. (1).

Theorem 5

Setting \(\lambda ={\mathop {\sup E\{| {\phi (\theta )}|\}}\limits _{-\tau \le \theta \le 0}}\), the solution of the linear stochastic time-delay system of Eq. (1) is delay-dependent uniformly asymptotically stable in the mean square if

$$\begin{aligned}&\tau \le \tau _{max}\equiv \frac{-1}{|ab|+b^2} \nonumber \\&\quad \left\{ a+b+\frac{(\sigma _1+\sigma _2)^2}{2}+ \frac{2|\sigma _0|(|\sigma _1|+|\sigma _2|)\lambda +\sigma _0 ^2}{2\lambda ^2}\right\} .\nonumber \\ \end{aligned}$$
(56)

Proof

Choosing the same Lyapunov–Razumikhin function candidate as in Eq. (13) as \(V(x(t))=\frac{1}{2}x^2(t)\) on \( \mathcal R \), and again, considering the time derivative along its trajectories in Ito’s sense, we can obtain

$$\begin{aligned} dV(x(t))&= \left\{ x(t)\left[ (a+b)x(t)-ab \int \limits _{t - \tau }^t {x(s)} ds\right. \right. \nonumber \\&-b^2\int \limits _{t - 2\tau }^{t- \tau } {x(s)} ds- b\int \limits _{t - \tau }^t (\bar{\sigma }_0+\bar{\sigma }_1x(s)\nonumber \\&\!\!\left. \left. +\bar{\sigma }_2x(t-\tau ))d\beta (s) \right] \right. \nonumber \\&+ \frac{1}{2}\left. (\sigma _0+\sigma _1x(t)+ \sigma _2x(t-\tau ))^2\right\} dt\nonumber \\&+x(t)\left[ \bar{\sigma }_0+\bar{\sigma }_1x(t)+\bar{\sigma }_2x(t-\tau )\right] d\beta (t). \end{aligned}$$
(57)

According to Lemma (1), the property \( V(x_t(\theta ))\le \rho V(x(t)) \) holds for some \( \rho >1 \), which implies Eq. (27).

Substituting Eq. (27) into Eq. (57) and taking expected value of the resulting equation yields

$$\begin{aligned} {\textit{dE}}\{V(x(t))\}&\le \left[ (a+b+\tau \sqrt{\rho }|ab|+ \tau \sqrt{\rho }b^2\right. \nonumber \\&\left. +\frac{1}{2}\sigma _1^2+\frac{1}{2}\rho \sigma _2^2+\sqrt{\rho }|\sigma _1||\sigma _2|)\right. \nonumber \\&\left. \times E\{x^2(t)\}+(|\sigma _0||\sigma _1|+ \sqrt{\rho }|\sigma _0||\sigma _2|)\right. \nonumber \\&\left. E\{x(t)\}+\frac{1}{2} \sigma _0^2\right] \nonumber \\&\le [A_2E\{x^2(t)\}+B_2E\{x(t)\}+\frac{1}{2}\sigma _0^2]dt \nonumber \\&\le -\gamma E\{x^2(t)\}dt, \end{aligned}$$
(58)

where \(A_2=a+b+\tau \sqrt{\rho }|ab|+\tau \sqrt{\rho }b^2+\frac{1}{2}\sigma _1^2+\frac{1}{2}\rho \sigma _2^2+\sqrt{\rho }|\sigma _1||\sigma _2|\) and \(B_2=|\sigma _0||\sigma _1|+\sqrt{\rho }||\sigma _0||\sigma _2|\). Following the same strategy as in Theorem (4), we can find that the system Eq. (1) is delay-dependent asymptotically stable in the mean square if

$$\begin{aligned} A_2+\gamma <0,\quad \forall \,\ 0 \le E\{x^2(t)\} \le - \frac{{\frac{1}{2}\sigma _0 ^2+B_2E\{|x(t)|\} }}{A_2+\gamma }. \nonumber \\ \end{aligned}$$
(59)

Hence, following the same strategy as in the previous section, the stability condition of Theorem 5 can be obtained.

We can also obtain a less general version of Eq. (56) with \(\sigma _2=0\) using the Lyapunov–Krasovskii based approach. Define a Lyapunov–Krasovskii functional candidate \(V (x_t(\theta ))\) on \(\mathcal C [-\tau ,0]\) as in Eq. (30). Taking the time derivative of \(V(x_t(\theta ))\) along the solutions of Eq. (1), yields

$$\begin{aligned} dV(x_t(\theta ))&= \left\{ 2((x(t) + b \int \limits _{t - \tau }^t {x(\theta )d\theta })(a + b)x(t)\right. \nonumber \\&\quad \left. +\left| {(a + b)b} \right| \int \limits _{t - \tau }^t {{x^2}( \theta )} d\theta -\left| {(a + b)b} \right| \right. \nonumber \\&\quad \left. \int \limits _{t - \tau }^t {{x^2}(t)d\theta }+(\sigma _0+\sigma _1 x(t))^2\right\} dt\nonumber \\&\quad +2((x(t) \!+\! b\int \limits _{t \!-\! \tau }^t {x(\theta )d\theta })( {\bar{\sigma }}_0\!+\!{\bar{\sigma }}_1 x(t)) d\beta (t).\nonumber \\ \end{aligned}$$
(60)
Fig. 4
figure 4

Stability region of the scalar linear stochastic time-delay system in Eq. (1) using the Lyapunov approach for \(\tau =1(sec), \lambda =2.5, \sigma _0=\sigma _1=1\), and \(\sigma _2=0\) (gray region) in comparison with the stability domain of the corresponding deterministic system using the frequency domain approach (yellow region). a Stability region of Eq. (38) (red dashed boundary) in comparison with the stability region of Eq. (66) (red solid boundary) using the LMI-based Lyapunov approach for \(d=6.6667\). d stability region of nonlinear system (green region) for \(\delta =0.3\). (Color figure online)

Full size image

After some simplification,

$$\begin{aligned} dV(x_t(\theta ))&= \left\{ (2a +2 b+ {\bar{\sigma }}_1^2)x^2(t)+2\sigma _0\sigma _1x(t) \right. \nonumber \\&\quad +2\left. (a + b)b \int \limits _{t - \tau }^t {{x}(t)x(\theta )d \theta }- \left| {(a + b)b} \right| \right. \nonumber \\&\quad \times \left. \int \limits _{t - \tau }^t {{x^2}(\theta )} d\theta \!+\! \tau \left| {(a \!+\! b)b} \right| {x^2}(t)\!+\!\sigma _0^2\right\} dt\nonumber \\&\quad +2((x(t) \!+\! b\int \limits _{t - \tau }^t {x(\theta )d\theta })( {\bar{\sigma }}_0\!+\!{\bar{\sigma }}_1 x(t)) d\beta (t).\nonumber \\ \end{aligned}$$
(61)

Now by using Eq. (32), the second term on the right hand side of Eq. (61) can be expressed as

$$\begin{aligned}&2(a + b)b\int \limits _{t - \tau }^t {x(t)x(\theta )d \theta } \le 2\left| {(a + b)b} \right| \nonumber \\&\quad \left[ \sqrt{{ \int \limits _{t - \tau }^t {{x^2}(t)d\theta } }}\,\right] \left[ {\sqrt{ \int \limits _{t - \tau }^t {{x^2}(\theta )d\theta } }}\,\right] \nonumber \\&\le \tau \left| {(a + b)b} \right| {x^2}(t) + \left| {(a + b)b} \right| \int \limits _{t - \tau }^t {{x(\theta )^2}d\theta }. \end{aligned}$$
(62)

Substituting Eq. (62) into Eq. (61) and taking the expected value of the resulting equation yields

$$\begin{aligned} {\textit{dE}}\{V(x_t(\theta ),t)\}&\le (2a \!+\!2 b\!+\! \sigma _1^2 \!+\! 2\tau \left| {(a \!+\! b)b} \right| )E\{x^2(t)\}\nonumber \\&+2\sigma _0\sigma _1E\{x(t)\}+\sigma _0^2. \end{aligned}$$
(63)

The asymptotic stability of the system is guaranteed if

$$\begin{aligned} 0<E\{x^2(t)\}<-\frac{\sigma _0^2+2|\sigma _0\sigma _1| E\{|x(t)|\}}{2a +2 b+\sigma _1^2 + 2\tau \left| {(a + b)b} \right| }, \end{aligned}$$
(64)

assuming that \(a<-b-\frac{1}{2}\sigma _1^2-\tau |(a+b)b|.\)Therefore the stability condition of Eq. (56) with \(\sigma _2=0\) is obtained by using Eqs. (44–46).\(\square \)

Fig. 5
figure 5

Stability region of the scalar linear stochastic time-delay system in Eq. (1) using the Lyapunov approach for \(\tau =1(sec)\) and \(\lambda =2.5\) (gray region) in comparison with the stability domain of the corresponding deterministic system using the frequency domain approach (dashed yellow region). (Color figure online)

Full size image
Fig. 6
figure 6

Stability region of the scalar linear stochastic time-delay system in Eq. (1) using the Lyapunov approach for \(\tau =1(sec), \sigma _0=\sigma _1=\sigma _2=1\) (gray region) in comparison with the stability domain of the corresponding deterministic system using the frequency domain approach (dashed yellow region). The crosses in a correspond to the simulations in Fig. 7. (Color figure online)

Full size image

The stability region of the scalar linear stochastic time-delay system in Eq. (1) derived in Theorems 4 and 5 for \(\sigma _0=1,\sigma _1=1\), and \(\sigma _2=0\) is shown in Fig 4. The supremum of the expected value of the initial function is also chosen as \(\lambda =2.5\). In order to have a comparison between the stochastic and deterministic system, the stability region of deterministic system obtained in Theorem 1 using the frequency domain approach is also shown by the yellow region and dashed line in all parts of Fig. 4. The corresponding delay-independent stability condition is given in Fig. 4a, and the corresponding delay-dependent stability is plotted in Fig. 4b. The entire stability region for the scalar linear stochastic time-delay system is also plotted in Fig. 4c, d, respectively.

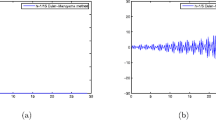
For the case of additive noise when \(\sigma _1=\sigma _2=0\), the delay dependent stability condition in Theorem 5 shrinks to \(\tau \le \tau _{max}\equiv \frac{-1}{|ab|+b^2}\left\{ a+b+\frac{\sigma _0 ^2}{2\lambda ^2}\right\} \), and for the case of multiplicative noise when \(\sigma _0=\sigma _2=0\), the stability region is defined as \( \tau \le \tau _{max}\equiv \frac{-1}{|ab|+b^2}\left\{ a+b+\frac{\sigma _1^2}{2}\right\} \). Note that these two expressions were also obtained in Mackey and Nechaeva [13]. These two cases along with the case of \(\sigma _0=\sigma _1=0\) and \(\sigma _2=1\) are depicted in Fig. 5 along with the deterministic stability boundary. For additive noise, we set \(\sigma _0=1\), and for two cases of multiplicative noise, \(\sigma _1=1\) or \(\sigma _2=1\), while the initial function is the same as before. Note that the initial function can affect the derived stability conditions in the parameter space. Figure 6 shows the change in the stability region of stochastic time-delay system in terms of different values of the initial function. As we can see in this figure, by increasing the value of the initial function, the stability domain will expand and moves toward the stability area of deterministic system which is depicted by the dashed yellow color. Figure 7 shows the mean absolute value of the response of Eq. (1) for \(\sigma _0=\sigma _1=\sigma _2=1\) and \(\lambda =0.5\). Note that in this figure the exponential stability is guaranteed for the stable gray region in Fig. 6a, while in the yellow region the response is not guaranteed to be exponentially stable, although it can be (Lyapunov) stable.

Fig. 7
figure 7

The mean absolute value of the response of the scalar linear stochastic time-delay system in Eq. (1) for \(\tau =1(sec), \sigma _0=\sigma _1=\sigma _2=1\), and \(\lambda =0.5\) (see Fig. 6a)

Full size image

Remark 3

Numerical LMI-based Lyapunov approaches can be also used to obtain the stability of scalar stochastic time-delayed systems. The main drawback of this method is that additive stochastic excitation term in Eq. (1), which also represents a nonhomogeneous term, cannot be analyzed by this method. Thus for \(\sigma _1=0\) the delay independent stability condition of Eq. (1) is obtained by using the same Lyapunov–Krasovskii functional as in Eq. (36) as

$$\begin{aligned} X^T(t)\left[ {\begin{array}{*{20}{c}} {2pa + q+p\sigma _1^2} &{} {p{b}+p\sigma _1\sigma _2} \\ {bp+p\sigma _1\sigma _2} &{} { - q+p\sigma _2^2} \\ \end{array}} \right] X(t)< -\gamma I_{2\times 2}, \nonumber \\ \end{aligned}$$
(65)

where \(I_{2\times 2}\) is a 2-by-2 identity matrix. Solving the above with \(\gamma \rightarrow 0\) yields

$$\begin{aligned} a<-\frac{q}{2p}-\frac{\sigma _1^2}{2}-\frac{p(b+ \sigma _1\sigma _2)^2}{2(q-p\sigma _2^2)}. \end{aligned}$$
(66)

To compare with Lyapunov–Krasovskii stability result, we set \(\sigma _2=0\) in Eq. (66) which results in

$$\begin{aligned} a<-\frac{q}{2p}-\frac{pb^2}{2q}-\frac{\sigma _1^2}{2}= -\frac{d}{2}-\frac{b^2}{2d}-\frac{\sigma _1^2}{2}. \end{aligned}$$
(67)

As seen from this condition, the maximum area of delay-independent asymptotic stability for Eq. (1), which is \(a<-|b|-\frac{1}{2}\sigma ^2_{1}\), will be obtained when \(d=\frac{q}{p}=|b|\). For comparison, the region of delay-independent asymptotic stability of Eq. (1) for the optimal constant value \(d=6.667\) from Remark 2 in Sect. 3 is plotted in Fig. 4a by red dashed boundary. It is noted that, unlike the deterministic case, the LMI-based stability boundary is not contained entirely inside the region described by Eq. (56).

Remark 4

In addition to the Lyapunov stability analysis of deterministic and stochastic time-delay systems, numerical approaches can be used for stability analysis of such systems. To compare our results obtained by the Lyapunov analysis with a numerical method, we apply the stochastic version of the semi-discretization technique used for stability analysis of stochastic time-delay systems in Elbeyli et al. [3]. Based on this approach, the stability of the stochastic system is equivalent to the spectral stability of the first and second moments. The stability diagram of the first order time-delay system of Eq. (1) when excited by purely multiplicative noise \((\sigma _0=\sigma _2=0,\sigma _1=1)\) is depicted in Fig. 8. The number of discretization points used to generate this stability chart is \(n=10\). The numerically obtained stability region is also compared with those based on Lyapunov theories in Fig. 8. Note that the first moment stability of the stochastic delayed system is the same as the frequency domain stability of the deterministic time-delay system. This is due to the fact that the expected value of the Brownian motion is zero. As is clear from the figure, the second moment stability is less conservative than those based on the Lyapunov theories.

5 Nonlinear scalar stochastic time-delay systems

In this section we extend the previous Lyapunov-based stability results to the case of nonlinear stochastic DDEs. For this purpose, let us assume that the nominal scalar SDDEs in Eq. (1) is perturbed by nonlinear functions of current and delayed states as

$$\begin{aligned} dx(t)&= (ax(t)+bx(t-\tau )+f_1(x(t))+f_2(x(t-\tau ))dt \nonumber \\&+(\bar{\sigma }_0+\bar{\sigma }_1x(t)+\bar{\sigma }_2x(t- \tau ))d\beta (t),t\ge 0 \nonumber \\ x(\theta )&= \phi (\theta ),\quad - \tau \le \theta \le 0, \end{aligned}$$
(68)

where \(f_1,f_2: \Omega \rightarrow \mathcal R \) are scalar nonlinear functions which satisfy \(f_1(0)=f_2(\theta )=0, -\tau <\theta <0\), and the Lipschitz conditions \(\left| f_1(x(t))\right| \le \delta _1\left| x(t)\right| , \left| f_2(x(t-\tau ))\right| \le \delta _2\left| x(t-\tau )\right| , \forall t>0\) in an open set \(\Omega \subset \mathcal C \) hold, where \(\delta _1,\delta _2\) are positive Lipschitz constants. We note that the nonlinearities \(f_1(x(t))\) and \(f_2(x(t-\tau ))\) could be higher order monomials resulting from a Taylor expansion about an equilibrium or perturbations representing modeling errors or uncertainties.

Stability of the nonlinear SDDE in Eq. (68) can be investigated analytically using Lyapunov-based methods. The Lyapunov–Razumikhin function candidate \( V (x(t)) \) on \(\mathcal C [-\tau ,0]\) is defined as in Eq. (13). Using Eq. (7), taking the time derivative of the above Lyapunov function along its trajectories in Ito’s sense, inserting Eq. (15) and the Lipschitz conditions into the derivative of the Lyapunov function, and taking the expected value from the resulting equation yields

$$\begin{aligned} {\textit{dE}}\{V(x(t))\}&\le [(a+\sqrt{\rho }\left| b \right| +\delta _1+\sqrt{\rho }\delta _2+\frac{1}{2}\sigma _1^2\nonumber \\&+ \frac{1}{2}\rho \sigma _2^2+\sqrt{\rho }|\sigma _1||\sigma _2|)E\{x^2 (t)\} \nonumber \\&+(|\sigma _0||\sigma _1|\!+\!\sqrt{\rho }|\sigma _0||\sigma _2|) E\{|x(t)|\} \!+\!\sigma _0^2]dt.\nonumber \\ \end{aligned}$$
(69)

Following the same procedure as in Theorem 4 by using Eqs. (44–46), the delay independent stability condition for the perturbed system in the parameter space can be obtained as

$$\begin{aligned} a \!<\! - \left| b \right| \!-\!\delta -\frac{1}{2}(\sigma _1+\sigma _2)^2- \frac{2{|\sigma _0|(|\sigma _1|\!+\! |\sigma _2|)}\lambda \!+\!{\sigma _0^2}}{{2\lambda ^2}}, \nonumber \\ \end{aligned}$$
(70)

where \(\delta =\delta _1+\delta _2\). For the delay dependent case, rewriting Eq. (55) corresponding to the nonlinear system with Eq. (68) yields

$$\begin{aligned}&dx(t) =\left[ (a+b)x(t)+f_1(x(t))+f_2(x(t-\tau )) \right. \nonumber \\&\qquad \qquad \left. -ab\int \limits _{t - \tau }^t {x(s)} ds-b\int \limits _{t - \tau }^t {f_1(s)} ds\right. \nonumber \\&\qquad \qquad -b^2\int \limits _{t - 2\tau }^{t-\tau } {x(s)} ds-\left. b \int \limits _{t - 2\tau }^{t-\tau } {f_2(s)}ds \right. \nonumber \\&\qquad \qquad \left. -b\int \limits _{t - \tau }^t {( \bar{\sigma }_0+\bar{\sigma }_1x(s)+\bar{\sigma }_2x(s-\tau ))d\beta (s)} \right] dt \nonumber \\&\qquad \qquad +(\bar{\sigma }_0+\bar{\sigma }_1x(t)+\bar{\sigma }_2x(t-\tau )) d \beta (t),\quad \nonumber \\&x(\theta ) = \phi (\theta )\, - \tau \le \theta \le 0. \end{aligned}$$
(71)

Using the same Lyapunov–Razumikhin function as in Theorem (5) and considering Eq. (27) and the Lipschitz conditions, we can obtain

$$\begin{aligned} d\!E\{V(x(t))\}&\le \left[ (a+b+\delta _1+\sqrt{\rho }\delta _2+\tau \sqrt{\rho }|ab|\right. \nonumber \\&\left. +\tau \sqrt{\rho }\delta |b|+\tau \sqrt{\rho }b^2+\frac{1}{2}\sigma _1^2+\frac{1}{2}\rho \sigma _2^2\right. \nonumber \\&+\left. \sqrt{\rho }|\sigma _1||\sigma _2|)E\{x^2(t)\} +(|\sigma _0||\sigma _1|\right. \nonumber \\&\left. +\sqrt{\rho }|\sigma _0||\sigma _2|)E\{x(t)\} +\frac{1}{2}\sigma _0^2\right] . \end{aligned}$$
(72)

Following the same procedure as in Theorem 5, the delay dependent stability condition of the nonlinear system is given as

$$\begin{aligned}&\!\!\!\tau \le \tau _{max}\equiv \frac{-1}{|ab|+\delta |b| +b^2}\nonumber \\&\!\!\!\times \left\{ a+b+\delta +\frac{(\sigma _1+\sigma _2)^2}{2}+ \frac{2|\sigma _0|(|\sigma _1|+|\sigma _2|)\lambda +\sigma _0 ^2}{2\lambda ^2}\right\} \!. \nonumber \\ \end{aligned}$$
(73)

It should be noted that the derived stability condition for both delay independent and delay dependent cases are valid in the open set \(\Omega \), where nonlinear functions \(f_1(x(t))\) and \(f_2(x(t-\tau ))\) satisfy the Lipschitz conditions. Moreover, in comparison with the delay independent stability region obtained for the linear system in Theorem 4, Eq. (70) is shifted to the left side in the parameter space \(Oab\) which implies that the stable region for the perturbed system is smaller than that for the nominal system, while for the delay dependent condition that is not the case. The entire stability region of the scalar nonlinear stochastic time-delay system derived in Eqs (70) and (73) for \(\delta =0.3\) is shown by the green region and dashed line in Fig. 4d. All other parameters are the same as in Fig. 4.

Fig. 8
figure 8

Stability region of the scalar linear stochastic time-delay system in Eq. (1) with multiplicative noise (\(\sigma _0=0, \sigma _1=1\), and \(\sigma _2=0\)) for \(\tau =1(sec)\) using numerical approach for the first moment (dashed blue), and the second moment (black), in comparison with the stability domain of the corresponding system using the time domain approach (green). (Color figure online)

Full size image

6 Conclusion

The Lyapunov-based stability of scalar linear and nonlinear stochastic systems in the parameter space was studied in this paper, where a known discrete time delay along with Brownian motion additive and multiplicative excitation was considered. First, the stability of the corresponding deterministic system was shown based on both exact frequency-domain criteria and Lyapunov-based criteria for both delay-independent and delay-dependent stability. Then, suitable Lyapunov–Razumikhin functions and Lyapunov–Krasovskii functionals were employed to derive analogous stability conditions for the stochastic delay differential equation. For the deterministic system, a comparison between derived stability conditions in the Lyapunov-based approach and the frequency domain approach shows the conservatism of the Lyapunov approach. Furthermore, for the stochastic system, we have shown that the additive Brownian motion stochastic process results in a larger region of stability in comparison with multiplicative Brownian motion. Moreover, by increasing the supremum value of initial function, the stability area expands and finally moves toward that of the deterministic system.

It was shown that the derived Lyapunov-based stability conditions are less conservative in comparison with other LMI-based approaches used in the literature. Finally, the numerical stability of the stochastic time-delayed system was analyzed from stability of the first and second moments using a stochastic version of the semidiscretization method recently proposed in literature, in which it was shown that the numerical second moment stability is less conservative than the stability conditions derived from the Lyapunov-based approaches.

A possible future extension of this work would be investigating the stability criteria for second-order stochastic time-delayed systems in the parameter space using the Lyapunov-based approaches. Such systems naturally occur in many areas of science and engineering. While the LMI-based Lyapunov approach may easily be extended to this case, however, the use of Lyapunov–Krasovskii functionals and Lyapunov–Razumikhin functions to obtain analytical stability criteria, as was done here for the scalar case, is much more difficult and requires further study.