1 Introduction

Physical systems are often subjected to noisy excitations and parametric uncertainties [4, 20, 23, 26]. The interplay between noise uncertainty and nonlinearity of dynamical systems can give rise to unexpected global changes in the dynamics, which have no analogue in the deterministic case, even under small noise inputs. For example, noise in nonlinear systems can induce chaos [12, 34], attractor and basin hopping [21, 27], complexity [38], bifurcations[15, 35] and crises [29, 30]. In general, noise is theoretically modeled as a random variable and a fuzzy set leading to the two categories of fuzzy and stochastic dynamics. An important problem is to understand the underlying mechanism for various bifurcations and complicated phenomena in noisy (fuzzy and stochastic) dynamics.

Chaos and bifurcation analysis of uncertain nonlinear dynamical systems is in general a difficult subject [1, 7, 8, 22, 36], partly because even the definition of chaos and bifurcations is open to discussion. For fuzzy nonlinear dynamics, the subject is even more difficult because the evolution of the membership function of the fuzzy response process can not be readily obtained analytically, especially for fuzzy chaotic response. A master equation has been derived for the evolution of membership functions of fuzzy processes [9, 10]. However, the solution to the equation is rare, particularly for nonlinear dynamical systems. Fuzzy generalized cell mapping [15, 32] is a discrete representation of the master equation. The FGCM method has been applied to study bifurcations of fuzzy nonlinear systems [15, 16]. It should be noted that there is little study in the literature on the bifurcation of fuzzy nonlinear dynamical systems. There are studies of bifurcations of fuzzy control systems where the fuzzy control law leads to a nonlinear and deterministic dynamical system. The bifurcation studies are practically the same as that of deterministic systems [5, 33]. The work by [28] deals with bifurcation of fuzzy dynamical systems having a fuzzy response. Numerical simulations are used to simulate the system response with a given parameter and fuzzy membership grade. The eigenvalues and the membership distribution are both used to describe the bifurcation. For a given membership grade, the bifurcation of the system is defined in the same manner as for the deterministic system.

In the theory of dissipative systems[2, 3], one often studies bifurcation phenomena as a single control parameter is varied. The most dramatic situations are so-called crises, namely the collision of a chaotic attractor with an unstable periodic orbit following the notation of [13] and [14], when a chaotic attractor undergoes a sudden discontinuous change. Of special interest are the mechanisms that induce crises. Two kinds of crises have been identified. A chaotic attractor suddenly disappears due to a boundary crisis or changes in size due to an interior crisis. Most physical systems usually contain several control parameters. When more than one parameter is changed simultaneously, a great variety of new phenomena may appear. In two-parameter dissipative systems, one of the most interesting phenomena is the coincidence and interaction of two distinct crises. An early example was due to [25] who defined a codimension two bifurcation of chaotic attractors of a forced damped pendulum with DC bias. Such an event has been called a double crisis and was also highlighted by [11] and [31], where a pattern involving a boundary crisis, an interior crisis, and a basin metamorphosis was examined using the laser ring cavity map and the Hénon map.

This paper applies the fuzzy generalized cell mapping (FGCM) method to analyze double crises in the presence of fuzzy noise. A fuzzy crisis is defined as a simultaneous sudden change both in the topology of a fuzzy chaotic attractor and in its membership distributions. Three distinct types of fuzzy chaotic basic sets are involved in the crisis analysis, namely, a chaotic attractor, a chaotic set on a fractal basin boundary, and a chaotic set in the interior of a basin and disjoint from the attractor. Rigorous set-theoretic definitions of all these chaotic entities for fuzzy dynamics are not available in the literature, to our knowledge. The double crisis induced by fuzzy noise has yet to be addressed.

The phase portrait diagrams [31] involving fuzzy chaotic basic sets of these three types are presented to understand a simultaneous sudden change in fuzzy chaotic sets. Any such sudden change results from the collision of a fuzzy chaotic set with a periodic or chaotic saddle and is also refered to as a fuzzy crisis, which may be an interior crisis, a boundary crisis, a basin metamorphosis. These crisis events generally lie on a smooth curve in two-dimensional parameter space. In this paper, the coincidence and interaction of four distinct fuzzy crises are determined at an exceptional point of a two-parameter plane by two examples of a chaotic pendulum and a duffing oscillator with fuzzy uncertainty.

The remainder of the paper is outlined as follows. Section 2 describes the FGCM method. Sections 3 and 4 present the study of the double crises of fuzzy chaotic oscillators. The paper concludes in Sect. 5.

2 The fuzzy generalized cell mapping method

We first review the GCM method for nonlinear dynamical systems with fuzzy uncertainties[32]. Consider a crisp ordinary differential equation,

$$\begin{aligned} {\dot{\mathbf{x}}}=\mathbf{f}(\mathbf{x},t,s); \mathbf{x} \in \mathbf{D}\subset \mathbf{R}^{n}, t\in \mathbf{R}^{1}, s\in \mathbf{R}^{1}, \end{aligned}$$
(1)

where \(\mathbf x \) is the state vector, \(t\) the time variable, \(s\) a system parameter, and \(\mathbf f \) is a vector-valued nonlinear function of its arguments. It is assumed to be periodic in \(t\) with period \(T\), and \(\mathbf D \) is a bounded domain of interest in the state space \(\mathbf R ^{n}\).

Let the system parameter \(s\) be a fuzzy number. Equation (1) becomes a fuzzy differential equation, which is to be interpreted as a fuzzy differential inclusion relation [6, 18, 19]

$$\begin{aligned} \dot{\mathbf{x}}\in \left[ \mathbf{f}(\mathbf{x},t,s)\right] ^{\alpha },\quad s\in \left[ S\right] ^{\alpha }, \quad 0\le \alpha \le 1, \end{aligned}$$
(2)

where \(\mathbf f \) is a fuzzy valued continuous function defined on \(\mathbf E ^{n}\), which is a collection of all normal, upper semi-continuous, convex, compact supported fuzzy subsets of \(\mathbf R ^{n}\). \(\left[ \mathbf f \right] ^{\alpha }\) denotes the \(\alpha \) cut of \(\mathbf f \), \(S\) is a fuzzy parameter and \(\left[ S\right] ^{\alpha }\) is the \(\alpha \) cut of the fuzzy set \(S\). We assume the right hand side to be continuous and bounded with respect to the Hausdorff distance \(d_{H}\) and that \(\mathbf f \) satisfies the Lipschitz condition \(d_{H}(\mathbf f \left( \mathbf x ,t,s\right) ,\mathbf f \left( \mathbf y ,t,s\right) )\le L\left| \mathbf x -\mathbf y \right| \) for all \(s\in \mathrm supp (S)\) and \((\mathbf x ,\) \(\mathbf y )\in \mathbf R ^{n}\times \mathbf R ^{n}\) with a Lipschitz constant \(L>0\) [18, 19]

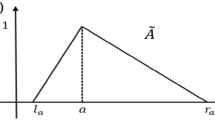
The cell mapping method proposes to further discretize the time and state variables in searching for the global solution of the system[17]. In order to apply the cell mapping method, we also need to discretize the fuzzy set \(S\). Suppose that \(S\) is a triangular fuzzy parameter with a membership function \(\mu _{S}(s)\in (0,1]\). We divide \(S\) into \(M\) segments of appropriate length and sample a value \(s_{k}\in \mathrm supp (S)\) \((k=1,\ldots ,M)\) in the middle of each segment. The division of \(S\) is such that there is at least one \(s_{k}\) with membership grade equal to one.

The domain \(\mathbf D \) is then discretized into \(N\) small cells. Each cell is identified by an integer ranging from \(1\) to \(N\). For a cell, say cell \(j\), \(N_{p}\) points are uniformly sampled from cell \(j\). By applying the method of numerical simulation of fuzzy differential inclusions similar to the one presented by [19], we generate \(M\times N_{p}\) fuzzy sample trajectories of one period \(T\) long. The length \(T\) is taken to be one mapping step. Each trajectory carries a membership grade determined by that of \(s_{k} \)’s. We then find the cells in which the end points of the trajectories fall. Assume that cell \(i\) is one of the image cells of cell \(j\), and that there are \(m\) \(\left( 0<m\leqslant MN_{p}\right) \)trajectories falling in cell \(i\). Define a quantity

$$\begin{aligned} p_{ij}=\underset{i_{k}}{\max }[\mu _{S}(s_{i_{k}})],\ \ 0<p_{ij}\leqslant 1, \end{aligned}$$
(3)

where \(i_{k}\) \((k=1,2,\ldots ,m)\) are referred to the trajectories falling in cell \(i\), and \(\mu _{S}(s_{i_{k}})\) are the membership grades of the corresponding trajectories. This procedure for computing \(p_{ij}\) is known as the sampling point method in the context of generalized cell mapping [17]

Now, assume that the membership grade of the system being in cell \(j\) at the \(n^{th}\) mapping step is \(p_{j}(n)\) \((0<p_{j}(n)\leqslant 1)\). Cell \(j\) is mapped in one step to cell \(i\) with the membership grade given by

$$\begin{aligned}&\max \left\{ \min \left[ \mu _{S}\left( s_{i_{1}}\right) ,p_{j}\left( n\right) \right] ,\min \left[ \mu _{S}\left( s_{i_{2}}\right) ,p_{j}\left( n\right) \right] ,\ldots ,\right. \nonumber \\&\left. \quad \quad \min \left[ \mu _{S}\left( s_{i_{m}}\right) ,p_{j}\left( n\right) \right] \right\} \\&\quad \quad =\min [\underset{i_{k}}{\max }\left( \mu _{S}\left( s_{i_{k}}\right) \right) ,p_{j}\left( n\right) ]=\min [p_{ij},p_{j}\left( n\right) ].\nonumber \end{aligned}$$
(4)

Considering all possible pre-images of cell \(i\), we have the membership grade of the system being in cell \(i\) at the \((n+1)^{th}\) step as

$$\begin{aligned} p_{i}\left( n+1\right) =\underset{j}{\max }\min \left[ p_{ij},p_{j}\left( n\right) \right] . \end{aligned}$$
(5)

Let \(\mathbf p \left( n\right) \) be a vector with components \(p_{i}\left( n\right) \), and \(\mathbf P \) a matrix with components \(p_{ij}\). Equation (5) can be written in a compact matrix notation

$$\begin{aligned} \mathbf p \left( n+1\right) =\mathbf P \circ \mathbf p \left( n\right) ,\ \ \mathbf p \left( n\right) =\mathbf P ^{n}\circ \mathbf p \left( 0\right) , \end{aligned}$$
(6)

where \(\mathbf P ^{n+1}=\mathbf P \circ \mathbf P ^{n}\) and \(\mathbf P ^{0}=\mathbf I \). The matrix \(\mathbf P \) is called the one-step transition membership matrix. The vector \(\mathbf p \left( n\right) \) is called the \(n\)-step membership distribution vector, and \(\mathbf p \left( 0\right) \) the initial membership distribution vector. The \((i,j)\mathrm{th}\) element \(p_{ij}\) of the matrix \(\mathbf P \) is called the one-step transition membership from cell \(j\) to cell \(i\).

Equation (6) is called a fuzzy generalized cell mapping system, which describes the evolution of the fuzzy solution process \(\mathbf x \left( t\right) \) and its membership function, and is a finite approximation to the fuzzy dynamical system (2) in \(\mathbf D \).

Consider the master equation for the possibility transition of continuous fuzzy processes[9, 10, 37]

$$\begin{aligned} p(\mathbf x ,t)=\sup _\mathbf{x _{0}\in \mathbf D }\left[ \min \{p(\mathbf x ,t|\mathbf x _{0},t_{0}),p(\mathbf x _{0},t_{0})\}\right] ,\,\, \mathbf x \in \mathbf D \end{aligned}$$
(7)

where \(\mathbf x \) is a fuzzy process, \(p(\mathbf x ,t)\) is the membership function of \(\mathbf x \), and \(p(\mathbf x ,t|\mathbf x _{0},t_{0})\) is the transition possibility function, also known as a fuzzy relation according to Yoshida [37]. Equation (5) of the FGCM can be viewed as a discrete representation of Eq. (7). Friedman and Sandler have derived a partial differential equation from Eq. (7) for continuous time processes [9, 10]. This equation is analogous to the Fokker–Planck–Kolmogorov equation for the probability density function of stochastic processes [24]. The solution to this equation is in general very difficult to obtain analytically. Numerically, the FGCM offers a very effective method for solutions to this equation, particularly, for fuzzy nonlinear dynamical systems.

3 A fuzzy double crisis in a forced damped pendulum

Our first example of a fuzzy double crisis occurs in the forced damped pendulum in the presence of multiplicative fuzzy noise.

$$\begin{aligned} \frac{d^{2}x}{dt^{2}}+\kappa \frac{dx}{dt}+\sin x=S\sin \omega t+C, \end{aligned}$$
(8)

where \(S\) is a fuzzy parameter of the forcing amplitude with a triangular membership function,

$$\begin{aligned} \mu _{S}\left( s\right) =\left\{ \begin{array}{ll} \left[ s-\left( s_{0}-\varepsilon \right) \right] /\varepsilon , &{} s_{0}-\varepsilon \leqslant s<s_{0}\\ -\left[ s-\left( s_{0}+\varepsilon \right) \right] /\varepsilon , &{} s_{0}\leqslant s<s_{0}+\varepsilon \\ 0, &{} \mathrm{otherwise} \end{array}\right. \end{aligned}$$
(9)

\(\varepsilon >0\) is a parameter characterizing the intensity of fuzziness of \(S\) and is called a fuzzy noise intensity. \(s_{0}\) is the nominal value of \(S\) with membership grade \(\mu _{S}\left( s_{0}\right) =1\). Here \(x\) represents the angle from the vertical of a pendulum subject to an external torque which varies sinusoidally in time with frequency \(\omega \) and the fuzzy forcing amplitude \(S\).

The deterministic counterpart of the pendulum equation (8) was studied by [25] when the forcing amplitude \(S\) is a deterministic value. In the present work, we are interested in the region of chaotic motions, in particular, we take \(\omega =0.55\), \(\kappa =0.5\), \(s_{0}=0.87\) and \(\varepsilon =0\) when the system has two coexistent chaotic attractors as shown in Fig. 1.

Fig. 1
figure 1

The phase portrait of the deterministic equation of the forced pendulum (8) with \(\omega =0.55\), \(\kappa =0.5\), \(C=0\), \(s_{0}=0.87\), and \(\varepsilon =0\)

Full size image

Within the context of the FGCM method, we define a fuzzy attractor as a stable and closed set of self-cycling cells, and a fuzzy saddle as an unstable and transient self-cycling set of cells. There are three types of fuzzy chaotic sets [31] , namely, a chaotic attractor, a chaotic set in a fractal basin boundary, and a chaotic set in the interior of a basin and disjoint from the attractor. A basic set is a maximal set with a dense trajectory. Maximal means that the basic set does not lie in a strictly bigger set having a dense trajectory. The fuzzy chaotic attractor is characterized by both its global topology in the phase space and steady state membership function. It can undergo sudden and discontinuous changes of the topology and membership function as the system control parameter varies. When this happens, we say that the system goes through a fuzzy crisis according to Grebogi’s definition of crises for deterministic chaotic systems [13, 14] . The phase diagrams of a fuzzy chaotic system are built upon the three kinds of basic sets: attractors \(A\), saddles \(B\) in basin boundaries, and saddles \(S\) in a basin interior. Arrows connecting basic sets describe a dynamical relation among them. An arrow from a basic set \(B\) to a basic set \(A\), for example, means that when the system is slightly disturbed from a trajectory in \(B\), it can tend to \(A\). Trajectories slightly disturbed from \(B\) follow its unstable set which is the ensemble of trajectories asymptotic to the saddle backward in time.

In the present work, we take the damping \(\kappa =0.5\), forcing frequency \(\omega =0.55\) and \(s_{0}=0.87\). When applying the FGCM method, a cell structure of \(141\times 141\) cells is used for the region of the state space \((-3.14\le x\le -1.9)\times (-0.4\le dx/dt\le -0.1)\), and \(5\times 5\) interior sampling points are used within each cell. The membership function is discretized into \(M=21\) segments. Hence out of each cell, there are \(525\) trajectories with varying membership grades. These trajectories are then used to compute the transition membership matrix.

Figure 2 shows two curves BC1 and BC2 of a fuzzy boundary crisis and two curves IC1 and IC2 of a fuzzy interior crisis, corresponding to two distinct fuzzy chaotic attractors A\(_{1}\) and A\(_{2}\). The four half-curves of crisis meet at a point of the \((C,\varepsilon )\) parameter space, located roughly at \((C,\varepsilon )\approx (0,0.0025)\), called a fuzzy double crisis vertex. In the south quadrant, there are two coexisting fuzzy chaotic attractors A\(_{1}\) and A\(_{2}\). In the west quadrant, there is only one fuzzy chaotic attractor A\(_{2}\). In the east, only one fuzzy chaotic attractor A\(_{1}\) exists. In the north, a single large fuzzy chaotic attractor A\(_{large}\) resides. The disappearance-appearance of the attractor A\(_{1}\) or A\(_{2}\) occurs when crossing the two curves BC1 and BC2 of the boundary crisis, respectively. The explosion-implosion of the attractor A\(_{1}\) or A\(_{2}\) occurs when crossing the two curves IC1 and IC2 of the interior crisis, respectively. Phase diagrams are given in each of the four quadrants involving three basic sets: fuzzy chaotic attractors \(A_{1}\), \(A_{2}\), \(A_{l\arg e}\), a regular saddle \(B\) in a smooth basin boundary, and chaotic saddles \(S_{1}\), \(S_{2}\) in a basin interior. An arrow joining two basic sets indicates robust trajectories from one to the other.

Fig. 2
figure 2

The double crisis vertex of the fuzzy forced pendulum equation (8) in the \((C,\varepsilon )\) parameter space. Phase diagrams in each of the four quadrants involving three basic sets: fuzzy chaotic attractors \(A_{1}\), \(A_{2}\), \(A_{l\arg e}\), a regular saddle \(B\) in a smooth basin boundary, and chaotic saddles \(S_{1}\), \(S_{2}\) in a basin interior. An arrow joining two basic sets indicates robust trajectories from one to the other

Full size image

Global phase portraits at \((C,\varepsilon )=(0,0.002)\), \((0,0.003)\), \((-0.001,0.0025)\), and \((0.001,0.0025)\) are shown in Figs. 3, 4, 5, and 6.

Fig. 3
figure 3

The phase diagram of the forced pendulum (8) with \((C,\varepsilon )=(0,0.002)\). In the upper figure of global topology, black colour denotes fuzzy chaotic attractors A\(_{1}\), A\(_{2}\) and A\(_{large}\), blue colour saddle, grey colour boundary. The membership function is shown in the lower figure. (Color figure online)

Full size image
Fig. 4
figure 4

The global diagram of the forced pendulum (8) with \((C,\varepsilon )=(0,0.003)\). The legends are the same as that in Fig. 3

Full size image
Fig. 5
figure 5

The global phase diagram of the forced pendulum (8) with \((C,\varepsilon )=(-0.001,0.0025)\). The legends are the same as that in Fig. 3

Full size image
Fig. 6
figure 6

The global phase diagram of the forced pendulum (8) with \((C,\varepsilon )=(0.001,0.0025)\). The legends are the same as that in Fig. 3

Full size image

A double crisis when \((C,\varepsilon )\) vary from \((0,0.002)\) to \((0,0.003)\) is shown in Figs. 3 and 4, in which two attractors A\(_{1}\) and A\(_{2}\) simultaneously collide with a period-one saddle in their smooth basin boundary before the crisis, and merge to form one single large attractor A\(_{large}\) after the crisis. In the meanwhile, there is a sudden discontinuous change in their membership distribution function.

A fuzzy boundary crisis, when \((C,\varepsilon )\) vary from \((0,0.002)\) to \((-0.001,0.0025)\) crossing the curve of a boundary crisis BC1, is shown in Figs. 3 and 5, in which a fuzzy chaotic attractor A\(_{1}\) collides with a period-one saddle in its smooth basin boundary before the crisis, and suddenly disappears, leaving behind a chaotic saddle in the place of the original chaotic attractor in the phase space after the crisis.

A fuzzy interior crisis, when \((C,\varepsilon )\) change from \((-0.001, 0.0025)\) to \((0,0.003)\) crossing the curve of an interior crisis IC2, is shown in Figs. 5 and 4, in which the attractor A\(_{2}\) collides with a chaotic saddle in its basin interior before the crisis, and suddenly increases its size after the crisis.

Moving from the south to west quadrant, a boundary crisis is shown in Figs. 3 and 6, in which the attractor A\(_{2}\) collides with a period-one saddle in its smooth basin boundary before the crisis, and suddenly disappears, leaving behind a chaotic saddle in the place of the original chaotic attractor in the phase space after the crisis. Moving from the west to north quadrant, a fuzzy interior crisis is shown in Figs. 6 and 4, in which the attractor A\(_{1}\) collides with a chaotic saddle in its basin interior before the crisis, and suddenly increases its size after the crisis.

4 A fuzzy double crisis in a forced duffing oscillator

The same two-parameter pattern of a fuzzy double crisis is observed in the forced duffing oscillator with multiplicative fuzzy noise

$$\begin{aligned} \frac{d^{2}x}{dt^{2}}+\kappa \frac{dx}{dt}+Sx+x^{3}=F\sin \omega t+C, \end{aligned}$$
(10)

where \(S\) is a fuzzy parameter with the same triangular membership function in the Eq. (9).

We take the damping \(\kappa =0.25\), forcing amplitude \(F=8.5\), forcing frequency \(\omega =1\) and \(s_{0}=0.23\). For the deterministic part of the forced duffing oscillator (10) with \(\varepsilon =0\) and \(C=0\), the system has two coexistent chaotic attractors, and a chaotic saddle on the basin boundary as shown in Fig. 7.

Fig. 7
figure 7

The phase portrait of the deterministic equation of the forced duffing system (10) with \(\kappa =0.25\), \(F=8.5\), \(\omega =1\), \(C=0\), \(s_{0}=0.23\), and \(\varepsilon =0\)

Full size image

In applying the FGCM method, a cell structure of \(141\times 141\) cells is used for the region of the state space \((-1.8\le x\le 1)\times (-1\le dx/dt\le 1)\), and \(5\times 5\) interior sampling points are used within each cell. The membership function is discretized into \(M=21\) segments.

Figure 8 shows two curves of a fuzzy boundary crisis and two curves of a fuzzy interior crisis, corresponding to two distinct fuzzy chaotic attractors. The four half-curves of crisis meet at a point of the \((C,\varepsilon )\) parameter space, located roughly at \((C,\varepsilon )\approx (0,0.009)\), called a fuzzy double crisis vertex. In the south quadrant, there are two coexisting fuzzy chaotic attractors A\(_{1}\) and A\(_{2}\). In the west quadrant, only one fuzzy chaotic attractor A\(_{2}\) exists. In the east, only one fuzzy chaotic attractor A\(_{1}\) exists. In the north, a single large fuzzy chaotic attractor A\(_{large}\) resides. The disappearance-appearance of the attractor A\(_{1}\) or A\(_{2}\) occurs when crossing two curves of the boundary crisis, respectively. The explosion-implosion of the attractor A\(_{1}\) or A\(_{2}\) occurs when \((C,\varepsilon )\) cross two curves of the interior crisis, respectively. Phase diagrams are given in each of the four quadrants involving three basic sets: fuzzy chaotic attractors \(A_{1}\), \(A_{2}\), \(A_{l\arg e}\), a chaotic saddle \(B\) in a fractal basin boundary, and chaotic saddles \(S_{1}\), \(S_{2}\) in a basin interior. An arrow joining two basic sets indicates robust trajectories from one to the other.

Fig. 8
figure 8

The fuzzy double crisis vertex of the fuzzy forced duffing equation (10) in the \((C,\varepsilon )\) parameter space. Phase diagrams in each of the four quadrants involving three basic sets: fuzzy chaotic attractors \(A_{1}\), \(A_{2}\), \(A_{l\arg e}\), a chaotic saddle \(B\) in a fractal basin boundary, and chaotic saddles \(S_{1}\), \(S_{2}\) in a basin interior. An arrow joining two basic sets indicates robust trajectories from one to the other

Full size image

Global phase portraits at \((C,\varepsilon )=(0,0.008)\), \((0,0.01)\), \((-0.001,0.009)\), and \((0.001,0.009)\), are shown in Figs. 9, 10, 11 and 12. A double crisis when \((C,\varepsilon )\) vary from \((0,0.008)\) to \((0,0.01)\) is shown in Figs. 9 and 10, in which two fuzzy chaotic attractors A\(_{1}\) and A\(_{2}\) simultaneously collide with a chaotic saddle in their fractal basin boundary before the crisis, and merge to form one single large fuzzy chaotic attractor A\(_{large}\) after the crisis. In the meanwhile, there is a sudden discontinuous change in their membership distribution.

Fig. 9
figure 9

The phase diagram of the fuzzy forced duffing oscillator (10) with \((C,\varepsilon )=(0,0.008)\). The legends are the same as that in Fig. 3

Full size image
Fig. 10
figure 10

The phase diagram of the fuzzy forced duffing oscillator (10) with \((C,\varepsilon )=(0,0.01)\). The legends are the same as that in Fig. 3

Full size image
Fig. 11
figure 11

The phase diagram of the fuzzy forced duffing oscillator (10) with \((C,\varepsilon )=(-0.001,0.009)\). The legends are the same as that in Fig. 3

Full size image
Fig. 12
figure 12

The phase diagram of the fuzzy forced duffing oscillator (10) with \((C,\varepsilon )=(0.001,0.009)\). The legends are the same as that in Fig. 3

Full size image

A fuzzy boundary crisis, when \((C,\varepsilon )\) vary from \((0,0.008)\) to \((-0.001,0.009)\) crossing the curve of a boundary crisis BC1, is shown in Figs. 9 and 11, in which a chaotic attractor A\(_{2}\) collides with a chaotic saddle in its fractal basin boundary before the crisis, and suddenly disappears, leaving behind a chaotic saddle in the place of the original chaotic attractor in phase space after the crisis.

A fuzzy interior crisis, when \((C,\varepsilon )\) change from (\(-\)0.001, 0.009) to (0,0.01) crossing the curve of a chaotic interior crisis IC1, is shown in Figs. 11 and 10, in which the attractor A\(_{1}\) collides with a chaotic saddle in its basin interior before the crisis, and suddenly increases its size after the crisis.

Moving from the south to west quadrant, a boundary crisis is shown in Figs. 9 and 12, in which the attractor A\(_{2}\) collides with a chaotic saddle in its fractal boundary before the crisis, and suddenly disappears, leaving behind a chaotic saddle in the place of the original chaotic attractor in phase space after the crisis. Moving from the west to north quadrant, a fuzzy interior crisis is shown in Figs. 12 and 10, in which a fuzzy chaotic attractor A\(_{1}\) collides with a chaotic saddle in its basin interior before the crisis, and suddenly increases its size after the crisis.

5 Concluding remarks

Two sinusoidally forced oscillators in the presence of fuzzy uncertainty have been studied by means of the FGCM method. A double crisis vertex is identified in a two-parameter space, at which four curves of fuzzy crisis meet and four distinct crises coincide. The crisis is characterized by the sudden discontinuous change of the global topology and membership function of a fuzzy chaotic attractor. Three types of fuzzy chaotic basic sets are involved in these crises, namely, an attractor, a chaotic set on a fractal basin boundary, and a chaotic set in a basin interior. The phase portrait diagrams involving fuzzy chaotic basic sets of these three types are presented to understand a simultaneous sudden change in fuzzy chaotic sets. Any such sudden change, which is called a fuzzy crisis, results from the collision of a fuzzy chaotic set with a periodic or chaotic saddle. These crisis events generally lie on a smooth curve in two-dimensional parameter space. Here we focus on the coincidence and interaction of four distinct fuzzy crises, which correspond to an exceptional vertex of two paramenter space. The dynamics of fuzzy chaotic systems is extremely rich at such a vertex. Understanding such coincidence and interaction facilitates the exploration of dynamical behaviors in multidimensional parameter space of nonlinear systems with fuzzy uncertainty.