1 Introduction

1.1 Motivation

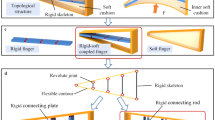
The effectiveness of a robot relies heavily on having the appropriate tooling for its designated tasks. While, specialized tools exist for specific applications like welding, robotic grippers play a crucial role in versatile applications, where adaptability is essential. Due to the increasing complexity of production lines and the rising lack of skilled workers in a variety of fields, these flexibility requirements for robots increase drastically. It is consequently of utterly importance to develop highly capable and versatile robotic grippers. While, rigid gripper concepts have to be designed for the parts they are intended to grasp, soft robotic grippers provide the highest conformability and, consequently also the highest flexibility [1]. Soft and flexible grippers can be designed with inherent force control via their structure, and they change their shape according to the geometry of an object. Thus, they are especially beneficial for handling soft or delicate objects such as fruits, eggs, bulbs, etc. They cause less impact and consequently also damage to the object’s surface than rigid grippers [2, 3]. Due to these advantages, soft robotic gripping is increasingly employed in various fields, such as food industry, medical and care, automotive, home applications, etc., for handling various shapes, sizes, and materials [4, 5]. Soft gripping can be achieved using multiple actuation principles such as vacuum, pneumatic, electrically controlled, fin ray effect (Fig. 1), reversible magnetorheological, and a lot more [6,7,8,9,10]. While, most of these need external energy sources, and grippers are based on the fin ray effect. The majority of works in the field optimize the grasping behavior of fin ray grippers alone. However, reduced energy consumption and resource efficiency are now more relevant than ever. Therefore, we utilize fin ray fingers that are inherently resource-efficient and maximize their capabilities by carefully minimizing weight and material costs during fabrication, while also taking their grasping behavior into account. Consequently, this work develops topology-optimized lightweight fin ray structures of triangular outer shape with a struts structure [11]. The optimization algorithm allows elastic deformation of the structure for better grasping [12].

Fig. 1
figure 1

3D-printed soft robotic finger’s force application and performance analysis a Various filling patterns are chosen based on fish fin ray effect, b the deflection coefficient Cd is calculated to compare the wrapping capability of the fingers, c The gripper, designed and printed with 3Dprinter to demonstrate the grasping of two different objects wooden block and coffee cup using Arduino microcontroller board and servo motors

Full size image

The fin ray principle draws inspiration from the properties of fish fins, which naturally bend in response to an applied force. By applying this principle to robotic fingers, they can easily wrap around objects without requiring external forces to do so.

Fin ray fingers are typically crafted using soft and extremely flexible polymers, ensuring high conformability. Their ability to wrap around objects without the need for an actuation system is achieved through reaction forces at the contact points. Such soft and flexible robotic fingers are highly adaptive in different fields because of their beneficial object-grasping capabilities [13, 14]. Here, we specifically employ 3D-printing for the fabrication of the developed fingers since it is material saving and the specific geometries can only be realized exploiting the high freedom in design that is uniquely offered by this technology.

1.2 Related work

In a study of Khaled et al., the fin ray jamming capabilities were experimentally analyzed, and successful grasping tasks for delicate objects were demonstrated [15]; the soft and flexible Ninjaflex, a commercially available form of thermoplastic polyurethane (TPU) material was employed for 3D-printing. The layer jamming effect improved the grasping of delicate objects, while generating higher contact forces. The Franka Emika Panda robotic arm and force sensors were used to show the grasping of various (fragile) objects such as; tomato, broccoli, egg, light bulb, and hammer. Later, the soft fin ray fingers were optimized using layer jamming to improve their stiffness. The strut’s inclination angle varied from 0° to 25°, and the stiffness of fingers was measured for applied forces. The best fingers at 10°–25° angles were 3D-printed; the simulation results were validated using a developed experimental setup [16]. Bu et al. focused on a flexible, three fingered end effector that utilized the fin ray effect to improve the efficiency of fruit harvesting [17]. It was demonstrated that adjustments in TPU stiffness, grasp distance, and fruit size significantly influenced the end-effector’s performance and enhancing automated fruit picking approach. Suder et al. analyzed various structures of fin ray fingers for the best wrapping of objects. Different filling patterns were considered such as: straight, with no filling, and branched struts. The thickness of the outer structure fixed at to = 2.8 mm without struts provided best wrapping capabilities; however, the fingers did not perform well at higher applied forces. For 3D-printing, the TPU 30D material, i.e., shore hardness of 30-D, was selected; the experimental setup was developed using ABB IRB 1600 and a force sensor. The experimental results matched with simulation results, and demonstrations of grasping different objects were provided for egg, bulb, lighter, and small blocks [18]. Yang et al. analyzed a robotic finger of mass 68 g with force feedback [19]. The grasping tasks are demonstrated for various objects with an embedded pressure sensor; however, the finger’s performance at various applied forces and their deflection were not evaluated. The fin ray finger structures were developed through a mathematical model with passive elements at assembly joints, and their validity was confirmed through multi-body simulation software [1]. Shin et al. conducted an experimental analysis of a soft robotic finger with larger gripping weight of up to 1200 g, and a modified finger improved the gripping weight by 40% [20]. Manoonpong et al. conducted an experimental analysis of the foot design, focusing on fin ray crossbeam angles for energy-efficient robot locomotion [21]. The effect of different angles of struts was analyzed under various payloads towards better durability of the soft robotic fingers. A large contact area was considered and evaluated by varying angles of the struts in active haptic control and assembly systems [22, 23]. The methodology was proposed for optimal fin ray finger design, evaluating the quality of the fingers’ grasping capability [24]. The framework was developed based on pseudo kinematics of soft fingers in learned simulations and with the required grasping force encoded in the form of a winding number. The effectiveness of the proposed method was tested using simulations and real-world examples. However, more complex designs and the combination of object shape and geometry of deformed. Nguyen et al. reviewed the field of bioinspired robotic grippers, emphasizing their design and application, inspired by human, animal, and plant mechanisms [25]. It highlighted the diversity and adaptability of these grippers including fin ray effect, underscoring their potential to innovate and enhance various industries and daily life. Few attempts were made in the field of compliant mechanisms using topology optimization (TO) for soft robotic grippers: Liu et al. analyzed compliant mechanisms of motor-driven three-finger soft robotic grippers [26]. A finite element method was developed to evaluate the stress, input force, and displacement; the mechanical advantage of various structures was tested. With the help of a three-finger gripper, objects with a size maximum of 140 mm and weight of 4.2 kg can be lifted. The optimal design was developed for grasping irregular objects with high mechanical advantage (MA) of compliant mechanism [27]. The MA is defined as the ratio of output force to the input force. TO of cable-driven soft robotic grippers was done considering geometric nonlinearity. Numerical simulations were performed using ANSYS software, and experimental results were performed to check the effectiveness of the developed algorithm [28]. Lakshmi and Javed conducted numerical simulations of the rectangular, elliptical, and trapezoidal structures for topologically optimized struts. However, the structures were not made up of soft material [29]. Recently, Yao et al. investigated soft robotic fingers inspired by the fin ray effect by integrating optimal design with intrinsic force sensing, demonstrating significant advancements in adaptability, dexterity, and safe handling capabilities [30]. The developed model combines the kinetostatic model with optimization and experimental validation, achieving enhanced adaptability and force estimation without embedded sensors. Milojević et al. developed a compliant two-finger soft robotic gripper mechanism for food-handling objects such as vegetables, sushi, fruits, and sweets [31] without needing additional sensors. However, the wrapping capabilities and performance of the soft robotic fingers were not analyzed in this study.

1.3 Contribution

The possibilities to grip more complex, delicate, and difficult-shaped geometries with soft fingers together with light weighting using topology optimization techniques are still an open topic of research. Most of the current work demonstrates the fingers’ wrapping by grasping various objects. However, lightweight TO method based on a mathematical and simulation analysis of wrapping quality is also still missing for the evolution of soft fingers. In this work, the wrapping quality of various filling patterns of fingers based on fish fin ray effect and mass reduced lightweight fingers are evaluated using the calculation of the deflection coefficient Cd, as shown in Fig. 1. Briefly, the deflection coefficient is the ratio of tip to the middle finger’s displacement. For better grasping and wrapping capabilities, the robotic finger should undergo large deformation (deflection). The maximum deflection value is in the denominator of equation of deflection coefficient; therefore, the fingers with lower Cd values possess more wrapping ability of the objects. The TPU 95A material is considered for the 3D printing of fingers due to its soft and flexible nature. However, the poor performance of flexible fingers is observed at high applied forces. To overcome this situation, TO is introduced to obtain both gripping capabilities and structural strength. The optimized structure allows the fingers into deformation for better wrapping of the object. The minimization of mass is selected as an objective function with constraints of displacement and von Mises stress threshold values. Various topologically optimized soft robotic fingers are generated for different volume fractions based on the loading and boundary conditions. The deflection coefficient of robotic fingers is calculated using SOLIDWORKS software. The performance of the soft robotic fingers, i.e., deflection (δ), von Mises stress (σ), and factor of safety (FOS), are analyzed by considering a range of applied force Fa = 5–30 N. The maximum applied force is targeted as 30 N, because the considered Emika Panda robot for grasping task has maximum payload of 3 kg. The FOS is ratio of yield stress to maximum permissible stress of the robotic finger; it is used to assure the designing does not occur any failure. If the design has higher FOS value, then the chance for design to be a failure is less. The experimental setup was developed to confirm the simulation values, and close accordance was demonstrated (< 3% deviation). The deformation zones are analyzed experimentally for the desired displacement value, i.e., d = 25 mm. In the end, grip testing is conducted to check the conformability of the fingers by considering two geometrically orthogonal objects such as a wooden block and a coffee cup. In future work, the fingers will be integrated with flexible [32] large-area tactile sensors to obtain real-time force and strain data, while grasping the various shapes and complex objects [33, 34].

The rest of manuscript is organized as follows: the filling patterns of various fingers, introduction of TO, evaluation of deflection coefficient, and experimental setup are shown in Sect. 2. The first simulations of measuring deflection coefficient, strength of finger, and experimental results are shown in Sect. 3. The conclusions of the findings in this research work are shown in Sect. 4.

2 Methodology

2.1 Various filling patterns of the soft robotic finger

The filling pattern of fin ray fingers is examined for various structures such as; rectangular, trapezoidal, straight struts, and inclined struts with angles + 45° and − 45°, based on fish fins, as shown in Fig. 2. To observe the effect of various internal struts on the deflection coefficient, the outer dimensions of all fingers are fixed to the same values, i.e., l = 100 mm, h = 60 mm, t = 20 mm, radius of curvature R = 2.5 mm. The width of fingers’ outer structure at the struts and fixed support are wc = 2 mm and wf = 8 mm, respectively. In all structures, the thickness of the struts changes from TS = 2–4 mm with a step value of sv = 0.5 mm. A total of 25 different finger variants are created based on the various strut patterns and thicknesses. When the thickness of the strut changes, other parameters are kept constant to evaluate the influence of the change in the deflection coefficient. Fingers are designed and evaluated in SOLIDWORKS software. As shown earlier, TPU 95A material is selected to make the fingers soft and flexible; it can withstand up to 580% elongation until failure, it is highly durable and recyclable [35].

Fig. 2
figure 2

Filling patterns of the finger: A Rectangular struts, B trapezoidal struts, C straight slot struts, D inclined struts with angles + 45° and E inclined struts with angles − 45°

Full size image

The material properties of TPU 95A are not available as part of software’s material library. In order to reflect the actual behavior in the simulations, the required material properties are obtained by conducting a tensile test. The specimen is prepared according to the ISO 527-2 standards with the help of 3D-printing, as shown in Fig. 3. 3D-printing in general provides a great variety of advantages over conventional machining, to name a few ease of manufacturing complex designs, reduced time, and material and energy savings [36, 37]. The material properties will be dependent on the placement of the part on the printer bed (part orientation), deposited amount of material for each layer (layer height), structure and shape of the material inside a part (infill), and other printer parameters. Therefore, all specimens and fingers have been printed with the same settings.

Fig. 3
figure 3

The specimen dimensions for tensile testing

Full size image

The Prusa-i3 MK3S printer is used for printing robotic fingers with TPU 95A material. The computer-aided design (CAD) model is imported into the Prusa Slicer version 2.4.2 software, and basic printing parameter settings are shown in Table 1. This slicing software divides the 3D model into layers and converts it into connecting points, then it will generate the G-codes based on these coordinate points; using storage cards, the G-code is imported to 3D-printer for printing.

Table 1 The basic Prusa Slicer parameter settings for 3D-printing
Full size table

The printed specimens are tested for tensile measurement using the Zwick Roell Z020 machine, as shown in Fig. 4. The test specimen is not subjected to failure because the deformation is still in the elastic phase, and the strain rate is about 24%. After this point, the plastic phase of deformation begins. However, for simulations, the stretch ratio is calculated based on the ratio of final length to initial length. The experiments are conducted three times to minimize the errors; the final properties of the TPU 95A are tabulated along mean and standard deviation (SD), as shown in Table 2.

Fig. 4
figure 4

The Zwick Roell Z020 tensile testing machine loaded with a test sample

Full size image
Table 2 The material properties of the TPU 95A (mean ± SD)
Full size table

2.2 Topology optimization of the soft robotic finger

The soft robotic fin ray fingers have good wrapping capabilities (Cd = 1.5–3); however, at high load application (Fa = 30 N), the performance of the fingers is poor. TO of the fingers optimizes the stiffness and achieves better performance at higher load applications. At the same time, due to the soft, flexible material and constraints of the TO, the final structure can provide better wrapping capabilities with high FOS. Topology optimization is the most common type of structural optimization; it is an effective method for allocating useful densities in design space [38]. The solid isotropic material with penalization (SIMP) method is used to discretize the design space into finite square elements and predict the optimized material distribution for provided load cases, boundary conditions, and constraints [39,40,41]. This method can also deal with mesh independency, numerical instabilities, checkerboard, slope constraints, and local minima problems [42,43,44]. The SIMP method can optimize the material distribution for complex, nonlinear systems, making it suited for developing soft robotic fingers. Its advantages in design versatility, computational efficiency, and compatibility with nonlinear behaviors contributed to the choice of this method. The SIMP method assigns the density values (ρe) for each element in the design space, and it helps to evaluate modulus of elasticity (Ee) within the bounding values [0, 1], as shown in Eq. 1.

$$ E_{{\text{e}}} (\rho_{{\text{e}}} ) = E_{\min } + \rho_{{\text{e}}}^{p} (E_{0} - E_{\min } ) \to \rho_{{\text{e}}} \in [0,1] $$
(1)

where ‘E0’ and ‘Emin’ are stiffness of material and less stiffness allocated to the no-material-space to avoid any singularity effect. This results in obtaining intermediate values between 0 and 1; it leads to the greyscale effect. The penalization factor (p) is introduced to minimize the greyscale effect; the ‘p’ value lies between 3 and 5 and regulates the elements of optimization, either solid (ρe = 1) or void (ρe = 0.001≈0). The objective function of the TO algorithm is selected as minimization of mass, as shown in Eq. 2. For the good conformability and better structural strength, the constraints are chosen as displacement, and von Mises stress [45,46,47]. The displacement constraint can conform to various object shapes through bending and is imposed to ensure sufficient flexibility. This constraint ensures that the optimized designs undergo large deformation, a characteristic vital for wrapping around and securely grasping objects of varying geometries without exerting excessive force that could lead to damage. The von Mises stress constraint limits the maximum stress within the material and prevents failure or excessive wear over time. Thereby, fingers can withstand repeated use in diverse grasping tasks without compromising their structural integrity. The topology optimization method distributes the material in the design space up to the given percentage of mass reduction. The user can specify the upper limit of displacement (δτ) and the optimization algorithm arranges densities in the design space in such a way that the maximum deflection and stress values should be less than or equal to the specified threshold values.

$$ \begin{aligned} & \mathop {\min }\limits_{\rho } : \, m(\rho ) = \sum\limits_{e = 1}^{N} {m_{e} \rho_{{\text{e}}} } \\ & {\text{s}}{\text{.t }}: \, \max \left( \sigma \right) \le \sigma_{\tau } \\ & \max \left( \delta \right) \le \delta_{\tau } \\ & 0 \le \rho_{{\text{e}}} \le 1 \\ \end{aligned} $$
(2)

where ‘m’ is the mass of the structure, and ‘N’ is the total number of elements in the design space. ‘σ’ and ‘δ’ are von Mises stress and displacement of the optimized structure. The sensitivity analysis is included in the optimization loop to evaluate the impact of variation in the densities based on the given objective function [48, 49]. Mathematically, the sensitivity analysis is represented as a derivative of mass and material densities. Initially, the solid soft robotic finger is modeled using the SOLIDWORKS software with the exact dimensions of a filling pattern of the finger. The finger one end is fixed, and Fa = 30 N (maximum applied force/payload) is considered based on the application and applied at the top middle, as shown in Fig. 5. The material properties are edited in the software, as shown in Table 2. From the structural static analysis, the maximum performance values are recorded as δ = 0.5406 mm, σ = 0.3219 MPa, and FOS = 26.72. The performance values are under safe limits; therefore, the topology optimization study is conducted to minimize the mass of finger. The mass of the robotic finger is chosen from 10 to 30% with a step value of sM = 5%, and δτ = 25 mm is considered based on maximum targeted displacement. The στ = 0.4095 MPa is selected based on the obtained minimum of the maximum stress value from all finger variants.

Fig. 5
figure 5

The boundary conditions of the solid soft robotic finger

Full size image

Due to restricting the structure with less mass, stress values, and allowing it to undergo large deformation, the final optimized finger provides better wrapping ability with high FOS. However, with the increase in mass percentage, the optimized structures become stiffer and provide the worst wrapping abilities. The average mass of the fin ray fingers is 46 g and minimum mass (10%) of the optimized finger is 39 g. The manufacturing controls are applied to the optimization process for easy operation of 3D-printing. In software, the preserved region settings are selected as user-defined, and the thickness is proved to be wc = 2 mm for outer structure and wf = 8 mm for the fixed end, the same case as filling pattern fingers. The preserved region is not included in the topology optimization algorithm; software will not remove the material from this region, which is known as non-design region (NDR). The symmetry control properties are applied to the solid soft robotic finger (Fig. 5) using a half symmetry (x–z plane) condition for an optimized design. The automatic solver is selected for the TO study, and the obtained structures are shown in Fig. 6. Generally, the default solver is the Intel direct spare for faster performance; however, FFEPlus (iterative) is used for frequency constraint problems. After TO, the boundaries are refined by selecting the smoothening tool and exported as STEP file.

Fig. 6
figure 6

Topologically optimized soft robotic fingers at mass reduced to A 10% B 15% C 20% D 25% E 30%

Full size image

2.3 Loading and boundary conditions of the finger

The soft robotic filling patterns and topologically optimized structures are evaluated with respect to their deflection coefficient to determine the wrapping and strength capabilities. The base of the test object has dimensions of dim = 55 × 20 × 20 mm. A circular pointer of thickness tp = 10 mm and length lp = 50 mm is pressed into the soft robotic finger, as shown in Fig. 7. The test object acts perpendicularly to the contact surface of the finger at a distance of df = 50 mm from the tip. It is the middle of the finger and most relevant zone for grasping different objects. However, in general the grasping position will depend on the considered object and other positions on the finger might be beneficial.

Fig. 7
figure 7

Loading conditions for benchmarking of the soft robotic fingers

Full size image

The loading test is conducted in three ways to examine the wrapping and strength of the finger against the applied force. In the first approach, the test object is pressed into the soft robotic finger from do = 1–8 mm in depth with a step value of sdo = 1 mm, known as prescribed displacement approach. In this process, the deflection coefficient is obtained from the simulations which are detailed in the following subsection. From these simulation results, the best finger, i.e., with the smallest deflection coefficient, is selected. In the second approach, the deformation, von Mises stress, and FOS values are recorded based on the applied force. In this study, the grasping strength of the fingers is tested against higher applied forces. In SOLIDWORKS, the forces Fa = 5–30 N are applied on the finger surface with step value of sF = 5. For this study, the best fingers are selected from each category based on the shown displacement simulations.

The third approach deals with validating second simulation results by comparing them with experimental data; the details of the experimental setup is shown in Sec. 2.5. The best finger variants and topologically optimized structures are 3D-printed, and displacements are measured at the considered forces with the help of a force sensor and the universal robot UR3e. The 3D-printed test object pointer is attached to the end effector and connected to the robot through an AXIA80 force and torque sensor (FT). The deflection vs. force graph is retrieved from this experimental study and thereby simulation results are validated.

2.4 Evaluation of soft robotic finger’s deflection coefficient and simulation settings

The soft robotic fingers are evaluated based on the deflection coefficient of various variants and topologically optimized structures under the prescribed displacement. The finger’s left end is subjected to the fixed support, and the test object is then pushed into the finger in a positive Z direction. In the simulations, the material is assumed to be isotropic and homogeneous for the soft robotic fingers, based on the averaged material properties obtained from tensile testing. This simplification does not account for variations in material properties due to manufacturing inconsistencies or the anisotropic nature of some 3D-printed materials. The object-wrapping ability of the finger is evaluated by computing the deflection coefficient with the help of three marker points, as shown in Fig. 8. The first marker point is positioned at the fixed joint, and the deflection at this point is zero. The second marker is located at the contact point between test object and finger; here, the deflection is maximum (Zmax). The third marker is placed at the end of the finger; the deflection is a nonzero value (Ztip). From these magnitudes, the deflection coefficient (Cd) of the finger is calculated as shown in Eq. 3

$$ C_{{\text{d}}} = \frac{{\sum\limits_{j = 1}^{n} {\frac{{Z_{{{\text{tip}}_{j} }} }}{{Z_{{\max_{j} }} }}} }}{n} $$
(3)

where ‘j’ is the given millimeter of compression and ‘n’ is the maximum displacement of do = 8 mm. The value of maximum displacement is taken from the past simulations for the same size and material. The deflection coefficient values vary from 1.5 to 3 based on the finger’s filling patterns, dimensions, and material properties.

Fig. 8
figure 8

The evaluation of the wrapping capability of the soft robotic finger

Full size image

In order to measure the deflection coefficient, the simulations are performed using a nonlinear static study. Because the TPU 95A material shows elastoplastic properties, nonlinear elastic behavior, and its stress–strain relationship does not follow Hooke’s Law across the range of finger deformations. Nonlinear static analysis can accurately interpolate this behavior, ensuring the simulation results closely match experimental performance. At the same time, the design of fin ray fingers, enables adaptive conformity to grasped objects by bending and large deforming, shows challenges for linear analysis but effectively addressed by nonlinear static analysis for realistic performance insights. The 2-D study is conducted to reduce the computational time by selecting t = 20 mm (thickness of finger). The material properties are entered manually in the software as given in Table 2. The test object can move in a positive Z direction, and the movement in X direction is prevented; the penetration between the contact surface of finger and test object is disabled. The prescribed displacement is selected within a range of do = 1–8 mm. Using the probe tool in SOLIDWORKS, the user can find the deflection at the tip of a finger, and the maximum deflection is highlighted later on in the results.

2.5 Experimental setup

The most suitable fingers from each variant are 3D-printed and tested with the help of developed experimental setup to validate the simulation results. The UR3e robotic arm is used for the experimental setup; its repetition accuracy is ± 0.1 mm (ISO 9283), and maximum speed of the robot joints from 1–3 to 4–6 is 180 and 360°/s, respectively. The robot UR3 teach pendent is used to provide the required displacement in a specific direction of the tool.

The AXIA80 is used to find the forces on the finger at the desired displacement. The sensor net mass is 0.28 kg and it measures the force in the range of ± 75 N, ± 75 N, and ± 470 N in x, y, and z direction, respectively; it has a resolution of 0.04 N in all axes. The robot end-effector is connected to the test object pointer through the force sensor, as shown in Fig. 9. The soft robotic fingers are rigidly fixed on the plank with the help of a nut and bolt; it is attached to the table using fixtures. The test object pointer is placed on the finger at required location and pushes the finger in positive Z direction until it reaches the targeted force values using UR3 teach pendant. Once the pointer touches the contact surface of the finger, the robot moves at a velocity of 0.1 mm/s. The GW instek GPD-3303S multiple output programmable power supply device is connected to the FT sensor. A PYTHON based code is developed to acquire the force values at the contact point of test object and finger. After reaching the targeted force values, the robot is stopped at the position, and displacement values are recorded.

Fig. 9
figure 9

The experimental setup to measure the force versus displacement using UR3 robot and force sensor

Full size image

3 Results and discussions

This section details the results obtained from nonlinear simulations as described above. The robotic fingers are manufactured with the help of a Prusa tabletop 3D-printer using TPU 95A flexible material to validate the simulation results and test the deformation zones of the finger. Finally, grasping is demonstrated for two structurally distinct objects, such as a coffee cup and a wooden block, to check the conformability of the fingers.

3.1 Deflection coefficient of fingers

In this nonlinear simulation, the deflection coefficient is measured using Eq. 3 with the help of SOLIDWORKS software, as shown in Sec. 2.4. The fingers with different filling variants and thicknesses are tabulated along with deflection coefficient and ranking, as shown in Table 3. The graph notations are given to the fingers based on the structure and parameter changes for easy communication in the graphs and text. The wrapping or grasping capacity of the fingers will be increased for the smallest deflection coefficient, which we refer to as best fingers. From the results, the smallest deflection coefficient is recorded as Cd = 0.1574 for straight slot structure C with struts thickness of TS = 2 mm (CTS2); out of all simulated results, this finger provides high wrapping capabilities. Poor wrapping around the object is obtained for fingers with inclined struts at an angle of + 45° and thickness TS = 4 mm (DTS4). In this structure, the struts are nearly parallel to the axis of applied force and thus will offer more resistance to the applied force, and the maximum deflection coefficient is recorded as Cd = 0.3134. Moreover, the interpretation of the results extends to thoughts of structural mechanics and material behavior. For instance, the observed trend of increasing deflection coefficient with thicker strut thicknesses highlights the role of material stiffness in governing deformation under load. The topologically optimized structure with volume fraction vf = 0.1 (FVF0.1) achieved highest wrapping capabilities with a deflection coefficient of Cd = 0.1896. The designs are categorized accordingly. In each category, the best fingers are arranged in terms of their wrapping capabilities determined based on the deflection coefficient, as shown in Eq. 4.

$$ {\text{CTS2}} > {\text{ETS2}} > {\text{FVF0}}{.1} > {\text{BTS2}} > {\text{ATS2}} > {\text{DTS2}} $$
(4)
Table 3 The replication of experimental combination parameters along with the mean performance values
Full size table

The topologically optimized structure with a volume fraction of vf = 0.1 attained third position based on wrapping capability compared to the other fin ray fingers. This method reduces the mass, where less critical functionality of the densities in the design space. A lightweight design is achieved without compromising strength or flexibility: this optimization leads to more energy-efficient operation of the robotic fingers and potentially increases the speed and precision of the movements. Following this methodology, the practitioners can also select the topologically optimized structure for better wrapping and stiffness of the finger. Along with the wrapping capabilities, the strength of the finger is equally essential; this is evaluated in the following subsection.

3.2 Performance analysis of the robotic fingers

The strength of the soft robotic fingers is equally crucial, along with the wrapping capabilities [16]. In the second simulation, the performance values of the fingers, such as deflection, von Mises stress, and FOS are simulated using SOLIDWORKS software. The CAD models of the best fingers from each category are imported into the software and analyzed using a static structural study. The left side of the fingers is realized as fixed support, and again the considered forces are applied on top of the finger from Fa = 5–30 N with step value of sF = 5. The performance values versus applied forces graphs are plotted for each finger, as shown in Fig. 10.

Fig. 10
figure 10

The performance values of the robotic fingers such as Max deflection (mm), Max stress (MPa), and FOS for A ATS2 B BTS2 C CTS2 D DTS2 E ETS2 F FVF0.1

Full size image

These findings disclose a linear increase in both maximum deflection and von Mises stresses as the applied force magnitude increases, while the factor of safety (FOS) decreases. This underscores the critical role of finger strength, particularly when the soft robotic gripper handles heavier objects. The high lifetime of fingers is possible when they are subject to less internal stresses and provide a high FOS at higher applied loads. From graphs, the variants CTS2 and ETS2 fingers show the best wrapping abilities of deflections at δ = 37.97 mm and 34.74 mm, respectively, at higher applied force (Fa = 30 N). However, the von Mises stress and FOS values are σ = 10.71 MPa, 8.007 MPa, and FOS = 0.803, 1.074. The topologically optimized finger FVF0.1 shows good wrapping ability of deflection δ = 31.96 mm, and at the same time, the von Mises stress and FOS values are σ = 5.504 MPa, 1.375; these values are better than CTS2. The variant DTS2 gives a poor grasping ability of deflection of δ = 19.272 mm; however, the FOS of the finger is 1.405. The practitioners can select a required structure of the soft robotic fingers based on the targeted performance value.

3.3 Experimental results

For the experimental evaluation, the fingers are placed on the plank and rigidly fixed using a nut and bolt; later, the test object is placed on the top surface of finger at the desired position. The test object is moved one millimeter in a positive Z direction, and force value is recorded, this process is continued until the value crosses Fa = 30 N. Later, the graph is plotted using these points in MATLAB, and deflection values are interpolated exactly at step value of forces Fa = 5–30 N. The deformed finger in the experiments and simulations are compared, as shown in Fig. 11. As shown in Fig. 11, the simulation results of deformed fingers are very closely related to the experimental results at the maximum applied force of Fa = 30 N. The fin ray fingers C and D are subjected to maximum and minimum deformation, respectively. The same simulation order is followed in the experiments regarding the deformation, as shown in Eq. 4. The deformation results exactly at the desired force values are interpolated from graphs using MATLAB software. The simulation and experimental deflection values are plotted and shown in Fig. 12. The simulated and experimental values of deflection values are in decent agreement with a maximum deviation of esim = 2.314%. The simulations results are relied on averaged material properties derived from tensile testing. However, the actual material properties of 3D-printed parts can vary due to variations in factors such as layer orientation, print speed, and temperature, which are not captured in the averaged values. These variations could lead to differences in the simulated and experimental values of deflection.

Fig. 11
figure 11

The soft robotic finger deflection is compared between experiments (left) and simulations (right) for A ATS2 B BTS2 C CTS2 D DTS2 E ETS2 F FVF0.1

Full size image
Fig. 12
figure 12

The simulations and experimental values of the deflection and applied force comparison for fingers left: ATS2, BTS2, DTS2 and right: CTS2, ETS2, and FVF0.1

Full size image

After applying force, robotic fingers are subject to deformation phase [50]. To understand the behavior of the designed fingers with respect to the deformation phases, a prescribed displacement of d0 = 25 mm is applied using a test object on all fingers, and force values are captured over time, as shown in Fig. 13. All fingers are reached maximum displacement within four see and the test object is stays at the same position until 5 s to check the settled force for deformation analysis. From these results, one can conclude that the fin ray fingers are showing more or less similar kind of trend in the deformation phase. To capture this effect, the percentage of change in maximum force to the settled force of the test object (ΔF) is measured and shown in Fig. 13. The DTS2 structure out of fin ray fingers shows the maximum value of ΔF = 11.3%; due to its inclined struts design, it inherently exhibits higher resistance to deformation at initial loading stages due to the geometric alignment of the struts in fin ray fingers. The FTF0.1 topologically optimized finger allows higher deformation change in the structure of ΔF = 34.2%, and provides a new method for designing soft fingers [12]. Due to the higher ΔF value, the finger can more effectively distribute contact pressures and adapt its shape to various objects, improving grip security and dexterity. Such features are particularly advantageous in applications requiring the handling of delicate or irregularly shaped objects. The design optimizations that led to the higher deformation change also contribute to the structural resilience of the FTF0.1 finger. By enabling larger deformations without failure, the finger can absorb and adapt to unexpected loads or impacts, reducing the risk of damage during operation. This deformation phase provides good wrapping and conformable abilities to the finger. The optimized finger force values are increased with higher slope compared to other fingers at large displacement due to the stiffness offered by the structure.

Fig. 13
figure 13

The deformation phases of the soft robotic fingers after the removal of force over time

Full size image

3.4 Demonstration of grasping tasks

The soft robotic fingers are used to grasp objects such as coffee cup and wooden block, as shown in Fig. 14. In the selected two objects, the coffee cup is cylindrical with a heavier mass of m = 260 g, and wooden block is cubic with a lighter mass of m = 80 g. The coffee cup makes a circular, whereas the wooden block makes point contact with the soft robotic fingers. The wrapping ability of the 3D-printed fingers can be seen from the grasping tasks, while the fingers hold the objects. From Fig. 14, all fingers smoothly adapt to the objects in the grasping task; however, the CTS2 and FVF0.1 fingers show good wrapping ability and contact area with the objects. The adaptability ensures a more distributed contact pressure, which is crucial for securely grasping and manipulating objects without causing damage, especially for delicate or irregularly shaped items. The increased contact area provided by the optimized design of these fingers enhances the frictional grip on objects. This feature is particularly helpful when handling smooth-surfaced items, where a larger contact area can significantly improve grasp stability. The practical deformation of the finger is hard to measure in this task; therefore, the quantification of its value is not provided here. The material properties of TPU 95A contribute significantly to the performance of finger; however, they also pose limitations. The repeated or prolonged use, particularly at high stress or strain levels, could lead to material fatigue or wear, affecting long-term reliability. The balance between flexibility and durability requires careful consideration in design and material selection. Our study mainly focused on mechanical design and performance of fingers. However, integrating tactile sensors to enhance control and responsiveness during grasping tasks presents an additional challenge. In future work, tactile sensors will be integrated into fingers to achieve precise control over the gripping force. Adapting to unexpected object movement or slippage during manipulation requires sensing and control strategies.

Fig. 14
figure 14

The demonstration of grasping task (left-1) coffee cup and (right-2) wooden block for A ATS2 B BTS2 C CTS2 D DTS2 E ETS2 F FVF0.1

Full size image

4 Conclusions

Soft robotic grippers can operate efficiently in dynamically changing environments and become more and more essential in modern developed end-effectors for industrial manipulators. The possibilities to grasp more complex, delicate, and difficult-shaped geometries with soft material and fin ray effects are very attractive to be researched. In this work, various filling patterns of robotic fingers are designed and evaluated using the deflection coefficient value. Generally, soft robotic fingers do not perform well in heavy-load applications. Consequently, the topology optimization of the fingers was introduced for obtaining both gripping capabilities and structural strength, while yielding the most lightweight designs. To this end, the objective function was chosen as minimization of mass with constraints of deflection and von Mises stress threshold values. The topologically optimized fingers were generated for volume fractions from vf = 0.1–0.3 with a step value of sM = 0.05. The 3D-printing material was selected as TPU 95A, which is soft and flexible. However, due to the nature of 3D-printing, material properties of the printed devices are not the same as those of standard bulk material, therefore tensile testing was conducted with the help of Zwick Roell Z020 to measure the material properties using 3D-printed specimen based on the ISO 527-2 standard. First, simulations were conducted using SOLIDWORKS software to find the wrapping ability of the fingers. For better grasping ability, the deflection coefficient value should be minimum. The variant CTS2 and DTS4 provided best and worst wrapping capabilities out of 35 variant fingers with deflection coefficients of Cd = 0.1574 and 0.3134, respectively. At maximum applied force of Fa = 30 N, the best wrapping finger (CTS2) performance values were recorded as δ = 37.97 mm, σ = 10.71 MPa, and FOS = 0.803. However, the finger was not performing well at the higher applied forces. The topologically optimized finger performance values (FVF0.1) were recorded as δ = 31.96 mm, σ = 5.504 MPa, and FOS = 1.375. Even though the finger has less deflection of 6.01 mm, it possesses FOS of 1.71 times stronger than CTS2. The experimental setup was developed to validate the simulation results with the help of an UR3e robotic arm, AXIA80 force sensor, and 3D-printed test object. The test object was moved using a teach pendent in the positive Z direction by a distance of 2 mm, and the force values were recorded up to it crossed 30 N. The graph was interpolated using MATLAB, and the deflection values were recorded precisely at the required forces from Fa = 5–30 N with a step value of sF = 5. The deformation zones are analyzed experimentally, and topologically optimized structure enters into the higher deformation zone with ΔF = 34.2% for good wrapping of the object. The simulation and experimental results were in good agreement, with a maximum deviation of esim = 2.314%. Finally, the grasping task of fingers was demonstrated with the help of a coffee cup and wooden block to show the conformability of the fingers.