1 Introduction

The transport of fluids in channels has been an interesting topic over many decades, with interesting applications in many fields of research in industry, biomechanics and medical engineering. Recent developments involve fluids with complex structure, industrial and biological fluids such as refrigerants, lubricants, bioliquids, and polymeric solutions and in the past two decades nanofluids in which the presence of nanoparticles helps to enhance and control the various thermophysical characteristics of the flow. A huge amount of literature exists on the subject, among which [1,2,3,4,5,6,7,8,9,10,11] just to cite a few, in which different factors are investigated which affect the fluid flow, for example the effect of electric and magnetic fields, the shape of the channel, the type of fluid and the thermal effects. Exact solutions could be found to few of these problems, but numerical methods are most popular to deal with the arising nonlinear systems of partial differential equations.

The cylindrical Couette flow has attracted the attention of many researchers in the two cases of axial or rotational motions, due to its numerous applications in industry and in biomechanics. Stability problems form an important trend in this field of research. Complex boundary conditions may be significant for a proper desription of the fluid–structure interaction at the interface. The dynamic wall slip involving a time derivative is an example of such boundary conditions. It emerged from laboratory experiments showing that the slip velocity of certain fluids exhibits a relaxational or delay behavior that requires introduction of a dynamic response of the fluid. Such a dynamic slip introduces a dissipative term and thus requires attention as it adds to the technical difficulties facing the process of finding solutions. Hatzikiriakos et al. [12] pointed out at the existence of slip in industrial applications involving fluids of complex structure, more specifically polymer melts. A mathematical analysis of Navier–Stokes-like problems with a dynamic slip boundary condition was developed by Abbatiello et al. [13]. Matthews and Hill [14] reviewed the continuum description of nanofluidics with altered boundary conditions at the fluid–structure interface. Gittler [15] studied the linear stability of axial parallel Poiseuille–Couette flow in an annulus between concentric cylinders, where it is shown that pure sliding Couette flow can become unstable if the radius ratio is below a specific threshold value. Kaoullas and Georgiou [16] derived analytical solutions for the Newtonian Poiseuille and Couette flows with dynamic wall slip. Malkin and Patlazhan [17] presented a review on the slip condition in complex liquids. Abou-Dina et al. [18] investigated a problem of plane Couette flow under dynamic wall slip. Analytical approximate solutions for the axial flow of polymer power-law fluids in an annular region were presented by Deterre et al. [19], but ignoring dynamic slip. Pitsillou et al. [20] considered various steady shearing Newtonian Couette or Poiseuille flows with logarithmic and Navier wall slip. Huilgol and Georgiou [21] developed a fast numerical scheme for the study of non-Newtonian fluid flow in pipes under pressure gradient.

A thorough review of the literature reveals that initial boundary value problems for Couette flow under dynamic slip boundary condition are very few in number. To the best of authors’ knowledge, no attempt was made to investigate the cylindrical annular Couette flow under dynamic wall slip condition.

In the present work we consider the transient annular Couette flow of a Newtonian viscous fluid between coaxial circular cylinders under dynamic wall slip, using Laplace transform technique. The inner cylinder is given a sudden axial velocity that is kept constant in subsequent times, while the outer cylinder is held stationary. The boundary condition on the outer cylinder is a dynamic slip condition and on the inner one a non-slip condition. The dynamic wall slip takes place in transient regimes and represents a dissipative retardation phenomenon that may have relevant effects on the flow (C.f. [17]). It is thus a problem of practical interest. It is the aim of the present work to assess the importance of the dynamic slip on the flow behavior. For this reason, the properties of the flowing liquid have been kept simple, involving only viscosity. Laplace transform technique and inversion by Laguerre polynomials is used here to find the solution of the governing equations and limiting conditions. It is known that the numerical inversion using Laguere polynomials gives high accuracy on a wide range of functions (C.f. [22]). Moreover, this method may be applied, in conjunction with perturbation methods, to solve difficult problems of nonlinear Couette flow and similar problems.

The material of this work is presented as follows: Sect. 1 is an Introduction; in Sect. 2, the governing equations and the boundary conditions of the start-up annular Couette flow of a Newtonian fluid are presented. The steady-state solution is derived and compared to the planar Couette case. In Sect. 3, the Laplace transform method for solving the flow problem is briefly presented and the numerical method used for the inversion of the Laplace transform is discussed. Section 4 is devoted to the numerical results. The calculated solution is tested against the steady-state solution, which it is eventually reached at infinite time. In Sect. 5, the conclusions are presented.

The obtained results illustrate the interplay between the two slip coefficients: Navier slip and dynamical slip. It is demonstrated that these two slip parameters yield damping effect on the evolution of the time-dependent solution as expected. More specifically, it turns out that in the presence of Navier slip, the dynamical slip has noticeable effect only when the corresponding parameter \(\Lambda \) is sufficiently large. The presence of dynamic wall slip produces retardation in reaching the steady state. This fact has important consequences in rheometry. The obtained results assess the effect of both slip parameters on the volumetric flow rate, which is one of the important factors for flow control. Comparison was carried out with the case of no dynamic slip. It is shown that the dynamic slip reduces the flux, but this reduction tends to disappear as steady state is approached.

It is important to note that the proposed method relying on the use of Laplace transform and numerical inversion by Laguerre polynomials, as for other techniques, loses efficiency when the thickness of the annulus decreases, and when the values of the slip parameter B are smaller.

2 Governing equations

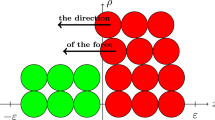
We consider the unidirectional, annular flow of a Newtonian viscous fluid occupying the region between two infinite circular coaxial cylinders of radii \(R_1\) and \(R_2\), \(R_1 < R_2\). The fluid is assumed to exhibit dynamic wall slip along the fixed outer cylinder and no-slip along the moving inner cylinder. The fluid is at rest, and suddenly, the inner cylinder starts moving axially at a speed \(U_0\), while the outer cylinder is kept fixed as illustrated in Fig. 1.

Fig. 1
figure 1

Geometry of annular shear flow

Full size image

Assuming that the effect of gravity is negligible and that all thermal effects can be neglected, the r-component of the momentum equation in cylindrical coordinates reduces to

$$\begin{aligned} \frac{\partial U}{\partial t}(r,t)=\nu \frac{1}{r}\frac{\partial }{\partial r } \left( r \frac{\partial U}{\partial r} \right) . \end{aligned}$$
(1)

The boundary conditions for this initial boundary value problem read:

$$\begin{aligned} U(r,t)=U_0 \, H(t) \hspace{70pt} \text {at} \, r=R_1, \end{aligned}$$
(2)
$$\begin{aligned} U(r,t)+\lambda \, \frac{\partial U}{\partial t}(r,t) = - \frac{1}{B} \frac{\partial U}{\partial r}(r,t) \hspace{50pt} \text {at} \, r=R_2, \end{aligned}$$
(3)

where H(t) denotes the Heaviside unit step function and \(\lambda , B\) are the non-negative dynamical slip and Navier slip numbers, respectively (see [18]). The added negative sign in the r.h.s. of equation (3) is due to the fact that the velocity gradient is negative throughout the flow, This sign should be removed in case the start-up velocity is placed at the outer boundary.

The initial condition is given by

$$\begin{aligned} U (r,0) = 0 \hspace{80pt} \text {at} \quad t\le 0. \end{aligned}$$
(4)

Here, U is the velocity, and the other parameters have their usual meaning (see [18]).

The simplified model under consideration allows to concentrate on the effect of the dynamic wall slip on the flow behavior, and on the interplay between this dynamic slip and Navier slip.

We shall now go to the dimensionless form of Eqs. (1)–(4). To this end, we introduce the characteristic velocity \(U_0\) and length \(R_1\):

$$\begin{aligned} R\equiv \frac{r}{R_1},\ \ \ \ \epsilon \equiv \frac{R_2}{R_1},\ \ \ \ V\equiv \frac{U}{U_0} ,\ \ \ \ T\equiv \frac{\nu t}{R_1^2} \end{aligned}$$

and

$$\begin{aligned} \Lambda \equiv \frac{\lambda \nu }{R_1^2}, \quad B' \equiv B R_1 \end{aligned}$$

are the dimensionless slip-relaxation and slip numbers, respectively. With the above scalings, after dropping the 'prime,’ the equations in dimensionless form read:

$$\begin{aligned} \frac{\partial V}{\partial T}(R,T)= \frac{\partial ^2 V}{\partial R ^2}(R,T)+\frac{1}{R}\frac{\partial V}{\partial R}(R,T) \end{aligned}$$
(5)

The initial and boundary conditions are given by:

$$\begin{aligned}{} & {} T\le 0: \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ V (R,0) = 0 \ \ \ \ \ \ \ \ \ \, \text {for} \, \, 1 \le R\le \epsilon \end{aligned}$$
(6)
$$\begin{aligned}{} & {} T>0: \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ V(R,T) = H(T) \ \ \ \ \ \ \ \ \ \ \ \ \ \text {at} \, \, R=1\ \ \end{aligned}$$
(7)
$$\begin{aligned}{} & {} V(R,T)+\Lambda \frac{\partial V}{\partial T}(R,T) = - \frac{1}{B} \frac{\partial V}{\partial R}(R,T) \hspace{20pt} \text {at} \, \, R=\epsilon \end{aligned}$$
(8)

2.1 The steady-state solution

For large values of time, a steady state practically establishes in the flow domain. This solution may be derived directly by setting to zero all time derivatives in the governing equation and boundary conditions. It reads:

$$\begin{aligned} V_{st}(R) = \frac{1 + B \epsilon \ln \frac{\epsilon }{R}}{1 + B \epsilon \ln \epsilon }, \end{aligned}$$
(9)

This steady-state profile is logarithmic, in contrast to the linear one for the Newtonian viscous flow between two plates (C.f. [18]). In case \(R = \epsilon \), i.e., at the outer cylinder, one gets the value of the steady-state velocity in the form:

$$\begin{aligned} V_{st}(\epsilon ) = \frac{1}{1 + B \epsilon \ln \epsilon }. \end{aligned}$$
(10)

Figure 2 represents the steady-state solution for three values of parameter B. Note that the no-slip case corresponds to \(B = \infty \), from which we get \(V_{st}(\epsilon ) =0\). The other limiting case corresponds to \(B = 0\), which implies that we have full slip. In this case the velocity profile in Eq. (23) is simply \(V_{st}(\epsilon )=1\).

The value of the steady-state slip velocity \(V_s\) for the plane Couette flow as given in [18] is \(V_s = \frac{1}{B+1}\). In reference to this value, the relative variation of the steady-state slip velocity between the annular and the plane Couette flows is given by:

$$\begin{aligned} \frac{\Delta V_s}{V_s} \equiv \frac{V_s^{annular} - V_s}{V_s} = B . \frac{1 - \epsilon \ln \epsilon }{1 + B \epsilon \ln \epsilon }. \end{aligned}$$
(11)

This expression vanishes for

$$\begin{aligned} \epsilon \ln \epsilon = 1, \end{aligned}$$

irrespective of the value of the Navier slip number B.

Fig. 2
figure 2

Profiles of the steady-state velocity for \(\epsilon = 1.4\) and three values of B as calculated from the final-value theorem of Laplace transform: \(B=1.0\) (dotted line); \(B=10.0\) (dash-dotted line); \(B=100.0\) (plain line)

Full size image

Figure 3 exhibits this relative variation as function of parameter \(\epsilon \), from which it is seen that that the steady-state slip velocity for the annular Couette flow is approximately the same as that of the plane Couette flow for values \(\epsilon \simeq 1.765\), but is different otherwise.

Fig. 3
figure 3

Relative variation of the steady-state slip velocity as function of \(\epsilon \) for three values of B, based on the slip velocity \(V_s\) of the plane Couette flow: \(B=1.0\) (dotted line); \(B=10.0\) (dash-dotted line); \(B=100.0\) (plain line)

Full size image

3 Time-dependent solutions

The standard Laplace transform method is used to derive the solution of problem (5)-(8), with Laguerre polynomials expansion to achieve the numerical inversion of Laplace transform for the determination of the initial velocity function V(R, T).

3.1 Solution by Laplace transform

Define the Laplace transform of V(R, T) as:

$$\begin{aligned} \bar{{V}}{(R,p)}= \int _{0}^{\infty } V(R,T) e^{-pT} dT. \end{aligned}$$
(12)

The transformed problem in terms of the new dependent variable \(\bar{{V}}{(R,p)}\) reads:

$$\begin{aligned}&\frac{d^2 \bar{V}(R,p)}{d R^2}+\frac{1}{R} \frac{ d\bar{V}(R,p)}{d R}- p \bar{V}(R,p)=0 \end{aligned}$$
(13)
$$\begin{aligned}&\bar{V}(R,0) = 0 \hspace{50pt} \ \ \ \ \ \ \text {for} \, \ 1\le R\le \epsilon \ \ \end{aligned}$$
(14)
$$\begin{aligned}&\bar{V}(1,p) =\frac{1}{p} \end{aligned}$$
(15)
$$\begin{aligned}&\frac{d\bar{V}}{d R}(\epsilon ,p)= - B (1+\Lambda p) \bar{V}(\epsilon ,p). \end{aligned}$$
(16)

The solution of Eq.(13) satisfying boundary conditions (15)–(16) is easily seen to be:

$$\begin{aligned} \bar{{V}}{(R,p)}= \alpha (p) I_0(\sqrt{p} R) + \beta (p) K_0(\sqrt{p} R), \end{aligned}$$
(17)

where \(I_0\) and \(K_0\) denote the well-known modified Bessel functions, and the coefficients \(\alpha (p)\) and \(\beta (p)\) are given as:

$$\begin{aligned} \alpha (p)&=\frac{- B (1+ \Lambda p) K_0(\sqrt{p}\epsilon ) + \sqrt{p} \, K_1(\sqrt{p}\epsilon )}{D}.\frac{1}{p} \end{aligned}$$
(18)
$$\begin{aligned} \beta (p)&= \frac{B (1+ \Lambda p) I_0(\sqrt{p}\epsilon ) + \sqrt{p} \, I_1(\sqrt{p}\epsilon ) }{D}.\frac{1}{p}, \end{aligned}$$
(19)

with

$$\begin{aligned}{} & {} D = - B.(1+ \Lambda p) \left[ K_0(\sqrt{p}\epsilon ) I_0(\sqrt{p}) - I_0(\sqrt{p}\epsilon ) ) K_0(\sqrt{p}) \right] \nonumber \\ {}{} & {} \quad + \sqrt{p} \left[ K_1(\sqrt{p}\epsilon ) I_0(\sqrt{p}) + I_1(\sqrt{p}\epsilon ) ) K_0(\sqrt{p}) \right] . \end{aligned}$$
(20)

The steady-state solution may be recovered within the above formulation by assigning sufficiently large values to the time. The final-value theorem of Laplace transform enables us to find the value of a function as time grows indefinitely large directly from its Laplace transform without the need for finding the inverse Laplace transform. This theorem is expressed as:

$$\begin{aligned} \lim _{t \rightarrow \infty } V(R,t) = \lim _{p \rightarrow 0} p \, \bar{V}{(R,p)}. \end{aligned}$$
(21)

Using the well-known asymptotic expressions for modified Bessel functions for small argument:

$$\begin{aligned}{} & {} I_{\alpha }(z) \sim \frac{1}{\Gamma (\alpha + 1)} \left( \frac{z}{2} \right) ^{\alpha }, \\{} & {} K_{\alpha }(z) \sim {\left\{ \begin{array}{ll} \frac{\Gamma (\alpha )}{2} \left( \frac{2}{z} \right) ^{\alpha }, &{} \alpha \ne 0 \\ - \ln \left( \frac{z}{2} \right) - \gamma , &{} \alpha = 0, \end{array}\right. } \end{aligned}$$

where \(\Gamma \) denotes the gamma function and \(\gamma \) is the Euler–Mascheroni constant (\(\gamma \simeq 0.577\)), one obtains after some manipulations the following expression for the steady-state solution:

$$\begin{aligned} \lim _{t \rightarrow \infty } V(R,t) = \frac{1 + B \epsilon \ln \frac{\epsilon }{R}}{1 + B \epsilon \ln \epsilon }, \end{aligned}$$
(22)

which matches exactly the solution given in (9).

3.2 Numerical inversion of Laplace transform by Laguerre polynomials

The inversion of the Laplace transform may be easily obtained by the method presented in [23], the main idea of which resides in finding a suitable representation of the given transform in its domain of regularity, using a certain class of functions whose inversion is known. The method is explained here briefly. Further details may be found in the cited reference. Other applications of the method are presented in [24, 25]. For this purpose:

  • The transform function \(\bar{{V}}{(R,p)}\) of the complex variable \(p = s + i \omega \), is assumed to be analytic in the right half-plane including the imaginary axis for all values of R. Moreover, suppose that

    $$\begin{aligned} \lim \left[ p \bar{{V}}{(R,p)} \right] \end{aligned}$$

    exists, is finite and uniquely determined as p approaches infinity in both directions of the imaginary axis and that \(\bar{{V}}{(R,p)}\) can be calculated numerically at arbitrary points of the imaginary axis. This is almost usually the case in practical situations.

  • Make the conformal transformation

    $$\begin{aligned} z=\frac{\zeta -p}{\zeta +p} \end{aligned}$$
    (23)

of the complex plane on itself, where \(\zeta \) is a real positive number, which maps the entire right half-plane into the interior of the unit circle. The unit circle itself becomes the image of the infinite imaginary axis. Parameter \(\zeta \) plays the important role, when properly chosen, of accelerating the convergence of some used series representation as explained in the sequel.

  • Introduce a new function

    $$\begin{aligned} F(R,p)= (\zeta +p) \bar{{V}}{(R,p)} \end{aligned}$$
    (24)

    that remains finite even as parameter p tends to \(\pm i \infty \). This new function allows to express the transform function \(\bar{{V}}{(R,p)}\) finally as a series expansion of functions which could be invertible and produce known expressions. Now express F(R, p) in terms of the new variable z and let the resulting function be denoted F(R, z). This function is finite on the unit circle and analytic in its interior.

  • Approximate function F(R, z) by an interpolating polynomial P(z) at n equidistant points on the unit circle:

    $$\begin{aligned} P(R,z) = \displaystyle \sum _{k=0}^{n-1} C_k(R) \, z^k \end{aligned}$$

  • Determine the coefficients \(C_k(R)\)

  • Find the inversion Laplace transform \(\mathcal {L}^{-1}\) in the form:

$$\begin{aligned} V(R,t) = \displaystyle \sum _{k=0}^{n-1} (-1)^k \xi _k(R) \,\ell _k(2 \zeta t), \end{aligned}$$
(25)

where \(\xi _k\) are the real parts of \(C_k\), and \(\ell _k\) are Laguerre polynomials defined as:

$$\begin{aligned} \ell _k(t)= \frac{e^{t/2}}{k!} \frac{d^k}{dt^k} \left( t^k \, e^{-t} \right) = e^{-t/2} L_k(t), \quad k=0,1,2, \ldots . \end{aligned}$$
(26)

It is known [26] that the functions \(\ell _k(t), \, k=0,1,2, \ldots \) form a set of orthonormal polynomials in the interval \((0, \infty )\).

4 Numerical results

The Laguerre series (25) is shown in [23] to converge uniformly (even absolutely) over every finite interval \(0 \le t \le t_0 < \infty \) towards the actual original function V(R, T). The derviatives of V(R, T) can be obtained by differentiating the Laguerre series for V(R, T) term-wise, which converge again uniformly (even absolutely) over the same time interval. A reasonable value for the parameter n appearing in the above sum compromises between accuracy and the calculation time. For our purposes, \(n \simeq 100\).

Many numerical experiments were carried out in order to assess the dependence of the solution on the value of the parameter \(\zeta \), the proper choice of which is of primordial importance for correct numerical results. It was noted that reliable results could be obtained only when \(\zeta \ge 2.5\). This is different from the case of plane Couette flow, the calculations of which have shown that \(\zeta \ge 1.1\).

The displayed numerical results have been obtained with \(\zeta = 2.5\) and radii ratio \(\epsilon = 1.4\). Figure 4 shows a normal cross section of the flow region, which is a moderately thick annulus. Generally, computations are more difficult to carry for thinner annuli.

Fig. 4
figure 4

Moderately thick flow region

Full size image

4.1 Case \(\Lambda =0\)

Figure 5 shows the velocity profile for \(\Lambda =0.0\) and slip number \(B=1\) at different time moments. The value of the slip velocity as calculated from the upper curve (steady state) matches that in Fig. 2. One may thus conclude that the steady state practically establishes and the flow may be considered as fully developed starting from time \(t=5\).

Fig. 5
figure 5

Velocity profile for \(\Lambda =0.0\) and \(B=1.0\) at different time moments

Full size image

Figure 6 shows the behavior of the slip velocity with time for different values of the Navier slip parameter B, with curves tending to saturation values which decrease as B increases.

Fig. 6
figure 6

Slip velocity for \(\Lambda =0.0\) and different values of parameter B

Full size image

4.2 Case \(\Lambda \ne 0\)

In the following figures, the dynamic slip parameter \(\Lambda \) will be given different nonzero values, in order to assess its influence on the flow. For the sake of comparison, this parameter will sometimes be given zero value.

At first we shall explore the effect of small values of the dynamic slip parameter \(\Lambda \) on the flow behavior. Figures 7 and 8 represent the velocity profiles at different time moments for \(B=1.0\), and for \(\Lambda =0.01, 0.1\), respectively. It is noticed that these two figures are close to each other, almost undistinguishable, although the value of parameter \(\Lambda \) was increased by 10 times. One may thus conclude that the small enough values of the dynamic slip parameter \(\Lambda \) yield almost the same effect on the flow.

Fig. 7
figure 7

Evolution of the velocity profiles for \(B = 1.0\), \(\Lambda =0.01\) and different values of time

Full size image
Fig. 8
figure 8

Evolution of the velocity profiles for \(B = 1.0\), \(\Lambda =0.1\) and different values of time

Full size image

Figures 9, 10 and 11 illustrate the evolution of the slip velocity for three values of Navier slip parameter B: \(B=1.0, 3.0, 10.0\) and four values of the dynamic slip parameter \(\Lambda \) ranging from 0.0 to 1.0. These figures will serve as reference for the evaluation of the effect of the dynamic slip parameter \(\Lambda \) on the slip velocity. As time grows, the curves tend asymptotically to saturation values which decrease monotonically as parameter \(\Lambda \) increases. The slip velocity decreases as B increases.

Fig. 9
figure 9

Time evolution of the slip velocity for \(B = 1.0\) (strong slip) and four values of \(\Lambda \)

Full size image
Fig. 10
figure 10

Time evolution of the slip velocity for \(B = 3.0\) and four values of \(\Lambda \)

Full size image
Fig. 11
figure 11

Time evolution of the slip velocity for \(B = 10.0\) (moderate slip) and four values of \(\Lambda \)

Full size image

4.3 Volumetric flux

In problems involving fluid flow in tubes and channels, it is of practical importance to secure accurate volumetric flux measurements, irrespective of the nature of the flowing fluid and the geometry of the tube or channel. Accurate measurement of the volumetric flux ensures an efficient fluid control. It can have a significant effect on output quality, reduction of waste and minimisation of environmental impact, a vital requirement in industry for cost efficiency, health and safety purposes.

Figure 12 represents the behavior of the volumetric flux as function of time for a case of strong Navier slip (\(B=1.0\)) for four values of the dynamic slip parameter \(\Lambda \), while Fig. 13 illustrates the flux as function of time for \(\Lambda =0.5\) and three values of parameter B. For the sake of comparison, we have represented in Fig. 14 the volumetric flux for the case of no dynamic slip and for three values of parameter B. Comparison shows that the volumetric flux has decreased by \(\simeq 33\%\) as parameter \(\lambda \) has changed value from 0 to 0.5.

Fig. 12
figure 12

Volumetric flux as function of time for \(B = 1.0\) (strong slip) and four values of \(\Lambda \)

Full size image
Fig. 13
figure 13

Volumetric flux as function of time for \(\Lambda = 0.5\) and three values of B

Full size image
Fig. 14
figure 14

Volumetric flux as function of time for \(\Lambda = 0.0\) and three values of B

Full size image

5 Discussion

As explained above, the simple nature of the flowing viscous fluid, and the exclusion of gravity and of any thermal effects in the present formulation, has allowed to concentrate on the effect of the dynamic slip with parameter \(\Lambda \) on the flow behavior, and the interplay with Navier slip with parameter B. In particular, the retardation influence of both slips was put in evidence in the figures illustrating the distribution of velocity in the annulus as function of time. Again, the influence of dynamic slip in decreasing the volumetric flux rate is shown in Figs. 12, 13 and 14. In all cases, it was found that for a given value of the Navier slip parameter B, the influence of the dynamic slip far from the steady state becomes significant only for larger values of the parameter \(\Lambda \), so that it is possible to neglect the effects arising from this parameter altogether in certain cases. However, it is believed that for fluids with complcated structure, it is necessary to include this dynamical slip parameter in the boundary condition for an efficient description of the flow.

The realistic shapes of the obtained curves for the velocity distribution in the annulus, and the volumetric flux rate for different values of the slip parameters, clearly indicate that the proposed method for the inversion of the Laplace transform by Laguerre polynomials yields reliable results. Further validation was realized by comparing the steady state solution with known ones. However, it is important to note that the influence of the geometrical parameter \(\ell \) occuring in the inversion formulas is crucial during calculations. This parameter needs to be chosen in a proper way that secures stability of the results when this parameter is changed, so as to guarantee the existence of an interval of continuous dependence of the solution, inside which this parameter can be varied safely. Our calculations have been carried out within this spirit.

6 Conclusions

The start-up Newtonian annular Couette flow between two long coaxial circular cylinders with dynamic slip along the fixed outer cylinder has been solved analytically using the Laplace transform method. The effects of the conformal mapping, slip and slip relaxation parameters have been discussed and representative ranges of the three parameters corresponding to certain numerical experiments were deduced. It is demonstrated that two slip parameters have a damping effect on the evolution of the time-dependent solution as expected. The numerical results suggest that if the dynamical slip parameter is small enough, it can be neglected altogether. However, this might not be true for other fluids of more complex nature, for which the dynamic slip consideration is necessary for a reliable description of the flow characteristics. It is noticed that the steady-state velocity profile is logarithmic, in contrast to the linear one for the plane Couete flow. Again, the annular Couette flow yields values of the slip velocity which are close to those of the plane Couette flow only when the radii ratio is \(\epsilon \simeq 1.765\).

The fact that reaching a steady state in the presence of dynamic wall slip may take very long times is of importance in rheometry. The analytical solution presented here may be useful in calculating the slip relaxation coefficients from transient experiments on Newtonian viscous fluids. As slip becomes stronger (i.e., for smaller values of parameter B), the effect of parameter \(\Lambda \), before reaching a steady state, becomes less noticeable.

The volumetric flow rate was calculated for different values of the slip parameters, as this is important for control purposes of the flow. Comparison was carried out with the case of no dynamic slip. The obtained results cleary show a decrease of the volumetric flux with increasing dynamical slip. Such a decrease understandably vanishes as a steady state is approached.

The technique for resolving the problem under consideration relies on the use of Laplace transform, with numerical inversion by Laguerre polynomials. It has been noted that computational difficulties arise for thinner annuli and for smaller values of the slip parameter B. In all cases, a proper choice of the geometrical parameter \(\ell \) involved in the inversion formulas is crucial in finding an interval of continuous dependence of the solution on this parameter, in which this parameter can be varied safely, and thus in obtaining reliable results

The presented method will be applied in a forthcoming work, in conjunction with perturbation methods, to solve difficult problems of nonlinear thermal Couette flow. More systematic experimental data on both Newtonian and non-Newtonian fluids will be most useful in understanding better the implications of dynamic slip in practice.