1 Introduction

Since their discovery in Japan in 1991, carbon nanotubes (CNTs) have always attracted the attention of researchers because of their extraordinary chemical, optical, electrical and mechanical properties like other carbon nanomaterials [1]. The fact that CNTs are an effective tool in improving the strength properties of composite (polymer, metal, ceramic and etc.) materials has been the subject of many studies and such studies continue today [2,3,4,5,6,7,8]. These studies present the thermo-mechanical properties, fabrication, functionalization and perspectives of composites reinforced with CNTs, as well as the outstanding challenges in applications in recent years. Due to their extraordinary properties, nanocomposites have been used frequently in various engineering fields such as spacecraft, machinery, automotive and civil engineering in the last decade, first as single-layer and then as laminated structural elements. Because of the laminated structural elements especially laminated plates, which are used as main carrier elements in various industries, are exposed to dynamic loadings in most cases, the investigation of their vibration behavior has always been the focus of attention. If the vibration behavior of single-layer structural elements was initially discussed in linear formulation and within the framework of classical theory (CT), in recent years the linear behavior of laminated plates containing heterogeneous nanocomposite layers has begun to be discussed within the framework of advanced theories [9,10,11,12,13,14,15,16,17,18,19]. The vibration of heterogeneous anisotropic nanocomposite plates should be addressed in nonlinear formulation when the deflections are comparable to the total thickness and sometimes reach several thicknesses [20,21,22,23,24,25,26,27,28,29].

Laminated composite plates with CNT reinforced layers, intended to be used for various purposes, are in contact with various types of foundations. Since soils have a very complex structure, it is very difficult to model the soil-structure interaction problem mathematically. For safe and economical design, it is necessary to accurately determine the mechanical behavior of the plates in contact with the ground. Since it is difficult to sample for tests that produce results consistent with soil behavior, simplifying assumptions are needed, which determine the types of foundation models. In general, the plate–foundation interaction is idealized as the plates resting on the elastic foundations. Various foundation models such as Winkler, Hetenyi, Timoshenko, Pasternak and Filonenko-Borodich are used in the literature, and one of the most realistic ones is the Pasternak-type foundation model (PT-EF) [30,31,32]. Considering the effect of elastic foundations, the number of studies on linear and nonlinear behavior of layered CNT plates is very limited. Among them, Zhang and Liew [33] performed the large deflection analysis of functionally graded (FG) CNT-reinforced composite skew plates resting on the Pasternak foundation using an element-free Ritz method. Banic et al. [34] investigated the effect of the Winkler–Pasternak foundation on the vibration behavior of plates and shells reinforced with agglomerated carbon nanotubes. Gao et al. [35] studied nonlinear free vibration of FG graphene platelets reinforced porous nanocomposite plates resting on elastic foundation within classical shell theory using three displacement functions. Shen and Wang [36] and Shen et al. [37] studied the linear and nonlinear vibrations of compressed and thermally post-buckled CNT reinforced composite single-layer and sandwich plates resting on elastic foundations. Yang et al. [38] examined the nonlinear bending behavior with negative Poisson's ratio of temperature-dependent FG-CNT-reinforced laminated beams resting on the Pasternak foundation. Avey et al. [39] carried out free vibration of thin-walled composite shell structures reinforced with smooth and linear carbon nanotubes: taking into account the effect of elastic foundation and nonlinearity. Alazwari et al. [40] studied hygrothermal buckling analysis of smart graphene/piezoelectric nanocomposite circular plates on an elastic substrate via DQM. Wu et al. [41] presented free vibration analysis of functionally graded graphene nanocomposite beams partially in contact with fluid. Jin et al. [42] presented a new electro-mechanical finite formulation for functionally graded graphene-reinforced composite laminated thick plates with piezoelectric actuator. The problems addressed in above studies are generally solved using numerical methods.

Each of the factors listed above alone can seriously affect the vibration behavior of laminated structural members. However, taking into account their combined effects further increases the difficulty of solving and analyzing the vibration problem of laminated nanocomposite structural members. Therefore, the development of an efficient and reliable analytical solution method for the nonlinear vibration of laminated plates made of CNT originating layers resting on elastic foundations (EFs) in the framework of FOPTs is a very current problem. The aim of this work is to study the nonlinear free vibration of laminated plates originating from CNTs in the presence of EFs, and to develop a methodology to establish the dependence of the nonlinear frequency from the amplitude. One of the most important and original aspects of this research is the first-order shear deformation plate theory proposed by Ambartsumyan [43], generalized to heterogeneous laminated nanocomposite plates and solved analytically by a semi-inverse method. Another important aspect is the nonlinearity of the correlations between frequency and amplitude, as well as the originality of all analyzes.

2 Basic relationships

2.1 Statement of the problem

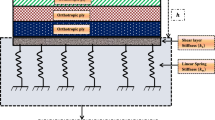
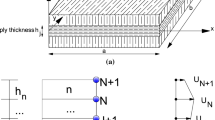
Consider the moderately thick laminated nanocomposite rectangular plate which consists of perfectly bounded \(N\) layers originating from CNTs is simply supported at four edges and rests on the PT-EF, as shown in Fig. 1a, b. The length, width and total thickness of the CNT originating laminated plate are \(a\), \(b\) and \(h\), respectively. Let the \(x,y\) and \(z\) be a set of coordinates with \(x,y\) axes located in the middle plane of the plate and \(z\) axis pointing downwards. The origin of the coordinate system \(Oxyz\) is located at the corner of the laminated plate on the mid-plane. The displacement components of the mid-plane along the \(x,y\) and \(z\) axes are designated by \(u,v\) and \(w\), respectively, \(F_{1}\) and \(F_{2}\) are the mid-plane rotations of the normals about \(y\) and \(x\) axes, respectively. The linear elastic foundation is presented by a two-parameter foundation model or PT-EF, and is modeled as \(P_{0} \, = \, k_{1} w \, - k_{2} \nabla w \,\), where \(P_{0} \,\) is the force per unit area, \(k_{1}\) is the Winkler foundation stiffness and \(k_{2}\) is the shear layer stiffness of the foundation, and \(\nabla\) is the Laplace operator according to the variables \(x\) and \(y\) [30,31,32]. Let \(F(x,y,t)\) be the stress function for the stress resultants defined by \(N_{11} = hF,_{yy} ,\,\,N_{12} = - hF,_{xy} ,\,\,N_{22} = hF,_{xx}\) where the comma is partial differentiation with respect to the corresponding coordinates.

Fig.1
figure 1

a Configuration of laminated rectangular plate with CNT patterns resting on the PT-EF, b cross-section of laminated plate, c CNT originating layers

Full size image

2.2 Mechanical properties of laminated nanocomposite plates

The extended mixing rule is used by introducing the CNT efficiency and the effective properties of nanocomposite layers can be expressed as [9, 11, 20, 24]:

$$\begin{aligned} E_{11}^{(k)} (\overline{z}) & = \eta_{1}^{(k)} V_{cn}^{(k)} Y_{11cn}^{(k)} + V_{m}^{(k)} Y_{m}^{(k)} ,\,\,\,E_{22}^{(k)} (\overline{z}) = \frac{{\eta_{2}^{(k)} Y_{m}^{(k)} Y_{22cn}^{(k)} }}{{Y_{22cn}^{(k)} V_{m}^{(k)} + Y_{m}^{(k)} V_{cn}^{(k)} }}, \\ G_{12}^{(k)} (\overline{z}) & = \frac{{\eta_{3}^{(k)} G_{m}^{(k)} G_{12cn}^{(k)} }}{{G_{12cn}^{(k)} V_{m}^{(k)} + G_{m}^{(k)} V_{cn}^{(k)} }},\,\,\,G_{13}^{(k)} (\overline{z}) = G_{12}^{(k)} (\overline{z}),\,\,\,G_{23}^{(k)} (\overline{z}) = 1.2G_{12}^{(k)} (\overline{z}), \\ \nu_{12}^{(k)} & = V_{cn}^{*(k)} \nu_{12cn}^{(k)} + V_{m}^{(k)} \nu_{m}^{(k)} \,,\,\,\rho_{t}^{(k)} = V_{cn}^{(k)} \rho_{cn}^{(k)} + V_{m}^{(k)} \rho_{m}^{(k)} ,\,\,\,\overline{z} = z/h, \\ & \quad - \frac{h}{2} + \frac{(k - 1)h}{N} \le z \le - \frac{h}{2} + \frac{kh}{N},\,\,\,k = 1,2,...,N \\ \end{aligned} $$
(1)

where \(E_{ii}^{(k)} (\overline{z}),\,\,\,G_{ij}^{(k)} (\overline{z}),\,\,\rho_{t}^{(k)} ,\,\,\nu_{12}^{(k)} \,\,(i = 1,2,j = 2,3)\), \(Y_{11cn}^{(k)} ,\,\,Y_{22cn}^{(k)} ,\,\,G_{12cn}^{(k)} ,\,\,\rho_{cn}^{(k)} ,\,\,\nu_{12cn}^{(k)}\) and \(Y_{m}^{(k)} ,\,\,G_{m}^{(k)} ,\,\,\rho_{m}^{(k)} ,\,\,\nu_{m}^{(k)}\) are the Young and shear moduli, density and Poisson's ratio of heterogeneous nanocomposite, CNT and matrix in the \(k^{th}\) layer, respectively, \(\eta_{i}^{(k)} (i = 1,2,3)\) are the efficiency parameters in the lamina \(k^{th}\). Here \(V_{cn}^{(k)}\) and \(V_{m}^{(k)}\) are the volume fractions of CNTs and lamina, respectively and satisfy \(V_{cn}^{(k)} + V_{m}^{(k)} = 1\).

The distribution of volume fractions of CNTs across the lamina thickness is modeled as the U-, Ʌ- and X-patterned: \({U}\,\,\,\,\,at\,\,\,\,\,V_{cn}^{(k)} = \,\,V_{cn}^{*(k)}\), \(\Lambda \,\,\,\,\,at\,\,\,\,\,V_{cn}^{(k)} = \,\,(1 + 2\overline{z})\,V_{cn}^{*(k)}\) and \({X}\,\,\,\,\,at\,\,\,\,\,V_{cn}^{(k)} = \,\,4\left| {\overline{z}} \right|\,V_{cn}^{*(k)}\)(See, Fig. 1c).

3 Basic equations

The basic relations for the layer \(k^{th}\) reinforced with CNTs in the framework of FOPT can be expressed as follows [24]:

$$\sigma_{11}^{(k)} = Q_{{11\overline{z}}}^{(k)} e_{11} \, + Q_{{12\overline{z}}}^{(k)} e_{22} ,\,\,\,\,\,\sigma_{22}^{(k)} = Q_{{21\overline{z}}}^{(k)} e_{11} \, + Q_{{22\overline{z}}}^{(k)} e_{22} ,\,\,\,\,\,\sigma_{12}^{(k)} = Q_{{66\overline{z}}}^{(k)} \gamma_{12}$$
(2a)

and

$$\sigma_{13}^{(k)} = Q_{{55\overline{z}}}^{(k)} \gamma_{13} ,\,\,\,\,\sigma_{23}^{(k)} = Q_{{44\overline{z}}}^{(k)} \gamma_{23} \,$$
(2b)

where \(\sigma_{11}^{(k)} ,\,\,\sigma_{22}^{(k)} ,\,\,\sigma_{12}^{(k)} ,\,\,\sigma_{13}^{(k)} ,\,\,\sigma_{23}^{(k)}\) are the stresses in the \(k^{th}\) layer. Here \(e_{11} ,e_{22} ,\gamma_{12} ,\gamma_{13} ,\gamma_{23}\) are the strains and \(Q_{{ij\overline{z}}}^{(k)} {, (}i{,}\,j = {1,2,6)}\) are the coefficients depending on the material properties of the nanocomposite lamina \(k^{th}\) and are expressed as:

$$\begin{aligned} Q_{{11\overline{z}}}^{(k)} & = \frac{{E_{11}^{\left( k \right)} (\overline{z})}}{{1 - \nu_{{{12}}}^{\left( k \right)} \, \nu_{21}^{\left( k \right)} }},\,\,\,Q_{{22\overline{z}}}^{(k)} = \frac{{E_{22}^{\left( k \right)} (\overline{z})}}{{1 - \nu_{{{12}}}^{\left( k \right)} \nu_{21}^{\left( k \right)} }},\,\,Q_{{12\overline{z}}}^{(k)} = \nu_{21}^{\left( k \right)} Q_{{11\overline{z}}}^{(k)} = \nu_{12}^{\left( k \right)} Q_{{22\overline{z}}}^{(k)} { = }Q_{{21\overline{z}}}^{(k)} {,} \\ Q_{{44\overline{z}}}^{(k)} & = G_{23}^{(k)} (\overline{z}),\,\,\,Q_{{55\overline{z}}}^{(k)} = G_{13}^{(k)} (\overline{z}),\,\,Q_{66}^{(k)} = G_{12}^{(k)} (\overline{z}) \\ \end{aligned}$$
(3)

The stresses \(\sigma_{13}^{(k)}\) and \(\sigma_{23}^{(k)}\) in the lamina \(k^{th}\) are also expressed by the \(F_{1}\) and \(F_{2}\) as follows [24, 43]:

$$\sigma_{13}^{(k)} = f_{1,z}^{(k)} {(}z{)}F_{1} {,}\,\,\sigma_{23}^{(k)} = f_{2,z}^{(k)} {(}z{)}F_{2}$$
(4)

Here \(f_{j}^{(k)} (j = 1,2)\) are the transverse shear stress shape functions in the layer \(k^{th}\).

Based on the von Kármán-type kinematic nonlinearity, the strains of any point not on the mid-plane of laminated CNT plates are defined by

$$\begin{gathered} e_{{{11}}} = e_{{{11}}}^{{0}} - zw,_{xx} + I_{1z}^{(k)} F_{1,x} ,\,\,e_{22} = e_{22}^{{0}} - zw,_{yy} + I_{2z}^{(k)} F_{2,y} , \hfill \\ \gamma_{{{12}}} = \gamma_{{{12}}}^{{0}} - {2}zw,_{xy} + I_{1z}^{(k)} F_{1,y} + I_{2z}^{(k)} F_{2,x} \hfill \\ \end{gathered}$$
(5)

where \(e_{11}^{{0}} ,e_{22}^{{0}} ,\,\gamma_{12}^{{0}}\) are the strain components in the mid-plane of laminated plates [43,44,45,46,47,48]:

$$e_{{{11}}}^{{0}} = u_{,x} { + 0}{.5}\left( {w_{,x} } \right)^{{2}} ,\,\,\,\,e_{{{22}}}^{{0}} = v_{,y} { + 0}{.5}\left( {w_{,y} } \right)^{{2}} ,\,\,\,\gamma_{{{12}}}^{{0}} = v_{,x} { + }u_{,y} { + }w_{,x} w_{,y}$$
(6)

\(I_{jz}^{(k)} (j = 1,2)\) are defined by

$$I_{1z}^{(k)} = \int\limits_{0}^{z} {\frac{{f_{1,z}^{(k)} }}{{G_{13}^{(k)} (\overline{z})}}{d}z} \,,\,\,\,I_{2z}^{(k)} = \int\limits_{0}^{z} {\frac{{f_{2,z}^{(k)} }}{{G_{23}^{(k)} (\overline{z})}}{d}z}$$
(7)

The in-plane forces \(\left( {N_{{{11}}} ,\,N_{22} ,N_{{{12}}} } \right)\), shear forces \(\left( {Q_{{1}} ,Q_{2} } \right)\) and moments \(\left( {M_{{{11}}} ,\,M_{22} ,M_{{{12}}} } \right)\) of the laminated plates are obtained from the following integrals [24, 43,44,45,46]:

$$\begin{gathered} \left( {N_{{{11}}} ,\,N_{22} ,N_{{{12}}} } \right) = \sum\limits_{k = 1}^{N} {\int\limits_{{ - {0}{.5}h{ + (k - 1)hN}^{ - 1} }}^{{ - {0}{.5}h{ + khN}^{ - 1} }} {\left( {\sigma_{11}^{(k)} ,\,\sigma_{22}^{(k)} ,\sigma_{12}^{(k)} } \right){dz},} } \,\,\,\left( {Q_{{1}} ,Q_{2} } \right) = \sum\limits_{k = 1}^{N} {\int\limits_{{ - {0}{.5}h{ + (k - 1)hN}^{ - 1} }}^{{ - {0}{.5}h{ + khN}^{ - 1} }} {\left( {\sigma_{13}^{(k)} ,\sigma_{23}^{(k)} } \right){dz},} } \hfill \\ \left( {M_{{{11}}} ,\,M_{22} ,M_{{{12}}} } \right) = \sum\limits_{k = 1}^{N} {\int\limits_{{ - {0}{.5}h{ + (k - 1)hN}^{ - 1} }}^{{ - {0}{.5}h{ + khN}^{ - 1} }} {(\sigma_{11}^{(k)} ,\,\sigma_{22}^{(k)} ,\sigma_{12}^{(k)} )z{d}z.} } \,\, \hfill \\ \end{gathered}$$
(8)

The set of equations of nonlinear motion for laminated plates consisting of carbon nanotube originating layers resting on the two parametric elastic foundation using Hamilton principle are expressed as [24, 43, 46]:

$$\begin{gathered} M_{{{11,}\,x}} + M_{{{12,y}}} - Q_{1} + \rho_{{1}} w,_{xtt} - \rho_{{2}} \psi_{{{1,}tt}} = {0} \hfill \\ M_{{{21,}\,x}} + M_{{{22,}\,y}} - Q_{2} + \rho_{{1}} w,_{ytt} - \rho_{{3}} \psi_{{{2,}tt}} = {0} \hfill \\ Q_{{{1, }x}} + Q_{{{2,}\,y}} + N_{{{11}}} w,_{xx} + 2N_{12} w,_{xy} + N_{22} w,_{yy} - k_{1} w + k_{2} (w,_{xx} { + }w,_{yy} {) } - \overline{\rho }w,_{tt} = 0 \hfill \\ \end{gathered}$$
(9)
$$e_{{{11,}yy}}^{{0}} + e_{{{22,}xx}}^{{0}} - e_{{{12,}xy}}^{{0}} - \left( {w,_{xy} } \right)^{{2}} + w,_{xx} w,_{yy} = 0$$
(10)

where t is the time, \(\overline{\rho }\) and \(\rho_{i} {(}i{ = 1,2,3)}\) are defined by:

$$\begin{gathered} \overline{\rho } = \sum\limits_{k = 1}^{N} {\int\limits_{{ - {0}{.5}h{ + (}k - {1)}hN^{ - 1} }}^{{ - {0}{.5}h{ + }khN^{ - 1} }} {\rho_{t}^{(k)} {d}z,} } \,\,\rho_{{1}} = \sum\limits_{k = 1}^{N} {\int\limits_{{ - {0}{.5}h{ + (}k - {1)}hN^{ - 1} }}^{{ - {0}{.5}h{ + }khN^{ - 1} }} {\rho_{t}^{(k)} z^{{2}} {d}z,} } \,\,\,\rho_{{2}} = \,\sum\limits_{k = 1}^{N} {\int\limits_{{ - - {0}{.5}h{ + (}k - {1)}hN^{ - 1} }}^{{ - {0}{.5}h{ + }khN^{ - 1} }} {I_{1z}^{(k)} \rho_{t}^{(k)} z{d}z,} } \hfill \\ \rho_{{3}} = \sum\limits_{k = 1}^{N} {\int\limits_{{ - {0}{.5}h{ + (}k - {1)}hN^{ - 1} }}^{{ - {0}{.5}h{ + }khN^{ - 1} }} {I_{2z}^{(k)} \rho_{t}^{(k)} z{d}z.} } \hfill \\ \end{gathered}$$
(11)

By using basic relations (1–8) and additionally considering relations between Airy stress function and in-plane force components, then substituting resulting expressions into (9) and (10), the set of equations of nonlinear motion for laminated plates consisting of carbon nanotube originating layers resting on elastic foundations based on the FOPT are derived as follows:

$$\begin{gathered} L_{11} (F) + L_{12} (w) + L_{13} (F_{{1}} ) + L_{14} (F_{2} ) = 0 \hfill \\ L_{21} (F) + L_{22} (w) + L_{23} (F_{{1}} ) + L_{24} (F_{2} ) = 0 \hfill \\ L_{31} (F) + L_{32} (w) + L_{33} (F_{{1}} ) + L_{34} (F_{2} ) + L_{35} (F,w) = 0 \hfill \\ L_{41} (F) + L_{42} (w) + L_{43} (F_{{1}} ) + L_{44} (F_{2} ) + L_{45} (w,w) = 0 \hfill \\ \end{gathered}$$
(12)

where

$$\begin{gathered} L_{11} (F) = h\left[ {{(}A_{{{11}}} - A_{{{31}}} {)}F,_{xxyy} + A_{{{12}}} F,_{xxxx} } \right],\,\,\,L_{12} (w) = \rho_{{1}} w,_{xxtt} - A_{{{13}}} w,_{xxxx} - \left( {A_{{{14}}} + A_{{{32}}} } \right)w,_{xxyy} , \hfill \\ L_{13} (F_{1} ) = A_{{{15}}} F_{1} ,_{xxx} + A_{{{35}}} F_{1} ,_{xyy} - I_{{3}} F_{1} ,_{x} - \rho_{{2}} F_{1} ,_{xtt} ,\,\,\,\,\,\,L_{14} (F_{2} ) = \left( {A_{{{18}}} + A_{{{38}}} } \right)F_{2} ,_{xxy} , \hfill \\ L_{21} (F) = h\left[ {A_{{{21}}} F,_{yyyy} + (A_{{{22}}} - A_{{{31}}} )F,_{xxyy} } \right],\,\,L_{22} (w) = - \left( {A_{{{32}}} + A_{{{23}}} } \right)w,_{xxyy} - A_{{{24}}} w,_{yyyy} + \rho_{{1}} w,_{xxtt} , \hfill \\ L_{23} (F_{{1}} ) = \left( {A_{{{35}}} + A_{{{25}}} } \right)F_{1} ,_{xyy} ,\,\,L_{24} (F_{2} ) = A_{{{38}}} F_{2} ,_{xxy} + A_{{{28}}} F_{2} ,_{yyy} - I_{{4}} F_{2} ,_{y} - \rho_{{3}} F_{2} ,_{ytt} , \hfill \\ L_{31} (F) = 0,\,\,\,\,\,L_{32} (w) = - \overline{\rho }w,_{tt} - k_{1} w + k_{2} \left( {w,_{xx} + w,_{yy} } \right),\,\,\,\,\,L_{33} (F_{{1}} ) = I_{{3}} F_{{1}} ,_{x} , \hfill \\ L_{34} (F_{2} ) = I_{{4}} F_{2} ,_{y} ,\,\,\,\,\,\,L_{35} (F,w) = h\left[ {F,_{yy} w,_{xx} - {2}F,_{xy} w,_{xy} + F,_{xx} w,_{yy} } \right], \hfill \\ L_{41} (F) = h\left[ {B_{{{11}}} F,_{yyyy} + (B_{{{12}}} + B_{{{21}}} + B_{{{31}}} )F,_{xxyy} + B_{{{22}}} F,_{xxxx} } \right], \hfill \\ L_{42} (w) = - B_{{{23}}} w,_{xxxx} - \left( {B_{{{24}}} + B_{{{13}}} - B_{{{32}}} } \right)w,_{xxyy} - B_{{{14}}} w,_{yyyy} , \hfill \\ L_{43} (F_{{1}} ) = B_{{{25}}} F_{1} ,_{xxx} + \left( {B_{{{15}}} + B_{{{35}}} } \right)F_{1} ,_{xyy} ,\,\,L_{44} (F_{2} ) = \left( {B_{{{28}}} + B_{{{38}}} } \right)F_{2} ,_{xxy} + B_{{{18}}} F_{2} ,_{yyy} , \hfill \\ L_{45} (w,w) = - \left( {w_{,xy} } \right)^{2} + w,_{xx} w,_{yy} \hfill \\ \end{gathered}$$
(13)

in which \(A_{ij} ,\,\,I_{j}\) and \(B_{ij}\) are described in Appendix A.

4 Solution method

Assuming that all edges of the laminated plate consisting of CNT originating layers are simply supported with no in-plane displacement, that is, movement in the x and y directions is inhibited; these boundary conditions can be mathematically expressed as [43,44,45,46,47,48]:

$$\begin{gathered} w{ = 0,}\,\,\,M_{{{11}}} { = 0,}\,\,\,F_{{2}} { = 0},\,\,\,{as}\,\,x{ = 0}\,\,{and}\,\,x{ = }a \hfill \\ \hfill \\ w{ = 0,}\,\,\,M_{{{22}}} { = 0,}\,\,F_{{1}} { = 0,}\,\,\,{as}\,\,y{ = 0}\,\,{and}\,\,y{ = b} \hfill \\ \end{gathered}$$
(14)

The functions \(w\), \(F_{{1}}\) and \(F_{2}\) of the laminated plate consisting of CNT originating layers are sought as follows [24, 47]:

$$w{ = }\overline{w}{(}t{)}\,{sin(}m_{1} x{)}\,{sin(}m_{2} y{),}\,\,F_{{1}} { = }\overline{F}_{{1}} {(}t{)}\,{cos(}m_{{1}} x{)}\,{sin(}m_{2} y{),}\,\,F_{{2}} { = }\overline{F}_{2} {(}t{)}\,{sin(}m_{{1}} x{)}\,{cos(}m_{{2}} y{)}$$
(15)

where \(\overline{w}{(}t{)},\,\,\,\overline{F}_{{1}} {(}t{)}\) and \(\overline{F}_{{2}} {(}t{)}\) are time-dependent functions, \(m_{{1}} = \frac{m\pi }{a}\) and \(m_{2} = \frac{n\pi }{b}\), and \(\left( {m,n} \right)\) is the wave numbers.

By substituting the functions given in (14) in the fourth equation of the system of the non-homogeneous PDEs system (12), \(F\) is found from the particular solution of the PDE as follows:

$$F(x,y,t) = D_{{1}} {cos(2}m_{1} x{) + }D_{{2}} {cos(2}m_{2} y{) + }D_{3} {sin(}m_{1} x{)sin(}m_{2} y{)}$$
(16)

where

$$D_{{1}} { = }\frac{{\delta_{{{14}}} \overline{w}^{2} (t)}}{{{32}m_{{1}}^{{4}} \delta_{{3}} }}{,}\,\,\,D_{{2}} { = }\frac{{\delta_{{{14}}} \overline{w}^{2} (t)}}{{{32}m_{2}^{{4}} \delta_{{1}} }}{,}\,\,\,\,D_{{3}} { = }\frac{{\delta_{{{11}}} \overline{w}(t){ + }\delta_{{{12}}} \overline{F}_{{1}} (t){ + }\delta_{{{13}}} \overline{F}_{{2}} (t)}}{{\delta_{{1}} m_{2}^{{4}} { + }\delta_{{2}} m_{{1}}^{{2}} m_{2}^{2} { + }\delta_{{3}} m_{{1}}^{{4}} }}$$
(17)

in which

$$\begin{gathered} \delta_{{1}} { = }B_{{{11}}} h,\,\,\,\delta_{{2}} { = (}B_{{{12}}} + B_{{{21}}} + B_{{{31}}} {)}h,\,\,\,\delta_{{3}} { = }B_{{{22}}} h,\,\,\delta_{{{11}}} { = }B_{{{23}}} m_{{1}}^{{4}} + {(}B_{{{24}}} + B_{{{13}}} - B_{{{32}}} {)}m_{1}^{{2}} m_{2}^{{2}} + B_{{{14}}} m_{2}^{{4}} , \hfill \\ \hfill \\ \delta_{{{12}}} { = } - B_{{{25}}} m_{{1}}^{{3}} - {(}B_{{{15}}} + B_{{{35}}} {)}m_{{1}} m_{2}^{{2}} ,\,\,\,\delta_{{{13}}} { = } - {(}B_{{{28}}} + B_{{{38}}} {)}m_{{1}}^{{2}} m_{2} - B_{{{18}}} m_{2}^{{3}} ,\,\,\,\delta_{{{14}}} = m_{{1}}^{{2}} m_{2}^{{2}} \hfill \\ \end{gathered}$$
(18)

By substituting the functions (15) and (16) into the first three equations of the system of PDEs (12), and then applying the Galerkin method, the following set of nonlinear ordinary differential equations (NL-ODE) is obtained:

$$\begin{gathered} q_{11} \overline{w} + q_{11}^{NL} \overline{w}^{2} + q_{11}^{t} \overline{w},_{tt} + q_{12} \overline{F}_{1} + q_{12}^{t} \overline{F}_{1} ,_{tt} + q_{13} \overline{F}_{2} = 0, \hfill \\ \hfill \\ q_{21} \overline{w} + q_{21}^{NL} \overline{w}^{2} + q_{21}^{t} \overline{w},_{tt} + q_{22} \overline{F}_{1} + q_{23} \overline{F}_{2} + q_{23}^{t} \overline{F}_{2} ,_{tt} = 0, \hfill \\ \hfill \\ \overline{\rho }\overline{w},_{tt} + q_{31} \overline{w} + q_{31}^{NL} \overline{w}^{2} + q_{32} \overline{w}^{3} + q_{33} \overline{F}_{1} + q_{34} \overline{F}_{2} = 0 \hfill \\ \end{gathered}$$
(19)

where \(q_{ij} {(}i = 1,2,3,j = 1,2,...,4{)}\) are given in Appendix B.

Due to the smallness of the inertia terms with the upper index t, ignoring these terms in set of Eqs. (19), and eliminating the functions \(\overline{F}_{1}\) and \(\overline{F}_{2}\), the following NL-ODE with quadratic and cubic nonlinearities for laminated nanocomposite plates resting on the PT-EF is obtained:

$$w_{1,tt} (t) + \left( {\Omega_{L}^{STwp} } \right)^{2} w_{1} (t) + \Gamma_{1} w_{1}^{2} (t) + \Gamma_{2} w_{1}^{3} (t) = 0$$
(20)

where \(w_{1} (t) = \overline{w}(t)/h\), \(\Gamma_{1} = \frac{{h\overline{q}_{31}^{NL} }}{{\overline{\rho }}},\,\,\Gamma_{2} = \frac{{h^{2} q_{32} }}{{\overline{\rho }}}\) and \(\Omega_{L}^{STwp}\) is the linear frequency of shear deformable laminated plate consisting of CNT originating layers resting on the PT-EF and defined as:

$$\Omega_{L}^{STwp} = \sqrt {\frac{{\overline{q}_{31} + k_{1} + k_{2} (m_{1}^{2} + m_{2}^{2} )}}{{\overline{\rho }}}}$$
(21)

in which

$$\begin{gathered} \overline{q}_{31} = q_{33} \frac{{q_{11} q_{23} - q_{21} q_{13} }}{{q_{22} q_{13} - q_{12} q_{23} }} - q_{34} \left( {\frac{{q_{21} }}{{q_{23} }} + \frac{{q_{22} }}{{q_{23} }}\frac{{q_{11} q_{23} - q_{21} q_{13} }}{{q_{22} q_{13} - q_{23} q_{12} }}} \right), \hfill \\ \hfill \\ \overline{q}_{31}^{NL} = q_{31}^{NL} - \frac{{q_{33} \left( {q_{11}^{NL} q_{23} - q_{13} q_{21}^{NL} } \right)}}{{q_{12} q_{23} - q_{13} q_{22} }} - \frac{{q_{34} q_{21}^{NL} }}{{q_{23} }} + \frac{{q_{34} q_{22} }}{{q_{23} }}\frac{{q_{11}^{NL} q_{23} - q_{13} q_{21}^{NL} }}{{q_{12} q_{23} - q_{13} q_{22} }} \hfill \\ \end{gathered}$$
(22)

When we apply the semi-inverse method to Eq. (20), the following integral is generated [49]:

$$\Lambda (w_{1} ) = \int\limits_{0}^{T/4} {\left\{ { - 0.5\left[ {w_{1,t} (t)} \right]^{2} + \left[ {0.5\left( {\Omega_{L}^{STwp} } \right)^{2} w_{1}^{2} (t) + \Gamma_{1} w_{1}^{3} (t)/3 + 0.25\Gamma_{2} w_{1}^{4} (t)} \right]} \right\}} {d}t$$
(23)

Here \(T = 2\pi /\Omega_{NL}^{STwp}\) is the nonlinear vibration period in which \(\Omega_{NL}^{STwp}\) denotes the nonlinear vibration frequency (NLF) of shear deformable laminated plate consisting of CNT originating layers resting on the PT-EF.

To satisfy the initial conditions \(w_{1} ({0}) = f,\,\,\,w_{1,t} ({0}) = 0\,\), \(w_{1} (t)\) is expressed by:

$$w_{1} (t) = f\cos \left( {\Omega_{NL}^{STwp} t} \right),\,\,\,\,\,\,\,f = w_{\max }$$
(24)

Considering the expression (24) in Eq. (23), the following equation is easily obtained:

$$\Lambda (f,\Omega_{NL}^{STwp} ) = - 0.125\pi \Omega_{NL}^{STwp} f^{2} + \left[ {\Omega_{NL}^{STwp} } \right]^{ - 1} \left[ {0.125\pi \left( {\Omega_{L}^{STwp} } \right)^{2} f^{2} + (2/9)\Gamma_{1} f^{3} + (3/64)\Gamma_{2} \pi f^{4} } \right]$$
(25)

Can be seen from (25) that \(\frac{{\partial \Lambda (f,\Omega_{NL}^{STwp} )}}{{\partial \Omega_{NL}^{STwp} }} < 0\), therefore, from the condition \(\frac{{\partial \Lambda (f,\Omega_{NL}^{STwp} )}}{\partial f} = 0\), the \(f\) dependence of the nonlinear vibration frequency of shear deformable laminated plate consisting of CNT originating layers resting on the PT-EF becomes as follows:

$$\Omega_{NL}^{STwp} = \sqrt {\left( {\Omega_{L}^{STwp} } \right)^{2} + (8/3\pi )\Gamma_{1} f + 0.75\Gamma_{2} f^{2} } \,$$
(26)

The non-dimensional \(\Omega_{1NL}^{STwp}\) for the shear deformable laminated plates consisting of CNT originating layers resting on the PT-EF is used as:

$$\Omega_{1NL}^{STwp} = \Omega_{NL}^{STwp} h\sqrt {\frac{{\rho_{m}^{(k)} }}{{E_{m}^{(k)} }}} \,\,$$
(27)

The \(f\) dependence of \(\Omega_{NL}^{STwp} /\Omega_{L}^{ST}\) ratio for laminated plates consisting of CNT originating layers resting on the PT-EF is obtained as follows:

$$\Omega_{NL}^{STwp} /\Omega_{L}^{ST} = \sqrt {\left( {\Omega_{L}^{STwp} /\Omega_{L}^{ST} } \right)^{2} + (8/3\pi )\Gamma_{1} f/\left( {\Omega_{L}^{ST} } \right)^{2} + 0.75\Gamma_{2} f^{2} /\left( {\Omega_{L}^{ST} } \right)^{2} }$$
(28)

where \(\Omega_{L}^{ST}\) denotes the linear vibration frequency of shear deformable laminated plate consisting of CNT originating layers without EFs.

When the effect of shear stresses is neglected from the formulas (21) and (26–28), the formulas are obtained for laminated plates consisting of CNT originating layers resting on PT-EF within the framework of CT.

Similarly, if we neglect the effect of PT-EF from the formulas (21) and (26–28), we arrive at the formulas for unconstrained laminated plates.

5 Numerical examples and discussion

5.1 Material properties and arrangement of nanocomposite layers

In this subsection, the laminated plate consisting of CNT reinforced layers consists of polymethyl methacrylate (PMMA) and the reinforcement element consists of the CNT. The material properties of PMMA and CNTs are assumed to be, respectively, as follows [20, 21]: \(Y_{m}^{(k)} = 2.5\, \times {10}^{9} {Pa,}\,\,\nu_{m}^{(k)} = 0.34{,}\,\rho_{m}^{(k)} = 1.15 \times 10^{3} \,{kg/m}^{3}\) and \(Y_{11cn}^{(k)} = 5.6466\,{TPa,}\,\,Y_{22cn}^{(k)} = 7.08\,{TPa,}\) \(G_{12cn}^{(k)} = 1.9445\,{TPa,}\,\,\nu_{12cn}^{(k)} = 0.175\). The efficiency parameters and total volume fraction of CNTs in the lamina \(k^{th}\) are given in Table 1.

Table 1 Efficiency parameters corresponding to the \(V_{cn}^{*(k)}\)
Full size table

The shear stresses of layers are defined as, \(f_{1}^{(k)} \left( z \right) = f_{2}^{(k)} \left( z \right) = z - 4z^{3} /3h^{2}\)[43, 44]. The layer arrays (0°), (0°/90°/0°), (90°/0°/90°), (0°/90°/90°/0°) and (90°/0°/0°/90°) that we will use in the analysis are shown in Fig. 2. The single-, three- and four-layer nanocomposite plates with U-, Ʌ-, and X-shaped patterns used in the analysis are shown in Figs. 3, 4 and 5.

Fig. 2
figure 2

a (0°)-monolayer, b (0°/90°/0°), c (90°/0°/90°), d (0°/90°/90°/0°) and e (90°/0°/0°/90°)-array plates

Full size image
Fig. 3
figure 3

CNT reinforced monolayer plate with a U-, b Ʌ- and c X-patterns

Full size image
Fig. 4
figure 4

Three-layered plate of CNT-reinforced layers with a U-, b Ʌ- and c X-patterns

Full size image
Fig. 5
figure 5

Four-layered plate of CNT-reinforced layers with a U-, b Ʌ- and c X-patterns

Full size image

5.2 Validation

The convergence of the proposed method is examined through three different free vibration analysis samples of single-layer and laminated plates and compared with other methods. In two comparisons, the nanocomposite material properties are used as follows [9, 50]:

\(Y_{m}^{(k)} = 2.1\,{GPa,}\,V_{cn}^{*(k)} = 0.11,\eta_{1}^{(k)} = 0.142,\eta_{2}^{(k)} = \eta_{3}^{(k)} = 0.934,\,V_{cn}^{*(k)} = 0.14, \, \eta_{1}^{(k)} = 0.15,\,\eta_{2}^{(k)} = \eta_{3}^{(k)} = 0.941,\,V_{cn}^{*(k)} = 0.17, \, \eta_{1}^{(k)} = 0.150,\,\,\eta_{2}^{(k)} = \eta_{3}^{(k)} = 1.381.\)

Other material properties are the same as in the previous sub-title.

The first comparison is conducted for the square single-layer monolayer (k = 1) nanocomposite plate. The nanocomposite plate characteristics are: \(a/b = 1, \, b/h = 50\). The values of linear dimensionless frequency parameter (L-DFP) of unconstrained composite plates with different CNT patterns are compared with the results obtained by higher-order shear deformation theory (HSDT) and finite element method (FEM) in the study of ref. [50]. The L-DFP is calculated using the formula \(\Omega_{1L}^{ST} = \Omega_{L}^{ST} \left( {\frac{{b^{2} }}{h}} \right)\sqrt {\frac{{\rho_{m}^{(1)} }}{{E_{m}^{(1)} }}}\), where \(\Omega_{L}^{ST}\) is the L-FP for the unconstrained single-layer nanocomposite plates, and is obtained from expression (19), when k = 1 and ground coefficients \(k_{1} = k_{2} = 0\). Table 2 shows that the \(\Omega_{1L}^{ST}\) for U and X-patterns of CNTs are in good agreement.

Table 2 Comparison of \(\Omega_{1L}^{ST}\) for single-layer composite plates with CNT patterns
Full size table

The second example, the comparison is made for square cross-ply laminated (k = 5) nanocomposite plate with \(\left( {0^{\circ} /90^{\circ} /0^{\circ} /90^{\circ} /0^{\circ} } \right)\) array whose geometrical properties and wave numbers are as follows: \(a/b = 1, \, b/h = 10,\,\,(m,n) = (1,1)\) (see, Table 3). The magnitudes of L-DFP for unconstrained cross-ply laminated composite plates with U- and X- patterns are compared with the results obtained by the kp-Ritz method in the study of Lei et al. [9]. The L-DFP is calculated using the formula \(\Omega_{1L}^{ST} = \Omega_{L}^{ST} \left( {\frac{{b^{2} }}{h}} \right)\sqrt {\frac{{\rho_{m}^{(k)} }}{{E_{m}^{(k)} }}}\), when k = 5 and \(k_{1} = k_{2} = 0\). From Table 3, it can be seen that the fundamental linear dimensionless frequency parameter values for cross-ply laminated (k = 5) nanocomposite plate are in good agreement.

Table 3 Comparison of \(\Omega_{1L}^{ST}\) for cross-ply laminated nanocomposite plates reinforced with U- and X-patterned CNT in the layers
Full size table

In the third example, the comparison is made with linear and nonlinear dimensionless vibration frequencies of unconstrained single-layer homogeneous orthotropic elastic plates presented in the book of Ambartsumyan [43]. The linear and nonlinear dimensionless frequency values in the second and fourth columns of the Table 4, respectively, are obtained using the formulas presented in Ref. [43]. The boron/epoxy material properties and plate characteristics used for comparison are as follows [44]:

$$\begin{gathered} E_{11} = 209 \times 10^{9} ({Pa}),\,\,E_{22} = 20.9 \times 10^{9} ({Pa}),\,\,G_{12} = G_{13} = 6.9 \times 10^{9} ({Pa}),\,\,G_{23} = 4.14 \times 10^{9} ({Pa}),\, \hfill \\ \hfill \\ \nu_{12} = 0.3,\rho_{t} = 1950\,{kg}/{m}^{3} ;\,\,a/b = 1,\,\,b = 10h \hfill \\ \end{gathered}$$
Table 4 Comparison of dimensionless linear and nonlinear frequency values for unconstrained single-layer homogeneous orthotropic plates
Full size table

It shows that the dimensionless linear frequencies values coincide with the results in Ref. [43], while the nonlinear frequency values are in very good agreement (see, Table 4).

5.3 Nonlinear analysis

The variation of the values of the NL-DFP of (0°), \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\) and \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array nanocomposite plates with U- and Ʌ-patterns versus the \(k_{1}\) and \(k_{2}\) are presented in Table 5. The following data are used: \(h/a = 0.10, \, a/b = 1, \, f = 1,V_{cn}^{*(k)} = 0.12\,(k = 1,3)\). It should be emphasized that in this subsection wave modes are \(\left( {m,n} \right) = \left( {1,1} \right)\). As can be seen from Table 5, the magnitudes of NL-DFP increase versus the increase of the elastic foundation coefficients \(k_{1}\) and \(k_{2}\). The influences of shear deformations on NL-DFPs decrease with the increase of the elastic foundation coefficients \(k_{1}\) and \(k_{2}\). For example, at \(k_{2} = 0\), depending on the increase \(k_{1}\) from 0 to \(2.5 \times 10^{9} \,\,(N/m^{3} )\), the influence of shear deformations on the frequency of the plate consisting of (0°)-aligned and U-origin layers decreases from 19.7% to 16%, while at \(k_{1} = 1.5 \times 10^{9} {N}/{m}^{3}\) and that effect decreases from 17.4% to 14.6% depending on the increase of \(k_{2}\) from 0 to \(1.2 \times 10^{6} (N/m)\). The largest shear deformations effect on the nonlinear frequency is obtained in the \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array nanocomposite plate, while the smallest shear deformations effect occurs in the \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-array. For example, while the effect of shear deformations is approximately 2.5% larger in the \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array plate than in the (0°)-monolayer plate, the effect is approximately 0.7% smaller in the \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-array plate than in the (0°)-plate. The effect of shear deformations on the frequency of the nanocomposite plate with Ʌ-pattern is smaller than that of U-pattern. The difference of shear deformations effect between the (0°) and \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-array plates is 6%, while it is approximately 7% for the \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array plate.

Table 5 Distribution of dimensionless nonlinear free vibration frequency of laminated plates reinforced with CNTs depending on the coefficients \(k_{1}\) and \(k_{2}\)
Full size table

The influence of the Ʌ-profile on the nonlinear frequency of laminated plates decreases with the increase of the \(k_{1}\) and \(k_{2}\). For example, the effect of the Ʌ-profile on the frequency of \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array plate within FOPT decreases from (-7.9%) to (-6.9%), due to the increase of \(k_{1}\) from 0 to \(2.5 \times 10^{9} \,\,(N/m^{3} )\) for \(k_{2} = 0\), while the effect change of the Ʌ-profile in the \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array is smaller than 1% due to the increase of \(k_{2}\) from 0 to \(1.2 \times 10^{6} (N/m^{3} )\) for \(k_{1} = 1.5 \times 10^{9} {N}/{m}^{3}\). The largest influence Ʌ-profile on the nonlinear frequency is obtained in the (90°/0°/90°)-array plates, while the smallest effect occurs in the \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-array plates. For example, the Ʌ-pattern effect within CT is smaller 1.1% in the (0°)-sequence than in the \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)- sequence, while in the \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-sequence gets smaller 2.2% compared to the (90°/0°/90°)-sequence. The difference of the Ʌ-profile effect on the NL-DFP between the two theories is approximately 7% for the (0°) and \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-array plates, while this difference is approximately 8% in the \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array plate.

The elastic foundation effects on the nonlinear frequencies of laminated nanocomposite plates increase with the increase of \(k_{1}\) and \(k_{2}\). For example, when \(k_{2} = 0\), the elastic foundation effect on the frequencies of the (0°)-plate consisting of Ʌ-pattern layer increases from 9.3% to 15.1%, depending on the increase of \(k_{1}\) from \(1.5 \times 10^{9}\) to \(2.5 \times 10^{9}\). Likewise, it increases from 12.1% to 25.4% depending on the increase of \(k_{2}\) from 0 to \(1.2 \times 10^{6}\) for \(k_{1} = 2 \times 10^{9} {N}/{m}^{3}\). In addition, the difference of elastic foundation effect between the layer arrays increases with the increase of \(k_{1}\) and \(k_{2}\). For example, the highest foundation effect difference between the (0°) and \(\left( {90^{\circ} /0^{\circ} /90^{\circ} } \right)\)-sequences is 2.5%, while it is less than 1% for difference between the (0°) and \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-sequences. The elastic foundation difference between the two theories increases with the increase of \(k_{1}\) and \(k_{2}\). For example, the elastic foundation effect difference between FOPT and CT for \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\)-array is 2.9% due to the increase of \(k_{1}\) from \(1.5 \times 10^{9}\) to \(2.5 \times 10^{9}\) when \(k_{2} = 0\), while this difference is 5.3% for the \(\left( {0^{\circ} /90^{\circ} /0^{\circ} } \right)\) -array U-plate due to the increase of \(k_{2}\) from 0 to \(1.2 \times 10^{6}\) when \(k_{1} = 2.5 \times 10^{9} {N}/{m}^{3}\).

The distribution of the ratio of nonlinear and linear free vibration frequencies (NLF/LF) of (0°), \(\left( {0^{\circ} /90^{\circ} /90^{\circ} /0^{\circ} } \right)\) and \(\left( {90^{\circ} /0^{\circ} /0^{\circ} /90^{\circ} } \right)\)-arrays rectangular plates made of U- and X- originating layers resting on the Pasternak elastic foundation, depending on the amplitude \(f\), is presented in Table 6, Figs. 6 and 7 for different \(V_{cn}^{*(k)}\). Other plate and soil parameters used are as follows: \(b = 2a,\,\,h = 0.1a\) and \(\left( {k_{1} ,k_{2} } \right) = \left( {1 \times 10^{9} , \, 1.8 \times 10^{6} } \right)\). The effect of geometric nonlinearity on the free vibration frequencies of laminated plates made of U- and X- originating layers in grounded and ungrounded conditions increases significantly, depending on the increase of \(f\). In addition, the NLF/LF ratio of laminated plates varies depending on the increase of \(V_{cn}^{*(k)}\) for fixed \(f\). The smallest values of the NLF/LF ratio of laminated plates composed of U and X-originating layers with and without PT-EF are obtained at \(V_{cn}^{*(k)} = 0.17\), while the largest ratio is obtained at \(V_{cn}^{*(k)} = 0.28\). When the \(\left( {0^{\circ} /90^{\circ} /90^{\circ} /0^{\circ} } \right)\) and \(\left( {90^{\circ} /0^{\circ} /0^{\circ} /90^{\circ} } \right)\)-arrayed plates are compared with (0°)-single-layer nanocomposite plates, the NLF/LF ratio is more effective in the laminated plates (see, Figs. 6, 7, also). In grounded and ungrounded cases, taking into account shear deformations reduces the effect of geometric nonlinearity on the frequency, and this decrease becomes more pronounced as the \(f\) increases. In addition, when compared with (0°)-single-layer plate, the change of layer arrangement changes the influence of nonlinearity on the frequency. For example, the effects of nonlinearity on the frequency in X-patterned plates with \(\left( {0^{\circ} /90^{\circ} /90^{\circ} /0^{\circ} } \right)\) and \(\left( {90^{\circ} /0^{\circ} /0^{\circ} /90^{\circ} } \right)\)-arrays for \(V_{cn}^{*(k)}\) = 0.12 and \(f\) = 1.4 in the groundless case are 1.94% and 3.32%, while those effects decrease in the case of the Pasternak ground and vary around 1.53% and 1.88%, respectively, in the framework of FOPT. For \(V_{cn}^{*(k)}\) = 0.28 and \(f\) = 1.4, those influences change around 1.92% and 2.65% in the presence of the Pasternak ground, while those effects are 2.15% and 3.31% in the absence of the foundation. The presence of the Pasternak soil weakens the effect of the layer arrangement on the geometric nonlinear frequency. The effect of the X-pattern on the NLF/LF ratio is more pronounced in \(\left( {0^{\circ} /90^{\circ} /90^{\circ} /0^{\circ} } \right)\)-array plates compared to plates with other arrays. For example, the effects of X-pattern in comparison with U-pattern on the NLF/LF ratio for (0°), \(\left( {0^{\circ} /90^{\circ} /90^{\circ} /0^{\circ} } \right)\) and \(\left( {90^{\circ} /0^{\circ} /0^{\circ} /90^{\circ} } \right)\)-array plates without elastic foundation are (-10.65%), (-12.42%) and (-9.16%), while in plates on PT-EF those are (-11.08%), (-12.62%) and (-9.7%), respectively.

Table 6 Distribution of the nonlinearity effect on the frequency of laminated plates made of U- and X- originating layers versus the \(f\) for different \(V_{cn}^{*(k)}\) in grounded and ungrounded cases
Full size table
Fig.6
figure 6

Variation of the \(\Omega_{1NL}^{ST} /\Omega_{1L}^{ST}\) of (0°) and (0°/90°/90°/0°)-array plates made of U- and X- originating layers versus the \(f\) with and without Pasternak foundation

Full size image
Fig.7
figure 7

Variation of the \(\Omega_{1NL}^{ST} /\Omega_{1L}^{ST}\) of (0°) and (90°/0°/0°/90°)-array plates made of U- and X-originating layers versus the \(f\) with and without Pasternak foundation

Full size image

6 Conclusions

The nonlinear vibration behaviors of laminated plates composed of CNT originating layers are investigated in the framework of FOPT in elastic environments. The Galerkin and semi-inverse methods are used to solve the NL-PDEs which derived using Donnell-type nonlinear shell theory. Three distributions of CNTs across the thickness of the layers such as uniformly and functionally graded distributions are considered. The nonlinear frequency–amplitude relationship for laminated plates consisting of CNT originating layers resting on the PT-EF is established within FOPT. The accuracy of the above procedure has been verified by comparison with the available literature. The elastic ground characteristics, when combined with other factors such as CNT volume fraction, CNT distribution, layer arrangement and number, and geometric parameters, have a significant effect on the nonlinear frequency of laminated plates with CNT patterned layers.