1 Introduction

A flapping airfoil power generator (FAPG) is a new type of power generator that is inspired by the swimming of aquatic animals and the flying of insects and birds. Compared to conventional rotational power generators, FAPG has a simple structure, low noise, environmental friendliness, and high-power extraction efficiency under low-speed fluids [1,2,3].

The power extraction efficiency of the FAPG flapping airfoil can be improved by three methods: by improving the kinematic parameters of the flapping airfoil, by applying the active flow control technology on the flapping airfoil, and by changing the airfoil structure of the flapping airfoil [4, 5]. Among these, the methods to improve the kinematic parameters of the flapping airfoil have been widely studied, and several noteworthy conclusions have been obtained [6,7,8,9]. Yet further improvement in the power extraction efficiency of the flapping airfoil is still needed by active flow control or modifying the airfoil structure method.

Le et al. [10] proposed a bionic airfoil to imitate dragonfly wings and analyzed its power extraction performance by numerical approach. It was shown that the optimized bionic airfoil can extract more power from the fluid as compared to the baseline NACA0012 airfoil. Guo et al. [11] designed a flapping airfoil with a wavy leading edge. It was concluded that the flapping airfoil with a larger leading edge wavelength and amplitude can generate a larger lift than that of a traditional smooth leading edge. Graham [12] performed a numerical study to investigate the effect of the Gurney flap on the power extraction performance of the flapping airfoil. The results revealed that the thickness and height of the Gurney flap can be varied to improve the aerodynamic characteristics of the flapping airfoil.

Suction and blowing jet technology is one of the active flow control technologies and is widely used to improve the lift drag ratio of vertical axis wind turbine and rotor aircraft blades [13, 14]. The FAPG is used to extract the fluid flow power by reciprocating flapping driven by the lift of the airfoil. It is believed that the suction and blowing jet have a reasonable influence on the power extraction performance of the flapping airfoil. But so far, only a few studies unfold the influence of suction and blowing combined jet on the power extraction performance of the flapping airfoil [15, 16], and the mechanism of the effect of suction and blowing combined jet on the power extraction performance of the flapping airfoil is still vague.

In addition, Taguchi method is one of the effective methods for multi-parameter optimization problems, which has been widely used in many fields. For instance, Bao et al. [17] studied the influence of design parameters on the performance of a metal hydride reactor by CFD-Taguchi combined method. It was concluded that the method is effective to search for optimum reactor design scheme. Qasemi et al. [18] used the Taguchi method to optimize the power performance of a vertical axis wind turbine augmented with a flat plate deflector. It was reported that compared to the bare turbine, utilizing the deflector with optimum parameters increased the efficiency of the wind turbine by 16.42%. Zhu et al. [19] performed a numerical study to investigate the energy harvesting properties of a semi-active flapping wing with cooperative jet based on Taguchi method. The results indicated that the energy harvesting efficiency can be improved by 11.06% by selecting appropriate parameters. Meanwhile, the levels of parameters can be optimized under limited pairs of combinations according to the Taguchi method instead of full factorial design, which substantially reduces the computational time with an improved efficiency.

Therefore, in this work, the investigation on the flow field of flapping airfoil with suction and blowing jet is carried out using CFD. The effects of jet parameters, including jet position, aperture, and velocity amplitude, on the power extraction performance of the airfoil, are systematically studied. The Taguchi method [20] is employed to examine the weight of these parameters effect and to identify the optimal combination of these jet parameters.

2 Problem description

To study the effect of suction and blowing combined jet on the power extraction performance of the flapping airfoil, the kinetics of the flapping airfoil is simplified as the coupling form of plunging motion h(t) and pitching motion θ(t), as shown in Fig. 1. These two kinds of motion are defined by harmonic functions with the same frequency; the motions and their velocities are given as:

$$ h\left( t \right) = H\sin \left( {2\pi ft + \varphi } \right) $$
(1)
$$ v_{y} \left( t \right) = 2\pi fH\cos \left( {2\pi ft + \varphi } \right) $$
(2)
$$ \theta \left( t \right) = \theta_{0} \sin \left( {2\pi ft} \right) $$
(3)
$$ \omega \left( t \right) = 2\pi f\theta_{0} \cos \left( {2\pi ft} \right) $$
(4)

where H is the plunging amplitude, vy(t) is the plunging velocity, θ0 is the pitching amplitude, ω(t) is the pitching velocity, t is the time, f is the plunging and pitching frequency, and φ is the phase difference of the two motions. Kinsey and Dumas [21] studied the influence of the pitching-center location on the performance of the flapping airfoil. It was found that the pitching-axis is located at 1/3 chord length from the leading edge is a reasonable choice for the airfoil to achieve better performance. Thus, in the present simulation, the distance between the rotation center cp of pitching motion and the leading edge of the flapping airfoil is fixed at c/3, where c is the chord length of the flapping airfoil. Moreover, the pitching frequency is normalized as f* = fc/U∞, where U∞ is the velocity of the incoming stream.

Fig. 1
figure 1

Plunging and pitching motions of flapping airfoil

Full size image

The flapping airfoil model with blowing and suction compound jet is shown in Fig. 2, where Cf represents the distance between the center of the jet hole and the leading edge of the flapping airfoil and D shows the width of the jet hole. It should be mentioned that the hole blows a jet in the normal direction to the wall, and the suction hole draws in the same mass flow. The velocity equations of suction and blowing jet are as follows:

$$ u_{1} \left( t \right) = U\sin \left( {2\pi ft} \right) $$
(5)
$$ u_{2} \left( t \right) = - U\sin \left( {2\pi ft} \right) $$
(6)

where U is the jet velocity amplitude, u1(t) is the jet velocity of the blowhole in the downward movement and the jet velocity of the suction hole in the upward movement of the flapping airfoil, u2(t) is the jet velocity of the suction hole in the downward movement and the jet velocity of the blowhole in the upward movement of the flapping wing. The relative jet velocity with respect to the incoming stream is described by the jet velocity coefficient and is given as Cu = U/ U∞.

Fig. 2
figure 2

Schematic of the NACA0015 airfoil with blowing and suction jet

Full size image

The power extracted by the reciprocating plunging motion of the flapping airfoil Py(t) is the product of the lift Fy(t) and the plunging velocity vy(t), and the power extracted by pitching motion Pθ(t) is the product of pitching moment M(t) and pitching angular velocity ω(t). Py(t) and Pθ(t) are given as:

$$ P_{y} (t) = F_{y} (t)v_{y} (t) $$
(7)
$$ P_{\theta } (t) = M(t)\omega (t) $$
(8)

Compared to the base airfoil, the flapping airfoil with jet needs to provide the power Pu(t) consumed by the jet and is described as:

$$ P_{u} (t) = \frac{1}{2}\rho \left| {u\left( t \right)} \right|^{3} Dl $$
(9)

where u(t) is the jet velocity, ρ is the fluid density and l is the span of flapping airfoil which is taken unity in the present study. Therefore, the net power extracted by the flapping airfoil with suction and blowing jet can be defined by the following equation:

$$ P_{T} = P_{y} (t) + P_{\theta } (t) - P_{u} (t) $$
(10)

where T is the flapping cycle.

To compare the flapping airfoil performance, the extracted power is usually expressed in the form of a coefficient, which is defined as:

$$ C_{p} = \frac{{P_{T} }}{{0.5\rho U_{\infty }^{3} c}} $$
(11)

The mean power coefficient and the efficiency of power extraction from flapping airfoil are defined as:

$$ \overline{{C_{p} }} = \frac{1}{T}\int_{t}^{t + T} {C_{p} {\text{d}}t} $$
(12)
$$ \eta = \frac{{\overline{{P_{T} }} }}{{0.5\rho U_{\infty }^{3} d}} = \overline{{C_{p} }} \frac{c}{d} $$
(13)

where d is the maximum distance reached by the airfoil, as shown in Fig. 1.

3 Numerical method and validation

3.1 Computational domain and boundary conditions

In the present study, the Reynolds number of the flow is found to be 1.99 × 106 based on the inflow velocity and the chord length of the airfoil for the flow field analysis of the flapping wing using ANSYS Fluent software. The results of reference [22] showed that the Spalart–Allmaras (S–A) model [23] can calculate the aerodynamic force of the flapping airfoil with reasonable accuracy, and the model is insensitive to the grid quality. Therefore, the Spalart–Allmaras(S–A) model is chosen as the turbulence model in this study. The flow field solver adopts a pressure-based separation solution algorithm and the coupled equations of pressure–velocity are solved by the SIMPLEC algorithm. The Green-Gauss method based on nodes is used as the interpolation method for the gradient calculation. The second-order upwind scheme is used as the discrete scheme for pressure, momentum, and turbulent viscosity coefficients, and the first-order implicit scheme is used for time integration. The convergence criterion for residuals is defined as 1 × 10–5.

As demonstrated by Le et al. [24], although the real turbine has a finite airfoil span, the adopted two-dimensional (2D) numerical simulation can give reasonable results with acceptable accuracy and variation trends. Thus, the 2D geometrical configuration is adopted in the present simulations.

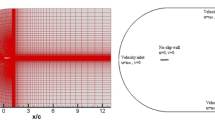
The grids scheme of the airfoil is shown in Fig. 3. The computational domain is divided into two parts: the inner domain moves with the flapping airfoil, keeping the grid topology steady; the outer domain is a fixed domain, and the remeshing is carried out near the interface of the two domains according to the moving inner part technique. The inlet velocity is defined at the left, upper, and lower boundaries of the computational domain, and the outlet pressure is specified at the right boundary. The surface of the airfoil adopts the no-slip wall boundary condition, and the position of the jet hole is set as the velocity inlet boundary condition. The plunging and pitching motions of the airfoil are realized by the dynamic mesh method, and the dynamic characteristics of the airfoil are obtained by user-defined function (UDF).

Fig. 3
figure 3

Grids of the computational domain

Full size image

3.2 Validation

To validate the numerical model for grid independence and time-step, the mesh system of airfoil surface with cell spacing of 0.001c, 0.0005c and 0.00025c and the time-step of T/1000, T/2000 and T/4000 are analyzed by keeping the grid size growth rate of 1.08 from the airfoil surface to the outer-domain boundary. The variations of the flapping airfoil plunging power coefficient (\(\overline{C}_{py} = \frac{1}{T}\int_{t}^{t + T} {{{P_{y} (t)} \mathord{\left/ {\vphantom {{P_{y} (t)} {\left( {0.5\rho U_{\infty }^{3} c} \right)}}} \right. \kern-0pt} {\left( {0.5\rho U_{\infty }^{3} c} \right)}}} {\text{d}}t\)) for different cell spacings and time-step are shown in Fig. 4. It is found that the simulation results vary insignificantly with regard to mesh numbers and time-step, and for the mesh system of 0.0005c and time-step of T/2000, the percentage of error of the time-averaged \(\overline{C}_{py}\) is below 0.7%. Therefore, to reduce the computation time and ensure higher accuracy, the mesh cell and time-step are adopted as 0.0005c and T/2000, respectively, for the rest of the simulations.

Fig. 4
figure 4

Comparison of numerical results of power coefficient

Full size image

To test the legitimacy of the numerical method for analyzing the power extraction performance of the flapping airfoil, the input parameters (Re = 5 × 105, θm = 75°, H = 1c, f* = 0.14) are chosen in line with Kinsey et al. [25], which ensures that both effective angle of attack αeff are the same during the whole flapping cycle, as shown in Fig. 5. Meanwhile, the validation curve of the flapping airfoil lift coefficient (CL = Fy(t)/(0.5ρU2∞c) with respect to the time is also presented in Fig. 5. It is evident from the plot that the lift coefficient CL of the present numerical data are in good agreement with those of Kinsey et al. [25], which confirms the accuracy of the numerical simulation model in this work.

Fig. 5
figure 5

The contrast curve of lift coefficient

Full size image

4 Taguchi experiment design and result analysis

4.1 Taguchi experiment design

Taguchi is a theoretical method of optimization for comprehensive experimental design, which can optimize the model under limited factors and levels, without calculating all possible combinations. It substantially reduces the simulation time and efforts with an improved experimental efficiency [26, 27]. The procedure of Taguchi method can be divided into six steps, which are as follows:

  1. (1)

    Identify optimization objective.

  2. (2)

    Select relevant parameters and levels.

  3. (3)

    Select orthogonal table.

  4. (4)

    Conduct experiments or CFD numerical simulation.

  5. (5)

    Analyze results.

  6. (6)

    Determine the optimized scheme.

In this paper, the Taguchi method and CFD technique are used to thoroughly study the effect of suction and blowing compound jet on the power extraction efficiency of the flapping airfoil. The jet parameters include the distance between the center point of the jet hole and the leading edge of the flapping airfoil Cf, the width of the jet hole D, and the ratio of jet velocity to inflow velocity Cu. For each parameter, four different levels are considered, as is shown in Table 1.

Table 1 The factors and levels
Full size table

Based on parameters and levels given in Table 1, the L16(43) orthogonal table is shown in Table 2. Taguchi method considers the signal-to-noise (S/N) ratio as a measure of robustness and better quality. The larger-the-better of the signal-to-noise ratio is defined using the efficiency parameter \(\eta\), given as:

$$ S/N = - 10\lg (1/\eta^{2} ) $$
(14)
Table 2 Orthogonal table and simulated results
Full size table

4.2 Analysis of Taguchi experiment results

The power extraction efficiency η of the flapping airfoil is taken as the input of the Taguchi experiment since it is an important parameter to assess the performance of the airfoil. The power extraction efficiency η and the S/N ratio of the 16 different cases are also illustrated in Table 2, where the results of the base airfoil are also presented for comparison. The results show that the power extraction efficiency of the flapping airfoil increases as the distance between the jet position and trailing edge of the airfoil reduces. The maximum and minimum values of the S/N ratio are found to be 31.531 and 26.277 for case 15 and case 4. The efficiency of case 15 is increased by 29.27% with reference to the baseline airfoil, which indicates that the power extraction efficiency of the flapping airfoil can be improved by applying the compound jet at the trailing edge under specific conditions.

Moreover, the Taguchi method can also be used to determine the weighted order and the optimal combination of different parameters. The order of weighted impact of each parameter on the power extraction performance can be determined by the difference between the largest mean S/N ratio and the smallest mean S/N ratio:

$$ E_{j} = \max \left( {G_{j1} ,G_{j2} ,G_{j3} ,G_{j4} } \right) - \min \left( {G_{j1} ,G_{j2} ,G_{j3} ,G_{j4} } \right) $$
(15)

where Gji represents the average S/N ratio of j = Cf, D, Cu factors at the level of i = 1,2,3,4.

The mean S/N ratio of each parameter was generated by Minitab17 software. The difference between the maximum and minimum S/N ratio of each factor Ej is shown in Table 3.

Table 3 The mean S/N ratios
Full size table

Based on Table 3, Fig. 6 shows the plot of mean S/N ratios for different values of each jet parameter. It is seen that the mean S/N ratios of the Cf and D increase as the level increases, while the mean S/N ratio of the Cu increases up to level 2 and then decreases as the level increases. The results show that the combination of A4, B4, and C2 (Cf = 0.9c, D = 0.07c, Cu = 1) yields the maximum efficiency.

Fig. 6
figure 6

The mean S/N ratios of the various levels of the jet parameters

Full size image

Figure 7 shows the order of impact of Cf, D, and Cu on the power extraction performance of the flapping airfoil are found to be 2.86, 0.12, and 1.87, respectively. This implies that the position of the jet hole Cf is the most significant parameter that affects the power extraction performance of flapping airfoil whereas the width of the jet hole D has the least impact.

Fig. 7
figure 7

The order of impact of the considered factors

Full size image

5 Mechanism of the compound jet affecting the power extraction performance

Numerical simulation of the optimal combination of jet parameters (Cf = 0.9c, D = 0.07c, Cu = 1) shows that the efficiency of flapping airfoil reaches 40.31%, which is 38.14% greater than that of the base airfoil. Besides, the minimum power extraction efficiency is 20.60% corresponding to case 4 as listed in Table 3. A thorough analysis of flapping airfoil with and without jet is presented in the following sections to explore the mechanism of the effect of suction and blowing compound jet on the power extraction efficiency of the flapping airfoil.

5.1 Force and momentum characteristics of flapping airfoil under optimal jet parameters

Referring to Eqs. (7)–(10), the power extraction efficiency of the flapping airfoil is a function of lift, plunging velocity, pitching moment, and pitching angular velocity. Figure 8 shows the variation of the lift coefficient, plunging velocity, pitching moment coefficient (CM = M(t)/( 0.5ρU2∞c2)), and pitching velocity of the airfoil as a function of time for the optimal jet parameters. The plunging velocity and pitching angular velocity of the flapping airfoil with jet and base airfoil are given in Eqs. (2) and Eq. (4), respectively.

Fig. 8
figure 8

Variations of lift coefficient, pitching moment coefficient, plunging power coefficient and pitching power coefficient when Cf = 0.9c, D = 0.07c, Cu = 1

Full size image
Fig. 9
figure 9

The lift coefficient as a function of the effective angle of attack when Cf = 0.9c, D = 0.07c, Cu = 1

Full size image

It is seen from Fig. 8a that the lift coefficient for both types of flapping airfoils varies in a similar fashion with respect to time. It is found that the amplitude of lift coefficient for flapping airfoil with the jet is slightly larger than that of the flapping base airfoil. In addition, the lift coefficient of the flapping airfoil with jet has better synchronicity with the plunging velocity. It results in the plunging motion of the flapping airfoil with optimal jet parameters that extracts more fluid power than that of the base airfoil, as shown in Fig. 8c.

It is seen from Fig. 8b that the pitching moment coefficient and pitching angular velocity are in the opposite phase for the specified period. It indicates the negative work done by the pitching moment during the said period. It can be observed from the plot that the amplitude of the pitching moment coefficient of the flapping airfoil with the jet is similar to that of the base flapping airfoil. However, the negative work produced by the flapping airfoil with a jet in the given period increases (see Fig. 8d), this is attributed to the deterioration of synchronicity between pitching moment and angular velocity of the flapping airfoil with jet, and when the pitching moment reaches the peak, the airfoil has a larger angular velocity.

In addition, it is found from Fig. 8c and d that the magnitude of \(\overline{C}_{p\theta }\) are much smaller than that of \(\overline{C}_{py}\), which indicates that the overall power extraction is dominated by the plunging motion. Meanwhile, the lift of the airfoil is associated with effective angle of attack [28], and the angle of attack of two studied cases in present work is the same, this explains the similar variation trend in the lift coefficient for both types of flapping airfoils. However, from β = 90–180° (phase of the plunging motion) and 270–360(0°), there is a obvious increase in the lift coefficient, which is related to the suction effect of the evolution of the leading edge vortex (LEV) (Fig. 9).

To make a comparison, the total power coefficient of a jet flapping airfoil is defined as \(C_{p1} = {{(p_{y} (t) + p_{\theta } (t))} \mathord{\left/ {\vphantom {{(p_{y} (t) + p_{\theta } (t))} {0.5\rho U_{\infty }^{3} c}}} \right. \kern-0pt} {0.5\rho U_{\infty }^{3} c}}\), and the jet consumption power coefficient is defined as \(C_{p2} = {{p_{u} (t)} \mathord{\left/ {\vphantom {{p_{u} (t)} {0.5\rho U_{\infty }^{3} c}}} \right. \kern-0pt} {0.5\rho U_{\infty }^{3} c}}\). According to Eq. (11): \(C_{p} = C_{p1} - C_{p2}\). The variation of the power coefficient with the time is plotted in Fig. 10. It can be seen from Fig. 10 that using the optimal jet parameters, the positive work done by the plunging motion is greater than the sum of the negative work done by the pitching motion and the power consumed by the jet, so the overall power extraction efficiency of the flapping airfoil with the jet is increased.

Fig. 10
figure 10

Variations of power extraction coefficients when Cf = 0.9c, D = 0.07c, Cu = 1

Full size image

5.2 Force and momentum characteristics of the flapping airfoil under the worst jet parameters

It can be seen from Table 3 that the minimum power extraction efficiency is 20.60% which corresponds to case 4. To analyze the reasons for the low efficiency of the flapping airfoil with jet (Cf = 0.6c, D = 0.07c, Cu = 2), Fig. 10 is plotted to see the variation of the lift coefficient, plunging velocity, pitching moment coefficient, and pitching angular velocity of the flapping airfoil with the jet as a function of the time.

Figure 11a depicts that the lift coefficient has a synchronized variation for the plunging velocity in the entire flapping cycle. After the jet is applied, the lift coefficient of the flapping airfoil has better synchronicity with the plunging velocity; however, the amplitude of the lift coefficient of the flapping airfoil with the jet is smaller, which is the reason for the two studied airfoils almost having identical plunging motion power coefficients with only the difference in phase, as shown in Fig. 11c.

Fig. 11
figure 11

Variations of lift coefficient, pitching moment coefficient, plunging power coefficient and pitching power coefficient when Cf = 0.6c, D = 0.07c, Cu = 2

Full size image

It is seen from Fig. 11b that compared to the base airfoil, the application of the jet increases the synchronicity of pitching moment and pitching angular velocity at t/T = 0.1–0.2 and t/T = 0.6–0.7, which represents the more positive work done by airfoil with jet at the moment, and this conclusion can be supported by Fig. 11d. On the other hand, the pitching moment coefficient of the flapping airfoil with jet reaches the higher value at (t/T) of 0.3–0.5 and 0.8–1.0 relative to that of the base flapping airfoil. As a result, the airfoil with worst jet parameters has a larger negative power consumption range than the base airfoil during the said period.

It is observed from Fig. 12 that similar to the optimized case, the deep dynamic stall is also not apparent. However, the formation and evolution of the LEV are affected by the jet under the worst parameters, which results in the peak value of the lift decrease, and the plunging power coefficient also decreases in the whole flapping cycle.

Fig. 12
figure 12

The lift coefficient as a function of the effective angle of attack when Cf = 0.6c, D = 0.07c, Cu = 2

Full size image

Figure 13 shows the variation of the power coefficient with respect to time. It is seen that the total power coefficient Cp1 profile of the flapping airfoil with the jet is slightly above the profile of power coefficient Cp for the base airfoil. It reveals that the power extracted by the plunging and pitching motion of the jet airfoil is improved relative to the base airfoil, but this increase in power is insufficient to compensate for the power consumed by the jet; therefore, the net power of the flapping airfoil decreases.

Fig. 13
figure 13

Variations of power extraction coefficients when Cf = 0.6c, D = 0.07c, Cu = 2

Full size image

5.3 Flow regimes of the flapping airfoil with and without jet

To further analyze the effect of suction and blowing compound jet on the power extraction performance of the flapping airfoil, the flow regimes with and without jet need to be examined. Figure 14 shows the vortex contours and pressure contours for the base airfoil and the two cases of the jet airfoil. A comparative analysis of the flow structure shows that at (t/T) of 0.15 and 0.25, it is seen that the vortex is generated on the pressure surface of the flapping airfoil in the vicinity of the jet. The vortex shrinks as the location of the jet is shifted to the trailing end of the airfoil. It can be seen from the pressure contours that the larger pressure is observed on the flapping airfoil pressure surface and a smaller pressure is found on the suction surface. However, when the position of the jet is far from the trailing edge of the flapping airfoil, a low-pressure area is formed in the pressure surface of the airfoil due to the existence of the jet, which is in favor of the counterclockwise pitching movement. For (t/T) of 0.35, the vortex contours show that the vortex on the pressure surface begins to separate from the surface of the flapping airfoil with jet, while the separation of the vortex on the suction surface from the lower surface of the airfoil is delayed due to the presence of jet. As shown by the pressure contours, the pressure on the suction surface of the flapping airfoil with the jet is smaller and the range is larger, which is contributing to the plunging movement of the airfoil. These observations are supported by Figs. 8a and 11a. It can be observed at (t/T) of 0.45 that the trailing edge of the suction surface of the flapping airfoil with the worst jet parameters has a partial positive pressure area, which is neither helpful for the downward movement nor to its clockwise pitching movement. Therefore, the flapping airfoil's plunging movement extracts less power, while the pitching movement consumes more power at this moment. The same conclusion is also drawn from Fig. 11.

Fig. 14
figure 14

Contour of z-vorticity and pressure

Full size image

6 Conclusions

In this work, the effects of the suction and blowing jet on the power extraction performance of the flapping airfoil are studied using the combined application of the Taguchi method and CFD technique. The major findings of this work are as follows:

  1. (1)

    The power extraction efficiency can be improved by applying suction and blowing jet on the trailing edge of the flapping airfoil. The optimal jet parameters are found to be Cf = 0.9c, D = 0.07c, Cu = 1 using the Taguchi method. The power extraction efficiency of the flapping airfoil is improved by 38.14% by adopting the optimal jet parameters.

  2. (2)

    When the jet is positioned near the center of the flapping airfoil at the rear half-edge, the vortex will be generated in the positive pressure area of the flapping airfoil, which results in an increase in power extraction less than the power consumed by the jet. It causes a reduction in the power extraction performance of the flapping airfoil.

  3. (3)

    The weighted order of the parameters that affect the power extraction performance of the airfoil is Cf, Cu, D.

The results obtained in this work can be useful for the design of a high-performance prototype of the flapping airfoil power extraction generator.