Accurate trajectory tracking control with adaptive neural networks for omnidirectional mobile robots subject to unmodeled dynamics

Abstract

Omnidirectional mobile robots have gained a lot of attention in recent years due to their maneuverability capabilities. However, ensuring accurate trajectory tracking with this class of robots is still challenging control system designers. In this work, a novel intelligent controller is introduced for accurate trajectory tracking of omnidirectional robots subject to unstructured uncertainties. An adaptive neural network is adopted within a Lyapunov-based nonlinear control scheme to deal with frictional forces and other unmodeled dynamics or external disturbances that may occur. Online learning, rather than supervised offline training, is employed to allow the robot to learn on its own how to compensate for uncertainties and disturbances by interacting with the environment. The adoption of a combined error signal as the single input in the neural network significantly reduces the computational complexity of the disturbance compensation scheme and enables the resulting intelligent controller to be implemented in the embedded hardware of mobile robots. The boundedness and convergence properties of the proposed control scheme are proved by means of a Lyapunov-like stability analysis. The effectiveness of the proposed intelligent controller is numerically evaluated and experimentally validated using an omnidirectional mobile robot. The comparative analyses of the obtained results show that the adoption of an intelligent compensation scheme based on adaptive neural networks allows reductions of more than $95\%$ in the tracking error, thus guaranteeing an accurate tracking and confirming the great superiority of the proposed control strategy.

1 Introduction

Mobile robots are autonomous devices that are able to move themselves and interact with the environment [1, 2]. It is noteworthy that mobile robotics is a cutting-edge research field and one of the most rapidly growing technologies at the moment, with applications ranging from warehouse logistics and surveillance operations to healthcare services and planetary exploration [3,4,5]. In addition, a special class of mobile robots, namely mecanum-wheeled omnidirectional robots, has gained a lot of attention lately due to their great maneuverability [6]. Independently driven mecanum wheels allow robots to move in an arbitrary direction with simultaneous translation and rotation, which grants them the ability to perform complex maneuvers [7] and navigate in narrow spaces [8, 9]. However, despite all these advantages, mecanum wheels can also lead to imprecise motion caused by wobbly contact between the free rollers with the ground [3, 8], which makes the design of accurate controllers for trajectory tracking with omnidirectional mobile robots (OMR) an urgent and imperative requirement [9, 10].

Although conventional controllers such as computed torque and other feedback linearization-based approaches have been successfully employed in industrial robotics [11], this is usually not the most suitable choice for trajectory tracking problems in mobile robotics. Mobile robots are often subject to unstructured environments, modeling inaccuracy and external disturbances, which in fact pose major challenges for the design of classical control laws [12, 13]. Furthermore, special attention should be also paid to the effects of friction on trajectory tracking with omnidirectional robots [14,15,16]. The contact of a mecanum wheel with the floor is theoretically limited to only one point, which causes the robot to slide and change its position/orientation abruptly even when subjected to only small changes in the friction force [16]. Thus, it is essential that the adopted control approach is also capable of dealing with the uncertainties arising from friction [9, 14].

In order to address the issues of modeling inaccuracies and imperfect information, computational intelligence offers a very attractive option for the control of mobile robots. On this basis, both fuzzy logic [8,9,10, 16,17,18,19] and artificial neural networks [20,21,22,23,24,25] based schemes have been adopted in the control of omnidirectional mobile robots. Cao et al.[8], for example, present a fuzzy adaptive PID controller for an OMR with eight mecanum wheels. In [9], backstepping is combined with fuzzy approximators to compensate for friction effects as well as other modeling inaccuracies, and the effectiveness of the proposed scheme is evaluated through numerical simulations considering a four-wheeled OMR. Zou et al.[10] propose a type 2 adaptive range fuzzy controller for a four-wheeled OMR, and its performance is compared with a PID scheme by means of computer simulations. A fuzzy proportional-integral (PI) controller is presented in [16] to improve the heading accuracy of a four-wheeled OMR. In [17], Mamdani hierarchical fuzzy systems are employed to allow a three-wheeled OMR to navigate in an unstructured environment. Trajectory tracking with three-wheeled OMR is also addressed in [18], but using an adaptive fuzzy sliding mode controller. Abiyev et al.[19] introduce a Z-number-based fuzzy inference system for the control of omnidirectional soccer robots.

Due to their universal approximation capability [26], radial basis function (RBF) networks are also widely employed for trajectory control with OMR. Zijie et al.[20], for instance, combine RBF networks with PID to enhance the heading precision of a four-wheeled OMR. In [21], RBF networks are used to estimate uncertain nonlinear functions in a sliding mode scheme, with the control performance being evaluated through numerical simulations. RBF networks have been also combined with Dynamic surface control to handle the trajectory tracking problem with four-wheeled [22, 23] and three-wheeled [24] OMR.

Despite the ability of control schemes based on computational intelligence to compensate for uncertainties and disturbances, there are some fundamental requirements that are often overlooked and not fulfilled:

• 1. The control scheme must be able to handle the robot dynamics, rather than just taking its kinematics into account, if accurate trajectory tracking is desired. Dynamic effects are the main source of uncertainty in mobile robotics and, if neglected, usually lead to degraded control performance.

• 2. Online learning, rather than offline training, should be used to allow the mobile robot to continuously learn by interacting with its surroundings. This is actually a very important feature because the control scheme must be able to continuously improve its overall performance even when subjected to a dynamically changing environment.

• 3. The intelligent algorithm should learn to deal with uncertainties and disturbances indirectly, as they are usually not available to be measured. The compensation scheme, in this case, should not rely on direct measurements of the signal to be estimated.

• 4. The resulting intelligent controller must be simple enough to avoid computational complexity, so that it can be implemented on the low-power embedded hardware of mobile robots. The computational complexity of neural networks and fuzzy systems is directly related to the number of neurons in the input layer or fuzzy variables in the premise of the rules, respectively.

As a matter of fact, none of the aforementioned control schemes satisfies all these four essential conditions.

In this work, a novel multivariable intelligent controller is introduced for three-wheeled omnidirectional mobile robots that is able to successfully handle these four requirements. The proposed scheme employs an adaptive radial basis function neural network to represent the robot uncertain dynamics within a Lyapunov-based nonlinear control law. In order to keep computational complexity low, the architecture adopted for the network requires only a combined error measure as the single input neuron. Moreover, the weight vector of the neural net can be updated online by minimizing the combined error measure, which allows the controller to be continuously improved as the robot moves around and does not need direct measurements of the disturbance that must be compensated. In fact, the proposed approach can be understood as an extension for a multiple-input and multiple-output system of the control strategy presented by Dos Santos and Bessa [27] for electrohydraulic actuators and by Bessa et al.[28] for a micro-diving cell. The boundedness and convergence properties of the tracking error are rigorously proved by means of a Lyapunov-like stability analysis. In addition, the effectiveness of the intelligent controller is evaluated not only via computer simulations, but also through experiments performed with an omnidirectional mobile robot. The superiority of the proposed control strategy can be clearly seen through the obtained results: the adoption of an intelligent compensation scheme guarantees a reduction of tracking error by more than $95\%$. It should also be highlighted that the proposed control approach presents a good trade-off between simplicity and efficacy, which allows its implementation in the low-power embedded hardware normally used in mobile robotics.

2 Omnidirectional mobile robot

An omnidirectional mobile robot like Robotino®, Fig. 1, has its individually controllable wheels arranged in such a manner that it can perform both translation and rotation motions independently.

Fig. 1

Three-wheeled omnidirectional mobile robot

In order to start designing the control law, a mathematical model representing the omnidirectional robot is quite useful. Dynamic models for such systems are well documented in the literature [24, 29,30,31]. In this section, we first present the kinematic relationship between the angular velocities of the wheels and the velocities described in the inertial frame. Then, the equation of motion of the system is obtained by means of Lagrangian mechanics.

2.1 Robot kinematics

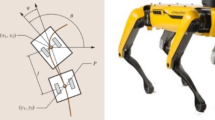
A schematic representation of the mobile robot with the adopted coordinate systems is shown in Fig. 2.

Fig. 2

Schematic top view of the omnidirectional robot

Considering that each wheel touches the ground at a single point and rolls without slipping, the velocity of the center point can be computed by:

$$\begin{aligned} {}_{B_i}\dot{\varvec{r}}_{w,i} = {}_{B_i}\dot{\varvec{r}}_{p,i} + {}_{B_i}\dot{\varvec{\theta }}_i \times {}_{B_i}\varvec{r}_w \end{aligned}$$

(1)

where ${}_{B_i}\dot{\varvec{\theta }}_i = [\omega _i ~ 0 ~ 0]^\top$, with $\omega _i$ being the angular velocity of the wheel, ${}_{B_i}\varvec{r}_w = [0 ~ 0 ~ r]^\top$ the vector with wheel radius r, and ${}_{B_i}\dot{\varvec{r}}_{p,i} = [\dot{n}_i ~ 0 ~ 0]^\top$ standing for the velocity due to the other two wheels.

Equation (1) can be also represented in the inertial frame using the appropriate transformation matrices:

$$\begin{aligned} {}_{I}\dot{\varvec{r}}_{w,i} = \varvec{T}_\varphi \varvec{T}_i\, {}_{B_i}\dot{\varvec{r}}_{w,i} \end{aligned}$$

(2)

where $\varvec{T}_\varphi$ is the transformation matrix between the inertial and the robot’s fixed reference frames, ${}_{I}\varvec{r} = \varvec{T}_\varphi {}_{\bar{B}}\varvec{r}$:

$$\begin{aligned} \varvec{T}_\varphi = \begin{bmatrix} \cos \varphi &{} -\sin \varphi &{} 0 \\ \sin \varphi &{} \cos \varphi &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$

(3)

and $\varvec{T}_i$ is the transformation matrix relating the center of the ith wheel to the robot’s center of mass $\bar{x}\bar{y}$, ${}_{\bar{B}}\varvec{r} = \varvec{T}_i {}_{B_i}\varvec{r}$:

$$\begin{aligned} \varvec{T}_1&= \varvec{T}_3^\top = \begin{bmatrix} \cos \beta &{} -\sin \beta &{} 0 \\ \sin \beta &{} \cos \beta &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$

(4a)

$$\begin{aligned} \varvec{T}_2&= {{\,\textrm{diag}\,}}\{-1, -1, 1 \} \end{aligned}$$

(4b)

with $\beta$ being the angle between the wheel axes, as depicted in Fig. 2.

Now, the velocity of each wheel is obtained by combining the translational velocity of the robot ${}_{I}\dot{\varvec{r}}_{t}$ with its rotational velocity ${}_{I}\dot{\varvec{r}}_{r}$:

$$\begin{aligned} {}_{I}\dot{\varvec{r}}_{w,i} = {}_{I}\dot{\varvec{r}}_{t} + {}_{I}\dot{\varvec{r}}_{r} \end{aligned}$$

(5)

where

$$\begin{aligned} {}_{I}\dot{\varvec{r}}_{t} = [\dot{x}~\dot{y}~0]^\top \end{aligned}$$

(6)

and

$$\begin{aligned} {}_{I}\dot{\varvec{r}}_{r} = {}_{I}\dot{\varvec{\varphi }} \times (\varvec{T}_\varphi {}_{\bar{B}}\varvec{r}_i) \end{aligned}$$

(7)

with ${}_{I} \dot{\varvec{\varphi }}$ being the resulting angular velocity of the robot:

$$\begin{aligned} {}_{I}\dot{\varvec{\varphi }} = \begin{bmatrix} 0 \\ 0 \\ \dot{\varphi } \end{bmatrix} + \varvec{T}_\varphi \sum _{i=1}^3 \varvec{T}_i {}_{B_i}\dot{\varvec{\theta }}_i \end{aligned}$$

(8)

and ${}_{\bar{B}}\varvec{r}_i$ being the center of rotation of each wheel with respect to the center of the robot:

$$\begin{aligned} {}_{\bar{B}}\varvec{r}_i = \varvec{T}_i \begin{bmatrix} l \\ 0 \\ 0 \end{bmatrix} \end{aligned}$$

(9)

By combining Eqs. (2) and (5), the angular velocities of the wheels and the speed of the robot, $\varvec{\dot{q}} = [\dot{x}~\dot{y}~\dot{\varphi }]^\top$, can be related as follows:

$$\begin{aligned} \varvec{\dot{q}} = \varvec{T}_r\,\varvec{\omega } \end{aligned}$$

(10)

with $\varvec{T}_r \in \mathbb {R}^{3 \times 3}$ being the corresponding transformation matrix [30], as detailed in Appendix A, and $\varvec{\omega } = [\omega _1~\omega _2~\omega _3]^\top$.

2.2 Robot dynamics

In order to derive the equations of motion for the omnidirectional robot using the Lagrangian approach, the generalized coordinates of the system need to be defined first:

$$\begin{aligned} \varvec{\theta } = [\theta _1~\theta _2~\theta _3]^\top \end{aligned}$$

(11)

with $\dot{\varvec{\theta }} = \varvec{\omega }$.

In addition to uniquely describing the robot’s position, the chosen coordinates are directly related to the input torques $\varvec{\tau } = [\tau _1~\tau _2~\tau _3]^\top$.

In this work it is considered that the robot moves freely on a flat surface. Thus, the equations of motion can be obtained from the Euler–Lagrange equation:

$$\begin{aligned} \frac{d}{dt} \left( \frac{\partial \mathcal {K}(\varvec{\theta }, \varvec{\omega })}{\partial \varvec{\omega }} \right) - \frac{\partial \mathcal {K}(\varvec{\theta }, \varvec{\omega })}{\partial \varvec{\theta }} = \varvec{\tau } \end{aligned}$$

(12)

with $\mathcal {K}(\varvec{\theta }, \varvec{\omega })$ being the kinetic energy.

Basically, a three-wheeled mobile robot is composed by four rigid bodies: a main body and the three driving blocks. However, as the controller to be proposed in the next section is capable of handling unmodeled dynamics, only the main body of the robot will be considered in kinetic energy:

$$\begin{aligned} \mathcal {K}(\varvec{\theta }, \varvec{\omega }) = \frac{1}{2} m_r {}_{I}\dot{\varvec{r}}_{t}^\top {}_{I}\dot{\varvec{r}}_{t} + \frac{1}{2} {}_{I}\dot{\varvec{\varphi }}^\top {}_{I} \varvec{I}_{r} {}_{I}\dot{\varvec{\varphi }} \end{aligned}$$

(13)

where ${}_{I}\dot{\varvec{\varphi }} = [0~0~\dot{\varphi }]^\top$ and ${}_{I} \varvec{I}_{r}$ is the inertia matrix of the main body:

$$\begin{aligned} {}_{I} \varvec{I}_{r} = m_r {{\,\textrm{diag}\,}}\left\{ \frac{h_r^2 + 3 R_r^2}{12}, \frac{h_r^2 + 3 R_r^2}{12}, \frac{R_r^2}{2} \right\} \end{aligned}$$

(14)

with $m_r$, $h_r$, and $R_r$ being the mass, height, and radius of the robot, respectively.

So, applying (6), (7), and (14) into (13), it follows that:

$$\begin{aligned} \mathcal {K}(\varvec{\theta }, \varvec{\omega }) = \frac{1}{2} m_r \left( \dot{x}^2 + \dot{y}^2 + \frac{1}{2} R_r^2 \dot{\varphi }^2 \right) \end{aligned}$$

(15)

Therefore, using the transformation matrix (10) to replace the variables $\dot{x}$, $\dot{y}$, $\dot{\varphi }$, the equation of motion for a omnidirectional mobile robot becomes [30, 31]:

$$\begin{aligned} \varvec{M} \varvec{\dot{\omega }} = \varvec{\tau } \end{aligned}$$

(16)

where $\varvec{M} \in \mathbb {R}^{3 \times 3}$ is the inertia matrix, which is detailed in Appendix B.

Finally, by combining the time derivative of (10) with (16), the robot dynamics can be expressed in the following vector form:

$$\begin{aligned} \varvec{\ddot{q}} = \varvec{f} + \varvec{T}_r \varvec{M}^{-1} \varvec{\tau } + \varvec{d} \end{aligned}$$

(17)

where $\varvec{f} = \varvec{\dot{T}}_r \varvec{T}_r^{-1} \varvec{\dot{q}}$, and $\varvec{d}$ is introduced to represent not only external disturbances but also modeling inaccuracies.

3 Intelligent controller

Intelligent controllers are able to adapt themselves, learn by interacting with the environment and can fairly predict the outcome of their own actions. They have been successfully used to control robotic [28, 32], underactuated [33,34,35], chaotic [36, 37] and other uncertain nonlinear systems [27, 38].

First, following the feedback linearization method [39], the control law for the omnidirectional mobile robot is defined as follows:

$$\begin{aligned} \varvec{\tau } = \varvec{M} \varvec{T}_r^{-1} (-\varvec{f} - \varvec{\hat{d}} + \varvec{\ddot{q}}_\text {d} - 2 \varvec{\Lambda } \varvec{\dot{\tilde{q}}} - \varvec{\Lambda }^2 \varvec{\tilde{q}}) \end{aligned}$$

(18)

with $\varvec{\hat{d}}$ being the estimate of $\varvec{d}$, $\varvec{\Lambda } \in \mathbb {R}^{3 \times 3}$ a diagonal matrix with strictly positive entries $\lambda _i$, and $\varvec{\tilde{q}} = \varvec{q} - \varvec{q}_\text {d}$ the tracking error vector.

By applying the control law (18) to the robot dynamics (17), the error dynamics becomes

$$\begin{aligned} \varvec{\ddot{\tilde{q}}} + 2 \varvec{\Lambda } \varvec{\dot{\tilde{q}}} + \varvec{\Lambda }^2 \varvec{\tilde{q}} = \varvec{d} - \varvec{\hat{d}} \end{aligned}$$

(19)

Inspired by the sliding mode method, a combined error vector is adopted:

$$\begin{aligned} \varvec{s} = \varvec{\dot{\tilde{q}}} + \varvec{\Lambda } \varvec{\tilde{q}} \end{aligned}$$

(20)

Thus, if (20) is considered in the description of the closed-loop system, Eq. (19) becomes:

$$\begin{aligned} \dot{\varvec{s}} + \varvec{\Lambda } \varvec{s} = \varvec{d} - \varvec{\hat{d}} \end{aligned}$$

(21)

From (19) to (21), it can be verified that in the ideal case, i.e., when $\varvec{\hat{d}}=\varvec{d}$ (perfect estimation), both tracking error $\varvec{\tilde{q}}$ and combined error $\varvec{s}$ exponentially converge to zero. If it is not the case, closed-loop dynamics is driven by the approximation error. Furthermore, it also suggests that the combined error $\varvec{s}$ represents a reasonable metric for tracking success and can be used to help calculate the estimate $\varvec{\hat{d}}$.

Then, assuming that artificial neural networks can ensure universal approximation [26] with an arbitrary precision $\varepsilon _i$, it follows that $d_i = \hat{d}_i^*+ \varepsilon _i$, with $\hat{d}_i^*$ being the output related to the optimal weight vector $\varvec{w}_i^*$.

Let us now turn the proposed control law into an intelligent scheme, allowing the estimate $\varvec{\hat{d}}$ to be calculated by RBF neural networks:

$$\begin{aligned} \hat{d}_i = \varvec{w}^\top _i \varvec{\psi }_i(s_i),\quad i=1,2,3 \end{aligned}$$

(22)

where $\hat{d}_i$ are the components of $\varvec{\hat{d}}$, $\varvec{w}_i = [w_{i,1} \ldots w_{i,n_i}]^\top$ stand for the weight vectors, and $\varvec{\psi }_i(s_i) = [\psi _{i,1} \ldots \psi _{i,n_i}]^\top$ represent the vectors with the activation functions $\psi _{i,j}$, with $i=1,2,3$, $j = 1, \ldots , n_i$, and $n_i$ being the number of neurons in the hidden layer of the corresponding ith component of $\varvec{\hat{d}}$. Figure 3 presents the architecture of the radial basis function network.

Fig. 3

Architecture of the RBF neural network

The boundedness and convergence properties of closed-loop signals in the presence of modeling inaccuracies can now be proved by means of a Lyapunov-type stability analysis. Thus, let a positive-definite function $V_i$ be defined for each component of $\varvec{s}$:

$$\begin{aligned} V_i(t) = \frac{1}{2} s_i^2 + \frac{1}{2\eta _i} \varvec{\delta }_i^\top \varvec{\delta }_i \end{aligned}$$

(23)

with $\eta _i$ being a strictly positive constant and $\varvec{\delta }_i = \varvec{w}_i - \varvec{w}_i^*$.

Since $\dot{\varvec{\delta }}_i = \dot{\varvec{w}}_i$, the time derivative of $V_i$ is

$$\begin{aligned} \begin{aligned} \dot{V}_i(t)&= s_i \dot{s}_i + \eta _i^{-1} \varvec{\delta }_i^\top \dot{\varvec{w}}_i\\&= [-\lambda _i s_i + d_i - \hat{d}_i]s_i + \eta _i^{-1} \varvec{\delta }_i^\top \dot{\varvec{w}}_i \\&= -[\lambda _i s_i - (\hat{d}_i^*+ \varepsilon _i - \hat{d}_i) ]s_i + \eta _i^{-1} \varvec{\delta }_i^\top \dot{\varvec{w}}_i\\&= -[\lambda _i s_i - \varepsilon _i + \varvec{\delta }_i^\top \varvec{\psi }_i ]s_i + \eta _i^{-1} \varvec{\delta }_i^\top \dot{\varvec{w}}_i\\&= -[\lambda _i s_i - \varepsilon _i ]s_i + \eta _i^{-1} \varvec{\delta }_i^\top [\dot{\varvec{w}}_i - \eta _i s_i\varvec{\psi }_i] \end{aligned} \end{aligned}$$

Hence, by updating $\varvec{w}_i$ according to $\dot{\varvec{w}}_i = \eta _i s_i \varvec{\psi }_i$, the time derivative $\dot{V}_i$ becomes

$$\begin{aligned} \begin{aligned} \dot{V}_i(t)&= -[\lambda _i s_i - \varepsilon _i ]s_i\\&\le - [\lambda _i \vert s_i\vert - \epsilon _i ]\vert s_i\vert \end{aligned} \end{aligned}$$

which means that $\dot{V}_i$ is negative definite when $\vert s_i\vert > \epsilon _i / \lambda _i$. Thus, the bounds of $\varvec{w}_i$ cannot be ensured with $\dot{\varvec{w}}_i = \eta _i s_i \varvec{\psi }_i$ when $\vert s_i\vert \le \epsilon _i / \lambda _i$. Fortunately, the projection algorithm [40] can be evoked to guarantee that $\varvec{w}_i$ will remain within a convex region $\mathcal {W}_i = \{\varvec{w}_i \in \mathbb {R}^n : \varvec{w}_i ^\top \varvec{w}_i \le \mu _i^2 \}$:

$$\begin{aligned} \dot{\varvec{w}}_i = \left\{ \begin{array}{ll} \eta _i s_i \varvec{\psi }_i &{} \text {if}~\Vert \varvec{w}_i \Vert _2< \mu _i ~\text {or} \\ &{} \text {if}~\Vert \varvec{w}_i \Vert _2 = \mu _i ~\text {and}~ \\ &{} \qquad \qquad \eta _i s_i \varvec{w}_i^\top \varvec{\psi }_i < 0 \\ \left( \varvec{I} - \frac{\varvec{w}_i \varvec{w}_i^\top }{\varvec{w}_i^\top \varvec{w}_i} \right) \eta _i s_i \varvec{\psi }_i &{} \text {otherwise} \end{array} \right. \end{aligned}$$

(24)

where $\mu _i$ is the desired upper bound of $\Vert \varvec{w}_i \Vert _2$.

Since $\Vert \varvec{w}_i(0) \Vert _2 \le \mu _i$, it follows that $\vert s_i\vert \le \epsilon _i / \lambda _i$ and $\Vert \varvec{w}_i(t) \Vert _2 \le \mu _i$ as $t \rightarrow \infty$. Then, recalling that $s_i = \dot{\tilde{q}}_i + \lambda _i \tilde{q}_i$, it follows that

$$\begin{aligned} -\lambda _i^{-1}\epsilon _i \le \dot{\tilde{q}}_i + \lambda _i \tilde{q}_i \le \lambda _i^{-1}\epsilon _i \end{aligned}$$

(25)

Multiplying (26) by $e^{\lambda _i t}$ and integrating the resulting inequalities between 0 and t, yields

$$\begin{aligned} -\lambda _i^{-1}\epsilon _i e^{\lambda _i t}&\le \left( \dot{\tilde{q}}_i + \lambda _i \tilde{q}_i\right) e^{\lambda _i t} \le \lambda _i^{-1}\epsilon _i e^{\lambda _i t}\\ -\lambda _i^{-1}\epsilon _i e^{\lambda _i t}&\le \frac{d}{dt} \left( \tilde{q}_i e^{\lambda _i t} \right) \le \lambda _i^{-1}\epsilon _i e^{\lambda _i t} \end{aligned}$$

Integrating between 0 and t, and dividing by $e^{\lambda _i t}$, gives

$$\begin{aligned} -\frac{\epsilon _i}{\lambda _i^2} - \left[ \vert \tilde{q}_i (0)\vert + \frac{\epsilon _i}{\lambda _i^2} \right] e^{- \lambda _i t} \le \tilde{q}_i \le \frac{\epsilon _i}{\lambda _i^2} + \left[ \vert \tilde{q}_i (0)\vert + \frac{\epsilon _i}{\lambda _i^2} \right] e^{- \lambda _i t} \end{aligned}$$

For $t \rightarrow \infty$, it becomes:

$$\begin{aligned} -\frac{\epsilon _i}{\lambda _i^2} \le \tilde{q}_i \le \frac{\epsilon _i}{\lambda _i^2} \end{aligned}$$

(26)

Applying (26) to (25), yields

$$\begin{aligned} -2\frac{\epsilon _i}{\lambda _i} \le \dot{\tilde{q}}_i \le 2\frac{\epsilon _i}{\lambda _i} \end{aligned}$$

(27)

This implies that the proposed control scheme ensures the exponential convergence of the tracking error to the closed region $\mathcal {Q} = \{ (\varvec{\tilde{q}},\varvec{\dot{\tilde{q}}}) \in \mathbb {R}^6 : \vert \tilde{q}_i\vert \le \epsilon _i\lambda _i^{-2} \, \text {and} \, \vert \dot{\tilde{q}}_i\vert \le 2\epsilon _i\lambda _i^{-1}\}$.

It is important to emphasize that the proposed control scheme, defined by Eqs. (18), (22) and (24), has all the required features, namely adaptation, learning and prediction, which enables it to be called an intelligent controller according to Bessa et al.[41].

The block diagram of the proposed intelligent control scheme is shown in Fig. 4.

Fig. 4

Block diagram of the intelligent control scheme

4 Numerical and experimental results

The effectiveness of the proposed control scheme is now evaluated first through numerical studies and then with the help of a three-wheeled OMR.

4.1 Numerical studies

Numerical simulations were performed in C++, by applying the proposed control scheme to the robot dynamics (17). The system of ordinary differential equations was numerically solved using the fourth-order Runge–Kutta method with sampling rates of 10 Hz for the controller and 400 Hz for the dynamic model. The Armadillo C++ library [42] was used to assist in scientific computing tasks. To evaluate control performance in the presence of modeling uncertainties and external disturbances, the term $\varvec{d}$ is calculated as $\varvec{d} = \Delta \varvec{M} \ddot{\varvec{q}} - \varvec{\xi }$, where $\Delta \varvec{M} \ddot{\varvec{q}}$ takes into account the uncertainty in the inertia matrix and $\varvec{\xi } = \varvec{\Xi } \dot{\varvec{q}}$ stands for the unknown friction effects, with $\varvec{\Xi } = {{\,\textrm{diag}\,}}\{ 5; 4; 12 \}$.

Regarding the other model parameters, they are chosen as: $m_r = 11.2$ kg, $l=0.294$ m, $\beta = 60^\circ$, $r = 0.051$ m, $R_r = 0.27$ m, and $g=9.81$ m/s$^2$. In the control design, an error of 10% is assumed with respect the inertial matrix and the gains are set to $\lambda _i = 1$. Considering the network architecture presented in Fig. 3, three RBF networks are considered, one for each state variable, where each one contains one input ($s_i$), one output ($\hat{d}_i$) and seven neurons in the hidden layer. The number of neurons was chosen to ensure a good trade-off between control accuracy and computational burden. Gaussian functions are adopted for the neurons in the hidden layer: $\psi _i(s_i; c_i, \sigma _i) = \exp \{ -0.5[(s_i - c_i)/\sigma _i]^2 \}$, where $c_i = [-\gamma _i/2; -\gamma _i/4; -\gamma _i/8; 0.0; \gamma _i/8; \gamma _i/4; \gamma _i/2]$ and $\sigma _i = [\gamma _i/3; \gamma _i/5; \gamma _i/15; \gamma _i/30; \gamma _i/15; \gamma _i/5; \gamma _i/3]$, with $\varvec{\gamma } = [0.5; 0.5; 3.0]$. In order to let the robot learn about its environment from scratch, the weight vector is initialized as $\varvec{w}_i = \varvec{0}$ and updated according to (24), with learning rates $\varvec{\eta } = [30; 30; 35]$. Figure 5 shows the tracking performance associated with the trajectory $\varvec{q}_\text {d} = [r\cos (\alpha t)~-r\sin (\alpha t)~-(\alpha t +\pi /2)]^\top$, with $r = 0.5$ and $\alpha = \pi /15$. The influence of the neural network on the control performance is evaluated by comparing the proposed intelligent approach with a conventional nonlinear controller, namely the computed torque scheme, which is commonly used in robotics. In fact, the computed torque scheme can be easily obtained from the intelligent approach by simply disregarding the contribution of the RBF networks to the control signal, i.e., by setting $\varvec{\hat{d}} = \varvec{0}$.

Fig. 5

Numerical results for the tracking of $\varvec{q}_\text {d} = [r\cos (\alpha t)~-r\sin (\alpha t)~-(\alpha t +\pi /2)]^\top$

By observing the obtained numerical results, it can be seen that the intelligent controller is capable of tracking the desired trajectory, presenting a strongly improved performance when compared to the conventional approach, Fig. 5a. The efficacy of the proposed control scheme can also be verified by noting that the conventional controller presented a significant residual tracking error, while the intelligent approach was able to practically zero it, Fig.  5b, with a comparable control effort, Fig. 5c. This improved tracking response, as a matter of fact, is due to the capacity of the neural network to compensate for modeling uncertainties and external disturbances, Fig. 5d, which quite often degrade the performance of conventional controllers.

4.2 Experimental validation

The performance of the intelligent controller is now assessed by means of experimental results obtained with the omnidirectional mobile robot Robotino®. The robot consists of three controllable mecanum-like wheels equipped with optical encoders, nine infrared distance sensors, a bumper sensor, a digital gyroscope, and an embedded PC 104 with real-time Linux operating system. The proposed control scheme was implemented in C++ using the Robotino® API. All control parameters are the same used in numerical studies. Uncertainties regarding the inertia matrix and no prior knowledge of the friction effects are once again assumed. The robot’s position and orientation are provided by the odometry system using the gyroscope and motor encoders. It should be noted that, instead of torques, the robot requires the angular speeds of the wheels as control inputs, which is easily obtained with a first order filter. Moreover, as both conventional and intelligent controllers need the robot speed, i.e., $\varvec{\dot{q}} = [\dot{x}~\dot{y}~\dot{\varphi }]^\top$, sliding mode observers [43] are used for this purpose. The deployed computer code and all obtained experimental data can be accessed at https://github.com/RoboteamUFRN/Intelligent-Control-Robotino.

Figures 6 and 7 show the obtained results for the tracking of $\varvec{q}_\text {d} = [r\cos (\alpha t)~-r\sin (\alpha t)~-(\alpha t +\pi /2)]^\top$.

Fig. 6

Experimental results and overlaid video frames for the trajectory tracking with Robotino®

Fig. 7

Experimental results for the tracking of $\varvec{q}_\text {d} = [r\cos (\alpha t)~-r\sin (\alpha t)~-(\alpha t +\pi /2)]^\top$

As shown in Fig. 6, the intelligent controller allows the robot to track the desired trajectory with a small associated error. Some video frames captured during the experiment are also overlaid to allow a better understanding of the obtained results. Furthermore, the results presented in Fig. 7 confirm the much superior performance of the proposed controller, as well as the effectiveness of the adaptive neural network in compensating for uncertainties and disturbances, Fig. 7d. As can be seen in Fig. 7b, the intelligent control scheme is able to provide a much smaller tracking error when compared to the conventional approach.

In fact, for a quantitative comparison, the absolute errors obtained in steady-state can be summed according to the equation below:

$$\begin{aligned} E_{\tilde{z}}=\int ^{t_2}_{t_1}\vert \tilde{z}\vert \text {d}t \end{aligned}$$

(28)

with $\tilde{z}$ representing the tracking error for one of the three states. Table 1 shows the results for both conventional and intelligent controllers, related to the tracking errors in Fig. 7b obtained from $t_1=30$ s to $t_2=60$ s.

Table 1 Comparative analysis of the tracking error obtained with conventional and intelligent controllers: sum of the absolute errors during the steady-state phase

From Table 1 it can be observed that when incorporating the RBF networks in the control law, the tracking error obtained with the intelligent controller in the steady-state phase is from 95.83 to 99.73% lower, which confirms its much superior performance when compared to the conventional approach.

The full video of the trajectory tracking with Robotino®, as well as the animated plots with both control schemes, can be accessed at https://youtu.be/GT9OINhxZpo.

5 Concluding remarks

This work introduces a novel intelligent controller for accurate trajectory tracking with omnidirectional mobile robots. The proposed scheme takes advantage of a Lyapunov-based nonlinear approach, but adaptive neural networks are also included in the control law to deal with modeling uncertainties and external disturbances. The boundedness and convergence properties of all closed-loop signals are analytically proved.

Moreover, the proposed intelligent controller is able to fulfill the four essential requirements mentioned at the beginning of this work:

• 1. The intelligent control scheme can adequately handle the dynamic effects associated with the robot’s motion, rather than just kinematic control, which allows accurate trajectory tracking even when subjected to unmodeled dynamics;

• 2. Online learning, rather than offline training, is adopted to allow the robot to continuously improve its overall performance in a dynamically changing environment;

• 3. The neural network can learn to compensate for uncertainties and disturbances by minimizing the combined error measurement, making direct measurements of the signal to be estimated (which is not possible in real applications) completely unnecessary;

• 4. As only $s_i$ is used as input to the neural networks, instead of the states or state errors, the complexity of the intelligent compensation scheme can be considered quite low, making its implementation possible even on the low-power embedded hardware of mobile robots.

Finally, the effectiveness of the proposed control scheme is evaluated both numerically, through simulation studies, and experimentally with a three-wheeled omnidirectional mobile robot. Both numerical and experimental results confirm the greatly improved performance achieved by the intelligent controller. The quantitative comparison of the experimental results obtained with the conventional and intelligent controllers showed that the proposed approach is capable of providing tracking errors from 95.83 to 99.73% lower, thus ensuring accurate trajectory tracking even in the presence of high levels of uncertainty.

From the results presented in this work, it can be verified that intelligent control schemes are essential to deal with the high level of uncertainties to which mobile robots are subject. However, it is worth mentioning that control systems, whether they are intelligent or not, still depend on a previously established reference. In mobile robotics, this reference is often defined by a path planning algorithm, which along with perception, localization and tracking control is also one of the most researched subjects nowadays. Path planning is, nonetheless, a NP (nondeterministic polynomial-time) hard problem and in some applications, such as self-driving cars, it usually involves many ethical issues. Therefore, future works in mobile robotics should focus on the development of integrated strategies for simultaneous motion planning and control, where a single algorithm is able to plan and control the trajectory to be followed in a smooth and holistic way.

Appendices

Appendix A: Transformation matrix

$$\begin{aligned} \varvec{T}_r&= \begin{bmatrix} t_{11} &{} t_{12} &{} t_{13} \\ t_{21} &{} t_{22} &{} t_{23} \\ t_{31} &{} t_{32} &{} t_{33} \end{bmatrix} \end{aligned}$$

(29)

$$\begin{aligned} t_{11}&= \frac{r [\sin (\beta - \varphi ) + \sin \varphi ]}{\cos 2\beta - 1} \end{aligned}$$

(30)

$$\begin{aligned} t_{12}&= \frac{r \sin \varphi }{\cos \beta + 1} \end{aligned}$$

(31)

$$\begin{aligned} t_{13}&= \frac{r [\sin \varphi - \sin (\beta + \varphi )]}{\cos 2\beta - 1} \end{aligned}$$

(32)

$$\begin{aligned} t_{21}&= \frac{r [\cos (\beta - \varphi ) - \cos \varphi ]}{\cos 2\beta - 1} \end{aligned}$$

(33)

$$\begin{aligned} t_{22}&= -\frac{r \cos \varphi }{\cos \beta + 1} \end{aligned}$$

(34)

$$\begin{aligned} t_{23}&= \frac{r [\cos (\beta + \varphi ) - \cos \varphi ]}{\cos 2\beta - 1} \end{aligned}$$

(35)

$$\begin{aligned} t_{31}&= t_{33} = \frac{r}{2 l (\cos \beta + 1)} \end{aligned}$$

(36)

$$\begin{aligned} t_{32}&= \frac{r \cos \beta }{l (\cos \beta + 1)} \end{aligned}$$

(37)

Inertia matrix

$$\begin{aligned} \varvec{M}&= \begin{bmatrix} m_{11} &{} m_{12} &{} m_{13} \\ m_{21} &{} m_{22} &{} m_{23} \\ m_{31} &{} m_{32} &{} m_{33} \end{bmatrix} \end{aligned}$$

(38)

$$\begin{aligned} m_{11}&= m_{33} = \frac{m_r r^2 \sec ^4(\beta /2) [2 l^2 \csc ^2 (\beta /2) + R_r^2]}{32 l^2} \end{aligned}$$

(39)

$$\begin{aligned} m_{12}&= \frac{m_r r^2 \sec ^4(\beta /2) (R_r^2\cos \beta - 2 l^2)}{16 l^2} \end{aligned}$$

(40)

$$\begin{aligned} m_{13}&= m_{31} = \frac{m_r r^2 \sec ^4(\beta /2) \left( \dfrac{4 l^2 \cos \beta }{\cos \beta - 1} + R_r^2 \right) }{32 l^2} \end{aligned}$$

(41)

$$\begin{aligned} m_{22}&= \frac{m_r r^2 \sec ^4(\beta /2) (2 l^2 + R_r^2 \cos ^2\beta )}{8 l^2} \end{aligned}$$

(42)

$$\begin{aligned} m_{21}&= m_{23} = m_{32} = m_{12} \end{aligned}$$

(43)