1 Introduction

Owing to their vast industrial applications, pitching motion and dynamic stall behavior of airfoils have been of great interest to many researchers. To illustrate, output power of wind turbines could be controlled either by pitch to feather or stall where the latter, as the name suggests, brings about dynamic stall on the blade [1, 2]. Furthermore, airplane maneuver, MAVs motion and turbomachines performance are highly affected by dynamic stall. As a result, in the last decades some theoretical [3,4,5], experimental [6,7,8,9] and numerical [10,11,12,13,14] attempts have been made to investigate dynamic stall.

Many researchers attempted to investigate different aspects of dynamic stall through understanding effects of geometrical parameters [15,16,17], turbulence [18,19,20] and vortex structures formation [20, 21]. For instance, Visbal and Garmann [22] studied the dynamic stall of a 3-D wing by the employment of large eddy simulation (LES) method. It was shown that before the formation of the dynamic stall vortex (DSV) a laminar separation bubble (LSB) appears on the leading edge of the airfoil.

Due to the fact that stall leads to a drop in the lift coefficient and the subsequent detrimental effects, postponement of flow separation by various control methods has been a topic of interest for the researchers in this field as well. Active flow controllers like synthetic jets and plasma as well as passive controllers have been studied for dynamic stall control in recent years owing to their high performance [23,24,25,26,27,28,29,30]. In a study, Tadjfar and Asgari [31] attempted to find the optimal location of a synthetic jet. It was reported that at optimum location the drag coefficient decreased significantly. It was found that the employment of synthetic jets at lower frequencies delays the dynamic stall better compared to higher amplitudes.

Rain as a sporadic meteorological phenomenon could impose penalties to the aerodynamic efficiency of an airborne device which cannot be thoroughly considered in the design process. As a result, the investigation of rain effect on the aerodynamic characteristics has been an ongoing issue explained in different studies. For instance, the work of Rhode [32], Luers [33] and Hess and Spectron [34] could be regarded as the first attempts to shed light to the physics of rain and air flow interaction. In the following years, Bezos et al. [35, 36] performed an experimental study on the effect of raindrop on the aerodynamic performance of an airfoil under heavy rain condition. Thompson et al. [37] derived the correlation between the surface-film behavior and aerodynamic coefficients for a wing with a NACA-4412 airfoil profile by means of experimental methods. It should be noted with the advances in the computational resources, numerical techniques began to be implemented to describe the physics of raindrop on the aerodynamic behavior of an airborne. The Eulerian–Lagrangian method is the general framework of modelling raindrops in the literature which will be discussed in details in the following sections. In this regard, the study conducted by Valentine and Decker [38] is one of the very first attempts to numerically simulate the raindrop effect on an airfoil. Wu et al. [39], Wu and Cao [40] and Ismail et al. [41] also implemented a numerical study to find the penalty in the aerodynamic coefficients as a result of the raindrops and the airfoil interaction. Fatahian et al. [42, 43] studied the performance of gurney flaps and slatted airfoils under rainy condition. In another study, Fatahian et al. [44] investigated the effect of rain on aeroacoustics behavior of an airfoil employing Volume of Fluid (VOF), an Eulerian–Eulerian approach, for the film formation on the airfoil, along with Eulerian–Lagrangian reference of frame to take the raindrops into consideration. It should be noted that there is a common finding in in the literature that indicates the presence of rain leads to a decrease in the aerodynamic performance of an airfoil. Another aspect of rainy condition which needs to be taken care of with more details is on airfoils utilized in energy production machines e.g., wind turbines. Cai et al. [45] developed a Eulerian–Lagrangian method to study the performance of a wind turbine airfoil under rainy condition. It was reported that the two-phase model successfully simulated the rain effect on the airfoil and the results suggested a considerable penalty on the aerodynamic performance. Aiden and Arastoopour [46] studied the effect of rain and the water-film formation on the aerodynamic performance of an airfoil of a wind turbine blade by Discrete Phase Model (DPM) and Volume of Fluid (VOF), respectively. It should be noted that DPM is a Eulerian–Lagrangian method which solves the discrete phase in the Lagrangian frame of reference moving along with the particles e.g., raindrops, and the primary phase is solved in the stationary frame of reference known as Eulerian. Wu et al. [47] investigated the effect of rain on the performance of vertical axis wind turbine. Similar to the previous studies, it was demonstrated that the presence raindrops leads to the exacerbation of aerodynamic performance the wind turbine. Nevertheless, airfoil has not been the only topic of interest for researchers. To illustrate, Jian et al. [48] investigated the effect of rain drop on the liquid film thickness formed on the windshield of a train. Yu et al. [49] investigated the aerodynamics of an Ahmet body under heavy rain condition.

Generally, most of the research in this field focused on the dynamic stall in the dried conditions, and moreover, the raindrop investigations were mainly aimed to understand the physics of static aerodynamic bodies. However, moving airborne devices, such as pitching airfoil, may undergo dynamic stall in the rainy conditions as well. Having considered the studies conducted so far, one comes to this conclusion that the effect of raindrops on the characteristics of the dynamic stall, which is very common in real life applications of this phenomenon, has remained unnoticed. In fact, the presence of raindrops in the upstream flow can affect the aerodynamic loads and flow characteristics downstream of the pitching airfoil. Due to the presence of the raindrops which adds more momentum to the upstream flow, and also considering the interaction between the raindrops and the turbulent flow structures, some variations in flow characteristics compared to the baseline case could be expected. In the following sections, the effect of the rainy condition on the dynamic stall of a NACA-0012 airfoil and the mechanisms leading to aerodynamic characteristics variation will be investigated by means of numerical methods namely, two-phase flow methods and turbulence modelling technique.

2 Problem description

In this study the effect of the rain on flow characteristics over a pitching airfoil oscillating around its one quarter chord in dynamic stall condition has been numerically investigated by means of Ansys Fluent v18. It should be noted that the geometry and the pitching were set according to that of [24]. The oscillating airfoil is a NACA-0012 profile with a chord length of 0.58 m which has been subjected to a uniform flow with the inlet velocity being equal to 24.93 (m/s). Therefore, the mentioned parameters result in a Reynolds number equal to 106 In addition, the NACA-0012 airfoil undergoes a sinusoidal motion according to Eq. 1 as follows:

$$\theta = \theta_{0} + A{\text{sin}}\left( {2\pi ft} \right)$$
(1)

where \({\theta }_{0}\) is the initial incidence angle of the airfoil being equal to \(14.98^\circ\). Moreover, A is the amplitude of the motion which was set to be 10 degrees. As a result, the amplitude of the airfoil fluctuation ranges from \(4.98^\circ\) to \(24.98^\circ\). Also, f is the frequency of motion however, as demonstrated in the literature, reduced frequency, which is denoted by k, is preferred to frequency as it also takes the free stream velocity into consideration which leads to a more thorough description of the motion. Reduced frequency is calculated by Eq. 2 and it should be mentioned that for this study its value was considered to be equal to 0.15.

$$k = \frac{\pi fc}{{U_{\infty } }}$$
(2)

In addition, because the main non-dimensional number ruling the physics of incompressible flows is the Reynolds number, this number was set to be equal for both the dry and rainy cases. The parameter which needs to be adjusted to make the Reynolds number of the wet and dry cases equal is the inlet velocity as the density and viscosity for both the wet and dry cases are obtained by equations as follows:

$$\rho = \alpha .\rho_{{{\text{water}}}} + \left( {1 - \alpha } \right).\rho_{{{\text{air}}}}$$
(3)
$$\mu = \alpha .\mu_{{{\text{water}}}} + \left( {1 - \alpha } \right).\mu_{{{\text{air}}}}$$
(4)

where α, ρ and μ are the mass fraction of water, density, and viscosity, respectively. The simulation was decided to be performed at a relatively low amount of liquid water content to avoid much difference in the inlet velocity as this study is intended to take the effect of the waterdrops into consideration only. Therefore, the water liquid content was set to 2.1 g/m3 as suggested in [34]. The lift and drag coefficients were calculated, respectively, based on the density obtained from Eq. 3 as presented in Eqs. 5–6. It should be noted that the vertical relative velocity component of raindrops was neglected to study the pure effect of drops interacting with the airfoil and the airflow. The role of the vertical relative velocity component could be investigated in future studies.

Obviously, the mass fraction of water for the dry case was set to zero.

$$C_{L} = L/0.5\rho U_{\infty }^{2} A$$
(5)
$$C_{D} = D/0.5\rho U_{\infty }^{2} A$$
(6)

where \(L\) and \(D\) correspond to lift and drag force magnitude, respectively. Also, the reference area as denoted by \(A\), is the surface of a rectangle which is parallel to the flow confined to the chord and span lines of the airfoil.

3 Numerical method

Considering the fact that the Reynolds number lies in the range of turbulent flow regime, 2-D unsteady Reynolds averaged Navier–Stokes (URANS) presented in Eq. 7 was numerically solved by ANSYS FLUENT Version 18.0 commercial code.

$$\frac{{\partial U_{i} }}{\partial t} + U_{j} \frac{{\partial U_{j} }}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{\partial P}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {\frac{\mu }{\rho }\frac{{\partial U_{i} }}{{\partial x_{j} }}} \right) + \frac{{\partial \left( { - u_{i}^{^{\prime}} u_{j}^{^{\prime}} } \right)}}{{\partial x_{j} }}$$
(7)

To solve Eq. 7 k−ω Shear–Stress Transport (SST) method was utilized owing to its widely known capabilities in precisely localizing the separation and also predicting the flow characteristics both in pre- and post-stall condition. This method. i.e., k−ω SST, is a two-equation URANS model which solves the region in the vicinity of the wall by standard k−ω turbulence model, while the flow variables of the far field region are obtained by k−ɛ model, thanks to their capabilities in predicting the boundary layer separation and the free stream characteristics, respectively. In order for the turbulence modelling equation to be able to switch from k−ω to k−ɛ interchangeably, it is multiplied by a blending function whose value is considered to be one in the near wall and null in the far field region.

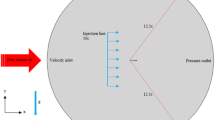
The boundary conditions applied to the systems of equations has been presented in Fig. 1. The airfoil surface was considered to be wall with no-slip condition. In addition, at the upper and lower bounds of the numerical domain, as seen in Fig. 1, the gradients of all the variables were assumed to be zero. This boundary condition has been specified as “symmetry” as shown in Fig. 1. Moreover, to impose pitching motion to the airfoil, the domain has been decomposed into two separate regions called inner and outer region. It should be mentioned that the pitching motion was imposed to the inner region using the sliding mesh technique. As a result, no mesh stretching/compression and mesh destruction/generation was employed which makes the solution far more accurate. Also, note that the type of the surrounding circle is “interface” meaning that conservation of the flux of flow variables on either side of the boundary would be guaranteed. For solving mentioned equations, a pressure-based solver using SIMPLE pressure–velocity coupling was implemented. In addition, all the spatial and temporal terms in the equations presented above were discretized by second order upwind and second order method. In addition, least square cell base method was employed to discretize the gradients.

Fig. 1
figure 1

Boundary condition and zone names in the numerical domain

Full size image

To take the effect of raindrops into consideration, two multiphase models which were DPM and Dispersed Multiphase (DMP), which is a Eulerian–Eulerian method which models a dispersed phase (rain) in a primary phase (air) both in a stationary frame of reference, were employed. DPM is a Lagrangian–Eulerian method which regards the primary phase i.e., the phase whose volume fraction is far more dominating than that of the other phase, to be solved by Eulerian approach. As a result, the primary phase flow field is obtained by working out Eq. 7 presented earlier. Further, in DPM, the behavior of secondary phase, which is the phase with considerably lower amount of volume fraction, is described by Lagrangian approach. To predict the trajectory of the secondary phase, the resulting force acting on the particles needs to be calculated and by striking the force balance, the inertial force will be equal to the force exerted by the primary phase. As a result, Eq. 8 presented below will be the governing equation of the Lagrangian equation whose result specifies the particles trajectories.

$$m_{p} \frac{{du_{p} }}{dt} = m_{p} \frac{{\left( {u - u_{p} } \right)}}{{\tau_{r} }} + \frac{{g_{x} \left( {\rho_{p} - \rho } \right)}}{{\rho_{p} }} + F_{x}$$
(8)

where the first term on the right-hand side of the equation above is the drag force, and Fx represents additional forces acting on the particles. It should be noted that \({\tau }_{r}\) is the droplet or particle relaxation time obtained as follows:

$$\tau_{r} = \frac{{\rho_{P} d_{p}^{2} }}{18\mu }\frac{1}{{f_{r} }}$$
(9)

A further discussion of the relaxation time is found in Sect. 4.4.

Many attempts have been made to present a relationship between the drag function, fr, and the primary flow characteristics. Nevertheless, Schiller and Naumann correlation has been employed in this study to predict the drag function:

$$f_{r} = \frac{{C_{D} {\text{Re}}}}{24}$$
(10)

where

$$C_{D} = \left\{ {\begin{array}{*{20}l} {24\left( {1 + 0.15{\text{Re}}^{0.687} } \right), {\text{Re}} < 1000} \\ {0.44 , {\text{Re}} \ge 1000} \\ \end{array} } \right.$$
(11)

In Discrete Phase Model (DPM) it is assumed that the dispersed phase, which possesses a lower amount of volume fraction, has been scattered throughout the flow field. DMP, unlike DPM, includes an Euler–Euler system of equation. In addition, in each cell the volume fraction is obtained through the continuity equation. On the other hand, the continuity equation needs to be calculated for each phase. As a result, the set of equations for DMP are as follows:

$$\frac{\partial }{\partial t}\int\limits_{v} {\alpha_{i} \rho_{i} {\text{d}}V} + \oint\limits_{A} {\alpha_{i} \rho_{i} v_{i} .{\text{d}}a} = 0$$
(12)
$$\frac{\partial }{\partial t}\smallint \alpha_{i} \rho_{i} v_{i} {\text{d}}V + \oint\limits_{A} {\alpha_{i} \rho_{i} v_{i} \times v_{i} .{\text{d}}a} = - \int\limits_{v} {\alpha_{i} \nabla p{\text{d}}V + F_{ij}^{D} }$$
(13)

where αi, ρi and \({v}_{i}\) are volume fraction, density and velocity component of the dispersed phase \(i\). Moreover, \({F}_{ij}^{D}\) is the drag forced exerted by the primary phase to the dispersed phase \(j\). Also, \(p\) stands for the static pressure which includes the buoyancy force.

4 Parameters independency and validation

To verify the performance and the choice of numerical parameters in the numerical simulation the parameters affecting the results need to be thoroughly investigated. The parameters which are going to be studied in this section are mesh and time step independency, numerical solution validation against experimental results and multiphase accuracy. Having performed the mentioned studies, one may ensure the validity of the numerical solution to draw reasonable conclusions in the following sections.

4.1 Mesh independency

To investigate the sensitivity of the numerical solution to the mesh size, three different meshes with 50,000, 150,000 and 250,000 cells were generated and the variation of lift and drag coefficient with the mesh size is plotted in Fig. 2. It is evident in Fig. 2 that after 1,50,000 cells the variation in lift and drag coefficients is less than one percent. Therefore, the mesh with 1,50,000 cells was selected to perform the further numerical simulations on it. Moreover, the value of \({y}^{+}\) was calculated all over the airfoil and its maximum number is 1.8. In Fig. 3 the graphical and qualitative presentation of the mesh generated around the airfoil can be observed. It should be noted that the Angle of Attack (AOA) has been presented in degrees in all the figures of this paper.

Fig. 2
figure 2

Mesh independency study

Full size image
Fig. 3
figure 3

Mesh generated around the airfoil

Full size image

4.2 Time step independency

To implement time step independency study, three different time steps were considered. The time step size was determined with respect to the amount of time the airfoil needs to sweep one period of the oscillating movement. As a result, considering the angular velocity of the airfoil, which is the time derivation of the pitching motion presented in Eq. 1, time steps as long as one period T divided by 180, 360 and 720 were generated to perform the time step independency study. The hysteresis curve of the lift coefficient for all time steps is plotted in Fig. 4. It is evident that the discrepancy among the time step lengths is quite negligible and the results for the finest time steps i.e., \(T/360\) and \(T/720\), are so close that the curves are on top of the other It should be noted that T stands for the time required for the completion of one period of movement which is equal to \(0.49(\text{s})\). As a result, the time step sizes for the implementation of this study are \(2.72\times {10}^{-3},1.36\times {10}^{-3}\) and \(6.8\times {10}^{-4}\) s. It should be noted that the simulations for the time step study were performed for the dry case.

Fig. 4
figure 4

Time step study (dry case)

Full size image

4.3 Numerical solution validation

The numerical results obtained for the dry case, using the parameters which were proven to satisfy the independency conditions, were compared with both experimental (McAlister et al. [7]) and numerical data (Tadjfar and Asgari [31]) and presented in Fig. 5. It is evident that the numerical results could capture the trend of the aerodynamic forces as well as location of dynamic stall occurrence properly. It should be noted that there are some non-smooth changes in the experimental results indicating lack of sampling. As a result, the experimental data could not capture the lift oscillations at the beginning of the dynamic stall, while both numerical results show some oscillations.at the same angles of attack. The largest amount of difference between numerical results with the experimental data occurs during the downstroke near \(AoA=18^\circ\). At this point, both numerical studies fail to capture physics of dynamic stall. This point corresponds to separation of Trailing Edge Vortex (TEV) which will be discussed in details in the following sections.

Fig. 5
figure 5

Validation with experimental and numerical data in the literature (dry case)

Full size image

As discussed in the introduction part, DPM is mainly employed as the main method for the rain simulation in different applications. In this work, in order to perform a validation study on the DPM simulation, the wet results of a static NACA-0012 airfoil at different angles of attacks were compared with that of the experimental and numerical studies conducted respectively by Bezos et al. [35] and Ismail et al. [41]. In Fig. 6 the aerodynamic coefficients of the airfoil under rainy condition have been presented. As seen in Fig. 6 the wet results of the current simulation are in a good agreement with that of the experimental work of Bezos et al. [35]. It should be noted that the same DPM settings will be used for the investigation of the rain effect on the dynamic stall.

Fig. 6
figure 6

Validation with experimental and numerical data in the literature (wet case)

Full size image

4.4 Multiphase model accuracy

As mentioned at the beginning of Sect. 3, in order to find the most accurate multiphase model to predict the behavior of pitching airfoil in the rainy weather condition, DPM and DMP methods were employed. For the implementation of DPM, a two-way coupling method was utilized. Particle relaxation time is defined as follows in Eq. 14 [50]:

$$\tau = \frac{{\left( {\frac{{\rho_{p} }}{{\rho_{f} }}*d^{2} *C_{c} } \right)}}{18\nu }$$
(14)

where in this study the slip correction factor, \({C}_{c},\) is about unity. Regarding the droplet density, air density, droplet diameter and air viscosity as \({\rho }_{p}\), \({\rho }_{f}\), \(d\) and \(\nu\) respectively, the relaxation time of particles will be \(3\times {10}^{-4}\text{s}\). To be on the safe side, only three percent of the calculated relaxation time was considered as the particle time step, i.e., \(\Delta {t}_{p}={10}^{-5}\text{s}\). Another parameter which is required to be determined is the order of coupling. Fig. 7 demonstrates the particles coupling order in terms of volume fraction, \({\alpha }_{P}\), and relative relaxation time, \({\tau }_{P}/{\tau }_{f}\) presented by Elghobashi [51]. Considering the amount of volume fraction and the relaxation time of flow and particle, this problem requires to be modeled by two-way coupling.

Fig. 7
figure 7

Classification of particle–turbulence interactions (Elghobashi [51])

Full size image

In Fig. 8 the lift, drag and moment coefficients have been presented under both rainy and dry condition.

Fig. 8
figure 8

Multiphase Model accuracy investigation

Full size image

Unlike DPM, there have been few reports on utilizing Eulerian–Eulerian reference of frame for modelling raindrops in the air [52], which may be associated with the disperse nature of water drops. However, one should keep in mind that less significant deal of computational cost is imposed to the system in this method. Hence, it is wise to compare the results obtained from Eulerian–Eulerian and Eulerian–Lagrangian references of frame for simulating water drops in air. The accuracy of the Eulerian–Lagrangian method, namely DPM, has been validated in Sect. 4.3. In addition, based on the literature, the presence of raindrops cannot make significant alterations in the trend of aerodynamic forces. However, as seen in Fig. 8, the results of the Eulerian–Eulerian method, i.e., DMP, demonstrate a totally different patterns especially at the angles of attack near the dynamic stall. Thus, the DMP method is not appropriate in capturing the physics of dynamic stall of a pitching airfoil under the rainy condition. Also, as can be observed by looking in Fig. 8a at the lift coefficient, DMP method fails to capture the physics of dynamic stall. On the other hand, DPM demonstrates an excellent capability to yield physically meaningful results in both the pre- and post-stall conditions. Ergo, in the following steps, DPM method was chosen to study the effect of the raindrops. Also, it should be noted that the liquid water content and droplet diameter were assumed to be \(2.1 {\text{g}}/{\text{m}}^{3}\) and \({10}^{-5\;{\text{m}}}\) respectively as suggested in [53]. In addition, as [53] suggests when the We number ranges from five to ten, which is the working range of this study, the interaction between the airfoil and the raindrops is assumed to be of the rebound type.

5 Results and Discussion

Having evaluated the accuracy of the numerical simulation, we discuss the effect of raindrops on the aerodynamic characteristics by comparing lift and drag coefficients with those of the dry case. To achieve this goal, the lift and drag coefficient hysteresis curves of the dry and the wet cases are presented in Fig. 9. Also, to understand the physics of this phenomenon, the vorticity contours of the dry and the wet cases at different angles of attack are presented in Fig. 10. It should be noted that the points on Fig. 9 correspond to the angles of attack in Fig. 10. Also, the upwards and downwards arrows in Fig. 9 indicate upstroke and downstroke motion, respectively. As stated in Sects. 2 and 4.4, the raindrop diameter and liquid water content were set to be 1e − 5 m and \(2.1 {\text{g}}/{\text{m}}^{3}.\)

Fig. 9
figure 9

Points of interest

Full size image
Fig. 10
figure 10figure 10figure 10

Vorticity contours at different angles of attack (left and right contours correspond to dry and rainy condition, respectively)

Full size image

Overall, both the dry and wet cases follow the same trend and the overall value of the aerodynamic coefficients of the wet case is smaller than that of the dry case. Nevertheless, it is evident in Fig. 9 that there is a lead in the trend of the wet case as peaks and valleys occurred ahead of that of the dry case. Due to the fact that both cases suggest a similar trend in the lift and drag coefficient variation, in the following the aerodynamic phenomena regarding the pitching motion both in the dry and the wet case is investigated. The vorticity contours at different angles of attack during up and downstroke have been presented in Fig. 10. Figure 10a shows that at the beginning of the pitching upstroke motion the vortical structure in both cases is quite narrow. As the angle of attack increases the vortical structure begins to grow as seen in Fig. 10b. As the angle of attack rises to about 23 degrees, in Fig. 10c, the first cores of the leading-edge vortex (LEV) start to appear on the leading edge of the airfoil. It should be noted that the LEVs are typical of dynamic stall phenomenon and they come into existence due to the difference between the free stream and the leading-edge relative velocities leading to Kelvin–Helmholtz instability. Also, the presence of the LEV benefits the lift growth and it is the main responsible for the stall prognostication as it causes the velocity to increase on the suction side and at the same time decelerates the flow passing the pressure side. Obviously, by increasing the angle of attack the LEV is intensified thanks to the rise in the relative velocity between the flow and the airfoil leading edge as demonstrated in Fig. 10d. Therefore, when the angle of attack exceeds a certain limit the LEV detaches, and the lift coefficient drops dramatically as can be seen in Fig. 10e. The detachment of the LEV leads to a sharp drop in the lift coefficient and a sudden rise in the drag coefficient and this observation corresponds to the point “e” in Fig. 9. Up to this angle of attack i.e. the LEV detachment at 25 degrees, the vortical structures formation in both dry and wet cases are similar. However, straight after the LEV detachment a lead in the formation of the vortical structures is witnessed. To illustrate, the same vortical structure reported in the wet case at \(24.79^\circ\) (Fig. 10e-right) is exactly observed in the dry case at \(22.70^\circ\) (Fig. 10f-left). Moreover, the same trend is observed until the airfoil reaches very low angles of attacks as illustrated in Fig. 10j. Therefore, the flow separation and the succeeding phenomena, in the wet case, happen at a lower angle of attack, during the upstroke motion, compared to the dry case.

It should also be noted that during the downstroke motion another phenomenon known as trailing edge vortex (TEV) rises into importance as the downward motion favors its formation as a result of the velocity gradient at the trailing edge. Contrary to the LEV, TEV is a counterclockwise (CCW) vortex generated at the trailing edge of the airfoil and its formation is an adverse factor to the lift coefficient growth. This is ascribed to the fact that, because of the direction of its rotation, the TEV decelerates the flow on the suction side and accelerates the flow on the pressure side resulting in a lift drop. In order to better understand the effect of the TEV on the aerodynamic behavior of the airfoil, the vortical structures at the beginning of the TEV formation and its detachment need to be taken into consideration. To begin with, the first symptoms of the TEV formation can be observed at the beginning of the dynamic stall in Fig. 10e (shown in red) where the LEV starts to detach. A little after the LEV detachment, as demonstrated in Fig. 10f and g, the TEV grows and then detaches. Unlike the LEVs, TEV growth leads to a lift coefficient sharp drop and its detachment results in a rise in the lift coefficient as marked in Fig. 9a by the points “f” and “g”. In other words, the LEV and TEV formation and separation correspond to a local minimum and maximum, respectively. As a result, the oscillations in the lift and drag coefficients, mainly at higher angles of attack during the downstroke motion, are due to the TEV formation and separation.

The main outcome of the description on the comparison between the vorticity contours and the aerodynamic characteristics is that the lift and drag coefficient of the rainy case is slightly lower than that of the dry case and also a lead in the aerodynamic phenomena is observed. At the first thought, these phenomena could be attributed to the lower Reynolds number of air in the wet case leading to lower amount of lift coefficient and a lead in the TEV separation. However, a numerical simulation was performed for the dry case with the air inlet velocity equal to that of the current wet case and the results showed almost the same value for the aerodynamic coefficients and with absolutely no lead or lag in their behavior. As a result, the explanation for these phenomena needs to be sought in the interaction between the primary and secondary phases. Therefore, the contour of velocity magnitude difference (UWET − UDRY) between the wet and the dry case along with the vectorial difference is presented in Fig. 11 to have a better understanding of the interaction. It is evident in Fig. 11 that at the leading edge the difference vectors tend downwards suggesting that the airfoil sees a lower amount of angle of attack which corresponds to a lower amount of lift coefficient. Also, at the trailing edge, the difference vectors show a TEV like vortical structure. As discussed earlier, the presence of a CCW vortex at the trailing edge has an adverse effect on the lift generation of the pitching airfoil which is one of the mechanisms leading to a lower amount of lift coefficient of the wet case compared to the dry case. Further, regarding the vector differences, it is evident in Fig. 11 that the flow in the suction side experiences a deceleration, while on the pressure side it accelerates. In other words, an LEV with an unfavorable rotation direction (CCW) is seen at the leading edge. All the observations from Fig. 11 imply that due to the two-way coupling the air velocity vectors of the upstream flow undergoes an alteration due to the forces exerted by the secondary phase.

Fig. 11
figure 11

Velocity difference between the wet and the dry case at \(AOA=22.96^\circ\) Upstroke

Full size image

6 Conclusion and summary

In this study the effect of raindrops on the dynamic stall of a NACA-0012 pitching airfoil at a Reynolds number equal to 106 was investigated. The well-known \(k-\omega {\text{SST}}\) model was utilized to account for the turbulent phenomena. In addition, to exploit the maximum accuracy of this model, \({y}^{+}\sim 1\) was considered for the airfoil boundary. The rain condition was set as suggested in [53]. Hence, the raindrop diameters and liquid water content were set \({10}^{-5} {\text{m}}\) and \(2.1 {\text{g}}/{\text{m}}^{3}\), respectively. To implement an accurate two-phase study two different well-known models were compared and the most accurate one called Discrete Phase Model (DPM) was selected as the main two-phase model. It was shown that the Disperse Multiphase (DMP) method is not capable of capturing the physics of the dynamic stall. As a result, DPM was employed to investigate the effect of raindrops on the pitching airfoil. Furthermore, to ensure the accuracy of the numerical results, the grid and time step independency were implemented, respectively. In the end, the numerical solution was validated against an experimental [7] and a numerical [31] studies.

The comparison between the lift and drag coefficients revealed that a lead and drop in both the coefficients occurred. More precisely, wet condition phenomena occurred in advance of that of the dry one with slightly lower magnitude. Firstly, it was discussed that Reynolds number does not play a pivotal role in the lift reduction or phase lead as the hysteresis curves of the aerodynamic coefficients for the dry cases with the inlet velocity being equal to the main dry case and the wet case were stated to be very close in value and no phase shift was observed. Secondly, the two-way coupling of air and raindrops, causes the flow to undergo an alteration in its direction near the leading edge. The velocity difference contours proved the direction of velocity in the rainy case lies in the adverse direction, as a result of two-way coupling, which leads to a lower amount of aerodynamic coefficients in general. The vorticity contours of the dry and the wet cases showed that the Leading Edge Vortex (LEV) and Trailing Edge Vortex (TEV) of the wet case tend to separate anterior to the dry case. Also, it was illustrated that the LEV formation contributed to lift augmentation, while the presence of TEV results in a reduction in the lift coefficient. Hence, their separation counteracts their positive or negative effects on the aerodynamic coefficients to a considerable extent. Therefore, to sum up, the main findings of this study are as follows:

  • DPM is a more accurate solution for modelling raindrops effects on a pitching airfoil than DMP is. Since the latter has been proven to be not able to capture the physics of the flow.

  • Raindrops cause a reduction in the magnitude of lift and drag coefficients.

  • Raindrops do not alter the main trend of the aerodynamic coefficients but they bring a lead in the trend.

  • The lower Reynolds number of the wet case was shown not to have a considerable effect on the lower amount of the aerodynamic coefficients and phase shift.

  • The two-way coupling between the primary and the secondary phases was found to change the local angle of attack affecting the aerodynamic of the airfoil.

  • The interaction between the primary and secondary phases was found to be the most important factor resulting in the observed phenomena.