Polyconvex hyperelastic modeling of rubberlike materials

Abstract

In this work a number of selected, isotropic, invariant-based hyperelastic models are analyzed. The considered constitutive relations of hyperelasticity include the model by Gent (G) and its extension, the so-called generalized Gent model (GG), the exponential-power law model (Exp-PL) and the power law model (PL). The material parameters of the models under study have been identified for eight different experimental data sets. As it has been demonstrated, the much celebrated Gent’s model does not always allow to obtain an acceptable quality of the experimental data approximation. Furthermore, it is observed that the best curve fitting quality is usually achieved when the experimentally derived conditions that were proposed by Rivlin and Saunders are fulfilled. However, it is shown that the conditions by Rivlin and Saunders are in a contradiction with the mathematical requirements of stored energy polyconvexity. A polyconvex stored energy function is assumed in order to ensure the existence of solutions to a properly defined boundary value problem and to avoid non-physical material response. It is found that in the case of the analyzed hyperelastic models the application of polyconvexity conditions leads to only a slight decrease in the curve fitting quality. When the energy polyconvexity is assumed, the best experimental data approximation is usually obtained for the PL model. Among the non-polyconvex hyperelastic models, the best curve fitting results are most frequently achieved for the GG model. However, it is shown that both the G and the GG models are problematic due to the presence of the locking effect.

1 Introduction

At present the polymeric materials play a crucial role in different branches of industry. It is the reason why a good description of the mechanical properties of polymers becomes an important issue. In the case of elastomers, the hyperelasticity theory is usually used to describe the material behavior, cf, e.g., [12, 22]. Nowadays the hyperelasticity is also a basis utilized to formulate some more elaborate constitutive equations, such as the nonlinear viscoelastic or the damage models, e.g., [2, 13, 25, 30, 31]. Furthermore, the hyperelastic material models can be used for solving multifield problems, e.g., [8]. Consequently, a proper formulation and perfecting of the constitutive equations of hyperelasticity are indispensible.

In this study our attention is focused on the isotropic, invariant-based hyperelastic models due to the fact that the finite element (FE) implementation of such models is much simpler than in the case of models formulated using the principal stretches such as the model by Ogden [22], for instance. The invariant-based models are also characterized by a lower computational cost of the FE analysis. What is more, the common assumption of material full incompressibility is adopted for further simplification.

The reason behind the concepts presented in the subsequent paragraphs can be summarized as follows. The Mooney–Rivlin (MR) hyperelastic model [21, 23] and the model by Gent (G) [9], which both follow from the statistically-based neo-Hookean (NH) stored energy function, are the starting point for further analysis. An idea of combining the advantages of MR and G models leads to the formulation of the so-called generalized Gent model (GG) [16]. As it will be shown further in the text, the GG model is characterized by a very good approximation of the experimental data. However, the presence of a logarithmic term is the source of troublesome locking effect in both the G and the GG models. A need for eliminating the locking effect yields the concept of replacing the logarithmic term with an exponential one which results in the definition of the exponential-power law stored energy function (Exp-PL) [15]. This model formulation can be further simplified by eliminating the strongly nonlinear exponential term in favor of an additional power term which leads to the power law model (PL) [14].

The analyzed stored energy functions (GG, Exp-PL and PL) depend both on the first and the second deformation invariants in order to properly capture the material response in both the uniaxial and the biaxial stress states [14, 18]. Thus, in order to determine the material parameter values the experimental data from the uniaxial tension test and the biaxial tension test are required. In addition, the test data collected in a simple shear experiment can be utilized during the material parameter evaluation. However, in this case the shear test results play a secondary role, since during this particular experiment the values of the first and the second invariants are equal, cf, e.g., [14, 18], making it difficult to assess the influence of a particular invariant.

The GG, the Exp-PL and the PL models are phenomenological. Thus, the material parameters of these models have no clear physical meaning. This is the reason why the term “material parameters” is used instead of “material constants”. Nevertheless, for each of the considered hyperelastic models the initial value of the shear modulus can be calculated using the given material parameter values. The formulas for the initial shear modulus have been given in the paper.

All the three aforementioned stored energy functions are nonlinearly dependent on the material parameter values. Thus, the nonlinear optimization tools require to be utilized in order to evaluate the material parameters of hyperelasticity¹. It should be emphasized that the material parameters cannot be clearly determined using the methods of nonlinear optimization and their evaluation process leads to alternative, different parameter sets which are characterized by some very similar values of the residual square error. A need for additional mathematical conditions arises that would reduce the non-uniqueness of solutions associated with the nonlinear optimization process, thus allowing to more specifically determine the material parameter values.

The constitutive models of hyperelasticity are viewed here as tools developed in order to solve different boundary value problems both analytically or numerically using the FE analysis, for instance. Thus, assuming the elastic energy as a polyconvex function appears to be a natural choice, since it ensures the existence of solution to a properly defined boundary value problem². Other mathematical conditions such as the stored energy’s positivity or the condition of convexity with respect to the principal stretches are either insufficient or too restrictive, cf [3, 14, 27]. The specific limitations regarding material parameter values can be derived from the polyconvexity conditions, e.g., [26]. Thus, the non-uniqueness of material parameter identification is reduced when the energy polyconvexity conditions are applied.

In the present study, the material parameters for each of the three analyzed hyperelastic models have been identified using eight different experimental data sets, i.e., [1, 5, 11, 20, 28, 33]. It is shown that the best curve-fitting quality is usually achieved for the material parameter set which is in an agreement with the commonly used conditions that were proposed by Rivlin and Saunders [24]. However, it is demonstrated that the conditions by Rivlin and Saunders are in a contradiction with the requirements of stored energy polyconvexity. This matter is discussed further in the text, and some explanation is proposed for this phenomenon.

It is found that for the considered group of hyperelastic models the application of polyconvexity conditions leads to only a slight decrease in the curve fitting quality. It is shown that in the case of a polyconvex stored energy function the best test data approximation is usually achieved when the power law (PL) model is used. If the polyconvexity conditions are omitted, the best curve fitting results are often obtained for the generalized Gent model (GG). Nevertheless, it is highlighted that the locking effect which is exhibited by both the model by Gent and its generalization presents itself a serious obstacle to a correct identification of material parameter values. Moreover, it is shown further in the text that the much celebrated Gent’s model does not always allow to obtain an acceptable quality of the experimental data approximation.

Finally, it is demonstrated that in many cases the analyzed Exp-PL and PL stored energy functions can be significantly simplified without any serious decrease in the curve-fitting quality. The considered simplifications included the omission of selected terms within the stored energy function and the assumption that some of the exponents are equal to one. Such simplifications allow to limit the number of material parameters which need to be identified and decrease the computational cost of numerical calculations due to the reduction of model’s nonlinearity.

2 Hyperelastic models of rubberlike materials

2.1 Stored energy functions and constitutive relations

The rubberlike materials are usually analyzed as the isotropic and incompressible hyperelastic materials which satisfy the following internal constraints:

$$\begin{aligned} J-1=\det \mathbf{F}-1=0, \end{aligned}$$

(1)

where $\mathbf{F}$ is the deformation gradient tensor, e.g., [12]. Due to the incompressibility constraints given by Eq. (1), a rubberlike material can undergo only isochoric deformations, i.e., deformations without a volume change. The stored energy function $W(\overline{\mathbf{F}})={\overline{W}}({\bar{I}}_{1},{\bar{I}}_{2})$ is a function of two basic invariants of the isochoric deformation, i.e., ${\bar{I}}_{1}$ and ${\bar{I}}_{2}$:

$$\begin{aligned} {\bar{I}}_{1}={{\,\mathrm{tr}\,}}\overline{\mathbf{C}}={{\,\mathrm{tr}\,}}\overline{\mathbf{B}}, \qquad {\bar{I}}_{2}={{\,\mathrm{tr}\,}}\overline{\mathbf{C}}^{-1}={{\,\mathrm{tr}\,}}\overline{\mathbf{B}}^{-1}, \end{aligned}$$

(2)

where $\overline{\mathbf{B}}=\overline{\mathbf{F}}\overline{\mathbf{F}}^{{{\,\mathrm{T}\,}}}$ and $\overline{\mathbf{C}}=\overline{\mathbf{F}}^{{{\,\mathrm{T}\,}}}\overline{\mathbf{F}}$ are the left and the right Cauchy–Green deformation tensor, respectively. The multiplicative decomposition of the deformation gradient tensor $\mathbf{F}$ into its volumetric component $(\det \mathbf{F})^{1/3}{} \mathbf{I}$ (with $\mathbf{I}$ being the identity tensor) and the isochoric component $\overline{\mathbf{F}}$, $\mathbf{F}=(\det \mathbf{F})^{1/3}\overline{\mathbf{F}}$ is utilized.

Due to the incompressibility constraints given by Eq. (1), the constitutive relation in the body’s deformed configuration defines only the deviatoric component of the Cauchy stress tensor. It takes the following form, e.g., [14]:

$$\begin{aligned} \varvec{\sigma }= -p\mathbf{I}+{\bar{\beta }}_{1}\overline{\mathbf{B}}+{\bar{\beta }}_{-1}\overline{\mathbf{B}}^{-1}, \end{aligned}$$

(3)

where p is the unknown hydrostatic pressure, whereas

$$\begin{aligned} {\bar{\beta }}_{1}=2\frac{\partial {\overline{W}}({\bar{I}}_{1},{\bar{I}}_{2})}{\partial {\bar{I}}_{1}}, \quad {\bar{\beta }}_{-1}=-2\frac{\partial {\overline{W}}({\bar{I}}_{1},{\bar{I}}_{2})}{\partial {\bar{I}}_{2}}. \end{aligned}$$

(4)

In the case of incompressibility constraints the basic invariants ${\bar{I}}_{1}$ and ${\bar{I}}_{2}$ can be viewed as the functions of two independent principal values of the stretch tensors, i.e.,

$$\begin{aligned} {\bar{I}}_{1}={\bar{\lambda }}_{1}^{2}+{\bar{\lambda }}_{2}^{2}+({\bar{\lambda }}_{1} {\bar{\lambda }}_{2})^{-2}, \quad {\bar{I}}_{2}={\bar{\lambda }}_{1}^{-2}+{\bar{\lambda }}_{2}^{-2}+({\bar{\lambda }}_{1} {\bar{\lambda }}_{2})^{2}. \end{aligned}$$

(5)

In Eqs (5) ${\bar{\lambda }}_{1}$ and ${\bar{\lambda }}_{2}$ are the independent but unarranged eigenvalues of tensors $\overline{\mathbf{U}}=\sqrt{{\overline{\mathbf{C}}}}$ and $\overline{\mathbf{V}}=\sqrt{{\overline{\mathbf{B}}}}$, [12, 22]. The invariant ${\bar{I}}_{1}$, unlike ${\bar{I}}_{2}$, is a convex function of the stretches ${\bar{\lambda }}_{1}$ and ${\bar{\lambda }}_{2}$, e.g., [14].

The incompressibility constraints given by Eq. (1) implicate the following relationship between the Cauchy stress tensor $\varvec{\sigma }$ and the first Piola–Kirchhoff (P–K) stress tensor $\mathbf{S}$:

$$\begin{aligned} \mathbf{S}=\varvec{\sigma } {{\,\mathrm{Cof}\,}}\mathbf{F}=\varvec{\sigma }\left( \mathbf{F}^{-1} \right) ^{{{\,\mathrm{T}\,}}}, \end{aligned}$$

(6)

where ${{\,\mathrm{Cof}\,}}\mathbf{F}=J (\mathbf{F}^{-1} )^{{{\,\mathrm{T}\,}}}=(\mathbf{F}^{-1} )^{{{\,\mathrm{T}\,}}}$ in the case of $J=1$. The constitutive relationship formulated using the first P-K stress tensor can be obtained using Eqs (3) and (6).

2.2 Conditions imposed on stored energy function

2.2.1 Polyconvexity

In the mathematical theory of hyperelasticity, it is assumed that the stored elastic energy function is polyconvex [3, 27]. This assumption guarantees the existence of solutions to a wide class of boundary value problems³.

The elastic energy function $W(\mathbf{F})$ is polyconvex if the extended function, i.e.,

$$\begin{aligned} W(\mathbf{X},\mathbf{F})={\mathcal {W}}(\mathbf{X},\mathbf{F}, {{\,\mathrm{Cof}\,}}\mathbf{F}, \det \mathbf{F}), \end{aligned}$$

(7)

is a convex function. The domain of function ${\mathcal {W}}(\mathbf{X},\mathbf{F}, {{\,\mathrm{Cof}\,}}\mathbf{F}, \det \mathbf{F})$ takes the form of a nineteen-dimensional set $Lin \times Lin \times (0, \infty )$.

An extension of the stored energy function’s domain is necessary due to the fact that for the function $W(\mathbf{F})$ the tensor $\mathbf{F}$ is an element of $Lin^{+}$ which is a non-convex set⁴. The smallest convex set which contains $Lin^{+}$ is Lin.

A polyconvex function ${\mathcal {W}}(\mathbf{F}, {{\,\mathrm{Cof}\,}}\mathbf{F}, \det \mathbf{F})=W(\mathbf{C})$ must also satisfy the requirements which follow from the conditions of proper growth for:

$$\begin{aligned} \Vert \mathbf{C} \Vert \rightarrow 0^{+}, \quad \Vert {{\,\mathrm{Cof}\,}}\mathbf{C} \Vert \rightarrow 0^{+}, \quad \det \mathbf{C} \rightarrow 0^{+}, \end{aligned}$$

(8)

and analogous conditions when the quantities listed above tend to infinity, e.g., [3, 14, 27].

In the case of incompressible materials (the constraints given by Eq. (1)), the function $W(\overline{\mathbf{F}})$ is a polyconvex one if an extension of this function exists which takes the form of another function ${\mathcal {W}}(\mathbf{F}, {{\,\mathrm{Cof}\,}}\mathbf{F})$ which is convex with respect to $\mathbf{F} \in Lin$ and ${{\,\mathrm{Cof}\,}}\mathbf{F} \in Lin$ (cf [3, 27]), i.e.,

$$\begin{aligned} W(\overline{\mathbf{F}})={\mathcal {W}}(\mathbf{F}, {{\,\mathrm{Cof}\,}}\mathbf{F}). \end{aligned}$$

(9)

For the sake of simplicity, it is assumed that:

$$\begin{aligned} W(\overline{\mathbf{F}})={\mathcal {W}}_{1}(\mathbf{F})+{\mathcal {W}}_{2}({{\,\mathrm{Cof}\,}}\mathbf{F}), \end{aligned}$$

(10)

where:

$$\begin{aligned}&{\mathcal {W}}_{1}(\mathbf{F})=W_{1}(I_{1}), \quad I_{1}={{\,\mathrm{tr}\,}}(\mathbf{F}^{{{\,\mathrm{T}\,}}}{} \mathbf{F})= {{\,\mathrm{tr}\,}}(\mathbf{F}{} \mathbf{F}^{{{\,\mathrm{T}\,}}}), \end{aligned}$$

(11)

$$\begin{aligned}&{\mathcal {W}}_{2}({{\,\mathrm{Cof}\,}}\mathbf{F})=W_{2}(I_{2}), \quad I_{2}={{\,\mathrm{tr}\,}}\left[ \left( {{{\,\mathrm{Cof}\,}}\mathbf{F}}\right) ^{{{\,\mathrm{T}\,}}}{{\,\mathrm{Cof}\,}}\mathbf{F}\right] \nonumber \\&\quad = {{\,\mathrm{tr}\,}}\left[ {{\,\mathrm{Cof}\,}}\mathbf{F}\left( {{{\,\mathrm{Cof}\,}}\mathbf{F}}\right) ^{{{\,\mathrm{T}\,}}}\right] . \end{aligned}$$

(12)

The function given by Eq. (10) is polyconvex if and only if the function in Eq. $(11)_{1}$ is convex with respect to $\mathbf{F}$ and the function in Eq. $(12)_{1}$ is convex with respect to ${{\,\mathrm{Cof}\,}}\mathbf{F}$. For the analysis in the following sections, it is important that the function $\left[ {{\,\mathrm{tr}\,}}(\mathbf{A}^{{{\,\mathrm{T}\,}}}\mathbf{A})\right] ^{q}=\left\| \mathbf{A}\right\| ^{2q}$, where $q > 1$, is convex with respect to any second order tensor $\mathbf{A}$. Moreover, any ascending function of a convex function (such as $\exp \left( \left\| \mathbf{A}\right\| ^{2}\right)$, for example) is convex as well [3, 27]. The extension of stored energy function, i.e., ${\mathcal {W}}(\mathbf{F}, {{\,\mathrm{Cof}\,}}\mathbf{F})$, is a proper one because for $J=1$, the tensor $\mathbf{F}$ is equal to $\overline{\mathbf{F}}$ and $I_{1}={\bar{I}}_{1}$, $I_{2}={\bar{I}}_{2}$, cf Eqs (2), $(11)_{2}$ and $(12)_{2}$.

2.2.2 Conditions derived experimentally

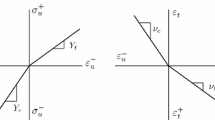
In their classical work on the elastic properties of rubber, Rivlin and Saunders [24] postulated that the stored energy function could be assumed as a sum of two terms, one of which depends solely on the first invariant of the deformation with the other one being a function of the second invariant [24], i.e.,

$$\begin{aligned} W={\overline{W}}_{1}({\bar{I}}_{1})+{\overline{W}}_{2}({\bar{I}}_{2}). \end{aligned}$$

(13)

The gathered experimental results lead to a number of conditions which should be satisfied by the derivatives of stored energy function given by Eq. (13). For the moderately large stretches ${\overline{W}}_{1}({\bar{I}}_{1})$ should meet the following conditions:

$$\begin{aligned} {\bar{\beta }}_{1}=2\frac{\partial {\overline{W}}_{1}({\bar{I}}_{1})}{\partial {\bar{I}}_{1}}={{\,\mathrm{const}\,}}>0, \quad \frac{\partial {\bar{\beta }}_{1}}{\partial {\bar{I}}_{1}}=0. \end{aligned}$$

(14)

It was also observed that ${\bar{\beta }}_{1}({\bar{I}}_{1})$ begins increasing rapidly in the plot region immediately preceding fracture.

Based on the experimental data, the function ${\overline{W}}_{2}({\bar{I}}_{2})$ should satisfy the conditions:

$$\begin{aligned} \frac{\partial {\overline{W}}_{2}({\bar{I}}_{2})}{\partial {\bar{I}}_{2}} >0, \quad \frac{\partial ^{2} {\overline{W}}_{2}({\bar{I}}_{2})}{\partial {\bar{I}}_{2}^{2}}<0, \end{aligned}$$

(15)

which, according to Eq. (4), result in:

$$\begin{aligned} {\bar{\beta }}_{-1}=-2\frac{\partial {\overline{W}}_{2}({\bar{I}}_{2})}{\partial {\bar{I}}_{2}}<0, \quad \frac{\partial {\bar{\beta }}_{-1}}{\partial {\bar{I}}_{2}}=-2\frac{\partial ^{2}{\overline{W}}_{2}({\bar{I}}_{2})}{\partial {\bar{I}}_{2}^{2}}>0. \end{aligned}$$

(16)

The concepts presented by Rivlin and Saunders in [24] were later extended in other research works, e.g., [6, 10, 32]. Among other results, it was shown that for the very high values of ${\bar{I}}_{1}$ the function ${\bar{\beta }}_{1}$ depends exponentially on the first invariant of the deformation. Furthermore, it was demonstrated that the derivatives $\frac{\partial {\overline{W}}_{1}({\bar{I}}_{1})}{\partial {\bar{I}}_{1}}$ and $\frac{\partial {\overline{W}}_{2}({\bar{I}}_{2})}{\partial {\bar{I}}_{2}}$ can be viewed as singular in the natural state.

It was emphasized both in [6] and [24] that the conditions presented in Eqs (14) and (16) could be affected by the relatively large experimental errors. Furthermore, the inelastic effects which were undoubtedly present during the experiments performed in large deformations could have played an important role, as well. Nevertheless, the conditions proposed by Rivlin and Saunders are used in the development of new invariant-based hyperelastic models, e.g., [10, 19]. In the subsequent paragraphs it is discussed to what extent the aforementioned conditions are in agreement with the material parameter identification results and the mathematical conditions of polyconvexity.

2.3 Universal relationships for basic experimental tests

In the case of material full incompressibility, for the uniaxial tension/compression (UT/UC) ${\bar{\lambda }}_{1}={\bar{\lambda }}_{1}^{-1/2}$ and

$$\begin{aligned} {\bar{I}}_{1}={\bar{\lambda }}_{1}^{2}+2{\bar{\lambda }}_{1}^{-1}, \quad {\bar{I}}_{2}={\bar{\lambda }}_{1}^{-2}+2{\bar{\lambda }}_{1}, \end{aligned}$$

(17)

thus

$$\begin{aligned} S_{1}=(1-{\bar{\lambda }}_{1}^{-3})\left( {\bar{\lambda }}_{1}{\bar{\beta }}_{1}- {\bar{\beta }}_{-1}\right) , \end{aligned}$$

(18)

where $S_{1}$ is the first P–K stress tensor component. It follows from the relationships given in [26] that in the case of equibiaxial tension (BT) ${\bar{\lambda }}_{1}={\bar{\lambda }}_{2}$ and the following relations for the components of first P-K stress tensor hold:

$$\begin{aligned} S_{1}=S_{2}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-5})\left( {\bar{\beta }}_{1}-{\bar{\lambda }}_{1}^{2} {\bar{\beta }}_{-1}\right) . \end{aligned}$$

(19)

In this test the invariants of the isochoric deformation are given as:

$$\begin{aligned} {\bar{I}}_{1}=2{\bar{\lambda }}_{1}^{2}+{\bar{\lambda }}_{1}^{-4}, \quad {\bar{I}}_{2}=2{\bar{\lambda }}_{1}^{-2}+{\bar{\lambda }}_{1}^{4}. \end{aligned}$$

(20)

In the case of pure shear (PS), i.e., the uniaxial tension for the plane strain state, the following relations hold:

$$\begin{aligned}&{\bar{\lambda }}_{2}=1, \quad {\bar{\lambda }}_{3}={\bar{\lambda }}_{1}^{-1}, \quad {\bar{I}}_{1}={\bar{I}}_{2}={\bar{\lambda }}_{1}^{2}+{\bar{\lambda }}_{1}^{-2}+1, \end{aligned}$$

(21)

$$\begin{aligned}&S_{1}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-3})\left( {\bar{\beta }}_{1}- {\bar{\beta }}_{-1}\right) , \quad S_{2}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-2})\left( {\bar{\beta }}_{1}- {\bar{\lambda }}_{1}^{2}{\bar{\beta }}_{-1}\right) . \end{aligned}$$

(22)

Eq. $(22)_{2}$ is not utilized for the experiment interpretation.

3 Classical material models—neo-Hookean, Gent and Mooney–Rivlin

3.1 Models formulation

The simplest model of incompressible material (the so-called incompressible neo-Hookean material, NH) can be obtained by assuming the following form of the stored elastic energy function (cf [12, 16]):

$$\begin{aligned} W={\overline{W}}_{NH}({\bar{I}}_{1})=\frac{\mu _{0}}{2}({\bar{I}}_{1}-3), \end{aligned}$$

(23)

where $\mu _{0}$ is the shear modulus (identical as in the linear Hooke’s law). The material parameter $\mu _{0}$ can be determined from a single mechanical test such as uniaxial tension, or simple shear, for instance. In the simplest microstructural model of a polymeric material, which follows from the assumption of Gaussian statistics, the function given by Eq. (23) is the Helmholtz’s free energy, with $\mu _{0}=kNT$ (where k is the Boltzmann’s constant, N the number of polymer chains in a unit volume, and T the absolute temperature), cf, e.g., [16].

A modification of the stored energy function given by Eq. (23) was proposed by Gent [9] who introduced an additional parameter associated with the limited extensibility of the polymer chains. The stored energy function according to Gent (1996) takes the following form:

$$\begin{aligned} W={\overline{W}}_{G}({\bar{I}}_{1})=-\frac{\mu }{2} a\ln \left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) , \end{aligned}$$

(24)

where $\mu >0$, $a>0$ and ${\bar{I}}_{1}<3+a$. If ${\bar{I}}_{1}\longrightarrow 3+a$, then ${\overline{W}}_{G}\longrightarrow +\infty$. It is easy to notice that:

$$\begin{aligned} \lim _{a \rightarrow + \infty } {\overline{W}}_{G}=\frac{\mu _{0}}{2}({\bar{I}}_{1}-3)\equiv {\overline{W}}_{NH}({\bar{I}}_{1}) \end{aligned}$$

(25)

where ${\overline{W}}_{NH}({\bar{I}}_{1})$ is the stored energy function of the incompressible neo-Hookean material (NH). In the vicinity of the natural state (${\bar{I}}_{1}\cong 3$), the stored energy function given by Eq. (24) can be approximated according to the following relationship:

$$\begin{aligned} {\overline{W}}_{G}({\bar{I}}_{1}) \approx {\overline{W}}_{NH}({\bar{I}}_{1})+\frac{\mu }{2}\sum _{n=2}^{N}\frac{({\bar{I}}_{1}-3)^{n}}{na^{n-1} }+O({\bar{I}}_{1}-3)^{N+1}, \end{aligned}$$

(26)

which means that $\mu \equiv \mu _{0}$ is the so-called initial shear modulus.

If one substitutes the first invariant of the isochoric deformation, as given by Eq. $(5)_{1}$, into Eq. (24) it is found that:

$$\begin{aligned}&W={\overline{U}}_{G}({\bar{\lambda }}_{1},{\bar{\lambda }}_{2})=-\frac{\mu _{0}}{2} a\ln [L({\bar{\lambda }}_{1},{\bar{\lambda }}_{2})], \nonumber \\&L({\bar{\lambda }}_{1},{\bar{\lambda }}_{2})=1-\frac{{\bar{\lambda }}_{1}^{2}+{\bar{\lambda }}_{2}^{2}+(\lambda _{1}\lambda _{2})^{-2}-3}{a}. \end{aligned}$$

(27)

The domain of the convex function ${\overline{U}}_{G}({\bar{\lambda }}_{1},{\bar{\lambda }}_{2})$ is limited by the curve $L({\bar{\lambda }}_{1},{\bar{\lambda }}_{2})=0$ which has a mechanical interpretation of a locking condition. The value of parameter a, which follows from the assumption of the limited extensibility of polymer chains [9], can be evaluated using standard test data by utilizing the nonlinear optimization methods.

In the case of the model by Gent, the material functions that should be substituted into the universal relationships and the constitutive equations take the form:

$$\begin{aligned} {\bar{\beta }}_{1}=2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{1}}= \mu \left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}, \quad {\bar{\beta }}_{-1}=-2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{2}}=0. \end{aligned}$$

(28)

The axial component of the first P-K stress tensor during a UT/UC process is found by the substitution of Eqs (28) into Eq. (18), with the first invariant of deformation given by Eq. $(17)_{1}$, i.e.,

$$\begin{aligned} S_{1}=\mu ({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-2}) \left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}, \quad \lim _{a \rightarrow + \infty } S_{1}=\mu _{0}\frac{1-{\bar{\lambda }}_{1}^{3}}{{\bar{\lambda }}_{1}^{2}}. \end{aligned}$$

(29)

The limit in Eq. $(29)_{2}$ reflects the case of neo-Hookean material. Some exemplary plots of functions given by Eqs (27) and (29) can be seen in Fig. 1.

Fig. 1

Results produced by Gent’s model for $a=2$, a normalized nominal stress–stretch relationship for uniaxial tension/compression test, b contour plots of stored energy function (normalized using $\mu _{0}$), cf [17]

The relation for the nominal stresses in a BT process is found by inserting Eqs (28) into Eq. (19), i.e.,

$$\begin{aligned} S_{1}=S_{2}=\mu ({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-5})\left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}, \end{aligned}$$

(30)

with ${\bar{I}}_{1}$ being given by Eq. $(20)_{1}$.

Substituting Eqs (28) into Eqs (22) leads to the formulas for the nominal stress components in the case of PS:

$$\begin{aligned}&S_{1}=\mu ({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-3})\left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}, \nonumber \\&S_{2}=\mu ({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-2})\left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}, \end{aligned}$$

(31)

where ${\bar{I}}_{1}$ is given by Eq. $(21)_{3}$.

Many material models of incompressible materials, for which the stored energy function depends on first invariant solely, i.e., $W(\bar{\mathbf{F}})={\overline{W}}({\bar{I}}_{1})$, have been proposed in the literature. A thorough discussion and evaluation of that kind of models’ application range can be found in [18], for instance. From the mathematical point of view, the fundamental disadvantage of such models is the fact that the stored energy function is not polyconvex and does not satisfy the proper growth condition (there is no extension as given by Eq. (9) as the function does not depend on the variable ${{\,\mathrm{Cof}\,}}\mathbf{F} \in Lin$).

If the stored energy function given by Eq. (23) is modified by adding a term which linearly depends on the invariant ${\bar{I}}_{2}$, we obtain the so-called incompressible Mooney–Rivlin hyperelastic material model (MR), cf Mooney [21] and Rivlin [23]. The MR model is the simplest example of a model with a polyconvex stored energy function, which takes the form:

$$\begin{aligned} {\overline{W}}=C_{10}({\bar{I}}_{1}-3)+C_{01}({\bar{I}}_{2}-3). \end{aligned}$$

(32)

The material parameters can be defined in a way which better reflects their mechanical interpretation, i.e.,

$$\begin{aligned} 2C_{10}=\mu _{0}f, \quad 2C_{01}=\mu _{0}(1-f), \end{aligned}$$

(33)

where $f \in (0,1]$. For $C_{10}>0$ and $C_{01}>0$ the stored energy function of MR model is polyconvex.

In the case of MR model the material functions are given as:

$$\begin{aligned} {\bar{\beta }}_{1}=2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{1}}= \mu _{0} f, \quad {\bar{\beta }}_{-1}=-2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{2}}=-\mu _{0}(1-f). \end{aligned}$$

(34)

It is seen that the MR model only partially satisfies the experimentally based conditions presented by Rivlin and Saunders [24], cf Eqs (14) and (16). By substituting Eqs (34) into Eq. (3), the constitutive relationship of the MR model is obtained:

$$\begin{aligned} \varvec{\sigma }= -p\mathbf{I}+\mu _{0}f\overline{\mathbf{B}}-\mu _{0}(1-f)\overline{\mathbf{B}}^{-1}. \end{aligned}$$

(35)

Of course, assuming $f=1$ in Eq. (35) leads to the constitutive equation of NH model.

Substitution of Eqs (34) into Eq. (18) leads to the relation for nominal stress in the case of UT/UC process, i.e.,

$$\begin{aligned} S_{1}=\mu _{0}(1-{\bar{\lambda }}_{1}^{-3})\left[ 1+({\bar{\lambda }}_{1}-1)f\right] . \end{aligned}$$

(36)

By inserting Eqs (34) into Eq. (19), it is found that in the case of BT the nominal stresses are given as:

$$\begin{aligned} S_{1}=S_{2}=\mu _{0}({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-5})\left[ f+{\bar{\lambda }}_{1}^{2}(1-f)\right] . \end{aligned}$$

(37)

Furthermore, after substituting Eqs (34) into Eqs (22) the formulas for the nominal stress components during the PS process are obtained:

$$\begin{aligned} S_{1}=\mu _{0}({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-3}), \quad S_{2}=\mu _{0}({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-2})\left[ f+ {\bar{\lambda }}_{1}^{2}(1-f)\right] . \end{aligned}$$

(38)

In the case of $\mu _{0}>0$ and $f \in (0,1)$ the stored energy function of the MR model given by Eq. (32) is polyconvex. Let us notice that the function ${\overline{U}}({\bar{\lambda }}_{1},{\bar{\lambda }}_{2})$ of the NH model, which follows from Eq. (32), is a convex function of stretches. Generally, for $f \in (0,1)$ and sufficiently large stretches, the stored energy function as given by Eq. (32) is not a convex function of ${\bar{\lambda }}_{1}$ and ${\bar{\lambda }}_{2}$ even if it is polyconvex.

3.2 Material parameter determination

3.2.1 Gent model

In this study the hyperelastic model proposed by Gent was utilized to approximate a wide range of experimental data [1, 5, 11, 20, 28, 33]. The least squares method was used for the material parameter determination. The process equations, i.e., Eqs $(29)_{1}$, (30) and $(31)_{1}$, were used to calculate the minimized total square error. The results of curve fitting are presented in Figs. 2 and 3, whereas the identified material parameters are gathered in Table 1. The information about residue (Residual Sum of Squares—RSS) has been included in the figures.

Some satisfactory approximation results were obtained for certain experimental data sets: the data by Meunier et al. [20] for unfilled silicone rubber (Fig. 2a and b), the data by Heuillet and Dugautier [11] for santoprene (Fig. 2g and h), the Zhao’s data [33] for thermoplastic elastomer (Fig. 3a) and the Treloar’s data [28] for rubber (Fig. 3b).

Fig. 2

Comparison of experimental and theoretical results for hyperelastic model proposed by Gent: (UT—uniaxial tension, UC—uniaxial compression, BT—equibiaxial tension, PS—pure shear): (a) and (b) Meunier’s data for silicone rubber, (c) Brieu’s data for natural rubber, (d) Brieu’s data for cured rubber, (e) and (f) Heuillet’s data for natural rubber, (g) and (h) Heuillet’s data for santoprene

Fig. 3

Comparison of experimental and theoretical results for hyperelastic model proposed by Gent: (UT—uniaxial tension, BT—equibiaxial tension, PS—pure shear): a Zhao’s data for thermoplastic elastomer, b Treloar’s data for rubber, c Alexander’s data for neoprene

Table 1 Material parameters of model by Gent determined using different experimental data (UT—uniaxial tension, UC—uniaxial compression, BT—equibiaxial tension, PS—pure shear), NR—natural rubber, CR - cured rubber, S—santoprene

The curve fitting quality is unsatisfactory for a group of experimental data which includes the data by Brieu et al. [5] for both the natural (Fig. 2c) and cured rubber (Fig. 2d), the data by Heuillet and Dugautier [11] for natural rubber (Fig. 2e and f) and the data by Alexander [1] for neoprene (Fig. 3c). In the case of data by Heuillet and Dugautier, a very high value of the parameter a was determined for both the natural rubber and the santoprene (cf Table 1) which makes the theoretical predictions very close to those that would be produced by the NH model. What is more, it can be seen in Figs. 2 and 3 that the stresses predicted by the model during a BT process are usually underestimated.

It can be concluded that the hyperelastic model by Gent is less universal than it is usually claimed. It should be emphasized that the locking effect, which has been discussed in the previous paragraph, presented a serious obstacle in the determination of material parameters. An asymptote of the stress-stretch curve can appear within the range of considered stretches, which naturally excludes a particular set of material parameters from further analysis as non-physical. A question arises, about some possible modifications to the model by Gent, that would allow to eliminate the aforementioned imperfections.

3.2.2 Mooney–Rivlin and neo-Hookean models

In Fig. 4 the curve-fitting results obtained for rubber are presented. The Mooney–Rivlin (MR) and neo-Hookean (NH) models were used to approximate Treloar’s experimental data [28], i.e., uniaxial tension (UT), equibiaxial tension (BT) and pure shear (PS). The determination of material parameters was performed in several variants by utilizing different combinations of test data (i.e., UT, BT and PS), cf [14, 18].

It can be seen in Fig. 4a and b that the determination of MR model parameters based on UT test data leads to a completely wrong approximation. The stress produced by the model in the case of BT process is seriously overestimated. Much better results are obtained when $\mu _{0}$ and f are evaluated based on the BT data (Fig. 4c). Simultaneous utilization of UT and BT data (Fig. 4d) or UT, BT and PS data (Fig. 4e) results in slightly worse approximation of the BT curve. On the other hand, the quality of the curve-fitting obtained for both UT and PS is slightly improved. In Fig. 4f the approximation obtained by the use of NH model is presented. All three data sets were used for the determination of $\mu _{0}$ in this case. The determined material parameter values of both the MR and the NH models are gathered in Table 2.

Fig. 4

Comparison of theoretical results (MR—Mooney–Rivlin model, NH—neo-Hookean model) and Treloar’s experimental data (UT—uniaxial tension, BT—equibiaxial tension, PS—pure shear) [14, 18, 28]: a MR parameters determined from UT, ${\bar{\lambda }}_{1} \in [1,2.5]$, b MR parameters determined from UT, ${\bar{\lambda }}_{1} \in [1,4.2]$, c MR parameters determined from BT, ${\bar{\lambda }}_{1} \in [1,4.5]$, d MR parameters determined from UT and BT, ${\bar{\lambda }}_{1} \in [1,2.5]$, e MR parameters determined from UT, BT and PS ${\bar{\lambda }}_{1} \in [1,2.5]$, f NH parameters determined from UT, BT and PS ${\bar{\lambda }}_{1} \in [1,2.5]$

Table 2 Material parameters of Mooney–Rivlin (MR) and neo-Hookean (NH) models determined using Treloar’s test data (UT—uniaxial tension, BT—equibiaxial tension, PS—pure shear), cf [14, 18]

In the case of a hyperelastic model whose stored energy function depends on both invariants, i.e., ${\bar{I}}_{1}$ and ${\bar{I}}_{2}$, the material parameters evaluated from the UT data lead to a completely wrong description of the material response in BT, cf Fig. 4a, b. It can be seen in Fig. 4c–e that an acceptable curve fitting of the BT experimental results is achieved only when the BT test data are utilized during the material parameter identification process. This fact can be explained by analyzing the values of both ${\bar{I}}_{1}$ and ${\bar{I}}_{2}$ during UT and BT tests as seen in Fig. 5. In the case of UT test, ${\bar{I}}_{2}$ reaches values that are substantially lower than that of ${\bar{I}}_{1}$ (Fig. 5a). Thus, when the UT test results are the only data used for the curve fitting, all the stored energy terms which depend solely on ${\bar{I}}_{2}$ will play a negligible role during the minimization of the total square error. In this case the total square error can reach the searched minimum even if the determined values of the material parameters that are associated with ${\bar{I}}_{2}$-dependent energy terms are incorrect, i.e., they do not describe the material response in BT with an acceptable accuracy. On the other hand, during a BT process the value of ${\bar{I}}_{2}$ is much higher than that of ${\bar{I}}_{1}$ (Fig. 3b) which explains why all the ${\bar{I}}_{2}$-dependent energy terms are crucial for the description of material response in BT.

Fig. 5

Isochoric deformation invariants as functions of stretch ratio: a uniaxial tension/compression and pure shear (${\bar{I}}_{1}={\bar{I}}_{2}$), b equibiaxial tension/compression [26]

It can be seen in Fig. 4f that the NH model provides an inaccurate approximation of the BT test data. The results obtained for NH and MR lead to a conclusion that a stored energy function should depend on the second invariant of deformation in order to properly describe the material response in BT. Furthermore, when the stored energy is a function of ${\bar{I}}_{1}$ and ${\bar{I}}_{2}$, usually both the UT and the BT test data should be used during the material parameter determination. During the PS process the deformation invariants are equal (${\bar{I}}_{1}={\bar{I}}_{2}$). Thus, the experimental measurements obtained in the PS test are insufficient for determining how the stored energy function depends on ${\bar{I}}_{1}$ or ${\bar{I}}_{2}$. The PS data play a secondary role during the material parameter evaluation process.

The main aim of the following paragraphs of this work is analyzing some possible generalizations of the models by Gent, Mooney and Rivlin which improve the quality of the test data approximation. Subsequently, the mathematical conditions of polyconvexity are imposed on the selected stored energy functions in order to guarantee the existence of solution and reduce the non-uniqueness in material parameter identification process.

4 Possible modifications of classical hyperelastic models

4.1 Generalized Gent model

The generalized Gent model (GG) was introduced in [16] and further discussed in [17]. This formulation of stored energy function is based on two concepts. The first is adding an ${\bar{I}}_{1}$-dependent power term to the stored energy by Gent, thus allowing the model to more accurately reproduce the stress-stretch curve for UT. The other idea is adding an ${\bar{I}}_{2}$-dependent power term in order to capture the material response in BT. Thus, the stored energy function of GG model takes the form:

$$\begin{aligned}&W={\overline{W}}({\bar{I}}_{1}, {\bar{I}}_{2})= -\frac{\mu }{2}a {{\,\mathrm{ln}\,}}\left( 1-\frac{{\bar{I}}_{1}-3}{a} \right) \nonumber \\&\quad +b\left( {\bar{I}}_{1}^{\alpha }-3^{\alpha }\right) + c\left( {\bar{I}}_{2}^{\beta }-3^{\beta }\right) , \end{aligned}$$

(39)

where, similarly as in Eq. (24), $\mu >0$, $a>0$ and ${\bar{I}}_{1}<3+a$, whereas b, c, $\alpha$ and $\beta$ are additional material parameters. Since the term containing the logarithmic function is not convex, the stored energy function of GG model is not a polyconvex function by definition.

Expanding the stored energy given by Eq. (39) into a series yields the following initial shear modulus:

$$\begin{aligned} \mu _{0}=\mu +\frac{2}{3}(\alpha b 3^{\alpha }+\beta c 3^{\beta }). \end{aligned}$$

(40)

After substituting Eq. (39) into Eqs (4) the material functions are found, i.e.,

$$\begin{aligned}&{\bar{\beta }}_{1}=2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{1}}= \mu \left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}+2b\alpha {\bar{I}}_{1}^{\alpha -1}, \nonumber \\&{\bar{\beta }}_{-1}=-2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{2}}=-2c \beta {\bar{I}}_{2}^{\beta -1}, \end{aligned}$$

(41)

that subsequently, can be inserted into the constitutive equation and the universal formulas. It follows from Eq. $(41)_{2}$ that the experimentally established conditions given in Eqs (16) are satisfied for $c\beta > 0$ and $\beta < 1$, cf [24].

The substitution of Eqs (41) into Eq. (18) leads to the relation for nominal stress in the case of UT/UC:

$$\begin{aligned}&S_{1}=(1-{\bar{\lambda }}_{1}^{-3})\left\{ {\bar{\lambda }}_{1} \left[ \mu \left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}+2b\alpha {\bar{I}}_{1}^{\alpha -1} \right] \right. \nonumber \\&\quad \left. +2c \beta {\bar{I}}_{2}^{\beta -1} \right\} , \end{aligned}$$

(42)

where the deformation invariants are given by Eqs (17).

Inserting Eqs (41) into Eq. (19) results in the following formulas for the nominal stress during a BT process:

$$\begin{aligned}&S_{1}=S_{2}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-5})\left[ \mu \left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}+2b\alpha {\bar{I}}_{1}^{\alpha -1}\right. \nonumber \\&\quad \left. +2{\bar{\lambda }}_{1}^{2}c \beta {\bar{I}}_{2}^{\beta -1} \right] , \end{aligned}$$

(43)

with the deformation invariants defined by Eqs (20).

In the case of PS, substituting Eqs (41) into Eq. $(22)_{1}$ results in the formulae determining the nominal stress, i.e.,

$$\begin{aligned}&S_{1}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-3})\left[ \mu \left( 1-\frac{{\bar{I}}_{1}-3}{a}\right) ^{-1}\right. \nonumber \\&\quad \left. +2b\alpha {\bar{I}}_{1}^{\alpha -1}+2c \beta {\bar{I}}_{2}^{\beta -1} \right] , \end{aligned}$$

(44)

where the deformation invariants are equal and given by Eq. $(21)_{3}$.

The universal relations derived for GG were used for the curve fitting of a wide range of experimental data. Every considered experimental data set was fitted separately by a simultaneous approximation of all available test data. The obtained approximation results are presented in Figs. 6, 7 and 8, whereas the determined values of material parameters are gathered in Table 3 along with the residue (RSS). The obstacles associated with the locking effect proved to be an even greater problem than in the case of the original Gent’s formulation of the stored energy function. It can be seen in Fig. 6b that the asymptote of the stress-stretch curve is situated within the range of the analyzed stretches.

It follows from the analysis of Figs. 7 and 8 that adding the additional power terms to the stored energy by Gent results in a substantial improvement of the curve fitting quality. In particular, the material response in BT is now captured much better due to the presence of the ${\bar{I}}_{2}$-dependent power term. However, the locking effect seriously hinders the material parameter identification process (Fig. 6b) and can be a potential source of errors during numerical simulations. Thus, the GG stored energy function requires further modifications aimed at eliminating the locking effect. The approximation results for santoprene data are not included here because the obtained quality of the curve fitting did not present any substantial improvement compared to Fig. 2g, h.

Fig. 6

Comparison of Heuillet’s experimental data for natural rubber and theoretical results generated by GG hyperelastic model: (UT—uniaxial tension, UC—uniaxial compression, BT—equibiaxial tension, PS—pure shear): a uniaxial tension (UT), equibiaxial tension (BT) and pure shear (PS), b uniaxial compression (UC)

Fig. 7

Comparison of experimental and theoretical results for GG hyperelastic model: (UT—uniaxial tension, UC—uniaxial compression, BT—equibiaxial tension, PS—pure shear): (a) and (b) Meunier’s data for silicone rubber, (c) Brieu’s data for natural rubber, (d) Brieu’s data for cured rubber

Fig. 8

Comparison of experimental and theoretical results for GG hyperelastic model (UT—uniaxial tension, BT—equibiaxial tension, PS—pure shear): a Zhao’s data for thermoplastic elastomer, b Treloar’s data for rubber, c Alexander’s data for neoprene

Table 3 Material parameters of GG model determined for different experimental data: 1—unfilled silicone rubber (Meunier et al. [20]), 2—natural rubber (Brieu et al. [5]), 3—cured rubber (Brieu et al. [5]), 4—natural rubber (Heuillet and Dugautier [11]), 5—santoprene (Heuillet and Dugautier [11]), 6—thermoplastic elastomer (Zhao [33]), 7—rubber (Treloar [28]), 8—neoprene (Alexander [1])

4.2 Exponential-power law model

In the vicinity of the natural state (${\bar{I}}_{1}\cong 3$) the following approximation holds:

$$\begin{aligned}&{\overline{W}}_{G}({\bar{I}}_{1})-\frac{\mu }{2a}\left[ e^{a({\bar{I}}_{1}-3)}-1 \right] \nonumber \\&\quad \cong \frac{\mu }{2}\left[ \frac{a^{2}({\bar{I}}_{1}-3)^{3}}{6}+\frac{5a^{3}({\bar{I}}_{1}-3)^{4}}{24}\right] +\dots , \end{aligned}$$

(45)

where ${\overline{W}}_{G}({\bar{I}}_{1})$ is given by Eq. (24). This leads to the idea of replacing the natural logarithm in Eq. (39) with an exponential function of ${\bar{I}}_{1}$. The modification is motivated by the elimination of locking effect exhibited by GG model with a simultaneous preservation of model’s curve fitting abilities. This way the so-called exponential-power law (Exp-PL) stored energy function is formulated, cf [15, 17], i.e.,

$$\begin{aligned}&W={\overline{W}}({\bar{I}}_{1}, {\bar{I}}_{2})= \frac{\mu }{2a}\left[ e^{a({\bar{I}}_{1}-3)}-1 \right] \nonumber \\&\quad +\frac{b}{2 \alpha }\left( {\bar{I}}_{1}^{\alpha }-3^{\alpha } \right) +\frac{c}{2 \beta }\left( {\bar{I}}_{2}^{\beta }-3^{\beta } \right) , \end{aligned}$$

(46)

where: $\mu \ge 0$, $a \ge 0$, $b \ge 0$, $c \ge 0$, $\alpha$ and $\beta$ are the material parameters. In the case of $\mu =0$ and $\alpha =\beta =1$, the function given by Eq. (46) is reduced to the stored energy of Mooney–Rivlin model [15]. On the other hand, if one assumes $b=0$ and $c=0$ in Eq. (46), the soft tissue model is obtained, cf [7]. In the case of $\alpha \ge 1$ and $\beta \ge 1$ the stored energy is polyconvex.

The following material functions should be inserted in the constitutive equations and the universal relationships:

$$\begin{aligned} {\bar{\beta }}_{1}=2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{1}}= \mu e^{a({\bar{I}}_{1}-3)}+b{\bar{I}}_{1}^{\alpha -1}, \quad {\bar{\beta }}_{-1}=-2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{2}}= -c {\bar{I}}_{2}^{\beta -1}. \end{aligned}$$

(47)

It follows from Eq. $(47)_{2}$ that the conditions by Rivlin and Saunders given in Eqs (16) are satisfied for $c>0$ and $\beta <1$, cf [24], which is in a clear contradiction to the requirements of energy function polyconvexity.

By expanding the stored energy given by Eq. (46) in a series, the initial shear modulus is found:

$$\begin{aligned} \mu _{0}=\mu +\frac{1}{3}(b3^{\alpha }+c3^{\beta })>0. \end{aligned}$$

(48)

The substitution of Eqs (47) into Eqs (18), (19) and $(22)_{1}$ yields the following expressions for the nominal stress components in the case of: UT/UC (with the deformation invariants given by Eqs (17))

$$\begin{aligned} S_{1}=(1-{\bar{\lambda }}_{1}^{-3})\left[ {\bar{\lambda }}_{1} \left( \mu e^{a({\bar{I}}_{1}-3)}+b{\bar{I}}_{1}^{\alpha -1}\right) +c{\bar{I}}_{2}^{\beta -1} \right] , \end{aligned}$$

(49)

BT (with the invariants as defined by Eqs (20))

$$\begin{aligned} S_{1}=S_{2}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-5}) \left( \mu e^{a({\bar{I}}_{1}-3)}+b{\bar{I}}_{1}^{\alpha -1} +{\bar{\lambda }}_{1}^{2}c{\bar{I}}_{2}^{\beta -1} \right) , \end{aligned}$$

(50)

and PS (where the invariants are given by Eq. $(21)_{3}$)

$$\begin{aligned} S_{1}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-3}) \left( \mu e^{a({\bar{I}}_{1}-3)}+b{\bar{I}}_{1}^{\alpha -1} +c{\bar{I}}_{2}^{\beta -1} \right) . \end{aligned}$$

(51)

Equations (49–51) were utilized for the approximation of experimental data. Every considered experimental data set was fitted separately by a simultaneous approximation of all available test data. The curve fitting plots that were obtained for the test data by Meunier et al. [20], Heuillet and Dugautier [11] (santoprene) and Brieu et al. [5] are not included, since visually they present no significant improvement compared to the approximations seen in Figs. 2 and 7. The material parameters of Exp-PL model determined for all the aforementioned experimental data sets are gathered in Tables 4, 5, 6. Two approaches to model simplification were analyzed. The first was omitting selected energy terms. The second was assuming the selected exponents as equal one a priori.

In many cases it was possible to determine several alternative material parameter sets which are characterized by a very similar approximation quality. The nonlinearity of the material parameter value optimization task is the reason of this phenomenon. The question of non-uniqueness of solution to the parameter evaluation problem is one of the reasons why additional criteria are required that limit the possible values of material parameters.

The material parameters which were evaluated for unfilled silicone rubber using the data by Meunier et al. [20] are gathered in Table 4. It is seen that two completely different material parameter sets were obtained that are characterized by a very close values of RSS. The second parameter set does not satisfy the condition of $a>0$. Both the material parameter sets given in Table 4 correspond to non-polyconvex stored energy functions.

Table 4 Material parameters of Exp-PL model determined for unfilled silicone rubber (Meunier et al. [20])

The experimental data for cured rubber (Brieu et al. [5]) were used to evaluate the parameters of Exp-PL model in two variants, see Table 5. The first material parameter set was determined for the full version of Exp-PL model. Subsequently, the parameter values of simplified model variant, in which the ${\bar{I}}_{1}$-dependent power term is omitted, were evaluated (set no. 2). Based on the RSS values it can be concluded, that in this particular case the model simplification results in a negligible decrease of the approximation quality.

Table 5 Material parameters of Exp-PL model determined for cured and natural rubber (Brieu et al. [5])

Table 6 Material parameters of Exp-PL model determined for natural rubber and santoprene (Heuillet and Dugautier, 1997, [11])

In the case of the experimental data by Heuillet and Dugautier [11], obtained for natural rubber, three alternative material parameter sets were evaluated, see Table 6. The set no. 1 was determined for the full version of Exp-PL model. The curve-fitting results can be seen in Fig. 9. Only slightly worse approximation is achieved for the material parameters which were determined for the simplified version of the model (set no. 2). Imposing the condition of $\beta =1$ results in further worsening of the curve fitting quality (parameter set no. 3). The set no. 3 corresponds to a polyconvex stored energy function. For santoprene two alternative material parameter sets were evaluated, i.e., set no. 1 for the full version of Exp-PL model and set no. 2 for the simplified version of the model. Both sets correspond to non-polyconvex stored energy functions. Again, the considered model simplification results in a negligible decrease of the approximation quality.

Fig. 9

Comparison of Heuillet’s experimental data for natural rubber and theoretical results generated by Exp-PL hyperelastic model: (UT—uniaxial tension, UC—uniaxial compression, BT—equibiaxial tension, PS—pure shear): a uniaxial tension (UT), equibiaxial tension (BT) and pure shear (PS), b uniaxial compression (UC)

In the case of the experimental results by Zhao [33], Treloar [28] and Alexander [1], an effort was made to identify both polyconvex and non-polyconvex stored energy functions for each one of the data sets. The aforementioned experimental measurements include the approximately exponential stress growth which occurs in rubber prior to the failure. Thus, the conclusions which are drawn below are more firmly based on the experiment. The determined material parameter values which correspond to the polyconvex and non-polyconvex version of the Exp-PL model are gathered in Table 7. The curve fitting results can be seen in Fig. 10. It should be observed that the RSS always reaches its minimum for the non-polyconvex stored energies whose material parameters are in an agreement with the conditions formulated by Rivlin and Saunders [24], cf Table 7.

It can be seen in Fig. 10 and Table 7 that imposing the conditions of polyconvexity leads to slight worsening of the curve fitting quality. As it was mentioned before, the material parameter sets which correspond to a polyconvex stored energy function of the Exp-PL model, automatically do not satisfy the conditions derived experimentally by Rivlin and Saunders [24].

Table 7 Material parameters of exponential-power law (Exp-PL) model determined for experimental data sets by Zhao [33], Treloar [28] and Alexander [1]

Fig. 10

Comparison of experimental and theoretical results for Exp-PL hyperelastic model: (UT—uniaxial tension, BT—equibiaxial tension, PS—pure shear): a Zhao’s data for thermoplastic elastomer (non-polyconvex energy), b Zhao’s data for thermoplastic elastomer (polyconvex energy), c Treloar’s data for rubber (non-polyconvex energy), d Treloar’s data for rubber (polyconvex energy), e Alexander’s data for neoprene (non-polyconvex energy), f Alexander’s data for neoprene (polyconvex energy)

In the case of Treloar’s data for rubber and Alexander’s data for neoprene, the stored energy contour plots were generated in order to compare the results obtained for the polyconvex and non-polyconvex Exp-PL models. It can be seen in Fig. 11 that in both cases a relatively good agreement is found between the plots of the polyconvex energy function and those of the non-polyconvex energy. In Fig. 11a the stored energy is a convex function of the principal stretches for both the polyconvex and non-polyconvex version of the Exp-PL model. In Fig. 11b the non-polyconvex energy function is seen to be a non-convex function of stretches, while the polyconvex stored energy is a convex function. Generally, a polyconvex energy function does not have to correspond to a convex function of stretches.

In [26] a slightly worse approximation of the data by Treloar and Alexander is presented that was performed using the Exp-PL model. However, the values of RSS reported there are comparable to those from the present study, despite the fact that the parameter values are completely different. It is another illustration of the fact that the parameter value optimization problem does not lead to a unique solution. The presence of the exponential function, which is utilized in the Exp-PL model, significantly complicates this optimization task. Thus, it is reasonable to consider a simplified version of the model where the exponential term has been replaced with an additional power term.

Fig. 11

Contour plots of stored elastic energy generated with Exp-PL model: a rubber (Treloar [28]), b neoprene (Alexander [1]), solid line—non-polyconvex energy, dashed line—polyconvex energy (material parameter values as given in Table 7); curves corresponding to UT/UC, BT and PS processes are plotted in red

4.3 Power law model

The stored energy function of the power law (PL) model takes the form [14]:

$$\begin{aligned} W={\overline{W}}({\bar{I}}_{1}, {\bar{I}}_{2})= \frac{1}{2}\sum _{i=1}^{2}\frac{\alpha _{i}}{ \beta _{i}}\left( {\bar{I}}_{1}^{\beta _{i}}-3^{\beta _{i}}\right) + \frac{\alpha _{3}}{2 \beta _{3}}\left( {\bar{I}}_{2}^{\beta _{3}}-3^{\beta _{3}}\right) , \end{aligned}$$

(52)

where $\alpha _{i}$ and $\beta _{i}$ ($i=1,2,3$) are the material parameters. For $\alpha _{i}>0$ and $\beta _{i}\ge 1$ the function given by Eq. (52) is polyconvex (one of the parameters, i.e., either $\alpha _{1}$ or $\alpha _{2}$ can be equal zero).

For this particular model the following material functions should be substituted in the universal relationships and the constitutive equations:

$$\begin{aligned} {\bar{\beta }}_{1}=2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{1}}= \alpha _{1}{\bar{I}}_{1}^{\beta _{1}-1}+ \alpha _{2}{\bar{I}}_{1}^{\beta _{2}-1}, \quad {\bar{\beta }}_{-1}=-2\frac{\partial {\overline{W}}}{\partial {\bar{I}}_{2}}= -\alpha _{3}{\bar{I}}_{2}^{\beta _{3}-1}. \end{aligned}$$

(53)

It follows from Eq. $(53)_{2}$ that the experimentally established conditions (cf Rivlin and Saunders [24]) given in Eqs (16) are satisfied for $\alpha _{3}>0$ and $\beta _{3}<1$. This is in a clear contradiction with the requirements that follow from the energy polyconvexity assumption.

By inserting Eqs (53) into Eqs (18) and (19), we obtain the following relations for the nominal stress in the UT/UC and BT processes, respectively:

$$\begin{aligned}&S_{1}=(1-{\bar{\lambda }}_{1}^{-3})\left[ {\bar{\lambda }}_{1} (\alpha _{1}{\bar{I}}_{1}^{\beta _{1}-1}+ \alpha _{2}{\bar{I}}_{1}^{\beta _{2}-1}) +\alpha _{3}{\bar{I}}_{2}^{\beta _{3}-1}\right] , \end{aligned}$$

(54)

$$\begin{aligned}&S_{1}=S_{2}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-5})\left[ \alpha _{1}{\bar{I}}_{1}^{\beta _{1}-1}+ \alpha _{2}{\bar{I}}_{1}^{\beta _{2}-1} +{\bar{\lambda }}_{1}^{2}\alpha _{3}{\bar{I}}_{2}^{\beta _{3}-1}\right] , \end{aligned}$$

(55)

where the proper relationships defining the isochoric deformation invariants are given in Eqs (17) and (20), respectively.

According to Eq. $(21)_{3}$, for the PS test the invariants of the isochoric deformation are equal. The nominal stress component given by Eq. $(22)_{1}$ takes the form:

$$\begin{aligned} S_{1}=({\bar{\lambda }}_{1}-{\bar{\lambda }}_{1}^{-3})( \alpha _{1}{\bar{I}}_{1}^{\beta _{1}-1}+ \alpha _{2}{\bar{I}}_{1}^{\beta _{2}-1} +\alpha _{3}{\bar{I}}_{2}^{\beta _{3}-1}). \end{aligned}$$

(56)

Expanding the stored energy given by Eq. (52) in a series leads to the following initial shear modulus:

$$\begin{aligned} \mu _{0}=\sum _{i=1}^{3}3^{\beta _{i}-1}\alpha _{i}. \end{aligned}$$

(57)

The derived Eqs (54–56) were utilized during the curve fitting process. Every considered experimental data set was fitted separately by a simultaneous approximation of all available test data. Below the tabularized values of the material parameters determined for the considered test data sets are gathered. Some of the figures presenting the experimental data approximation have not been included due to their visual similarity to the plots already presented in the previous sections.

A group of alternative material parameter sets was evaluated using the experimental data by Meunier et al. [20]. The determined material parameters are gathered in Table 8. The parameter sets no. 1 and 2 are characterized by the lowest value of residue and result in non-polyconvex stored energy functions. The experimentally derived conditions given in Eq. (16), cf [24], are satisfied. It can be seen in Table 8 that for the PL model a small difference in RSS (sets no. 1 and 2) results in a slight change of the material parameter values. This was not the case for the Exp-PL model (cf Table 4). Thus, it can be concluded that the replacement of the exponential function with an additional power term reduces the non-uniqueness associated with the material parameter evaluation process, as it was expected. The material parameter sets no. 3 and 4 correspond to a polyconvex stored energy function. Again, a small difference of RSS results only in a slight change of the material parameter values. The imposition of the polyconvexity conditions does not cause any significant decrease in the curve fitting quality.

The material parameter sets no. 5–9 represent different model simplifications applied to both polyconvex and non-polyconvex stored energy functions. As before, two possible kinds of simplifications were considered. The first was omitting selected energy terms. The second was assuming a priori the values of selected exponents as equal one. It can be seen in Table 8 that the applied model simplifications do not result in any significant decrease in the approximation quality.

Table 8 Material parameters of PL model determined for unfilled silicone rubber (Meunier et al. [20])

In Table 9 the material parameters of the PL model evaluated for the experimental data by Brieu et al. [5] are gathered. The determined value of $\alpha _{2}$ parameter was negligible for both the natural and the cured rubber. Thus, the simplified version of the PL model is sufficient in capturing the stress-stretch relations of those materials. Both parameter sets satisfy the conditions formulated by Rivlin and Saunders [24].

In Table 10 the material parameter values determined for the experimental data by Heuillet and Dugautier [11] are presented. In the case of natural rubber the parameter set no. 1, which is characterized by the lowest value of RSS, satisfies the experimentally derived conditions formulated by Rivlin and Saunders [24]. The parameter sets no. 2 and 3 were evaluated for the natural rubber assuming the simplified versions of the PL model. The parameter set no. 4 corresponds to a polyconvex stored energy function. In this particular case the PL model has been reduced to the MR model. For santoprene the material parameter sets no. 1 and 2 (Table 10) satisfy neither the mathematical conditions of polyconvexity nor the experimentally-based conditions proposed by Rivlin and Saunders. The parameter set no. 4 corresponds to a polyconvex stored energy. It is seen that for both the natural rubber and the santoprene applying the conditions of polyconvexity leads to a certain decrease in the curve fitting quality.

In Table 11 the material parameter values determined for the experimental measurements by Zhao [33], Treloar [28] and Alexander [1] are gathered. Both the cases of polyconvex and non-polyconvex stored energies were analyzed. It is seen in Table 11 that the best approximation results were obtained in the case of non-polyconvex PL model for which the material parameters satisfy the experimentally-based conditions formulated by Rivlin and Saunders [24]. It can be seen that for all three data sets the identified material parameter values are close despite the fact that they were determined for different materials. This remark refers especially to the case of polyconvex energy function. Applying the polyconvexity conditions results in a slight worsening of the curve fitting. The approximation results obtained for the reported parameter values can be seen in Fig. 12.

Fig. 12

Comparison of experimental and theoretical results for PL hyperelastic model: (UT—uniaxial tension, BT—equibiaxial tension, PS—pure shear): a Zhao’s data for thermoplastic elastomer (non-polyconvex energy), b Zhao’s data for thermoplastic elastomer (polyconvex energy), c Treloar’s data for rubber (non-polyconvex energy), d Treloar’s data for rubber (polyconvex energy), e Alexander’s data for neoprene (non-polyconvex energy), f Alexander’s data for neoprene (polyconvex energy)

Table 9 Material parameters of PL model determined for cured and natural rubber (Brieu et al. [5])

Table 10 Material parameters of PL model determined for natural rubber and santoprene (Heuillet and Dugautier [11])

Table 11 Material parameters of power law (PL) model determined for experimental data sets by Zhao [33], Treloar [28] and Alexander [1]

5 Conclusions

In this work several recently developed constitutive models of hyperelasticity were analyzed. The attention was focused on isotropic, invariant-based hyperelastic models, which can be relatively easily implemented into the FE software. The considered constitutive equations included the model by Gent [9] and its modification, the so-called generalized Gent model (GG) [16, 17], the exponential-power law model (Exp-PL) [15] and the power law model (PL) [14]. The aforementioned models of hyperelasticity were checked for their ability to capture the mechanical properties of elastomeric materials using a number of experimental data sets [1, 5, 11, 20, 28, 33].

It was found that the model by Gent in several cases fails to generate an acceptable approximation of the experimental data, cf Figs. 2 and 3. The proposed GG model allows for a much better curve fitting, cf Figs. 7 and 8. However, a major drawback of both the Gent model and its generalization is the presence of the locking effect (Figs. 1 and 6). The locking effect significantly complicates the material parameter identification process and may be a source of errors during the FE analysis.

In order to eliminate the difficulties arising from the locking effect, the Exp-PL and the PL hyperelastic models were proposed [14, 15]. In this study it is shown that for all the considered experimental data sets both models produced very good curve fitting results, cf Figs. 9, 10 and 12.

The mathematical conditions of polyconvexity were utilized in order to guarantee the existence of solution to a properly defined boundary value problem. Although it was found that the best approximations of the experimental data are always achieved for non-polyconvex hyperelastic models, application of the polyconvexity condition usually only slightly decreases the curve fitting quality. What is more, it can be seen in Table 11 that for the PL model the material parameter values identified for different rubberlike materials are close. One should expect such a result because the thermoplastic elastomer, the natural rubber and the neoprene are all characterized by similar mechanical properties. It was possible to obtain similar parameter values for this group of materials due to the replacement of the exponential term in the Exp-PL model with a power term in the PL model. The assumption of selected exponents as equal one, in order to fulfill the conditions of energy polyconvexity, made the parameter values even closer.

In Table 12 the models which allowed to achieve the best data approximations are listed both in the case of the polyconvex and the non-polyconvex stored energy function. It is seen that as far as the non-polyconvex stored energies are considered, the GG model is often the one that produces the best approximation of the experimental data. On the other hand, when the conditions of polyconvexity are taken into account, the best curve fitting quality is commonly obtained for the PL model. In the case of the experimental measurements by Brieu et al. [5] the determined material parameter values that resulted in a good curve fitting did not satisfy the conditions which follow from the requirement of energy polyconvexity.

Table 12 The best approximations of analyzed experimental data sets for both non-polyconvex and polyconvex stored energy functions (GG—generalized Gent model, Exp-PL—exponential-power law model, PL—power law model)

It was found that the determined material parameter sets which result in the best curve fitting (the lowest residue) usually satisfy the experimentally derived conditions formulated by Rivlin and Saunders [24], cf Eqs. (14) and (16). Furthermore, it was demonstrated that for the considered group of hyperelastic models the conditions by Rivlin and Saunders are in a contradiction with the mathematical conditions of polyconvexity. This fact can be explained by considering the limitations of hyperelasticity theory. The hyperelasticity is an idealization aimed at simulating the mechanical behavior of rubberlike materials. It assumes ideal elasticity and no dissipation taking place in the material under loading. However, the real deformation processes are dissipative, as follows from the second law of thermodynamics. There is an extensive literature regarding different rheological effects which are observed in real materials (e.g., stress relaxation, hysteresis loop, Mullins effect, strain rate dependence, etc., cf [2, 13, 25, 30, 31]). The analyzed deviation of the conditions presented by Rivlin and Saunders from the mathematical conditions of energy polyconvexity can be interpreted as the influence of dissipative processes that were registered experimentally but not analyzed in [24]. Substantial stress relaxation must have occurred during the long lasting, static tensile tests reported in [24]. However, the collected experimental data were utilized to draw conclusions regarding the formulation of ideally elastic constitutive models. This could lead to the discussed discrepancies between the conditions proposed by Rivlin and Saunders and the requirements of stored energy polyconvexity.

It can be concluded that for the purpose of solving boundary value problems it is recommended to utilize the polyconvex versions of the Exp-PL and the PL models. Usually the usage of PL model leads to a better approximation of the experimental data. What is more, in the case of PL model the material parameter identification process is less influenced by the non-uniqueness of solutions. This is achieved by the usage of a power energy term instead of an exponential function and by the application of polyconvexity conditions.