1 Introduction

In the local area of pump flow passage during operation, transporting liquid is vaporized to bubbles when the absolute pressure of liquid (generally water) is lower than the vapor pressure under current temperature. Furthermore, gases dissolved in liquid will be precipitated as bubbles. The process from initial formation to expansion of these bubbles is called cavitation. With the flowing development, the increased local pressure may influence flowing liquid and thereby inhibit the growth of bubbles, but make them implode and finally disappear. The development and breakage process of bubbles occur in an extremely short period on the nanosecond level, accompanied by production of abundant blast waves. Breakage of bubbles occurs exceptionally easily on the surface of the flow passage and may form a high-speed microjet at the boundaries of solids. When the shock pressure produced by the implosion of bubbles is stronger than the ultimate mechanical strength of materials, pits that are micrometers big in diameter are formed on the solid wall. These pits accumulate continuously and finally develop into sponge-like plastic deformation and fall off. The cavitation is accompanied by abundant bubbles that block the main channel of the flow passage, thereby causing energy loss and changing the flow characteristics of hydraulic machinery. Consequently, a series of serious problems, such as vibration of unit, noise, and material failures, threaten the safety operation of the pump [1,2,3]. Cavitation generally occurs in hydraulic machinery, including channels in fluid flow machines such as hydroturbines and water pumps. On the one hand, miniaturization is inevitable for pumps to reduce material and processing cost, which proposes higher requirements on designed rotating speed, thereby causing a deterioration in the intake performance of pumps. On the other hand, with rapid economic development, diversified market demands have emerged for pumps along with unreasonable mode selection of users, which may cause pumps to be used in non-designed conditions. Excess high-speed and non-designed working conditions are two principal causes of pump cavitation [4, 5]. Cavitation is one of the three types of damage that easily occurs during the operation of fluid machinery. One core problem of the centrifugal pump industry lies in the cavitation, which can influence operation efficiency and production of vibration noises of a centrifugal pump. Besides, serious cavitation may destroy flow passage in a centrifugal pump and thereby influence the stability and reliability of the pump operation. To relieve pump damage caused by cavitation, many scholars have discussed its occurrence mechanism and influencing factors, and have achieved certain results [6,7,8]. Some studies have reported that cavitation number could greatly influence the distribution of bubbles on the blade surface of a centrifugal pump. Influencing factors of cavitation of a centrifugal pump include physical structure and chemical properties of media. Among them, roughness is an important physical factor that influences cavitation performance of hydraulic machinery and relevant studies are mainly based on axial flow pump and pump turbine [9,10,11]. Nevertheless, previous studies on the effects of roughness on hydraulic machinery have been conducted under good working conditions of the hydraulic machinery [12]. The operation of hydraulic machinery is often accompanied by vibration, cavitation, and noise. Under these circumstances, effects of roughness on the operation of hydraulic machinery remain unknown.

In this study, influencing laws of roughness on the performance of a centrifugal pump under special working conditions were investigated by combining roughness and the pump cavitation process. A numerical simulation of the cavitation of a mode of centrifugal pump under the rated flow rate was conducted by ANSYS CFX software. Cavitation was divided into cavitation inception, cavitation development, critical cavitation, and fracture cavitation. Transient behaviors of the centrifugal pump in each cavitation stage were analyzed by changing wall roughness at the impeller blade. This study aims to provide references to improve the cavitation characteristics of centrifugal pumps by changing roughness.

2 Methodology

During the operation of pumps, cavitation may cause material damage and distortion deformation of the flow passage [13,14,15]. Many scholars have conducted in-depth research on the occurrence mechanism and damage of cavitation for a long period. For example, Ferrari et al. [16] proposed a mechanical model of a high-pressure pump for a common-rail fuel system. Through a comparative verification between experimental instant torque of the pump shaft and lifting data of the pump piston, the researchers found that cavitation might occur in the inlet and early compression stage of pump circulation during operation of a fuel metering apparatus. However, they did not propose any measure to relieve the cavitation degree of a light pump. Liu et al. [17] predicted the influencing law of cavitation number on the bubbles on the blade surface of a centrifugal pump based on three cavitation models. They found that with the decrease in cavitation number, bubbles were produced near the inlet side of the blade suction surface, which would then extend toward the outlet and blade pressure surface along the blade suction surface. Reduction of total pressure coefficient of the impeller mainly occurs on the upstream section, and cavitation development influences the downstream section very slightly. On the contrary, cavitation can influence load distribution on the blade surface significantly. Azad et al. [18] conducted an experimental study on the cavitation phenomenon in a transparent centrifugal pump by using viscoelastic fluid and found that the formation and development of bubbles were highly sensitive to the concentration of polymers, cavitation number, and degradation. Bubbles began to be delayed in polymer solution, which was further evident under a high concentration of polymer solution. Previous studies have disclosed influences of cavitation number, but lack an analysis of the occurrence mechanism of cavitation in different stages.

Marchis et al. [19] reported a large-eddy simulation of wall resolution for completely developed turbulent passage flow on two surfaces with different roughness, in which influences of irregular two-dimensional and three-dimensional roughness on turbulence were analyzed. The researchers concluded that three-dimensional irregular rough surface could influence anisotropism more than two-dimensional by analyzing the ratio of different Reynolds stress components and studying the trend of anisotropism. Khoeini et al. [20] conducted a numerical and experimental study on the state and behavior of different viscous fluids in typical horizontal single-stage centrifugal pumps and improved the performance of the pumps by increasing the throat area of volute. The researchers found that the fluid with the highest viscosity consumed the largest amount of energy and its absorbing power was approximately 55% higher than that of the fluid with the lowest viscosity. However, they did not conduct a specific experimental study. Shi et al. [21] simulated and tested an axial flow pump impeller by using various turbulence models to study the cavitation characteristics of the impeller region in the axial pump. They verified the adaptation of various turbulence and multiphase flow models and discussed the cavitation characteristics in the impeller region. Mahmoodi et al. [22] proposed three models based on the gene expression program (GEP) and evaluated the hydrodynamic performance of propellers and the amount of cavitation under different geometric physical conditions. This study assured the reasonable accuracy of the final model between the observation value and prediction results of GEP, but did not propose an explicit introduction to specific occurrence stages of cavitation.

In addition, few studies discuss the influence of roughness on the hydraulic performance of a centrifugal pump. Deshmukh et al. [23] conducted a three-dimensional numerical analysis on the flow characteristics of fluid on a rough surface when an electric submersible pump was working under the designed and non-designed conditions. In the numerical analysis, the flow rate, the rotating speed of impeller, and roughness were changed. Results showed that the strong interaction between rough wall and fluid changed the pressure, speed gradient, and turbulence parameters in boundaries, thereby influencing the overall performance of pumps. Dierich et al. [24] found that surface roughness increased turbulence and increased heat transfer coefficient near the wall surface; however, the researchers did not disclose the influence of roughness on turbulence intensity and the occurrence mechanism of cavitation.

Fu et al. [25] studied the cavitation characteristics of a centrifugal charging pump in nuclear power stations and designed and developed a special chopped-off prototype. According to numerical simulation results, the number of bubbles in impeller along radial position increases quickly with the occurrence of cavitation, so that volume fraction of bubbles increases gradually. When cavitation develops to a certain extent, eddies occur in the impeller and the eddy area is expanded continuously. Pressure fluctuates regularly during cavitation inception, and the dynamic and static interferences of the impeller and volute take a dominant role. Subsequently, cavitation becomes a major factor that controls the pressure fluctuation law in the pump.

Tao et al. [26] studied cavitation on the runner blade of a reversible pump turbine and found that this phenomenon was more obvious under the water pump mode. To evaluate the cavitation phenomenon of blades, which is easy to neglect, the researchers conducted a numerical test under 26 combined conditions of the opening angle of the guide vane and flow rate. Results demonstrate that cavitation mainly occurs at the leading and trailing edges of the guide vane, and it might be observed on the leading edge of a fixed guide vane and vaneless space. Moreover, a cavitation phenomenon of the jet vortex also occurs in the impeller passage. Although the researchers characterized a reasonable starting law of the water pump mode, they did not analyze the cavitation process and verify the relevant data.

In other words, some studies have discussed the causes of cavitation and bubble distribution law in a centrifugal pump, but none have analyzed the occurrence mechanism of cavitation under different wall roughness [27,28,29,30]. To address existing research limitations, this study conducted a numerical simulation on cavitation in a mode of the centrifugal pump under a rated flow rate and divided the cavitation into four stages. Instant characteristics in each cavitation stage were analyzed by changing the wall roughness at the impeller blade to disclose the cavitation characteristics of centrifugal pumps and further study the occurrence mechanism of cavitation.

The rest of this study is organized as follows. Section 3 describes the basic performance parameters of a centrifugal pump. In this section, three-dimensional modeling, domain discretization, grid independence test, setting of boundary conditions, and selection of cavitation model are introduced. Section 4 verifies the reliability of the model setting and analyzed the distribution pattern of bubbles under different roughness and complicated working conditions. This section finds that wall roughness can influence the pressure distribution and cavitation performance. Section 5 provides conclusions.

3 Numerical model

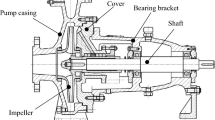
Construction accuracy of a three-dimensional model determines the accuracy of numerical simulation calculation in reflecting the real situation of flow. However, the three-dimensional model of a centrifugal pump is ideal because parts of the pump exhibit certain errors during casting, processing, assembling, and overall test. A three-dimensional full-flow field model of the flow passage of a centrifugal pump was constructed rather than an overall model of a centrifugal pump. This model was used to discuss flow laws in the flow field of the pump. A mode of volute horizontal single-stage centrifugal pump was chosen as the computational region model. As the high-speed rotation of the impeller may disturb speed distribution in the passage of the pump inlet at the blade inlet and cause early diffusion of numerical values, the inlet and outlet sections of the flow passage at the inlet and outlet of the pump are extended appropriately. External characteristic parameters of a centrifugal pump are listed in Table 1.

Table 1 External Characteristic Parameters of a Centrifugal Pump
Full size table

The specific speed ns is defined as

$$ n_{s} = \frac{n\sqrt Q }{{H^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}}} }} $$
(1)

where n is rotational speed(rpm), Q is designed flow rate(m3/s), and H is pump head(m).

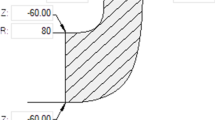
First, a three-dimensional model of the flow passage in a centrifugal pump was constructed by using the Professional Engineer three-dimensional modeling software according to equal proportions. The entire model was divided into inlet, impeller, volute, and outlet sections to decrease calculation errors. The model structure is shown in Fig. 1.

Fig. 1
figure 1

Three-dimensional model of pump flow passage

Full size image

3.1 Meshing scheme and grid independence verification

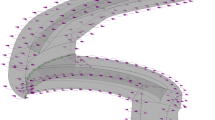
During the numerical simulation, the orthogonal quality of grids may exert non-negligible effects on the accuracy and precision of calculated results. According to incomplete statistics, time for meshing, which is the primary task of numerical calculation, accounts for over 60% of the entire numerical calculation process. In general, the calculation error can be controlled by refined meshing [31,32,33]. However, excess grids may consume considerable calculation time. Therefore, selecting the appropriate number of grids is important. In this study, the entire pump flow passage was meshed by the integrated computer engineering and manufacturing code for computational fluid dynamics software, and unstructured hybrid tetrahedral meshing with strong adaptation was implemented. Meshing of the flow passage of the impeller was further refined, which showed that the total grid orthogonal quality was higher than 0.3. The processes of impeller section meshing and local mesh refining are shown in Fig. 2.

Fig. 2
figure 2

Local Mesh Refinement in Impeller Region

Full size image

The same calculation model, meshing scheme, boundary conditions, and wall roughness were applied during the calculation to analyze the effects of the number and quality of grids on the simulation error. Grid independence was analyzed using the same model under the designed flow rate and seven different grid numbers. The analysis results are presented in Fig. 3. When the grid number is higher than 4,886,547, head and efficiency, which are obtained from the numerical calculation, do not fluctuate violently with the increase in the grid number (the overall error is less than 1%), thereby indicating the weak correlation between the grid number and calculated results. To capture the flow field information accurately and considering the computer configuration and computing time, the study determined the number of grids as 4,886,547.

Fig. 3
figure 3

Grid independence verification

Full size image

3.2 Governing equation

Reynolds normalization group k-epsilon (RNG k-ε) two-equation model has been widely applied in turbulence models because of its high stability and calculation accuracy. The characteristic length of the equation of the turbulent energy dissipation rate ε is equal to the dissipation scale and can be calculated from the corresponding partial differential equation. Numerous calculated results have proved that the RNG k-ε two-equation model can calculate the complex three-dimensional turbulence accurately. In this case study, the RNG k-ε turbulence model and closed momentum equation set of the equation of continuity were applied. The RNG k-ε turbulence model was applicable to solve flow in a centrifugal pump with a large radius of curvature and was particularly applicable to the numerical calculation of the flow field in the selected mode of the centrifugal pump.

3.3 Cavitation model

According to the Rayleigh–Plesset equation, gas cores grow quickly when the intensity of pressure in the passage is lower than the steam pressure. With the development of flow, bubbles collapse and disappear when they are transformed to regions with high pressure. The process of bubble collapse and perishing is highly complicated and is determined to influence surface tension, viscosity of liquid, and non-condensed gas. Zwart cavitation model based on the Rayleigh–Plesset equation in bubble kinetics was applied as the cavitation model for calculation, without consideration for the influence of soluble gases in water on cavitation. The cavitation model ignores the effects of surface tension and other factors in order to ensure the stability of the calculation process. As the increase in volume fraction of steam is accompanied by a reduction of the fluid density of gas cores, the mass cavitation equation was corrected by the Zwart cavitation model. The governing equation is:

$$ \dot{m} = \left\{ {\begin{array}{*{20}l} {F_{e} \frac{{3r_{nuc} \left( {1 - \alpha } \right)\rho_{v} }}{{R_{B} }}\sqrt {\frac{2}{3}\frac{{P_{v} - P}}{{\rho_{L} }}} } \hfill & {{\text{if}}} \hfill & {P < P_{v} } \hfill \\ {F_{c} \frac{{3\alpha \rho_{v} }}{{R_{B} }}\sqrt {\frac{2}{3}\frac{{P - P_{v} }}{{\rho_{L} }}} } \hfill & {{\text{if}}} \hfill & {P < P_{v} } \hfill \\ \end{array} } \right. $$

where Pv is the gas-phase pressure, P is saturated pressure of vapor, rnuc is the gas-phase volume fraction at the nucleation position, RB is the radius of bubbles at the nucleation position, and Fe and Fc are two empirical parameters in the gasification and compression processes. These parameters are set as follows: rnuc = 5.0 × 10–4, RB = 2.0 × 10–6 m, Fe = 5.0, and Fc = 0.01.

3.4 Boundary conditions and computing method

Boundary conditions involved in the numerical simulation were set as follows. A total pressure inlet boundary condition was applied at the inlet of the centrifugal pump. The stage and degree of cavitation in the centrifugal pump were controlled by adjusting the overall pressure at the inlet. The outlet boundary condition was set as the fixed mass flow rate. The solid wall used insulation non-slip boundary conditions and the near-wall region used the standard wall function. A frozen rotor interface was set at the intersection of the impeller, volute, and inlet sections for the coupling of dynamic and static parts. The convective term used the first-order upwind scheme, while the diffusion term applied the second-order central difference scheme. The semi-implicit method for pressure-linked equations (SIMPLE) algorithm, which belongs to the pressure correction method, was applied as the discrete method. Convergence accuracy of the iterative computing residual error of the flow field was set at 10–4.

The simulation process was mainly divided into two steps. The first step was single-phase constant numerical simulation of fluid, and the second step was the computing of cavitation flow by using the constant calculated results as the initial value. In the two-phase flow mixing model, the continuous phase was set as water and the dispersed phase was set as bubbles. In the initial calculation, the volume fraction of water at the inlet was set at 100% and the volume fraction of bubbles was set as 0. The saturated vapor pressure of liquid was 3.17 kPa, and the average diameter of bubbles was 2 × 10–6 m. The blade surface of the impeller was set with different roughness in the numerical simulation, namely 0 (absolute smoothness), 0.06, 0.12, 0.18, 0.24, and 0.3 mm.

4 Results and discussion

4.1 Comparison between numerical simulation and experimental performance curves

To verify the accuracy of numerical simulation on flow law in the internal flow field of a centrifugal pump, the test results of the external characteristics of the pump were compared with the predicted results in numerical simulation under constant conditions. Comparative results are presented in Fig. 4.

Fig. 4
figure 4

Performance curve comparison of numerical simulation with experiment

Full size image

Figure 4 shows that the numerical simulation curve basically agrees with the experimental curve. The error between them is less than 3% under rated conditions. A slight deviation occurs under a small flow rate, which is mainly due to numerical calculation accuracy under such a rate. In general, the numerical simulation performance curve and experimental performance curve show basically consistent variation trends, indicating that numerical simulation can reflect the flow state in the flow field of centrifugal pumps in a relatively accurate manner.

4.2 Performance analysis under single-phase non-cavitation condition

The three-dimensional model of the full-flow field can consider volume loss through numerical simulation, thereby enabling the elimination of calculation error from the simulation results caused by the simplification of the flow field and avoiding correction of calculated error based on an empirical formula. The streamlined flow field under single-phase non-cavitation condition is presented in Fig. 5.

Fig. 5
figure 5

Streamlined Diagram of Single-phase Non-cavitation Condition

Full size image

First, the numerical calculation of the flow field under single-phase non-cavitation conditions was conducted. Accuracy of the simulation results was verified by comparing the constant simulation results under the standard designed flow rate Q = 500 m3/h and test results under rated flow rate. Before verification of accuracy, we have to analyze whether the flow structure of the flow field is reasonable. As shown in Fig. 5, liquid flows in from the inlet passage, runs through the impeller passage and pumping chamber, and then discharges from the outlet section. The entire streamline is smooth, and the spaces between streams of different fluid particles are uniform. The flow speed conforms to the flow law completely, without eddies and reflux. These results confirm that the constructed model can effectively reflect flow conditions in a centrifugal pump. Numerical simulation results were compared with the test value under rated flow rate (Table 2). The relative error between the numerical simulation results and rated values in terms of head, efficiency, and shaft power is 7.78%, 3.09%, and 5.42%, respectively. Relative errors are within a small range (less than 10%). Considering the influences of grid size on meshing quality, we can view the numerical simulation results in high accordance with the rated values of characteristic parameters, which proves the reasonability of the model setting and reliability of the calculated results. These results enable us to analyze the influences of wall roughness on the cavitation process.

Table 2 Steady numerical simulation results compared with rated condition parameters
Full size table

4.3 Evolution laws of bubbles

Bubbles are produced when local pressure in a centrifugal pump is lower than the saturated vapor pressure under the working temperature of the transmitting liquid. Based on numerical simulation convergence under single-phase non-cavitation conditions, a cavitation model is loaded and the overall pressure at the inlet is controlled to divide cavitation into the following stages: cavitation inception, cavitation development, critical cavitation, and fracture cavitation. A distribution cloud diagram of bubble volume in different cavitation stages is shown in Fig. 6. In cavitation inception, few bubbles are produced at the inlet of the impeller initially. The reason is that the circular velocity of the fluid particles at the inlet of the impeller is higher than that at other positions of the inlet and the velocity of fluid increases due to centrifugal force. According to the velocity triangle, the pressure drop caused by pressure loss streaming at the inlet increases accordingly, which easily causes bubble generation. The maximum volume fraction of bubbles in the cavitation inception is only 0.55, and the distribution area of the bubbles is small. When cavitation is developed to a certain extent, the bubble region is expanded and the maximum volume fraction of bubbles is increased to 0.85. In critical cavitation, the number of bubbles increases significantly and the bubbles extend to the working face of the blades. The maximum volume fraction of the bubbles reaches 0.94. In fracture cavitation, the volume fraction of the bubbles increases from the inlet side of the impeller along the radius direction and reaches the peak as it approaches the middle position of the blades. Therefore, bubbles are initiated at the inlet of the impeller and developed to the extreme state in the middle position of the blades. Under this circumstance, bubbles collapse and perish when fluid pressure changes, thereby causing strong impacts and noise loss, and bringing negative influences on flow passage.

Fig. 6
figure 6

Volume fraction contour of gas phase on impeller. a Cavitation inception. b Cavitation development. c Critical cavitation. d Fracture cavitation

Full size image

According to bubble distribution in the impeller, bubbles are mainly produced at the inlet of the impeller during cavitation inception and then extend toward the middle of the impeller, finally occupying approximately half the area of the entire blade. As the volute tongue can influence the flow process, the distribution of bubbles is asymmetric to a certain extent. Such instability is due to pressure fluctuation, which is induced by the disturbance of fluids between adjacent blades. The maximum volume fraction of the bubbles is in the range of 0.55–0.94 throughout the development of cavitation.

4.4 Effects of roughness on pressure distribution in impeller

Bubbles are generally produced by saturated vapor pressure. Cavitation occurs when local pressure in a centrifugal pump is lower than the saturated vapor pressure under the working temperature of the transmitting liquid. Roughness on the blade surface mainly influences the degree of cavitation indirectly by local pressure distribution in the flow passage of the impeller. Critical cavitation with evident cavitation characteristics was selected to analyze the effects of roughness on pressure distribution in the impeller passage. Changes of pressure distribution in the impeller with roughness during the critical cavitation are shown in Fig. 7. Obviously, a low-pressure region mainly distributes at the inlet of the impeller and low pressure is approximately 3000 Pa, which is close to the saturated vapor pressure of the bubbles. Requirements on the pressure for cavitation are met. Therefore, the impeller inlet is the first region where cavitation occurs. However, the low-pressure region occupies 1/3 at the most and expands continuously with the increase in roughness. Cavitation extends from the impeller inlet to the blade outlet. According to analysis, cavitation in the flow passage of the impeller is mainly caused by local pressure in the flow passage under different surface roughness of the blade. The area of the low-pressure region is positively related to the volume fraction of bubbles and the cavitation area. In other words, wall roughness can greatly influence the development of cavitation.

Fig. 7
figure 7

Impeller surface total pressure distribution at different roughness

Full size image

4.5 Gas volume distribution in impeller

The relation curve between gas volume fraction in the impeller and r/R2 (r is radial position and R2 is outer diameter of the impeller) at the dimensionless radial position is shown in Fig. 8, which can be used to analyze the effective distribution of the bubble volume fraction in the impeller. Under this condition, the distribution law of bubble volume is quantified in analysis.

Fig. 8
figure 8

Volume fraction of gas in radial distribution

Full size image

In Fig. 8, the peak volume fraction of bubbles is only 55% during cavitation inception. Bubbles mainly distribute in the radial scope of 0.17–0.20 at inlet of the impeller. The volume fraction of bubbles is increased dramatically to over 85% during the cavitation development, and the bubbles mainly distribute in the radial scope of 0.12–0.19. The peak volume fraction of bubbles reaches 90% during critical cavitation, and the bubbles mainly distribute in the radial scope of 0.13–0.21. The peak volume fraction of bubbles further increases to 94% during fracture cavitation. The bubbles mainly distribute in the radial scope of 0.08–0.35. In the fracture cavitation stage, distribution area of bubbles reaches the maximum value.

With the continuous development of cavitation, the peak volume fraction of bubbles increases gradually and the final peak ranges within 85%–94%. Meanwhile, the distribution area of bubbles expands continuously. Bubbles mainly concentrate on the dimensionless radial scope of 0.08–0.35. In each stage of cavitation, the volume fraction of bubbles increases with the increase in roughness, and the peak volume fraction extends toward the outlet of the blades. Ultimately, bubbles occupy and block more than 50% of the flow area in the impeller passage.

4.6 Effects of roughness on pump performance

The occurrence and development of cavitation can influence the external characteristics of the centrifugal pump. Changes in the head, efficiency, and shaft power of a centrifugal pump with roughness in different cavitation stages are shown in Fig. 9. The head and efficiency both decrease with the increase in roughness, while the shaft power shows the opposite.

Fig. 9
figure 9

Influence of wall roughness on pump cavitation performance. a Effect of roughness on head. b Effect of roughness on efficiency. c Effect of roughness on shaft power

Full size image

Variation trends of performance parameters differ significantly across the cavitation stages. At cavitation inception, the variation curves of the head and efficiency decrease stably and slightly (0.34% and 0.89% on average). The shaft power also increases slightly, and the average growth rate is only 1.35%. Characteristic parameters of the pump become increasingly stable. Therefore, bubbles begin to be produced and cause local energy loss, and the cavitation performance of the pump remains basically the same with changes in roughness during cavitation inception. In cavitation development and critical cavitation, variation curves of the head and efficiency decline gradually and significantly, with an average reduction rate of 1.86% and 2.14%. On the contrary, the shaft power increases continuously and greatly. The average growth rate of the shaft power is 3.94% during the cavitation development and 2.33% during the critical cavitation. The performance curves present similar variation trends in these two stages. The variation curves of efficiency, head, and shaft power all show large slopes. During fracture cavitation, the variation curves of head and efficiency are smooth and decrease slightly (0.67% and 1.31% on average), whereas those of shaft power achieve a small growth (0.79% on average). At this stage, the flow passage in the pump is filled with bubbles that are produced from the cavitation and block the flow passage in the impeller. Energy loss increases sharply, which leads to reduction of the head and efficiency of the pump. This condition can be interpreted from two perspectives.

The pump performance change slightly with the increasing of roughness during cavitation inception and fracture cavitation, but fluctuate greatly in the cavitation development and critical cavitation. The reason for this phenomenon is the formation of a few bubbles does not affect flow significantly during the cavitation inception. And during fracture cavitation, bubbles produced from the cavitation block the entire flow passage, which would be influencing the machine performance seriously. Under these two conditions, wall roughness can slightly influence the pump performance. Change roughness is suggested to improve the cavitation performance of centrifugal pumps during design process. Such an improvement is better during cavitation development and critical cavitation. Controlling wall roughness during the cavitation development and critical cavitation can prevent sharp reductions of the head and efficiency curves and decrease the flow energy loss.

5 Conclusions and future perspectives

Design, mode selection, and operation conditions of centrifugal pumps are improved to discuss the influences of wall roughness on the cavitation performance of centrifugal pumps and reveal the occurrence mechanism and control method of cavitation. In this study, a numerical simulation of the cavitation of a mode of the centrifugal pump is conducted based on computational fluid dynamics (CFD) technology. A comparative analysis of the evolution laws of bubbles in different cavitation stages is conducted to discuss the influences of wall roughness on pressure in the impeller and the efficiency and head of pumps systematically. The following conclusions can be drawn:

  1. (1)

    With the increase in wall roughness, the volume fraction of bubbles in the impeller increases. Accordingly, the distribution area of the maximum volume fraction of bubbles is expanded and is mainly in the dimensionless radial scope of 0.08–0.35 on the blade. The distribution area of the maximum volume fraction of bubbles extends toward the outlet of the blades. The variation curves of pump efficiency decreased by 0.89% on average at cavitation inception, by 2.14% on average at cavitation development and critical cavitation, by 1.31% on average at fracture cavitation.

  2. (2)

    With the increase in roughness, the low-pressure region in the impeller expands with the development of cavitation and further increases the volume fraction of bubbles on the blade surface as well as the flow loss. The wall roughness influences the development of cavitation significantly.

  3. (3)

    The head and efficiency of the centrifugal pumps decrease greatly with the development of cavitation, whereas the shaft power increases gradually. During the cavitation development and critical cavitation, the influence of wall roughness on the external characteristics of the pump is more obvious compared with those during the cavitation inception and fracture cavitation.

  4. (4)

    In the design process of centrifugal pumps, decreasing the wall roughness appropriately during the cavitation development and critical cavitation is important to effectively improve the cavitation performance of pumps.

In this study, the occurrence mechanism and cavitation development are described accurately with comprehensive consideration of the influencing laws of wall roughness at different cavitation stages, which can provide a technological reference for the design and operation of centrifugal pumps in engineering practices. In this study, the cavitation characteristics of centrifugal pumps are studied by changing the wall roughness. However, only a qualitative analysis of the influences of wall roughness on the external characteristics of centrifugal pumps is reported. This study still has certain limitations in examining the influence of dynamic and static interferences at the casing tongue on the cavitation process during the actual operation.

According to the research results, it can be predicted that surface tension and flowing state of liquid, rotating speed of the impeller, and coefficient of viscosity of fluids can influence the cavitation to a certain extent. The influencing mechanisms of these factors can be analyzed through reasonable experimental design and simple accurate numerical simulation. These influencing factors can be considered in future studies.