Skip to main content
SpringerLink
Log in

Buckling analysis of functionally graded beams with periodic nanostructures using doublet mechanics theory

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

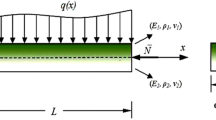
Buckling analysis of functionally graded (FG) nanobeams is examined using doublet mechanics theory. The material properties of FG nanobeams change with the thickness coordinate. A periodic nanostructure model is considered in FG nanobeams which has a simple crystal square lattice type and Euler–Bernoulli beam theory is used in the formulation. Softening or hardening material behaviour has been observed by changing chiral angle of the considered FG periodic nanobeams in the present doublet mechanics theory. Unlike other size dependent theories such as nonlocal stress gradient elasticity theory, couple stress theory, strain gradient theory, this mechanical response (softening or hardening) is seen for the first time in doublet mechanics theory. Mechanical material responses are directly affected by the atomic structure of the considered material in the doublet mechanics theory. Firstly, micro-stress and micro-strain relations are obtained for the considered nanostructure model in doublet mechanics theory. Then, these microequations are transformed to macroequations in the present doublet mechanics theory. Thus, more physical and accurate mechanical results can be obtained in nanostructures using the doublet mechanics theory. After developing the mathematical formulations of FG periodic nanobeams, Ritz method is applied to obtain the critical buckling loads for different boundary conditions. Comparison of example studies with the present doublet mechanics model is presented for verification, and effects of chiral angle on stability response of periodic FG nanobeams are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Şimşek M, Yurtcu HH (2013) Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos Struct 97:378–386

    Article  Google Scholar 

  2. Miyamoto Y, Kaysser WA, Rabin BH, Kawasaki A, Ford RG (1999) Functionally graded materials: design, processing and applications. Kluwer Academic Publihers, London

    Book  Google Scholar 

  3. Sankar BV (2001) An elasticity solution for functionally graded beams. Compos Sci Technol 61:689–696

    Article  Google Scholar 

  4. Chakraborty A, Gopalakrishnan S, Reddy JN (2003) A new beam finite element for the analysis of functionally graded materials. Int J Mech Sci 45:519–539

    Article  MATH  Google Scholar 

  5. Wattanasakulpong N, Prusty BG, Kelly DW (2011) Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int J Mech Sci 53:734–743

    Article  Google Scholar 

  6. Aydogdu M, Taskin V (2007) Free vibration analysis of functionally graded beams with simply supported edges. Mater Des 28:1651–1656

    Article  Google Scholar 

  7. Li XF (2008) A unified approach for analysing static and dynamic behaviors of functionally graded Timoshenko and Euler-Bernoulli beams. J Sound Vib 318:1210–1229

    Article  Google Scholar 

  8. Sina SA, Navazi HM, Haddadpour H (2009) An analytical method for free vibration analysis of functionally graded beams. Mater Des 30:741–747

    Article  Google Scholar 

  9. Reddy JN (2011) Microstructure-dependent couple stress theories of functionally graded beams. J Mech Phys Solids 59:2382–2389

    Article  MathSciNet  MATH  Google Scholar 

  10. Nguyen TK, Nguyen BD, Vo TP, Thai HT (2017) Hygro-thermal effects on vibration and thermal buckling behaviours of functionally graded beams. Compos Struct 176:1050–1060

    Article  Google Scholar 

  11. Arefi M, Zenkour AM (2017) Wave propagation analysis of a functionally graded magneto-electro-elastic nanobeam rest on Visco-Pasternak foundation. Mech Res Commun 79:51–62

    Article  Google Scholar 

  12. Hasanyan DJ, Batra RC, Harutyunyan S (2008) Pull-in instabilities in functionally graded microthermoelectromechanical systems. J Therm Stress 31:1006–1021

    Article  Google Scholar 

  13. Janghorban M, Zare A (2011) Free vibration analysis of functionally graded carbon nanotubes with variable thickness by differential quadrature method. Phys E 43:1602–1604

    Article  Google Scholar 

  14. Eltaher MA, Emam SA, Mahmoud FF (2012) Free vibration analysis of functionally graded size-dependent nanobeams. Appl Math Comput 218:7406–7420

    MathSciNet  MATH  Google Scholar 

  15. Şimşek M, Reddy JN (2013) A unified higher order beam theory for buckling of a functionally graded microbeam embedded in elastic medium using modified couple stress theory. Compos Struct 101:47–58

    Article  Google Scholar 

  16. Ansari R, Gholami R, Sahmani S (2011) Free vibration analysis of size-dependent functionally graded microbeams based on the strain gradient Timoshenko beam theory. Compos Struct 94:221–228

    Article  Google Scholar 

  17. Akgöz B, Civalek Ö (2013) Free vibration analysis of axially functionally graded tapered Bernoulii–Euler microbeams based on the modified couple stress theory. Compos Struct 98:314–322

    Article  Google Scholar 

  18. Akgöz B, Civalek Ö (2013) Buckling analysis of functionally graded microbeams based on the strain gradient theory. Acta Mech 224:2185–2201

    Article  MathSciNet  MATH  Google Scholar 

  19. Abo-bakr HM, Abo-bakr RM, Mohamed SA, Eltaher MA (2021) Multi-objective shape optimization for axially functionally graded microbeams. Compos Struct 258:113370

    Article  Google Scholar 

  20. Eltaher MA, Fouda N, El-midany T, Sadoun AM (2018) Modified porosity model in analysis of functionally graded porous nanobeams. J Braz Soc Mech Sci Eng 40:141

    Article  Google Scholar 

  21. Esen I, Özarpa C, Eltaher MA (2021) Free vibration of a cracked FG microbeam embedded in an elastic matrix and exposed to magnetic field in a thermal environment. Compos Struct 261:113552

    Article  Google Scholar 

  22. Abo-bakr RM, Abo-bakr HM, Mohamed SA, Eltaher MA (2021) Optimal weight for buckling of FG beam under variable axial load using Pareto optimality. Compos Struct 258:113193

    Article  Google Scholar 

  23. Abo-bakr RM, Eltaher MA, Attia MA (2020) Pull-in and freestanding instability of actuated functionally graded nanobeams including surface and stiffening effects. Eng Comput. https://doi.org/10.1007/s00366-020-01146-0

    Article  Google Scholar 

  24. Abo-bakr HM, Abo-bakr RM, Mohamed SA, Eltaher MA (2020) Weight optimization of axially functionally graded microbeams under buckling and vibration behaviors. Mech Based Design Struct Mach. https://doi.org/10.1080/15397734.2020.1838298

    Article  Google Scholar 

  25. Eringen AC (1976) Nonlocal polar field models. Academic Press, New York

    Google Scholar 

  26. Mindlin RD (1964) Micro-structure in linear elasticity. Arch Ration Mech Anal 16:51–78

    MathSciNet  MATH  Google Scholar 

  27. Cosserat E, Cosserat F (1909) Sur la théorie des corps déformables. Herman, Paris (In French)

    MATH  Google Scholar 

  28. Mohamed N, Eltaher MA, Mohamed SA, Seddek LF (2019) Energy equivalent model in analysis of postbuckling of imperfect carbon nanotubes resting on nonlinear elastic foundation. Struct Eng Mech 70(6):737–750

    Google Scholar 

  29. Eltaher MA, Mohamed N, Mohamed S, Seddek LF (2019) Postbuckling of curved carbon nanotubes using energy equivalent model. J Nano Res 57:136–157

    Article  Google Scholar 

  30. Eltaher MA, Almalki TA, Ahmed KIE, Khalid H (2019) Characterization and behaviors of single walled carbon nanotube by equivalent-continuum mechanics approach. Adv Nano Res 7(1):39–49

    Google Scholar 

  31. Mohamed N, Mohamed SA, Eltaher MA (2020) Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model. Eng Comput. https://doi.org/10.1007/s00366-020-00976-2

    Article  Google Scholar 

  32. Granik VT (1978) Microstructural mechanics of granular media. Technique report IM/MGU Inst Mech Moscow State Univ, pp 78–241

  33. Eltaher MA, Mohamed N (2020) Nonlinear stability and vibration of imperfect CNTs by doublet mechanics. Appl Math Comput 382:125311

    MathSciNet  MATH  Google Scholar 

  34. Eltaher MA, Mohamed N, Mohamed SA (2020) Nonlinear buckling and free vibration of curved CNTs by doublet mechanics. Smart Struct Syst 26(2):213–226

    MATH  Google Scholar 

  35. Ferrari M, Granik VT, Imam A (1997) Introduction to doublet mechanics, Advances in Doublet Mechanics. Springer, Berlin, Heidelberg, pp 1–26

    Book  MATH  Google Scholar 

  36. Gul U, Aydogdu M, Gaygusuzoglu G (2017) Axial dynamics of a nanorod embedded in an elastic medium using doublet mechanics. Compos Struct 160:1268–1278

    Article  Google Scholar 

  37. Gul U, Aydogdu M (2018) Structural modelling of nanorods and nanobeams using doublet mechanics theory. Int J Mech Mater Des 14:195–212

    Article  Google Scholar 

  38. Gul U, Aydogdu M (2018) Noncoaxial vibration and buckling analysis of embedded double-walled carbon nanotubes by using doublet mechanics. Compos Part B 137:60–73

    Article  Google Scholar 

  39. Gul U, Aydogdu M (2018) Vibration and buckling analysis of nanotubes (nanofibers) embedded in an elastic medium using Doublet Mechanics. J Eng Math 109:85–111

    Article  MathSciNet  MATH  Google Scholar 

  40. Reddy JN (2004) Mechanics of laminated composite plates and shells: theory and analysis. CRC Press, Boca Raton

    Book  MATH  Google Scholar 

  41. Leissa AW (2005) The historical bases of the Rayleigh and Ritz methods. J Sound Vib 287(4–5):961–978

    Article  Google Scholar 

Download references

Funding

The author received no financial support for the research, authorship, and/or publication of this article.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Trakya University, Edirne, 22030, Turkey

    Ufuk Gul & Metin Aydogdu

Authors
  1. Ufuk Gul
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Metin Aydogdu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ufuk Gul.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Technical Editor: Aurelio Araujo.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gul, U., Aydogdu, M. Buckling analysis of functionally graded beams with periodic nanostructures using doublet mechanics theory. J Braz. Soc. Mech. Sci. Eng. 43, 254 (2021). https://doi.org/10.1007/s40430-021-02972-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-021-02972-z

Keywords

Search

Navigation