A lattice Boltzmann study of 2D steady and unsteady flows around a confined cylinder

Abstract

In this work, the lattice Boltzmann (LB) method was applied to simulate incompressible steady and unsteady low Reynolds number (Re) flows around a confined cylinder. In the LB method, different collision models (Bhatnagar–Gross–Krook model, two-relaxation-time model, multi-relaxation-time model, and entropic lattice Boltzmann model) and a regularization model were used, and the results were compared. Numerical results pertaining to a two-dimensional flow around a cylinder are reported and compared with numerical and experimental data available in the literature. The results agree with the predictions made from the literature. A correlation for Strouhal number (St) for 55 $\le$ Re $\le$ 300 is suggested.

1 Introduction

The lattice Boltzmann (LB) method is a numerical tool based around a discrete form of statistical–mechanical Boltzmann equation [1]. One of LB’s primary uses is hydrodynamics computations. Several collision models have been proposed in the past, that include the Bhatnagar–Gross–Krook model—BGK [2], the two-relaxation-time model—TRT [3], the multi-relaxation-time model—MRT [4], the entropic lattice Boltzmann model—ELB [5], and, although technically not a collision model, the regularized lattice Boltzmann model—RLB [6]. By applying the right parameters, all of these models can reproduce the Navier–Stokes equations. However, each collision model has a specific window of application, which for some is wider, for others narrower. The “better” collision models usually carry a greater computational cost, and different problems require different approaches in terms of collision model choice. Different collision models have been put head-to-head before, e.g., their performance in finding a steady-state solution of a 2D lid-driven cavity flow benchmark was compared [7]; however, the ELB implementation therein received a follow-up comment [8].

Another popular computational fluid dynamics (CFD) benchmark is fluid flow around a cylinder [9]. The flow around a cylinder is often considered for testing different solid boundary conditions. Curved walls of the cylinder represent a challenge to be modeled properly, especially in LB computations, as these are usually performed on square lattices [10,11,12,13,14,15,16]. This benchmark serves well in comparing different CFD approaches. However, flow around a cylinder is also a good starting point for testing the solver’s performance in solving flow through complex geometries [17, 18]. With the onset of an unsteady solution at Reynolds numbers (Re) above its critical value (Re$_{\mathrm{crit}}$), where a vortex street (von Kármán vortex street) appears, flow around a cylinder is also popular for testing the performance in solving unsteady flows [19,20,21] and turbulent flows [22].

The aim of this work is to: first verify and validate an in-house-developed LB solver, utilizing the BGK, TRT, MRT, ELB, and RLB models, via the CFD benchmark for flow around a cylinder in both states—steady and unsteady [9]; and second to study the flow around a confined cylinder using the verified model. The first part is also meant to compare the different models’ performance in solving the benchmark problem. In the second part Re$_{\mathrm{crit}}$, as well as the correlation between the Strouhal number (St) and Re in the laminar and transition vortex shedding modes [23], will be investigated.

2 Methods and materials

2.1 The lattice Boltzmann method

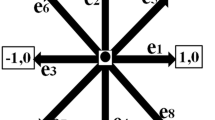
The LB method is performed on a square lattice where at each node there is a discrete number of directions in which the fluid particles can move. In this study, a 2D model with nine lattice velocities—the D2Q9, will be discussed and applied.

Fig. 1

D2Q9 basic lattice velocity directions

A general form of the LB equation can be written as follows [1]:

$$\begin{aligned} f_i\left( \varvec{x} + \varvec{e}_i \varDelta t, t + \varDelta t\right) - f_i\left( \varvec{x}, t\right) = \varOmega _i^{\mathrm{coll}}\left( \varvec{x}, t\right) , \end{aligned}$$

(1)

where $f_i$ is a discrete distribution function at position $\varvec{x}$, with average particle lattice velocity $\varvec{e}_i$, pointing in direction i (see Fig. 1), at time t. $\varOmega ^{\mathrm{coll}}$ is the collision operator, and will be discussed later. $\varvec{e}_i = (e_{x,i}, e_{y,i})$ is the directional vector and it takes the following values:

$$\begin{aligned} \varvec{e} = \left( \begin{matrix} e_{x,0}, \ e_{x,1}, \ldots \ e_{x,8}\\ e_{y,0}, \ e_{y,1}, \ldots \ e_{y,8} \end{matrix} \right) = \left( \begin{matrix} 0, 1, 0, -1, 0, 1, -1, -1, 1 \\ 0, 0, 1, 0, -1, 1, 1, -1, -1 \end{matrix} \right) . \end{aligned}$$

(2)

The local fluid density $\rho$ is computed as the sum of all $f_i$’s on site. The expression for D2Q9 lattice model is the following:

$$\begin{aligned} \rho \left( \varvec{x}, t\right) = \sum _{i = 0}^{8} f_i \left( \varvec{x}, t\right) . \end{aligned}$$

(3)

The local fluid velocity $\varvec{u} = \left( u_x, u_y\right)$ can be computed from the expression for local momentum:

$$\begin{aligned} \rho \left( \varvec{x}, t\right) \varvec{u} \left( \varvec{x}, t\right) = \sum _{i = 1}^{8} f_i \left( \varvec{x}, t\right) \varvec{e}_i. \end{aligned}$$

(4)

2.2 Bhatnagar–Gross–Krook model

The Bhatnagar–Gross–Krook (BGK) model has the simplest form of the presented collision operators, which reads as follows [1, 2]:

$$\begin{aligned} \varOmega _i^{\mathrm{coll}} = -\omega \left( f_i \left( \varvec{x}, t\right) - f_i^{\mathrm{eq}} \left( \varvec{x}, t\right) \right) . \end{aligned}$$

(5)

$f_i^{\mathrm{eq}}$ is the local equilibrium distribution function, and is computed from the local macroscopic velocity $\varvec{u}$, and local density $\rho$:

$$\begin{aligned} f_i^{\mathrm{eq}}\left( \varvec{u}, \rho \right)= & {} w_i \rho \left( \varvec{x}, t\right) \left[ 1 + 3 \, \varvec{e}_i \cdot \varvec{u}\left( \varvec{x}, t\right) + \frac{9}{2} \left( \varvec{e}_i \cdot \varvec{u} \left( \varvec{x}, t\right) \right) ^2\right. \nonumber \\&\left. - \frac{3}{2} \, \varvec{u}\left( \varvec{x}, t\right) \cdot \varvec{u}\left( \varvec{x}, t\right) \right] , \end{aligned}$$

(6)

where $w_i$ is the equilibrium weight factor in the ith direction. Its values add up to 1, and in D2Q9 they equal:

$$\begin{aligned} \varvec{w} = \left( w_0, w_1, \ \ldots \ w_8\right) = \left( \frac{4}{9}, \frac{1}{9}, \frac{1}{9}, \frac{1}{9}, \frac{1}{9}, \frac{1}{36}, \frac{1}{36}, \frac{1}{36}, \frac{1}{36}\right) . \end{aligned}$$

(7)

$\omega$ is the relaxation rate and is the inverse of the relaxation time $\tau = \frac{1}{\omega }$. From the relaxation rate, the fluid’s kinematic viscosity $\nu$ can be calculated:

$$\begin{aligned} \nu = \frac{1}{3} \left( \frac{1}{\omega } - \frac{1}{2}\right) . \end{aligned}$$

(8)

2.3 Two-relaxation-time model

The two-relaxation-time (TRT) collision model is an improved form of the BGK, and at the same time a reduced, and simpler form of the multi-relaxation time model, which will be discussed later. It takes the following form [3]:

$$\begin{aligned} \varOmega _i^{\mathrm{coll}}= & {} -\omega ^+\left( f_i^+\left( \varvec{x}, t\right) - f_i^{\mathrm{eq}+}\left( \varvec{x}, t\right) \right) \nonumber \\&- \omega ^-\left( f_i^-\left( \varvec{x}, t\right) - f_i^{\mathrm{eq}-}\left( \varvec{x}, t\right) \right) . \end{aligned}$$

(9)

The $f_i^+$ and $f_i^-$ are, respectively, the symmetric and anti-symmetric parts of the ith distribution function, and are defined as follows:

$$\begin{aligned} f_i^+ = \frac{f_i + f_{\bar{i}}}{2}, \, f_i^- = \frac{f_i - f_{\bar{i}}}{2}, \end{aligned}$$

(10)

where the index $\bar{i}$ stands for the direction opposite of the direction of index i (see Fig. 1). Expressions for $f_i^{\mathrm{eq}+}$ and $f_i^{\mathrm{eq}-}$ follow suit, but f is replaced by $f^{\mathrm{eq}}$ which can be calculated using Eq. 6:

$$\begin{aligned} f_i^{\mathrm{eq}+} = \frac{f_i^{\mathrm{eq}} + f_{\bar{i}}^{\mathrm{eq}}}{2}, \, f_i^{\mathrm{eq}-} = \frac{f_i^{\mathrm{eq}} - f_{\bar{i}}^{\mathrm{eq}}}{2}. \end{aligned}$$

(11)

$\omega ^+$ and $\omega ^-$ are relaxation rates of the model. They are linked via the “magic parameter” $\varLambda$:

$$\begin{aligned} \varLambda = \left( \frac{1}{\omega ^+} - \frac{1}{2}\right) \left( \frac{1}{\omega ^-} - \frac{1}{2}\right) . \end{aligned}$$

(12)

For almost all of the benchmarking, $\varLambda = \frac{1}{4}$ was used as this was proven to be its most stable value [24]. Indeed, this $\varLambda$ gave the best results, but it was numerically unstable in some cases. There $\varLambda = 10^{-5}$ was used. The positive relaxation rate $\omega ^+$ plays an identical role in TRT as $\omega$ does in BGK, and therefore directly correlates with the kinematic viscosity of the fluid $\nu$:

$$\begin{aligned} \nu = \frac{1}{3} \left( \frac{1}{\omega ^+} - \frac{1}{2}\right) . \end{aligned}$$

(13)

2.4 Multi-relaxation-time model

The multi-relaxation-time (MRT) model was developed almost simultaneously with the LB method itself [4]. The form of MRT presented and used in this study is of the Gram–Schmidt type [25, 26]. The algorithm of MRT collision is as follows: the $f_i$’s at a node in the population space are transformed into the moment space to moments $m_i$’s via the transformation matrix $\varvec{M}$, where the collision is carried out through the relaxation matrix $\varvec{S}$, and finally $m_i$’s are transformed back to $f_i$’s via the inverse of the transformation matrix $\varvec{M}^{-1}$. In general, the MRT collision operator can be written as:

$$\begin{aligned} \varOmega _i^{\mathrm{coll}} = \left( -\varvec{M}^{-1} \varvec{S} \varvec{M} \left[ \varvec{f}\left( \varvec{x}, t\right) - \varvec{f}^{\mathrm{eq}}\left( \varvec{x}, t\right) \right] \right) _i, \end{aligned}$$

(14)

where $\varvec{f} = \left( f_0, f_1, \ldots , f_8\right)$, and $\varvec{f}^{\mathrm{eq}} = \left( f^{\mathrm{eq}}_0, f^{\mathrm{eq}}_1, \ldots , f^{\mathrm{eq}}_8\right)$. The streaming step is carried out with $f_i$’s in the population space. Gram–Schmidt $\varvec{M}$ for the D2Q9 model takes the following form:

$$\begin{aligned} \varvec{M} = \begin{bmatrix} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ -4 &{}\quad -1 &{}\quad -1 &{}\quad -1 &{}\quad -1 &{}\quad 2 &{}\quad 2 &{}\quad 2 &{}\quad 2 \\ 4 &{}\quad -2 &{}\quad -2 &{}\quad -2 &{}\quad -2 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad -1 &{}\quad 0 &{}\quad 1 &{}\quad -1 &{}\quad -1 &{}\quad 1 \\ 0 &{}\quad -2 &{}\quad 0 &{}\quad 2 &{}\quad 0 &{}\quad 1 &{}\quad -1 &{}\quad -1 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad -1 &{}\quad 1 &{}\quad 1 &{}\quad -1 &{}\quad -1 \\ 0 &{}\quad 0 &{}\quad -2 &{}\quad 0 &{}\quad 2 &{}\quad 1 &{}\quad 1 &{}\quad -1 &{}\quad -1 \\ 0 &{}\quad 1 &{}\quad -1 &{}\quad 1 &{}\quad -1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad -1 &{}\quad 1 &{}\quad -1 \end{bmatrix}. \end{aligned}$$

(15)

The inverse matrix $\varvec{M}^{-1}$ can be looked up in the literature [25, 26] or it can be computed with the help of a computer solver. After the transformation to moment space, the moments relax toward the equilibrium moments $m_i^{\mathrm{eq}}$ which are:

$$\begin{aligned} m_0^{\mathrm{eq}}&= \rho , \nonumber \\ m_1^{\mathrm{eq}}&= \rho \left[ -2 + 3 \left( u_x^2 + u_y^2\right) \right] , \nonumber \\ m_2^{\mathrm{eq}}&= \rho \left[ 1 - 3 \left( u_x^2 + u_y^2\right) \right] , \nonumber \\ m_3^{\mathrm{eq}}&= \rho u_x, \nonumber \\ m_4^{\mathrm{eq}}&= -\rho u_x, \nonumber \\ m_5^{\mathrm{eq}}&= \rho u_y, \nonumber \\ m_6^{\mathrm{eq}}&= -\rho u_y, \nonumber \\ m_7^{\mathrm{eq}}&= \rho \left( u_x^2 - u_y^2\right) , \nonumber \\ m_8^{\mathrm{eq}}&= \rho u_x u_y. \end{aligned}$$

(16)

The relaxation is done through $\varvec{S}$, which in Gram–Schmidt procedure takes the form of a diagonal matrix, and can thus be written as:

$$\begin{aligned} \varvec{S} = {\mathrm{diag}}(0, \omega _e, \omega _{\epsilon }, 0, \omega _q, 0, \omega _q, \omega _{\nu }, \omega _{\nu }), \end{aligned}$$

(17)

where $\omega _{\nu }$ is of particular interest, as it correlates with the fluid’s kinematic viscosity in the same way as $\omega$ in BGK:

$$\begin{aligned} \nu = \frac{1}{3}\left( \frac{1}{\omega _{\nu }} - \frac{1}{2}\right) . \end{aligned}$$

(18)

$\omega _{\epsilon }$ is correlated with the fluid’s bulk viscosity. However, it, along with the other relaxation rates (except $\omega _{\nu }$) is usually set to a fixed value, which requires some tuning on the user’s part to find the optimal values. For the purpose of this study, the following values were used $\varvec{S} = {\mathrm{diag}}(0, 1.95, 1.95, 0, 1.4, 0, 1.4, \omega _{\nu }, \omega _{\nu })$.

2.5 Entropic lattice Boltzmann model

The entropic lattice Boltzmann (ELB) model was derived by finding the entropy functions through which the Navier–Stokes equations could be recovered [5, 27]. For ELB, the collision operation can be written as:

$$\begin{aligned} \varOmega _i^{\mathrm{coll}} = -\alpha \beta \left( f_i\left( \varvec{x}, t\right) - f_i^{\mathrm{eq}}\left( \varvec{x}, t\right) \right) . \end{aligned}$$

(19)

At the first glance, Eq. 19 seems very similar to BGK equation (Eq. 5), and indeed, if $\alpha = 2$ it becomes the BGK collision operator, as $\beta = \frac{1}{2 \tau }$. $\beta$ is therefore directly correlated with the fluid’s kinematic viscosity $\nu$:

$$\begin{aligned} \nu = \frac{1}{3}\left( \frac{1}{2 \beta } - \frac{1}{2}\right) . \end{aligned}$$

(20)

However, $f^{\mathrm{eq}}$ in ELB take a slightly different form:

$$\begin{aligned} f_i^{\mathrm{eq}}\left( \varvec{u}, \rho \right) = \rho \left( \varvec{x}, t\right) w_i \prod _{s} \left( 2 - \sqrt{1 + 3 u_s^2}\right) \left[ \frac{2 u_s + \sqrt{1 + 3 u_s^2}}{1 - u_s}\right] ^{e_{s,i}}; \ s = x, \ y. \end{aligned}$$

(21)

To understand the parameter $\alpha,$ the entropy function H should be considered first. In D2Q9, H is defined as:

$$\begin{aligned} H\left( \varvec{f}\right) = f_0 \ln \left( \frac{f_0}{8}\right) + \sum _{i = 1}^{4} f_i \ln \left( \frac{f_i}{2}\right) + \sum _{i = 5}^{8} f_i \ln \left( 2 f_i\right) . \end{aligned}$$

(22)

$\alpha$ should then be numerically determined as the non-trivial solution of the following equation, using the $f^{\mathrm{eq}}$ calculated with Eq. 21:

$$\begin{aligned} H\left( \varvec{f}\right) = H\left( \varvec{f} + \alpha \left( \varvec{f}^{\mathrm{eq}} - \varvec{f}\right) \right) . \end{aligned}$$

(23)

2.6 Regularized lattice Boltzmann model

The regularized lattice Boltzmann (RLB) model actually incorporates the BGK collision, but it includes a regularization of the $f_i$’s before the collision step itself [6]. There are several related regularization procedures in the literature [6, 28, 29]. In this study, the high-order regularization with filtered central moments by Mattila et al. was used [29]. First, let there be a non-equilibrium distribution function $f_i^{\mathrm{neq}}$ introduced:

$$\begin{aligned} f_i^{\mathrm{neq}} = f_i - f_i^{\mathrm{eq}}. \end{aligned}$$

(24)

Then by combining Eqs. 1, 5, and 24, the LB equation can be rearranged as follows:

$$\begin{aligned} f_i\left( \varvec{x} + \varvec{e}_i \varDelta t, t + \varDelta t\right) = f_i^{\mathrm{eq}}\left( \varvec{x}, t\right) + \left( 1 - \omega \right) f_i^{\mathrm{neq}}\left( \varvec{x}, t\right) . \end{aligned}$$

(25)

The high-order $f^{\mathrm{eq}}_i$ is computed as:

$$\begin{aligned} f_i^{\mathrm{eq}}\left( \varvec{u}, \rho \right)&= w_i \rho \left( \varvec{x}, t\right) \left[ 1 + 3 \, \varvec{e}_i \cdot \varvec{u}\left( \varvec{x}, t\right) + \frac{9}{2} \left( \varvec{e}_i \cdot \varvec{u} \left( \varvec{x}, t\right) \right) ^2 \right. \nonumber \\&\quad - \frac{3}{2} \, \varvec{u}\left( \varvec{x}, t\right) \cdot \varvec{u}\left( \varvec{x}, t\right) \nonumber \\&\quad + \frac{27}{2} u_x^2\left( \varvec{x}, t\right) u_y\left( \varvec{x}, t\right) \left( e_{x,i}^2 - \frac{1}{3}\right) e_{y,i} \nonumber \\&\quad + \frac{27}{2} u_y^2\left( \varvec{x}, t\right) u_x\left( \varvec{x}, t\right) \left( e_{y,i}^2 - \frac{1}{3}\right) e_{x,i} \nonumber \\&\quad + \left. \frac{81}{4}u_x^2\left( \varvec{x}, t\right) u_y^2\left( \varvec{x}, t\right) \left( e_{x,i}^2 - \frac{1}{3}\right) \left( e_{x,i}^2 - \frac{1}{3}\right) \right] . \end{aligned}$$

(26)

The actual regularization step occurs by computing $f_i^{\mathrm{neq}}$ as:

$$\begin{aligned} f_i^{\mathrm{neq}}\left( \varvec{x}, t\right)&= w_i \left( \varvec{x}, t\right) \left\{ \frac{9}{2}\left[ \varTheta _{xx}\left( e_{x,i}^2 - \frac{1}{3}\right) + \varTheta _{yy}\left( e_{y,i}^2 - \frac{1}{3}\right) + 2 \varTheta _{xy} e_{x,i}e_{y,i}\right] \right. \nonumber \\&\quad + \frac{27}{2}\left( u_y\left( \varvec{x}, t\right) \varTheta _{xx} + 2 u_x\left( \varvec{x}, t\right) \varTheta _{xy}\right) \left( e_{x,i}^2 - \frac{1}{3}\right) e_{y,i} \nonumber \\&\quad + \frac{27}{2}\left( u_x\left( \varvec{x}, t\right) \varTheta _{yy} + 2 u_y\left( \varvec{x}, t\right) \varTheta _{xy}\right) \left( e_{y,i}^2 - \frac{1}{3}\right) e_{x,i} \nonumber \\&\quad + \frac{81}{4}\left[ u_x^2\left( \varvec{x}, t\right) \varTheta _{yy} + u_y^2\left( \varvec{x}, t\right) \varTheta _{xx}\right. \nonumber \\&\quad + \left. \left. 4 u_x\left( \varvec{x}, t\right) u_y\left( \varvec{x}, t\right) \varTheta _{xy}\right] \left( e_{x,i}^2 - \frac{1}{3}\right) \left( e_{y,i}^2 - \frac{1}{3}\right) \right\} , \end{aligned}$$

(27)

where:

$$\begin{aligned} \varTheta _{kl} = \sum _{i=1}^{8}e_{k,i}e_{l,i}\left( f_i\left( \varvec{x}, t\right) - f_i^{\mathrm{eq}}\left( \varvec{x}, t\right) \right) ; \ k = x, \ y; \ l = x, \ y. \end{aligned}$$

(28)

2.7 Boundary conditions

As a cylinder (or its 2D projection—a circle) requires the use of curved boundaries, the multi-reflection (MR) boundary condition was used for solid walls [30]. Unlike other approaches to curved boundaries, MR formulation is independent of the distance of the wall from the wet node q [31]. This property makes the MR fairly easy to implement and does not greatly increase the overall computational costs, especially in its reduced form [31, 32]:

$$\begin{aligned} f_i\left( B, t + \varDelta t\right) = f_{\bar{i}}\left( B, t\right) + \frac{1 - 2 q}{1 + 2 q}\left( f_{\bar{i}}\left( N, t\right) - f_i\left( B, t\right) \right) . \end{aligned}$$

(29)

q takes a value between 0 and 1, and represents the relative distance between the actual wall position and the boundary node. The positional parameters B and N represent the boundary, and neighboring nodes, respectively, $N = B + \varvec{e}_i \varDelta t$. Straight walls had the value of q set to 0.5, which reduces Eq. 29 to the standard no-slip bounce-back boundary condition.

The inlet boundary condition can be a simple Dirichlet boundary condition, where the multi-reflection boundary is slightly modified:

$$\begin{aligned} f_i^{in}\left( B, t + \varDelta t\right) = f_i\left( B, t + \varDelta t\right) + 6 e_{x,i} \rho _{\mathrm{in}} {u_x}_{\mathrm{in}}\left( y\right) , \end{aligned}$$

(30)

where the ${u_x}_{\mathrm{in}}$ is the inlet velocity, a function of y-coordinate, as in computations in this study a parabolic inlet velocity profile was applied. $\rho _{\mathrm{in}}$ is the density at inlet, and it can be calculated as [33]:

$$\begin{aligned} \rho _{\mathrm{in}} = \frac{f_0\left( B, t\right) + f_2\left( B, t\right) + f_4\left( B, t\right) + 2 \left( f_3\left( B, t\right) + f_6\left( B, t\right) + f_7\left( B, t\right) \right) }{1-u_{\mathrm{in}}\left( y\right) }. \end{aligned}$$

(31)

For the outlet boundary conditions, the non-equilibrium boundary was utilized [34]. This one is formulated in the following manner:

$$\begin{aligned} f_i \left( B\right) = f_i^{\mathrm{eq}} \left( \varvec{u}\left( N\right) , \rho _0\right) + \left[ f_i\left( N\right) - f_i^{\mathrm{eq}}\left( \varvec{u}\left( N\right) , \rho \left( N\right) \right) \right] , \end{aligned}$$

(32)

where the parameters for $f_i^{\mathrm{eq}}$ indicate the values that are used in its computation. $\rho _0$ takes a user-defined value and represents the constant density (pressure) at the outlet.

2.8 Benchmarking the code

The code was first tested in a simple setup—steady and unsteady 2D flow around a cylinder. The benchmark is such as described by Schäfer et al. [9]. A 2D domain, which is bounded on the north and south sides by static no-slip walls, was designed. A cylinder was positioned slightly off-midstream (Fig. 2); the inlet boundary condition is a fully developed parabolic profile, and the outlet boundary condition can be chosen freely. In this study, the boundary conditions were chosen as described above. For MR, at straight walls q equaled 0.5.

The benchmarking is done at two different benchmark Reynolds numbers, Re$_{\mathrm{bm}}$:

$$\begin{aligned} \hbox {Re}_{\mathrm{bm}} = \frac{\bar{u}_x D}{\nu }, \end{aligned}$$

(33)

where $\bar{u}_x$ is the mean flow speed in the x-direction at the inlet, D is the cylinder diameter, and $\nu$ is the fluid’s kinematic viscosity. The benchmark for the steady flow is set at Re$_{\mathrm{bm}} = 20$, while the unsteady case is studied at Re$_{\mathrm{bm}} = 100.$

The tested values were: the drag coefficient $c_D$, the lift coefficient $c_L$, the recirculation length $L_a$ at Re$_{\mathrm{bm}} = 20$, the Strouhal number St$_{\mathrm{bm}}$ at Re$_{\mathrm{bm}} = 100$, and the downstream pressure drop at the cylinder $\varDelta P$:

$$\begin{aligned} c_D= & {} \frac{2 F_D}{\rho \bar{u}_x^2 D}, \end{aligned}$$

(34)

$$\begin{aligned} c_L= & {} \frac{2 F_L}{\rho \bar{u}_x^2 D}, \end{aligned}$$

(35)

$$\begin{aligned} L_a= & {} x_r - x_e, \end{aligned}$$

(36)

$$\begin{aligned} \hbox {St}_{\mathrm{bm}}= & {} \frac{f_{\mathrm{sh}} D}{\bar{u}_x}, \end{aligned}$$

(37)

$$\begin{aligned} \varDelta P= & {} P\left( x_a\right) - P\left( x_e\right) , \end{aligned}$$

(38)

where $F_D$ and $F_L$ are the drag and lift components of the force acting on the cylinder ($\varvec{F} = \left( F_D, \, F_L\right)$), respectively, and $\rho$ is the fluid density. $x_r$ is the x-coordinate downstream from the cylinder, where $u_x$ equals 0, $x_e$ is the x-coordinate on the edge of the cylinder that is the furthest downstream, equaling 0.25, and $x_a$ lies on the opposing side of the cylinder upstream. $f_{\mathrm{sh}}$ is the vortex shedding frequency, and it was determined as the frequency at which there was a maximum of the Fourier transformed data of $c_L$.

Fig. 2

Benchmarking domain [9]. Displayed are the inlet and outlet positions (the fluid flows west to east). The domain dimensions are written in terms of cylinder diameter D

In the steady case, the resulting $c_D$ and $c_L$ were the steady solutions, whereas in the unsteady case both parameters in question were their maximum values, $c_D^{\mathrm{max}}$ and $c_L^{\mathrm{max}}$, when a periodic steady state was reached (the von Kármán vortex street). $F_D$ and $F_L$ were calculated as the change of momentum in a time period $\varDelta t$ in a given direction, also accounting for the curved wall position q [30]:

$$\begin{aligned} F_D= & {} \sum _{i = 1}^{8} e_{x,i} \left[ \left( \frac{1}{2} + q\right) \left( f_i\left( B, \, t\right) + f_{\bar{i}}\left( N, \, t\right) \right) \right. \nonumber \\&\left. + \left( \frac{1}{2} - q\right) \left( f_i\left( N, \, t\right) + f_{\bar{i}}\left( N + 1, \, t\right) \right) \right] \varDelta t, \end{aligned}$$

(39)

$$\begin{aligned} F_L= & {} \sum _{i = 1}^{8} e_{y,i} \left[ \left( \frac{1}{2} + q\right) \left( f_i\left( B, \, t\right) + f_{\bar{i}}\left( N, \, t\right) \right) \right. \nonumber \\&\left. + \left( \frac{1}{2} - q\right) \left( f_i\left( N, \, t\right) + f_{\bar{i}}\left( N + 1, \, t\right) \right) \right] \varDelta t. \end{aligned}$$

(40)

B represents all solid cylinder boundary nodes, N represents $B + \varvec{e}_i \varDelta t$ if the said point is fluid, and $N + 1$ represents $B + 2 \varvec{e}_i \varDelta t$.

The benchmarks were performed at different D’s: 8, 16, 32, and 64. Additionally, different collision models were used, to test any differences in the obtained results. For TRT, $\varLambda = \frac{1}{4}$ was used for all computations, with the exception of $D = 8$ and $D = 16$ at Re$_{\mathrm{bm}} = 100$, as the benchmark was numerically more stable with $\varLambda = 10^{-5}$.

2.9 Simulation setup

Again a cylinder is put between two walls in a 2D system. Unlike in the benchmark, here a channel with a cylinder placed midstream and a fifth of the channel length downstream was set up. The channel width was 8 times the cylinder diameter D, and channel length was 4 times the channel width. The channel-width-to-cylinder-diameter of 8 (blockage ratio of 0.125) was found to reproduce the results of an unbounded cylinder [35]. These dimensions also made sure that the inlet and outlet boundary conditions did not interfere with the computations. The setup is represented in Fig. 3. The boundary conditions used were the same as above.

Fig. 3

Simulation domain. Displayed are the inlet and outlet positions (the fluid flows west to east). The domain dimensions are written in terms of cylinder diameter D. Marked are also the points at which local $\rho$’s were logged. The difference of the two values is proportional to the pressure drop in the y-direction

The computations logged the density difference $\varDelta \rho$ through the middle of the cylinder in the y-direction. These measurements are proportional to the pressure drop in the same direction. By processing these data, the frequency of vortex shedding $f_{\mathrm{sh}}$ could be obtained. The simulations were performed in a range of Reynolds numbers Re between 50 and 300. Re is defined as follows:

$$\begin{aligned} \hbox {Re} = \frac{\bar{u}^\star D}{\nu }. \end{aligned}$$

(41)

The flow speed $\bar{u}^\star$ is calculated as the average x-component of the velocity, $u_x$, at inlet over the obstacle’s projection onto the inlet [36], in this case:

$$\begin{aligned} \bar{u}^\star = \int _{3.5D}^{4.5D} u_x\left( \mathrm{inlet}, \, y\right) {\mathrm{d}}y. \end{aligned}$$

(42)

According to Chen et al., this formulation of average flow speed allows for comparison of bounded and unbounded cylinders [36]. Additionally, the critical Reynolds number Re$_{\mathrm{crit}}$ was determined by increasing Re between 50 and 60 in increments of 1. Re$_{\mathrm{crit}}$ is the Re at which an instability in flow occurs.

To compare the present results to the ones found in other published work, $f_{\mathrm{sh}}$ was converted to the Strouhal number St. This was then plotted against Re. St is defined as:

$$\begin{aligned} {\mathrm{St}} = \frac{f_{\mathrm{sh}} D}{\bar{u}^\star }. \end{aligned}$$

(43)

The simulations ran for a total of 200 000 time steps per value of Re. The output data were then transformed with the Fourier transformation to obtain the vortex shedding frequency spectra. The simulations for Re$_{\mathrm{crit}}$ ran for 2 000 000 time steps, as it took longer for instabilities to develop at lower Re.

The cylinder diameter chosen for the simulations was $D = 32$. Computations were performed with the MRT collision model.

2.10 Hardware and software

The computations were carried out with an in-house-developed LB solver, written in CUDA C++. The code ran on two separate machines, namely the benchmarking was performed on an Intel^® Core™ i7-6700HQ, 16 GB RAM, NVIDIA^® GeForce^® GTX 960M 4 GB laptop, and the simulations ran on an Intel^® Core™ i7-8700K, 8 GB RAM, NVIDIA^® GeForce^® GTX 1060 6 GB desktop computer. Both machines were using Ubuntu 18.04.1 LTS operating system, NVIDIA^® CUDA^® Compiler Driver (nvcc) from NVIDIA^® Toolkit version 9.1, and GNU C++ (g++) compiler version 7.3.0. Data analysis was performed with ParaView 5.4.1, and Python 3.6.5, using the numpy, scipy, and matplotlib libraries. The Fourier transform utilized was the scipy.fftpack.fft. To smooth out the datasets computed in the benchmark (especially for the $c_L^{\mathrm{max}}$ and $c_D^{\mathrm{max}}$ determination), the Savitzky–Golay filter (scipy.signal.savgol_filter) was applied. This reduced the errors significantly.

3 Results

3.1 Benchmarks

The benchmarking results are given in Table 1, and are graphically depicted in Figs. 4 and 6. Also displayed are examples of velocity profiles of fully developed flows in Figs. 5 and 7. At Re$_{\mathrm{bm}} = 20$ it can be noticed, that at the smallest D (8) the performance is the worst, and it gets better as the value of D increases. The errors for all methods are the greatest for $c_L$, followed by $c_D$. In both cases, the methods converged to the prescribed limits with greater resolution. ELB and RLB, however, were not able to fall within the limits, except RLB for $c_L$ at $D = 64$. $\varDelta P$ errors converge with increased grid resolution. $L_a$ results are in good agreement with the expected values, apart from the outlying ELB results. For $D = 32$ and 64, the results for all of the collision models seem to fall more or less within the range prescribed in [9].

Table 1 Results from benchmarks for both Re$_{\mathrm{bm}}$: 20 and 100. The presented values are: drag coefficient $c_D$, lift coefficient $c_L$, recirculation length $L_a$, and pressure drop $\varDelta P$ (Re$_{\mathrm{bm}} = 20$); and maximum drag coefficient $c_D^{\mathrm{max}}$, maximum lift coefficient $c_L^{\mathrm{max}}$, Strouhal number St$_{\mathrm{bm}}$, and pressure drop $\varDelta P$ (Re$_{\mathrm{bm}} = 100$). All models (BGK, TRT, MRT, ELB, and RLB) were benchmarked at different sizes of D, which determined the domain size and grid resolution

At Re$_{\mathrm{bm}} = 100$ the trend is similar to the Re$_{\mathrm{bm}} = 20$—higher resolution computations performed better. ELB again failed to perform well in $c_D^{\mathrm{max}}$ and $c_L^{\mathrm{max}}$ tests, but it captured the emergent flow properties (St$_{\mathrm{bm}}$) well. Similarly as at Re$_{\mathrm{bm}} = 20$ the errors are the greatest for $c_L^{\mathrm{max}}$ and $c_D^{\mathrm{max}}$. $\varDelta P$ was the most accurate at $D = 64$. It is, however, surprising that St$_{\mathrm{bm}}$ was the same for all methods, with only difference being at $D = 8$, where ELB, RLB, and MRT differ from TRT and BGK. At higher D, there are no differences between the methods.

Fig. 4

Graphical representation of the results from Table 1 at Re$_{\mathrm{bm}} = 20$ for different cylinder diameters D and collision models: a drag coefficient $c_D^{\mathrm{max}}$, b lift coefficient $c_D$, c recirculation length $L_a$, and d pressure drop $\varDelta P$. Plotted are also the lower and upper bounds for each measured value from [9]

Fig. 5

An example of a fully developed flow at Re$_{\mathrm{bm}} = 20$. Displayed is the velocity profile. The collision model utilized here is TRT, and $D = 64$. No vortex shedding can be observed in the cylinder’s wake

From these results, it is evident that the emerging flow pattern remains pretty much unaffected by the size of D (results for St$_{\mathrm{bm}}$) and the choice of the collision operator. However, MRT and RLB were the most stable, but MRT required shorter computation times (data not shown), so further computations were performed using it. $D = 32$ appears to be a good enough resolution for further computations, as $D = 64$ does not greatly improve the results, and smaller D would result in greater errors. All the presented models performed better in the unsteady (Re$_{\mathrm{bm}} = 100$) case, which is good for this study, as the flow in the transition range of Re that was investigated later does not give a steady-state solution. The overall benchmarking results suggest that the presented approach is suitable for simulating 2D fluid flow around a cylinder. Overall the computation time of the BGK, TRT, and MRT models was similar ($\pm 6\%$), whereas ELB and RLB computation time was about twice as long (data not shown). It should be noted, however, that RLB implementation here was not as far optimized as the other models’.

Fig. 6

Graphical representation of the results from Table 1 at Re$_{\mathrm{bm}} = 100$ for different cylinder diameters D and different collision models: a maximum drag coefficient $c_D^{\mathrm{max}}$, b maximum lift coefficient $c_L^{\mathrm{max}}$, c Strouhal number St$_{\mathrm{bm}}$, and d pressure drop $\varDelta P$. Plotted are also the lower and upper bounds for each measured value from [9]

Fig. 7

An example of a fully developed flow at Re$_{\mathrm{bm}} = 100$. Displayed is the velocity profile. The collision model utilized here is ELB, and $D = 8$. Vortex shedding can be observed in the cylinder’s wake

3.2 Simulations

3.2.1 Re$_{\mathrm{crit}}$ determination

Fig. 8

Re$_{\mathrm{crit}}$ determination. a Maximum peak size plotted against Re. From this graph, it is evident that a disturbance in the flow becomes significant at Re = 55. Plotted is also a best-fit line across 55 $\le$ Re $\le$ 57. b $u_y$ at the channel mid-point plotted along the x-axis for Re = 53, 54, 55, all after 2 000 000 time steps. The lines for Re= 53, 54 appear identical, whereas a significant disturbance is seen at Re = 55

Blockage ratio of the channel has an effect on Re$_{\mathrm{crit}}$, which is the lowest Re at which a disturbance in the wake of the cylinder can be noticed. In general, Re$_{\mathrm{crit}}$ increases with greater blockage ratio. Sahin and Owens investigated this phenomenon [37]; however, in that study Re$_{\mathrm{crit}}$ was not determined for blockage ratio of 0.125, which was used here. By interpolating their data, it was determined that in this case Re$_{\mathrm{crit}}$ should be about Re = 54.6. The results of the numerical experiments, which were used to determine Re$_{\mathrm{crit}}$ of the investigated system, are displayed in Fig. 8. In Fig. 8a, the maximum peak size of the Fourier transform of the data log was plotted against Re. The peak size is affected by the frequency and the amplitude of the signal. A more intense (higher amplitude) wave produces a higher peak size. Because the disturbance appears sooner in flows with higher Re, only the last 150,000 logged points were used in the Fourier transform. At this point, the disturbances were already fully developed, and the comparison between the signals could be made. Figure 8b displays the $u_y$ at the channel mid-point along the x-axis after 2,000,000 time steps. The plots shown are for Re = 53, 54, 55. This shows that practically no change in flow pattern occurs between Re 53 and 54, but a significant disturbance appears at Re = 55. Both plots mentioned above suggest that Re$_{\mathrm{crit}} = 55.0\pm 0.5$, which favors the prediction made above (Figs. 6, 7).

3.2.2 Correlation between St and Re

The correlation between St and Re was investigated and compared to some results found in the literature, which were both experimental and computational [23, 38,39,40,41,42]. The results of these simulations are presented in Fig. 9, and an example of a velocity profile of fully developed flow at Re = 250 is displayed in Fig. 10. The present results agree well with the others. A general trend of St increasing with higher Re can be observed. At lower Re, St increases faster, but the increase slows down at higher Re. In particular, the agreement is good between the present results and [38, 39] in the range $55\left( =\hbox {Re}_{\mathrm{crit}}\right) \le {\mathrm{Re}} \le 100$. A function to fit the data was also calculated:

$$\begin{aligned} {\mathrm{St}} = 0.228 \left( 1 - \frac{35.2}{\mathrm{Re}} + \frac{641}{\hbox {Re}^2}\right) ; \ 55 \le {\mathrm{Re}} \le 300. \end{aligned}$$

(44)

Fig. 9

St versus Re. Plotted are the results from the present study along with a best-fit line (second-order polynomial)—Eq. 44, and others found in the literature. The results of Roshko [23], Tritton (1 and 2) [38], and Norberg [39] are based on experimental results, whereas the results of Zhang [40], Behara [41], Mittal [42], and Singha [35] are from computer simulations

Fig. 10

An example of a fully developed flow at Re = 250. Displayed is the velocity profile. A von Kármán vortex street can be observed in the cylinder’s wake

4 Conclusions

A brief overview of the LB collision models was presented, along with the benchmark model for 2D flow around a cylinder [9]. The presented LB collision models were applied to the benchmark, and were compared among one another. For the specific problem, no significant differences between the models were noticed, especially at higher grid resolutions, and all were able to reproduce the flow, as prescribed by the benchmark, as indicated by correctly computed $L_a$ and St$_{\mathrm{bm}}$. The computations of $c_D$, $c_L$, $c_D^{\mathrm{max}}$, and $c_L^{\mathrm{max}}$ set the models further apart (especially ELB). The poor performance of ELB in the benchmark is surprising. However, the method is said to have an edge over others, especially in high Re flows which exceed the range of the presented study [8]. ELB also does not require any parameter tuning, unlike MRT, which makes its use easier for the end user. Similarly, RLB also did not appear to have an edge over other methods, apart from great stability, but like ELB it involves no parameter tuning, and it is (in these authors’ humble opinion) even simpler to implement. Also surprising is poor stability of TRT at Re$_{\mathrm{bm}} = 100$ that caused the need to use a different $\varLambda$ in this case. The instability developed from the inlet boundary condition (data not shown), which suggests its poor compatibility with TRT. Among the collision models, there is no clear-cut winner in this application.

The flow around a confined cylinder was studied and compared to diverse data from the literature, mainly data for an unconfined cylinder. For the purpose of these computations, the MRT collision model was used. Re$_{\mathrm{crit}}$ for the cylinder with the blockage ratio 0.125 was determined to be $55.0\pm 0.5$, which agrees with the earlier prediction from the literature. The results from the laminar and transition vortex shedding modes agree well with the literature. A correlation for St in $55 \le {\mathrm{Re}} \le 300$ was suggested.