Chemically reactive flow of upper-convected Maxwell fluid with Cattaneo–Christov heat flux model

Abstract

This attempt concentrates on impact of chemically reactive flow of upper-convected Maxwell liquid. Nonlinear slip condition for Maxwell fluid is employed. The processes of heat and mass transfer through theory of Cattaneo–Christov flux are studied. Ordinary differential systems have been considered. Convergent solutions are constructed for the governing equations. Incoming nonlinear modeled problems have been computed for the velocity, temperature and concentration. The impact of emerging variables, namely Deborah number (β), Schmidt number (Sc), Thermal relaxation parameter (γ), Prandtl number (Pr) and chemical reaction parameter (δ) on quantities of interest is graphically investigated. Both temperature and concentration fields decay when thermal relaxation and chemical reaction parameters are increased.

1 Introduction

There is a wide range of chemical reactions in nature which have widespread practical applications. These reactions are involved in various processes, especially in fog formation and dispersion, food processing, hydrometallurgical industry, air and water pollutions, atmospheric flows, fibers insulation and crops damage due to freezing, etc. In these processes the molecular diffusion of species on the boundary or inside the chemical reaction is very intricate. Some of the reactions have the capacity to proceed gradually or do not react at the moment without catalyst. In this direction Merkin [1] studied a model for isothermal homogeneous–heterogeneous reactions in boundary layer flow over a flat plate. Forced convection stagnation point flow of viscous fluid with homogeneous–heterogeneous reactions was explored by Chaudhary and Merkin [2]. Impact of nanoparticles in flow of viscous liquid with homogeneous/heterogeneous reactions is explored by Krishnamurthy et al. [3]. Khan and Pop [4] put forward such effects on the flow of viscoelastic fluid bounded a stretching sheet. The boundary layer flow of Maxwell fluid over a stretching surface with homogeneous–heterogeneous reactions was examined by Khan et al. [5]. The characteristics of homogeneous–heterogeneous reactions in the region of stagnation point flow of carbon nanotubes towards a stretching cylinder with Newtonian heating were also explored by Hayat et al. [6]. Analysis of homogeneous–heterogeneous reactions in slip flow of Casson liquid towards permeable stretched/shrinked surface is presented by Sheikh and Abbas [7]. Bachok et al. [8] reported heterogeneous–homogeneous reactions in stagnation-point flow towards a stretchable surface. Kameswaran et al. [9] discussed heterogeneous–homogeneous reactions in flow of nanomaterial induced by a permeable stretchable surface. Imtiaz et al. [10] addressed unsteady hydromagnetic flow past a curved stretchable surface subject to heterogeneous–homogeneous reactions. Recently Khan et al. [11] studied heterogeneous–homogeneous reactions in flow of viscous fluid in the presence of viscous dissipation and Joule heating. Hydromagnetic stagnation point flow of viscous liquid toward stretched–shrinked surface with slip condition and heterogeneous–homogeneous reactions is scrutinized by Abbas et al. [12]. Impact of nonlinear thermal radiation and induced magnetic field in flow of viscoelastic material with heterogeneous and homogeneous reactions is reported by Animasaun et al. [13]. Raju et al. [14] examined induced magnetic field effects in flow of Casson liquid with heterogeneous and homogeneous reactions. Qayyum et al. [15] examined heterogeneous–homogeneous reactions flow of silver-water and copper-water nanoparticles in the presence of nonlinear thermal radiation.

It is greatly acknowledged that in circumstances comprising extremely small times, maximal temperatures or thermal gradients nearby absolute zero, heat diffusion concept provided by Fourier becomes imprecise and non-Fourier consequence becomes decisive in characterizing the diffusion mechanism and anticipating temperature distribution. Practical prospects where deviance from the Fourier’s model turns noteworthy may be encountered, for example, in microelectronic materials including IC chips, heating of laser pulse with high heat flux or exceptionally short duration for hardening of semiconductors, impulse drying and laser surgery in biomedical engineering. Numerous investigations have been reported in order to present new formulation for heat conduction. For instance Straughan [16] disclosed thermal convection phenomenon utilizing non-Fourier heat conduction concept. Non-Fourier heat conduction effectiveness in stretching flow of Maxwell liquid is presented by Han et al. [17]. Waqas et al. [18] extended the idea presented in [17] considering temperature-dependent conductivity. Analysis of radiation and non-Fourier flux in differentially heated two-dimensional square cavity is developed by Sasmal and Mishra [19]. Chemical reaction and stagnation point characteristics in stratified variable thermal conductivity stretched flow of Eyring–Powell material in presence of non-Fourier heat conduction is explored by Hayat et al. [20]. Upper-convected Maxwell liquid flow with non-Fourier heat flux is studied by Saleem et al. [21]. Makinde et al. [22] presented magnetohydrodynamic flow over various geometries with Cattaneo–Christov heat flux.

The aforestated investigations witness that slip effects are not explored correctly. No doubt wall slip appears in complex liquids comprising suspensions, emulsions, foams and polymer analysis. The liquids which communicate boundary slip characteristics possess considerable demands in internal cavities and artificial heart valves [23]. MHD slip flow near a stagnation point in the presence of variable thicked surface is investigated by Khan et al. [24] and Babu and Sandeep [25]. Thermal radiation and mixed convection effects in stagnation point slipped flow of viscous liquid is explored by Rashad et al. [26]. Aly and Sayed [27] presented a comparative analysis considering four types of nanoparticles in MHD radiative stretched flow of viscous liquid. Simultaneous influences of mixed convection and magnetohydrodynamics in axisymmetric stretched flow of viscous material through slip effects and convective conditions are analyzed by Ganesh et al. [28]. Hayat et al. [29] established numerical solutions for radiative viscous nanomaterial considering melting effects.

It has been found from the existing information that mostly the flow of non-Newtonian fluid in the presence of slip condition valid for viscous fluid is considered. This is not correct. No doubt the stress in non-Newtonian material even for incompressible case is different than the viscous fluid. Thus, in reality the slip conditions for viscous and non-Newtonian fluids are distinct. Motivated in such fact our prime intention here was to report the slip effects in Maxwell material induced by stretchable surface. This model is capable of predicting relaxation time characteristics [30,31,32,33,34]. Polymer having low molecular weight is the best example for Maxwell material. Note that slip condition in viscous fluid is linear whereas it becomes nonlinear in Maxwell fluid situation. Also the generalized concept of heat and mass fluxes are imposed. Such concept has been used in view of Cattaneo–Christov theory. Another important feature is related to the consideration of stretching surface with chemical reaction. Besides this homotopy concept [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50] is implemented for arising nonlinear problems. Velocity, temperature and concentration are described for meaningful discussion considering important variables.

2 Formulation

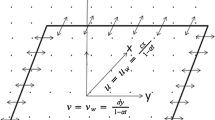
Let us consider flow of an incompressible Maxwell fluid over a stretching sheet with slip effect. Heat and mass fluxes have been characterized using Cattaneo–Christov theory. Further, we assume $T_{\text{w}}$ and $C_{\text{w}}$ as the temperature and concentration of stretched surface at $y = 0$ while $T_{\infty }$ and $C_{\infty }$ denote the ambient temperature and concentration. The present flow is governed by the following basic expressions:

$${\text{div}}\;{\mathbf{V}} = 0,$$

(1)

$$\rho \frac{{{\text{d}}{\mathbf{V}}}}{{{\text{d}}t}} = {\text{div}}\;\tau ,$$

(2)

$$\rho c_{p} \frac{{{\text{d}}T}}{{{\text{d}}t}} = \tau .{\mathbf{L - }}{\text{div}}\;{\mathbf{q}},$$

(3)

$$\frac{{{\text{d}}C}}{{{\text{d}}t}} = - {\mathbf{\nabla }}.{\mathbf{j}},$$

(4)

$${\mathbf{j}} = - D^{ * } {\mathbf{\nabla }}C.$$

(5)

Now (4) gives

$$\frac{{{\text{d}}C}}{{{\text{d}}t}} = D^{ * } {\mathbf{\nabla }}^{2} C,$$

(6)

in which C represents the concentration of species, D ^* the mass diffusivity and j the mass flux.

The Cauchy stress tensor for Maxwell fluid model is

$$\tau = - p{\mathbf{I + S}},$$

(7)

where the extra stress tensor ${\mathbf{S}}$ satisfies the following relation:

$${\mathbf{S + }}\lambda_{1} \frac{{D{\mathbf{S}}}}{Dt} = \mu {\mathbf{A}}_{1} ,$$

(8)

$${\mathbf{A}}_{1} = {\mathbf{L + L}}^{T} ,\, \, {\mathbf{L = \nabla V}}.$$

(9)

The velocity, temperature and concentration fields are

$$V = [u(x,\,y),\, \, v(x,\,y),\, \, 0],\, \, T = T(x,\,y),\, \, C = C(x,\,y).$$

(10)

The boundary layer equations now are

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$

(11)

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right),$$

(12)

with

$$u - ax + \lambda_{1} \left[ {u\frac{\partial u}{\partial x} - au + v\frac{\partial u}{\partial y}} \right] = \alpha \frac{\partial u}{\partial y},\, \, v = 0\quad {\text{at }}y = 0,$$

(13)

$$u \to 0\;{\text{when }}y \to \infty .$$

To study the characteristics of heat and mass transfer we have

$${\mathbf{q + }}\lambda_{2} \left( {\frac{{\partial {\mathbf{q}}}}{\partial t} + {\mathbf{v}}.\nabla {\mathbf{q - q}}.\nabla {\mathbf{v + }}\left( {\nabla .{\mathbf{v}}} \right)\,{\mathbf{q}}} \right) = - k\nabla T.$$

(14)

For λ ₂ = 0 the above equation reduces to Fourier law of heat conduction. For incompressible fluid $\nabla .{\mathbf{v = 0}}$ and then Eq. (14) gives

$${\mathbf{q + }}\lambda_{2} \left( {\frac{{\partial {\mathbf{q}}}}{\partial t} + {\mathbf{v}}.\nabla {\mathbf{q - q}}.\nabla {\mathbf{v}}} \right) = - k\nabla T.$$

(15)

The energy equation is

$$\rho c_{p} {\mathbf{v}}.\nabla T = - \nabla .{\mathbf{q}}.$$

(16)

Equations (15) and (16) yield

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + \lambda_{2} \left( {\begin{array}{*{20}c} {u^{2} \tfrac{{\partial^{2} T}}{{\partial x^{2} }} + v^{2} \tfrac{{\partial^{2} T}}{{\partial y^{2} }} + 2uv\tfrac{{\partial^{2} T}}{\partial y\partial x} +\, u\tfrac{\partial u}{\partial x}\tfrac{\partial T}{\partial x}} \\ { +\, u\tfrac{\partial v}{\partial x}\tfrac{\partial T}{\partial y} + v\tfrac{\partial u}{\partial y}\tfrac{\partial T}{\partial x} + v\tfrac{\partial v}{\partial y}\tfrac{\partial T}{\partial y}} \\ \end{array} } \right) = \frac{k}{{\rho c_{p} }}\frac{{\partial^{2} T}}{{\partial y^{2} }},$$

(17)

with boundary conditions

$$T = T_{w} \quad {\text{at}}\; \, y = 0,\quad T \to T_{\infty } \quad {\text{when}}\; \, y \to \infty .$$

(18)

The concentration equation is

$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D^{ * } \frac{{\partial^{2} C}}{{\partial y^{2} }} - K\left( {C - C_{\infty } } \right),$$

(19)

$$C = C_{\text{w}} \quad {\text{at}}\;y = 0,\quad C \to C_{\infty } \quad {\text{when}}\;y \to \infty .$$

(20)

Employing the transformations

$$\begin{aligned} u = & \frac{\partial \psi }{\partial y},\quad \upsilon = - \frac{\partial \psi }{\partial x},\quad \eta = y\sqrt {\frac{a}{\nu }} ,\quad \psi = x\sqrt {\nu a} f\left( \eta \right), \\ \theta = & \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\quad \varphi = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }}, \\ \end{aligned}$$

(21)

the mass conservation law (11) is identically fulfilled and Eqs. (12, 13, 17, 19, 20) are reduced to the forms:

$$f^{\prime \prime \prime } + f^{\prime 2} + ff^{\prime \prime } + \beta \left( {2ff^{\prime } f^{\prime \prime } - f^{2} f^{\prime \prime \prime } } \right) = 0,$$

(22)

$$\theta^{\prime \prime } + \mathop {Pr}\limits f\theta^{\prime } - \mathop {Pr}\limits \gamma \left( {ff^{\prime } \theta^{\prime } + f^{2} \theta^{\prime \prime } } \right) = 0,$$

(23)

$$\varphi^{\prime \prime } + Sc\left( {f\varphi^{\prime } - \delta \varphi } \right) = 0,$$

(24)

with

$$f\left( \eta \right) = 0,\quad f^{\prime}\left( \eta \right) = 1 - \beta \left[ {f^{\prime 2} - f^{\prime}} \right] + bf^{\prime\prime}\left( \eta \right),\quad \theta \left( \eta \right) = 1,\quad \varphi \left( \eta \right) = 1\quad {\text{at}}\;\eta = 0,$$

(25)

$$f^{\prime}\left( \eta \right) \to 0,\quad \theta \left( \eta \right) \to 0,\quad \varphi \left( \eta \right) \to 0\quad {\text{when}}\;\eta \to \infty .$$

(26)

The dimensionless variables are

$$\begin{aligned} \beta = & \lambda_{1} a,\quad \mathop {Pr}\limits = \frac{{\mu c_{p} }}{k},\quad \gamma = \lambda_{2} a,\quad b = \alpha \sqrt {\frac{a}{\nu }} , \, \\ Sc = & \frac{\nu }{{D^{ * } }},\quad \delta = \frac{K}{a}. \\ \end{aligned}$$

(27)

Homotopic solutions and convergence analysis.

We consider f(η), θ(η) and φ(η) via set of base functions

$$\left\{ {\eta^{k} \exp \left( { - n\eta } \right)\,k/k \ge 0,\, \, n \ge 0} \right\},$$

(28)

in the forms

$$f\left( \eta \right) = a_{0,\,0} + \mathop \sum \limits_{k = 0}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } a_{k,\,n} \eta^{k} \exp \left( { - n\eta } \right)$$

(29)

$$\theta \left( \eta \right) = \mathop \sum \limits_{k = 0}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } b_{k,\,n} \eta^{k} \exp \left( { - n\eta } \right)$$

(30)

$$\varphi \left( \eta \right) = \mathop \sum \limits_{k = 0}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } a_{k,\,n} \eta^{k} \exp \left( { - n\eta } \right),$$

(31)

where $a_{k,\;n} ,$ $b_{k,\,n}$ and $c_{k,\,n}$ are coefficients. Thus all the approximations of $f\left( \eta \right),$ $\theta \left( \eta \right)$ and $\varphi \left( \eta \right)$ must obey the above expressions. The initial approximations and operators are

$$\begin{array}{l} {f_{0} \left( \eta \right) = \tfrac{1}{1 + b}\left( {1 - \exp ( - \eta )} \right),} \\ {\theta_{0} \left( \eta \right) = \exp \left( { - \eta } \right),} \\ {\varphi_{0} \left( \eta \right) = \exp \left( { - \eta } \right),} \\ \end{array}$$

(32)

$${\mathbf{L}}_{f} \left( f \right) = \frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta^{3} }} - \frac{{{\text{d}}f}}{{{\text{d}}\eta }},\quad {\mathbf{L}}_{\theta } \left( \theta \right) = \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} - \theta ,\quad {\mathbf{L}}_{\varphi } \left( \varphi \right) = \frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}\eta^{2} }} - \varphi ,$$

(33)

with

$$L_{\text{f}} \left[ {C_{1} + C_{2} \exp (\eta ) + C_{3} \exp ( - \eta )} \right] = 0,$$

(34)

$${\mathbf{L}}_{\theta } \left[ {C_{4} \exp (\eta ) + C_{5} \exp ( - \eta )} \right] = 0,$$

(35)

$${\mathbf{L}}_{\varphi } \left[ {C_{6} \exp (\eta ) + C_{7} \exp ( - \eta )} \right] = 0,$$

(36)

in which $C_{i}$ $\left( {i = 1 - 7} \right)$ are the arbitrary constants.

The general solutions $\left( {f_{\text{m}} ,\;\theta_{\text{m}} \;{\text{ and}}\; \, \varphi_{\text{m}} } \right)$ in terms of special solutions $\left( {f_{m}^{ * } ,\, \, \theta_{m}^{ * } {\text{ and }}\varphi_{m}^{ * } } \right)$ are

$$f_{\text{m}} \left( \eta \right) = f_{\text{m}}^{*} \left( \eta \right) + C_{1} + C_{2} {\text{e}}^{\eta } + C_{3} {\text{e}}^{ - \eta } ,$$

(37)

$$\theta_{\text{m}} \left( \eta \right) = \theta_{\text{m}}^{*} \left( \eta \right) + C_{4} {\text{e}}^{\eta } + C_{5} {\text{e}}^{ - \eta } ,$$

(38)

$$\varphi_{\text{m}} \left( \eta \right) = \varphi_{\text{m}}^{*} \left( \eta \right) + C_{6} {\text{e}}^{\eta } + C_{7} {\text{e}}^{ - \eta } ,$$

(39)

where

$$\begin{aligned} C_{2} = \,& C_{4} = C_{6} = 0,\\C_{1} =\,& - \frac{1}{{\left( {1 + b} \right)}}\left( {\left. {\frac{{\partial f_{\text{m}}^{*} \left( \eta \right)}}{\partial \eta }} \right|_{\eta = 0} - b\left. {\frac{{\partial^{2} f_{\text{m}}^{*} \left( \eta \right)}}{{\partial \eta^{2} }}} \right|_{\eta = 0} } \right) - f_{\text{m}}^{*} \left( 0 \right), \\ C_{3} =\, & \frac{1}{{\left( {1 + b} \right)}}\left( {\left. {\frac{{\partial f_{\text{m}}^{*} \left( \eta \right)}}{\partial \eta }} \right|_{\eta = 0} - b\left. {\frac{{\partial^{2} f_{\text{m}}^{*} \left( \eta \right)}}{{\partial \eta^{2} }}} \right|_{\eta = 0} } \right),\quad C_{5} = - \theta_{\text{m}}^{ * } \left( \eta \right), \, \\ C_{7} =\, & - \varphi_{\text{m}}^{ * } \left( \eta \right). \\ \end{aligned}$$

(40)

The convergence of series solutions in HAM procedure is quite necessary. Such convergence analysis heavily depends upon the auxiliary variables $\hbar$. Thus $\hbar -$ curves for $f,$ $\theta$ and $\varphi$ have been displayed in Fig. 1. Figure clearly depicts that the acceptable ranges for values of $\hbar_{\text{f}} ,$ $\hbar_{\theta }$ and $\hbar_{\varphi }$ are $\left( { - 0.7 \le \hbar_{\text{f}} \le - 0.4,\; - 1.7 \le \hbar_{\theta } \le - 0.4\;{\text{and}}\; - 1.9 \le \hbar_{\varphi } \le - 0.8} \right)$.

Fig. 1

The $\hbar$-curves for $f^{\prime\prime}(0),$ $\theta^{\prime}(0)$ and $\varphi^{\prime}(0)$ when $\gamma = 0.2,$ $\beta = 0.3,$ $Pr = 1.2,\,\delta =$ $1,$ $b = 0.1$ and Sc = 1.2

3 Discussion

This portion presents the impacts of various pertinent parameters like Deborah number $(\beta ),$ thermal relaxation parameter $\left( \gamma \right),$ chemical reaction parameter $\left( \delta \right),$ Prandtl number $\left( {\Pr } \right),$ and Schmidt number $(Sc)$ on the non-dimensional velocity $f^{\prime}(\eta ),$ temperature $\theta (\eta )$ and concentration $\varphi (\eta ).$ Rheological behavior of Deborah number $\left( \beta \right)$ on the velocity $f^{\prime}(\eta )$ is presented in Fig. 2. It is observed that velocity $f^{\prime}(\eta )$ reduces with enhancement of Deborah number $\left( \beta \right).$ From a physical point of view when shear stress is eliminated fluid will come to rest. This sort of phenomenon is shown in many polymeric liquids that cannot be defined in the viscous fluid model. Higher estimation of Deborah number $\left( \beta \right)$ will produce a retarding force between two adjacent layers in the flow. Due to this fact there is a reduction in the velocity and associated layer thickness. The results of viscous fluid are obtained when $\beta = 0.$ Figure 3 is sketched for the effect of $(\gamma )$ on temperature $\theta (\eta ).$ It is scrutinized that temperature $\theta (\eta )$ shows recessive behavior for higher estimation of thermal relaxation parameter $\left( \gamma \right).$ It is found that larger values of $\gamma$ decreases both temperature field and thermal layer thickness. Physically for higher estimation of thermal relaxation parameter $\left( \gamma \right)$ a material requires more time to transfer heat from more energetic particles to low energetic particles, i.e., it demonstrates the features of a non-conducting material. Therefore, temperature $\theta (\eta )$ decays. Further, it is noted that for $\left( {\gamma = 0} \right)$ the heat transfers without any delay through the whole material. Thus temperature $\theta (\eta )$ dominants for Fourier law (i.e., for $\gamma = 0$) in comparison to Cattaneo–Christov heat flux model. Behavior of Prandtl number $\left( {\Pr } \right)$ on temperature $\theta (\eta )$ is examined in Fig. 4. Higher estimation of $Pr$ decays the temperature field and thermal layer thickness. It is due the fact that Pr is the combination of thermal diffusivity to momentum diffusivity. Therefore, small values of $Pr,$ $(Pr \ll 1)$ mean the thermal diffusivity dominates. For higher estimation of $Pr,$ $(Pr \gg 1)$ the momentum diffusivity dominates. Brownian diffusion coefficient decreases due to which concentration boundary layer is reduced. Influence of chemical reaction parameter $\left( \delta \right)$ on concentration $\varphi (\eta )$ is displayed in Fig. 5. As anticipated, a reduction in concentration $\varphi (\eta )$ is observed when the chemical reaction parameter $\left( {\delta > 0} \right)$ is increased. Figure 6 illustrates the behavior of Schmidt number $(Sc)$ on concentration $\varphi (\eta ).$ Ratio of viscous to molecular diffusion rate is known as Schmidt number. Larger viscous diffusion rate is observed when Schmidt number is increased and consequently fluid concentration enhances. Table 1 is constructed to show the order of convergence. $f^{\prime\prime}(0),$ $\theta^{\prime}(0)$ and $\varphi^{\prime}(0)$ converge at 15th and 16th order of approximations, respectively. To examine the correctness of flow problem, we have compared our results with the published results of Makinde et al. [51] in Table 2. The results are found in an excellent agreement.

Fig. 2

Variation of β for f′

Fig. 3

Variation of γ for θ

Fig. 4

Variation of Pr for θ

Fig. 5

Variation of δ for φ

Fig. 6

Variation of Sc for φ

Table 1 Series solutions convergence when $\gamma = 0.2,$ $\beta = 0.3,$ $Pr = 1.2,\,\delta = 1,$ $b = 0.1,$ $h = - 1.2$ and Sc = 1.2

Table 2 Comparative analysis of present results with [51] for distinct values of $Pr$ when γ = 0

4 Closing remarks

In this paper we employ the upper-convected Maxwell model and non-Fourier heat flux model to investigate heat and mass transfer above a stretching plate with velocity slip. The numerical results suggest the following:

• Velocity decays for higher estimation of $\beta .$

• Temperature field decreases for larger $Pr$ and $\gamma .$

• Both $\theta$ and $\varphi$ decay by increasing $\gamma$ and $\delta .$

• Concentration of fluid decreases for higher estimation of $Sc.$