GENERIC-compliant simulations of Brownian multi-particle systems: modeling stochastic lubrication

Abstract

A stochastic Lagrangian model for simulating the dynamics and rheology of a Brownian multi-particle system interacting with a simple liquid medium is presented. The discrete particle model is formulated within the GENERIC framework for Non-Equilibrium Thermodynamics and therefore it satisfies discretely the First/Second Laws of Thermodynamics and the Fluctuation Dissipation Theorem (FDT). Long-range fluctuating hydrodynamics interactions between suspended particles are described by an explicit solvent model. To this purpose, the Smoothed Dissipative Particle Dynamics method is adopted, which is a GENERIC-compliant Lagrangian meshless discretization of the fluctuating Navier–Stokes equations. In dense multi-particle systems, the average inter-particle distance is typically small compared to the particle size and short-range hydrodynamics interactions play a major role. In order to bypass an explicit—computationally costly—solution for these forces, a lubrication correction is introduced based on semi-analytical expressions for spheres under Stokes flow conditions. We generalize here the lubrication formalism to Brownian conditions, where an additional thermal-lubrication contribution needs to be taken into account in a way that discretely satisfies FDT. The coupled lubrication dynamics is integrated in time using a generalized semi-implicit splitting scheme for stochastic differential equations. The model is finally validated for a single particle diffusion as well as for a Brownian multi-particle system under homogeneous shear flow. Results for the diffusional properties as well as the rheological behavior of the whole suspension are presented and discussed.

1 Introduction

Particles suspended in liquids are ubiquitous in nature, with slurries, gels or pharmaceuticals as some common examples [21]. When the particle size starts to enter the sub-micrometer regime, thermal fluctuations of the surrounding environment start to play a relevant role, leading to an increased diffusional properties, i.e Brownian motion [8]. An accurate and efficient description of Brownian multi-particle systems is critical in many applications and the understanding of their dynamics and mechanical response is both of high scientific importance and industrial relevance [20]. In the context of microrheology [35], for example, it is possible to infer the non-Newtonian properties of suspending fluids and/or the heterogeneity of the microscopic environments, uniquely from the diffusional patterns of immersed nano-particles. More specifically, in terms of biomedical applications, intra-cellular microrheology [44] can allow to infer altered mechanical properties of the liquid environment which can define novel biomarkers to several pathologies [18]. On the other hand, in the context of material engineering, Brownian suspensions are generally characterized by a fluid’s viscosity that drops, a response known as “shear thinning” [29]. That rheology is engineered into a range of consumer products, from shampoos and paints to liquid detergents, to make them to flow easily under a weak stress [43]. Opposite shear-thickening can also occur at very high shear-rates as effects of short-range lubrications [43] and contact forces [33].

When modelling Brownian particles immersed in a liquid medium, hydrodynamics, thermal fluctuations and mass diffusion needs to be consistently taken into account. There is a large number of numerical techniques that have allowed accurate simulations for these systems in the past, for which a complete review is out of the scope of this paper. Generally speaking, these techniques belong to two main classes: (a) implicit-solvent and (b) explicit-solvent methods [25]. In the first class, the solvent medium is not described, whereas the forces acting between suspended particles are obtained from Green’s function theory in the over-damped Stokes limit, leading to far-field Oseen or Rotne–Prager–Yamakawa hydrodynamics approximations. Brownian Dynamics [11] or Stokesian Dynamics techniques [4] are two popular examples of implicit solvers. Although being highly efficient, the application of these methods to more complex systems, e.g. arbitrary-shape particles, non-Newtonian solvent media or interaction with complex boundaries, is difficult.

In the second class of methods, as the word suggests, the liquid behavior is explicitly described in terms of extra computational degrees of freedoms. Forces and torques are then simply computed on-the-fly from the fluid phase and exerted on the dispersed solid phase. In this class we finds standard direct numerical simulations approaches for the discretization of the liquid phase such as Finite Elements methods [5], Finite Volumes methods [34], Lattice Boltzmann method [16] or Lagrangian particle-based techniques such as the Smoothed Particle Hydrodynamics [22] and Dissipative Particle Dynamics [15]. In the latter class of explicit schemes, a crucial modelling feature is related to the algorithm’s ability to accurately simulate fluid dynamics and thermal fluctuations at the same time, i.e the so-called Landau and Lifshitz Fluctuating Hydrodynamic (FH) regime [17]. Among several Brownian explicit solvers available on the markets, there is only a limited number of tools that have paid special attention to the exact (i.e. discrete¹) enforcement of thermodynamic properties. In fact, the direct incorporation of the FH equations in a standard discretization scheme, such as the finite element/volumes method [5] is not straightforward. In order to have the correct level of thermal fluctuations at all resolved scales, the FDT must be fulfilled at the discrete level (not only in the continuum limit) which is not generally the case [34]. In the Finite Volume-based scheme proposed by Donev et al. [7], for example, the Fluctuation–Dissipation Theorem was proved to be satisfied at the discrete level in virtue of the specific construction of the skew-adjoint relation between the discretized gradient and divergence operators.

Here we consider another Lagrangian stochastic particle solver, named Smoothed Dissipative Particle Dynamics (SDPD) [10, 12]. In SDPD, Lagrangian elements (i.e. fluid particles) are considered to computationally map the fluid domain, which interact via pair-wise repulsive, dissipative and random forces. The SDPD method is built within the so-called GENERIC framework (General Equation for Non-Equilibrium Reversible-Irreversible Coupling) [14] which allows to easily construct discrete models with a minimal set of geometrical constraints that enforce the Laws of Thermodynamics. In [39] it was shown that a stochastic SDPD formulation can be developed which describes the Fluctuating Hydrodynamics and, at the same time enjoys a number of physical features: (a) it conserves exactly (at the discrete level) the total energy of the system; (b) it has an entropy which, by construction, is a monotonically increasing function of time; (c) it satisfies discretely a Fluctuation–Dissipation Theorem; and (d) it posses fluctuations associated to the hydrodynamics variables which are distributed according to the equilibrium Boltzmann distribution. Moreover, in [39] it was also shown that in the limit of vanishing fluctuations the SDPD method can be interpreted as a specific Lagrangian meshless discretization of the deterministic Navier–Stokes equations, i.e. linking it to the Smoothed Particle Hydrodynamics (SPH) method. The comparison of the GENERIC-derived particle model with SPH is precisely needed to determine the explicit expressions of the amplitudes of the thermal noise which, in turn, produce a consistent SDPD discretization of the FH with prescribed input transport coefficients. All these features make it a suitable numerical tool to study flow problems under Brownian conditions.

In relation to solid particles immersed in liquid, in [3] it was shown that hydrodynamic interactions between suspended solid Brownian particles are correctly captured by the SDPD technique as long as the flow is fully resolved. In more exact terms, by considering two moving solid particles of radii a, placed at a center-to-center distance d, forces and correlations mediated by the interstitial fluid are correctly captured as long as the the numerical SDPD resolution is sufficiently large (i.e. the SDPD fluid particle size dx $\ll s=d-2a$, being s the gap length between their surfaces). On the other hand, if the gaps size $s\rightarrow d$x the problem is numerically under-resolved and hydrodynamic interactions are incorrect. In order to bypass this problem, in [2, 26, 41] we have incorporated a pairwise short-range lubrication contributions which “corrects” for the lack of numerical resolution when two solid particles becomes too close (i.e. for $s\approx d$x). The method has been shown to accurately reproduce the dynamics of two-mutually interacting non-Brownian particles as well as the dissipative response of a many-particle system [37].

In the present paper, we generalize the above-mentioned methodology to Brownian regimes, by extending the lubrication corrections to the stochastic case. Since lubrication leads to irreversible dissipative forces, they need also to satisfy FDT at the discrete level. We show here how a general stochastic lubrication model can be formulated in a way that complies precisely with GENERIC. The coupled lubrication dynamics is integrated in time using a generalized semi-implicit splitting schemes for stochastic differential equations, in the spirit of [19]. The resulting stochastic SDPD model allows to correctly reproduce fluctuating hydrodynamic interactions in a dense Brownian many-particle systems, from far-field to short-range conditions, in a way that is fully GENERIC compliant. The model is finally validated in a number of Brownian flow conditions including particle diffusion and Brownian suspension rheology, and the results discussed in relation with established data form literature.

2 The Brownian multi-particle model

2.1 The GENERIC framework

In this section we present a brief review of the GENERIC formalism [14]. Let’s consider a system with a vector of relevant variables $\varvec{x}$, a total energy E and a total entropy S. According to the GENERIC formalism, the deterministic part of the dynamics reads

$$\begin{aligned} \frac{d\varvec{x}}{dt}= & {} \varvec{L}\cdot \frac{\partial E}{\partial \varvec{x}} + \varvec{M}\cdot \frac{\partial S}{\partial \varvec{x}} \end{aligned}$$

(1)

Both entropy and energy of the system are functions of the relevant variables. The first term of the right hand side is corresponding to the reversible part of the dynamics of the system, while the second term is describing the irreversible part. $\varvec{L}$ and $\varvec{M}$ matrices must satisfy some properties: $\varvec{L}$ is antisymmetric and $\varvec{M}$ is symmetric and positive-definite. The next degeneration conditions must be held in order to fulfill the first and second Laws of Thermodynamics ($\dot{E} = 0$ and $\dot{S}\ge 0$), respectively:

$$\begin{aligned} \varvec{L}\cdot \frac{\partial S}{\partial \varvec{x}}= & {} 0 \nonumber \\ \varvec{M}\cdot \frac{\partial E}{\partial \varvec{x}}= & {} 0 \end{aligned}$$

(2)

If there were other dynamic invariants $I(\varvec{x})$ of the system, two more conditions should be considered

$$\begin{aligned} \frac{\partial I}{\partial \varvec{x}}\cdot \varvec{L}\cdot \frac{\partial E}{\partial \varvec{x}}= & {} 0 \nonumber \\ \frac{\partial I}{\partial \varvec{x}}\cdot \varvec{M}\cdot \frac{\partial S}{\partial \varvec{x}}= & {} 0 \end{aligned}$$

(3)

ensuring $\dot{I} = 0$.

Furthermore, if thermal fluctuations are relevant, instead of Eq. (1), the system dynamics follow the next stochastic differential equation

$$\begin{aligned} d\varvec{x}= & {} \left[ \varvec{L}\cdot \frac{\partial E}{\partial \varvec{x}} + \varvec{M}\cdot \frac{\partial S}{\partial \varvec{x}} + k_B\frac{\partial }{\partial \varvec{x}}\cdot \varvec{M}\right] dt + d\tilde{\varvec{x}} \end{aligned}$$

(4)

The stochastic term $d\tilde{x}$ is a linear combination of independent increments of the Wiener process, and satisfies the Itô rule

$$\begin{aligned} d\tilde{\varvec{x}}d\tilde{\varvec{x}}^T = 2k_B\varvec{M}dt \end{aligned}$$

(5)

where $k_B$ is the Boltzmann’s constant and Eq. (5) represents the Fluctuation–Dissipation Theorem. Note that this equation implies that matrix $\varvec{M}$ is symmetric and positive-definite. Another way to write the stochastic term is

$$\begin{aligned} d\tilde{\varvec{x}}^{\mu }= & {} \varvec{b}^{\mu \nu }(\varvec{x})d\varvec{W}^{\nu } \end{aligned}$$

(6)

where superindices refer to tensorial components, and where the noises $d\varvec{W}$ hold the mnemothecnical Itô rule

$$\begin{aligned} d\varvec{W}^{\mu }d\varvec{W}^{\nu } = \delta ^{\mu \nu } dt \end{aligned}$$

(7)

With this definition, matrix $\varvec{M}$ can be written as

$$\begin{aligned} \varvec{M}^{\mu \nu }= & {} \frac{1}{2k_B}\varvec{b}^{\mu \nu '}\varvec{b}^{\nu \nu '} \end{aligned}$$

(8)

When thermal fluctuations are considered, there is a stronger requirement than Eq. (2) to ensure that the total energy and the invariants do not change during the evolution of the system:

$$\begin{aligned} \frac{\partial E}{\partial \varvec{x}}\cdot d\tilde{\varvec{x}}= & {} 0 \nonumber \\ \frac{\partial I}{\partial \varvec{x}}\cdot d\tilde{\varvec{x}}= & {} 0 \end{aligned}$$

(9)

These equations represent a minimal guide to embed 1st and 2nd Laws of Thermodynamics and incorporate thermal noise in new models, and they can be explained in geometrical language. For example, considering the first equation, $E(\varvec{x}) = E_T$ can be seen as the hyper-surface of points of space defined by coordinates $\varvec{x}$, where the system has a total energy equal to $E_T$. Derivative $\frac{\partial E}{\partial \varvec{x}}$ of the total energy E respect to the relevant variables $\varvec{x}$, is a normal vector to such a hyper-surface, and Eq. (9) requires that infinitesimal movements of the system in this space (e.g. due to thermal fluctuations) must be tangent to the hyper-surface in order to conserve total energy. The same holds for further invariants.

2.2 SDPD model for the liquid medium

In this section we summarize the main results of the SDPD method for the thermodynamically-consistent discretization of the Fluctuating Hydrodynamics. For a recent overview of the technique the reader is referred to [10]. A set of computational fluid particles labelled by Latin indices $i,j=1,\ldots ,N$, will be considered here which is homogeneously distributed in the liquid domain. Positions are denoted by $\varvec{r}_i$, momenta by $\varvec{p}_i$ and entropies $s_i$, masses $m_i$ and temperatures $T_i$. In [12] it was shown that the geometrical set of equations for the irreversible dynamics of a discrete particle system obtained via GENERIC can be expressed as:

$$\begin{aligned} d{\varvec{r}}_i\arrowvert _{irrev}= & {} 0 \nonumber \\ d{\varvec{p}}_i\arrowvert _{irrev}= & {} -\left( \sum _j\left[ a_{ij}\varvec{v}_{ij}+ \left[ a_{ij}\left( 1-\frac{2}{D}\right) +b_{ij}\right] \varvec{e}_{ij}\varvec{e}_{ij}\cdot \varvec{v}_{ij}\right] \right) dt + d\tilde{\varvec{p}}_i\nonumber \\ d{s}_i\arrowvert _{irrev}= & {} - \left( \sum _j c_{ij}T_{ij} + \frac{1}{2}\sum _j\left[ a_{ij}v_{ij}^2 + a_{ij}\left( 1-\frac{2}{D}\right) +b_{ij}\right] \left( \varvec{v}_{ij}\cdot \varvec{e}_{ij}\right) ^2 \right) dt \nonumber \\&+ T_id\tilde{s}_i \end{aligned}$$

(10)

being dt a discrete time step, $\varvec{e}_{ij}=\left( \varvec{r}_i - \varvec{r}_j\right) /\left| \varvec{r}_i - \varvec{r}_j\right|$ and $\varvec{v}_{ij} = \varvec{v}_i - \varvec{v}_j$, being $\varvec{v}_i = \varvec{p}_i / m_i$ the velocity of the i particle. The term $T_{ij}$ is the difference of temperatures $T_i-T_j$ and $a_{ij}$, $b_{ij}$ and $c_{ij}$ are suitable coefficients that will be linked to fluid properties. The stochastic terms have been postulated to be of the form

$$\begin{aligned} d\tilde{\varvec{p}}_i = \sum _j d\tilde{\varvec{p}}_{ij} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, T_id\tilde{s}_i = \sum _jd\tilde{\epsilon }_{ij}+\sum _jd\tilde{q}_{ij} \end{aligned}$$

(11)

where $d\tilde{\varvec{p}}_{ij}=-d\tilde{\varvec{p}}_{ji}$, $d\tilde{q}_{ij} = -d\tilde{q}_{ji}$ and $d\tilde{\epsilon }_{ij}=-d\tilde{\epsilon }_{ji}$ represent spontaneous momentum and heat exchanges between particles i and j caused by a thermal fluctuation and are defined as

$$\begin{aligned} d\tilde{\varvec{p}}_{ij}= & {} \left( A_{ij}d\overline{\varvec{W}}_{ij} + B_{ij} \frac{\varvec{1}}{D}\text {tr}\left[ d\varvec{W}_{ij}\right] \right) \cdot \varvec{e}_{ij}\nonumber \\ d\tilde{\epsilon }_{ij}= & {} -\frac{1}{2} \left( A_{ij}d\overline{\varvec{W}}_{ij} + B_{ij} \frac{\varvec{1}}{D}\text {tr}\left[ d\varvec{W}_{ij}\right] \right) : \varvec{e}_{ij}\varvec{v}_{ij} \nonumber \\ d\tilde{q}_{ij}= & {} C_{ij}dV_{ij} \end{aligned}$$

(12)

being D the number of dimensions and $\varvec{1}$ the identity matrix. Term $dV_i$ is an independent increment of the Wiener process and $d\varvec{W}_{ij}$ is a matrix of independent increments of the Wiener processes which satisfy the following Itô mnemotechnical rules

$$\begin{aligned} d\varvec{W}_{ii'}^{\alpha \alpha '}d\varvec{W}_{jj'}^{\beta \beta '}= & {} \left[ \delta _{ij}\delta _{i'j'}+\delta _{ij'}\delta _{j'i}\right] \delta ^{\alpha \beta } \delta ^{\alpha '\beta '} dt \nonumber \\ dV_{ii'}dV_{jj'}= & {} \left[ \delta _{ij}\delta _{i'j'}-\delta _{ij'}\delta _{j'i}\right] dt \nonumber \\ dV_{ii'}d\varvec{W}_{jj'}^{\alpha \alpha '}= & {} \varvec{0}^{\alpha \alpha '} \end{aligned}$$

(13)

where $\delta$ is the Kronecker delta and Greek superindices here refer to tensorial components.

Finally, the matrix $d\overline{\varvec{W}}_{ij}$ in Eq. (12) is a traceless symmetric matrix given by

$$\begin{aligned} d\overline{\varvec{W}}_{ij}= & {} \frac{1}{2}\left( d\varvec{W}_{ij} + d\varvec{W}_{ij}^T\right) -\frac{\varvec{1}}{D}\text {tr}\left( d\varvec{W}_{ij}\right) \end{aligned}$$

(14)

and the terms $A_{ij}$, $B_{ij}$ and $C_{ij}$ appearing in Eq. (12) are the thermal noise amplitudes.

It is simple to show that, by defining the irreversible matrix according to the dyadic product Eq. (5) with the general noise terms in Eq. (12), the discrete irreversible dynamics obtained via GENERIC is precisely that reported in Eq. (10). However, this is is true only if the following matching of coefficients is considered

$$\begin{aligned} a_{ij} = \frac{A_{ij}^2}{8k_B}\left( \frac{1}{T_i}+\frac{1}{T_j}\right) \,\,\,\,\,\,\, b_{ij} = \frac{A_{ij}^2}{4Dk_B}\left( \frac{1}{T_i}+\frac{1}{T_j}\right) \,\,\,\,\,\,\, c_{ij} = \frac{C_{ij}^2}{2k_BT_iT_j} \end{aligned}$$

(15)

which correspond to the discrete SDPD Fluctuation Dissipation Theorem. In virtue of the compliance with GENERIC, this geometrical structure of the particle equations enforces automatically: (a) the conservation of the total and local linear momentum; (b) the conservation of the total energy; (c) the monotonic time increase of the total entropy; (d) the Boltzmann distribution of the thermal fluctuations; and (e) the validity of the Fluctuation Dissipation Theorem at the discrete level. For further details the reader is referred to [10, 12].

Note that Eq. (10) describes a general stochastic dissipative model for “particles” where no link has been established yet with fluid mechanics. Such a general structure can be compared to different particle-based discretizations of the non-isothermal Navier–Stokes equations, such as the Smoothed Particle Hydrodynamics [10, 12] or the mesoscopic Voronoi method [32] in order to obtain specific expressions of the amplitudes of the thermal noise and, consequently, a related irreversible dynamics. If a SPH model is chosen, the governing equations are given by [12]

$$\begin{aligned} \dot{\varvec{r}}_i= & {} \varvec{v}_i \nonumber \\ \dot{\varvec{p}}_i= & {} -\sum _j \left[ \frac{P_i}{d_i^2}+ \frac{P_j}{d_j^2}\right] W'_{ij}\varvec{e}_{ij} + \sum _j\frac{1}{r_{ij}} \frac{W'_{ij}}{d_id_j}\left( a\varvec{v}_{ij}+ b\varvec{e}_{ij}\varvec{e}_{ij}\cdot \varvec{v}_{ij}\right) \nonumber \\ \dot{s}_i= & {} 2\kappa \sum _j\frac{1}{r_{ij}}\frac{W'_{ij}}{d_id_j} T_{ij}-\frac{1}{2} \sum _j\frac{1}{r_{ij}} \frac{W'_{ij}}{d_id_j}\left( a v_{ij}^2+ b\left( \varvec{e}_{ij}\cdot \varvec{v}_{ij}\right) ^2\right) \end{aligned}$$

(16)

where a and b are transport coefficients related to the shear and bulk viscosities $\eta _s$ and $\zeta _s$ as

$$\begin{aligned} a = \frac{5\eta _s}{3}-\zeta _s, \,\,\,\,\, b = 5\left( \frac{\eta _s}{3} + \zeta _s\right) \end{aligned}$$

(17)

The terms $P_i$ correspond to pressure contributions associated to the particle i and can be defined based on local fluid densities (see Eq. (21) below). Note that the pressure forces appearing in the first summation on the r.h.s. of Eq. (16) represent a reversible contribution and they can be also derived through the GENERIC route by considering the generalized derivative of the energy function in Eq. (1). For further details the reader is referred to [10]. For the moment, it is sufficient to notice that these pressure forces are anti-symmetric by swapping particle index ($i \leftrightarrow j$) and therefore they preserve the linear and angular momentum locally.

The coefficient $\kappa$ is the thermal conductivity coefficient of the fluid. The SPH kernel $W_{ij} = W(r_{ij})$ is a normalized interpolation bell-shaped function with compact support of size $r_{cut}$, and $W'_{ij}=\partial W(r,r_{cut})/\partial r|_{r=r_{ij}}$ is its derivative. The quantity $d_i$ is the particle number density, related to the particle volume $\mathcal {V}_i$ as

$$\begin{aligned} d_i= & {} \frac{1}{\mathcal {V}_i} = \sum _j W\left( r_{ij}\right) \end{aligned}$$

(18)

The comparison with the GENERIC model allows to find the noise amplitudes which in this case read specifically

$$\begin{aligned} A_{ij}^2= & {} -8k_B\frac{T_iT_j}{T_i+T_j}a\frac{1}{r_{ij}}\frac{W'_{ij}}{d_id_j} \nonumber \\ B_{ij}^2= & {} -4Dk_B\frac{T_iT_j}{T_i+T_j}\left( b+a\left( \frac{2}{D}-1\right) \right) \frac{1}{r_{ij}}\frac{W'_{ij}}{d_id_j} \nonumber \\ C_{ij}^2= & {} -4\kappa k_B T_iT_j\frac{1}{r_{ij}}\frac{W'_{ij}}{d_id_j} \end{aligned}$$

(19)

Summarizing: Eq. (16) with the stochastic terms provided in Eqs. (11), (12) and the noise amplitudes given in Eq. (19), represent a GENERIC-compliant SDPD discretization of the the non-isothermal fluctuating Navier–Stokes equations [17].

It should be highlighted that Eq. (16) do not generally conserve the total angular momentum, due to the presence of the term proportional to $\varvec{v}_{ij}$ in the viscous inter-particle forces. Although it is possible to consider additional evolution equations for the particle spins [24], another simple way to restore angular momentum conservation is by an appropriate selection of the bulk viscosity to constrain the inter-particle forces to be central. This can be done by taking $\zeta _s = \frac{5}{3}{\eta _s}$. With this specific choice, the final governing equation for the momentum yields

$$\begin{aligned} d\varvec{p}_i= & {} \left[ - \sum _j \left[ \frac{P_i}{d_i^2} +\frac{P_j}{d_j^2}\right] \,W'_{ij}\varvec{e}_{ij} + 10\eta _s \sum _j \frac{\varvec{e}_{ij}\cdot \varvec{v}_{ij}}{r_{ij}} \, \frac{W'_{ij}}{d_i d_j} \varvec{e}_{ij}\right] dt + d\tilde{\varvec{p}}_i \end{aligned}$$

(20)

In the isothermal conditions considered in this work, Eq. (20) will be considered, however more general non-equilibrium conditions can be modelled. Finally, the isotropic particle pressure $P_i$ is computed by using an equation of state [22]

$$\begin{aligned} P_i= & {} p_0\left[ \left( \frac{\rho _i}{\rho _0}\right) ^\gamma -1\right] \end{aligned}$$

(21)

where $\rho _i=m_i d_i$ is the local mass density, and $p_0$ and $\rho _0$ are reference pressure and reference density respectively. Speed of sound $c_s=\sqrt{\gamma p_0/\rho _0}$ is chosen sufficiently large compared to other characteristic velocities, therefore enforcing a weakly-compressible regime of operation.

Finally, temporal integration of the SPH equations for the matrix fluid is performed with a modified velocity-Verlet scheme [15]. For the weighting function W, the present work adopts a quintic spline kernel [23] with cutoff radius $r_{cut} = 4\,$dx (dx being the mean SDPD particle spacing) [9].

2.3 Fluid-particle interaction: long-range fluctuating hydrodynamics

Fig. 1

Sketch of the model for a solid particle suspended in a SDPD liquid. Computational particles forming the solid suspended bead have been drawn in white color. In the figure, the suspended solid particle is interacting with the surrounding fluid particles (in transparent blue color)

Fluid-structure interaction with suspended inclusions of arbitrary shapes can be modelled using boundary particles located inside a solid region [3, 41] (see Fig. 1). The no-slip boundary condition at the liquid-solid interface is enforced during each interaction between fluid particle and boundary particle by assigning an artificial velocity to the boundary particle, which satisfies zero interpolation at the interface [23]. Additional artificial penetration of SDPD fluid elements into the solid structure is avoided by means of specular reflection boundary conditions discussed in Sect. 2.6. Finally, once all fluid-boundary forces are defined, a total force $\varvec{F}^{\text {sph}}_{\alpha }$ and torque $\varvec{T}^{\text {sph}}_{\alpha }$ exerted by the surrounding fluid on a given solid sphere labelled ${\alpha }=1,\ldots ,N_c$ can be calculated and the corresponding coordinates updated as a rigid-body translation/rotation [37, 38] as

$$\begin{aligned} \dot{\varvec{R}}_\alpha= & {} \varvec{V}_\alpha \nonumber \\ M_\alpha \dot{\varvec{V}}_\alpha= & {} \varvec{F}^{\text {sph}}_{\alpha } \nonumber \\ I_\alpha \dot{\varvec{\omega }}_\alpha= & {} \varvec{T}^{\text {sph}}_{\alpha } \end{aligned}$$

(22)

where $M_\alpha$ is the mass of the solid particle $\alpha$, $\mathbf{R}_\alpha$ its center of mass position, $\mathbf{V}_\alpha$ its linear velocity, $\varvec{\omega }_\alpha$ the angular velocity and $I_\alpha$ its moment of inertia. In this way, the interaction of a suspended solid particle with its surrounding fluid medium, as well as with other solid particles located at “sufficiently large” distances, is accurately reproduced by the explicit SDPD stochastic model. The terminology “sufficiently large” here is considered in the sense that the local flow in the gaps between solid particles needs to be fully-resolved numerically, that is, the surface-to-surface gap size s must be sufficiently larger than the resolution length dx in the SDPD model. Although this computational requirement does not represent an issue for dilute systems (where solid inter-particle distances are typically large), it might pose notable numerical difficulties in dense many-particle systems where particles are frequently in near-contact.

2.4 Solid particle-particle interaction: short-range stochastic lubrication

As mentioned in the previous section, long-range stochastic hydrodynamic interactions between suspended solid particles are mediated by the SDPD fluid and are accurately described by Eq. (22). As discussed in [2, 37], in order to reproduce accurately the short-range hydrodynamic behavior however, viscous lubrication as well as short-range inter-particle repulsion models need to be considered. Short-range inter-particle repulsion forces prevent spurious inter-particle overlap and can be physically associated to molecular Van-der-Walls or steric surface interactions [21].

More tricky is the way in which short-range lubrication forces between suspended solid particles are formally introduced, since they are irreversible and therefore they need to follow the global GENERIC structure. As discussed above, when a fixed numerical resolution dx is considered , there will always exist a limiting small distance between close solid particles for which the shearing/squeezing flow in that liquid gap will be under-resolved. This problem can be solved in two ways: either (i) by dynamically and adaptively refining the local SDPD resolution in the gaps, as done in [36], with associated computational costs; or (ii) by introducing a sub-particle model handling the unresolved short-range hydrodynamic interactions implicitly. In the Stokes limit usually considered in Brownian systems, it is possible to work out analytical expressions for the lubrication forces acting between pairs of spheres in arbitrary relative motion. In particular, the normal and tangential lubrication forces acting between close spheres (i.e. at distances $s \ll a$; a particle radius) read

$$\begin{aligned} \varvec{F}_{\alpha \beta }^{\text {lub},n}(s\le s_c^n)= & {} f_{\alpha \beta }(s)\varvec{V}_{\alpha \beta }\cdot \varvec{e}_{\alpha \beta }\varvec{e}_{\alpha \beta } \nonumber \\ \varvec{F}_{\alpha \beta }^{\text {lub},t}(s\le s_c^t)= & {} g_{\alpha \beta }(s) \varvec{V}_{\alpha \beta }\cdot \left( \varvec{1} - \varvec{e}_{\alpha \beta }\varvec{e}_{\alpha \beta }\right) \end{aligned}$$

(23)

where $\varvec{e}_{\alpha \beta }=\varvec{R}_{\alpha \beta }/R_{\alpha \beta }$ is the vector joining the centers of mass of solid particles $\alpha$ and $\beta$, $\varvec{V}_{\alpha \beta }$ is their relative velocity and $s={R}_{\alpha \beta }-(a_\alpha +a_\beta )$ is the distance in the gap between sphere-sphere surfaces and $a_\alpha$ and $a_\beta$ are the sphere’s radii. $s_c^n$ and $s_c^t$ are the normal and tangential cutoff distances below which the lubrication corrections are applied and they depend on the SDPD resolution length. Above those distances, lubrication corrections vanish since the hydrodynamics is correctly captured by the explicit SDPD fluid model. Analytical expressions for the scalar functions $f_{\alpha \beta }(s)$ and $g_{\alpha \beta }(s)$ are given by [37]

$$\begin{aligned} f_{\alpha \beta }(s)= & {} -6 \pi \eta _s\left[ \left( \frac{a_\alpha a_\beta }{a_\alpha + a_\beta }\right) ^2\frac{1}{s} + a_{\alpha }\left( \frac{1+7\frac{a_\beta }{a_\alpha } + \left( \frac{a_\beta }{a_\alpha }\right) ^2}{5\left( 1+\frac{a_\beta }{a_\alpha }\right) ^3}\right) \text {ln}\left( \frac{a_\alpha }{s}\right) \right] \nonumber \\ g_{\alpha \beta }(s)= & {} -6\pi \eta _s a_{\alpha }\left[ \frac{4\frac{a_\beta }{a_\alpha } \left( 2 + \frac{a_\beta }{a_\alpha } + 2\left( \frac{a_\beta }{a_\alpha }\right) ^2\right) }{15\left( 1 + \frac{a_\beta }{a_\alpha }\right) ^3}\right] \text {ln}\left( \frac{a_\alpha }{s}\right) \end{aligned}$$

(24)

Note that lubrication forces are irreversible and as such, in order to fulfill the Fluctuation–Dissipation Theorem, an associated fluctuating term needs to be associated in a GENERIC-compliant way. In order to propose an expression for it, we rely on the general structure of the GENERIC particle model. Its irreversible part should be given by Eq. (10) which in the case of a solid particle considered here, can be rewritten as

$$\begin{aligned} d\varvec{P}_\alpha \arrowvert _{irr}= & {} -\sum _\beta \left[ a_{\alpha \beta } \varvec{V}_{\alpha \beta } + \left( a_{\alpha \beta }\left( 1-\frac{2}{D}\right) + b_{\alpha \beta }\right) \left( \varvec{e}_{\alpha \beta }\cdot \varvec{V}_{\alpha \beta }\right) \varvec{e}_{\alpha \beta }\right] dt + \sum _\beta d\tilde{\varvec{P}}_{\alpha \beta }\nonumber \\ \end{aligned}$$

(25)

where $a_{\alpha \beta }$ and $b_{\alpha \beta }$ are suitable transport coefficients and, analogously, the stochastic term $d\tilde{\varvec{P}}_{\alpha \beta }$ is given by

$$\begin{aligned} d\tilde{\varvec{P}}_{\alpha \beta }= & {} \left( A_{\alpha \beta } d\overline{\varvec{W}}_{\alpha \beta } + B_{\alpha \beta }\frac{\varvec{1}}{D} \text {tr}\left[ d\varvec{W}_{\alpha \beta }\right] \right) \cdot \varvec{e}_{\alpha \beta } \end{aligned}$$

(26)

where the noise amplitudes $A_{\alpha \beta }, B_{\alpha \beta }$ are related to $a_{\alpha \beta },b_{\alpha \beta }$ via

$$\begin{aligned} a_{\alpha \beta } = \frac{A_{\alpha \beta }^2}{4 k_B T} \,\,\,\,\,\,\,\, b_{\alpha \beta } = \frac{B_{\alpha \beta }^2}{2Dk_B T} \end{aligned}$$

(27)

In the specific case of the lubrication correction between solid particles, the change of momentum due to the lubrication interaction is given by

$$\begin{aligned} d\varvec{P}_{\alpha }^{lub}= & {} \sum _{\beta \in \text {solid}} \left( \varvec{F}_{\alpha \beta }^{lub,n}(s) + \varvec{F}_{\alpha \beta }^{lub,t}(s)\right) dt + \sum _{\beta \in \text {solid}}d\tilde{\varvec{P}}_{\alpha \beta }^{lub} \end{aligned}$$

(28)

where the last summation represents the overall contribution to the stochastic term on the dynamics of the solid particle $\alpha$ coming from short-range lubrication interactions with (nearly-touching) neighbors.² Note that recent experiments [27] showed that the lubrication interactions between two Brownian beads in near-contact follow strictly the expression given in Eqs. (23, 24), which were previously validated in our deterministic model in [37].

For a cleaner comparison with Eq. (62), Eq. (28) can be re-written as

$$\begin{aligned} d\varvec{P}_{\alpha \beta }^{lub}= & {} \sum _{\beta \in \text {solid}} \left[ g_{\alpha \beta }(s)\varvec{V}_{\alpha \beta } + \left( f_{\alpha \beta }(s) - g_{\alpha \beta }(s)\right) \left( \varvec{e}_{\alpha \beta }\cdot \varvec{V}_{\alpha \beta }\right) \varvec{e}_{\alpha \beta }\right] dt + \sum _{\beta \in \text {solid}}d\tilde{\varvec{P}}_{\alpha \beta }^{lub}\nonumber \\ \end{aligned}$$

(29)

where Eq. (23) have been used. As a result, the general terms $a_{\alpha \beta }$ and $b_{\alpha \beta }$ in Eq. (62) will correspond to

$$\begin{aligned} a_{\alpha \beta }= & {} -g_{\alpha \beta }(s) \nonumber \\ b_{\alpha \beta }= & {} -f_{\alpha \beta }(s) + 2g_{\alpha \beta }(s)\left( 1-\frac{1}{D}\right) \end{aligned}$$

(30)

in the case of solid particles interacting through lubrication. The corresponding thermal noise term will therefore read

$$\begin{aligned} d\tilde{\varvec{P}}_{\alpha \beta }^{lub}= & {} \left( \mathcal {A}_{\alpha \beta } d\overline{\varvec{W}}_{\alpha \beta } + \mathcal {B}_{\alpha \beta }\frac{\varvec{1}}{D} \text {tr}\left[ d\varvec{W}_{\alpha \beta }\right] \right) \cdot \varvec{e}_{\alpha \beta } \end{aligned}$$

(31)

where a matrix $\varvec{W}_{\alpha \beta }$ of independent increments of the Wiener process has been introduced for every pair of solid interacting particles. The traceless symmetric part $d\overline{\varvec{W}}_{\alpha \beta }$, again, reads

$$\begin{aligned} d\overline{\varvec{W}}_{\alpha \beta }= & {} \frac{1}{2} \left[ d\varvec{W}_{\alpha \beta } + d\varvec{W}_{\beta \alpha }\right] - \frac{\varvec{1}}{3}\text {tr}\left[ d\varvec{W}_{\beta \alpha }\right] \end{aligned}$$

(32)

with the new lubrication-noise amplitudes $A_{\alpha \beta }$ and $B_{\alpha \beta }$ defined as

$$\begin{aligned} \mathcal {A}_{\alpha \beta }= & {} \sqrt{-4k_BTg^*_{\alpha \beta }(s)} \nonumber \\ \mathcal {B}_{\alpha \beta }= & {} \sqrt{2Dk_BT\left[ -f^*_{\alpha \beta }(s)+2g^*_{\alpha \beta }(s) \left( 1-\frac{1}{D}\right) \right] } \end{aligned}$$

(33)

where

$$\begin{aligned} f^*_{\alpha \beta }(s)= & {} f_{\alpha \beta }(s)-f_{\alpha \beta }(s_c^n) \nonumber \\ g^*_{\alpha \beta }(s)= & {} g_{\alpha \beta }(s)-g_{\alpha \beta }(s_c^t) \end{aligned}$$

(34)

The previous stochastic differential equations need to be integrated in time and the resulting force contributions updated (in addition to the forces coming from the SDPD solvent) in the rigid-body translational/rotational solid particle dynamics. Details on the derivation of the irreversible lubrication matrix and related GENERIC building block are provided in Appendix A.

2.5 Splitting scheme for the stochastic lubrication

Since the lubrication forces are singular (they diverge as 1/s or $\text {ln}(1/s)$ for vanishing gaps, see Eq. 24), the integration problem becomes stiff and extremely small time steps are needed for tracking the dynamics of nearly-touching spheres. A very efficient semi-implicit splitting scheme similar to the one developed in [19, 26, 37] can be adapted here for taking into account the stochastic lubrication contribution in the many-particle system. The main idea is that for each solid particle $\alpha$ (instead of estimating the total stochastic lubrication force coming from all the neighboring solid particles and therefore integrating it explicitly on time), it is possible to split the problem in many simple two-body interaction problems and then solve them iteratively over all the pairs of solid particles. The efficiency of this strategy comes from two main ingredients: (i) the control on the overall threshold error and (ii) the possibility to solve the two-body problem analytically, in a way that no numerical matrix inversion is needed. The latter aspect makes the iteration procedure very fast [26].

More specifically, for every pair of solid particles $(\alpha ,\beta )$ the velocity at the step $n+1$ is given by

$$\begin{aligned} \varvec{V}_{\alpha }^{n+1}= & {} \varvec{V}_{\alpha }^{n} + \varvec{F}^{det}_{\alpha \beta }\frac{dt}{M_{\alpha }} + \frac{d\tilde{\varvec{P}}_{\alpha \beta }}{M_{\alpha }} \end{aligned}$$

(35)

where $\varvec{F}^{det}_{\alpha \beta }= \varvec{F}_{\alpha ,\beta }^{lub,n}+\varvec{F}_{\alpha ,\beta }^{lub,t}$ is the deterministic part of the lubrication correction force. Given that we are splitting the time step in $N_{sweep}$ parts (so $dt_{sweep} = dt/N_{sweep}$), the velocity $\overline{\varvec{V}}_\alpha$, after a time $dt_{sweep}$

$$\begin{aligned} \overline{\varvec{V}}_\alpha= & {} \varvec{V}_\alpha + \overline{\varvec{F}}^{det}_{\alpha \beta }\frac{dt_{sweep}}{M_\alpha } + \frac{d\tilde{\varvec{P}}_{\alpha \beta }}{M_\alpha N_{sweep}} \end{aligned}$$

(36)

The two-body system to solve therefore reads

$$\begin{aligned} \overline{\varvec{V}}_\alpha= & {} \varvec{V}_\alpha ' + \overline{\varvec{F}}_{\alpha \beta }^{det} \frac{dt_{sweep}}{M_\alpha } + \frac{d\tilde{\varvec{P}}_{\alpha \beta }}{M_\alpha }\frac{1}{N_{sweep}} \nonumber \\ \overline{\varvec{V}}_\beta= & {} \varvec{V}_\beta ' - \overline{\varvec{F}}_{\alpha \beta }^{det} \frac{dt_{sweep}}{M_\beta } - \frac{d\tilde{\varvec{P}}_{\alpha \beta }}{M_\beta }\frac{1}{N_{sweep}} \end{aligned}$$

(37)

where $\varvec{\varvec{V}}'$ and $\overline{\varvec{V}}$ represent the old and new velocities respectively. The solution of this system is similar to the one discussed in our previous work [37], by replacing $\varvec{V}_{\alpha \beta }'$ by $\varvec{V}_{\alpha \beta }'+\frac{1}{N_{sweep}}\left( \frac{1}{M_\alpha } + \frac{1}{M_\beta }\right) d\tilde{\varvec{P}}_{\alpha \beta }$, so that it finally reads

$$\begin{aligned} \overline{\varvec{V}}_{\alpha \beta }= & {} \left( \frac{1}{1-D_{\alpha \beta }}\right) \nonumber \\&\times \left( \varvec{V}_{\alpha \beta }'+\frac{1}{N_{sweep}}\left( \frac{1}{M_\alpha } + \frac{1}{M_\beta }\right) d\tilde{\varvec{P}}_{\alpha \beta }\right) \cdot \left[ \varvec{1} + \left( \frac{C_{\alpha \beta } - D_{\alpha \beta }}{1 - C_{\alpha \beta }}\right) \varvec{e}_{\alpha \beta }\varvec{e}_{\alpha \beta }\right] \qquad \end{aligned}$$

(38)

where

$$\begin{aligned} C_{\alpha \beta }= & {} f^*_{\alpha \beta } dt_{sweep} \left[ \frac{1}{M_{\alpha }} + \frac{1}{M_{\beta }}\right] \nonumber \\ D_{\alpha \beta }= & {} g^*_{\alpha \beta } dt_{sweep} \left[ \frac{1}{M_{\alpha }} + \frac{1}{M_{\beta }}\right] \end{aligned}$$

(39)

Given that linear momentum conservation must be held, individual velocities of the particles are finally calculated as

$$\begin{aligned} \overline{\varvec{V}}_{\beta } = \frac{M_{\alpha }\left( \varvec{V}'_{\alpha } - \overline{\varvec{V}}_{\alpha \beta } \right) + M_\beta \varvec{V}'_{\beta }}{M_{\alpha } + M_{\beta }}, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \overline{\varvec{V}}_{\alpha } = \overline{\varvec{V}}_{\alpha \beta } + \overline{\varvec{V}}_{\beta } \end{aligned}$$

(40)

The whole solution is obtained by iteratively solving the above equations for each interacting pair $(\alpha ,\beta )$. To maintain the accuracy of the method and its robustness at all particle configurations, a pseudo time step $dt_{sweep} = dt/N_{sweep}$ is used. Here, the number of sub-iteration $N_{sweep}$ is dynamically determined to ensure it is high enough to get convergence while simultaneously being sufficiently small to speed up the calculations. Beginning with a large default value for $N_{sweep}$ , at each time step say nth, two different sweeps are carried-out with $N_{sweep} = 2m$ and $N_{sweep} = 2m-1$. Then, the difference in the particles velocities are computed through an $L_2$ norm and compared against the value of a predefined tolerance $\epsilon$. For further details, the reader is referred to [19, 26].

Finally, the additional repulsive force acting between solid particles is introduced to prevent artificial particle overlap [2, 37] $\varvec{F}_{\alpha \beta }^{\text {rep}} = F^{\text {rep}} {\tau e^{-\tau s}}/{(1 - e^{-\tau s})}\varvec{e}_{\alpha \beta }$ where $\tau ^{-1}$ determines the interaction range and $F^{\text {rep}}$ its magnitude. In order to model nearly hard-spheres, typically values of $\tau ^{-1}=0.001a$ and $F^{\text {rep}}=21.15$ have been used [37]. In this work $\tau ^{-1} = 0.05$ is chosen, corresponding to slightly longer repulsive forces. Since this represents a reversible contribution, it will not alter the GENERIC structure and therefore no particular treatment is needed here (beside enforcing its anti-symmetric form for particle swap which leads to local momentum conservation). All inter-particle interactions are implemented within the so-called Parallel Particle Mesh library (PPM) [31], a Fortran 90 software layer between the Message Passing Interface (MPI) and Client Applications for simulations of physical systems using Particle-Mesh methods with optimal scaling performance.

2.6 Specular reflection boundary conditions

Due to the presence of thermal noise, the SDPD particles can occasionally penetrate the solid regions (e.g. solid walls or regions occupied by solid suspended particles) within one time step. In order to prevent it, specular reflection boundary conditions are applied [28]: when a fluid particle i is penetrating into a solid boundary, its velocity projection normal to the solid boundary is inverted:

$$\begin{aligned} \varvec{v}'_i=&\varvec{v}_i - 2 d\varvec{v}_i \end{aligned}$$

(41)

where $\varvec{v}_i$ is the velocity before the application of the specular reflection, $\varvec{v}'_i$ is the velocity after the reflection. In the case of rigid walls, we have

$$\begin{aligned} d\varvec{v}_i\arrowvert _{wall}= & {} \left( \varvec{v}_i - \varvec{V}_{wall}\right) \cdot \varvec{n}_{wall}\varvec{n}_{wall} \end{aligned}$$

(42)

being $\varvec{n}_{wall}$ the normal vector of the wall surface. Note that in the case of simple shear flow considered in Sect. 3, walls are moving tangentially to the fluid, so its velocity projected along its normal vector is identically zero.

In the case of a solid particle $\alpha$, its normal velocity $\varvec{V}_{\alpha }$ to the surface should be considered, in such a way that

$$\begin{aligned} d\varvec{v}_i\arrowvert _{part}= & {} \left( \varvec{v}_i - \varvec{V}_{\alpha }\right) \cdot \varvec{n}_{\alpha }\varvec{n}_{\alpha } \end{aligned}$$

(43)

being $\varvec{n}_{\alpha }$ the normal unit vector to the surface of the suspended solid particle $\alpha$ in the region where SDPD fluid particle i is penetrating.

If the solid boundary is represented by a moving solid particle, both linear and angular momentum transferred to the solid sphere should be considered. The change of linear momentum produced by the specular reflection of the SDPD fluid particle i is given by

$$\begin{aligned} \varDelta \varvec{p}_i\arrowvert _{part} = m_i\left( \varvec{v}'_i - \varvec{v}_i\right) = -2 m_i \left( \varvec{v}_i - \varvec{V}_{\alpha }\right) \cdot \varvec{n}_\alpha \varvec{n}_\alpha \end{aligned}$$

(44)

while the change of angular momentum is

$$\begin{aligned} \varDelta \varvec{L}_i = \left( \varvec{r}_i - \varvec{R}_\alpha \right) \times \varDelta \varvec{p}_i \end{aligned}$$

(45)

being $\varvec{r}_i$ the position of the fluid particle i and $\varvec{R}_\alpha$ the position of the center of the solid particle $\alpha$. As a results of the overall possible reflections with SDPD fluid particles, the solid particle $\alpha$ will change its velocity $\varvec{V}_\alpha$ according to

$$\begin{aligned} \varvec{V}'_\alpha = \varvec{V}_\alpha -\sum _i\frac{\varDelta \varvec{p}_i}{M_\alpha } \end{aligned}$$

(46)

where a summation over all penetrating fluid particles has been made. Similarly, the change on the angular velocity $\varvec{\omega }_\alpha$ of the solid particle should be corrected as

$$\begin{aligned} \varvec{\omega }'_\alpha = \varvec{\omega }_\alpha - \sum _i \frac{\varDelta \varvec{L}_i}{I_\alpha } \end{aligned}$$

(47)

where $I_\alpha$ is its moment of inertia. In this way discrete conservation of linear and angular momentum is preserved.

In the case of penetration into the walls, there is no need to consider the transfer of linear moment to simulate the dynamics, since in the shear-flow simulations of Sect. 3 the wall velocity is fixed and prescribed. However, since the suspension viscosity will be inferred from tangential forces acting on the wall, an accurate force estimate is required. The extra force $\varDelta \varvec{F}$ on the wall due to the specular reflection reads

$$\begin{aligned} \varDelta \varvec{F}_{wall}= & {} \sum _i \frac{\varDelta \varvec{p}_i}{dt} \end{aligned}$$

(48)

where the summation is over all penetrating fluid particles into the wall, dt is the time step, and

$$\begin{aligned} \varDelta \varvec{p}_i\arrowvert _{wall} = -2 m \left( \varvec{v}_i-\varvec{V}_{wall}\right) \cdot \varvec{n}_{wall} \varvec{n}_{wall} \end{aligned}$$

(49)

Other possible choices for the velocity boundary conditions in SDPD include bounce-back and Maxwellian reflections. For a more detailed discussion on the effect of the several boundary conditions on the dynamics, the reader is referred, for example, to [28].

3 Numerical results

In this section we validate the single and multi-particle Brownian systems by checking their diffusional properties (e.g. velocity probability distribution function, particle mean square displacement and diffusion coefficient) as well as the rheological properties (i.e. the relative suspension viscosity) of the whole Brownian suspension. Results are compared with established data from the literature and discussed.

3.1 Isolated Brownian particle: diffusional properties

In this section, we validate the single solid particle diffusion. We consider a cubic simulation box of side $L=10$ and a solid particle of radius $a=1$ placed at the center. Physical parameters are: $k_BT=10.0$, fluid density $\rho _0=1$, fluid viscosity $\eta _s=4$. Solid particle mass is $M=\rho _0 \frac{4}{3}\pi a^3 = 4.188$ and its thermal velocity is estimated as $V_{th}=\sqrt{k_BT/M}= 1.545$. Resolution is taken as 5 SDPD particles per radius of the solid particle (see Fig. 1), so the mean fluid particle spacing is dx$=0.2a$. SDPD particle mass is $m=\rho _0 d$x$^3 = 0.008$, leading to a SDPD fluid thermal velocity $v_{th}=\sqrt{k_BT/m}= 35.355$. The speed of sound is chosen $c_s=80$ larger than $V_{th}$ to enforce a quasi-incompressible regime. With these parameters, the following time scales can be defined as follows: the sonic time scale $t_s=a/c_s=0.0125$, the viscous time scale $t_\nu =a^2/\nu =0.25$ and the diffusive time scale $t_d=a^2/D_0= 7.5$, where $D_0=k_BT/(6 \pi \eta _s a)$ is the solid particle diffusion coefficient. It is clear that the correct hierarchy of time scales is enforced, that is: $t_s \ll t_v \ll t_d$, as physically required [40].

The total number of SDPD particles in the simulation box is $N=125,000$. Simulations are running until times $t \gg t_d$ to ensure the correct achievement of the diffusive regime. The time step was $dt=5\times 10^{-4}$.

Figure 2 shows the velocity statistics and mean square displacement of the solid particle defined as

$$\begin{aligned} \text{ MSD } = \varDelta \varvec{R}^2(t) = \langle | \varvec{R}(t)-\varvec{R}(0)|^2\rangle \end{aligned}$$

(50)

with the average being performed over multiple independent realizations. From Fig. 2 (left) it can be seen that the velocity probability distribution function match well the Maxwell-Boltzmann distribution in a given direction (x) at the prescribed temperature

$$\begin{aligned} f(v_x)=(m/2\pi k_B T)^{1/2} \exp \left( (- m v_x)^2/2 k_BT\right) \end{aligned}$$

(51)

This is accurately reproduced both, for the SDPD solvent particles as well as for the suspended solid sphere.

Figure 2 (right) shows the MSD with the two characteristic regimes: ballistic ($\sim t^2$) and diffusive ($\sim t$) at time scales, respectively, smaller and larger than the viscous time $t_\nu$. An estimate of the diffusion coefficient D for the particle can be inferred from the MSD, leading to a computed value $D= 0.1\pm 0.01$. Since we are using periodic boundary conditions, this value should be compared with the corrected diffusion coefficient $D=D_0 \lambda$ obtained by taking into account the effect of the periodic images of the solid particles. Here $D_0$ is the limiting value obtained from Stokes–Einstein theory, whereas the factor $\lambda$ reads [30]:

$$\begin{aligned} \lambda (\phi ) = \left[ 1 - 1.7601 \phi ^{1/3} + \phi - 1.5593 \phi ^{2} + 3.9799 \phi ^{8/3} - 3.0734 \phi ^{10/3} + {\mathcal {O}} (\phi ^{11/3}) \right] \nonumber \\ \end{aligned}$$

(52)

where $\phi = 4 \pi a^3/(3 L^3)$ is the effective spheres concentration in a periodic domain. This is also in good agreement with the correction proposed in [45] $\lambda (a,L) = (1 - 2.84 a/L)$. Considering that in the present simulation $\phi = 0.0041888$, this gives an analytical estimate of the effective diffusion coefficient $D=0.09555$ in good agreement with the numerical value.

Fig. 2

Left: velocity PDF of the SDPD solvent and the solid particle compared to theory. Right: MSD of the solid particle showing ballistic and diffusive regimes

3.2 Brownian multi-particle system: rheology

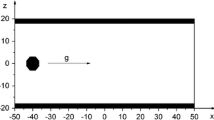
In this section we show results of the suspension viscosity for a mono-dispersed Brownian system and compare them with established data in a range of flow conditions and particle concentrations. To start, we define the concentration $\phi$ in the multi-particle system as

$$\begin{aligned} \phi= & {} \frac{4 N_c \pi a^3}{3 L^3} \end{aligned}$$

(53)

where a is the solid particle radius and $N_c$ is the total number of suspended solid particles. The system in this case is confined between two walls placed at a distance $L_z=10$ apart and moving in opposite directions $\pm V_{wall}$ (see Fig. 3). In this way a uniform linear velocity profile is generated within the suspension, characterized by a constant shear rate $\dot{\gamma }= 2 V_{wall}/L_z$. The shear rate provides a typical time scale of the flow denoted as $t_{f}=1/\dot{\gamma }$. In inertia-less Brownian systems, the other relevant physical time scale is the already defined viscous time $t_{d}=a^2/D_0$ associated to the diffusion of the solid particle. These two scales can be coupled together to define the so-called Péclet number

$$\begin{aligned} \text {Pe}= & {} \frac{t_{d}}{t_{f}}=\frac{a^2 \dot{\gamma }}{D_0} = \frac{6\pi \eta \dot{\gamma } a^3 }{k_B T} \end{aligned}$$

(54)

At small temperatures or large particle sizes, the diffusion is an extremely slow process, i.e. $t_{d}\gg t_{f} \rightarrow \text {Pe} \gg 1$ and the dynamics is governed by $t_{f}$. On opposite, for $\text {Pe}\ll 1$ the dynamics is governed by the particle diffusion. From the competition between these two time scales, a so-called “shear-thinning” rheological behavior for the suspension is typically observed where its viscosity generally shows a reduction trend for increasing Pe. At very large Pe, the viscosity shows a plateau corresponding to the deterministic limit, i.e. non-Brownian systems. However, depending on the specific short-range inter-particle forces, opposite shear-thickening can eventually sets in at large Pe. The effect is increased at large particle concentrations [13, 21]. In the next section we report the results for the suspension viscosity as a function of Pe and for two typical values of $\phi =0.1$ and $\phi =0.3$, respectively, in the semi-dilute and concentrated regimes. They correspond to systems with $N_c=24$ and $N_c=72$ suspended solid particles. In this section identical parameters to Sect. 3.1 are used. The Péclet number is modified by varying $V_{wall}$ in the range $\sim 0.066 - 66$.

3.2.1 Brownian suspension viscosity

Fig. 3

Sketch of the system considered in the rheology simulations. Computational SDPD particles forming the solid suspended beads have been drawn in white color, the walls in yellow and the solvent medium in transparent blue. A linear velocity profile is imposed and suspension viscosity extracted by measuring the force acting on the walls

In order to extract the viscosity from the simulations, we compute the wall shear stress from the total tangential force $\varvec{F}^{wall}$ exerted by the fluid and suspended solid particles on the walls. The component $\sigma _{xz}$ is related to the x component of $\varvec{F}^{wall}$ as $\sigma _{xz} ={F^{wall}_x}/{A}$ where A is the wall area. The total suspension viscosity for the given solid volume fraction $\phi$ finally yields

$$\begin{aligned} \eta (\phi )= & {} \frac{\sigma _{xz}}{\dot{\gamma }} = \frac{F^{wall}_x}{A\dot{\gamma }} \end{aligned}$$

(55)

The dimensionless relative suspension viscosity will be reported which is defined as $\eta _r(\phi )=\eta (\phi )/\eta _s$.

Fig. 4

Rheology of the Brownian suspension at two solid volume fractions: $\phi =0.1$ (semi-dilute regime: black) and $\phi =0.3$ (concentrated regime: red)

Figure 4 shows the relative suspension viscosity as a function of Pe for $\phi =0.1,0.3$. At low solid volume fraction ($\phi =0.1$, black points) no shear-thinning is observed with a constant value of $\eta _r\approx 1.3$ in excellent agreement with the theoretical result $\eta _r=1+2.5\phi +6.2 \phi ^2$ calculated by Batchelor [1] in the semi-dilute regime and previous numerical results [13] (dotted black line).

At larger solid volume fraction ($\phi =0.3$, red points) a marked shear-thinning behavior is observed. By fitting the relative suspension viscosity data with the following function

$$\begin{aligned} \eta _r({\text{ P }e})= & {} \eta _r^\infty + \frac{\eta _r^0 - \eta _r^\infty }{\left( 1 +\varGamma ^2 {\text{ P }e}^2 \right) ^{(1-n)/2}} \end{aligned}$$

(56)

the estimated values at low and large shear rates are, respectively, $\eta _r^0=3.83$ and $\eta _r^\infty =2.51$ which are in line with the values at $\phi =0.3$ obtained from the experimental correlations of de Kruif et al. [6] using a number of different Brownian samples, i.e. $\eta _r^0=3.24\pm 0.46$ and $\eta _r^\infty =2.77\pm 0.45$. Note that a mild shear-thickening sets-in at $Pe\approx 100$ in agreement with previous simulations results [13]. The present results show good agreement with experimental data and previous numerical calculations at the two given solid volume fractions and provide an indication on the accuracy of the present SDPD model for the simulation of Brownian multi-particle systems. More analysis is required to determine the effect of the rheometer gap-to-particle size ratio on the results as well as the repulsive parameter ($F_0$) and range of the repulsive forces ($\tau$), which is the matter of current numerical analysis.

4 Conclusions

In this work a stochastic Lagrangian model for simulating Brownian multi-particle systems interacting with a simple liquid medium is presented. The model is built within the framework of GENERIC and therefore it complies with the First and Second Laws of Thermodynamics and Fluctuation–Dissipation Theorem at the discrete level. More specifically, the model splits the description of hydrodynamic interactions between suspended particles in two parts: a far-field stochastic hydrodynamic contribution is taken into account by an explicit fluid model, namely the Smoothed Dissipative Particle Dynamics method which is a thermodynamically-consistent discretization of the fluctuating Navier–Stokes equations. Short-range hydrodynamics interactions are modelled by a generalization of the Lubrication Dynamics method and solved by a semi-implicit splitting procedure. The lubrication model is generalized to the stochastic case by incorporating the effect of a lubrication-induced thermal noise into the dynamics of closely interacting solid particles in a way that is GENERIC-compliant. Preliminary validations include Brownian diffusion as well as rheological response of a multi-particle system in the semi-dilute and concentrated regimes, showing good results.

Diffusivity analysis as well as rheological response in more concentrated systems is currently under work and should allow to validate the model in the highly-concentrated limit. Unlike other techniques such as Brownian Dynamics or Stokesian Dynamics, one of the benefits of the present SDPD-based model for Brownian suspensions is that, for example, the non-Newtonian properties of the liquid phase can be straightforwardly included. Viscoelasticity has been recently included in a GENERIC-compliant multi-particle model in the deterministic limit [42], and can be extended in the future to the stochastic regime of fluctuating viscoelasticity in a similar way to that proposed here.

Appendix A: Calculation of the GENERIC irreversible dynamics for a general particle model

In this appendix, the irreversible part of the equations of motion will be calculated. First, noises are introduced for the lubrication interaction between solid particles:

$$\begin{aligned} d\tilde{\varvec{P}}_\alpha= & {} \sum _\beta d\tilde{\varvec{P}}_{\alpha \beta } \nonumber \\ T_\alpha d\tilde{S}_\alpha= & {} \sum _\beta d\tilde{\mathcal {E}}_{\alpha \beta } + \sum _\beta d\tilde{Q}_{\alpha \beta } \end{aligned}$$

(57)

where the terms of spontaneous momentum transfer and heat fluxes between pairs of particles are postulated as follows

$$\begin{aligned} d\tilde{\varvec{P}}_{\alpha \beta }= & {} \left( \mathcal {A}_{\alpha \beta } d\overline{\varvec{W}}_{\alpha \beta } + \mathcal {B}_{\alpha \beta }\frac{\varvec{1}}{D}\text {tr} \left[ d\varvec{W}_{\alpha \beta }\right] \right) \cdot \varvec{e}_{\alpha \beta } \nonumber \\ d\tilde{\mathcal {E}}_{\alpha \beta }= & {} -\frac{1}{2}\left( \mathcal {A}_{\alpha \beta } d\overline{\varvec{W}}_{\alpha \beta } + \mathcal {B}_{\alpha \beta }\frac{\varvec{1}}{D}\text {tr} \left[ d\varvec{W}_{\alpha \beta }\right] \right) :\varvec{e}_{\alpha \beta } \varvec{V}_{\alpha \beta } \nonumber \\ d\tilde{Q}_{\alpha \beta }= & {} \mathcal {C}_{\alpha \beta }dV_{\alpha \beta } \end{aligned}$$

(58)

being $\varvec{W}_{\alpha \beta }$ a matrix of independent Wiener processes associated to particles $\alpha$ and $\beta$. The traceless symmetric part $d\overline{\varvec{W}}_{\alpha \beta }$ reads

$$\begin{aligned} d\overline{\varvec{W}}_{\alpha \beta }= & {} \frac{1}{2} \left[ d\varvec{W}_{\alpha \beta } + d\varvec{W}_{\beta \alpha }\right] - \frac{\varvec{1}}{3}\text {tr}\left[ d\varvec{W}_{\beta \alpha }\right] \end{aligned}$$

(59)

Note the similarity between these noise terms and the postulated ones for the model of liquid, Eqs. (11) and (12). The irreversible matrix M can be calculated via the dyadic product of the noise terms, Eq. (5), yielding

$$\begin{aligned} \varvec{M}_{\alpha \beta }= & {} \frac{1}{2 k_B T} \begin{pmatrix} \varvec{0} &{}&{} \varvec{0} &{}&{} \varvec{0} \\ \varvec{0} &{}&{} d\tilde{\varvec{P}}_\alpha d \tilde{\varvec{P}}_\beta &{}&{} d\tilde{\varvec{P}}_\alpha d\tilde{S}_\beta , \\ \varvec{0} &{}&{} d\tilde{S}_\alpha d\tilde{\varvec{P}}_\beta &{}&{} d\tilde{S}_\alpha d\tilde{S}_\beta \end{pmatrix}. \end{aligned}$$

(60)

The calculation of the irreversible matrix $\varvec{M}$ blocks leads to next equations

$$\begin{aligned} \varvec{M}_{\alpha \beta }^{pp}= & {} \frac{1}{2k_B} \left[ \delta _{\alpha \beta }\sum _{\gamma =1}^{N_F}\left( \frac{A_{\alpha \gamma }^2}{2} \left[ \varvec{1}+\varvec{e}_{\alpha \gamma }\varvec{e}_{\alpha \gamma }\right] + \left( B_{\alpha \gamma }^2-A_{\alpha \gamma }^2\right) \frac{\varvec{e}_{\alpha \gamma }\varvec{e}_{\alpha \gamma }}{D}\right) -\right. \nonumber \\&\left. \frac{A_{\alpha \beta }^2}{2} \left[ \varvec{1}+\varvec{e}_{\alpha \beta }\varvec{e}_{\alpha \beta }\right] - \left[ B_{\alpha \beta }^2-A_{\alpha \beta }^2\right] \frac{\varvec{e}_{\alpha \beta }\varvec{e}_{\alpha \beta }}{D}\right] \nonumber \\ \varvec{M}_{\alpha \beta }^{ps}=\varvec{M}_{\beta \alpha }^{sp}= & {} -\frac{\delta _{\alpha \beta }}{4k_BT_j}\sum _{\gamma =1}^{N_F}\left[ \frac{A_{\alpha \gamma }^2}{2}\left[ \varvec{v}_{\alpha \gamma } +\left( \varvec{e}_{\alpha \gamma }\cdot \varvec{v}_{\alpha \gamma }\right) \varvec{e}_{\alpha \gamma }\right] +\left( B_{\alpha \gamma }^2-A_{\alpha \gamma }^2\right) \frac{\left( \varvec{e}_{\alpha \gamma }\cdot \varvec{v}_{\alpha \gamma }\right) \varvec{e}_{\alpha \gamma }}{D} \right] \nonumber \\&-\frac{1}{4k_BT_j}\left[ \frac{A_{\alpha \beta }^2}{2}\left[ \varvec{v}_{\alpha \beta }+ \varvec{e}_{\alpha \beta }\left( \varvec{e}_{\alpha \beta } \cdot \varvec{v}_{\alpha \beta }\right) \right] + \left( B_{\alpha \beta }^2-A_{\alpha \beta }^2\right) \frac{\varvec{e}_{\alpha \beta }\left( \varvec{e}_{\alpha \beta } \cdot \varvec{v}_{\alpha \beta }\right) }{D} \right] \nonumber \\ \varvec{M}_{\alpha \beta }^{ss}= & {} \frac{\delta _{\alpha \beta }}{8k_BT_\alpha T_\beta }\sum _{\gamma =1}^{N_F}\left( \frac{A_{\alpha \gamma }^2}{2} \left[ \left( \varvec{v}_{\alpha \gamma }^2+ \left( \varvec{e}_{\alpha \gamma }\cdot \varvec{v}_ {\alpha \gamma }\right) ^2\right) \right] + \left( B_{\alpha \gamma }^2-A_{\alpha \gamma }^2\right) \frac{\left( \varvec{e}_{\alpha \gamma } \cdot \varvec{v}_ {\alpha \gamma }\right) ^2}{D}\right) \nonumber \\&+\frac{1}{8k_BT_\alpha T_\gamma }\left( \frac{A_{\alpha \beta }^2}{2} \left[ \left( \varvec{v}_{\alpha \beta }^2 + \left( \varvec{e}_{\alpha \beta }\cdot \varvec{v}_{\alpha \beta }\right) ^2\right) \right] + \left( B_{\alpha \beta }^2-A_{\alpha \beta }^2\right) \frac{\left( \varvec{e}_{\alpha \beta }\cdot \varvec{v}_ {\alpha \beta }\right) ^2}{D}\right) \nonumber \\&+\frac{1}{2k_BT_\alpha T_\beta }\left( \delta _{\alpha \beta }\sum _{\gamma =1}^{N_F}C_{\alpha \gamma }^2 -C_{\alpha \beta }^2\right) \end{aligned}$$

(61)

More details can be found in [12]. With this matrix $\varvec{M}$, the irreversible dynamics of the system can be finally calculated leading to the following equations of motion

$$\begin{aligned} d\varvec{P}_\alpha \arrowvert _{irr}= & {} -\sum _\beta \left[ a_{\alpha \beta } \varvec{V}_{\alpha \beta } + \left( a_{\alpha \beta }\left( 1-\frac{2}{D}\right) + b_{\alpha \beta }\right) \left( \varvec{e}_{\alpha \beta }\cdot \varvec{V}_{\alpha \beta }\right) \varvec{e}_{\alpha \beta }\right] dt + \sum _\beta d\tilde{\varvec{P}}_{\alpha \beta }.\nonumber \\ \end{aligned}$$

(62)