Truncation of tensors in the hierarchical format

Abstract

Tensors are in general large-scale data which require a special representation. These representations are also called a format. After mentioning the r-term and tensor subspace formats, we describe the hierarchical tensor format which is the most flexible one. Since operations with tensors often produce tensors of larger memory cost, truncation to reduced ranks is of utmost importance. The so-called higher-order singular-value decomposition (HOSVD) provides a save truncation with explicit error control. The paper explains in detail how the HOSVD procedure is performed within the hierarchical tensor format. Finally, we state special favourable properties of the HOSVD truncation.

1 Introduction

In the standard case, tensors of order d are quantities ${\mathbf {v}}$ indexed by d indices, i.e., the entries of ${\mathbf {v}}$ are ${\mathbf {v}}[i_{1} ,\ldots ,i_{d}],$ where e.g. all indices run from 1 to n. Hence the data size is $n^{d}.$ This shows that even number n and d of moderate size yield a huge value so that it is impossible to store all entries. Instead one needs some data-sparse tensor representation. In this paper we mention such representations. The optimal one is the hierarchical representation explained in Chapter 4. A slight generalisation is the tree-based format described in Falcó et al. [3].

Section 2 contains an introduction into tensor spaces and the used notation. We mainly restrict ourselves to the finite-dimensional case, in which we do not have to distinguish between the algebraic and topological tensor spaces. The latter tensor spaces are discussed in [3]. Since true tensor spaces—those of order $d\ge 3$—have less pleasant properties than matrices (which are tensors of order 2), one tries to interpret tensors as matrices. This leads to the technique of matricisation explained in Sect. 2.2. The range of the obtained matrices defines the minimal subspaces introduced in Sect. 2.3. The dimension of the minimal subspaces yields the associated ranks. The singular-value decomposition applied to the matricisations leads to the so-called higher-order singular-value decomposition (HOSVD) which will be important later. Finally, in Sect. 2.5, we discuss basis transformations.

In Sect. 3 we briefly discuss two classical representations of tensors: the r-term format (also called CP format) and the tensor subspace format (also called Tucker format). For the latter format the HOSVD is explained in Sect. 3.3: instead of applying HOSVD to the full tensor, we can apply it to the smaller core tensor. As a result of HOSVD we can introduce special HOSVD bases. These bases allow a simple truncation to smaller ranks (i.e., the data sparsity is improved; cf. Sect. 3.4).

Section 4 is devoted to the hierarchical tensor format. In principle it is a recursive application of the tensor subspace format. It is connected with a binary tree. The generalisation to a general tree yields the tree-based format in [3]. However, for practical reasons one should use a binary tree. a key point is the indirect coding of the bases discussed in Sect. 4.2. As a result only transfer matrices are stored instead of large-sized basis vectors. Basis transformations can be performed by simple matrix operations (cf. Sect. 4.3). Similarly, the orthonormalisation of the bases are performed by an orthonormalisation of the transfer matrices (cf. Sect. 4.4). The main challenge is the computation of the HOSVD bases. As demonstrated in Sect. 4.5 one can obtain these bases by singular-value decompositions only involving the transfer matrices. The corresponding truncation can be performed as in the previous chapter (cf. Sect. 4.6).

The SVD truncation to lower ranks can be regarded as a projection onto smaller subspaces. However, different from general projections, the SVD projection has particular properties which are discussed in the final Sect. 5. In Sect. 5.1 we consider the case of the tensor subspace representation of Sect. 3.2. It turns out that certain properties of the given tensor (e.g., side conditions or smoothness properties) are inherited by the projected (truncated) approximation. As proved in Sect. 5.2, the same statement holds for the best approximation in the format of lower ranks. Finally, this statement is generalised to the hierarchical tensor representation.

2 Tensor spaces

2.1 Definitions, notation

Let $V_{j}$ ($1\le j\le d$) be arbitrary vector spaces over the field $\mathbb {K},$ where either $\mathbb {K}=\mathbb {R}$ or $\mathbb {K}=\mathbb {C}.$ Then the algebraic tensor space ${\mathbf {V}}:=\left. _{a}\bigotimes _{j=1} ^{d}V_{j}\right.$ consists of all (finite) linear combinations of elementary tensors $\bigotimes _{j=1}^{d}v^{(j)}$ ($v^{(j)}\in V_{j}$). The algebraic definition of ${\mathbf {V}}$ and of the tensor product $\otimes :V_{1}\times \cdots \times V_{d}\rightarrow {\mathbf {V}}$ reads as follows (cf. Greub [4, Chap. I, §2]): Let U be any vector space over $\mathbb {K}$. Then, for any multilinear mapping $\varphi :V_{1}\times \cdots \times V_{d}\rightarrow U$, there exists a unique linear mapping $\,\varPhi :{\mathbf {V}}\rightarrow U\,$ such that $\varphi (v^{(1)},v^{(2)} ,\ldots ,v^{(d)})=\varPhi (\bigotimes _{j=1}^{d}v^{(j)})$ for all $\,v^{(j)}\in V_{j}.$

In the case of infinite-dimensional tensor spaces, one can equip the tensor space with a norm. The completion with respect to the norm $\left\| \cdot \right\|$ yields the topological tensor space $\left. _{\left\| \cdot \right\| }\bigotimes _{j=1}^{d}V_{j}\right.$ (cf. Hackbusch [5, § 4]). In this article, we restrict ourselves to the finite-dimensional case. Then the algebraic tensor space introduced above is already complete with respect to any norm and therefore it coincides with the topological tensor space. This fact allows us to avoid the affix ‘a’ in ${\mathbf {V}}=\left. _{a}\bigotimes _{j=1}^{d}V_{j}\right. .$ Instead, ${\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}$ is sufficient.

The simplest example of a tensor space is based on the vector spaces $V_{j}=\mathbb {K}^{n_{j}},$ where the vectors $v\in \mathbb {K}^{n_{j}}$ are indexed by $i\in I_{j}:=\{1,\ldots ,n_{j}\}.$ Instead of $\mathbb {K}^{n_{j}}$ we also write $\mathbb {K}^{I_{j}}.$ Then the elementary product ${\mathbf {v}} :=\bigotimes _{j=1}^{d}v^{(j)}$ is indexed¹ by d-tuples ${\mathbf {i}}\in {\mathbf {I}}:=I_{1}\times \ldots \times I_{d}$:

$$\begin{aligned} {\mathbf {v}}[{\mathbf {i}}]={\mathbf {v}}[i_{1},\ldots ,i_{d}]=\prod _{j=1}^{d} v^{(j)}[i_{j}]\qquad \text {for }{\mathbf {i}}=\left( i_{1},\ldots ,i_{d}\right) \in {\mathbf {I}}. \end{aligned}$$

(1)

Therefore the tensor space ${\mathbf {V}}$ is isomorphic to $\mathbb {K} ^{{\mathbf {I}}}.$

The second example is based on the matrix spaces $U_{j}=\mathbb {K} ^{m_{j}\times n_{j}}.$ Then the tensor space ${\mathbf {U}}:=\bigotimes _{j=1} ^{d}U_{j}$ can be interpreted as follows. Set ${\mathbf {V}}=\bigotimes _{j=1} ^{d}V_{j}$ with $V_{j}=\mathbb {K}^{n_{j}}$ as above, while ${\mathbf {W}} =\bigotimes _{j=1}^{d}W_{j}$ is generated by $W_{j}=\mathbb {K}^{m_{j}}.$ Matrices $M_{j}\in U_{j}$ define a linear map belonging to the vector space $L(V_{j},W_{j}).$ Now the elementary tensor ${\mathbf {M}}:=\bigotimes _{j=1} ^{d}M_{j}\in {\mathbf {U}}$ can be regarded as a linear map of $L({\mathbf {V}} ,{\mathbf {W}})$ defined by²

$$\begin{aligned} {\mathbf {M}}\left( \bigotimes _{j=1}^{d}v^{(j)}\right) =\bigotimes _{j=1} ^{d}\left( M_{j}v^{(j)}\right) \quad \text {for all } \, v^{(j)}\in V_{j}. \end{aligned}$$

(2)

The tensor product $\bigotimes _{j=1}^{d}M_{j}$ of matrices is also called the Kronecker product. In the finite-dimensional case, ${\mathbf {U}}$ coincides with $L({\mathbf {V}},{\mathbf {W}}).$

The definition of ${\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}$ by all linear combinations of elementary tensors ensures that any ${\mathbf {v}}\in {\mathbf {V}}$ has a representation

$$\begin{aligned} {\mathbf {v}}=\sum _{i=1}^{r}\bigotimes _{j=1}^{d}v_{i}^{(j)}\qquad (v_{i}^{(j)}\in V_{j}). \end{aligned}$$

(3)

The tensor rank of ${\mathbf {v}}$ is the smallest possible integer r in (3). It is denoted by ${\text {rank}}({\mathbf {v}}).$

If $d=2$ and $V_{j}=\mathbb {K}^{n_{j}},$ the tensor space ${\mathbf {V}} =V_{1}\otimes V_{2}$ is isomorphic to the matrix space $\mathbb {K} ^{n_{1}\times n_{2}}.$ The elementary tensor $v\otimes w$ corresponds to the rank-1 matrix $vw^{\mathsf {T}}.$ In this case the tensor rank coincides with the usual matrix rank.

$d=1$ is the trivial case where ${\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}$ coincides with $V_{1}.$ For $d=0,$ the empty product ${\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}$ is defined by the underlying field $\mathbb {K}.$

Remark 1

The dimension of ${\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}$ is $\dim ({\mathbf {V}})=\prod _{j=1}^{d}\dim (V_{j}).$ This fact implies that, e.g., $U\otimes V\otimes W,$ $\left( U\otimes V\right) \otimes W,$ $U\otimes \left( V\otimes W\right) ,$ and $\left( U\otimes W\right) \otimes V$ are isomorphic as vector spaces. Here $\left( U\otimes V\right) \otimes W$ is the tensor space of order 2 based on the vector spaces $X:=U\otimes V$ and W. However, these spaces are not isomorphic as tensor spaces. For instance they have different elementary tensors. ${\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}$ and ${\mathbf {W}}=\bigotimes _{j=1}^{d}W_{j}$ are isomorphic as tensor spaces if, for all $1\le j\le d,$ the vector spaces $V_{j}$ and $W_{j}$ are isomorphic.

2.2 Matricisation

Within the theory of tensor spaces, the matrix case corresponding to $d=2$ is an exceptional case. This means that most of the properties of matrices do not generalise to tensors of order $d\ge 3.$ An example is the tensor rank for $d\ge 3.$ In general its determination is NP hard (cf. Håstad [9]). Tensors in $\bigotimes _{j=1}^{d} \mathbb {R}^{n_{j}}$ can also be regarded as elements in $\bigotimes _{j=1} ^{d}\mathbb {C}^{n_{j}},$ but the corresponding tensor ranks may be different. Matrix decompositions like the Jordan normal form or the singular-value decomposition do not have an equivalent for $d\ge 3.$

To overcome these difficulties one may try to interpret tensors are matrices. According to Remark 1, for all $1\le j\le d,$ the tensor space ${\mathbf {V}}=\bigotimes _{k=1}^{d}V_{k}$ is isomorphic to

$$\begin{aligned} V_{j}\otimes V_{[j]},\qquad \text {where }V_{[j]}:=\bigotimes \nolimits _{k\ne j}V_{k}. \end{aligned}$$

Here $k\ne j$ means $k\in \{1,\ldots ,d\}\backslash \{j\}.$ The vector space isomorphism $\mathcal {M}_{j}:{\mathbf {V}}=\bigotimes _{k=1}^{d}V_{k}\rightarrow V_{j}\otimes V_{[j]}$ is defined by $\mathcal {M}_{j}(\bigotimes _{k=1} ^{d}v^{(k)})\mapsto v^{(j)}\otimes v^{[j]}$ with $v^{[j]}=\bigotimes _{k\ne j}v^{(k)}$ and called the j-th matricisation. In the case of $V_{k}=\mathbb {K}^{I_{k}},$ the image $\mathcal {M}_{j}({\mathbf {v}})$ of ${\mathbf {v}}\in {\mathbf {V}}$ is a matrix $M\in \mathbb {K}^{I_{j}\times {\mathbf {I}}_{[j]}}$ with ${\mathbf {I}}_{{[j]}} = {\times }_{{k \ne j}} I_{k}$

and the entries

$$\begin{aligned} M[i_{j},{\mathbf {i}}_{[j]}]={\mathbf {v}}[i_{1},\ldots ,i_{d}] \end{aligned}$$

for all $i_{j}\in I_{j}$ and ${\mathbf {i}}_{[j]}=(i_{1},\ldots ,i_{j-1} ,i_{j+1},\ldots ,i_{d})\in {\mathbf {I}}_{[j]}.$ An obvious generalisation reads as follows. Set $D:=\{1,\ldots ,d\}$ and choose a subset $\alpha \subset D$ with $\emptyset \ne \alpha \ne D.$ The complement is $\alpha ^{c}:=D\backslash \alpha .$ Define

and ${\mathbf {V}}_{\alpha }=\bigotimes _{j\in \alpha }V_{j}.$ The matricisation with respect to $\alpha$ uses the isomorphism

$$\begin{aligned} \mathcal {M}_{\alpha }:{\mathbf {V}}\rightarrow {\mathbf {V}}_{\alpha }\otimes {\mathbf {V}}_{\alpha ^{c}},\quad \mathcal {M}_{\alpha }({\mathbf {v}})[{\mathbf {i}} _{\alpha },{\mathbf {i}}_{\alpha ^{c}}]={\mathbf {v}}[{\mathbf {i}}]\quad \text {for }{\mathbf {i}}=\left( {\mathbf {i}}_{\alpha },{\mathbf {i}}_{\alpha ^{c}}\right) \in {\mathbf {I}}_{D}. \end{aligned}$$

(4)

Here ${\mathbf {i}}_{\alpha }$ is the tuple $(i_{j})_{j\in \alpha }\in {\mathbf {I}}_{\alpha }.\mathcal {M}_{\alpha }({\mathbf {v}})$ can be regarded as a matrix in $\mathbb {K}^{{\mathbf {I}}_{\alpha }\times {\mathbf {I}}_{\alpha ^{c}}}.$ For $\alpha =\{j\}$ we obtain the j-th matricisation $\mathcal {M}_{j}$ from above. For $\alpha =D,$ the set $\alpha ^{c}$ is empty. The formal definition $\bigotimes _{j\in \emptyset }V_{j}=\mathbb {K}$ explains that $\mathcal {M} _{D}:{\mathbf {V}}\rightarrow {\mathbf {V}}\otimes \mathbb {K}$. Regarding $\mathcal {M}_{D}({\mathbf {v}})$ as a matrix means that there is only one column containing the vectorised tensor ${\mathbf {v}}$. Analogously, $\mathcal {M} _{\emptyset }({\mathbf {v}})=\mathcal {M}_{D}({\mathbf {v}})^{\mathsf {T}}$ contains ${\mathbf {v}}$ as row vector.

The $\alpha$-rank of a tensor ${\mathbf {v}}$ is already defined by Hitchcock [10, p. 170] via the matrix rank of $\mathcal {M}_{\alpha }({\mathbf {v}})$:

$$\begin{aligned} {\text {rank}}_{\alpha }({\mathbf {v}}):={\text {rank}} \left( \mathcal {M}_{\alpha }({\mathbf {v}})\right) . \end{aligned}$$

For different $\alpha$ the $\alpha$-ranks are different. The only relations are

$$\begin{aligned} {\text {rank}}_{\alpha }({\mathbf {v}})&={\text {rank}}_{\alpha ^{c}}({\mathbf {v}}),\\ {\text {rank}}_{\alpha }({\mathbf {v}})&\le {\text {rank}}_{\alpha ^{\prime }}({\mathbf {v}} ){\text {rank}}_{\alpha ^{\prime \prime }}({\mathbf {v}} )\qquad \text {for }\alpha =\alpha ^{\prime }\,\dot{\cup }\,\alpha ^{\prime \prime } \end{aligned}$$

(cf. Hackbusch [5, Lemma 6.19], $\dot{\cup }$ is the disjoint union). The connection with the tensor rank introduced in Sect. 2.1 is

$$\begin{aligned} {\text {rank}}_{\alpha }({\mathbf {v}})\le {\text {rank}} ({\mathbf {v}}) \end{aligned}$$

(cf. Hackbusch [5, Remark 6.21]). For $\alpha =\{j\}$ we write ${\text {rank}}_{j}({\mathbf {v}}).$ The tuple $( {\text {rank}}_{1}({\mathbf {v}}),\ldots , {\text {rank}}_{d}({\mathbf {v}}))$ is also called the multilinear rank of ${\mathbf {v}}$.

Let ${\mathbf {M}}:=\bigotimes _{j=1}^{d}M^{(j)}$ be an elementary Kronecker product of matrices $M^{(j)}.$ The tensor ${\mathbf {Mv}}$ is defined by (2) and satisfies

$$\begin{aligned} \mathcal {M}_{\alpha }({\mathbf {Mv}})=\left( {\mathbf {M}}_{\alpha }\otimes {\mathbf {M}}_{\alpha ^{c}}\right) \mathcal {M}_{\alpha }({\mathbf {v}}), \end{aligned}$$

(5a)

where ${\mathbf {M}}_{\alpha }=\bigotimes _{j\in \alpha }M^{(j)}$ and ${\mathbf {M}} _{\alpha ^{c}}=\bigotimes _{j\in \alpha ^{c}}M^{(j)}$ are partial Kronecker products. Interpreting $\mathcal {M}_{\alpha }({\mathbf {v}})$ and $\mathcal {M} _{\alpha }({\mathbf {Mv}})$ as matrices, the equivalent statement is

$$\begin{aligned} \mathcal {M}_{\alpha }({\mathbf {Mv}})={\mathbf {M}}_{\alpha }\,\mathcal {M}_{\alpha }({\mathbf {v}})\,{\mathbf {M}}_{\alpha ^{c}}^{\mathsf {T}}. \end{aligned}$$

(5b)

2.3 Minimal subspaces

Given ${\mathbf {v}}\in {\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}$, there may be smaller subspaces $U_{j}\subset V_{j}$ such that ${\mathbf {v}}\in {\mathbf {U}} =\bigotimes _{j=1}^{d}U_{j}.$ The subspaces of minimal dimension are called the minimal subspaces and denoted by $U_{j}^{\min }({\mathbf {v}}).$ They satisfy

$$\begin{aligned} {\mathbf {v}}\in \bigotimes _{j=1}^{d}U_{j}^{\min }({\mathbf {v}}) \end{aligned}$$

(6)

while ${\mathbf {v}}\in \bigotimes _{j=1}^{d}U_{j}$ implies $U_{j}^{\min }({\mathbf {v}})\subset U_{j}.$

The generalisation to subsets $\alpha \subset D=\{1,\ldots ,d\}$ uses the isomorphism ${\mathbf {V}}\simeq {\mathbf {V}}_{\alpha }\otimes {\mathbf {V}}_{\alpha ^{c} }.$ ${\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})\subset {\mathbf {V}}_{\alpha }$ is defined as the subspace of minimal dimension such that ${\mathbf {v}} \in {\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})\otimes {\mathbf {V}}_{\alpha ^{c}}.$ The minimal subspaces can be characterised by

$$\begin{aligned} {\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}}):={\text {range}}\left( \mathcal {M}_{\alpha }({\mathbf {v}})\right) . \end{aligned}$$

(7)

This includes the case $\alpha =\{j\},$ for which ${\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})$ is written as $U_{j}^{\min }({\mathbf {v}}).$

In the infinite-dimensional case one cannot interpret $\mathcal {M}_{\alpha }({\mathbf {v}})$ as a matrix. Then the definition (6) must be replaced by

$$\begin{aligned} {\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}}):=\left\{ \phi _{\alpha ^{c}} ({\mathbf {v}}):\phi _{\alpha ^{c}}\in \left. _{a}\bigotimes \nolimits _{j\in \alpha ^{c}}V_{j}^{\prime }\right. \right\} , \end{aligned}$$

(8)

where $V_{j}^{\prime }$ is the dual space³ of $V_{j}.$ The application of $\phi _{\alpha ^{c}}=\bigotimes _{j\in \alpha ^{c}}\varphi ^{(j)}$ to ${\mathbf {v}}$ is defined by

$$\begin{aligned} \phi _{\alpha ^{c}}\left( \bigotimes _{j=1}^{d}v^{(j)}\right) :=\left( \prod _{j\in \alpha ^{c}}\varphi ^{(j)}(v^{(j)})\right) \bigotimes _{j\in \alpha }v^{(j)}\in {\mathbf {V}}_{\alpha }. \end{aligned}$$

In the general case the $\alpha$-rank is defined by ${\text {rank}}_{\alpha }({\mathbf {v}})=\dim ({\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})).$

An important property is that under natural conditions weak convergence ${\mathbf {v}}_{n}\rightharpoonup {\mathbf {v}}$ implies

$$\begin{aligned} {\text {rank}}_{\alpha }({\mathbf {v}})\le \underset{n\rightarrow \infty }{\lim \inf }{\text {rank}}_{\alpha }({\mathbf {v}}_{n}) \end{aligned}$$

(9)

(cf. Hackbusch [5, Theorem 6.24], Falcó–Hackbusch [2]).

2.4 Higher-order singular-value decomposition (HOSVD)

In the following we assume that all $V_{j}$ are pre-Hilbert spaces equipped with the Euclidean scalar product $\left\langle \cdot ,\cdot \right\rangle .$ The Euclidean scalar product in ${\mathbf {V}}_{\alpha }=\bigotimes _{j\in \alpha }V_{j}$ satisfies

$$\begin{aligned} \left\langle \bigotimes _{j\in \alpha }v^{(j)},\bigotimes _{j\in \alpha } w^{(j)}\right\rangle =\prod _{j\in \alpha }\left\langle v^{(j)},w^{(j)} \right\rangle . \end{aligned}$$

Interpreting $\mathcal {M}_{\alpha }({\mathbf {v}})$ as a matrix, one may determine its singular-value decomposition (SVD) $\sum _{i}\sigma _{i}^{(\alpha )}{\mathbf {b}}_{i}^{(\alpha )}({\mathbf {b}}_{i}^{(\alpha ^{c})})^{\mathsf {T}}$. The tensor representation is

$$\begin{aligned} \mathcal {M}_{\alpha }({\mathbf {v}})=\sum \limits _{i=1}^{r_{\alpha }}\sigma _{i}^{(\alpha )}{\mathbf {b}}_{i}^{(\alpha )}\otimes {\mathbf {b}}_{i}^{(\alpha ^{c} )}, \end{aligned}$$

(10)

where $r_{\alpha }={\text {rank}}_{\alpha }({\mathbf {v}})$ is the $\alpha$-rank and $\sigma _{1}^{(\alpha )}\ge \sigma _{2}^{(\alpha )}\ge \cdots \ge \sigma _{r_{\alpha }}^{(\alpha )}>0$ are the singular values, while $\{{\mathbf {b}}_{i}^{(\alpha )}:1\le i\le r_{\alpha }\}\subset {\mathbf {V}} _{\alpha }$ and $\{{\mathbf {b}}_{i}^{(\alpha ^{c})}:1\le i\le r_{\alpha }\}\subset {\mathbf {V}}_{\alpha ^{c}}$ are the orthonormal systems of the left and right singular vectors. De Lathauwer–De Moor–Vandewalle [1] introduced the name HOSVD for the simultaneous SVD of the matricisations $\mathcal {M}_{j}({\mathbf {v}}),$ $1\le j\le d.$ Note that in general the SVD spectra $(\sigma _{i}^{(j)})_{1\le i\le r_{j}}$ as well as $r_{j}={\text {rank}}_{j}({\mathbf {v}})$ do not coincide. Compare also Hackbusch–Uschmajew [8].

It will turn out that the important quantities in (10) are the singular values $\sigma _{i}^{(\alpha )}$ and the left singular vectors ${\mathbf {b}}_{i}^{(\alpha )}.$ These quantities are also characterised by the diagonalisation of the matrix $\mathcal {M}_{\alpha }({\mathbf {v}} )\mathcal {M}_{\alpha }({\mathbf {v}})^{\mathsf {H}}$:

$$\begin{aligned} \mathcal {M}_{\alpha }({\mathbf {v}})\mathcal {M}_{\alpha }({\mathbf {v}})^{\mathsf {H} }=\sum \limits _{i=1}^{r_{\alpha }} ( \sigma _{i}^{(\alpha )}) ^{2}{\mathbf {b}}_{i}^{(\alpha )} ( {\mathbf {b}}_{i}^{(\alpha )}) ^{\mathsf {H}}. \end{aligned}$$

In the case of $\alpha =\{j\},$ $\mathcal {M}_{j}({\mathbf {v}})$ is a matrix with $n_{j}=\dim (V_{j})$ rows and $n_{[j]}=\prod _{k\ne j}\dim (V_{k})$ columns. Note that $n_{[j]}$ may be a huge quantity. However, $\mathcal {M} _{j}({\mathbf {v}})\mathcal {M}_{j}({\mathbf {v}})^{\mathsf {H}}$ is only of the size $n_{j}\times n_{j}.$

2.5 Basis representations, transformations

The notation (1) refers to the unit vectors $e_{i}^{(j)}$ ($1\le i\le n_{j}$) of $V_{j}=\mathbb {K}^{n_{j}},$ i.e., the tensor is ${\mathbf {v}}=\sum _{i_{1}=1}^{n_{1}}\cdots \sum _{i_{d}=1}^{n_{d}}{\mathbf {v}} [i_{1},\ldots ,i_{d}]\,\bigotimes _{j=1}^{d}e_{i_{j}}^{(j)}.$ We may choose another basis $b_{i}^{(j)}$ ($1\le i\le n_{j}$) of $V_{j}=\mathbb {K}^{n_{j} }$ and obtain

$$\begin{aligned} {\mathbf {v}}=\sum _{i_{1}=1}^{n_{1}}\cdots \sum _{i_{d}=1}^{n_{d}}{\mathbf {c}} [i_{1},\ldots ,i_{d}]\,\bigotimes _{j=1}^{d}b_{i_{j}}^{(j)} \end{aligned}$$

(11)

with another coefficient tensor ${\mathbf {c}}\in {\mathbf {V}}:=\bigotimes _{j=1} ^{d}\mathbb {K}^{n_{j}}.$ The basis $b_{i}^{(j)}$ ($1\le i\le n_{j}$) yields the regular matrix $B_{j}=\left[ b_{1}^{(j)},\ldots ,b_{n_{j}}^{(j)}\right] .$ Forming the Kronecker product ${\mathbf {B}}:=\bigotimes _{j=1}^{d}B_{j}\in L({\mathbf {V,V),}}$ Eq. (11) becomes

$$\begin{aligned} {\mathbf {v}}={\mathbf {Bc}}. \end{aligned}$$

If $B_{j}$ and $B_{j}^{\prime }$ are two bases of $V_{j},$ there are transformations $T^{(j)}$ and $S^{(j)}=(T^{(j)})^{-1}$ with

$$\begin{aligned} B_{j}=B_{j}^{\prime }T^{(j)}\text { and }\,B_{j}^{\prime }=B_{j}S^{(j)} ,\quad \text {i.e.,}\quad b_{i}^{(j)}=\sum _{k=1}^{r_{j}}T_{ki}^{(j)} \,b_{k}^{\prime (j)}. \end{aligned}$$

Form ${\mathbf {T}}:=\bigotimes _{j=1}^{d}T^{(j)}$ and ${\mathbf {S}}:=\bigotimes _{j=1}^{d}S^{(j)}={\mathbf {T}}^{-1}.$ Then

$$\begin{aligned} {\mathbf {v}}={\mathbf {Bc}}={\mathbf {B}}^{\prime }{\mathbf {c}}^{\prime }\quad \text { holds with}\quad {\mathbf {B}}={\mathbf {B}}^{\prime }{\mathbf {T}},\;{\mathbf {B}}^{\prime }={\mathbf {B\,S,}}\;{\mathbf {c}}={\mathbf {Sc}}^{\prime }{\mathbf {,}}\;{\mathbf {c}} ^{\prime }={\mathbf {Tc}}. \end{aligned}$$

(12)

Remark 2

According to (5b), the matricisations of ${\mathbf {v}}$ and its core tensor ${\mathbf {c}}$ are related by $\mathcal {M} _{\alpha }({\mathbf {v}})={\mathbf {B}}_{\alpha }\,\mathcal {M}_{\alpha }({\mathbf {c}} )\,{\mathbf {B}}_{\alpha ^{c}}^{\mathsf {T}}$ with ${\mathbf {B}}_{\alpha } :=\bigotimes \nolimits _{j\in \alpha }B_{j}.$

3 Tensor representations

3.1 r-Term format

Often, the dimension $\prod _{j=1}^{d}n_{j}$ of $\bigotimes _{j=1}^{d} \mathbb {K}^{n_{j}}$ is much larger than the available computer memory. Therefore a naive representation of a tensor via its entries (1) is impossible. A classical tensor representation is the r-term format (also called the canonical or CP format) related to (3). Let ${\mathbf {V}}=\bigotimes _{j=1}^{d}V_{j}.$ We fix an integer $r\in \mathbb {N} _{0}=\mathbb {N}\cup \{0\}$ and define the set

$$\begin{aligned} \mathcal {R}_{r}:=\left\{ {\mathbf {v}}\in {\mathbf {V}}:{\mathbf {v}}=\sum _{i=1} ^{r}\bigotimes _{j=1}^{d}v_{i}^{(j)},\ v_{i}^{(j)}\in V_{j}\right\} , \end{aligned}$$

i.e., ${\mathbf {v}}$ is represented by r elementary tensors with the factors $v_{i}^{(j)}.$ Assuming $\dim (V_{j})=n_{j}\le n,$ the memory cost of ${\mathbf {v}}\in \mathcal {R}_{r}$ is rnd (unit: numbers in $\mathbb {K}$).

One checks that $\mathcal {R}_{r}=\left\{ {\mathbf {v}}:{\text {rank}} ({\mathbf {v}})\le r\right\} .$ As long as ${\text {rank}}({\mathbf {v}} )\le r$ holds with r of moderate size, this format yields a suitable representation. If ${\text {rank}}({\mathbf {v}})$ is too large, one may try to find an approximating tensor ${\mathbf {v}}^{\prime }$ of smaller rank. Another question is the implementation of tensor operations within this format. Adding ${\mathbf {u}}\in \mathcal {R}_{r}$ and ${\mathbf {v}}\in \mathcal {R}_{s},$ one obtains the representation of the sum ${\mathbf {w}} :={\mathbf {u}}+{\mathbf {v}}$ in $\mathcal {R}_{r+s}.$ Other operations let the representation rank increase even more. An example is the multiplication of the Kronecker matrix ${\mathbf {M}}:=\sum _{i=1}^{\rho }\bigotimes _{j=1}^{d} M_{i}^{(j)}$ by a tensor $v\in \mathcal {R}_{r}.$ The product belongs to $\mathcal {R}_{r\cdot s}.$Therefore one needs a truncation procedure which approximates a tensor from $\mathcal {R}_{t}$ (t too large) by an approximation in $\mathcal {R}_{r}$ for a suitable $r<t.$ Unfortunately, this task is rather difficult within the r-term format (cf. Hackbusch [5, §7, §9]).

3.2 Tensor-subspace format

A remedy is the Tucker format or tensor-subspace format, which is related to (6) and (11). Let $n_{j}=\dim (V_{j}).$ Assume that we know that ${\mathbf {v}}\in \bigotimes _{j=1}^{d}U_{j}$ holds for subspaces $U_{j}\subset V_{j}$ of (hopefully much) smaller dimension than $n_{j}.$ Choose any basis (or even only a generating system) $b_{i}^{(j)}$ ($1\le i\le r_{j}$) of $U_{j},$ i.e.,

$$\begin{aligned} U_{j}={\text {span}}\{b_{i}^{(j)}:1\le i\le r_{j}\}. \end{aligned}$$

(13a)

Then there is a tensor ${\mathbf {c}}\in \bigotimes _{j=1}^{d}\mathbb {K}^{r_{j}}$ – the so-called core tensor—such that

$$\begin{aligned} {\mathbf {v}}=\sum _{i_{1}=1}^{r_{1}}\cdots \sum _{i_{d}=1}^{r_{d}}{\mathbf {c}} [i_{1},\ldots ,i_{d}]\,\bigotimes _{j=1}^{d}b_{i_{j}}^{(j)}. \end{aligned}$$

(13b)

Note the difference to (11). The sums in (11) have $n_{j}$ terms, whereas (13b) only uses $r_{j}<n_{j}$ as upper bound.

Definition 1

We denote the set of all tensors in ${\mathbf {V}}$ with a representation (13b) by $\mathcal {T}_{{\mathbf {r}}}$, where ${\mathbf {r}}=(r_{1},\ldots ,r_{d})$ is a multi-index.

Remark 3

The optimal choice of $U_{j}$ is given by $U_{j}=U_{j}^{\min }({\mathbf {v}})$ (cf. Sect. 2.3), since then $r_{j}={\text {rank}}_{j}({\mathbf {v}})$ is minimal. The memory cost for the core tensor is $\prod _{j=1}^{d}r_{j}.$ Therefore this representation is unfavourable for large d.

Build the (rectangular) matrices $B_{j}=\left[ b_{1}^{(j)},\ldots ,b_{r_{j} }^{(j)}\right] \in \mathbb {K}^{n_{j}\times r_{j}}$ and the Kronecker product ${\mathbf {B}}:=\bigotimes _{j=1}^{d}B_{j}\in L(\bigotimes _{j=1}^{d} \mathbb {K}^{r_{j}}{\mathbf {,V)}}$ as in Sect. 2.5. Then (13b) is equivalent to

$$\begin{aligned} {\mathbf {v}}={\mathbf {Bc.}} \end{aligned}$$

(13c)

3.3 HOSVD

The first step are transformations into orthonormal bases $B_{j}^{\prime }$ with $B_{j}=B_{j}^{\prime }T_{j}$ (e.g., by a QR decomposition of $B_{j}$ yielding $B_{j}^{\prime }=Q$ and $T_{j}=R$). According to (12), we have ${\mathbf {v}}={\mathbf {B}}^{\prime }{\mathbf {c}}^{\prime }$ with ${\mathbf {c}}^{\prime }:={\mathbf {Tc.}}$ Denoting ${\mathbf {B}}^{\prime }$ and ${\mathbf {c}}^{\prime }$ again by ${\mathbf {B}}$ and ${\mathbf {c}},$ we obtain the representation (13b) with orthonormal bases $(b_{i}^{(j)})_{1\le i\le r_{j}}.$

The second step is the HOSVD applied to the core tensor ${\mathbf {c}} \in \bigotimes _{j=1}^{d}\mathbb {K}^{r_{j}}.$ Assume that the matricisation $C_{\alpha }:=\mathcal {M}_{\alpha }({\mathbf {c}})$ has the singular-value decomposition $C_{\alpha }=X_{\alpha }\varSigma _{\alpha }Y_{\alpha }^{\mathsf {T}}$ with diagonal $\varSigma _{\alpha }$ and unitary matrices $X_{\alpha },\ Y_{\alpha }.$ By Remark 2 the matricisation of ${\mathbf {v}}$ is $\mathcal {M}_{\alpha }({\mathbf {v}})={\mathbf {B}}_{\alpha }\,\mathcal {M}_{\alpha }({\mathbf {c}})\,{\mathbf {B}}_{\alpha ^{c}}^{\mathsf {T}}={\mathbf {B}}_{\alpha }\,X_{\alpha }\varSigma _{\alpha }Y_{\alpha }^{\mathsf {T}}\,{\mathbf {B}}_{\alpha ^{c} }^{\mathsf {T}}.$ This is the singular-value decomposition of $\mathcal {M} _{\alpha }({\mathbf {v}})$ with the unitary matrices ${\mathbf {B}}_{\alpha }\,X_{\alpha }$ and ${\mathbf {B}}_{\alpha ^{c}}Y_{\alpha }.$ Taking $\alpha =\{j\},$ we obtain a new basis transform by $B_{j}^{\prime }:=B_{j}\,X_{j}$ ($1\le j\le d$). The new basis $(b_{i}^{\prime (j)})_{1\le i\le r_{j}}$ is called the j-th HOSVD basis. The core tensor has to be transformed into ${\mathbf {c}}^{\prime }$ as above. Again denoting ${\mathbf {B}}^{\prime }$ and ${\mathbf {c}}^{\prime }$ by ${\mathbf {B}}$ and ${\mathbf {c}},$ we obtain the representation (13b) with respect to the HOSVD bases.

Since we do not need the right singular vectors in $Y_{\alpha },$ the practical computation first forms the product $P_{j}:=\mathcal {M}_{j}({\mathbf {c}} )\mathcal {M}_{j}({\mathbf {c}})^{\mathsf {H}}\in \mathbb {K}^{r_{j}\times r_{j}}.$ This is the most expensive step with an arithmetic cost of $\mathcal {O}( (\sum _{j=1}^{d}r_{j})\prod _{j=1}^{d}r_{j}).$ The second step is the singular-value decomposition of $P_{j}$ (cost: $\mathcal {O}(\sum _{j=1} ^{d}r_{j}^{3})$).

The representation of ${\mathbf {v}}\in \mathcal {T}_{{\mathbf {r}}}$ by the HOSVD bases allows two types of truncations. The number $r_{j}=\dim (U_{j})$ may be larger than necessary, i.e., larger than ${\text {rank}}_{j}({\mathbf {v}})=\dim (U_{j}^{\min }({\mathbf {v}})).$ This is detected by vanishing singular values. Assume that $\sigma _{s_{j}}^{(j)}>0,$ whereas $\sigma _{i}^{(j)}=0$ for $s_{j}<i\le r_{j}.$ Then the sums in (13b) can be shortened (replace $r_{j}$ by $s_{j})$. After this step, ${\mathbf {v}}\in \bigotimes _{j=1}^{d}U_{j}\subset \mathcal {T}_{{\mathbf {s}}}$ holds with $U_{j}=U_{j}^{\min }({\mathbf {v}})$ and $s_{j}={\text {rank}} _{j}({\mathbf {v}}).$ Note that the described procedure yields a shorter representation while the tensor is unchanged.

A truncation changing the tensor is described next.

3.4 HOSVD truncation

Assume again that the representation (13b) of ${\mathbf {v}} \in \mathcal {T}_{{\mathbf {r}}}$ uses the HOSVD bases. We are looking for an approximation ${\mathbf {u}}\in \mathcal {T}_{{\mathbf {s}}}$ with smaller dimensions $s_{j}<r_{j}$ of the corresponding subspaces $U_{j}.$ This problem has two answers. First there is a (not necessarily unique) best approximation ${\mathbf {u}}_{{\mathrm {best}}}\in \mathcal {T}_{{\mathbf {s}}}$ with

$$\begin{aligned} \left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {best}}}\right\| =\inf \{\left\| {\mathbf {v}}-{\mathbf {u}}\right\| :{\mathbf {u}}\in \mathcal {T}_{{\mathbf {s}}}\} \end{aligned}$$

($\left\| \cdot \right\|$ is the Euclidean norm). The computation must be done iteratively. It is hard to ensure that the corresponding minimisation method converges to the global minimum, since there may be many local minima.

A much easier approach is the HOSVD truncation: Given ${\mathbf {v}} \in \mathcal {T}_{{\mathbf {r}}}$ with HOSVD bases in (13b), omit all terms involving indices $i_{j}>s_{j}.$ The other terms are unchained. Obviously, the resulting tensor ${\mathbf {u}}_{{\mathrm {HOSVD}}}$ belongs to $\mathcal {T}_{{\mathbf {s}}}$ and its computation requires no arithmetical operation. In the case of matrices one knows that ${\mathbf {u}}_{{\mathrm {HOSVD}} }={\mathbf {u}}_{{\mathrm {best}}}.$ However, for $d\ge 3,$ ${\mathbf {u}} _{{\mathrm {HOSVD}}}$ is not necessarily the best, but the quasi-optimal approximation:

$$\begin{aligned} \left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {HOSVD}}}\right\| \le \sqrt{\sum _{j=1}^{d}\sum _{i=s_{j}+1}^{r_{j}}\left( \sigma _{i}^{(j)}\right) ^{2} }\le \sqrt{d}\,\left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {best}}}\right\| \end{aligned}$$

(14)

(cf. [5, Theorem 10.3]). Since the singular values $\sigma _{i}^{(j)}$ are known, the first inequality in (14) yields a precise error estimate. Given a tolerance $\varepsilon ,$ one can choose $r_{j}$ such that the error is below $\varepsilon .$ The second inequality proves quasi-optimality.

4 The hierarchical tensor format

4.1 Definition, notation

The tree-based tensor formats use a so-called dimension partition tree $T_{D}.$ The root of the tree is $D=\{1,\ldots ,d\},$ while the leaves are $\{1\},\ldots ,\{d\}.$ The tree describes how D is divided recursively. The vertices of the tree are subsets of D. Either a vertex $\alpha$ is a singleton (and therefore a leaf) or it has sons $\alpha _{i}$ with the property that $\alpha$ is the disjoint union of the $\alpha _{i}.$ Examples for $d=4$ are given below:

(15)

The first interpretation is that the tree (a) corresponds to $V_{1}\otimes V_{2}\otimes V_{3}\otimes V_{4},$ (b) to the isomorphic space $\left( V_{1}\otimes V_{2}\right) \otimes \left( V_{3}\otimes V_{4}\right) ,$ (c) to $\left( \left( V_{1}\otimes V_{2}\right) \otimes V_{3}\right) \otimes V_{4},$ and (d) to $\left( V_{1}\otimes V_{2}\otimes V_{3}\right) \otimes V_{4}.$

The second interpretation involves the associated subspaces. The tree (a) corresponds to the Tucker format in Sect. 3.2: All subspaces $U_{1},\ldots ,U_{d}$ are joined into $U_{1}\otimes U_{2}\otimes U_{3}\otimes U_{4}.$ In the case of tree (b) one first forms the subspaces $\left. U_{1}\otimes U_{2}\right.$ and $U_{3}\otimes U_{4}$ and determines subspaces $U_{\{1,2\}}\subset U_{1}\otimes U_{2}$ and $U_{\{3,4\}}\subset U_{3}\otimes U_{4}.$ Finally $U_{\{1,2\}}\otimes U_{\{3,4\}}$ is defined. The trees (c) and (d) lead to analogous constructions. The final subspace ${\mathbf {U}}_{D}$ must be such that ${\mathbf {v}}\in {\mathbf {U}}_{D}$ holds for the tensor ${\mathbf {v}}$ which we want to represent. Obviously, the one-dimensional subspace ${\mathbf {U}}_{D}={\text {span}}\{{\mathbf {v}}\}$ is sufficient.

Restricting ourselves to binary trees $T_{D},$ we obtain the hierarchical tensor format (cases (b), (c) in (15); cf. Hackbusch–Kühn [7]). The practical advantage of a binary tree is the fact that the quantities appearing in the later computations are matrices. The further restriction to linear trees as in case (c) of (15) leads to the so-called TT format or matrix product format (cf. Verstraete–Cirac [14], Oseledets–Tyrtyshnikov [11, 12]).

Consider a vertex $\alpha \subset D$ of the binary tree $T_{D}$ together with its sons $\alpha _{1}$ and $\alpha _{2}$:

$$\begin{aligned}{}\begin{array}[c]{ccccl} &{} &{} \alpha &{} \rightarrow &{} {\mathbf {U}}_{\alpha }\subset {\mathbf {U}}_{\alpha _{1} }{\mathbf {\otimes U}}_{\alpha _{2}}\\ &{} \diagup &{} &{} \diagdown &{} \\ {\mathbf {U}}_{\alpha _{1}}\leftarrow \alpha _{1} &{} &{} &{} &{} {{\alpha }} _{2}\rightarrow {\mathbf {U}}_{\alpha _{2}} \end{array} \end{aligned}$$

(16)

The sons are associated with subspaces ${\mathbf {U}}_{\alpha _{i}}\subset {\mathbf {V}}_{\alpha _{i}}=\bigotimes _{j\in \alpha _{i}}V_{j}$ ($i=1,2$), while ${\mathbf {U}}_{\alpha }\subset {\mathbf {U}}_{\alpha _{1}}\otimes {\mathbf {U}} _{\alpha _{2}}\subset {\mathbf {V}}_{\alpha }$ is the characteristic property of ${\mathbf {U}}_{\alpha }.$ If $\alpha =D,$ ${\mathbf {v}}\in {\mathbf {U}}_{D}$ is required. Therefore we can choose

$$\begin{aligned} {\mathbf {U}}_{D}={\text {span}}\{{\mathbf {v}}\}. \end{aligned}$$

(17)

The minimal subspaces ${\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})$ introduced in (7) and (8) satisfy⁴ the inclusion

$$\begin{aligned} {\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})\subset {\mathbf {U}}_{\alpha _{1}}^{\min }({\mathbf {v}})\otimes {\mathbf {U}}_{\alpha _{2}}^{\min }({\mathbf {v}}). \end{aligned}$$

This proves the following remark.

Remark 4

The existence of subspaces ${\mathbf {U}}_{\alpha }$ ($\alpha \in T_{D}$) with the required properties is ensured by the optimal choice ${\mathbf {U}}_{\alpha }={\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}}).$ Vice versa, ${\mathbf {U}}_{\alpha }\supset {\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})$ holds for all subspaces ${\mathbf {U}}_{\alpha }$ satisfying ${\mathbf {v}} \in {\mathbf {U}}_{D}$ und ${\mathbf {U}}_{\alpha }\subset {\mathbf {U}}_{\alpha _{1} }{\mathbf {\otimes U}}_{\alpha _{2}}$.

4.2 Implementation of the subspaces

In principle, all subspaces ${\mathbf {U}}_{\alpha }$ ($\alpha \in T_{D}$) are described by basis⁵ vectors:

$$\begin{aligned} {\mathbf {U}}_{\alpha }={\text {span}}\{{\mathbf {b}}_{\ell }^{(\alpha )} :1\le \ell \le r_{\alpha }\}. \end{aligned}$$

However, ${\mathbf {b}}_{\ell }^{(\alpha )}$ are already tensors of order $\#\alpha$ which should not be stored explicitly. Therefore we distinguish two cases.

Case A. $\alpha =\{j\}$ is a leaf. Then the basis vectors $b_{i}^{(j)}$ of ${\mathbf {U}}_{\alpha }=U_{j}$ are stored explicitly.

Case B. $\alpha$ is a non-leaf vertex with sons $\alpha _{1}$ and $\alpha _{2}.$ Note that $\{{\mathbf {b}}_{i}^{(\alpha _{1})}\otimes {\mathbf {b}}_{j}^{(\alpha _{2})}:1\le i\le r_{\alpha _{1}},1\le j\le r_{\alpha _{2}}\}$ is a basis of ${\mathbf {U}}_{\alpha _{1}}\otimes {\mathbf {U}} _{\alpha _{2}}.$ The inclusion ${\mathbf {U}}_{\alpha }\subset {\mathbf {U}} _{\alpha _{1}}\otimes {\mathbf {U}}_{\alpha _{2}}$ implies that the basis vector ${\mathbf {b}}_{\ell }^{(\alpha )}\in {\mathbf {U}}_{\alpha }$ must have a representation⁶

$$\begin{aligned} {\mathbf {b}}_{\ell }^{(\alpha )}=\sum _{i,j}c_{ij}^{(\alpha ,\ell )}{\mathbf {b}} _{i}^{(\alpha _{1})}\otimes {\mathbf {b}}_{j}^{(\alpha _{2})} \end{aligned}$$

(18)

with coefficients $c_{ij}^{(\alpha ,\ell )}$ forming an $r_{\alpha _{1}} \times r_{\alpha _{2}}$ matrix

$$\begin{aligned} C^{(\alpha ,\ell )}=(c_{ij}^{(\alpha ,\ell )})\qquad (1\le \ell \le r_{\alpha }). \end{aligned}$$

(19)

The tuple $\left( C^{(\alpha ,\ell )}\right) _{1\le \ell \le r_{\alpha }}$ of matrices can be regarded as a tensor ${\mathbf {C}}_{\alpha }$ of order 3 with entries ${\mathbf {C}}_{\alpha }[i,j,\ell ]=C_{ij}^{(\alpha ,\ell )}.$ In the case of $\alpha =D,$ $r_{D}=1$ holds. The desired representation of the tensor ${\mathbf {v}}$ is

$$\begin{aligned} {\mathbf {v}}=c_{1}^{(D)}{\mathbf {b}}_{1}^{(D)}. \end{aligned}$$

(20)

Remark 5

The representation of a tensor ${\mathbf {v}}$ by the hierarchical format uses the data $b_{i}^{(j)}$ ($1\le j\le d,\ 1\le i\le r_{j}$), $C^{(\alpha ,\ell )}$ ($1\le \ell \le r_{\alpha },\ \alpha$ non-leaf vertex of $T_{D}$), and $c_{1}^{(D)}.$ The memory cost of the hierarchical format is bounded by $dnr+\left( d-1\right) r^{3}+1,$ where $n:=\max _{j}\dim (V_{j})$ and $r:=\max _{\alpha \in T_{D}}r_{\alpha }.$

Although the representation of ${\mathbf {v}}$ by the quantities $(b_{i} ^{(j)},{\mathbf {C}}_{\alpha },c_{1}^{(D)})$ is rather indirect, all tensor operations can be performed by a recursion in the tree $T_{D}$ (either from the leaves to the root or in the opposite direction). Below we describe transformations, the orthonormalisation of the bases, and the HOSVD computation. Concerning other operations we refer to [5, § 13].

4.3 Transformations

We recall that the bases $\{{\mathbf {b}}_{\ell }^{(\alpha )}:1\le \ell \le r_{\alpha }\}$ are well-defined by (18), but they are not directly accessible except for leaves $\alpha \in T_{D}$. Transformations of the bases are described by the corresponding modifications of the matrices $C^{(\alpha ,\ell )}.$ As in Sect. 3.2 we form matrices ${\mathbf {B}} _{\alpha }=\left[ {\mathbf {b}}_{1}^{(\alpha )}\ \ldots \ {\mathbf {b}}_{r_{\alpha } }^{(\alpha )}\right]$ related to a linear map in $L(\mathbb {K}^{r_{\alpha } },{\mathbf {V}}_{\alpha }).$ For simplicity we will call ${\mathbf {B}}_{\alpha }$ the basis (of the spanned subspace).

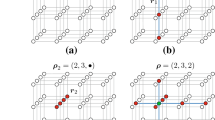
The left figure illustrates the connection of the basis $\,{\mathbf {B}}_{\alpha }$ with $\,{\mathbf {B}}_{\alpha _{1}}\,$ and $\,{\mathbf {B}}_{\alpha _{2}}\,$ at the son vertices via the data $\,{\mathbf {C}}_{\alpha }.$ Whenever one of these bases changes, also $\,{\mathbf {C}}_{\alpha }\,$ must be updated. Eq. (21) describes the update caused by a transformation of $\,{\mathbf {B}}_{\alpha },\,$ while (22) considers the transformations of $\,{\mathbf {B}}_{\alpha _{1}}\,$ and $\,{\mathbf {B}}_{\alpha _{2}}.$

Basis transformation in $\alpha .$ Assume that $\alpha$ is not a leaf and that ${\mathbf {B}}_{\alpha }$ and ${\mathbf {B}}_{\alpha }^{\prime }$ are two bases related by ${\mathbf {B}}_{\alpha }^{\prime }={\mathbf {B}}_{\alpha }S^{(\alpha )},$ i.e., ${\mathbf {b}}_{k}^{\prime (\alpha )}=\sum _{j=1}^{r_{\alpha }} S_{jk}^{(\alpha )}\,{\mathbf {b}}_{j}^{(\alpha )}$ $(1\le k\le r_{\alpha } ^{\prime }).$ The corresponding coefficient matrices $C^{(\alpha ,\ell )}$ and $C^{\prime (\alpha ,\ell )}$ satisfy

$$\begin{aligned} \,C^{\prime (\alpha ,k)}=\sum _{j=1}^{r_{\alpha }}S_{jk}^{(\alpha )}C^{(\alpha ,j)}\qquad \left( 1\le k\le r_{\alpha }^{\prime }\right) . \end{aligned}$$

(21)

Using the tensor ${\mathbf {C}}_{\alpha }$, this transformation becomes ${\mathbf {C}}_{\alpha }^{\prime }=\left( I\otimes I\otimes (S^{(\alpha )})^{\mathsf {T}}\right) {\mathbf {C}}_{\alpha }.$

Basis transformation in the son vertices $\alpha _{i}.$ Let $\alpha _{1},\,\alpha _{2}$ be the sons of $\alpha .$ Let ${\mathbf {B}}_{\alpha _{i}}$ and ${\mathbf {B}}_{\alpha _{i}}^{\prime }$ be two bases related by ${\mathbf {B}}_{\alpha _{i}}^{\prime }\,T^{(\alpha _{i})}={\mathbf {B}}_{\alpha _{i} }\ (i=1,2).$ The corresponding coefficient matrices $C^{(\alpha ,\ell )}$ and $C^{\prime (\alpha ,\ell )}$ are related by

$$\begin{aligned} C^{\prime (\alpha ,\ell )}=T^{(\alpha _{1})}\,C^{(\alpha ,\ell )}\,(T^{(\alpha _{2} )})^{\mathsf {T}}\qquad \text {for }\,1\le \ell \le r_{\alpha }. \end{aligned}$$

(22)

This is equivalent to ${\mathbf {C}}_{\alpha }^{\prime }=\left( T^{(\alpha _{1} )}\otimes T^{(\alpha _{2})}\otimes I\right) \,{\mathbf {C}}_{\alpha }.$

4.4 Orthonormalisation

Orthonormality of the (non-accessible) bases $\{{\mathbf {b}}_{\ell }^{(\alpha )}\}$ can be checked by corresponding properties of the coefficient matrices $C^{(\alpha ,\ell )}.$ The following sufficient condition is easy to prove.

Remark 6

Let $\alpha$ be a non-leaf vertex. The basis $\{{\mathbf {b}}_{\ell }^{(\alpha )}\}$ is orthonormal, if (a) the bases $\{{\mathbf {b}}_{i}^{(\alpha _{1})}\}$ and $\{{\mathbf {b}}_{j}^{(\alpha _{2})}\}$ of the sons $\alpha _{1},\alpha _{2}$ are orthonormal and (b) the matrices $C^{(\alpha ,\ell )}$ in (19) are orthonormal with respect to the Frobenius scalar product: $\left\langle C^{(\alpha ,\ell )},C^{(\alpha ,m)}\right\rangle _{\mathsf {F}}=\sum \nolimits _{ij}c_{ij}^{(\alpha ,\ell )}\overline{c_{ij}^{(\alpha ,m)}} =\delta _{\ell m}.$

The bases can be orthonormalised as follows. Orthonormalise the explicitly given bases at the leaves (e.g., by QR). As soon as $\{{\mathbf {b}}_{i} ^{(\alpha _{1})}\}$ and $\{{\mathbf {b}}_{j}^{(\alpha _{2})}\}$ are orthonormal, orthonormalise the matrices $C^{(\alpha ,\ell )}.$ The new matrices $C_{{\mathrm {new}}}^{(\alpha ,\ell )}$ define a new orthonormal basis $\{{\mathbf {b}}_{\ell ,{\mathrm {new}}}^{(\alpha )}\}$ via (21).

The above mentioned calculations require basis transformations. Here the following has to be taken into account (cf. Sect. 4.3 and [5, §11.3.1.4]).

• Case A1. Let $\alpha _{1}$ be the first son of $\alpha .$ Assume that the basis $\{{\mathbf {b}}_{i}^{(\alpha _{1})}\}$ is transformed into a new basis $\{{\mathbf {b}}_{i,{\mathrm {new}}}^{(\alpha _{1})}\}$ so that $\mathbf b _{i}^{(\alpha _{1})}=\sum \nolimits _{k}T_{ki}\,{\mathbf {b}}_{k,{\mathrm {new}} }^{(\alpha _{1})}.$ Changing $C^{(\alpha ,\ell )}$ into $C_{{\mathrm {new}} }^{(\alpha ,\ell )}:=TC^{(\alpha ,\ell )},$ the basis $\{{\mathbf {b}}_{\ell }^{(\alpha )}\}$ remains unchanged.

• Case A2. If $\mathbf b _{i}^{(\alpha _{2})}=\sum \nolimits _{k} T_{ki}{\mathbf {b}}_{k,{\mathrm {new}}}^{(\alpha _{2})}$ is a transformation of the second son of $\alpha ,$ $C^{(\alpha ,\ell )}$ must be changed into $C^{(\alpha ,\ell )}T^{\mathsf {T}}.$

• Case B. Consider a non-leaf vertex $\alpha .$ If the basis $\{{\mathbf {b}} _{\ell }^{(\alpha )}\}$ should be transformed into ${\mathbf {b}}_{\ell ,{\mathrm {new}}}^{(\alpha )}:=\sum \nolimits _{i}T_{\ell i}{\mathbf {b}}_{i} ^{(\alpha )},$ one has to change the coefficient matrices $C^{(\alpha ,\ell )}$ by $C_{{\mathrm {new}}}^{(\alpha ,\ell )}:=\sum \nolimits _{i}T_{\ell i} C^{(\alpha ,i)}.$ (In addition, this transformation causes changes at the father vertex according to Case A1 or Case A2).

As in Sect. 3.3, the bases have to be orthonormalised before the HOSVD bases are computed.

4.5 HOSVD bases

The challenge is the computation of the HOSVD, more precisely of the singular values $\sigma _{i}^{(\alpha )}$ and the left singular vectors (tensors) ${\mathbf {b}}_{i}^{(\alpha )}$ of $\mathcal {M}_{\alpha }({\mathbf {v}}).$ We recall that these data require the diagonalisation of the square matrix⁷$\mathcal {M}_{\alpha }({\mathbf {v}})\mathcal {M}_{\alpha }({\mathbf {v}})^{\mathsf {H} }.$ In the case of the tensor subspace representation of Sect. 3.3 it was possible to reduce $\mathcal {M}_{\alpha }({\mathbf {v}})\mathcal {M}_{\alpha }({\mathbf {v}})^{\mathsf {H}}$ to $\mathcal {M} _{\alpha }({\mathbf {c}})\mathcal {M}_{\alpha }({\mathbf {c}})^{\mathsf {H}}$ involving the (smaller) core tensor. Now we reduce the computation of $\mathcal {M}_{\alpha }({\mathbf {v}})\mathcal {M}_{\alpha }({\mathbf {v}})^{\mathsf {H}}$ to matrix operations only involving the data ${\mathbf {C}}_{\alpha }.$

The basis ${\mathbf {B}}_{\alpha }=\{b_{i}^{(\alpha )}:1\le i\le r_{\alpha }\}$ spans the subspace ${\mathbf {U}}_{\alpha }\subset {\mathbf {V}}_{\alpha } =\bigotimes _{j\in \alpha }V_{j}.$ The requirement ${\mathbf {v}}\in {\mathbf {U}}_{D}$ implies that ${\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}})\subset {\mathbf {U}}_{\alpha }$ (cf. Remark 4). Together with ${\mathbf {U}} _{\alpha }^{\min }({\mathbf {v}})={\text {range}}(\mathcal {M}_{\alpha }({\mathbf {v}}))$ (cf. (7)) we conclude that $\mathcal {M} _{\alpha }({\mathbf {v}})\mathcal {M}_{\alpha }({\mathbf {v}})^{\mathsf {H}}$ must be of the form

$$\begin{aligned} X_{\alpha }:=\mathcal {M}_{\alpha }({\mathbf {v}})\mathcal {M}_{\alpha } ({\mathbf {v}})^{\mathsf {H}}=\sum _{i,j=1}^{r_{\alpha }}e_{ij}^{(\alpha )} {\mathbf {b}}_{i}^{(\alpha )}({\mathbf {b}}_{j}^{(\alpha )})^{\mathsf {H}} ={\mathbf {B}}_{\alpha }E_{\alpha }{\mathbf {B}}_{\alpha }^{\mathsf {H}} \end{aligned}$$

(23)

with some coefficients $e_{ij}^{(\alpha )}$ which form an $r_{\alpha }\times r_{\alpha }$ matrix

$$\begin{aligned} E_{\alpha }=\big (e_{ij}^{(\alpha )}\big )_{i,j=1}^{r_{\alpha }}. \end{aligned}$$

To simplify matters we assume that the bases are already orthonormal⁸ (cf. Sect. 4.4). We start with the root $\alpha =D$ of the tree $T_{D}.$ Since $r_{D}=1,$ $E_{D}=e_{11}^{(D)}$ is a scalar. The definition of $\mathcal {M}_{D}({\mathbf {v}})$ in Sect. 2.2 shows that $X_{\alpha }={\mathbf {vv}}^{\mathsf {H}}.$ On the other hand, the equality ${\mathbf {v}}=c_{1}^{(D)}{\mathbf {b}}_{1}^{(D)}$ in (20) implies

$$\begin{aligned} E_{D}=e_{11}^{(D)}=|c_{1}^{(D)}|^{2}\qquad \text {and}\quad \sigma _{1} ^{(D)}=|c_{1}^{(D)}|, \end{aligned}$$

(24)

where $\sigma _{1}^{(D)}$ is the only singular value of $\mathcal {M} _{D}({\mathbf {v}}).$ Its left singular vector is ${\mathbf {v}}.$ The following recursion starts with $\alpha =D.$

We assume that for some non-leaf vertex $\alpha \in T_{D}$ the singular values $\sigma _{i}^{(\alpha )}$ and the matrix $E_{\alpha }$ are known. Now we want to determine $E_{\alpha _{1}}$ and $E_{\alpha _{2}}$ for the sons $\alpha _{1}$ and $\alpha _{2}$ of $\alpha .$ Concerning $X_{\alpha }$ and $X_{\alpha _{1}},$ we recall the definition of $\mathcal {M}_{\alpha }({\mathbf {v}})$ by (4 ). The entries of $X_{\alpha }$ are

$$\begin{aligned} X_{\alpha }[{\mathbf {i}}_{\alpha },{\mathbf {j}}_{\alpha }]&=\sum _{{\mathbf {k}} _{\alpha ^{c}}\in {\mathbf {I}}_{\alpha ^{c}}}\mathcal {M}_{\alpha }({\mathbf {v}} )[{\mathbf {i}}_{\alpha },{\mathbf {k}}_{\alpha ^{c}}]\,\overline{\mathcal {M}_{\alpha }({\mathbf {v}})[{\mathbf {j}}_{\alpha },{\mathbf {k}}_{\alpha ^{c}}]}\nonumber \\&=\sum _{{\mathbf {k}}_{\alpha ^{c}}\in {\mathbf {I}}_{\alpha ^{c}}}{\mathbf {v}}[\left( {\mathbf {i}}_{\alpha },{\mathbf {k}}_{\alpha ^{c}}\right) ]\,\overline{{\mathbf {v}}[\left( {\mathbf {j}}_{\alpha },{\mathbf {k}}_{\alpha ^{c}}\right) ]}. \end{aligned}$$

(25)

On the left-hand side, e.g.,

form the pair of matrix indices, while in the second line $\left( {\mathbf {i}}_{\alpha },{\mathbf {k}}_{\alpha ^{c} }\right) \in {\mathbf {I}}_{D}$ is the index of ${\mathbf {v.}}$ Analogously we have

$$\begin{aligned} X_{\alpha _{1}}[{\mathbf {i}}_{\alpha _{1}},{\mathbf {j}}_{\alpha _{1}}]=\sum _{{\mathbf {k}}_{\alpha _{1}^{c}}\in {\mathbf {I}}_{\alpha _{1}^{c}}}{\mathbf {v}}[\left( {\mathbf {i}}_{\alpha _{1}},{\mathbf {k}}_{\alpha _{1}^{c}}\right) ]\ \overline{{\mathbf {v}}[\left( {\mathbf {j}}_{\alpha _{1}},{\mathbf {k}}_{\alpha _{1}^{c} }\right) ]}. \end{aligned}$$

The complement of $\alpha _{1}$ is $\alpha _{1}^{c}=\alpha ^{c}\,\dot{\cup }\,\alpha _{2}$ so that ${\mathbf {I}}_{\alpha _{1}^{c}}={\mathbf {I}}_{\alpha ^{c} }\times {\mathbf {I}}_{\alpha _{2}}.$ Hence the summation over ${\mathbf {k}} _{\alpha _{1}^{c}}\in {\mathbf {I}}_{\alpha _{1}^{c}}$ becomes a double sum over ${\mathbf {k}}_{\alpha ^{c}}\in {\mathbf {I}}_{\alpha ^{c}}$ and ${\mathbf {k}} _{\alpha _{2}}\in {\mathbf {I}}_{\alpha _{2}}.$ The sum over ${\mathbf {k}}_{\alpha ^{c}}\in {\mathbf {I}}_{\alpha ^{c}}$ already appears in (25) so that

$$\begin{aligned} X_{\alpha _{1}}[{\mathbf {i}}_{\alpha _{1}},{\mathbf {j}}_{\alpha _{1}}]&=\sum _{{\mathbf {k}}_{\alpha _{2}}\in {\mathbf {I}}_{\alpha _{2}}}\sum _{{\mathbf {k}} _{\alpha ^{c}}\in {\mathbf {I}}_{\alpha ^{c}}}{\mathbf {v}}[\left( {\mathbf {i}} _{\alpha _{1}},{\mathbf {k}}_{\alpha _{2}},{\mathbf {k}}_{\alpha ^{c}}\right) ]\,\overline{{\mathbf {v}}[\left( {\mathbf {j}}_{\alpha _{1}},{\mathbf {k}}_{\alpha _{2}},{\mathbf {k}}_{\alpha ^{c}}\right) ]}\\&\underset{(25)}{=}\sum _{{\mathbf {k}}_{\alpha _{2}}\in {\mathbf {I}} _{\alpha _{2}}}X_{\alpha }[\left( {\mathbf {i}}_{\alpha _{1}},{\mathbf {k}} _{\alpha _{2}}\right) ,\left( {\mathbf {j}}_{\alpha _{1}},{\mathbf {k}}_{\alpha _{2} }\right) ]. \end{aligned}$$

Returning to the matrices $\mathcal {M}_{\alpha }({\mathbf {v}})$ and $\mathcal {M}_{\alpha _{1}}({\mathbf {v}}),$ the latter sum can be regarded as a matrix multiplication when we interpret ${\mathbf {b}}_{i}^{(\alpha )}$ in (23) as the $r_{\alpha _{1}}\times r_{\alpha _{2}}$ matrix $\sum _{\nu ,\mu }C_{\nu ,\mu }^{(\alpha ,i)}b_{\nu }^{(\alpha _{1})}(b_{\mu }^{(\alpha _{2})})^{\mathsf {T}}$:

$$\begin{aligned} X_{\alpha _{1}}&=\sum _{{\mathbf {k}}_{\alpha _{2}}\in {\mathbf {I}}_{\alpha _{2}} }X_{\alpha }[\left( {\mathbf {\cdot }},{\mathbf {k}}_{\alpha _{2}}\right) ,\left( {\mathbf {\cdot }},{\mathbf {k}}_{\alpha _{2}}\right) ]\\&=\sum _{{\mathbf {k}}_{\alpha _{2}}\in {\mathbf {I}}_{\alpha _{2}}}\left( \sum _{i,j=1}^{r_{\alpha }}e_{ij}^{(\alpha )}{\mathbf {b}}_{i}^{(\alpha )} ({\mathbf {b}}_{j}^{(\alpha )})^{\mathsf {H}}\right) [\left( {\mathbf {\cdot }},{\mathbf {k}}_{\alpha _{2}}\right) ,\left( {\mathbf {\cdot }},{\mathbf {k}} _{\alpha _{2}}\right) ]\\&=\sum _{i,j=1}^{r_{\alpha }}e_{ij}^{(\alpha )}{\mathbf {b}}_{i}^{(\alpha )}[\,{\mathbf {\cdot }},{\mathbf {k}}_{\alpha _{2}}]\,\overline{{\mathbf {b}} _{j}^{(\alpha )}[\,{\mathbf {\cdot }},{\mathbf {k}}_{\alpha _{2}}]}\\&\underset{(18)}{=}\sum _{i,j=1}^{r_{\alpha }}e_{ij}^{(\alpha )}\left( \sum _{\nu \mu }c_{\nu \mu }^{(\alpha ,i)}{\mathbf {b}}_{\nu }^{(\alpha _{1} )}\left( {\mathbf {b}}_{\mu }^{(\alpha _{2})}\right) ^{\mathsf {T}}\right) \left( \sum _{\lambda \varkappa }c_{\lambda \varkappa }^{(\alpha ,j)} {\mathbf {b}}_{\lambda }^{(\alpha _{1})}\left( {\mathbf {b}}_{\varkappa }^{(\alpha _{2})}\right) ^{\mathsf {T}}\right) ^{\mathsf {H}}. \end{aligned}$$

Since the basis is orthonormal, we obtain that ${\mathbf {b}}_{\nu }^{(\alpha _{1})}({\mathbf {b}}_{\mu }^{(\alpha _{2})})^{\mathsf {T}}\left( {\mathbf {b}} _{\lambda }^{(\alpha _{1})}({\mathbf {b}}_{\varkappa }^{(\alpha _{2})})^{\mathsf {T} }\right) ^{\mathsf {H}}={\mathbf {b}}_{\nu }^{(\alpha _{1})}({\mathbf {b}}_{\mu }^{(\alpha _{2})})^{\mathsf {T}}\overline{{\mathbf {b}}_{\varkappa }^{(\alpha _{2})} }({\mathbf {b}}_{\lambda }^{(\alpha _{1})})^{\mathsf {H}}=\left\langle {\mathbf {b}}_{\mu }^{(\alpha _{2})},{\mathbf {b}}_{\varkappa }^{(\alpha _{2} )}\right\rangle {\mathbf {b}}_{\nu }^{(\alpha _{1})}({\mathbf {b}}_{\lambda } ^{(\alpha _{1})})^{\mathsf {H}}=\delta _{\mu \varkappa }{\mathbf {b}}_{\nu } ^{(\alpha _{1})}({\mathbf {b}}_{\lambda }^{(\alpha _{1})})^{\mathsf {H}}$ ($\delta _{\mu \varkappa }$: Kronecker delta). Hence

$$\begin{aligned} X_{\alpha _{1}}=\sum _{i,j=1}^{r_{\alpha }}e_{ij}^{(\alpha )}\sum _{\nu ,\mu ,\lambda }c_{\nu \mu }^{(\alpha ,i)}\,\overline{c_{\lambda \mu }^{(\alpha ,j)} }\,\,{\mathbf {b}}_{\nu }^{(\alpha _{1})}\,({\mathbf {b}}_{\lambda }^{(\alpha _{1} )})^{\mathsf {H}}. \end{aligned}$$

This proves that (23) holds for $\alpha _{1}$ instead of $\alpha$ with coefficients $e_{\nu \lambda }^{(\alpha _{1})}=\sum _{i,j=1}^{r_{\alpha }} e_{ij}^{(\alpha )}\sum _{\lambda }c_{\nu \mu }^{(\alpha ,\ell )}\overline{c_{\lambda \mu }^{(\alpha ,\ell )}}$ forming the matrix $E_{\alpha _{1}}=\sum _{i,j=1}^{r_{\alpha }}e_{ij}^{(\alpha )}C^{(\alpha ,i)}(C^{(\alpha ,j)})^{\mathsf {H}}$ (cf. (19)). A similar treatment of $X_{\alpha _{2}}$ proves the following theorem.

Theorem 1

The matrices $E_{\alpha },$ $E_{\alpha _{1}},$ $E_{\alpha _{2}}$ are connected by

$$\begin{aligned} E_{\alpha _{1}}=\sum _{i,j=1}^{r_{\alpha }}e_{ij}^{(\alpha )}C^{(\alpha ,i)}(C^{(\alpha ,j)})^{\mathsf {H}},\quad E_{\alpha _{2}}=\sum _{i,j=1} ^{r_{\alpha }}e_{ij}^{(\alpha )}(C^{(\alpha ,i)})^{\mathsf {T}}\, \overline{C^{(\alpha ,j)}}. \end{aligned}$$

As in Sect. 3.3 the HOSVD bases $\{{\mathbf {b}}_{i,{\mathrm {HOSVD}} }^{(\alpha )}\}$ is defined by the diagonalisation of $X_{\alpha } :=\mathcal {M}_{\alpha }({\mathbf {v}})\mathcal {M}_{\alpha }({\mathbf {v}} )^{\mathsf {H}}=\sum _{i}(\sigma _{i}^{(\alpha )})^{2}{\mathbf {b}}_{i,{\mathrm {HOSVD}} }^{(\alpha )}({\mathbf {b}}_{i,{\mathrm {HOSVD}}}^{(\alpha )})^{\mathsf {H}}.$ A comparison with (23) shows that $X_{\alpha }$ is diagonalised if and only if

$$\begin{aligned} E_{\alpha }={\text {diag}}\{(\sigma _{1}^{(\alpha )})^{2},(\sigma _{2}^{(\alpha )})^{2},\ldots \}. \end{aligned}$$

(26)

Since $r_{D}=1$ at the root $\alpha =D,$ we have $\sigma _{1}^{(D)}=|c_{1} ^{(D)}|$ (cf. (24)) and ${\mathbf {b}}_{1}^{(D)}={\mathbf {b}} _{1,{\mathrm {HOSVD}}}^{(D)}.$ Assume that the HOSVD basis $\{{\mathbf {b}} _{i,{\mathrm {HOSVD}}}^{(\alpha )}\}$ is already chosen for the representation (we recall that the definition of ${\mathbf {b}}_{i,{\mathrm {HOSVD}}}^{(\alpha )}$ is implicitly given by the coefficient matrices $C^{(\alpha ,i)}$). Combining (26) with Theorem 1 we obtain

$$\begin{aligned} E_{\alpha _{1}}=\sum _{i=1}^{r_{\alpha }}(\sigma _{i}^{(\alpha )})^{2} C^{(\alpha ,i)}(C^{(\alpha ,i)})^{\mathsf {H}},\quad E_{\alpha _{2}}=\sum _{i=1}^{r_{\alpha }}(\sigma _{i}^{(\alpha )})^{2}(C^{(\alpha ,i)})^{\mathsf {T} }\,\overline{C^{(\alpha ,i)}}. \end{aligned}$$

Diagonalisation of the explicitly given matrices $E_{\alpha _{1}}$ and $E_{\alpha _{2}}$ yields

$$\begin{aligned} E_{\alpha _{1}}=U\varSigma _{\alpha _{1}}^{2}U^{\mathsf {H}},\qquad E_{\alpha _{2} }=V\varSigma _{\alpha _{2}}^{2}V^{\mathsf {H}} \end{aligned}$$

with orthogonal matrices U, V and diagonal matrices $\varSigma _{\alpha _{i} }={\text {diag}}\{\sigma _{1}^{(\alpha _{i})},\ldots \}$. Since also ${\mathbf {B}}_{\alpha _{i}}$ is orthogonal (i.e., ${\mathbf {B}}_{\alpha _{i} }^{\mathsf {H}}{\mathbf {B}}_{\alpha _{i}}=I),$ the diagonalisation is given by $X_{\alpha _{1}}=({\mathbf {B}}_{\alpha _{1}}U)\varSigma _{\alpha _{1}}^{2} ({\mathbf {B}}_{\alpha _{1}}U)^{\mathsf {H}}$, $X_{\alpha _{2}}=({\mathbf {B}} _{\alpha _{2}}V)\varSigma _{\alpha _{2}}^{2}({\mathbf {B}}_{\alpha _{2}}V)^{\mathsf {H} }.$ Hence ${\mathbf {B}}_{\alpha _{1}}^{{\mathrm {HOSVD}}}={\mathbf {B}}_{\alpha _{1}}U$ and ${\mathbf {B}}_{\alpha _{2}}^{{\mathrm {HOSVD}}}={\mathbf {B}}_{\alpha _{2}}V$ are the desired HOSVD bases at the vertices $\alpha _{1}$ and $\alpha _{2}$. If $\alpha _{i}$ is a leaf, this transformation is performed explicitly. Otherwise the coefficient matrices are modified according to Sect. 4.3. The procedure is repeated for the sons of $\alpha _{1},$ $\alpha _{2}$ until we reach the leaves. Then at all vertices HOSVD bases are introduced together with singular values $\sigma _{\nu }^{(\alpha )}.$

If there are vanishing singular values $\sigma _{i}^{(\alpha )}$, the corresponding contributions can be omitted. This reduces the associated subspace ${\mathbf {U}}_{\alpha }$ (cf. (16)) to the minimal subspace ${\mathbf {U}}_{\alpha }^{\min }({\mathbf {v}}).$ Correspondingly the value of $r_{\alpha }$ becomes ${\text {rank}}_{\alpha }({\mathbf {v}}).$

4.6 HOSVD truncation

We assume that following the procedure described above the hierarchical representation uses the HOSVD bases. The format $\mathcal {H}_{\mathfrak {r}}$ with $\mathfrak {r}=\left( r_{\alpha }\right) _{\alpha \in T_{D}}$ consists of all tensors ${\mathbf {v}}\in {\mathbf {V}}$ with ${\text {rank}}_{\alpha }({\mathbf {v}})\le r_{\alpha }.$ Given ${\mathbf {v}}\in \mathcal {H}_{\mathfrak {r}}$ we ask for an approximation ${\mathbf {u}}\in \mathcal {H}_{\mathfrak {s}}$ for a smaller tuple $\mathfrak {s}$ with $\mathfrak {s}\le \mathfrak {r}.$

The HOSVD truncation is similar to the procedure in Sect. 3.4. In terms of the (implicitly defined) bases the approximation ${\mathbf {u}} _{{\mathrm {HOSVD}}}$ is obtained by omitting all contributions involving the HOSVD basis vectors ${\mathbf {b}}_{i}^{(\alpha )}$ for $s_{\alpha }<i\le r_{\alpha }.$ In practice this means that the coefficient matrices $C^{(\alpha ,i)}$ are omitted for $s_{\alpha }<i\le r_{\alpha }$, while the remaining $r_{\alpha _{1}}\times r_{\alpha _{2}}$ matrices $C^{(\alpha ,i)}$ are reduced to size $s_{\alpha _{1}}\times s_{\alpha _{2}}$ by deleting the last $r_{\alpha _{1}}-s_{\alpha _{1}}$ rows and $r_{\alpha _{2}}-s_{\alpha _{2}}$ columns. If $\alpha =\{j\}$ is a leaf, the explicitly given basis $\{b_{i,{\mathrm {HOSVD}}}^{(j)}:1\le i\le r_{j}\}$ is replaced by $\{b_{i,{\mathrm {HOSVD}}}^{(j)}:1\le i\le s_{j}\}.$

The approximation error ${\mathbf {v}}-{\mathbf {u}}_{{\mathrm {HOSVD}}}$ satisfies (cf. [5, Theorem 11.58]), where ${\mathbf {v}}_{{\mathrm {HOSVD}} }$ is the truncated value of ${\mathbf {v}}$:

$$\begin{aligned} \left\| {\mathbf {v}}-{\mathbf {v}}_{{\mathrm {HOSVD}}}\right\| \le \sqrt{\sum _{\alpha }\sum _{\nu \ge s_{\alpha }+1}(\sigma _{\nu }^{(\alpha )})^{2}} \le \sqrt{2d-3}\left\| {\mathbf {v}}-{\mathbf {v}}_{{\mathrm {best}}}\right\| . \end{aligned}$$

(27)

The first inequality allows us to explicitly control the error with respect to the Euclidean norm by the choice of the omitted singular values. The second inequality proves quasi-optimality of this truncation. ${\mathbf {u}} _{{\mathrm {best}}}\in \mathcal {H}_{\mathfrak {s}}$ is the best approximation. The parameter d is the order of the tensor.

The number $2d-3$ on the right-hand side becomes smaller if $s_{\alpha }=r_{\alpha }$ holds for some vertices $\alpha .$ For instance, the TT format as described in [11] uses the maximal value $s_{j} =r_{j}=\dim (V_{j})$ for the leaves. Then (27) holds with $\sqrt{d-1}$ instead of $\sqrt{2d-3}.$

5 Properties of the SVD projection

5.1 Case of the tensor-subspace format

The HOSVD truncation of the tensor-subspace format in Sect. 3.4 is the Kronecker product

$$\begin{aligned} \varPi :=\bigotimes _{j=1}^{d}P_{j}, \end{aligned}$$

where $P_{j}:V_{j}\rightarrow {\text {span}}\{b_{i}^{(j)}:1\le i\le s_{j}\}$ with $s_{j}<r_{j}$ is the orthogonal projection. $\varPi$ is again an orthogonal projection onto $\bigotimes _{j=1}^{d}{\text {span}} \{b_{i}^{(j)}:1\le i\le s_{j}\}.$

The tensor product $\varPi$ of the single projections $P_{j}$ can also be written as a usual product $\varPi =\prod _{j=1}^{d}{\mathbf {P}}_{j}$ of

$$\begin{aligned} {\mathbf {P}}_{j}:={\mathbf {I}}_{[j]}\otimes P_{j}\qquad \text {with }{\mathbf {I}}_{[j]}:=\bigotimes \nolimits _{k\ne j}I_{j}, \end{aligned}$$

(28)

where $I_{j}$ is the identity map on $V_{j}$. Since the projections ${\mathbf {P}}_{j}$ commute, the order of the factors in $\prod _{j=1} ^{d}{\mathbf {P}}_{j}$ does not matter. We recall the singular-value decomposition of the matricisation $\mathcal {M}_{j}({\mathbf {v}})$ (cf. Sect. 2.4):

$$\begin{aligned} \mathcal {M}_{j}({\mathbf {v}})=\sum \limits _{i=1}^{r_{j}}\sigma _{i}^{(j)} b_{i}^{(j)}({\mathbf {b}}_{i}^{[j]})^{\mathsf {T}}, \end{aligned}$$

where the superscript $[j]=\{j\}^{c}$ denotes the complement of the leaf $\alpha =\{j\}.$ Using (5b), we get

$$\begin{aligned} \mathcal {M}_{j}({\mathbf {P}}_{j}{\mathbf {v}})=P_{j}\mathcal {M}_{j}({\mathbf {v}} )=\sum \limits _{i=1}^{r_{j}}\sigma _{i}^{(j)}\left( P_{j}b_{i}^{(j)}\right) ({\mathbf {b}}_{i}^{[j]})^{\mathsf {T}}=\sum \limits _{i=1}^{s_{j}}\sigma _{i} ^{(j)}b_{i}^{(j)}({\mathbf {b}}_{i}^{[j]})^{\mathsf {T}}. \end{aligned}$$

However, we may also define

$$\begin{aligned} {\hat{\mathbf {P}}}_{j}:={\mathbf {P}}_{[j]}\otimes I_{j}, \end{aligned}$$

(29)

where ${\mathbf {P}}_{[j]}$ is the orthogonal projection of ${\mathbf {V}} _{[j]}=\bigotimes \nolimits _{k\ne j}V_{k}$ onto ${\text {span}} \{{\mathbf {b}}_{i}^{[j]}:1\le i\le s_{j}\}$. As (5b) again shows

$$\begin{aligned} \mathcal {M}_{j}({\hat{\mathbf {P}}}_{j}{\mathbf {v}})=\mathcal {M}_{j}({\mathbf {v}} ){\mathbf {P}}_{[j]}^{\mathsf {T}}=\sum \limits _{i=1}^{r_{j}}\sigma _{i}^{(j)} b_{i}^{(j)}({\mathbf {P}}_{[j]}{\mathbf {b}}_{i}^{[j]})^{\mathsf {T}}=\sum \limits _{i=1}^{s_{j}}\sigma _{i}^{(j)}b_{i}^{(j)}({\mathbf {b}}_{i}^{[j]} )^{\mathsf {T}}, \end{aligned}$$

we obtain the identical value ${\mathbf {P}}_{j}{\mathbf {v}}={\hat{\mathbf {P}}} _{j}{\mathbf {v}}$ although the projections are different. This property has interesting consequences. We introduce

$$\begin{aligned} \varPi _{j}:=\left( \prod \nolimits _{k\ne j}{\mathbf {P}}_{k}\right) {\hat{\mathbf {P}}}_{j} \end{aligned}$$

and observe that $\varPi _{j}{\mathbf {v=(}}\prod _{k\ne j}{\mathbf {P}}_{k} ){\hat{\mathbf {P}}}_{j}{\mathbf {v=(}}\prod _{k\ne j}{\mathbf {P}}_{k}){\mathbf {P}} _{j}{\mathbf {v=}}\varPi {\mathbf {v}}$ holds for the special tensor ${\mathbf {v}}$ although $\varPi _{j}\ne \varPi$. Note that all maps ${\mathbf {P}}_{k}$ and ${\hat{\mathbf {P}}}_{j}$ are elementary tensors containing the identity $I_{j}:V_{j}\rightarrow V_{j}$ with respect to the j-th direction. This proves the next lemma for which we introduce the following notation. Let $\varphi _{j}:V_{j}\rightarrow W_{j}$ be a linear map. It gives rise to the elementary Kronecker product $\phi _{j}:=I_{1}\otimes \cdots \otimes I_{j-1}\otimes \varphi _{j}\otimes I_{j+1}\otimes \cdots \otimes I_{d}.$

Lemma 1

Let $\varphi _{j}:V_{j}\rightarrow W_{j}$ and $\phi _{j}$ as above. Then $\phi _{j}\varPi _{j}=\varPi _{j}\phi _{j}$ holds (the latter $\varPi _{j}$ contains the identity $I_{j}:W_{j}\rightarrow W_{j}$ instead of $I_{j} :V_{j}\rightarrow V_{j}$).

This allows the following estimate with respect to the Euclidean norm.

Conclusion 2

Given ${\mathbf {v}}\in {\mathbf {V}},$ let ${\mathbf {u}}_{{\mathrm {HOSVD}} }\in \mathcal {T}_{{\mathbf {s}}}$ be the HOSVD approximation defined in Sect. 3.4. With $\phi _{j}$ from above we have

$$\begin{aligned} \left\| \phi _{j}{\mathbf {u}}_{{\mathrm {HOSVD}}}\right\| \le \left\| \phi _{j}{\mathbf {v}}\right\| . \end{aligned}$$

(30)

Proof

${\mathbf {u}}_{{\mathrm {HOSVD}}}=\varPi _{j}{\mathbf {v}}$ shows that $\phi _{j} {\mathbf {u}}_{{\mathrm {HOSVD}}}=\phi _{j}\varPi _{j}{\mathbf {v}}=\varPi _{j}\phi _{j}{\mathbf {v}}.$ Since $\varPi _{j}$ is a product of orthogonal projection, $\left\| \varPi _{j}\phi _{j}{\mathbf {v}}\right\| \le \left\| \phi _{j}{\mathbf {v}}\right\|$ follows. $\square$

In the case of infinite-dimensional Hilbert spaces ${\mathbf {V}}$ we may consider unbounded linear maps $\phi _{j}{\mathbf {.}}$ The subspace of elements ${\mathbf {v}}$ for which $\phi _{j}{\mathbf {v}}$ is defined, is called the domain of $\phi _{j}.$

Conclusion 3

If $\,{\mathbf {v}}\in {\mathbf {V}}\,$ belongs to the domain of $\,\phi _{j},\,$ then also $\,{\mathbf {u}}_{{\mathrm {HOSVD}}}$ belongs to the domain and satisfies (30).

An important example is the topological tensor space ${\mathbf {V}}=L^{2} (\varOmega )=\bigotimes _{k=1}^{d}L^{2}(\varOmega _{j}),$ where $\varOmega$ is the Cartesian product of the $\varOmega _{j}.$ Set $\phi _{j}=\partial ^{k}/\partial x_{j}^{k}.$ If the function ${\mathbf {v}}\in {\mathbf {V}}$ possesses a k-th derivative with respect to $x_{j},$ then by Conclusion 3 also ${\mathbf {u}}_{{\mathrm {HOSVD}}}$ is k-times differentiable in the $L^{2}$ sense and satisfies $\left\| \partial ^{k}{\mathbf {u}}_{{\mathrm {HOSVD}}}/\partial x_{j}^{k}\right\| _{L^{2}}\le \left\| \partial ^{k}{\mathbf {v}}/\partial x_{j}^{k}\right\| _{L^{2}}.$ Assuming sufficient smoothness of ${\mathbf {v}}$ and using the Gagliardo–Nirenberg inequality, we proved in [6] estimates of $\left\| {\mathbf {v}}-{\mathbf {u}} _{{\mathrm {HOSVD}}}\right\| _{\infty }$ with respect to the maximum norm by means of the $L^{2}$ norm of ${\mathbf {v}}-{\mathbf {u}}_{{\mathrm {HOSVD}}}.$ This is important for the pointwise evaluation of the truncated function.

Another trivial conclusion from (30) is that $\phi _{j}{\mathbf {v}}=0$ implies $\phi _{j}{\mathbf {u}}_{{\mathrm {HOSVD}}}=0.$ For instance, let $\varphi _{j}\in V_{j}^{\prime }$ be a functional on $V_{j}$ (i.e., $W_{j}=\mathbb {K}).$ Examples of $\varphi _{j}$ are the mean value $\varphi _{j}(u)={\mathbf {1}}^{\mathsf {T}}u$ or a zero at a certain index $i^{*}$: $\varphi _{j}(u)=u_{i^{*}}=0.$ We say that ${\mathbf {v}}$ satisfies the side condition $\varphi _{j}$ if $\phi _{j}{\mathbf {v}}=0.$ We conclude that ${\mathbf {u}}_{{\mathrm {HOSVD}}}$ satisfies the same side condition. In the case of $\varphi _{j}(u)={\mathbf {1}}^{\mathsf {T}}u,$ also ${\mathbf {u}}_{{\mathrm {HOSVD}} }$ has a vanishing mean. If $\varphi _{j}(u)=u_{i^{*}},$ ${\mathbf {u}} _{{\mathrm {HOSVD}}}[{\mathbf {i}}]=0$ holds for ${\mathbf {i}}$ with $i_{j}=i^{*}.$

In the case of matrix spaces $V_{j},$ structural properties like symmetry or sparsity can be described by functionals. One concludes that the HOSVD approximations lead to matrices of the same structure.

5.2 Best approximation ${\mathbf {u}}_{{\mathrm {best}}}$

We recall that the HOSVD approximation ${\mathbf {u}}_{{\mathrm {HOSVD}}} \in \mathcal {T}_{{\mathbf {r}}}$ of ${\mathbf {v}}\in {\mathbf {V}}$ is not (necessarily) the best approximation defined by

$$\begin{aligned} {\mathbf {u}}_{{\mathrm {best}}}\in \mathcal {T}_{{\mathbf {r}}}\qquad \text {with}\quad \left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {best}}}\right\| =\inf \{\left\| {\mathbf {v}}-{\mathbf {u}}\right\| :{\mathbf {u}}\in \mathcal {T}_{{\mathbf {r}} }\} \end{aligned}$$

(31)

(cf. Definition 1). Nevertheless, ${\mathbf {u}}_{{\mathrm {best}}}$ has similar properties as ${\mathbf {u}}_{{\mathrm {HOSVD}}}.$

Define

$$\begin{aligned} U_{k}:=U_{k}^{\min }({\mathbf {u}}_{{\mathrm {best}}})\quad \text { for }\ 1\le k\le d. \end{aligned}$$

Let $P_{k}:V_{k}\rightarrow U_{k}$ be the orthogonal projection onto $U_{k}.$ Based on these projections we define ${\mathbf {P}}_{k}$ and $\varPi$ as in Sect. 5.1. Now we fix one index j and define $\varPi _{[j]}:=\prod _{k\ne j}{\mathbf {P}}_{k}.$ Set ${\mathbf {v}}_{j}:=\varPi _{[j]}{\mathbf {v}}\in U_{1}\otimes \ldots \otimes U_{j-1}\otimes V_{j}\otimes U_{j+1}\otimes \ldots \otimes U_{d}$ and note that ${\mathbf {P}}_{j}{\mathbf {v}} _{j}={\mathbf {u}}_{{\mathrm {best}}}.$ Based on the SVD of $\mathcal {M} _{j}({\mathbf {v}}_{j})$ we can determine its HOSVD approximation ${\mathbf {u}} _{{\mathrm {HOSVD}}}\in \mathcal {T}_{{\mathbf {r}}}$. Since it is the minimiser of $\min _{{\mathbf {u}}\in \mathcal {T}_{{\mathbf {r}}}}\left\| {\mathbf {v}} _{j}-{\mathbf {u}}\right\| ,$ we have $\left\| {\mathbf {v}}_{j} -{\mathbf {u}}_{{\mathrm {HOSVD}}}\right\| \le \left\| {\mathbf {v}} _{j}-{\mathbf {u}}_{{\mathrm {best}}}\right\|$. For an indirect proof assume that $\left\| {\mathbf {v}}_{j}-{\mathbf {u}}_{{\mathrm {HOSVD}}}\right\| <\left\| {\mathbf {v}}_{j}-{\mathbf {u}}_{{\mathrm {best}}}\right\| .$ Both ${\mathbf {u}}_{{\mathrm {HOSVD}}}$ and ${\mathbf {u}}_{{\mathrm {best}}}$ are in the range of $\varPi _{[j]},$ i.e.,

$$\begin{aligned} \left( I-\varPi _{[j]}\right) {\mathbf {u}}_{{\mathrm {HOSVD}}}=\left( I-\varPi _{[j]}\right) {\mathbf {u}}_{{\mathrm {best}}}=0. \end{aligned}$$

Pythagoras’ equality yields

$$\begin{aligned} \left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {HOSVD}}}\right\| ^{2}&=\left\| \varPi _{[j]}({\mathbf {v}}-{\mathbf {u}}_{{\mathrm {HOSVD}} })\right\| ^{2}+\left\| \left( I-\varPi _{[j]}\right) ({\mathbf {v}}-{\mathbf {u}}_{{\mathrm {HOSVD}}})\right\| ^{2}\\&=\left\| {\mathbf {v}}_{j}-{\mathbf {u}}_{{\mathrm {HOSVD}}}\right\| ^{2}+\left\| \left( I-\varPi _{[j]}\right) {\mathbf {v}}\right\| ^{2}\\&<\left\| {\mathbf {v}}_{j}-{\mathbf {u}}_{{\mathrm {best}}}\right\| ^{2}+\left\| \left( I-\varPi _{[j]}\right) {\mathbf {v}}\right\| ^{2}\\&=\left\| \varPi _{[j]}({\mathbf {v}}-{\mathbf {u}}_{{\mathrm {best}} })\right\| ^{2}+\left\| \left( I-\varPi _{[j]}\right) ({\mathbf {v}}-{\mathbf {u}}_{{\mathrm {best}}})\right\| ^{2}\\&=\left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {best}}}\right\| ^{2} \end{aligned}$$

in contradiction to the optimality of ${\mathbf {u}}_{{\mathrm {best}}}.$ Hence, $\left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {HOSVD}}}\right\| =\left\| {\mathbf {v}}-{\mathbf {u}}_{{\mathrm {best}}}\right\|$ must hold. Depending on the multiplicity of certain singular values, the SVD approximation may be unique. In this case ${\mathbf {u}}_{{\mathrm {HOSVD}}}={\mathbf {u}}_{{\mathrm {best}}}$ holds. If the SVD approximation is not unique, we may choose ${\mathbf {u}} _{{\mathrm {best}}}$ as ${\mathbf {u}}_{{\mathrm {HOSVD}}}={\mathbf {P}}_{j}{\mathbf {v}} _{j}.$ Knowing that ${\mathbf {P}}_{j}$ is a SVD projection, we may replace ${\mathbf {P}}_{j}$ by ${\hat{\mathbf {P}}}_{j}$ as defined in (29). The projection $\varPi _{j}:=\varPi _{[j]}{\hat{\mathbf {P}}}_{j}$ has the same properties as $\varPi _{j}$ in §5.1. This proves the following (cf. Uschmajew [13]).

Theorem 4

The statements of Lemma 1 and the Conclusions 2 and 3 also hold for the best approximation ${\mathbf {u}}_{{\mathrm {best}}}$ in (31) and the related mapping $\varPi _{j}$.

5.3 Case of the hierarchical format

The HOSVD truncation within the hierarchical format (cf. Sect. 4.6) can be expressed by orthogonal projections ${\mathbf {P}}_{\alpha }$ for all vertices $\alpha$ of the tree $T_{D}.$ However, different from Sect. 5.1, projections ${\mathbf {P}}_{\alpha }$ and ${\mathbf {P}}_{\beta }$ commute if and only $\alpha \cap \beta =\emptyset .$ The truncation is described by the product

$$\begin{aligned} \varPi :=\prod \nolimits _{\alpha \in T_{D}}{\mathbf {P}}_{\alpha }, \end{aligned}$$

where the factors are ordered in such a way that ${\mathbf {P}}_{\alpha }$ is applied before ${\mathbf {P}}_{\alpha _{1}}$ and ${\mathbf {P}}_{\alpha _{2}}$ ($\alpha _{1},\alpha _{2}$ sons of $\alpha$) follow. Because of these restrictions, the analysis is more involved. We refer the reader to Hackbusch [6, § 4]. As a result the statements in Sect. 5.1 also hold for the hierarchical format.