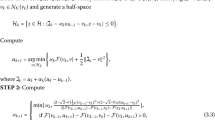1 Introduction

Let C be a nonempty closed and convex subset of a real Hilbert space H. Let \(f: H\times H\rightarrow {\mathbb {R}}\) be a bifunction with \(f(x,x)=0\) for all \(x\in C\). The equilibrium problem of the bifunction f on C, denoted by EP(f, C), is stated as follows:

$$\begin{aligned} \hbox {Find}~x^*\in C~\hbox {such that}~f(x^*,y)\ge 0,~\forall y\in C. \end{aligned}$$
(1)

Equilibrium problem is also called the Ky Fan inequality due to his contribution to this field (Fan 1972). Mathematically, EP(f, C) is a generalization of various important mathematical models including variational inequality problems, optimization problems and fixed point problems, see (Blum and Oettli 1994; Konnov 2000, 2007; Muu and Oettli 1992; Quoc and Muu 2012; Vuong and Strodiot 2020). EPs have been considered by many authors in recent years, e.g., see (Combettes and Hirstoaga 2005; Hieu et al. 2018; Iusem et al. 2009; Lyashko et al. 2011; Lyashko and Semenov 2016; Moudafi 2003; Nguyen et al. 2014; Strodiot et al. 2016; Tran et al. 2008; Vinh and Muu 2019; Vuong et al. 2015, 2012) and the references therein. Some notable methods for EPs have been proposed such proximal point methods (PPM) (Flam and Antipin 1997; Moudafi 1999), auxiliary problem principle methods (Mastroeni 2000) and gap function method (Mastroeni 2003). For an excellent collection of equilibrium modelling and applications, solutions existence as well as solution methods for EPs, we refer the readers to a recent monograph (Bigi et al. 2019).

The PPM is often used for solving monotone EPs, in which a regularized equilibrium problem is formed at each iteration. This sub-problem is strongly monotone, hence the solution is unique and can be computed more easily than solutions of the original problem. Solution approximations generated by the PPM will converge finitely or asymptotically to some solution of the original EPs (Flam and Antipin 1997; Moudafi 1999).

For solving pseudomonotone EPs, a powerful algorithm is the extragradient methods (EGM) studied originally by Korpelevich (1976) for variational inequalities and saddle point problems. This algorithm was extended to EPs in Tran et al. (2008) where the equilibrium bifunctions are pseudomonotone and satisfy a Lipschitz-type assumption. Under suitable conditions imposed on parameters and bifunctions, the iterative sequences generated by the EGM are proved to be convergent to some solution of EP(f, C). In recent years, the extragradient methods have received great attention from the many authors, see, e.g., Censor et al. (2011); Nguyen et al. (2014); Vuong et al. (2015). The advantage of the extragradient method (Vinh and Muu 2019) is that the sub-problems are easier to solve than the PPM. Moreover, it can be applied to the more general class of bifunctions.

The main drawback of EGM is that the chosen step-size depends on the Lipschitz-type constants of the bifunctions (Dang 2017; Lyashko et al. 2011; Lyashko and Semenov 2016; Moudafi 1999). This fact can make some restrictions in applications because the Lipschitz-type constants are often unknown or difficult to estimate. In this work, we propose a new inertial extragradient method for solving strongly pseudo-monotone equilibrium problem. Note that, an extragradient method with inertial effect for solving EPs can be found in Vinh and Muu (2019) where the inertial parameters were chosen depending on the iteration gap and a summable sequence. In addition, no convergence rate was obtained in Vinh and Muu (2019).

The EGM variant proposed in this paper uses a new step-size rule which does not require the knowledge of the Lipschitz-type constants of the bifunction as in Vinh and Muu (2019). Moreover, the inertial parameter can be chosen independently to the iterations. Under suitable conditions on the parameters, we establish the linear convergence of the iterations to the unique solution of the EPs. As a consequence, we provide a linear convergence rate of a modified extragradient method for solving variational inequality problems in Hilbert spaces.

This paper is organized as follows: in Sect. 2, we collect some definitions and preliminary results for further use. Section 3 deals with analyzing the convergence of the proposed algorithm. Finally, we discuss the applications to variational inequalities in Sect. 4, following with some numerical examples in Sect. 5.

2 Preliminaries

Let C be a nonempty closed convex subset of H. We begin with some concepts of monotonicity of a bifunction (Blum and Oettli 1994; Muu and Oettli 1992). A bifunction \(f:H\times H\rightarrow {\mathbb {R}}\) is said to be:

(i) strongly monotone on C if there exists a constant \(\gamma >0\) such that

$$\begin{aligned} f(x,y)+f(y,x)\le -\gamma ||x-y||^2, \quad \forall x,y\in C. \end{aligned}$$

(ii) strongly pseudomonotone on C if there exists a constant \(\gamma >0\) such that

$$\begin{aligned} f(x,y)\ge 0 \Longrightarrow f(y,x)\le -\gamma ||x-y||^2, \quad \forall x,y\in C. \end{aligned}$$

(iii) satisfied Lipschitz-type condition on C if there exist two positive constants \(c_1,c_2\) such that

$$\begin{aligned} f(x,y) + f(y,z) \ge f(x,z) - c_1||x-y||^2 - c_2||y-z||^2, \quad \forall x,y,z \in C. \end{aligned}$$

From the definitions above, it is obvious that \(\mathrm (i) \Longrightarrow (ii)\).

The normal cone \(N_C\) to C at a point \(x\in C\) is defined by

$$\begin{aligned} N_C(x)=\left\{ w\in H:\left\langle w,x-y\right\rangle \ge 0, \forall y\in C\right\} . \end{aligned}$$

For every \(x\in H\), the metric projection \({ P_C(x)}\) of x onto C is defined by

$$\begin{aligned} { P_C(x)}=\arg \min \left\{ \left\| y-x\right\| :y\in C\right\} . \end{aligned}$$

Since C is nonempty, closed and convex, \({ P_C(x)}\) exists and is unique.

For each \(x,z\in H,\) by \(\partial f(z,x),\) we denote the subdifferential of convex function \(f(z,\cdot )\) at x, i.e.,

$$\begin{aligned} { \partial f(z,x)}:=\{u\in H:f(z,y)\ge f(z,x)+\langle u,y-x\rangle , \forall y\in H\}. \end{aligned}$$

In particular,

$$\begin{aligned} {\partial f(z,z)}=\{u\in H:f(z,y)\ge \langle u,y-z\rangle , \forall y \in H\}. \end{aligned}$$

For proving the convergence of the algorithm, we need the following lemma.

Lemma 2.1

(Peypouquet 2015, Proposition 3.61) Let C be a nonempty closed convex subset of H and \(g:H\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a proper, convex and lower semicontinuous function on H. Assume either that g is continuous at some point of C, or that there is an interior point of C where g is finite. Then, \(x^*\) is a solution to the following convex problem \( \min \left\{ g(x):x\in C\right\} \) if and only if   \(0\in \partial g(x^*)+N_C(x^*)\), where \(\partial g(\cdot )\) denotes the subdifferential of g and \(N_C(x^*)\) is the normal cone of C at \(x^*\).

Definition 2.1

(Ortega and Rheinboldt 1970) Let \(\{x_n\}\) be a sequence in H.

(i) \(\{x_n\}\) is said to converge R-linearly to \(x^*\) with rate \(\rho \in [0, 1)\) if there is a constant \(c>0\) such that

$$\begin{aligned} \Vert x_n-x^*\Vert \le c\rho ^n \quad \forall n\in {\mathbb {N}}. \end{aligned}$$

(ii) \(\{x_n\}\) is said to converge Q-linearly to \(x^*\) with rate \(\rho \in [0, 1)\) if

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert \le \rho \Vert x_n-x^*\Vert \quad \forall n\in {\mathbb {N}}. \end{aligned}$$

3 Convergence analysis

Now, we are in a position to present a modified version of inertial extragradient method in Vinh and Muu (2019) for solving equilibrium problems.

figure a

Remark 3.1

The self-adaptive stepsizes \(\{\lambda _n\}\) chosen as in (2) is allowed to increase from iteration to iteration showing that the self-adaptive stepsize in this work is different from the studied self-adaptive stepsize in the literature (Hieu et al. 2018; Dang 2017; Muu and Quoc 2009; Tran et al. 2008; Vinh and Muu 2019). The initial stepsize \(\lambda _1\) chosen in (2) could be arbitrary large allowing fast convergence from the beginning of the iterations. In particular, (Vinh and Muu 2019, Algorithm 1) proposed an inertial extragradient method for solving pseudo-monotone EPs with fixed stepsize and inertial parameters were chosen along the course of iterations depending on a summable series, which were different from Algorithm (3.1). In addition, the linear convergence rate was not investigated in (Vinh and Muu 2019).

In order to establish the convergence of Algorithm 3.1, we assume that bifunction \(f:H\times H\rightarrow {\mathbb {R}}\) satisfies the following conditions.

Condition 1

(A1) f is \(\gamma \)-strongly pseudomonotone on C.

(A2) f satisfies Lipschitz-type condition on H with two constants \(c_1\) and \(c_2\).

(A3) \(f(x,\cdot )\) is convex and lower semicontinuous on H for every fixed \(x\in H.\)

(A4) Either \(int C \ne \emptyset \) or \(f (x,\cdot )\) is continuous at some point in C for every \(x \in H\).

Remark 3.2

From the condtions (A1) and (A2) we get \(f(x,x)=0\) for all \(x\in C.\) It is also known that under Condition 1, the problem EP(f,C) has unique solution (Muu and Quy 2015). It is easy to see that the uniqueness of solution is guaranteed by the strong pseudomonotonicity of the bifunction f. For generic conditions of solution existence and their relaxations, we refer the readers to an excellent survey (Bigi et al. 2013, Section 2). In particular, the most simplest conditions for solution existence are: C is a bounded and convex set; \(f(x, \cdot )\) is convex for each \(x\in C\) and \(f(\cdot , y)\) is continuous for each \(y\in C\).

Next, we will establish the convergence rate of Algorithm 3.1. We start with the following lemmas which play an important role in proving the convergence of the proposed algorithm.

Lemma 3.1

(Yang 2020) Let Condition 1 be satisfied. Let \(\{\lambda _n\}\) be a sequence generated by Algorithm 3.1. Then

$$\begin{aligned} \lim _{n\rightarrow \infty }\lambda _{n}=\lambda \in \bigg [\min \bigg \{ \dfrac{\mu }{2\max \{c_1,c_2\}}, \lambda _1\bigg \},\lambda _1+\tau \bigg ], \end{aligned}$$

where \(\tau =\sum _{n=1}^\infty \tau _n.\)

Lemma 3.2

For any \(\lambda > 0\) and \(x,t \in H\), let

$$\begin{aligned} z = \underset{y\in C}{\text{ argmin }}\, \left\{ \lambda f(x,y) + \frac{1}{2}\Vert y-t\Vert ^2\right\} , \end{aligned}$$
(3)

then

$$\begin{aligned} \lambda \left( f(x,y) -f(x, z) \right) \ge \left\langle t-z, y-z\right\rangle \quad \forall y \in C. \end{aligned}$$

Proof

Since z is the unique solution of the strongly convex minimization problem (3). The optimality condition (Lemma 2.1) implies that there exists \(s \in { \partial f(x, z)}\) such that

$$\begin{aligned} 0 \in \lambda s + z - t + N_{C}(z), \end{aligned}$$

Hence, by definition of this cone, we obtain that

$$\begin{aligned} \langle t-z- \lambda s,y-z \rangle \le 0 \quad \forall y \in C. \end{aligned}$$
(4)

On the other hand, since \(s \in { \partial f(x, z)}\), we have

$$\begin{aligned} f(x,y) -f(x, z) \ge \langle s,y-z\rangle \quad \forall y \in C. \end{aligned}$$
(5)

Combining (4) and (5), we obtain

$$\begin{aligned} \lambda \left( f(x,y) -f(x, z) \right) \ge \langle \lambda s,y-z\rangle \ge \left\langle t-z, y-z\right\rangle \quad \forall y \in C. \end{aligned}$$

Lemma 3.3

Let C be a nonempty, closed and convex subset of H and \(f:H\times H \rightarrow {\mathbb {R}}\) be a bifunction satisfying Condition 1. Let u be the unique solution of EP(f, C). Then the following inequality holds

$$\begin{aligned} \Vert u_{n+1}-u\Vert ^2&\le \Vert t_n-u\Vert ^2 -\bigg (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\bigg )\Vert t_n-v_n\Vert ^2-\bigg (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}} \bigg )\Vert u_{n+1}-v_n\Vert ^2 \nonumber \\&\quad \, -2\lambda _n\gamma \Vert v_n-u\Vert ^2. \end{aligned}$$
(6)

Proof

From

$$\begin{aligned} u_{n+1}= \underset{y\in C}{\hbox {argmin}} \left\{ \lambda _n f(v_n, y) +\frac{1}{2}\Vert y-t_n\Vert ^2\right\} , \end{aligned}$$

by Lemma 3.2, we get

$$\begin{aligned} \lambda _n (f(v_n,y)-f(v_n,u_{n+1}))\ge \langle t_n-u_{n+1},y-u_{n+1}\rangle \quad \forall y\in C. \end{aligned}$$

Substituting \(y:=u \in C\), we obtain

$$\begin{aligned} \lambda _n (f(v_n,u)-f(v_n,u_{n+1}))\ge \langle t_n-u_{n+1},u-u_{n+1}\rangle . \end{aligned}$$
(7)

Since u is the unique solution of EP(f, C) and \(v_n\in C\), we have \(f(u,v_n)\ge 0\). By the strong pseudomonotonicity assumption of f, we obtain \(f(v_n,u)\le -\gamma \Vert v_n-u\Vert ^2.\) It implies from (7) that

$$\begin{aligned} -\lambda _n f(v_n,u_{n+1})&\ge \langle t_n-u_{n+1},u-u_{n+1}\rangle -\lambda _n f(v_n,u)\nonumber \\&\ge \langle t_n-u_{n+1},u-u_{n+1}\rangle +\lambda _n \gamma \Vert v_n-u\Vert ^2. \end{aligned}$$
(8)

Again, since

$$\begin{aligned} v_n= \underset{y\in C}{\hbox {argmin}} \left\{ \lambda _n f(t_n, y) +\frac{1}{2}||y-t_n||^2\right\} , \end{aligned}$$

Lemma 3.2 implies

$$\begin{aligned} \lambda _n(f(t_n,u_{n+1})-f(t_n,v_n))\ge \langle t_n-v_n,u_{n+1}-v_n\rangle . \end{aligned}$$
(9)

Adding (8) and (9) we get

$$\begin{aligned}&2\lambda _n(f(t_n,u_{n+1})-f(t_n,v_n)-f(v_n,u_{n+1}))\\&\quad \ge 2\langle t_n-v_n,u_{n+1}-v_n\rangle + 2\langle t_n-u_{n+1},u-u_{n+1}\rangle +2\lambda _n \gamma \Vert v_n-u\Vert ^2\\&\quad =(\Vert t_n-v_n\Vert ^2+\Vert u_{n+1}-v_n\Vert ^2-\Vert u_{n+1}-t_n\Vert ^2)+\\&\qquad +(\Vert t_n-u_{n+1}\Vert ^2+\Vert u_{n+1}-u\Vert ^2-\Vert t_n-u\Vert ^2)+2\lambda _n \gamma \Vert v_n-u\Vert ^2\\&\quad =\Vert t_n-v_n\Vert ^2+\Vert u_{n+1}-v_n\Vert ^2+\Vert u_{n+1}-u\Vert ^2 -\Vert t_n-u\Vert ^2+2\lambda _n\gamma \Vert v_n-u\Vert ^2. \end{aligned}$$

This implies that

$$\begin{aligned} \Vert u_{n+1}-u\Vert ^2&\le \Vert t_n-u\Vert ^2-\Vert t_n-v_n\Vert ^2-\Vert u_{n+1}-v_n\Vert ^2+2\lambda _n(f(t_n,u_{n+1}) \nonumber \\&\quad \, -f(t_n,v_n)-f(v_n,u_{n+1})) - 2\lambda _n\gamma \Vert v_n-u\Vert ^2. \end{aligned}$$
(10)

On the other hand, from the definition of the sequence \(\lambda _n\) we get

$$\begin{aligned} 2(f(t_n,u_{n+1})-f(t_n,v_n)-f(v_n,u_{n+1}))\le \dfrac{\mu }{\lambda _{n+1}}\bigg (\Vert t_n-v_n\Vert ^2+\Vert u_{n+1}-v_n\Vert ^2\bigg ).\nonumber \\ \end{aligned}$$
(11)

Substituting (10) into (11) we obtain

$$\begin{aligned} \Vert u_{n+1}-u\Vert ^2&\le \Vert t_n-u\Vert ^2-\bigg (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\bigg )\Vert t_n-v_n\Vert ^2-\bigg (1-\mu \dfrac{\lambda _n}{\lambda _{n+1}} \bigg )\Vert u_{n+1}-v_n\Vert ^2\nonumber \\&\quad - 2\lambda _n\gamma \Vert v_n-u\Vert ^2. \end{aligned}$$

In the following theorem we will show that the sequence \(\{u_n\}\) generated by Algorithm 3.1 converges strongly to the unique solution u with a R-linear rate.

Theorem 3.1

Let C be a nonempty closed convex subset of H. Let \(f: H \times H \rightarrow {\mathbb {R}}\) be a bifunction satisfying Condition 1. Let \(\theta \in (0,1)\) be arbitrary and \(\rho \) be a real number such that

$$\begin{aligned} 0 \le \rho \le \dfrac{\omega \epsilon }{\omega \epsilon +2\omega +\epsilon }, \end{aligned}$$
(12)

where \(\omega :=1-\min \bigg \{\dfrac{(1-\mu )\theta }{ 4},\dfrac{\gamma \lambda }{2} \bigg \}\) and \(\epsilon :=\dfrac{1}{ 2}(1-\mu )(1-\theta )\theta \). Then the sequence \(\{u_n\}\) generated by Algorithm 3.1 converges in norm to the unique solution u of the problem EP(f,C) with a R-linear rate.

Proof

First, we show that there exists \(N_1\in {\mathbb {N}}\) such that

$$\begin{aligned} \Vert u_{n+1}-u\Vert ^2\le&\, \omega \Vert t_n-u\Vert ^2-\epsilon \Vert u_{n+1}- t_n\Vert ^2 \ \ \forall n\ge N_1. \end{aligned}$$
(13)

Indeed, it follows from Lemma 3.1 that \(\lim _{n \rightarrow \infty } \lambda _n = \lambda > 0\) and since \({ \mu < 1}\), there exists \(N>0\) such that

$$\begin{aligned} \left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) >0 \quad \forall n\ge N. \end{aligned}$$

Thanks to (6) and \(\theta \in (0,1)\), we have for all \(n\ge N\) that

$$\begin{aligned} \begin{aligned} \Vert u_{n+1}-u\Vert ^2&\le \Vert t_n-u\Vert ^2 -\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) \Vert v_n- t_n\Vert ^2 \\ {}&\quad -\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) (1-\theta )\Vert u_{n+1}-v_n\Vert ^2 -2\lambda _n\gamma \Vert v_n-u\Vert ^2\ \\&=\Vert t_n-u\Vert ^2 -\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) \theta \Vert v_n- t_n\Vert ^2\\&\quad -\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) (1-\theta )\bigg [\Vert v_n- t_n\Vert ^2 +\Vert u_{n+1}-v_n\Vert ^2\bigg ]-2\lambda _n\gamma \Vert v_n-u\Vert ^2 \\&\le \Vert t_n-u\Vert ^2 -\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) \theta \Vert v_n- t_n\Vert ^2\\&\quad - \dfrac{1}{2}\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) (1-\theta )\Vert u_{n+1}- t_n\Vert ^2 -2\lambda _n\gamma \Vert v_n-u\Vert ^2, \end{aligned} \end{aligned}$$
(14)

where we have used the Cauchy–Schwartz inequality in the last estimation. Moreover, we get

$$\begin{aligned}{} & {} \lim _{n\rightarrow \infty }\dfrac{1}{2}\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) (1-\theta ) =\dfrac{1}{2}(1-\mu )(1-\theta )> \dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta , \\ {}{} & {} \lim _{n\rightarrow \infty }\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) \theta =(1-\mu )\theta> 2\min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2}\bigg \}, \\ {}{} & {} \lim _{n\rightarrow \infty }\lambda _n\gamma =\lambda \gamma > \min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2} \bigg \}. \end{aligned}$$

Using the definition of the limit, there exists \(N_1\in {\mathbb {N}}\) and \(N_1\ge N\), such that for all \(n\ge N_1\)

$$\begin{aligned}{} & {} \dfrac{1}{2}\left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) (1-\theta ) \ge \dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta , \\{} & {} \left( 1-\mu \dfrac{\lambda _n}{\lambda _{n+1}}\right) \theta \ge 2\min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2} \bigg \}, \end{aligned}$$

and

$$\begin{aligned} \lambda _n\gamma \ge \min \bigg \{\dfrac{(1-\mu )\theta }{4}, \dfrac{\gamma \lambda }{2} \bigg \}. \end{aligned}$$

Using (14) we obtain for all \(n\ge N_1\) that

$$\begin{aligned} \Vert u_{n+1}-u\Vert ^2&\le \Vert t_n-u\Vert ^2 -2\min \bigg \{\dfrac{(1-\mu )\theta }{4}, \dfrac{\gamma \lambda }{2} \bigg \}\Vert v_n- t_n\Vert ^2 \\&\quad -\dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta \Vert u_{n+1}- t_n\Vert ^2\nonumber \\&\quad -2\min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2} \bigg \} \Vert v_n-u\Vert ^2 \nonumber \\&= \Vert t_n-u\Vert ^2-\dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta \Vert u_{n+1}- t_n\Vert ^2\nonumber \\&\quad -2\min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2} \bigg \}(\Vert v_n- t_n\Vert ^2+\Vert v_n-u\Vert ^2)\ \nonumber \\&\le \Vert t_n-u\Vert ^2-\dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta \Vert u_{n+1}- t_n\Vert ^2\\&\quad -\min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2} \bigg \}\Vert t_n-u\Vert ^2\ \ \nonumber \\&= \bigg (1-\min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2}\bigg \}\bigg )\Vert t_n-u\Vert ^2- \dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta \Vert u_{n+1}- t_n\Vert ^2 \ \nonumber \\&\le \bigg (1-\min \bigg \{\dfrac{(1-\mu )\theta }{4},\dfrac{\gamma \lambda }{2}\bigg \}\bigg )\Vert t_n-u\Vert ^2- \dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta \Vert u_{n+1}- t_n\Vert ^2 \ \nonumber \\&=\omega \Vert t_n-u\Vert ^2- \epsilon \Vert u_{n+1}- t_n\Vert ^2. \ \nonumber \end{aligned}$$

Next, we show that the sequence \(\{u_n\}\) converges strongly to the unique solution u of the problem EP(f, C). Indeed, we have

$$\begin{aligned} \Vert t_n-u\Vert ^2&=\Vert (1+\rho )(u_n-u)-\rho (u_{n-1}-u)\Vert ^2\\&=(1+\rho )\Vert u_n-u\Vert ^2-\rho \Vert u_{n-1}-u\Vert ^2+\rho (1+\rho )\Vert u_n-u_{n-1}\Vert ^2 \end{aligned}$$

and

$$\begin{aligned} \Vert u_{n+1}-t_n\Vert ^2&=\Vert u_{n+1}-u_n-\rho (u_n -u_{n-1})\Vert ^2\\&= \Vert u_{n+1}-u_n\Vert ^2 + \rho ^2 \Vert u_n - u_{n-1}\Vert ^2- 2 \rho \left\langle u_{n+1} -u_n, u_n -u_{n-1}\right\rangle \\&\ge \Vert u_{n+1}-u_n\Vert ^2 + \rho ^2 \Vert u_n - u_{n-1}\Vert ^2- 2 \rho \Vert u_{n+1} -u_n\Vert \Vert u_n -u_{n-1}\Vert \\&\ge \Vert u_{n+1}-u_n\Vert ^2 + \rho ^2 \Vert u_n - u_{n-1}\Vert ^2- \rho \Vert u_{n+1} -u_n\Vert ^2 -\rho \Vert u_n -u_{n-1}\Vert ^2\\&= (1-\rho )\Vert u_{n+1}-u_n\Vert ^2 - \rho (1-\rho ) \Vert u_n - u_{n-1}\Vert ^2. \end{aligned}$$

Combining these inequalities with (13) we obtain

$$\begin{aligned} \Vert u_{n+1}-u\Vert ^2&\le \omega (1+\rho )\Vert u_n-u\Vert ^2-\omega \rho \Vert u_{n-1}-u\Vert ^2+\omega \rho (1+\rho )\Vert u_n-u_{n-1}\Vert ^2\\&\quad - \epsilon (1-\rho )\Vert u_{n+1}-u_n\Vert ^2 + \epsilon \rho (1-\rho ) \Vert u_n - u_{n-1}\Vert ^2 \quad \forall n\ge N_1, \end{aligned}$$

or equivalently

$$\begin{aligned}&\Vert u_{n+1}-u\Vert ^2 - \omega \rho \Vert u_{n}-u\Vert ^2 + \epsilon (1-\rho )\Vert u_{n+1}-u_n\Vert ^2\\&\quad \le \, \omega \left[ \Vert u_n-u\Vert ^2-\rho \Vert u_{n-1}-u\Vert ^2+ \epsilon (1-\rho ) \Vert u_n - u_{n-1}\Vert ^2\right] \\&\qquad - \left( \omega \epsilon (1-\rho )-\omega \rho (1+\rho )- \epsilon \rho (1-\rho )\right) \Vert u_n - u_{n-1}\Vert ^2\quad \forall n\ge N_1. \end{aligned}$$

Setting

$$\begin{aligned} \Sigma _n:= \Vert u_n-u\Vert ^2-\rho \Vert u_{n-1}-u\Vert ^2+ \epsilon (1-\rho )\Vert u_n - u_{n-1}\Vert ^2, \end{aligned}$$

since \(\omega \in (0,1)\), we can write

$$\begin{aligned} \Sigma _{n+1} \le&\, \Vert u_{n+1}-u\Vert ^2 - \omega \rho \Vert u_{n}-u\Vert ^2 + \epsilon (1-\rho )\Vert u_{n+1}-u_n\Vert ^2\\ \le&\, \omega \Sigma _n - \left( \omega \epsilon (1-\rho )-\omega \rho (1+\rho )- \epsilon \rho (1-\rho )\right) \Vert u_n - u_{n-1}\Vert ^2\ \ \forall n\ge N_1. \end{aligned}$$

We show that

$$\begin{aligned} \omega \epsilon (1-\rho )-\omega \rho (1+\rho )- \epsilon \rho (1-\rho ) \ge 0. \end{aligned}$$

Indeed, from (12) we get \(\rho \in [0,1)\), thus we obtain \(1+ \rho \le 2\) and \(\rho (1-\rho )\le \rho \), hence

$$\begin{aligned} \omega \epsilon (1-\rho )-\omega \rho (1+\rho )- \epsilon \rho (1-\rho )&\ge \omega \epsilon (1-\rho )-2 \omega \rho - \epsilon \rho \\&= \omega \epsilon -\rho ( \omega \epsilon +2\omega +\epsilon )\ge 0. \end{aligned}$$

Therefore

$$\begin{aligned} \Sigma _{n+1} \le \omega \Sigma _n \quad \forall n\ge N_1. \end{aligned}$$

Next, we show that \(\Sigma _n\ge 0\) for all n. From (12) we deduce

$$\begin{aligned} \rho \le \dfrac{\omega \epsilon }{\omega \epsilon +2\omega +\epsilon } \le \dfrac{\omega \epsilon }{w\epsilon +2\omega }= \frac{\epsilon }{2+\epsilon }, \end{aligned}$$

which implies \(\rho \le \frac{\epsilon (1-\rho )}{2}\). Using this fact, we obtain

$$\begin{aligned} \Sigma _n&= (1-\epsilon (1-\rho )) \Vert u_n-u\Vert ^2 + \epsilon (1-\rho ) \left( \Vert u_n-u\Vert ^2+\Vert u_n - u_{n-1}\Vert ^2\right) -\rho \Vert u_{n-1}-u\Vert ^2\\&\ge (1-\epsilon (1-\rho )) \Vert u_n-u\Vert ^2 +\frac{\epsilon (1-\rho )}{2} \Vert u_{n-1}-u\Vert ^2 -\rho \Vert u_{n-1}-u\Vert ^2 \\&\ge (1-\epsilon (1-\rho )) \Vert u_n-u\Vert ^2 \ge 0. \end{aligned}$$

Hence

$$\begin{aligned} \Sigma _{n+1} \le \omega \Sigma _n \le \cdots \le \omega ^{n-N_1+1}\Sigma _{N_1}. \end{aligned}$$
$$\begin{aligned} \Vert u_n-u\Vert ^2\le \dfrac{\Sigma _{N_1}}{\omega ^{N_1-1}}\omega ^n, \end{aligned}$$

which means that \(\left\{ u_n \right\} \) converges R-linearly to u.

Remark 3.3

Using the similar technique in Vinh and Muu (2019); Yang (2020), one can obtain the weak convergence of Algorithm 3.1 under conditions: f is pseudomonotone on C; \(f(\cdot ,y)\) is weakly upper semicontinuous on C, (A2), (A3), (A4) and the solution set \(EP(f,C)\ne \emptyset \). We omit the proof here.

4 Application to variational inequalities

In this Section, we discuss the applications of the main result obtained in Sect. 3 for solving variational inequality problems in Hilbert spaces. Let \( f(x, y) = \langle { F(x)}, y- x\rangle , \ \forall x, y \in C\), where \(F: H \rightarrow H\) is a continuous mapping. Then the equilibrium problems (1) becomes the variational inequality problem, i.e., find \(x^*\in C\) such that

$$\begin{aligned} \langle { F(x^*)}, y - x^*\rangle \ge 0 \quad \forall y \in C. \end{aligned}$$
(15)

The solution set of (15) is denoted by Sol(F, C). Moreover, we have

$$\begin{aligned} v_n= \underset{y\in C}{\hbox {argmin}} \{ \lambda _n f(t_n, y) +\frac{1}{2}||y-t_n||^2\}= P_C(t_n - \lambda _n { F(t_n)}). \end{aligned}$$

We recall that the mapping F is \(\delta \)-strongly pseudomonotone on C if there exists a constant \(\delta >0\) such that

$$\begin{aligned} \langle { F(x)},y-x \rangle \ge 0 \Longrightarrow \langle { F(y)},y-x \rangle \ge \delta \Vert x-y\Vert ^2 \ \ \ \forall x,y \in C. \end{aligned}$$

If F is L-Lipschitz continuous and strongly pseudomonotone, then the conditions (A1)-(A4) hold for f with \(c_1 = c_2 = \dfrac{L}{2}\). Note that, under these assumption, Sol(F, C) is nonempty and singleton (Kim et al. 2016). For solving variational inequality, we propose the following algorithm.

figure b

The following result is a direct consequence of Theorem 3.1.

Theorem 4.1

Assume that \(F: H\rightarrow H\) is L-Lipschitz continuous on H and \(\delta \)-strongly pseudomonotone on C. Let \(\theta \in (0,1)\) be arbitrary and \(\rho \) be a real number such that

$$\begin{aligned} 0 \le \rho \le \dfrac{\omega \epsilon }{\omega \epsilon +2\omega +\epsilon }, \end{aligned}$$

where \(\omega :=1-\min \bigg \{\dfrac{(1-\mu )\theta }{4}, \dfrac{\gamma \lambda }{2}\bigg \}\) and \(\epsilon :=\dfrac{1}{{ 2}}(1-\mu )(1-\theta )\theta \). Then the sequence \(\{u_n\}\) generated by Algorithm 4.1 converges in norm to the unique solution \(u \in \mathrm{Sol(F,C)}\) with a R-linear rate.

Remark 4.1

As a consequence of Remark 3.3 we can also obtain the weak convergence of Algorithm 4.1 under conditions: F is pseudomonotone on H; F is L-Lipschitz continuous on H; F is sequentially weakly continuous on C and the solution set \(Sol(F,C)\ne \emptyset \).

5 Numerical Illustrations

In this section, we consider some numerical results to illustrate the linear convergence of Algorithm 3.1 and compare its performance with the relaxed projection algorithm (Vuong and Strodiot 2020) and the inertial extragradient algorithm proposed by Vinh and Muu (2019). The codes are implemented in MATLAB.

Example 1: The bifunction f of the equilibrium problem comes from the Cournot-Nash equilibrium model considered by Quoc and Muu (2012). It is defined for each \(x,y \in {\mathbb {R}}^5\), by

$$\begin{aligned} f(x,y) = \langle Px + Qy + r, y-x \rangle \end{aligned}$$

where \(r \in {\mathbb {R}}^5\), and P and Q are two square matrices of order 5 such that \(P-Q\) is symmetric positive definite. It was proved by Quoc and Muu (2012) that the function f is strongly pseudo-monotone with modulus \(\gamma =\lambda _{min}(P-Q)\), the smallest eigenvalue of \(P-Q\) and f satisfies the Lipschitz-type condition with modulus \(c_1 = c_2 = \frac{1}{2}\Vert P-Q\Vert \). As in Quoc and Muu (2012), in our test, the vector r and the matrices P and Q are chosen as follows:

$$\begin{aligned} r = \left[ \begin{array}{r}1\\ {}-2\\ {}-1\\ 2\\ {}-1 \end{array}\right] ; \quad P = \left[ \begin{array}{ccccc}3.1 &{} 2 &{} 0 &{} 0&{} 0\\ 2&{} 3.6&{} 0&{} 0&{} 0\\ 0 &{} 0&{} 3.5&{} 2&{} 0\\ 0&{} 0&{} 2&{} 3.3&{} 0\\ 0&{} 0&{} 0&{} 0&{} 3\end{array}\right] ; \quad Q = \left[ \begin{array}{ccccc}1.6&{} 1&{} 0&{} 0 &{}0\\ 1&{} 1.6&{} 0 &{}0&{} 0\\ 0&{} 0&{} 1.5&{} 1&{} 0\\ 0&{} 0 &{}1&{} 1.5&{} 0\\ 0&{} 0&{} 0&{} 0 &{}2\end{array}\right] . \end{aligned}$$

The constraint set of this problem is defined by

$$\begin{aligned} C= \left\{ x \in {\mathbb {R}}^5 \, | \, \sum _{i=1}^{5} x_i \ge 0, \quad -5 \le x_i \le 5, \quad i=1,2,3,4,5 \right\} , \end{aligned}$$

and its solution \(x^*\) is given by

$$\begin{aligned} x^*=(-0.725388, 0.803109, 0.72000, -0.866667, 0.200000)^T. \end{aligned}$$

In this example, \(\gamma =\lambda _{min}(P-Q)=0.7192\) and \(L = \Vert P-Q\Vert ,\) \(c_1 =c_2 = \frac{1}{2}\Vert P-Q\Vert = 1.45 \). The stopping condition is ErrorBound = \(\Vert u_{n+1}-u_n\Vert \le 10^{-5}\).

For the projection type algorithms in Vuong and Strodiot (2020), we choose \(\lambda = 1.9 * \gamma /L^2\) with the non-relaxed parameter (\(\alpha = 1\), red curve in Fig. 1) and \(\lambda = \gamma /L^2\) with the over-relaxed parameter (\(\alpha _{max} = 1.014\), black curve in Fig. 1). Moreover, the blue curve in Fig. 1 presents the inertial extragradient algorithm in Vinh and Muu (2019) with the stepsize \(\lambda = \frac{1}{2c_2}, \delta = 0.6\) and \(\epsilon _n=\frac{1}{n^2}, n=1,2,....\). Figure 1 presents the comparisons of the performance of these methods with \(u_0= u_1= (2,1,4,-1,-2)^T\) and the stopping condition \(10^{-5}\). It is clear that Algorithm 3.1 (green curve in Fig. 1) outperforms the others thanks to the very large initial stepsize (\(\lambda _1=5000\)) and inertial effect even though it is quite small (\(\rho = 0.003\)). The sequence \(\{\tau _n\}\) is chosen the same as \(\{\epsilon _n\}\). It is also noticed that the error estimates in Algorithm 3.1 has some oscillation phenomenon, which is well understood in algorithms with inertial effects for solving optimization problems. We believe that this is also the case for algorithms with inertial effects for solving EPs.

Fig. 1
figure 1

Performance of different algorithms when \(u_0=u_1=(2,1,4,-1,-2)^T\)

Full size image

Example 2: Similar to Krawczyk and Uryasev (2000); Quoc and Muu (2012), in this example, we consider the problem of River basin pollution game. There are three players \(j =1,2,3\) located along a river. Each agent is engaged in an economic activity (paper pulp producing) at a chosen level \(x_j\), but the players must meet the environmental condition set by a local authority. Pollutants may be expelled into the river, where they disperse. Two monitoring stations are located along the river, at which the local authority has set maximum pollutant concentration levels. The revenue and the expenditure for player j are

$$\begin{aligned} R_j(x)=[a_1-a_2(x_1+x_2+x_3)]x_j, \end{aligned}$$

and

$$\begin{aligned} F_j(x)=(b_{1j}+b_{2j}x_j)x_j, \end{aligned}$$

respectively, where the parameters \(a_1=3.0, a_2=0.01, b_{1j}=0.1, 0.12, 0.15,\) and \(c_{2j}=0.01, 0.05, 0.01\) for \(j=1, 2, 3\), respectively. The profit of player j is

$$\begin{aligned} K_j(x)=R_j(x)-F_j(x). \end{aligned}$$

The constraint on emission imposed by the local authority at location is

$$\begin{aligned} q_i(x)=\sum _{j=1}^3{u_jv_{ij}x_j \le 100, \quad i = 1,2,} \end{aligned}$$

where \(u_j=0.5, 0.25, 0.75, v_{1j}=6.5, 5.0, 5.5\) and \(v_{2j}=4.583, 6.25, 3.75\) for \(j =1,2,3\), respectively. The level \(x_j\) is nonnegative for \(j = 1,2,3\). Players try to maximize their profit \(K_j(x)\) satisfying the condition \(q_i(x) \le 100, i = 1,2\) and \(x \ge 0.\)

This problem can be reformulated as the equilibrium problem, where

$$\begin{aligned} P=\left[ \begin{array}{ccccc}a_2+b_{21} &{} a_2 &{} a_2\\ a_2&{} a_2+b_{22}&{} a_2\\ a_2 &{} a_2&{} a_2+b_{23}\end{array}\right] ; \quad Q=\left[ \begin{array}{ccccc}a_2+b_{21} &{} 0 &{} 0\\ 0&{} a_2+b_{22}&{} 0\\ 0 &{} 0&{} a_2+b_{23}\end{array}\right] \end{aligned}$$

and \(r=\left[ \begin{array}{r}b_{11}-a_1\\ b_{12}-a_1\\ b_{13}-a_1\end{array}\right] .\) Note that since \(P-Q\) is not positive definite, this linear equilibrium problem is not strongly monotone. However, since \(P+Q\) and Q are positive definite, we can choose matrix \(T=0.1\times \textrm{diag}(b_{21},b_{22},b_{23})\) such that this problem is equivalent to a strongly monotone linear equilibrium problem as in Example 1 when \(P_1 = P+T, Q_1 = Q-T\) and \(r_1 = r\) (see Quoc and Muu (2012) for more details). For this choice, the corresponding parameters are \(\gamma = \lambda _{min}(P_1-Q_1) = 0.019\) and \(L = \frac{1}{2}\Vert P_1-Q_1\Vert = 0.055.\) The other parameters are similar to Example 1 except \(\alpha _{max} = 1.5\). We also compare the performance of four algorithms with \(u_0= u_1= (0,0,0)^T\) and the stopping condition ErrorBound\(=\Vert u_{n+1}-u_n\Vert \le 10^{-5}\) in Fig. 2. Once again, Algorithm 3.1 demonstrates its effectiveness thanks to the large initial stepsize (\(\lambda _1 =5000\)) and inertial effects.

Fig. 2
figure 2

Performance of different algorithms when \(u_0=u_1=(0,0,0)^T\)

Full size image

Example 3: We continue with a very interesting model namely the Nash-Cournot oligopolistic equilibrium models of electricity markets introduced by Contreras et al. (2004). This model was reformulated as a strongly monotone equilibrium problem in Muu and Quy (2015); Quoc et al. (2012). Consider a Nash-Cournot oligopolistic equilibrium model arising in electricity markets with \(n^c \) \((n^c = 3)\) generating companies and each company i \((i=1,2,3)\) (com.  #) possesses several generating units \(n_i^c \,(gen. \, \#)\). The quantities x and \(x^c\) are the power generation of a unit and a company, respectively. The lower and upper bounds of the power generation of the generating units and companies are given in Table 1. The parameters of the cost function are pointed out in Table 2.

Table 1 The lower and upper bounds of the power generation of the generating unit and companies \((n^g =6)\)
Full size table
Table 2 The parameters of the generating unit cost functions \(c_j\ (j=1\dots , 6)\)
Full size table

The cost of a generating unit j (\(j=1,\dots ,6\)) is determined as follows

$$\begin{aligned} c_j(x_j) = \max \{{\hat{c}}_j(x_j), {\tilde{c}}_j(x_j)\} \end{aligned}$$

where

$$\begin{aligned} \begin{array} {lll} &{}{\hat{c}}_j(x_j) =\displaystyle \frac{{\hat{\alpha }}_j}{2}x_j^2 + {\hat{\beta }}_j x_j + {\hat{\gamma }}_j, \\[0.1in] &{}{\tilde{c}}_j(x_j) = {\tilde{\alpha }}_j x_j + \displaystyle \frac{{\tilde{\beta }}_j}{{\tilde{\beta }}_j + 1} {\tilde{\gamma }}_j^{\frac{-1}{{\tilde{\beta }}_j}} (x_j)^{\frac{{\tilde{\beta }}_j +1}{{\tilde{\beta }}_j}}. \end{array} \end{aligned}$$

It turns out that the cost of the generating unit j does not depend on other generating units. Let us denote \(n^g\) by the number of generating units of all companies (i.e. \(n^g = \sum _{i=1}^{n^c} n_i^c\)) and \(I_i\) by the index set of all generating units of the company i.

If the selling price of a unit of electricity is fixed at \(378.4 - 2 \sum _{l=1}^{n^g} x_l \) then the profit of the company i that owns \(n_i^c\) generating units will be defined by

$$\begin{aligned} f_i(x) = \left( 378.4 - 2 \sum _{l=1}^{n^g} x_l \right) \sum _{j\in I_i} x_j - \sum _{j\in I_i} c_j(x_j) \end{aligned}$$

where \((x_{min}^g)_j \le x_j \le (x_{max}^g)_j \, (j=1,\dots , n^g)\).

For each \(i=1,\dots ,n^c\), let us define

$$\begin{aligned} \varphi _i(x,y) = \left[ 378.4 - 2 \left( \sum _{j \not \in I_i} x_j + \sum _{j\in I_i} y_j \right) \right] \sum _{j\in I_i} y_j - \sum _{j\in I_i} c_j(y_j). \end{aligned}$$

The Nikaido-Isoda function is defined as

$$\begin{aligned} f(x,y) = \sum _{i=1}^{n^c} \left[ \varphi _i(x,x) - \varphi _i(x,y) \right] . \end{aligned}$$
Fig. 3
figure 3

Performance of different algorithms when \(u_0=u_1=(0,0,0,0,0,0)^T\)

Full size image

Since each company intends to maximize their profit, the oligopolistic equilibrium model of electricity markets can be reformulated as an equilibrium problem of finding \(x^*\in C^g\) such that

$$\begin{aligned} f(x^*,y) \ge 0, \,\, \forall y\in C^g \end{aligned}$$

where \(C^g\) is the feasible set given by

$$\begin{aligned} C^g = \{ x^g \in {\mathbb {R}}^{n^g} | (x_{min}^g)_j \le x_j \le (x_{max}^g)_j \, (j=1,\dots , n^g) \}. \end{aligned}$$

To figure out the properties of the bifunction f, first let us introduce two vectors \(q^i = (q_1^i,q_2^i, \dots , q_{n^g}^i)^T\) and \({\bar{q}}^i = ({\bar{q}}^i_1,\dots ,{\bar{q}}^i_{n^g})^T\) in which

$$\begin{aligned} q^i_j = {\left\{ \begin{array}{ll} 1 &{}if \,\, j\in I_i \\ 0&{}otherwise\end{array}\right. } \end{aligned}$$

and \({\bar{q}}^i_j=1-q^i_j \, (j=1,\dots ,n^g)\). By (Quoc et al. 2012, Lemma 7), the equilibrium problem being solved can be formulated as

$$\begin{aligned} x^* \in C^g: \, f(x^*,y) = \left[ \left( A+1.5B\right) x + 0.5By + a \right] ^T (y-x) + c(y) - c(x) \quad \forall y \in C^g, \end{aligned}$$

where the two matrices A, B, the vector a, and the cost function are identified as follows

$$\begin{aligned} \begin{array}{lll} &{}A = 2 \displaystyle \sum _{i=1}^{n^c} {\bar{q}}^i (q^i)^T, \quad B = 2 \sum _{i=1}^{n^c} q^i (q^i)^T\\[0.1in] &{}a = -378.4 \displaystyle \sum _{i=1}^{n^c} q^i, \quad c(x) = \sum _{i=1}^{n^c} \sum _{j\in I_i} c_j(x_j) = \sum _{j=1}^{n^g} c_j(x_j). \end{array} \end{aligned}$$

It is worth knowing that since c is a nonsmooth convex function and B is symmetric positive semidefinite, f is continuous on \(C^g \times C^g\) and \(f(x,\cdot )\) is convex but not smooth for all \(x\in C^g\). In addition, the function f is only monotone but it can be transformed equivalently to a strongly monotone equilibrium problem by considering the following bifunction (see (Muu and Quy 2015, Lemma 4)).

$$\begin{aligned} f_1(x,y) = f(x,y)- \frac{1}{2}(y-x)^TB(y-x). \end{aligned}$$

We test the Algorithm 3.1 with \(u_0=u_1=(0,0,0,0,0,0)^T,\) the initial stepsize \(\lambda _1 = 100\), the stopping condition ErrorBound=\(\Vert u_{n+1}-u_n\Vert \le 10^{-3}\) and small inertial effect (\(\rho = 0.003\)). For the other three algorithms, since the Lipschitz constants are not available, we select a positive stepsize so that the algorithms converge. We choose \(\lambda = 0.02\) for the projection algorithm and \(\lambda = 0.03, \alpha = 0.5\) for the relaxed projection algorithm. The inertial extragradient also uses the same stepsize with the relaxed projection. The sequences \(\{\tau _n\}\) and \(\{\epsilon _n\}\) are similar to Example 1. The results are reported in Fig. 3. We realize that the Algorithm 3.1 is still effective for this problem. We also notice that Algorithm 3.1 converges even faster with larger inertial effect, for example \(\rho =0.5\), but in this case condition (12) is not guaranteed.