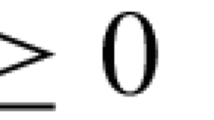1 Introduction

The equilibrium problem (EP for short) is a very general mathematical model in the sense that it includes, as special cases, the optimization problem, the variational inequality, the saddle point problem, the Nash equilibrium problem in noncooperative games, the fixed point problem, and others; see, for instance, [1,2,3,4,5,6,7] and references quoted therein. The interest of this problem is that it unifies all these particular problems in a convenient way. In recent years, a large number of applications have been described successfully via the concept of equilibrium solution and therefore many researchers devoted their efforts to study EPs. For an excellent survey on existence of equilibrium points and solution methods for finding them, we refer the readers to the new monograph [8].

Since EP is a general model, the methods for solving particular problems can be often extended to EPs; see for example, [8,9,10,11,12,13,14,15,16,17,18,19]. Among them, fixed point-type methods play an important role, because they are simple in form and useful in practice. The idea of these methods comes from the proximal point and the projection methods for solving a variational inequality (VI for short) [1, 2, 13, 20]. It is proved in [19] that fixed point methods can efficiently solve the class of strongly monotone EPs and that the convergence rate of these methods is linear [17].

In recent years, dynamical systems have been widely investigated for solving fixed point problems, variational inequalities and monotone inclusions [21,22,23,24,25,26,27,28,29]. As a natural extension, it is interesting to study EPs from a continuous time perspective. This is the aim of this paper. To do so, we first look at the EP as a fixed point problem of a suitable operator. Then, the solutions set of the EP is approached by considering a dynamical system associated with the fixed point map. Under standard assumptions, namely strong pseudo-monotonicity and Lipschitz continuity, we prove that the proposed dynamical system has a unique equilibrium point. Moreover, we also prove that this equilibrium solution is globally exponentially stable. A discrete version of the proposed dynamical system is also considered, allowing one to prove the linear convergence of the corresponding algorithms. Finally, we provide global error bounds in order to estimate the distance between any arbitrary trajectory and the unique solution under the given assumptions.

The remaining part of the paper is organized as follows. In Sect. 2, we recall some preliminary results. Section 3 describes the proposed dynamical system and its global stability. Global error bounds are discussed in Sect. 4. Finally, some numerical experiments are reported in Sect. 5 to illustrate the obtained theoretical results.

2 Preliminaries

Let H be a real Hilbert space endowed with an inner product and its induced norm denoted \(\langle \cdot ,\cdot \rangle \) and \(\Vert \cdot \Vert \), respectively. Let C be a nonempty, closed and convex subset of H and let f be a function from \(C \times C\) to \(\mathbb {R}\) satisfying for each \(x \in C\), \(f(x,x)=0\) and such that the function \(f(x,\cdot )\) is convex, l.s.c and subdifferentiable on C. The equilibrium problem associated with f, in the sense of [4], is denoted by \(\text {EP}(f,C)\), and consists in finding a point \(x^* \in C\) such that

$$\begin{aligned} f(x^*,y) \ge 0 \quad \text{ for } \text{ every } y \in C. \end{aligned}$$

The set of solutions of \(\text {EP}(f,C)\) is denoted \(\text {Sol}(f,C) \).

When \(f(x,y)=\langle F(x), y-x \rangle \) for all \(x,y \in H\), the equilibrium problem \(\text {EP}(f,C)\) reduces to the classical variational inequality VI(F, C), which consists in finding a point \(x^* \in C\) such that

$$\begin{aligned} \left<F(x^*), y-x^*\right>\ge 0 \quad \text{ for } \text{ every } y \in C, \end{aligned}$$

where \(F: H \rightarrow H\) is a continuous mapping. The solution set of this problem is abbreviated to \(\text {Sol}(F,C)\).

Another important particular case of equilibrium problem is the saddle point problem: Given two sets \(C_1 \subset H_1\) and \(C_2 \subset H_2\), where \(H_1\) and \(H_2\) are two real Hilbert spaces, a saddle point of a function \(G : C_1 \times C_2 \rightarrow \mathbb {R}\) is any \(x^* = ( x_1^* , x_2^* ) \in C_1 \times C_2 \) such that

$$\begin{aligned} G ( x_1^* , y_2 ) \le G ( x_1^* , x_2^* ) \le G ( y_1 , x_2^* ) \end{aligned}$$

holds for any \(y =(y_1,y_2)\in C_1 \times C_2\). Finding a saddle point of G amounts to solving \(\text {EP}(f, C)\) with \(C = C_1 \times C_2\) and

$$\begin{aligned} f ((x_1, x_2), (y_1, y_2)) = G (y_1, x_2) - G (x_1, y_2). \end{aligned}$$
(1)

Indeed, a saddle point of G is a Nash equilibrium in a two-person zero-sum game, that is a noncooperative game where the cost function of the first player is G and the cost function of the second player is \(-G\) (see, e.g., [2, 8].)

We recall some well-known definitions useful in the sequel.

A mapping \(f: C \times C \rightarrow \mathbb R \) is said to be

  1. (a)

    strongly monotone with modulus \(\gamma >0\) on C, if

    $$\begin{aligned} f(x,y)+f(y,x) \le -\gamma \Vert x-y\Vert ^2 \quad \forall x,y \in C; \end{aligned}$$
  2. (b)

    monotone on C, if

    $$\begin{aligned} f(x,y)+f(y,x) \le 0 \quad \forall x,y \in C; \end{aligned}$$
  3. (c)

    strongly pseudo-monotone with modulus \(\gamma >0\) on C, if

    $$\begin{aligned} f(x,y) \ge 0 \Rightarrow f(y,x) \le -\gamma \Vert x-y\Vert ^2 \end{aligned}$$

    for all \(x,y \in C\);

  4. (d)

    pseudo-monotone on C, if

    $$\begin{aligned} f(x,y) \ge 0 \Rightarrow f(y,x) \le 0 \end{aligned}$$

    for all \(x,y \in C\).

Remark 2.1

The implications (a)\(\Longrightarrow \)(b), (a)\(\Longrightarrow \)(c), (c)\(\Longrightarrow \)(d) and (b)\(\Longrightarrow \)(d) are evident. Note also that property (c) guarantees that \(\text {EP}(f,C)\) cannot have more than one solution. Indeed, if \(x^*, y^*\in \text {Sol}(f,C)\) and if (c) is satisfied, then \(f(y^*,x^*)\ge 0\) and \(-f(y^*,x^*)\ge \gamma \Vert y^*-x^*\Vert ^2\). Adding these inequalities yields \(0\ge \gamma \Vert y^*-x^*\Vert ^2\) which forces \(y^*=x^*\).

We provide in the following a class of functions f, which is strongly pseudo-monotone but not strongly monotone. The example is a generalization of examples given in [30,31,32].

Example 2.1

Let \(H=l_2\), \(C \subset H\) and let \(f: C\times C \rightarrow \mathbb {R}\) be defined as

$$\begin{aligned} f(x,y):= \xi (x) g(x,y), \end{aligned}$$

where \(\xi : C \rightarrow \mathbb {R}_{++}\) be a positive function satisfying \(\xi (x) \ge \xi >0\) for all \(x \in C\) and \(g: C\times C \rightarrow \mathbb {R} \) is \(\gamma \)-strongly monotone. We shall prove that f is strongly pseudo-monotone on C. Indeed, let \(x,y \in C\) be such that \(f(x,y) \ge 0\). Since \(\xi (x) \ge \xi >0\), we have \(g(x,y) \ge 0\). This and the strong monotonicity of g imply

$$\begin{aligned} f(y,x)&= \xi (y) g(y,x) \\&\le \xi (y) \left( g(y,x) + g(x,y)\right) \\&\le - \xi (y) \gamma \Vert x-y\Vert ^2 \\&\le - \xi \gamma \Vert x-y\Vert ^2 \end{aligned}$$

i.e., f is \(\xi \gamma \)- strongly pseudo-monotone. In general f is not (strongly) monotone. For example, we can take \(\xi (x): = a-\Vert x\Vert \), \(g(x,y) = \left\langle x,y-x \right\rangle \) and

$$\begin{aligned} C =\{x\in H: \Vert x\Vert \le b\}, \end{aligned}$$

where \(0< a/2< b<a\). Then, f is not monotone. Indeed, take

$$\begin{aligned} x = \left( a/2,0,0, \ldots \right) \quad \text {and} \quad y = \left( b,0,0, \ldots \right) , \end{aligned}$$

then

$$\begin{aligned} f(x,y) + f(y,x) = \frac{a}{2} \frac{a}{2} \left( b-\frac{a}{2} \right) +(a-b)b\left( \frac{a}{2}-b\right) = \left( b-\frac{a}{2} \right) ^3 >0. \end{aligned}$$

Remark 2.2

When EP reduces to VI, i.e., \(f(x,y) = \left\langle F(x), y-x\right\rangle \) for all \(x,y \in H\), the (generalized) monotonicity of function f defined above corresponds to the well known (generalized) monotonicity of mapping F (see [33]).

On the other hand, a mapping \(f: C \times C \rightarrow \mathbb R \) is said to satisfy a Lipschitz-type condition on C if there exists a constant \(L>0\) such that

$$\begin{aligned} f(x,y)+f(y,z) \ge f(x,z)-L\Vert x-y\Vert \Vert y-z\Vert \quad \forall x,y,z \in C. \end{aligned}$$
(2)

Remark 2.3

The Lipschitz-type condition (2) was introduced by Quoc and Muu [10]. We note that (2) is weaker than the Lipschitz-type condition introduced by Antipin [2], which can be written as

$$\begin{aligned} |f(x,y) - f(x,z) +f(u,y)-f(u,z)| \le L \Vert x-u\Vert \Vert y-z\Vert \quad \forall u,x,y,z \in C. \end{aligned}$$
(3)

Indeed, taking \(u=z\) in (3) we obtain (2). On the other hand, (2) implies the Lipschitz-type condition in the sense of Mastroeni [19]

$$\begin{aligned} f(x,y)+f(y,z) \ge f(x,z)-c_1\Vert x-y\Vert ^2- c_2 \Vert y-z\Vert ^2 \quad \forall x,y,z \in C, \end{aligned}$$

where \(c_1, c_2\) are two given positive constants.

If \(f(x,y) = \left\langle F(x), y-x\right\rangle \) for all \(x,y \in H\), i.e., EP collapses to a VI problem, then f satisfies (2) if F is Lipschitz continuous with a Lipschitz constant \(L > 0\). Indeed, since F is Lipschitz continuous, using the Cauchy–Schwarz inequality, we have

$$\begin{aligned} f(x,y)+f(y,z)- f(x,z)= & {} \left\langle F(y)- F(x), z-y \right\rangle \\\ge & {} -\Vert F(x)-F(y)\Vert \Vert y-z\Vert \\\ge & {} -L\Vert x-y\Vert \Vert y-z\Vert \quad \forall x,y,z \in C. \end{aligned}$$

To establish the main results of the paper, we need to recall the stability concepts of an equilibrium point of the general dynamical system

$$\begin{aligned} \dot{x}(t) = T(x(t)), \quad t \ge 0 \end{aligned}$$
(4)

where T is a continuous mapping from H to H and \(x:[0, +\infty [ \rightarrow H, \, t \rightarrow x(t)\).

Definition 2.1

[24]

  1. (a)

    A point \(x^*\in H\) is an equilibrium point for (4) if \(T(x^*)=0\);

  2. (b)

    An equilibrium point \(x^*\) of (4) is stable if, for any \(\epsilon >0\), there exists \(\delta >0\) such that, for every \(x_0 \in B(x^*, \delta ) \), the solution x(t) of the dynamical system with \(x(0)=x_0\) exists and is contained in \(B(x^*, \epsilon )\) for all \(t>0\), where \(B(x^*, r )\) denotes the open ball with center \(x^*\) and radius r;

  3. (c)

    A stable equilibrium point \(x^*\) of (4) is asymptotically stable if there exists \(\delta >0\) such that, for every solution x(t) of (4) with \(x(0) \in B(x^*, \delta )\), one has

    $$\begin{aligned} \lim _{t \rightarrow +\infty } x(t)=x^*; \end{aligned}$$
  4. (d)

    An equilibrium point \(x^*\) of (4) is exponentially stable if there exist \(\delta >0\) and constants \(\mu >0\) and \(\eta >0\) such that, for every solution x(t) of (4) with \(x(0) \in B(x^*, \delta )\), one has

    $$\begin{aligned} \Vert x(t) -x^* \Vert \le \mu \, \Vert x(0)-x^*\Vert \, e^{- \eta t} \quad \forall t \ge 0. \end{aligned}$$
    (5)

    Furthermore, \(x^*\) is globally exponentially stable if (5) holds true for all solutions x(t) of (4).

3 A Fixed Point-Type Dynamical System

For every \(\lambda >0\), we define a function \(\psi _\lambda : C \rightarrow C\) by

$$\begin{aligned} \psi _\lambda (x)= \text {argmin}_{y \in C}\,\left\{ \lambda f(x,y) + \frac{1}{2}\Vert y-x\Vert ^2\right\} \quad \forall x \in C. \end{aligned}$$
(6)

Since \(f(x,\cdot )\) is convex, for every \(x \in C\) and \(\lambda >0\), the problem

$$\begin{aligned} \min _{y \in C}\,\left\{ \lambda f(x,y) + \frac{1}{2}\Vert y-x\Vert ^2\right\} \end{aligned}$$
(7)

is a strongly convex problem, hence it has a unique solution. Therefore, the function \(\psi _\lambda \) is well defined and has single values on C. Moreover, if \(x^*\) is a fixed point of function \(\psi _\lambda \) then \(x^* \in \text {Sol}(f,C)\). Indeed, we have

Theorem 3.1

For any \(\lambda > 0\), \(x\in \text {Sol}(f,C)\) if and only if \(x = \psi _\lambda (x)\).

Proof

See e.g., [11].

Remark 3.1

If \(f(x,y) = \left\langle F(x), y-x \right\rangle \) for all \(x,y \in H\) then (6) becomes

$$\begin{aligned} \psi _\lambda (x)= & {} \text {argmin}_{y \in C}\,\left\{ \lambda f(x,y) + \frac{1}{2}\Vert y-x\Vert ^2\right\} \\= & {} \text {argmin}_{y \in C}\,\left\{ \lambda \left\langle F(x), y-x \right\rangle + \frac{1}{2}\Vert y-x\Vert ^2\right\} \\= & {} \text {argmin}_{y \in C}\,\left\{ \Vert y-(x-\lambda F(x))\Vert ^2\right\} =P_C (x-\lambda F(x)), \end{aligned}$$

where \(P_C\) denotes the projection operator onto C. In this case, Theorem 3.1 reduces to the well-known characterization of the solution of VI(F, C): For any \(\lambda > 0\), x is a solution of VI(F, C) if and only if \(x = P_C (x-\lambda F(x))\), see e.g., [20].

For solving \(\text {EP}(f,C)\), we consider the following dynamical system

$$\begin{aligned} \dot{x}(t) = -\rho (x(t)-\psi _{\lambda }(x(t))), \end{aligned}$$
(8)

where \(\rho , \lambda > 0\).

Remark 3.2

The explicit discretization of dynamical system (8) with respect to the time variable t, with step size \(h_n>0\) and initial point \(x_0 \in C\), yields the following iterative scheme:

$$\begin{aligned} \frac{x_{n+1}-x_n}{h_n}=-\rho \{x_n - \psi _{\lambda } (x_n)\}, \end{aligned}$$

or equivalently

$$\begin{aligned} x_{n+1}=(1-\rho h_n)x_n+\rho h_n \psi _{\lambda } (x_n), \end{aligned}$$
(9)

which is the relaxed projection-type method for solving \(\text {EP}(f,C)\) with relaxation parameter \(\rho h_n\). The convergence of this method without relaxation, i.e., \(\rho h_n = 1\) for all n, was investigated in [17, 19] when the function f is strongly monotone.

Remark 3.3

If \(f(x,y) = \left\langle F(x), y-x \right\rangle \) for all \(x,y \in H\), then the dynamical system (8) reduces to the projected dynamical system

$$\begin{aligned} \dot{x}(t) = -\rho (x(t)-P_C (x(t)-\lambda F(x(t)))), \end{aligned}$$

investigated in [21, 22, 24, 28].

It is known that, if the function f is strongly pseudo-monotone and continuous, then the equilibrium problem \(\text {EP}(f,C)\) has a unique solution \(x^*\), see [32]. It follows from Theorem 3.1 that \(x^*\) is a fixed point of \(\psi _{\lambda }\), i.e., \(x^*\) is the unique equilibrium point of dynamical system (8). Therefore, as a consequence, we have the following existence result.

Corollary 3.1

Suppose that the function f is continuous and strongly pseudo-monotone with modulus \(\gamma >0\) on a nonempty closed convex set C. Then, the dynamical system (8) has a unique equilibrium point, which is the unique solution of \(\text {EP}(f,C)\).

We are now in a position to establish the globally stability of dynamical system (8). For that purpose, we first give an estimation which plays the main role in the study of stability of the dynamical system (8).

Proposition 3.1

Let C be a nonempty closed convex subset of a real Hilbert space H. Let f be a \(\gamma \)-strongly pseudo-monotone function from \(C \times C\) into \(\mathbb {R}\) satisfying the Lipschitz-type condition with modulus \(L>0\). Let \(x^*\) be the unique solution of \(\text {EP}(f,C)\) and \(\lambda > 0\). Then,

$$\begin{aligned} \left[ 1+\lambda (2\gamma -\lambda L^2)\right] \Vert \psi _{\lambda } (x)-x^*\Vert ^2\le \Vert x-x^*\Vert ^2 \quad \forall x \in C. \end{aligned}$$
(10)

Proof

Since f satisfies the Lipschitz-type condition (2), using the Cauchy–Schwarz inequality, we have for all \(x,y,z \in C\) that

$$\begin{aligned} f(x,y)+f(y,z)\ge & {} f(x,z)-L\Vert x-y\Vert \Vert y-z\Vert \\\ge & {} f(x,z) - \frac{1}{2 \lambda } \Vert x-y\Vert ^2 - \frac{\lambda L^2}{2} \Vert y-z\Vert ^2. \end{aligned}$$

Hence, (10) can be deduced from [34, Proposition 4.2]. \(\square \)

We establish now the main result of this section.

Theorem 3.2

Let all the assumptions in Proposition 3.1 be satisfied and let \(\lambda < \frac{2\gamma }{L^2}\). Then, the unique equilibrium solution \(x^*\) of the dynamical system (8) is globally exponentially stable.

Proof

Consider the Lyapunov function

$$\begin{aligned} V(x(t))=\frac{1}{2}\Vert x(t)-x^*\Vert ^2 \quad \forall x(t) \in C. \end{aligned}$$

From (8), time derivative of V can be expressed as

$$\begin{aligned} \dot{V} (t)= & {} \left\langle x(t)-x^*, \dot{x}(t)\right\rangle \\= & {} \rho \langle x(t)-x^*, \psi _{\lambda } (x(t)) - x(t)\rangle \\= & {} \rho \left[ \left\langle x(t)-x^*, \psi _{\lambda } (x(t)) -x^*\right\rangle -\Vert x(t)-x^*\Vert ^2\right] . \end{aligned}$$

Therefore, it follows from Cauchy–Schwarz inequality and (10) that

$$\begin{aligned} \dot{V} (t)\le & {} \rho \left[ \Vert x(t)-x^*\Vert \Vert \psi _{\lambda } (x(t))-x^*\Vert -\Vert x(t)-x^*\Vert ^2\right] \\\le & {} \rho \left[ \frac{1}{\sqrt{1+\lambda (2\gamma -\lambda L^2)}}-1 \right] \Vert x(t)-x^*\Vert ^2 \\= & {} -\alpha \Vert x(t)-x^*\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} \alpha =\rho \left[ 1-\frac{1}{\sqrt{1+\lambda (2\gamma -\lambda L^2)}}\right] >0. \end{aligned}$$
(11)

Therefore, for all \(t>0\), we have

$$\begin{aligned} \Vert x(t)-x^*\Vert \le \Vert x(0)-x^*\Vert e^{-\alpha t}. \end{aligned}$$

This means that the equilibrium solution \(x^*\) of the dynamical system (8) is globally exponentially stable. \(\square \)

Remark 3.4

According to Theorem 3.2, the unique equilibrium point \(x^*\) is globally exponentially stable if parameter \(\lambda \) is small enough. Therefore, it is interesting to study the value of \(\lambda \) which maximizes the convergence rate of the trajectories. Considering \(\alpha \) in (11) as a function of \(\lambda \in \left]0,2\gamma /L^2 \right[\), we can see that the maximum convergence rate of the trajectory x(t) is

$$\begin{aligned} \alpha ^*=\rho \left[ 1-\frac{L}{\sqrt{L^2+\gamma ^2}}\right] , \end{aligned}$$

which is attained at \(\lambda =\lambda ^*=\gamma /L^2\).

Since any strongly monotone function f is strongly pseudo-monotone, we have directly the following consequence:

Corollary 3.2

Let C be a nonempty closed convex subset of a real Hilbert space H. Let f be a \(\gamma \)-strongly monotone function from \(C \times C\) into \(\mathbb {R}\) satisfying the Lipschitz-type condition with modulus \(L>0\). Let \(x^*\) be the unique solution of \(\text {EP}(f,C)\) and \(\lambda \in \left] 0, \frac{2 \gamma }{L^2}\right[ \). Then, \(x^*\) is globally exponentially stable.

In the following, we prove the linear convergence of a discrete version of the dynamical system (8), i.e., the scheme (9).

Theorem 3.3

Let all the assumptions in Proposition 3.1 be satisfied and let \(\lambda < \frac{2\gamma }{L^2}\). Let \(\left\{ \rho _n\right\} \subset [\underline{\rho }, 1] \) for all \(n\ge 0\) where \(\underline{\rho }>0\) and let \(x_0 \in C\). Then, the sequence \(\left\{ x_n\right\} \) generated by

$$\begin{aligned} x_{n+1} = (1-\rho _n) x_n + \rho _n \psi _\lambda (x_n) \end{aligned}$$
(12)

converges linearly to the unique solution \(x^*\) of \(\text {EP}(f,C)\).

Proof

Denoting \(y_n:= \psi _\lambda (x_n)\) and \(q= \frac{1}{1+\lambda (2 \gamma - \lambda L^2)} \in ]0,1[\), we have from (10) that

$$\begin{aligned} \Vert y_{n}-x^*\Vert ^2 \le q \Vert x_{n}-x^*\Vert ^2 \quad \forall n \ge 0. \end{aligned}$$
(13)

Therefore,

$$\begin{aligned} \nonumber \Vert x_{n+1}-x^*\Vert ^2= & {} \Vert (1-\rho _n)(x_{n}-x^*)+\rho _n(y_{n}-x^*)\Vert ^2\\ \nonumber= & {} (1-\rho _n) \Vert x_{n}-x^*\Vert ^2 + \rho _n \Vert y_{n}-x^*\Vert ^2 - \rho _n (1-\rho _n) \Vert x_{n}-y_n\Vert ^2 \\\le & {} (1-\rho _n) \Vert x_{n}-x^*\Vert ^2 + \rho _n q \Vert x_{n}-x^*\Vert ^2\\\le & {} (1-\rho _n(1-q)) \Vert x_{n}-x^*\Vert ^2 \\\le & {} (1-\underline{\rho }(1-q)) \Vert x_{n}-x^*\Vert ^2. \end{aligned}$$

This means that the sequence \(\left\{ x_n\right\} \) converges linearly to \(x^*\). \(\square \)

Remark 3.5

In the case \(\rho _n = 1\) for all \(n \ge 0\), (12) reduces to the proximal point algorithm studied by Antipin in [2], where the linear convergence was obtained under strong convexity assumption. The linear convergence of proximal point algorithm for solving strongly pseudo-monotone EPs is established in [34, Theorem 4.4]. A three-step proximal point algorithm can be found in [35, Theorem 3], where the speed of convergence is slower than linearity.

It is known that the over-relaxation may sometimes improve the convergence performance. We give an over-relaxation result in the following Theorem.

Theorem 3.4

Let all the assumptions in Proposition 3.1 be fulfilled and let \(\lambda < \frac{2\gamma }{L^2}\). Let \(\left\{ \rho _n\right\} \subset [1, \overline{\rho }] \) for all \(n\ge 0\), where \(\overline{\rho } < \frac{2}{1+\sqrt{q}}\) and let \(x_0 \in C\). Then, the sequence \(\left\{ x_n\right\} \) generated by

$$\begin{aligned} x_{n+1} = (1-\rho _n) x_n + \rho _n \psi _\lambda (x_n) \end{aligned}$$

converges linearly to the unique solution \(x^*\) of \(\text {EP}(f,C)\).

Proof

From (13), we have

$$\begin{aligned} \Vert y_{n}-x^*\Vert \le \sqrt{q} \Vert x_{n}-x^*\Vert \quad \forall n \ge 0. \end{aligned}$$

Hence,

$$\begin{aligned} \nonumber \Vert x_{n+1}-x^*\Vert= & {} \Vert (1-\rho _n)(x_{n}-x^*)+\rho _n(y_{n}-x^*)\Vert \\ \nonumber\le & {} (\rho _n-1) \Vert x_{n}-x^*\Vert + \rho _n \Vert y_{n}-x^*\Vert \\\le & {} (\rho _n-1) \Vert x_{n}-x^*\Vert + \rho _n \sqrt{q} \Vert x_{n}-x^*\Vert \\= & {} (\rho _n(1+\sqrt{q})-1) \Vert x_{n}-x^*\Vert \\\le & {} (\overline{\rho }(1+\sqrt{q})-1) \Vert x_{n}-x^*\Vert \end{aligned}$$

Since \(\overline{\rho } < \frac{2}{1+\sqrt{q}}\), we obtain \(\overline{\rho }(1+\sqrt{q})-1 \in (0,1)\). Therefore, \(\left\{ x_n\right\} \) converges linearly to \(x^*\). \(\square \)

As a consequence of Theorems 3.3 and 3.4, we have that the sequence \(\{x_n\}\) converges linearly to the unique solution of \(\text {EP}(f,C)\) when \(\rho _n \subset [\underline{\rho }, \overline{\rho }]\).

When \(f(x,y) = \left\langle F(x), y-x \right\rangle \) for all \(x,y \in H\), we obtain the relaxed version of the projected gradient method for solving variational inequalities considered in [30].

Corollary 3.3

Let F be Lipschitz continuous with modulus \(L>0\) and strongly pseudo-monotone with modulus \(\gamma > 0\). Let \(\lambda < \frac{2\gamma }{L^2}\) and \(\left\{ \rho _n\right\} \subset [\underline{\rho }, \overline{\rho }] \subset \left]0, \frac{2}{1+\sqrt{q}}\right[ \) for all \(n\ge 0\) and let \(x_0 \in C\). Then, the sequence \(\left\{ x_n\right\} \) generated by

$$\begin{aligned} x_{n+1} = (1-\rho _n) x_n + \rho _n P_C(x_n-\lambda F(x_n))\quad \forall n \end{aligned}$$

converges linearly to the unique solution \(x^*\) of VI(F, C).

Remark 3.6

When f(x, y) is defined as in (1), the results in Theorem 3.3 and Theorem 3.4 generalize the convergence of proximal point methods for solving saddle point problems studied in [1, 2].

4 Global Error Bounds

In this section, our aim is to establish a global bound for the distance between any arbitrary trajectory x and the solution set of strongly pseudo-monotone EPs. Specially, given an arbitrary trajectory \(x \in C\), we wish to measure how close x is to the unique solution \(x^*\) of the problem \(\text {EP}(f,C)\) and to obtain a bound on such measures in terms of some easily computable quantities depending solely on x and the data of \(\text {EP}(f,C)\).

Theorem 4.1

Let C be a nonempty closed convex subset of a real Hilbert space H. Let f be a \(\gamma \)-strongly pseudo-monotone function from \(C \times C\) into \(\mathbb {R}\) satisfying the Lipschitz-type condition with modulus \(L>0\). Let \(x^*\) be the unique solution of \(\text {EP}(f,C)\) and \(\lambda > 0\). Then, for every arbitrary vector \(x \in C\), it holds that

$$\begin{aligned} \Vert x-x^*\Vert \le \frac{1+\lambda \gamma +\lambda L}{\lambda \gamma } \Vert x- \psi _{\lambda } (x)\Vert . \end{aligned}$$

Proof

For every \(x \in C\), denote by \(z:= \psi _\lambda (x) \in C\), the unique solution of the strongly convex minimization problem (7). The optimality condition associated with (7) implies that there exists \(s \in \partial _2 f(x, z)\) such that

$$\begin{aligned} 0 \in \lambda s + z - x + N_{C}(z), \end{aligned}$$

where \(N_{C}(z)\) denotes the normal cone to C at z. Hence, by definition of this cone, we obtain that

$$\begin{aligned} \langle x-z- \lambda s,y-z \rangle \le 0 \quad \forall y \in C . \end{aligned}$$
(14)

On the other hand, since \(s \in \partial _2 f(x, z)\), we have

$$\begin{aligned} f(x,y) -f(x, z) \ge \langle s,y-z\rangle \quad \forall y \in C . \end{aligned}$$
(15)

Combining (14) and (15), we obtain

$$\begin{aligned} \lambda \left( f(x,y) -f(x, z) \right) \ge \langle \lambda s,y-z\rangle \ge \left\langle x-z, y-z\right\rangle \quad \forall y \in C . \end{aligned}$$
(16)

Substituting \(y:=x^* \in C\) into (16), we obtain

$$\begin{aligned} \lambda \left( f(x,x^*) -f(x, z) \right) \ge \left\langle x-z, x^*-z\right\rangle . \end{aligned}$$
(17)

Since \(x^*\) is the unique solution of \(\text {EP}(f,C)\) and \(z \in C\), we have \( f(x^*, z) \ge 0 \) and by the strong pseudo-monotonicity of f

$$\begin{aligned} f(z,x^*) \le -\gamma \Vert z-x^*\Vert ^2. \end{aligned}$$
(18)

Combining (17) and (18), we obtain

$$\begin{aligned} \lambda \left( f(x,x^*) -f(x, z)- f(z,x^*) \right) \ge \left\langle x-z, x^*-z\right\rangle + \gamma \lambda \Vert z-x^*\Vert ^2. \end{aligned}$$
(19)

On the other hand, the Lipschitz-type continuity of f gives

$$\begin{aligned} f(x, z) + f(z,x^*) - f(x,x^*) \ge -L \Vert x-z\Vert \Vert z-x^*\Vert , \end{aligned}$$

which implies

$$\begin{aligned} \lambda \left( f(x,x^*) -f(x, z)- f(z,x^*) \right) \le \lambda L \Vert x-z\Vert \Vert z-x^*\Vert . \end{aligned}$$
(20)

It follows from (19), (20) and the Cauchy–Schwarz inequality that

$$\begin{aligned} \lambda \gamma \Vert z-x^*\Vert ^2\le & {} - \left\langle x-z, x^*-z\right\rangle + \lambda L \Vert x-z\Vert \Vert z-x^*\Vert \nonumber \\\le & {} \Vert x-z\Vert \Vert z-x^*\Vert +\lambda L \Vert x-z\Vert \Vert z-x^*\Vert , \end{aligned}$$
(21)

which implies

$$\begin{aligned} \Vert z-x^*\Vert \le \frac{1+\lambda L}{\lambda \gamma } \Vert x- z\Vert . \end{aligned}$$

Using again the Cauchy–Schwarz inequality, we deduce

$$\begin{aligned} \Vert x-x^*\Vert \le \Vert x-z\Vert + \Vert z-x^*\Vert \le \frac{1+\lambda \gamma + \lambda L}{\lambda \gamma } \Vert x- z\Vert , \end{aligned}$$

which completes the proof. \(\square \)

Remark 4.1

Since the error bound holds globally, it can be used as a stopping condition in the algorithm for solving \(\text {EP}(f,C)\), i.e., one can stop the algorithm when \(\Vert x_n - \psi _\lambda (x_n)\Vert \) is small enough.

When \(f(x,y) = \left\langle F(x), y-x \right\rangle \) for all \(x,y \in C\), we recover the following global error bound for variational inequality as established in [31].

Corollary 4.1

Let F be Lipschitz continuous with modulus \(L>0\) and strongly pseudo-monotone with modulus \(\gamma > 0\). Let \(x^*\) be the unique solution of VI(F, C) and \(\lambda > 0\). Then, for every arbitrary vector \(x \in C\), it holds that

$$\begin{aligned} \Vert x-x^*\Vert \le \frac{1+\lambda \gamma +\lambda L}{\lambda \gamma } \Vert x- P_C(x-\lambda F(x))\Vert . \end{aligned}$$

The following result states that the distance from an arbitrary vector x to the solution set of \(\text {EP}(f,C)\) can also be lower bounded by the quantity \(\Vert x- \psi _{\lambda } (x)\Vert \).

Theorem 4.2

Let C be a nonempty closed convex subset of a real Hilbert space H. Let f be a \(\gamma \)-strongly pseudo-monotone function from \(C \times C\) into \(\mathbb {R}\) satisfying the Lipschitz-type condition with modulus \(L>0\). Let \(x^*\) be the unique solution of \(\text {EP}(f,C)\) and \(\lambda > 0\). Then, for every arbitrary vector \(x \in C\), it holds that

$$\begin{aligned} \left( 1-\frac{\lambda L^2}{4 \gamma }\right) \Vert x- \psi _{\lambda } (x)\Vert \le \Vert x-x^*\Vert . \end{aligned}$$
(22)

Proof

Setting \(z:= \psi _{\lambda }(x) \in C\), it follows from (21) that

$$\begin{aligned} \left\langle x-z, z-x^*\right\rangle \ge \lambda \gamma \Vert z-x^*\Vert ^2 - \lambda L \Vert x-z\Vert \Vert z-x^*\Vert . \end{aligned}$$

Hence,

$$\begin{aligned} \left\langle x -\psi _{\lambda }(x), x-x^* \right\rangle \nonumber= & {} \left\langle x -z, x-z+z-x^* \right\rangle \\ \nonumber= & {} \Vert x -z\Vert ^2 + \left\langle x -z,z-x^* \right\rangle \\ \nonumber\ge & {} \Vert x -z\Vert ^2 + \lambda \gamma \Vert z-x^*\Vert ^2 - \lambda L \Vert x-z\Vert \Vert z-x^*\Vert \\\nonumber= & {} \left( 1- \frac{\lambda L^2}{4 \gamma }\right) \Vert x -z\Vert ^2 \\\nonumber&\quad + \frac{\lambda L^2}{4 \gamma } \Vert x -z\Vert ^2+\lambda \gamma \Vert z-x^*\Vert ^2 - \lambda L \Vert x-z\Vert \Vert z-x^*\Vert \\\ge & {} \left( 1- \frac{\lambda L^2}{4 \gamma }\right) \Vert x -z\Vert ^2, \end{aligned}$$
(23)

where we have used the Cauchy–Schwarz inequality in the last estimation. Therefore,

$$\begin{aligned} \left( 1- \frac{\lambda L^2}{4 \gamma }\right) \Vert x -\psi _{\lambda }(x)\Vert ^2 \le \Vert x -\psi _{\lambda }(x)\Vert \Vert x-x^* \Vert . \end{aligned}$$

If \(\lambda \le \frac{4 \gamma }{L^2}\) then (22) follows from the last inequality. Otherwise, it is trivial. \(\square \)

When \(f(x,y) = \left\langle F(x), y-x \right\rangle \) for all \(x,y \in C\), we obtain a new result of global error bound for variational inequality.

Corollary 4.2

Let F be Lipschitz continuous with modulus \(L>0\) and strongly pseudo-monotone with modulus \(\gamma > 0\). Let \(x^*\) be the unique solution of VI(F, C) and \(\lambda > 0\). Then, for every arbitrary vector \(x \in C\), it holds that

$$\begin{aligned} \left( 1- \frac{\lambda L^2}{4 \gamma }\right) \Vert x- P_C(x-\lambda F(x))\Vert \le \Vert x-x^*\Vert . \end{aligned}$$

Remark 4.2

When f(x, y) is defined as in (1), the results in Theorem 4.1 and Theorem 4.2 provide error bounds for the saddle point problems.

5 Numerical Illustrations

In this section, we consider some numerical results to illustrate the global exponential stability of the unique equilibrium point of dynamical system (8). The codes are implemented in MATLAB. The STOP condition is \(\Vert x(t)-\psi _{\lambda }(t)\Vert \le \epsilon \) for all test problems, where \(\epsilon =10^{-5}\).

Problem 1 The bifunction f of the equilibrium problem comes from the Cournot–Nash equilibrium model considered in [10]. It is defined for each \(x,y \in \mathbb {R}^5\), by

$$\begin{aligned} f(x,y) = \langle Px + Qy + r, y-x \rangle \end{aligned}$$

where \(r \in \mathbb {R}^5\), and P and Q are two square matrices of order 5 such that \(P-Q\) is symmetric positive definite. It was proved in [10] that the function f is strongly monotone with modulus \(\gamma =\lambda _\mathrm{min}(P-Q)\), the smallest eigenvalue of \(P-Q\) and f satisfies the Lipschitz-type condition with modulus \(L=\Vert P-Q\Vert \). As in [10], in our test, the vector r and the matrices P and Q are chosen as follows:

The constraint set of this problem is defined by

$$\begin{aligned} C= \left\{ x \in \mathbb {R}^5 \, | \, \sum _{i=1}^{5} x_i \ge 0, \quad -5 \le x_i \le 5, \quad i=1,2,3,4,5 \right\} , \end{aligned}$$

and its solution \(x^*\) is given by

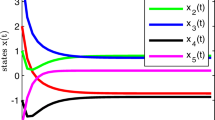
$$\begin{aligned} x^*=(-0.725388, 0.803109, 0.72000, -0.866667, 0.200000)^{\text {T}}. \end{aligned}$$

For this problem, \(\gamma =\lambda _{\min }(P-Q)=0.7192\) and \(L=\Vert P-Q\Vert =2.905\), and we choose \(\lambda =1.9 * \gamma /L^2\). Figure 1 displays the trajectories generated by the dynamical system (8). It is clear that x(t) converges exponentially to the unique equilibrium point \(x^{*}\).

Fig. 1
figure 1

The trajectory of dynamical system (8) when \(x_0=(2,1,4,-1,-2)^\mathrm{T}\) and \(\rho =1\)

Full size image

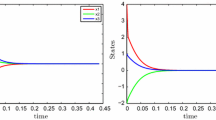
Figure 2 compares the behavior of the non-relaxed algorithm (\(\rho =1\)) with the inner-relaxed algorithm (\(\rho =0.8\)) and the over-relaxed algorithm (\(\rho =1.2\)) when \(x_0=(2,1,4,-1,-2)^\mathrm{T}\). We can see that the over-relaxed version takes advantage in this example.

Fig. 2
figure 2

Comparison of the non-relaxed algorithm (\(\rho _n=1\)) with the lower-relaxed (\(\rho _n=\rho =0.8\)) and over-relaxed (\(\rho _n=1.2\)) algorithms when \(x_0=(2,1,4,-1,-2)^\mathrm{T}\)

Full size image

Problem 2 Let f be given as in Example 2.1 with \(\xi (x): = a-\Vert x\Vert \), \(g(x,y) = \left\langle x,y-x \right\rangle \) and

$$\begin{aligned} C =\{x\in H : \Vert x\Vert \le b\}, \end{aligned}$$

where \(0< a/2< b<a\). We know that f is strongly pseudo-monotone with modulus \(\gamma = a-b >0 \) and not (strongly) monotone. Moreover, f satisfies the Lipschitz-type condition with \(L= a + 2b\) and \(x^*=0\) is the unique solution of \(\text {EP}(f,C)\). Indeed, re-writing \(g(x,y) = \left\langle \xi (x) x, y-x \right\rangle \), it follows from [30] that \(F(x):= \xi (x) x\) is Lipschitz continuous with \(L=a+2b\). Hence, the conclusion follows from (4). In Fig. 3, we present a simulation for Problem 2 where \(H=\mathbb {R}^5\), \(a= 10, b= 6\) and \(\lambda = \gamma /L^2\).

Fig. 3
figure 3

The trajectory of dynamical system (8) when \(x_0=(5,4,3,-1,-3)^\mathrm{T}\) and \(\rho =1\)

Full size image

Figure 4 compares the behavior of the non-relaxed algorithm (\(\rho =1\)) with the inner-relaxed algorithm (\(\rho =0.8\)) and the over-relaxed algorithm (\(\rho =1.2\)) with a random initial \(x_0\). Again, the over-relaxed version takes advantage in this example.

Fig. 4
figure 4

Comparison of the non-relaxed algorithm (\(\rho _n=1\)) with the lower-relaxed (\(\rho _n=\rho =0.8\)) and over-relaxed (\(\rho _n=1.2\)) algorithms with a random initial \(x_0\)

Full size image

6 Conclusions

We have proposed and studied a dynamical system for solving equilibrium problems in Hilbert spaces. Under mild conditions, we have established the solution existence and uniqueness as well as the stability of the solution of the equilibrium problem. We have also provided the linear convergence analysis of a discrete version of the proposed dynamical system. Relaxing the strong (pseudo)-monotonicity assumption could be an interesting topic for further research.