Analytical solutions of linear delay-differential equations with Dirac delta function inputs using the Laplace transform

Abstract

In this paper, we propose a methodology for computing the analytic solutions of linear retarded delay-differential equations and neutral delay-differential equations that include Dirac delta function inputs. In numerous applications, the delta function serves as a convenient and effective surrogate for modeling high voltages, sudden shocks, large forces, impulse vaccinations, etc., applied over a short period of time. The solutions are obtained using the Laplace transform method, in conjunction with the Cauchy residue theorem. The accuracy of these solutions are assessed by comparing them with the ones provided by the method of steps. Numerical examples illustrating the methodology are presented and discussed. These examples show that the Laplace transform solution is very reliable for linear retarded delay-differential equations, because the analytic solution, for a single delta function input, is continuous. However, for linear neutral delay-differential equations with a delta function input the analytic solution is discontinuous. Consequently, the well-known Gibbs phenomenon is observed in the vicinity of the discontinuities. However, for neutral delay differential equations, we show that in some cases, the magnitude of the jumps at the discontinuities decrease, as time increases. Therefore, the Gibbs phenomenon of the Laplace solution dissipates.

1 Introduction

Delay-differential equations (DDEs) are equations where time delays appear in the state variables and/or in their time derivatives. There are many applications in applied mathematics, physics, epidemiology and engineering (Aljahdaly and El-Tantawy 2021; Alfifi 2021; Arino and Van Den Driessche 2006; van den Berg et al. 2007; Ebaid et al. 2019; Halanay and Safta 2020; Nelson et al. 2000; Ruschel et al. 2019; Smith 2011). There are a variety of types of DDEs with different features. For instance, retarded DDEs (RDDEs) are equations where the time delay only appears in the state variable, whereas neutral DDEs (NDDEs) are equations in which the time delays appear in both the state variables and their time derivatives. In general, DDEs are more complex than ordinary differential equations (ODEs). The time delay can make the equation unstable and periodic solutions can appear (Smith 2011). There are a variety of studies devoted to developing methods for finding analytical or numerical solutions of DDEs (Bellour et al. 2020; Chamekh et al. 2019; Cimen and Uncu 2020; Ebaid et al. 2019; Eftekhari 2015; Jaaffar et al. 2020; Jamilla et al. 2020a; Jhinga and Daftardar-Gejji 2019; Jornet 2021; Peykrayegan et al. 2021; Senu et al. 2022; Shampine and Thompson 2009). For instance, in García et al. (2018), the authors developed nonstandard numerical schemes for linear delay-differential models. The classical method for analytically solving linear and nonlinear DDEs is the method of steps (MoS) (Bauer et al. 2013; Kalmár-Nagy 2009; Kaslik and Sivasundaram 2012; Smith 2011). This method generates the exact analytical solution by solving the relevant (updated) ODE on each successive interval. However, oftentimes the MoS is unable to produce the solution due to the phenomenon of expression swell (Bauer et al. 2013; Heffernan and Corless 2006; Kerr and González-Parra 2022). Therefore, the MoS is rarely able to provide insight into the long-time behavior of the solution. This is also the case with numerical methods. Some DDEs that do not include Dirac delta function inputs have, however, been solved using the MoS or different numerical methods (Enright and Hayashi 1998; Jamilla et al. 2020a). For instance, a method based on the Galerkin Finite-Element Method has been used for solving linear NDDEs (Qin et al. 2019). In Fabiano and Payne (2018), the authors presented an interesting spline-based semidiscrete approximation scheme for linear autonomous neutral delay-differential equations, where the Gibbs phenomenon is observed. The Laplace transform has been recently utilized to solve linear DDEs (Chakraborty 2015; Cimen and Uncu 2020; Kalmár-Nagy 2009; Kerr and González-Parra 2022). In Kalmár-Nagy (2009), the authors used the Laplace method to investigate the stability of linear DDEs.

There are a variety of real-world applications where the Dirac delta function is suitable for modeling spikes related to high voltages, large forces, impulse vaccinations, etc. (Abouelkheir et al. 2019; Belmiloudi 2015; Eftekhari 2015). Mathematical computational software has also been used to solve many delay-differential equations that do not include Dirac delta function inputs. However, it has been noted (Legua et al. 2008) that the solutions of ODEs provided by Matlab may occasionally neglect Heaviside step functions in the solution when instant impulses or piecewise continuous functions appear in the input. Thus, it is important to develop mathematical methods to solve differential equations, that account for impulses and piecewise continuous functions. In this paper, we use the Laplace transform method to obtain the analytical solutions of linear DDEs with Dirac delta function inputs. In Yan et al. (2016), the authors used the Laplace transform to derive a closed-form solution to a free-vibrating differential equation that included a Dirac’s delta function. In Chakraborty (2015), the authors proposed a method to obtain the exact solution of a time-dependent Schrödinger equation that includes a Dirac delta potential and they relied on the Laplace transform. In Tornberg and Engquist (2004), the authors used numerical regularization to deal with the Dirac delta function. The main idea there was to replace the Dirac delta function by a more regular function, which can be used on the grids in order to compute the numerical solution of differential equations, with singular source terms. There are a variety of approaches to approximate the Dirac delta function for numerical purposes related to ordinary and partial differential equations (Bojović et al. 2014; Eftekhari 2015; Nedeljkov and Oberguggenberger 2012; Zahedi and Tornberg 2010). One classical way to deal with linear differential equations that include the Dirac delta function is by means of the Laplace transform (Bellman and Roth 1984; Debnath 2016; Eltayeb and Kilicman 2010). In this paper, we study and develop the Laplace transform method to analytically solve linear DDEs that include Dirac delta function inputs. To the best of our knowledge, this is the first work related to this specific topic. The Laplace transform method is particularly well suited for handling linear DDEs with delta function inputs. It produces an algebraic equation for the Laplace transformation of the solution, from which the inverse can be obtained via the Laplace shifting property. There are (however) an infinite number of poles. For RDDEs, one can obtain a formula for the poles, in terms of the Lambert W function. For NDDEs, we used some recently derived formulas for the approximate location of the poles (Kerr and González-Parra 2022), as the initial guesses for computing the (actual) poles. The correct poles were then computed using symbolic computational software (for instance, using fsolve in Maple). We can then apply the inverse Laplace transform to obtain the solution in the original t-space. This requires the use of Cauchy’s residue theorem (Brown and Churchill 2009; Conway 2012). After the computation of the inverse Laplace transform, one obtains the analytical solution in the form of a non-harmonic Fourier series (Kerr and González-Parra 2022; Russell 1967; Sedletskii 2000; Sherman et al. 2023; Young 2001). This infinite series (from a practical viewpoint) needs to be truncated, in order to evaluate the solution at time t. In this work, we assess the accuracy of the Laplace transform solutions by comparing them with the analytical solutions provided by the MoS. However, as we have already mentioned, the MoS oftentimes can only generate the analytical solution over the first handful of intervals. In previous works, the Laplace method and MoS have also been compared with the numerical solution (Jaaffar et al. 2020; Jamilla et al. 2020a; Kerr and González-Parra 2022; Kerr et al. 2022). However, when dealing with Dirac delta function inputs, the computation of numerical solutions becomes a more difficult task, due to the unique nature of the delta function. It is unlike the ordinary functions of mathematics which are defined to have a single value at each point in certain domain. Indeed, Dirac himself, referred to it as an improper function (Dirac 1981). Therefore, we cannot rely, in a straightforward way, on the standard numerical routines which are currently available in software such as Matlab or Maple.

The remainder of this paper proceeds as follows. In the next section, we recall some basic definitions for DDEs and the Laplace transform method that are necessary to develop the proposed methodology. In Sect. 2, we present the methodology for solving linear retarded and neutral DDEs with the Laplace transformation method when the DDE includes the Dirac delta function input. In Sect. 3, we present some numerical results of the implementation of the proposed methodology to solve linear DDEs. We evaluate the reliability and accuracy of the solutions generated by the Laplace transform using the analytical solutions provided by the MoS. Section 4 is devoted for discussion and conclusions.

2 Framework for linear DDEs and Laplace transform

In this paper, we are interested in solving the following general linear DDE with a Dirac delta function as an input:

$$\begin{aligned} y'(t)= & {} a\,y(t)+b\,y'(t-\tau )+cy(t-\tau )+w\,\delta (t-t^*), \quad t >0,\nonumber \\ y(t)= & {} h(t), \, -\tau \le t \le 0. \end{aligned}$$

(1)

Without loss of generality, we will assume that $t^*\in [0,\tau ]$. As it is well known the DDE needs some initial condition, referred to as the history function h(t) defined in the interval $[-\tau ,0]$. Now, for the sake of clarity, let us assume $h(t)=0$. If the history function is not zero, we can obtain the complete solution using the principle of superposition, for linear equations. The interested reader is referred to Kerr and González-Parra (2022), where the same solution approach was employed for solving homogeneous DDEs, where all the examples featured non-zero history functions.

It is standard to denote the important class of retarded delay equations that occurs when $b=0$, i.e., the delay appears only in the state variable and not in the time derivative of the state variable. On the other hand, if $b\ne 0$, we have a NDDE. In this work, we deal with both classes. Furthermore, throughout this paper, we will assume that $w\ne 0$ in order to deal with the discontinuity on the input function. The case where $w=0$ has already been studied in Kerr and González-Parra (2022), Kerr et al. (2022), Sherman et al. (2022).

The linear NDDE (1) can be solved using the Laplace transform method, which is well suited for handling discontinuous functions (Bellman and Roth 1984; Debnath 2016; Spiegel 1965). Determining the solution requires one to find the infinite sequence of poles (Jamilla et al. 2020a, b; Kerr and González-Parra 2022; Kerr et al. 2022; Sherman et al. 2022), then use Cauchy’s residue theorem to obtain the solution in the original t-space (Conway 2012). For DDEs, the form of solution is a non-harmonic Fourier series (Kerr et al. 2022; Sedletskii 2000; Young 2001).

2.1 Laplace transform method to solve linear DDEs with Dirac delta function inputs

Let us begin by deriving the standard Laplace transform solution. If we assume $\mathcal {L}\left( y(t)\right) =Y(s)$, then

$$\begin{aligned} \mathcal {L}\left( y(t-\tau )\right) = e^{-s\tau }Y(s)+e^{-s\tau }\int _{-\tau }^{0}y(v)\,e^{-sv}{dv}, \end{aligned}$$

(2)

and

$$\begin{aligned} \mathcal {L}\left( y^{\prime }(t-\tau )\right) =s\,e^{-s\tau }Y(s) +s\,e^{-s\tau }\int _{-\tau }^{0}y(v)\,e^{-sv}\,dv -y(-\tau ). \end{aligned}$$

(3)

Applying the Laplace transform on Eq. (1) (with $h(t)=0$), we obtain the algebraic equation

$$\begin{aligned} sY=aY+b\,s\,e^{-s\tau }Y+c\,e^{-s\tau }Y +w\,e^{-st^*}. \end{aligned}$$

(4)

Solving this equation for Y, one gets

$$\begin{aligned} Y(s)=\dfrac{w\,e^{-st^*}}{s-a-(bs+c)\,e^{-s\tau }}. \end{aligned}$$

(5)

We can then find the inverse Laplace via the shifting property:

$$\begin{aligned} \mathcal {L}^{-1}\left( e^{-\alpha s}F(s)\right) =H(t-\alpha )\,f(t-\alpha ) \end{aligned}$$

(6)

where $f(t)=\mathcal {L}^{-1}\left( F(s)\right)$ and H(t) is the Heaviside function, in which case

$$\begin{aligned} y(t)=w\,H(t-t^*)\,g(t-t^*) \end{aligned}$$

(7)

with

$$\begin{aligned} g(t)=\mathcal {L}^{-1}\left( \dfrac{1}{s-a-(bs+c)e^{-s\tau }}\right) . \end{aligned}$$

(8)

Computing g(t) requires one to begin by determining the relevant poles, which are given by the roots of the equation

$$\begin{aligned} D(s)=s-a-(bs+c)\,e^{-s\tau }=0 . \end{aligned}$$

(9)

The exact number (0,1 or 2) of real roots is determined by the parameters a, b, c and $\tau$. The remaining (infinite) sequence of poles are complex.

Dividing the Eq. (9) by s reveals that the approximate location of the poles (for $\left| s\right|$ large and $\mathfrak {Im}(s)>0$) is ( see (Diekmann et al. 2012; Kerr and González-Parra 2022))

$$\begin{aligned} s_{k}=\frac{\ln (b)+2k\pi i}{\tau }\text {, }k\in \mathbb {N} \end{aligned}$$

(10)

when $b>0$ and

$$\begin{aligned} s_{k}=\frac{\ln (\left| b\right| )+(2k-1)\pi i}{\tau }\text {, }k\in \mathbb {N} \end{aligned}$$

(11)

for $b<0$. This is due to the fact that as $\left| s\right|$ increases the coefficients a and c play a less important role than b on the location of the poles.

These estimates can be used as the initial guesses for determining the actual poles, with the relevant system of equations given by

$$\begin{aligned} \begin{array}{ccc} 1-\dfrac{ax}{R_{2}}-be^{-\tau x}\cos (\tau y)+\dfrac{ce^{-\tau x}(y\sin (\tau y)-x\cos (\tau y))}{R_{2}} &{} = &{} 0, \\ {} &{} &{} \\ \dfrac{ay}{R_{2}}+be^{-\tau x}\sin (\tau y)+\dfrac{ce^{-\tau x}(x\sin (\tau y)+y\cos (\tau y))}{R_{2}} &{} = &{} 0 \end{array} \end{aligned}$$

(12)

where $R_{2}=x^{2}+y^{2}$ and $s=x +iy$ (where here y is the imaginary part of s).

We can then obtain g(t) from Eq. (8) by computing the inverse Laplace transform which requires the use of Cauchy’s residue theorem. Applying L’Hopital’s, the residues at the poles are given by

$$\begin{aligned} c_{k}=\dfrac{1}{1+(br_{k}\tau -b+c\tau )e^{-r_{k}\tau }}, \end{aligned}$$

(13)

where $r_k$ are the actual poles. For more details, we refer the interested readers to previous works (Kerr and González-Parra 2022; Kerr et al. 2022). Once the poles have been determined, we can apply the Cauchy residue theorem to determine g(t). For the sake of clarity, let us assume that there is one real root, $r_{0}$, then we can write the solution as

$$\begin{aligned} y(t)=wH(t-t^*)g(t-t^*), \end{aligned}$$

(14)

in which

$$\begin{aligned} g(t)=c_{0}\,e^{r_{0}t}+2\sum _{k=1}^{\infty }\mathfrak {Re}\left( c_{k}\,e^{r_{k}t}\right) , \end{aligned}$$

(15)

and where $r_{k},k\in \mathbb {N}$ are the sequence of complex poles above the imaginary axis. Note, to distinguish the actual poles from the approximates given by equation (10), for $b>0$, we shall use $r_{k}$. Before proceeding with the Laplace method solution, let us discuss one of the potentially major challenges that solving Eq. (1) presents.

2.2 Method of steps for solving linear DDEs with Dirac delta function inputs

Using symbolic computational software to solve DDE (1), by successively computing y(t) for $t\in [k\tau ,(k+1)\tau ],$ $k\in \mathbb {N}$, reveals that the solution is discontinuous, at $t=t^*+k\tau ,k\in \mathbb {N}$. This is attributable to the fact that the solution in the first interval includes a Heaviside function. Which, when substituted into the $y'(t-\tau )$ term (for the second interval), then introduces a Dirac delta function. As a consequence, the MoS is oftentimes unable to (reliably) solve Eq. (1) beyond the fourth or fifth time interval. One can gain further insight into this behavior (the discontinuities), and extend the MoS solution beyond these first few intervals, by switching to the intervals $t\in (t^*+k\tau ,t^*+(k+1)\tau ), k\in \mathbb {N}$.

The solution on the interval $(0,t^*]$ is $y(t)=0$. Thus, on the interval $t\in (t^*,t^*+\tau )$ the solution is

$$\begin{aligned} y(t)=w\,H(t-t^*)\,e^{a(t-t^*)} \end{aligned}$$

(16)

Therefore, the ODE that needs to be solved for the interval $t\in [t^*+\tau ,t^*+2\tau )$ is given by

$$\begin{aligned} y'(t)-ay(t)= & {} \!wb\,(\delta (t-\tau -t^*)\,e^{a(t-\tau -t^*)}\nonumber \\{} & {} +aH(t-\tau -t^*)e^{a(t-\tau -t^*)})+wcH(t-\tau -t^*)e^{a(t-\tau -t^*)}. \end{aligned}$$

(17)

Integrating over the small interval $(t^*+\tau -\epsilon ,t^*+\tau +\epsilon )$, we find the jump condition

$$\begin{aligned} y(t^*+\tau +\epsilon )-y(t^*+\tau -\epsilon )=wb. \end{aligned}$$

(18)

We also note that Eq. (17) can be simplified to

$$\begin{aligned} y'(t)-ay(t)=w(ba+c)\,e^{a(t-(\tau +t^*))},\;t\in (t^*+\tau ,t^*+2\tau ), \end{aligned}$$

(19)

with initial condition

$$\begin{aligned} y(t^*+\tau )=wb+e^{a\tau }. \end{aligned}$$

(20)

Continuing this process, we find that the jumps at the sequence of (discontinuity) points $t=t^*+k\tau ,\;k\in \mathbb {N}$ are equal to $wb^{k}$. And that the initial condition for subsequent intervals is $y(t^{*+}+k\tau )=wb^k+y(t^{*-}+k\tau )$. The $+$ superscript is included to indicate the initial y value on the kth interval, with the − superscript denoting the final (end point) value from the previous interval. Programming customized do loops, which incorporate these facts, enables one to compute the analytic (MoS) solution over a larger number of time intervals. These facts may also prove useful in developing and coding numerical algorithms, designed for solving Eq. (1).

These jumps also present a problem for the Laplace solution (14), because the truncated series (being comprised of exponentials, sines and cosines) is continuous $\forall t>t^*$. Therefore, Gibbs phenomenon behavior is observed in the vicinity of the jump points

$$\begin{aligned} t=t^*+(k-1)\tau ,\;k\in \mathbb {N}. \end{aligned}$$

(21)

The jumps decrease when $\left| b\right| <1$ and increase when $\left| b\right| >1$. However, in the latter case, the complex roots will also have a positive real part. Therefore, this behavior would only be present in applications where the solution was strongly divergent. In the former case, this (Gibbs phenomenon) shortcoming effectively resolves itself because the magnitude of the jumps decrease (geometrically). Therefore, as t increases, the solution converges to an essentially continuous function. Thus, enabling one to evaluate and analyze the long-term behavior of the solution. Which is one of the main advantages of the Laplace solution: its ability to accurately compute y(t) for intervals upon which t is large.

Despite the aforementioned limitation of the Laplace transform method in the vicinity of the points $t=t^*+(k-1)\tau \;,\;k\in \mathbb {N}$, we will see in the next section that the solution provided by the Laplace transform method is otherwise very accurate. Notice that for relatively large t oftentimes the MoS is unable to generate a solution. Therefore, the methodology proposed here provides an alternative for computing the solution at any time t.

3 Numerical results

In this section, we present some examples which illustrate the implementation of our proposed methodology for obtaining solutions to the linear DDE (1). In particular, we consider two examples of RDDEs ($b=0$) and three examples of NDDEs. First, we consider the examples for RDDEs. Later on, we solve the NDDEs examples with magnitudes of the coefficient b greater and smaller than zero since the jumps at the discontinuity points depend on the magnitude of b. We also include examples with positive and negative values for b since this affects the direction of the jumps. We compute the solutions of the linear DDEs using the Laplace transform method and make comparisons with the analytical solutions provided by the MoS. In addition, we compute the absolute and relative errors to analyze the accuracy and reliability of the Laplace transform method. We rely on the computational symbolic software Maple to compute the Laplace transform method and the MoS solutions.

For this section, let us introduce the following notation:

• $e_{A}(t) = |y_\textrm{MoS}(t) - y_\textrm{LT}(t)|$: Absolute error in the solution y(t) between MoS and Laplace transform method (LT) via Maple.

• $e_{R}(t) = \biggr |\frac{y_\textrm{MoS}(t) - y_\textrm{LT}(t)}{y_\textrm{MoS}(t)}\biggr |$: Relative error in the solution y(t) between MoS and LT.

3.1 Linear RDDEs

Example 1: Consider the following RDDE:

$$\begin{aligned} y'(t)&= -\frac{3}{5}y(t - \tau ) + 6\delta (t - t^{*}),\; t > 0, \nonumber \\ y(t)&= \phi _0(t) = 0,\;\;\;\; \qquad \qquad \quad \qquad t \in [-\tau , 0], \end{aligned}$$

(22)

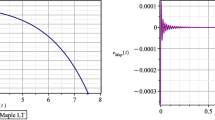
where $\tau = 2$ and $t^{*} = 1$. Figure 1 shows the exact solution computed by the MoS, and the solution generated by the Laplace transform method. On the right hand side of Fig. 1, we show the graph of the absolute error, over the same interval. In this example, it can be seen that the solution generated by the Laplace transform method is relatively accurate and its error decreases over the selected interval. It is important to remark that the analytical solution generated by the MoS is continuous for $t>t^*$. This only happens for the linear RDDEs ($b=0$).

Fig. 1

Solution results of RDDE (22) over $t \in [0,10\tau ]$: Plot of a MoS (solid) and Laplace transform method ($N=200$) solutions. b Absolute error $e_{A}(t)$ (without using the absolute value)

Example 2: Now, let us consider the linear RDDE (23):

$$\begin{aligned} y'(t)&= -\frac{3}{8}y(t) - \frac{5}{6}y(t - \tau ) + 3\delta (t - t^{*}), \nonumber \\ y(t)&= \phi _0(t) = 0,\;\; t \in [-\tau ,0], \end{aligned}$$

(23)

where $\tau = 4$ and $t^{*} = \frac{3}{2}$. Figure 2 shows the exact solution computed by the MoS, and the solution generated by the Laplace transform method. The figure also includes the evolution of the absolute error over the whole interval. It can be seen that in this example the solution generated by the Laplace transform method is accurate. The absolute error of the Laplace method solution decreases over the considered interval. In the next section, we apply the Laplace transform method to NDDEs, where we will see that the discontinuities of the analytical solution present additional challenges.

Fig. 2

Solution results of RDDE (23) over $t \in [0,10\tau ]$: Plot of a MoS (solid) and Laplace transform method ($N=200$) solutions. b Absolute error $e_{A}(t)$ (without using the absolute value)

3.2 Linear NDDE examples

Example 1 Now, let us consider the linear NDDE (24):

$$\begin{aligned} y'(t)&= -\frac{3}{8}y(t) - \frac{7}{8}y(t - \tau ) - 2y'(t - \tau ) + \frac{1}{2}\delta (t - t^{*}), \nonumber \\ y(t)&= \phi _0(t) = 0,\;\; t \in [-\tau ,0], \end{aligned}$$

(24)

where $\tau = 4$ and $t^{*} = 2$. Figure 3 shows the solutions of the NDDE (20). For this particular example, we used $N=900$ for the truncated non-harmonic Fourier series. Recall, the nth jump is given by $wb^n$, which for the chosen parameter set gives us the jump discontinuity sequence $\frac{1}{2}(-2)^n$. Therefore, the jumps at the discontinuity points become larger as t increases. Moreover, the direction of the jumps alternate, going upward and downward. It is also worth noting that in this example (where $\vert b\vert >1$) all the complex poles have a positive real part. This fact, coupled with the increases at the jumps, causes the absolute value of the solution y(t) to increase at a fairly rapid rate. When this is the case, the absolute error tends to increase, as t gets larger. Nevertheless, it can be observed that the solution generated by the Laplace transform method is relatively accurate, and that the relative error decreases over the considered interval, and it is relatively small. It is important to remark that at $t=t^*+(k-1)\tau ,\;k\in \mathbb {N}$ the analytic solution provided by the MoS is discontinuous, but the solution of the Laplace transform method is continuous. This has been pointed out in the previous section and it is a main shortcoming of the Laplace method approach when the NDDE includes Dirac delta function inputs. This shortcoming is, however, consistent with, e.g., Fourier series solutions and spline solutions, at points where the analytic solution is discontinuous (Abdi and Hosseini 2008; Amat et al. 2018). We also note that there is compelling evidence to suggest that, at the jump points, the Laplace solution exhibits the same behavior as a regular Fourier series. In particular, it is in agreement with the Fourier pointwise convergence theorem, which states that the series converges to the average of the left and right limits (Brown and Churchill 2009), which in our case would be that

$$\begin{aligned} y_{L}(t_{0})=\frac{y_{a}(t_{0}^{+})+y_{a}(t_{0}^{-})}{2}, \end{aligned}$$

(25)

where the subscript L is used to denote the Laplace series solution, with subscript a denoting the analytic (MoS) solution. The approximate values one obtains at $t_{0}=2$ are

$$\begin{aligned} y_{L}(2)\simeq 0.24994\text { and }\frac{y_{a}(2^{+})+y_{a}(2^{-})}{2}\simeq 0.25000, \end{aligned}$$

(26)

and the approximate values one obtains at $t_{0}=6$ are

$$\begin{aligned} y_{L}(6)\simeq -0.38833\text { and }\frac{y_{a}(6^{+})+y_{a}(6^{-})}{2} \simeq -0.38843. \end{aligned}$$

(27)

Figure 4 shows the solutions of the NDDE (24) with a small number of terms ($N=10$) for the truncated non-harmonic Fourier series. Notice, that the Gibbs phenomenon can be clearly seen.

Fig. 3

Solution results for the system in Eq. (24). a Plot of solution y(t) for MoS (solid) and LT (dash) methods. b The absolute error between the MoS and LT solutions. c The relative error ($e_{R}(t)$)

Fig. 4

Solution results for the system in Eq. (24). Plot of solution y(t) for MoS (solid) and LT (dash) methods. Here, only $N=10$ terms are used in the LT solution. The Gibbs phenomenon can be seen

Example 2 Now, let us consider the linear NDDE (28) with a history function $\phi _0(t)$ equal to zero:

$$\begin{aligned} y'(t)&= -\frac{5}{8}\,y(t)-\frac{9}{10}\,y'(t-\tau )+\frac{3}{4}\,y(t-\tau )+\delta (t-t^*),\nonumber \\ y(t)&= \phi _0(t) = 0,\;\; t \in [-\tau ,0], \end{aligned}$$

(28)

where $\tau =2$ and $t^{*}=1/2$. Figure 5 shows the solutions of the NDDE (28). For this particular example, we used $N=200$ for the truncated non-harmonic Fourier series. Recall, the nth jump is given by $wb^n$, which for the chosen parameter set gives us the jump discontinuity sequence $(-\frac{9}{10})^n$. Therefore, in this example, the jumps at the discontinuity points become smaller as t increases. And, as was the case in Example 1, the direction of the jumps alternate, going upward and downward. However, in this example, all the complex poles have a negative real part. Therefore, the growth rate of the absolute value of the solution y(t) is significantly smaller than that of the previous example. This can be seen in Fig. 5a, where the Laplace solution appears indistinguishable from the MoS solution, except at the discontinuity points. Note also that the absolute error decreases despite the fact that the solution y(t) increases. Furthermore, the relative error decreases over the considered interval and it is relatively small. It is important to remark that at $t=t^*+(k-1)\tau \;,\;k\in \mathbb {N}$, the analytical solution provided by the MoS is discontinuous, but the solution of the Laplace transform method is continuous. As was noted previously, this is the main weakness with the Laplace method approach when the NDDE includes Dirac delta function inputs.

Fig. 5

Solution results for the system in Eq. (28). a (Top) Plot of solution y(t) for MoS (solid) and LT (dash) methods. b (Left—bottom) The absolute error between the MoS and LT solutions ($e_{A}(t)$ without using the absolute value). c (Right—bottom) The relative error ($e_{R}(t)$ without using the absolute value)

Example 3: Now, let us consider the linear NDDE (29) with a history function $\phi _0(t)$ equal to zero:

$$\begin{aligned} y'(t)&= -\frac{5}{8}\,y(t)+\frac{11}{12}\,y'(t-\tau )+\frac{29}{41}\,y(t-\tau )+\delta (t-t^*),\nonumber \\ y(t)&= \phi _0(t) = 0,\;\; t \in [-\tau ,0], \end{aligned}$$

(29)

where $\tau =2$ and $t^{*}=1/2$. Figure 6 shows the solutions of the NDDE (29). Again in this particular example, we use $N=200$ for the truncated non-harmonic Fourier series. Notice, that for the selected parameter set in this NDDE that the jump discontinuity sequence is given by $(\frac{11}{12})^n$. Therefore, the jumps at the discontinuity points become smaller as t increases, while the direction of the jumps do not change (they are all positive). And, all the complex poles have a negative real part. Therefore, once again, the Laplace transform solution appears indistinguishable from the MoS solution except at the discontinuity points. Note also that the absolute error decreases despite the fact that y(t) increases and the relative error is relatively small.

Fig. 6

Solution results for the system in Eq. (29). a (top) Plot of solution y(t) for MoS (solid) and LT (dash) methods. b (Left—bottom) The absolute error between the MoS and LT solutions ($e_{A}(t)$ without using the absolute value). c (Right—bottom) The relative error ($e_{R}(t)$ without using the absolute value)

4 Conclusions

In this paper, we used the Laplace transform method to obtain analytic solutions for linear RDDEs and NDDEs with Dirac delta function inputs. Particularly, for NDDEs, these equations are more demanding to be solve, because the analytic solution has an infinite sequence of discontinuities (jumps). This is attributable to the (delayed) derivative term in the state variable. The solution process requires one to compute the relevant (infinite) sequence of poles, then determine the Laplace inverse, via the Cauchy residue theorem. For RDDEs a formula for the poles can be obtained in terms of the Lambert W function. For NDDEs, there is no analogous formula, and the poles must be computed numerically. However, we derived a formula which provides an excellent approximate for the location of these poles. We then used computer algebra software and numerical methods to find the desired number of poles. The proposed approach modifies and extends the Laplace methodology developed previously by the authors for linear RDDEs and NDDEs with continuous input functions. One of the main advantages of the Laplace solution is that it enables one to evaluate the solution for any t (time) value, and becomes more accurate for larger t values. Thus, enabling one to study and analyze the long-term behavior of the solution of the DDEs. This is definitely one of the major strengths of the Laplace solution, particularly for DDEs with delta function inputs. The MoS can only be relied upon over the first handful of intervals, and it is generally agreed that numerical solutions struggle when dealing with delta function inputs.

The developed Laplace transform methodology produces solutions that are based on truncated non-harmonic Fourier series. It is noteworthy that the Laplace solution is in some way able to handle the discontinuities of the analytical solution without any special mathematical artifact. At the points of discontinuity, the well-known Gibbs phenomenon appears in the Laplace solution. However, when more terms are included in the Laplace solution, this phenomenon is less evident. We can expect similar behavior for any other discontinuous function inputs. Finally, we can see that the Laplace transform solution, despite involving some relatively advanced mathematics, allows us to obtain accurate solutions for linear RDDEs and NDDEs that include Dirac delta function inputs.