1 Introduction

Delay differential equations (DDEs) appear in many applications from different fields of science [1,2,3,4,5,6,7,8,9,10]. For instance, several studies of climate models related to the global energy balance or the fundamental workings of the El Niño Southern Oscillation (ENSO) system have been presented using DDEs [11]. In general, the analysis of DDEs is more cumbersome than ordinary differential equations (ODEs). The infinite-dimensional nature of DDEs permits them to generate richer dynamics even with a limited number of variables and parameters [10, 11].

The introduction of delays can change the stability of equilibrium points and Hopf bifurcations may arise [10]. During the last few decades, there have been some new developments for finding different types of solutions of DDEs [5, 12,13,14,15,16,17,18,19,20,21,22]. The method of steps (MoS) is the most well-known method for analytically solving DDEs and it provides the exact solution. This method involves utilizing integration properties to obtain an exact analytical solution by solving the relevant (updated) ODE on each successive interval [23]. The MoS, however, oftentimes is only capable of calculating the solution over a limited set of t values, and therefore, the long-term behavior cannot be easily determined or analyzed [10, 24,25,26,27,28].

The Laplace transform method (LTM) in combination with other methods has been used to solve linear DDEs of retarded (RDDE) and neutral (NDDE) type [14, 25, 28,29,30,31,32]. RDDEs are equations where the time delay only appears in the state whereas NDDEs are equations where the time delay can appear in both the state variable and their time derivative. In addition, the LTM has been used to do stability analysis of DDEs [26, 27, 33,34,35]. Recently, the LT has been used to compute the solutions of models based on Caputo fractional derivatives [36]. The LTM requires the computation of contour integrals. In some earlier works, these integrals have been utilized to solve boundary value problems that involve the computation of residues [37, 38]. In this article, we extend the LTM to derive solutions of linear RDDEs and NDDEs that have real and complex poles of higher order. Furthermore, we present first-order linear DDEs that feature resonance phenomena, where the solutions are composed of exponentials, sines, and cosines with increasing amplitudes as a function of time. To the best of our knowledge, this has not been addressed before. The special case of poles of order two is briefly discussed in [25] but only for the RDDE case. The procedure for obtaining the solution by means of the LTM can be divided into three stages: (i) apply the LT to the DDE, (ii) determine the real and complex poles of the characteristic equation and the corresponding residues, and (iii) compute the inverse LT (ILT) of the solution in the s-space by using Cauchy’s residue theorem [39, 40]. When there are poles of higher order (greater than order \(M=1\)), the required modifications introduce additional terms. These are different from the ones that are present in the solution when there are no higher order poles. We shall show that these terms can cause a bounded solution to become unbounded. For RDDEs, the poles can be obtained in terms of the Lambert W function but for NDDEs, the complex poles, in almost all cases, must be computed numerically. In [28], the authors derived a formula which provides an approximation for the location of the complex poles. In some cases, however, this formula does provide one with the exact location of the poles and therefore numerical methods are not required.

In this article, we show that an important feature of first-order linear RDDES and NDDES with poles of higher order is that it is possible to generate the resonance phenomena, which in the counterpart ordinary differential equation cannot appear. This phenomenon can occur (for instance) when a complex pole has order two. Previous works have obtained resonance for nonlinear DDEs but not for linear ones [6, 11, 41, 42]. We show that despite the presence of higher order real and complex poles or resonance phenomena, the solutions generated by the LTM for linear RDDEs and NDDEs that have higher order poles are accurate and especially for larger t values. Moreover, the steady-state behavior of the solutions can be calculated by the LTM. On the other hand, oftentimes the MoS can just produce the solution for a short time.

The remainder of this article proceeds as follows. In the next section, we develop the procedure to obtain the solutions of linear RDDEs and NDDEs with higher order poles by means of the LTM. In Sect. 3, we present numerical results for linear RDDEs and NDDEs with higher order poles. We measure the accuracy of the solutions produced by the LTM using the solutions obtained by the MoS. In Sect. 4, we present our conclusions.

2 Solving linear DDEs considering the presence of higher order poles

Here, we develop the procedure to obtain the solutions of linear RDDEs and NDDEs with higher order poles by means of the LTM. The process to obtain the solution by means of the LTM can be summarized in a series of steps; (i) first, the LT is applied to the DDE, (ii) we compute all the real poles and a finite number of complex poles of the denominator of the solution in the s-space, and (iii) we compute the ILT of the solution in the s-space by using Cauchy’s residue theorem [39, 40]. The special case of poles of order \(M=2\) is briefly discussed in [25], but only for the RDDE case. For the interested readers, we refer them to previous works [25, 28, 29], where the details of the methodology are presented in greater detail. However, we present some crucial steps in this section and in particular for the cases of poles of higher order for both RDDE and NDDE systems.

First, let us describe the role of the Lambert W function in solving linear DDEs. The characteristic equation of a linear DDE can take on the form of a quasi-polynomial which could have an infinite number of roots. The Lambert W Function provides a means for expressing these roots in terms of Lambert W branches. The equation takes on the form \(z = W(z)\textrm{e}^{W(z)}\) where z is some complex number and W(z) is the complex multi-valued function solution of the equation. For each integer k, we denote \(W_k(z)\) as the k-th branch of the Lambert function. The branch \(W_0(z)\) is called the principal branch. For real numbers, the branches \(W_{0}\) and \(W_{-1}\) can be used to solve the equation \(y\textrm{e}^{y} = x\) with real numbers x and y if \(x \ge -\frac{1}{\textrm{e}}\). The solution, y, can be found using the following conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} y = W_{0}(x), &{} \text {if} \quad x \ge 0, \\ y = W_{-1}(x) \quad \text {or} \quad y = W_{0}(x) &{} \text {if} \quad -\frac{1}{\textrm{e}} \le x < 0. \end{array}\right. } \end{aligned}$$

We note that the second condition implies that in the interval \(-\frac{1}{\textrm{e}} \le x < 0\), the equation \(y\textrm{e}^y = x\) has two real solutions. Further details and applications of the Lambert function can be found in literature such as [43, 44].

Now, let us assume that f(z) is an analytic function in the complex region \(\mathcal {R}\) defined by \(0< |z - z_0| < d\), or the neighborhood of a point \(z = z_0 \in \mathbb {C}\). An isolated singularity is a pole if f(z) can be written as [45, 46]:

$$\begin{aligned} f(z) = \frac{\psi (z)}{(z-z_0)^M}, \end{aligned}$$
(1)

where \(M \in \mathbb {N}\) is the order of the pole, \(\psi (z_0) \ne 0\) and \(\psi (z)\) is an analytic function in \(\mathcal {R}\).

Residues of Poles: From Eq. (1), if \(M = 1\), then f(z) has a simple pole at \(z_0\). At a simple pole \(z_0 \in \mathbb {C}\), the residue of f(z) is given by

$$\begin{aligned} C_{-1} = \text {Res}(f(z),z_0) = \lim _{z\rightarrow z_0}\left( (z-z_0)f(z)\right) = \psi (z_0). \end{aligned}$$
(2)

Now, suppose f(z) can be written as \(f(z)=\frac{N(z)}{D(z)}\), where N(z) and D(z) are analytic functions in \(\mathcal {R}\) and D(z) has a zero at \(z_0\). Let us assume that \(D(z) = (z-z_0)^M\hat{D}(z)\) where \(\hat{D}(z)\) is analytic in \(\mathcal {R}\) and \(\hat{D}(z_0)\) is nonzero. Using the Taylor series expansion of N(z) and \(\hat{D}(z)\), the residue is given as [45, 46]:

$$\begin{aligned} C_{-1}= \psi (z_0) = \frac{N(z_0)}{D'(z_0)}. \end{aligned}$$
(3)

Now if we have that \(M\ge 2\), it can be shown through the Taylor Series Expansion of \(\psi (z)\) about \(z_0\) that the residue is given by [45, 46]:

$$\begin{aligned} C_{-1} = \frac{\psi ^{(M-1)}(z_0)}{(M-1)!} = \frac{1}{(M-1)!}\lim \limits _{z \rightarrow z_0}\left( \frac{\,\textrm{d}^{M-1}}{\,\textrm{d}z^{M-1}}\left( (z-z_0)^Mf(z)\right) \right) . \end{aligned}$$
(4)

After these basic definitions,we can proceed to solve linear RDDEs and NDDEs with the LTM.

2.1 Solving linear RDDEs in the presence of higher order poles

Let us consider the following linear RDDE with a non-homogeneous term g(t),

$$\begin{aligned} y'(t)=a\,y(t)+b\,y(t-\tau )+g(t), \quad t >0,\, y(t)=\phi _0(t), \quad -\tau \le t \le 0. \end{aligned}$$
(5)

Let us define \(\mathcal {L}\left( y(t)\right) =Y(s)\). Considering the homogeneous case and employing the LT to Eq. (5), we obtain the LT transform, \(Y(s) = \frac{N(s)}{D(s)}\) of y(t):

$$\begin{aligned} Y(s) = \frac{y(0)\textrm{e}^{s\tau } + b\int \limits _{-\tau }^{0}\phi _0(v)\textrm{e}^{-sv}\,\textrm{d}v}{(s - a)\,\textrm{e}^{s\tau } - b}. \end{aligned}$$

Setting \(D(s) = 0\), we find that the poles of Y(s) occur at \(s_k = a + \frac{1}{\tau }W_k\left( {\tau b\textrm{e}^{-a\tau }}\right) \) for \(k \in \mathbb {Z}\). From the definition of the Lambert function it can be shown that if \(\tau b\textrm{e}^{-a\tau } \ne -\frac{1}{\textrm{e}}\), then the poles \(s_k\) are of order \(M=1\) and employing the ILT, one gets

$$\begin{aligned} y(t) = \sum \limits _{k \in \mathbb {Z}} \text {Re}\left( \lim \limits _{s\rightarrow s_k}\left( C_{-1,k} \,\textrm{e}^{st} \right) \right) , \end{aligned}$$
(6)

where the coefficients \(C_{-1,k}\)’s are the calculated residues and the real part is taken due to the definition of the ILT.

Now, if \(\tau b\textrm{e}^{-a\tau } = -\frac{1}{\textrm{e}}\), then we encounter a case where the real pole \(s=a-\frac{1}{\tau }\) is of order \(M=2\) (since \(s_0 = s_{-1}\) by definition of the \(W_0\) and \(W_{-1}\) Lambert branches). Then, from Eq. (4), the residue for a pole \(s_0 = s_{-1}\) of order \(M=2\), we get

$$\begin{aligned} \text {Res}\{Y(s),\; s_0\}&= \lim \limits _{s \rightarrow s_0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left[ (s-s_0)^2Y(s)\right] \right) . \end{aligned}$$

Employing the ILT, one obtains

$$\begin{aligned} y(t)&= \sum \limits _{k \in \mathbb {Z}}\text {Res}\{Y(s)\textrm{e}^{st},\; s_k\} \nonumber \\&= 2\sum \limits _{k = 1}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k}\left( C_{-1,k}\textrm{e}^{st}\right) \right) + \lim \limits _{s \rightarrow s_0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_0)^2Y(s)\textrm{e}^{st}\right) \right) \end{aligned}$$
(7)

for \(s_0 = a - \frac{1}{\tau }\).

For a linear non-homogeneous RDDE, one gets

$$\begin{aligned} Y(s) = \frac{N(s)}{D(s)} + \frac{G(s)}{D(s)}, \end{aligned}$$
(8)

where G(s) is the LT of the function g(t). We denote the additional poles introduced by G(s) as \(s_{v,i}\) for \(i = 1,2,\ldots ,V\), \(V \in \mathbb {Z}^{+}\), with corresponding residues \(c_{v,i}\). Employing the ILT and the residue theorem, and assuming \(s_k \ne s_{v,i}\) for all \(k,\; i\), we obtain the solution

$$\begin{aligned} y(t) = \sum \limits _{k \in \mathbb {Z}} \text {Re}\left( \lim \limits _{s\rightarrow s_k}\left( C_{-1,k} \textrm{e}^{st} \right) \right) + \sum \limits _{i = 1}^{V} \text {Re}\left( \lim \limits _{s\rightarrow s_{v,i}}\left( \frac{c_{v,i}}{(s - a)\textrm{e}^{s\tau } - b}\textrm{e}^{st}\right) \right) , \end{aligned}$$
(9)

where

$$\begin{aligned} C_{-1,k}&= {\left\{ \begin{array}{ll} \frac{N(s_k) + G(s_k)}{D'(s_k)},\;\; k \in \mathbb {Z}\;\; &{}\text {if}\,\, s_k\,\, \text {is of order}\,\, M=1\\ \lim \limits _{s \rightarrow s_k}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_k)^2Y(s)\right) \right) \;\; &{}\text {if}\,\, s_k\,\, \text {is of order}\,\, M=2.\\ \end{array}\right. } \end{aligned}$$

It is possible that the roots of D(s) and the poles of G(s) may be the same. In which case, the term, Res\(\{Y(s)\textrm{e}^{st};s_{v,i}\}\), is computed according to Eq. (4) for the poles that are the same (when \(s_k = s_{v,i}\) for some k, i). In this paper,we consider the case when a small subset of the poles of G(s) coincide with any of the infinite sequence of the roots of D(s).

2.2 Solving linear NDDEs in the presence of higher order poles

Let us consider the following linear NDDE,

$$\begin{aligned} y'(t)=a\,y(t)+b\,y(t-\tau )+c\,y'(t-\tau )+g(t), \quad t >0,\, y(t)=\phi _0(t), \quad -\tau \le t \le 0. \end{aligned}$$
(10)

Considering the non-homogeneous case, we obtain the LT transform, \(Y(s) = \frac{N(s) + G(s)}{D(s)}\), of y(t):

$$\begin{aligned} Y(s)&= \frac{y(0) - cy(-\tau ) + b\textrm{e}^{-s\tau }\int \limits _{-\tau }^{0} y(v)\,\textrm{e}^{-sv}\,\textrm{d}v + cs\textrm{e}^{-s\tau }\int \limits _{-\tau }^{0}y(v)\,\textrm{e}^{-sv}\,\textrm{d}v\,+G(s)}{s - a - b\textrm{e}^{-s\tau } - cs\,\textrm{e}^{-s\tau }},\nonumber \\&= \dfrac{N(s)}{D(s)}+\frac{G(s)}{D(s)}. \end{aligned}$$
(11)

where \(D(s) = s - a - b\textrm{e}^{-s\tau } - cs\textrm{e}^{-s\tau }\) and G(s) is the LT of g(t). The roots of D(s) are denoted by \(s_k\) for \(k \in \mathbb {Z}\). We denote the additional poles introduced by G(s) as \(s_{v,i}\) for \(i = 1,2,\ldots ,V\), \(V \in \mathbb {Z}^{+}\), with corresponding residues \(C_{v,i}\). It can be shown that when \(ac+b=0\), D(s) can be factored as \(D(s)=(s-a)(1-c\,\textrm{e}^{-s\tau }).\) Therefore when \(c>0\), there are two real poles, \( s_{-1}=a\) and \(s_{0}=\ln (c)/\tau .\) However, when \(c<0\), there will be only one real pole at \(s_{0}=a\). The second term in the factorization also provides one with the exact location of the complex poles above the x axis:

$$\begin{aligned} s_k = \frac{\ln (c) + 2k\pi i}{\tau }\;\; (c > 0), \end{aligned}$$
(12)

and

$$\begin{aligned} s_k = \frac{\ln (|c|) + (2k-1)\pi i}{\tau }\;\; (c < 0) \end{aligned}$$
(13)

for \(k \in \mathbb {N}\). Depending on the LT of the non-homogeneous term, g(t), we may also obtain a repeated real or complex pole. However, we will see in the next section that a special case arises where we obtain a repeated real pole when \(ac + b \ne 0\) and \(g(t) = 0\).

As in the RDDE case, we may encounter \(s_k = s_{v,i}\) for some k, i. In which case, the term, Res\(\{Y(s)\textrm{e}^{st};s_{v,i}\}\), is computed according to Eq. (4). Otherwise, employing the ILT and the residue theorem, assuming \(s_k \ne s_{v,i}\) for all \(k, \; i\), one gets

$$\begin{aligned} y(t) = \sum \limits _{k \in \mathbb {Z}} \text {Re}\left( \lim \limits _{s\rightarrow s_k}\left( C_{-1,k} \textrm{e}^{st} \right) \right) + \sum \limits _{i = 1}^{V} \text {Re}\left( \lim \limits _{s\rightarrow s_{v,i}}\left( \frac{c_{v,i}}{s - a - b\textrm{e}^{-s\tau } - cs\textrm{e}^{-s\tau }}\textrm{e}^{st}\right) \right) , \end{aligned}$$
(14)

where

$$\begin{aligned} C_{-1,k}&= {\left\{ \begin{array}{ll} \frac{N(s_k) + G(s_k)}{D'(s_k)},\;\; k \in \mathbb {Z}\;\; &{}\text {if}\, s_k\, \text {is of order}\,\, M=1,\\ \lim \limits _{s \rightarrow s_k}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_k)^2Y(s)\right) \right) \;\; &{}\text {if}\, s_k\, \text {is of order}\,\, M=2.\\ \end{array}\right. } \end{aligned}$$

If \(r = s_k\) or \(r = s_{v,i}\) is a complex pole of order \(M=2\), then we have a complex conjugate pole and we could take advantage of this fact to compute the residue via,

$$\begin{aligned} 2\,\text {Re}\left( \lim \limits _{s \rightarrow r}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-r)^2Y(s)\,\textrm{e}^{st}\right) \right) \right) . \end{aligned}$$

In this way, we reduce the number of operations and therefore the computation time, even though it is not significant. Notice that the procedure that takes longer is the development of the analytical solution which varies depending on the order of the poles, the non-homogeneous term, and the history function.

3 Results

In this section, we present the solutions of a variety of linear RDDEs and NDDEs with higher order poles. We assess the accuracy of the LTM solutions by comparing them with the analytical solutions provided by the MoS.

We rely on Maple to obtain the solution by the LTM. For this section, let us introduce the next notation:

\(\textrm{e}_{Map}(t) = y_{Maple,MoS}(t) - y_{Maple,LT}(t)\): error in the solution y(t) between the MoS and LTM via Maple.

Now, let us proceed with a variety of linear RDDEs and NDDEs examples.

3.1 Linear RDDE examples

In this subsection, we consider several RDDEs in order to show different phenomena that can be obtained depending on the type of poles and the order of them.

Example 1

Consider the next RDDE:

$$\begin{aligned} y'(t)&= y(t) - \frac{\textrm{e}}{2}y(t - \tau ),\quad t > 0,\nonumber \\ y(t)&= \phi _0(t) = 1,\;\; \quad t \in [-\tau , 0], \end{aligned}$$
(15)

where \(\tau = 2\). Taking the LT, we obtain the quasi-polynomial \(D(s) = (s - 1)\textrm{e}^{2s} + \frac{\textrm{e}}{2}\), which has a real pole at \(s_0 = \frac{1}{2}\). We notice that the condition \(\tau b \textrm{e}^{-a\tau } = -\textrm{e}^{-1}\) is satisfied for the pole of order \(M=2\) given by \(s_0 = s_{-1} = a - \frac{1}{\tau } = \frac{1}{2}\). The remaining poles and residues are as follows: \(s_k = 1 + \frac{1}{2}W_k(-\textrm{e}^{-1})\), \(k \in \mathbb {Z}{\backslash }\{0,-1\}\), with property \(s_{-k-1} = \overline{s_k}\), and \(C_{-1,k} = \frac{N(s_k)}{D'(s_k)}\). Employing the ILT, one gets the LTM solution of y(t):

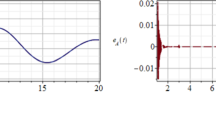
$$\begin{aligned} y(t) = 2\sum \limits _{k=1}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k}\left( C_{-1,k}\textrm{e}^{st}\right) \right) + \lim \limits _{s \rightarrow s_0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_0)^2Y(s)\textrm{e}^{st}\right) \right) . \end{aligned}$$

The solution of Example 1 via MoS (over \(m = 5\) intervals) and LTM (\(n = 100\)) is shown on the left-hand side of Fig. 1. We notice that as \(t \rightarrow \infty \), \(y(t) \rightarrow -\infty \). The solution is unstable due to the presence of a positive real pole. The right-hand side of Fig. 1 shows the graph of the error. It can be observed that the solution generated by the LTM is accurate and its error decreases as t increases.

Fig. 1
figure 1

Solution results of Eq. (15) over \(t \in [0,5\tau ]\) (\(n = 100\) terms): plot of (left) the solution y(t) via MoS and LTM and (right) error \(\textrm{e}_{Map}(t)\)

Full size image

Example 2

Consider the next RDDE:

$$\begin{aligned} y'(t)&= \frac{1}{3}y(t) - \textrm{e}^{-2/3}y(t - \tau ),\quad t > 0,\nonumber \\ y(t)&= \phi _0(t) = -2(t-1)^3,\quad t \in [-\tau , 0], \end{aligned}$$
(16)

where \(\tau = 1\). Taking the LT, we obtain the quasi-polynomial \(D(s) = (s - \frac{1}{3})\textrm{e}^{s} + \textrm{e}^{-2/3}\), which has a real pole at \(s_0 = -\frac{2}{3}\). We notice that the condition \(\tau b \textrm{e}^{-a\tau } = -\textrm{e}^{-1}\) is satisfied for the pole of order \(M=2\) given by \(s_0 = s_{-1} = a - \frac{1}{\tau } = -\frac{2}{3}\). The remaining poles and residues are: \(s_k = \frac{1}{3} + W_k(-\textrm{e}^{-1})\), \(k \in \mathbb {Z}{\backslash }\{0,-1\}\), with property \(s_{-k-1} = \overline{s_k}\), and \(C_{-1,k} = \frac{N(s_k)}{D'(s_k)}\). Employing the ILT, one gets the LTM solution of y(t):

$$\begin{aligned} y(t) = 2\sum \limits _{k=1}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k}\left( C_{-1,k}\textrm{e}^{st}\right) \right) + \lim \limits _{s \rightarrow s_0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_0)^2Y(s)\textrm{e}^{st}\right) \right) . \end{aligned}$$

The solution of Example 2 via MoS (over \(m = 10\) intervals) and LTM (\(n = 100\)) is shown on the left-hand side of Fig. 2. We notice that as \(t \rightarrow \infty \), \(y(t) \rightarrow 0\). The solution is stable since all of the poles have negative real parts. The right-hand side of Fig. 2 shows the graph of the error. It can be observed that the solution generated by the LTM is accurate and its error decreases as t increases.

Fig. 2
figure 2

Solution results of Eq. (16) over \(t \in [0,10\tau ]\) (\(n = 100\) terms): plot of (left) the solution y(t) via MoS and LTM and (right) error \(\textrm{e}_{Map}(t)\)

Full size image

Example 3

Consider the next RDDE:

$$\begin{aligned} y'(t)&= \frac{1}{3}y(t) - \frac{1}{3}y(t - \tau ) + \frac{\textrm{e}^{-t/6}}{2},\quad t > 0,\nonumber \\ y(t)&= \phi _0(t) = -3t,\quad t \in [-\tau , 0], \end{aligned}$$
(17)

where \(\tau = 3\). Denote \(G(s) = \frac{1}{2(s + 1/6)}\) as the LT of the function \(g(t) = \frac{\textrm{e}^{-t/6}}{2}\). The additional pole introduced by G(s) is denoted as \(s_{v,1} = -\frac{1}{6}\) with residue \(c_{v,1} = \frac{1}{2}\). Taking the LT, we obtain the quasi-polynomial \(D(s) = \big (s - \frac{1}{3}\big )\textrm{e}^{3s} + \frac{1}{3}\), which has a real pole at \(s_0 = 0\). We notice that the condition \(\tau b \textrm{e}^{-a\tau } = -\textrm{e}^{-1}\) is satisfied for the pole of order \(M=2\) given by \(s_0 = s_{-1} = a - \frac{1}{\tau } = 0\). The remaining poles and residues are as follows: \(s_k = \frac{1}{3} + \frac{1}{3}W_k(-\textrm{e}^{-1})\), \(k \in \mathbb {Z}{\backslash }\{0,-1\}\), with property \(s_{-k-1} = \overline{s_k}\), and \(C_{-1,k} = \frac{N(s_k) + G(s_k)}{D'(s_k)}\). Employing the ILT, one gets the LTM solution of y(t):

$$\begin{aligned} y(t)&= 2\sum \limits _{k=1}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k}\left( C_{-1,k}\textrm{e}^{st}\right) \right) + \lim \limits _{s \rightarrow s_0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_0)^2Y(s)\textrm{e}^{st}\right) \right) \\&\quad + \lim \limits _{s\rightarrow s_{v,1}}\left( \frac{c_{v,1}}{D(s)}\textrm{e}^{st}\right) \end{aligned}$$

The solution of Example 3 via MoS (over \(m = 5\) intervals) and LTM (\(n = 100\)) is shown on the left-hand side of Fig. 3. We notice that as \(t \rightarrow \infty \), \(y(t) \rightarrow -\infty \), and thus the system is unstable. The right-hand side of Fig. 3 shows the graph of the error. It can be observed that the solution generated by the LTM is accurate and its error decreases as t increases.

Fig. 3
figure 3

Solution results of Eq. (17) over \(t \in [0,5\tau ]\) (\(n = 100\) terms): plot of (left) the solution y(t) via MoS and LTM and (right) error \(\textrm{e}_{Map}(t)\)

Full size image

Example 4

Consider the next RDDE:

$$\begin{aligned} y'(t)&= \left( \frac{1}{2} - \ln (2)\right) y(t) - \frac{1}{8}y(t - \tau ) + t^2\left( \frac{1}{2}\right) ^t,\quad t > 0,\nonumber \\ y(t)&= \phi _0(t) = 2,\quad t \in [-\tau , 0], \end{aligned}$$
(18)

where \(\tau = 2\). The characteristic equation of the system is

$$\begin{aligned} D(s) = \left( s - \left( \frac{1}{2} - \ln (2)\right) \right) \textrm{e}^{2s} + \frac{1}{8}. \end{aligned}$$

First, we note that the condition \(\tau b \textrm{e}^{-a\tau } = -\textrm{e}^{-1}\) is satisfied so we obtain a pole \(s_0 = s_{-1} = a - \frac{1}{\tau } = -\ln (2)\) of order \(M = 2\). The Laplace transform of the non-homogeneous term, \(\mathcal {L}\{t^2\left( \frac{1}{2}\right) ^t\} = G(s) = \frac{2}{(s + \ln (2))^3}\), which means \(s_0\) is actually a pole of order \(M=5\). The exact location of the remaining complex poles is given by: \(s_k = \left( \frac{1}{2} - \ln (2))\right) + \frac{1}{2}W_k(-\textrm{e}^{-1})\) for \(k \in \mathbb {Z}{\backslash }\{0,-1\}\). These poles have the property \(s_{-k-1} = \overline{s_k}\) and residue \(C_{-1,k} = \frac{N(s_k) + G(s_k)}{D'(s_k)}\). We also find that Re\((s_k) < 0\) for all integers k and thus, we expect the solution to be asymptotically stable. Employing the ILT, one gets the LTM solution of y(t):

$$\begin{aligned} y(t)&= 2\sum \limits _{\begin{array}{c} k = 1 \end{array}}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k} \left( C_{-1,k}\textrm{e}^{st} \right) \right) + \frac{1}{(4)!}\left( \lim \limits _{s \rightarrow s_0}\left( \frac{\,\textrm{d}^{4}}{\,\textrm{d}s^{4}}\left( (s-s_0)^5Y(s)\textrm{e}^{st}\right) \right) \right) . \end{aligned}$$

The solution of RDDE Example 4 via MoS (over \(m = 9\) intervals) and LTM (\(n = 100\) terms) in Maple is shown on the left-hand side of Fig. 4. We notice that as \(t\rightarrow \infty \), \(y(t) \rightarrow 0\). The solution is stable since all of the poles have negative real parts. The right-hand side of Fig. 4 shows the graph of the error between MoS and LTM. It can be observed that the solution generated by the LTM is accurate and its error decreases as t increases.

Fig. 4
figure 4

Solution results of Eq. (18) over \(t \in [0,9\tau ]\) (\(n = 100\) terms): plot of (left) the solution y(t) via MoS and LTM and (right) error \(\textrm{e}_{Map}(t)\)

Full size image

Example 5

Consider the following RDDE:

$$\begin{aligned} y'(t)&= -\pi \,y(t) - \sqrt{2}\pi \,y(t - \tau ) + \sin (\pi t),\quad t > 0,\nonumber \\ y(t)&= \phi _0(t) = 0,\quad t \in [-\tau , 0], \end{aligned}$$
(19)

where \(\tau = \frac{3}{4}\). The characteristic equation of the system is:

$$\begin{aligned} D(s) = (s + \pi )\textrm{e}^{(3/4)s} + \sqrt{2}\pi . \end{aligned}$$

There are no real poles and there are an infinite number of complex poles, including \(s_0 = \pi \,i\) and \(s_{-1} = -\pi \,i\). The LT of the non-homogeneous term, \(\mathcal {L}\{\sin (\pi \,t)\} = G(s) = \frac{\pi }{s^2 + \pi ^2}\), which means \(s_0\) and \(s_{-1}\) are actually complex poles of order \(M=2\) with zero real part. The exact location of the remaining complex poles is: \(s_k = (-\pi ) + \frac{4}{3}W_k\left( -\frac{3\sqrt{2}\pi }{4}\textrm{e}^{3\pi /4} \right) \) for \(k \in \mathbb {Z}{\backslash }\{0,-1\}\), with property \(s_{-k-1} = \overline{s_k}\), and \(C_{-1,k} = \frac{N(s_k) + G(s_k)}{D'(s_k)}\). We also find that Re\((s_k)\le 0\) for all integers k. However, due to the repeated complex pole with zero real part, we expect that the solution will oscillate with larger amplitudes as t increases. Employing the ILT, one gets the LTM solution of y(t):

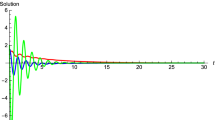
$$\begin{aligned} y(t)&= 2\sum \limits _{k=1}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k} \left( C_{-1,k}\textrm{e}^{st} \right) \right) + \sum \limits _{k = -1}^{0} \text {Re}\left( \lim \limits _{s \rightarrow s_k}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_k)^2Y(s)\textrm{e}^{st}\right) \right) \right) . \end{aligned}$$

The solution of RDDE Example 5 via MoS and LTM (\(n=50\) terms) in Maple is shown on the left-hand side of Fig. 5. We note that as \(t\rightarrow \infty \), \(y(t)\rightarrow (A_{1}t+A_{0})\cos (\pi t)+(B_{1}t+B_{0})\sin (\pi t),\) where the coefficients \(A_{1},A_{0},B_{1}\) and \(B_{0}\) are constants. These terms are introduced because of the order 2 poles at \(s=\pm \textrm{i}\pi .\) Therefore, mathematically the solution assumes the same form as that of a mass-spring system, when the external force is chosen to induce resonance. The complex poles at \(s=\pm \textrm{i}\pi \) effectively constitute a natural frequency for the DDE (19). The resonance is caused by the inclusion of the non-homogeneous forcing function, with this same frequency. However, from the right-hand side of Fig. 5, it can be observed that the error of the LTM solution decreases as \(t\rightarrow \infty \). Note that despite the fact that the real part of all the poles is non-positive, the solution is unstable due to the repeated complex poles.

Fig. 5
figure 5

Solution results of Eq. (19) over \(t \in [0,17]\) (\(n = 50\) terms): plot of (left) the solution y(t) via MoS and LTM and (right) error \(\textrm{e}_{Map}(t)\)

Full size image

3.2 Linear NDDE examples

Example 1

Consider the following NDDE:

$$\begin{aligned} y'(t)&= -\frac{1}{2}y(t) + \frac{1}{2}y(t - \tau ) + y'(t - \tau ) + \sin (2\pi t),\;\;\;\;{} & {} t > 0,\nonumber \\ y(t)&= \phi _0(t) = 0,\;\;\;\;{} & {} t \in [-\tau , 0], \end{aligned}$$
(20)

where \(\tau = 2\). The characteristic equation of the system is:

$$\begin{aligned} D(s) = s + \frac{1}{2} - \frac{\textrm{e}^{-2s}}{2} - s\textrm{e}^{-2s}, \end{aligned}$$

which has two real poles at \(r_0 = 0\) and \(r_1 = -\frac{1}{2}\). The Laplace transform of the non-homogeneous term, \(\mathcal {L}\{\sin (2\pi t)\} = G(s) = \frac{2\pi }{(s + 2\pi \textrm{i})(s - 2\pi \textrm{i})}\), introduces two additional poles, \(s_{v,1} = 2\pi \textrm{i}\) and \(s_{v,2} = -2\pi \textrm{i}\).

Since the condition \(ac + b = 0\) is satisfied, then the exact location of the remaining complex poles is given by: \(s_k = \frac{\ln (c) + 2k\pi \textrm{i}}{\tau } = k\pi \textrm{i}\) for \(k \in \mathbb {Z}{\backslash }\{0\}\). Note, when \(k = -2,2\), then \(s_{-2} = s_{v,2}\) and \(s_{2} = s_{v,1}\) are complex poles of order \(M = 2\). Employing the ILT, one gets the LTM solution of y(t) (note, here \(N(s) = 0\)):

$$\begin{aligned} y(t)&= \sum \limits _{i = 0}^{1}\left( \lim \limits _{s \rightarrow r_i} \left( \frac{G(s)}{D'(s)}\textrm{e}^{st} \right) \right) + 2\sum \limits _{\begin{array}{c} k = 1 \\ k\ne 2 \end{array}}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k} \left( \frac{G(s)}{D'(s)}\textrm{e}^{st} \right) \right) \\&\quad + \sum \limits _{i = 1}^{2}\left( \lim \limits _{s \rightarrow s_{v,i}}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-s_{v,i})^2Y(s)\textrm{e}^{st}\right) \right) \right) . \end{aligned}$$

The solution of NDDE Example 1 via MoS (over \(m = 8\) intervals) and LTM (\(n = 50\) terms) in Maple is shown on the left-hand side of Fig. 6. We notice that as \(t\rightarrow \infty \), \(y(t) \rightarrow \infty \). The right-hand side of Fig. 6 plots the error between MoS and LTM. Note that despite all poles have negative or zero real parts, the solution is unstable due to the resonance phenomenon. It can be observed that the solution generated by the LTM is accurate and its error decreases as t increases.

Fig. 6
figure 6

Solution results of Eq. (20) over \(t \in [0,8\tau ]\) (\(n = 50\) terms): plot of a the solution y(t) via MoS and LTM and b error \(\textrm{e}_{Map}(t)\)

Full size image

Example 2

Consider the following NDDE:

$$\begin{aligned} y'(t)&= -\frac{1}{3}y(t) + \frac{1}{6}y(t - \tau ) + \frac{1}{2}y'(t - \tau ) + \left( \frac{1}{2}\right) ^t,\;\;\;\;{} & {} t > 0,\nonumber \\ y(t)&= \phi _0(t) = 2t,\;\;\;\;{} & {} t \in [-\tau , 0], \end{aligned}$$
(21)

where \(\tau =1\). The characteristic equation of the system is:

$$\begin{aligned} D(s) = s + \frac{1}{3} - \frac{\textrm{e}^{-s}}{6} - \frac{s}{2}\textrm{e}^{-s}, \end{aligned}$$

which has two real poles at \(r_0 = -\ln (2)\) and \(r_1 = -\frac{1}{3}\). The Laplace transform of the non-homogeneous term, \(\mathcal {L}\{\left( \frac{1}{2}\right) ^t\} = G(s) = \frac{1}{s + \ln (2)}\), introduces an additional real pole, \(s_{v,1} = -\ln (2)\). Thus, \(r_0 = s_{v,1}\) is a negative real pole of order \(M = 2\).

Since the condition \(ac + b = 0\) is satisfied, then the exact location of the remaining complex poles is given by: \(s_k = \frac{\ln (c) + 2k\pi \textrm{i}}{\tau } = -\ln (2) + 2k\pi \textrm{i}\) for \(k \in \mathbb {Z}{\backslash }\{0\}\). Note that Re\((r_0) < 0\), Re\((r_1)< 0\), and Re\((s_k) < 0\) for all k. Thus, we expect the solution to be asymptotically stable. Employing the ILT, one gets the LTM solution of y(t):

$$\begin{aligned} y(t)&= \lim \limits _{s \rightarrow r_1} \left( \frac{N(s) + G(s)}{D'(s)}\textrm{e}^{st} \right) + 2\sum \limits _{k = 1}^{\infty }\text {Re}\left( \lim \limits _{s \rightarrow s_k} \left( \frac{N(s) + G(s)}{D'(s)}\textrm{e}^{st} \right) \right) \\&\quad + \lim \limits _{s \rightarrow r_0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( (s-r_0)^2Y(s)\textrm{e}^{st}\right) \right) . \end{aligned}$$

The solution of NDDE Example 2 via MoS (over \(m = 20\) intervals) and LTM (\(n = 100\) terms) in Maple is shown on the left-hand side of Fig. 7. We notice that as \(t\rightarrow \infty \), \(y(t) \rightarrow 0\). This is due to the fact that all poles have negative real parts. The right-hand side of Fig. 7 plots the error between MoS and LTM.

Fig. 7
figure 7

Solution results of Eq. (21) over \(t \in [0,20\tau ]\) (\(n = 100\) terms): plot of (left) the solution y(t) via MoS and LTM and (right) error \(\textrm{e}_{Map}(t)\)

Full size image

Example 3

Consider the following NDDE:

$$\begin{aligned} y'(t)&= \frac{1}{10}y(t) - \frac{1}{10}y(t - \tau ) + \frac{9}{10}y'(t - \tau ),\;\;&t > 0,\nonumber \\ y(t)&= \phi _0(t) = 1 + 5t(\tau + t),\;\;&t \in [-\tau , 0], \end{aligned}$$
(22)

where \(\tau =1\). The characteristic equation of the system is:

$$\begin{aligned} D(s)=s-\frac{1}{10}+\frac{\textrm{e}^{-s}}{10}-\frac{9s}{10}\textrm{e}^{-s}, \end{aligned}$$

which has a real pole at \(r_{0}=0\) of order \(M=2\). In [28], it was shown that when \(c>0\) and for sufficiently large \(k\in \mathbb {Z}{\backslash }\{0\} \), the remaining complex poles lie relatively close to the imaginary axis, and can be approximated with the initial guesses \(s_{k}\approx \frac{\ln (c)+2k\pi \textrm{i}}{\tau }\approx -0.1054+2k\pi \textrm{i}\). Employing the ILT, one gets the LTM solution of y(t):

$$\begin{aligned} y(t)=2\sum \limits _{k=1}^{\infty }\text {Re}\left( \lim \limits _{s\rightarrow s_{k}}\left( \frac{N(s)}{D^{\prime }(s)}\textrm{e}^{st}\right) \right) +\lim \limits _{s\rightarrow 0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}\left( s^{2}Y(s)\textrm{e}^{st}\right) \right) . \end{aligned}$$
(23)

The solution of NDDE Example 3 via MoS (over \(m=24\) intervals) and the LTM (\( n=100\) terms) in Maple is shown on the left of Fig. 8. The terms in the infinite sum become negligible as \(t\rightarrow \infty \) because all of the complex poles have negative real parts. Therefore, as \(t\rightarrow \infty \), \( y(t)\rightarrow \infty \). More specifically

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }y(t)=\lim \limits _{s\rightarrow 0}\left( \frac{\,\textrm{d}}{\,\textrm{d}s}(s^{2}Y(s))\right) +\left( \lim \limits _{s\rightarrow 0}(s^{2}Y(s))\right) t=\frac{1363}{6498}+\frac{5}{57}t. \end{aligned}$$
(24)

Notice that the real pole at \(r_{0}=0,\) of order 2, introduces the linear growth term, resulting in a behavior that is in some way analogous to the resonance phenomenon. Figure 8b plots the error between MoS and LTM.

Fig. 8
figure 8

Solution results of Eq. (22) over \(t \in [0,24\tau ]\) (\(n = 100\) terms): plot of a the solution y(t) via MoS and LTM and b error \(\textrm{e}_{Map}(t)\)

Full size image

4 Conclusions

In this work, we extended the Laplace transform method to obtain the analytic solutions for linear RDDEs and NDDEs which have real and complex poles of higher order. The procedure is similar to the one where all of the poles are order one, but requires one to use the appropriate modifications when using Cauchy’s Residue Theorem for the poles of higher order. This, as a consequence, introduces at least one additional term in the series solution which is typically of a different form to those at the simple poles. The process for obtaining the solution relies on computing the relevant infinite sequence of poles and then determining the Laplace inverse, via the Cauchy residue theorem. For RDDEs, the poles can be obtained in terms of the Lambert W function, but for NDDEs,the complex poles, in almost all cases, must be computed numerically. In [28],the authors derived a formula which provides an approximation for the location of the complex poles. In some cases, however, this formula does provide one with the exact location of the poles, and therefore, numerical methods are not required.

We found that an important feature of first-order linear RDDES and NDDES with poles of higher order is that it is possible to incite the resonance phenomena, which, in the counterpart ordinary differential equation, cannot appear. This phenomenon can occur for instance when a complex pole has order two. For any NDDE which requires one to compute the complex poles numerically, it is essentially impossible to introduce a non-homogeneous term that guarantees a repeated complex pole. Since the complex poles are computed with numerical methods, almost always these complex poles have infinitely many digits, and therefore, it is difficult to have a non-homogeneous term that generates this type of complex pole. However, it is possible to select parameter sets that ensure that the formula for the approximate location of the complex poles provides one with the exact location of these poles. Therefore, we were able to design NDDEs with complex poles of higher order. We show that despite the presence of higher order real and complex poles or resonance phenomena, the LTM is able to generate accurate solutions of linear RDDEs and NDDEs. These solutions are even more accurate for larger t values. This is a main strength of the method since oftentimes the MoS can only provide the solution for the first few time intervals.