On b-acyclic chromatic number of a graph

Abstract

Let G be a graph. We introduce the acyclic b-chromatic number of G as an analogue to the b-chromatic number of G. An acyclic coloring of a graph G is a map $c:V(G)\rightarrow \{1,\ldots ,k\}$ such that $c(u)\ne c(v)$ for any $uv\in E(G)$ and the induced subgraph on vertices of any two colors $i,j\in \{1,\ldots ,k\}$ induces a forest. On the set of all acyclic colorings of G we define a relation whose transitive closure is a strict partial order. The minimum cardinality of its minimal element is then the acyclic chromatic number A(G) of G and the maximum cardinality of its minimal element is the acyclic b-chromatic number $A_{\textrm{b}}(G)$ of G. We present several properties of $A_{\textrm{b}}(G).$ In particular, we derive $A_{\textrm{b}}(G)$ for several known graph families, derive some bounds for $A_{\textrm{b}}(G),$ compare $A_{\textrm{b}}(G)$ with some other parameters and generalize some influential tools from b-colorings to acyclic b-colorings.

1 Introduction

The computation of chromatic number $\chi (G)$ of a graph G is a well-known difficult problem that is NP-hard. As such one often tries to find some approximate values for it. For this one first needs a (proper) coloring of G. There are some simple approaches how to find such a coloring. Let us recall two of them. First is the greedy approach, also sometimes called first-fit, where one starts with a totally uncolored graph. Vertices are then colored in some arbitrary order by the rule that an uncolored vertex receives the minimum color that is not present in its neighborhood until that moment. At the end of this procedure, we obtain a coloring of G and the number of colors is an upper bound for $\chi (G).$ The other approach starts at the other end where all vertices are colored by a different color from $\{1,\ldots ,|V(G)|\}.$ In what follows we need to find at each step a color class that is without a vertex having neighbors of all the remaining colors. Every vertex of such a class can then be recolored with some color, the one that is missing in its neighborhood, and we obtain a new coloring with one color less than before. We stop with this when every color class has a vertex with all the other colors in its neighborhood. Again the number of the colors at the last stage is an upper bound for $\chi (G).$

Both mentioned procedures can result in a coloring with the number of colors that are close to $\chi (G)$ and if we are lucky, then even with $\chi (G)$ colors. However, the difference between the obtained number of colors and $\chi (G)$ can also be arbitrarily large. For both a wide range of studies deals with the worst case. In the greedy approach the worst number of colors that can be obtained is called the Grundy chromatic number $\Gamma (G)$ of G and the worst case in the other presented procedure is called the b-chromatic number $\varphi (G)$ of G.

The Grundy chromatic number was introduced by Christen and Selkow (1979) and then investigated by numerous authors. Let us cite just a few results. Erdös et al. (1987) proved that for every finite graph the Grundy chromatic number is equal to the ochromatic number (the one corresponding to the parsimonious proper coloring). Telle and Proskurowski in Telle and Proskurowski (1997) presented the first polynomial-time algorithm for computing the Grundy number of partial k-trees. DeVilbiss et al. (2018) proved the values of this graph invariant for the line graphs of the regular Turán graphs. The complexity of finding the Grundy number was analyzed e.g. by Zaker (2006) and Bonnet et al. (2018).

The b-chromatic number was introduced by Irving and Manlove (1999). They have shown that determining the b-chromatic number of a graph is an NP-hard problem. The problem is still NP-hard for connected bipartite graphs as shown by Kratochvíl et al. (2002). In contrast, the exact result for $\varphi (T)$ for every tree T was presented already in Irving and Manlove (1999). A similar approach was later transformed to cactus graphs (Campos et al. 2009), to outerplanar graphs (Maffray and Silva 2012), and to graphs with large enough girth (Campos et al. 2012, 2015; Kouider and Zamime 2017). For further reading about b-chromatic number and related concepts we recommend survey (Jakovac and Peterin 2018).

There exist many variants of graph (vertex) colorings with some special extra condition(s). They usually yield a special chromatic number like acyclic chromatic number, star chromatic number, Thue chromatic number and many others. Their computational complexity is usually NP-hard and, similarly as in the case of chromatic number, we desire for some simple procedures that yield an upper bound for the mentioned invariants. Again, the information on how much can go wrong in such a case is an interesting question. Therefore we start in this work with the analysis of acyclic b-chromatic number, that is the worst possible number of colors obtained by the second mentioned procedure which is limited in our case only to acyclic colorings of G.

The paper is organized as follows. In the next section we present basic notations and concepts, among others we recall two graph invariants: acyclic chromatic number and b-chromatic number. This part is followed by the definition of the acyclic b-chromatic number and some basic results about this parameter in Sect. 3. Then we generalize an upper bound from the b-chromatic number to the acyclic b-chromatic number in Sect. 4. This allows us to present an upper bound that is quadratic with respect to the maximum degree of the graph. In Sect. 5 we present some results about the acyclic b-colorings of joins of graphs. The last section contains some final remarks and open problems.

2 Preliminaries

In this work, we consider only graphs $G=(V(G),E(G))$ that are finite and simple, that is without loops and multiple edges. We use $n_G$ for the order and $m_G$ for the size of G. As usually, we denote by $N_G(v)$ the open neighborhood $\{u\in V(G):uv\in E(G)\}$ of $v\in V(G)$ and $N_G[v]=N_G(v)\cup \{v\}$ is the closed neighborhood of v. The degree of $v\in V(G)$ is denoted by $d_G(v)$ and is defined as $d_G(v)=\vert N_G(v)\vert .$ By $\Delta (G)$ and $\delta (G)$ we denote the maximum and the minimum degree of a vertex in G,  respectively. The clique number of G is denoted by $\omega (G).$ For $S\subseteq V(G)$ we denote by G[S] the subgraph of G induced by S. Graph $\overline{G}$ is the complement of G. We use [k] to denote the set $\{1,\ldots ,k\}$ and [j, k] to denote the set $\{j,\ldots ,k\}$ (so, in particular, $[1,k]=[k]$).

A graph G is a cactus graph if any two cycles intersect in at most one vertex. A graph G is called an odd cycle graph if G does not contain any cycle of even length. To the best of our knowledge, we are not aware of the existence of the following result in the literature. Although it is quite simple, we present the proof for the sake of completeness.

Proposition 2.1

A graph G is an odd cycle graph if and only if G is a cactus graph with only odd cycles.

Proof

A cactus graph with only odd cycles is clearly an odd cycle graph by the definition. Otherwise, suppose that two cycles C and $C'$ intersect in at least two vertices u and v. We wish to show that there exists a cycle of even length. If C or $C'$ is an even cycle, then we are done. So, we may assume that C and $C'$ are odd cycles. We choose u and v in such a way that a (u, v)-path $P\subseteq C$ does not contain any vertex from $C'$ other than u and v. Now $C^\prime$ splits into two (u, v)-paths $P_1$ and $P_2$ having no vertices in common with P except their ends u and v. Since $C'$ is odd, $P_1$ and $P_2$ have different parity. If $P_1$ has the same parity as P,  then $P\cup P_1$ is an even cycle. Otherwise, $P_2$ has the same parity as P and $P\cup P_2$ form an even cycle. So, G is not an odd cycle graph. $\square$

2.1 Acyclic chromatic number

A map $c:V(G)\rightarrow \{1,\ldots ,k\}$ is called proper vertex coloring with k colors if $c(x)\ne c(y)$ for every edge $xy\in E(G).$ We consider here only proper vertex colorings, therefore we omit the terms “proper” and “vertex” and call c a coloring or a k-coloring of G in the remainder of the paper. The trivial coloring of G is the coloring where every vertex obtains a different color. The minimum number k,  for which there exists a k-coloring, is called the chromatic number of G and is denoted by $\chi (G).$ Every k-coloring c yields a partition of V(G) into independent sets $V_i=\{u\in V(G):c(u)=i\},$ for every $i\in [k],$ called color classes of c. We denote by $V_{i,j}$ the union $V_i\cup V_j$ and by $V_{i,j,\ell }$ the union $V_i\cup V_j\cup V_{\ell }$ for any $i,j,\ell \in [k].$ In particular we use $V_{i,j,\ell }(v)$ for component of $G[V_{i,j,\ell }]$ that contains vertex v. By $CN_c(v)$ we denote the set of all the colors that are present in $N_G(v)$ under coloring c,  that is $CN_c(v)=\{c(u):u\in N_G(v)\}.$ In addition we have $CN_c[v]=CN_c(v)\cup \{c(v)\}.$

A coloring c is an acyclic coloring of G if $G[V_{i,j}]$ is a forest for any $i,j\in [k].$ In other words, the subgraph induced by any two color classes does not contain any cycle. Notice that $G[V_{i,i}]$ is even edgeless since c is a coloring of G. The minimum number of colors of an acyclic coloring of G is the acyclic chromatic number denoted by A(G). Clearly, $A(G)\ge \chi (G)$ as every acyclic coloring is also a coloring of G.

Acyclic colorings were introduced by Grünbaum (1973), who proved that the acyclic chromatic number of any planar graph is not greater than 9 and conjectured that in fact this bound is equal to 5. This was finally proved by Borodin (1979). Mondal et al. (2012) proved that every triangulated plane graph G has an acyclically 3-colorable subdivision, where the number of division vertices is not greater than $2.75n_G-6,$ and an acyclically 4-colorable subdivision, where the number of division vertices is not greater than $2n_G-6.$ Alon et al. (1991) showed that $A(G)\le \lceil 50\Delta ^{4/3}\rceil ,$ where $\Delta =\Delta (G),$ which proved the conjecture attributed to Erdös (see Jensen and Toft 1995, p. 89), stating that $A(G)=o(\Delta ^2).$ Recently, Gonçalves et al. (2020) used the entropy compression method to prove that for every graph G,  $A(G)\le \frac{3}{2}\Delta ^{4/3}+O(\Delta ).$ Alon et al. (1991) proved also that there exist graphs for which $A(G)=\Omega (\Delta ^{4/3}/(\log \Delta )^{1/3}).$Alon et al. (1996) showed that the acyclic chromatic number of the projective plane is 7,  while for every G embeddable on a surface of Euler characteristic $\chi =-\gamma ,$ $A(G)=O(\gamma ^{4/7}).$ Moreover, for every $\gamma >0$ there exist graphs embeddable on surfaces of Euler characteristic $-\gamma ,$ for which $A(G)=\Omega (\gamma ^{4/7}/(\log \gamma )^{1/7}).$ This disproved the conjecture due to Borodin (see Jensen and Toft 1995, p. 70) that acyclic chromatic number is equal to the chromatic number for all surfaces other than a plane. Acyclic colorings of graphs with a bounded degree were studied e.g. by Frtin and Raspaud (2008), Hocquard and Montassier (2010) and Yadav et al. (2011). Mondal et al. (2012) proved that deciding whether a graph with $\Delta \le 6$ is acyclically 4-colorable, is NP-complete.

2.2 b-Chromatic number

Let ${\mathcal {F}}(G)$ be the set of all colorings of G and let $c\in {\mathcal {F}}(G)$ be a k-coloring. A vertex v of G with $c(v)=i$ is a b-vertex (of color i), if v has all the colors of c in its closed neighborhood, that is $CN_c[v]=[k].$ If a vertex v with $c(v)=i$ is not a b-vertex, then (at least) one color is missing in $N_G[v],$ say j. We can recolor v with j and a slightly different coloring is obtained. Hence, if there exists no b-vertex of color i,  then we can recolor every vertex v colored with i with some color not present in $N_G[v],$ say $j_v.$ This way we obtain a new coloring $c_i:V(G)\rightarrow [k]{\setminus }\{i\}$ by

$$\begin{aligned} c_i(v)=\left\{ \begin{array}{ll} c(v): &{}\quad c(v)\ne i \\ j_v : &{}\quad c(v)=i \end{array} \right. . \end{aligned}$$

Clearly $c_i$ is a $(k-1)$-coloring of G. We call the above procedure a recoloring step. By the recoloring algorithm we mean an iterative performing of recoloring steps while it is possible where we start with a trivial coloring of G. Notice that one could also start with any other coloring from ${\mathcal {F}}(G).$

Next we define the relation $\triangleleft$ on ${\mathcal {F}}(G)\times {\mathcal {F}}(G).$ We say that $c'\in {\mathcal {F}}(G)$ is in relation $\triangleleft$ with $c\in {\mathcal {F}}(G),$ $c'\triangleleft c,$ if $c'$ can be obtained from c by a recoloring step of one fixed color class of c. Clearly, $\triangleleft$ is asymmetric. The transitive closure $\prec$ of $\triangleleft$ is then a strict partial order on ${\mathcal {F}}(G).$ Since there are finitely many different colorings of any graph G,  this order has some minimal elements. The maximum number of colors of a minimal element of $\prec$ is called the b-chromatic number of G and is denoted by $\varphi (G),$ in contrast with the chromatic number $\chi (G),$ which is the minimum number of colors of a minimal element of $\prec .$

Every color class of every minimal element of $\prec$ needs to have a b-vertex. So, one can use the following alternative definition, as already mentioned in Irving and Manlove (1999). A coloring c of G is a b-coloring if every color class contains a b-vertex. The b-chromatic number is then the maximum number of colors in a b-coloring of G. This definition was later used in almost all publications on the b-chromatic number.

There exists a very natural upper bound for $\varphi (G).$ Namely, every b-coloring with $\varphi (G)$ colors needs at least $\varphi (G)$ vertices with $d_G(v)\ge \varphi (G)-1.$ The m-degree m(G) is defined as

$$\begin{aligned} m(G)=\max \{i: i-1\le d_G(v_i)\}, \end{aligned}$$

where $v_1,\ldots ,v_{n_G}$ are ordered by the degrees $d_G(v_1)\ge \cdots \ge d_G(v_{n_G}).$ It was shown already in Irving and Manlove (1999) that $\varphi (G)\le m(G).$

Every run of the recoloring algorithm gives a minimal element of $\prec$ and it is straightforward to see that it consists of at most $n_G-\chi (G)$ recoloring steps. In every recoloring step we need to find which color classes are without a b-vertex. If we use $\ell$ colors at some step of the recoloring algorithm, then only vertices of degree at least $\ell -1$ can be b-vertices (of a certain color). Hence we need to check only closed neighborhoods of such vertices and this can be done in $O(m_G)$ time in the worst case. Let us also mention that if a vertex v with $c(v)=i$ is a b-vertex at some stage of the recoloring algorithm, then it remains a b-vertex of color i after each recoloring step that still follows. Finally, when we have a color class j without a b-vertex, we need to find for every vertex v satisfying $c(v)=j$ a color that is not present in $N_G(v)$ and this can be done in $O(m_G)$ time again. Altogether, recoloring algorithm is polynomial algorithm and its time complexity is at most $O\left( (n_G-\chi (G))(m_G)^2\right) .$

With this we have a heuristic polynomial algorithm that produces a coloring of G and gives an upper bound for $\chi (G).$ This way the study of $\varphi (G)$ became the study of the worst possible case that can happen while using the recoloring algorithm. A similar approach can be applied to the Grundy number $\Gamma (G),$ which corresponds with the study of the worst possible performance of the greedy algorithm. A comparative study on the b-chromatic number and the Grundy number was presented by Masih and Zaker (2021, 2022).

3 Definition and some basic results

Our goal in this part is to define the acyclic b-chromatic number of a graph G. For that reason, we could be interested in colorings of G that are acyclic and b-colorings at the same time. Unfortunately this is not possible for all graphs. Let us observe cycle $C_4.$ Notice that $\varphi (C_4)=\chi (C_4)=2$ and the only b-coloring of $C_4$ is the 2-coloring that is not acyclic. So, both conditions, being an acyclic coloring and being a b-coloring, are not always fulfilled. This is probably one of the reasons why this problem was not studied yet.

We can avoid this problem if we focus more strictly on the original definition of $\varphi (G).$ For this let ${\mathcal{A}\mathcal{F}}(G)$ be the set of all acyclic colorings of G. A recoloring step for $c\in {\mathcal{A}\mathcal{F}}(G)$ that produces coloring $c'$ is an acyclic recoloring step if $c'\in {\mathcal{A}\mathcal{F}}(G).$ This means that we can reduce some color of c only when a new coloring $c'$ is also acyclic. The acyclic recoloring algorithm is the use of an acyclic recoloring step until this is possible when starting with a trivial coloring of G. Also the acyclic recoloring algorithm has polynomial time complexity, because we need, in addition to the recoloring algorithm, after each acyclic recoloring step to check whether the new coloring is still acyclic. This can clearly be done in polynomial time since there are at most $O(n_G^2)$ pairs of different colors.

We define relation $\triangleleft _a\subseteq {\mathcal{A}\mathcal{F}}(G)\times {\mathcal{A}\mathcal{F}}(G)$ by $c'\triangleleft _a c$ when $c'$ can be obtained by an acyclic recoloring step from $c\in {\mathcal{A}\mathcal{F}}(G).$ Similarly as $\triangleleft ,$ $\triangleleft _a$ is also asymmetric. Let $\prec _a$ be its transitive closure. Hence, $\prec _a$ is a strict partial order of ${\mathcal{A}\mathcal{F}}(G).$ The trivial coloring is the greatest element of $\prec _a$ (sometimes also called the maximum element). Again, as G is finite, also ${\mathcal{A}\mathcal{F}}(G)$ is finite and at least one minimal element of $\prec _a$ exists.

Proposition 3.1

Let G be a graph and $t\in {\mathcal{A}\mathcal{F}}(G)$ be a trivial coloring. If $c\in {\mathcal{A}\mathcal{F}}(G),$ then there exists a chain

$$\begin{aligned} c\triangleleft _a c_1\triangleleft _a c_2\triangleleft _a\cdots \triangleleft _a c_{\ell -1}\triangleleft _a t. \end{aligned}$$

Proof

Let c be any k-coloring from ${\mathcal{A}\mathcal{F}}(G).$ Let $\ell =n_G-k,$ $c_{\ell }=t$ and $c_0=c.$ We may assume that the k colors from c are the first k colors from t. Let $v_1,\ldots ,v_k,v_{k+1},\ldots ,v_{n_G}$ be vertices of G ordered in such a way that $c(v_i)=i$ for every $i\in [k],$ the rest of the ordering being arbitrary. For every $i\in [\ell ]$ we define coloring $c_i$ from $c_{i-1}$ by

$$\begin{aligned} c_i(v)=\left\{ \begin{array}{ll} c_{i-1}(v) &{} \quad \text {if}\ v\ne v_{k+i}, \\ k+i &{} \quad \text {if}\ v=v_{k+i}. \end{array} \right. \end{aligned}$$

In other words, if we reverse the order of colorings, then we obtain c from t by recoloring every vertex at most once. Clearly, $c_i\in {\mathcal{A}\mathcal{F}}(G)$ for every $i\in [\ell ]$ because $c\in {\mathcal{A}\mathcal{F}}(G).$ Moreover, we can obtain $c_{i-1}$ from $c_i$ by a recoloring of vertex $v_{k+i}.$ By the construction of $c_i$ from $c_{i-1}$ it is clear that $v_{k+i}$ is not a b-vertex for $c_i$ because the color $c_{i-1}(v_{k+i})$ is not in the closed neighborhood of $v_{k+i}$ in coloring $c_i.$ Hence we have an acyclic recoloring step from $c_i$ to $c_{i-1}$ and $c_{i-1}\triangleleft _a c_i$ follows for every $i\in [\ell ].$ $\square$

With this the following definition is justified. The acyclic b-chromatic number $A_{\textrm{b}}(G)$ is the maximum number of colors in a minimal element of $\prec _a$:

$$\begin{aligned} A_{\textrm{b}}(G)=\max \{|c|:c\in {\mathcal{A}\mathcal{F}}(G) \text { is a minimal element of }\prec _a\}. \end{aligned}$$

The acyclic b-chromatic number of a graph G describes the worst case to appear while using the acyclic recoloring algorithm to estimate A(G). An acyclic coloring of G with $A_{\textrm{b}}(G)$ colors that arise from a minimal element of $\prec _a$ is called an $A_{\textrm{b}}(G)$-coloring. We have the following inequality chain

$$\begin{aligned} \omega (G)\le \chi (G)\le A(G)\le A_{\textrm{b}}(G)\le n_G, \end{aligned}$$

(1)

where the fact that every acyclic b-coloring is also an acyclic coloring implies $A(G)\le A_{\textrm{b}}(G).$ Next we characterize the graphs for which $A_{\textrm{b}}(G)=n_G.$

Proposition 3.2

We have $A_{\textrm{b}}(G)=n_G$ if and only if $G\cong K_{n_G}.$

Proof

If $G\cong K_n,$ then $A_{\textrm{b}}(G)=n=n_G$ by (1). Conversely, if $G\ncong K_n,$ then there exist different and nonadjacent $u,w\in V(G).$ For a trivial coloring t of G, 

$$\begin{aligned} c(v)=\left\{ \begin{array}{ll} t(v) :&{}\quad \text {if}\ v\ne u, \\ t(w) :&{} \quad \text {if}\ v=u, \end{array} \right. \end{aligned}$$

is a coloring obtained by an acyclic recoloring step. Hence t is not a minimal element of $\prec _a$ and $A_{\textrm{b}}(G)<n_G.$ $\square$

The b-chromatic number $\varphi (G)$ has an elegant description as a maximum number of colors for which b-vertex exists in every color class. For the acyclic b-chromatic number this is not enough as already shown for $C_4.$ Namely, arbitrary recoloring can also trigger a bi-chromatic cycles and we need to avoid this. To formulate appropriate condition, we define the concept of a weak acyclic b-vertex.

Definition 3.3

Let G be a graph with an acyclic coloring $c:V(G)\rightarrow [k].$ A vertex $v\in V_i,$ $i\in [k],$ is a weak acyclic b-vertex if it satisfies

$$\begin{aligned} \forall \ell \in [k]-CN_c[v], \exists j\in CN_c(v): G[V_{j,\ell }\cup \{v\}] \text { contains a cycle}. \end{aligned}$$

(2)

Note that every b-vertex v is also weak acyclic b-vertex, since $[k]-CN_c[v]=\emptyset$ in this case. If v is a weak acyclic b-vertex and $\ell \in [k]-CN_c[v],$ then there exists a bi-colored path of even length between two neighbors of v (both colored by j). For two colors $\ell ,m\in [k]-CN_c[v]$ such two paths can have a common inner vertex of color j if both paths start (and end) with the same color j.

As already suggested by “weak”, the notion of weak acyclic b-vertex does not generalize b-vertices to acyclic b-vertices in all the cases. For this observe Fig. . On the left, we have a colored 8-cycle where only color 1 has a weak acyclic b-vertex (that is actually a b-vertex), while colors 2 and 3 have no weak acyclic b-vertex. However, the presented coloring cannot be reduced with an acyclic recoloring step. Even more tricky is the example on the right graph G of Fig. 1. There are two similar colorings of this graph with only a difference in vertex z. In the first coloring z is colored by 2 and in the second coloring by 4. Vertices a, b, c are b-vertices for colors 1, 2, 4,  respectively, so only color 3,  which is without weak acyclic b-vertex, can be recolored. In the first coloring, this is possible as w and v can be recolored with 4,  and u and t with 2 and we get an acyclic coloring. On the other hand, an acyclic recoloring of G is not possible for the second coloring (i.e. the one in which $c(z)=4$), because u and v can be recolored only with 2 and this yields a bi-chromatic cycle.

Fig. 1

Colorings without weak acyclic b-vertices of all colors that can sometimes be acyclic recolored and sometimes not

Both colorings of G in Fig. 1 show that sometimes also an even cycle C can prevent the acyclic recoloring step for a color i and not a weak acyclic b-vertex. This is possible only if C is colored with exactly three colors, say i, j, k,  and i appears at least twice on C. Further, one of the other two colors, say j,  must be on every second vertex. We call such a cycle an i-critical cycle or i-CC for short. Note, that color k can appear only once, say on vertex v,  on C and in such a case v cannot be recolored with i by condition (2) (when v is a weak b-acyclic vertex). However, if also k appears at least twice on C,  then C is k-CC as well and we say that C is i, k-critical cycle or i, k-CC for short. Color i of i-CC is called principal while in i, k-CC we have two principal colors i and k. Clearly, i-CC is of the length at least six and i, k-CC of the length at least eight. Note that $C_8$ from Fig. 1 is 2, 3-CC and the 8-cycle from G on the same figure is 2, 3-CC as well. Further, in Fig.  C is 1-CC and $C'$ is 1, 5-CC.

Fig. 2

Cycles C and $C'$ form a critical cycle system

Critical cycles that have a common vertex of principal color can further influence on each other. For this observe a simple example in Fig. 2. Here C is 1-CC and $C'$ is 1, 5-CC and they have a common vertex d of principal color 1. Notice that b, c, g are b-vertices of colors 2, 4, 5,  respectively. In addition, e is a weak acyclic b-vertex. So the only candidate for acyclic recoloring is color 1. In this case, notice that f can be recolored only with 5. Now, d can be recolored with 3 or 5,  but we cannot recolor both d and f with 5,  because then $C'$ is bi-colored. So, d must receive color 3. Finally, a can be recolored only with 3,  which yields bi-colored cycle C. Hence, acyclic recoloring of this coloring is not possible.

Let c be an acyclic coloring of G. Let ${\mathcal {C}}$ be a collection of all critical cycles for c. A critical cycle system for color i or CCS(i) for short is a subcollection of i-CC from ${\mathcal {C}}$ that form a maximal connected subgraph of G and where different critical cycles intersect only in vertices of color i (there can be more than one CCS(i) in one coloring of G). The color that is not principal on a critical cycle C appears exactly once on C or on half of vertices of C. If it appears only once, then the condition (2) prevents the recoloring with i if necessary. The other color, say j,  can be always recolored on C (if there is no weak acyclic b-vertex of this color or some other CCS(j)). In Fig. 2$\{C,C'\}$ is the collection of all 1-CC as well as the only CCS(1) for the presented coloring. On the other hand, $C'$ is the only 5-CC and with this also CCS(5).

Let i be a principal color without any weak acyclic b-vertex in a coloring of a graph G. Let v be a vertex of color i in a CCS(i). An available color for v is every color that is not in the neighborhood of v and is not on a bi-colored path of even length between two neighbors of v. By $A_v$ we denote the set of all available colors of v. In Fig. 2 we have $A_a=\{3\},$ $A_d=\{3, 5\}$ and $A_f=\{5\}$ for CCS(1). On the same figure for CCS(5),  both sets of available colors are empty, because there exists a weak acyclic b-vertex g of color 5.

Let $D\subseteq {\mathcal {C}}$ be a CCS(i) for an acyclic coloring of graph G. If there exists a principal color i among the colors used on D such that for every vertex v from D colored with i there exists a color $j_v\in A_v,$ such that recoloring all such v with $j_v$ results in an acyclic coloring, then D is recolorable. Otherwise, D is not recolorable. CCS(1) $\{C,C'\}$ from Fig. 2 is not recolorable. As we have already observed, the recoloring of color 1 leads to a bi-chromatic cycle. Vertices of color 5 could be recolored in CCS(5),  however, vertex g is a b-vertex of color 5 and with this also a weak acyclic b-vertex and color 5 cannot be recolored. It is also easy to see that the critical cycle $C_8$ from Fig. 1 is not recolorable as well as the second coloring of G on the same figure. However, the first coloring of this graph is recolorable. Now everything is settled for the definition of acyclic b-vertices.

Definition 3.4

Let G be a graph with an acyclic coloring $c:V(G)\rightarrow [k].$ A vertex $v\in V_i,$ $i\in [k],$ is an acyclic b-vertex if it satisfies

$$\begin{aligned}{} & {} \forall \ell \in [k]-CN_c[v], \exists j\in CN_c(v): (G[V_{j,\ell }\cup \{v\}] \text { contains a cycle }\vee \nonumber \\{} & {} \quad \text {there exists a CCS }(i)\text { of }G\text { that contains }v\text { and is not recolorable}). \end{aligned}$$

(3)

Now we can describe minimal elements of $\prec _a$ of graph G as follows.

Theorem 3.5

An acyclic k-coloring c is a minimal element of $\prec _a$ if and only if every color class $V_i,$ $i\in [k],$ contains an acyclic b-vertex.

Proof

Let an acyclic k-coloring c be a minimal element of $\prec _a$ of a graph G. This means that we cannot present an acyclic recoloring step for c. There are two possible reasons for that for any color class $V_i,$ $i\in [k].$ Firstly, $V_i$ has a b-vertex or secondly, by any recoloring of $V_i$ we get a bi-chromatic cycle of colors, say j and $\ell ,$ different than i. Let $v_1v_2\dots v_qv_1$ be such a cycle C where $v_1\in V_i$ and $c(v_2)=c(v_q)=j.$ Clearly, C can be different after different recolorings. Since the recoloring is arbitrary, we may assume that $\ell \notin CN_c[v_1]$ is arbitrary. If $v_1$ is the only vertex of color i on C,  then path $v_2\dots v_q$ is bi-colored by c. Hence, $G[V_{j,\ell }\cup \{v\}$ contains a cycle and the first part of condition (3) holds. Otherwise, there exists more vertices of color i on C. Then there exists CCS(i) that contains $v_1,$ because C contains more than one vertex of color i and some i-CC from the mentioned CCS(i) is bi-chromatic after any recoloring. So, there exists CCS(i) that is not recolorable and the second part of condition (3) is fulfilled. In both cases, we have an acyclic b-vertex for every color $i\in [k].$

Conversely, if c is not a minimal element of $\prec _a,$ then we can perform an acyclic recoloring step for some color i. This means that for every $v\in V_i$ there exists a color $\ell _v\notin CN_c[v]$ such that for every $j\in CN_c(v)$ there is no cycle in $G[V_{j,\ell _v}\cup \{v\}]$ and every CCS(i) (if it exists) is acyclic recolorable. But then condition (3) is not fulfilled and $V_i$ is without acyclic b-vertex and we are done. $\square$

Corollary 3.6

The acyclic b-chromatic number $A_{\textrm{b}}(G)$ of a graph G is the largest integer k,  such that there exists an acyclic k-coloring,  where every color class $V_i,$ $i\in [k],$ contains an acyclic b-vertex.

Corollary 3.7

Let G be a graph with all even cycles being 4-cycles. The acyclic b-chromatic number $A_{\textrm{b}}(G)$ of G is the largest integer k,  such that there exists an acyclic k-coloring,  where every color class $V_i,$ $i\in [k],$ contains a weak acyclic b-vertex.

Let us observe some simple facts.

Corollary 3.8

For every positive integers $n,k,\ell ,$ where $k\ge 3$ and $\ell \ge 5,$ we have

• $A_{\textrm{b}}(\overline{K}_n)=1.$

• $A_{\textrm{b}}(P_{\ell })=3.$

• $A_{\textrm{b}}(C_k)=3.$

Proof

$A_{\textrm{b}}(\overline{K}_n)\ge 1$ and $A_{\textrm{b}}(C_k)\ge 3$ follow from (1), while the coloring $c:V(P_{\ell })\rightarrow [3]$ guaranteeing $A_{\textrm{b}}(P_{\ell })\ge 3$ can be defined as $c(v_i)=(i\,\,({\textrm{mod}}\,3))+1,$ $i\in [\ell ]$ (every internal vertex is a b-vertex and thus there is an acyclic b-vertex in each color class). On the other hand, if $\overline{K}_n$ is colored with $p\ge 2$ colors, then every color is without an acyclic b-vertex and this coloring is not a minimal element of $\prec _a$ by Theorem 3.5. Similar is with $C_k$ and $P_{\ell }.$ If they are colored by $p\ge 4$ colors, then no color class contains an acyclic b-vertex and such a coloring in not a minimal element of $\prec _a$ by Theorem 3.5. The desired equalities now follow. $\square$

We end this section with a brief discussion of graphs where ${\mathcal {F}}(G)={\mathcal{A}\mathcal{F}}(G),$ or in other words, where every coloring of G is acyclic. Among such graphs are clearly odd cycle graphs described in Proposition 2.1, some cactus graphs and in particular trees. For such graphs we have $A_{\textrm{b}}(G)=\varphi (G).$ In particular, b-chromatic number of trees and cactus graphs was studied in Irving and Manlove (1999) and Campos et al. (2009), respectively. In both cases, it was shown that

$$\begin{aligned} m(G)-1\le \varphi (G)\le m(G), \end{aligned}$$

where the above holds for cactus graphs when $m(G)\ge 7.$ Moreover, the lower bound is achieved if and only if G is a pivoted graph. Notice that pivoted tree (see Irving and Manlove 1999) is defined differently than a pivoted cactus graph (see Campos et al. 2009) and that for pivoted trees we do not have a restriction that $m(G)\ge 7.$ It is also important to mention, that the authors of Campos et al. (2009) used an alternative definition of cacti, where two cycles can have arbitrarily many vertices in common, provided that they do not have a common edge. For that reason, their results are not consistent with the definitions used in our paper. However, we still can formulate the following.

Corollary 3.9

Let T be a tree. If T is a pivoted tree,  then $A_{\textrm{b}}(T)=m(T)-1$ and otherwise $A_{\textrm{b}}(T)=m(T).$

Corollary 3.9 implies in particular that the difference between $A_{\textrm{b}}(G)$ and A(G) can be arbitrarily large.

Corollary 3.10

There exists an infinite family of graphs $G_1, G_2, \dots$ such that $(A_{\textrm{b}}(G_n)-A(G_n))\rightarrow \infty$ as $n\rightarrow \infty .$

Proof

For $n\ge 1,$ let $G_n$ be a graph consisting of a star $K_{1,n+1}$ with n pendant edges attached to each of its leaves. Graph $G_n$ has exactly $n+2$ vertices of degree $n+1$ and $n(n+1)$ vertices of degree 1,  so $m(G_n)=n+2.$ Also, $G_n$ is not a pivoted tree, so $A_{\textrm{b}}(G_n)=m(G_n)=n+2.$ On the other hand, any proper coloring of $G_n$ is its acyclic coloring, so $A(G)=2.$ Thus $A_{\textrm{b}}(G_n)-A(G_n)=n$ for every $n\ge 1$ and $(A_{\textrm{b}}(G_n)-A(G_n))\rightarrow \infty$ as $n\rightarrow \infty .$ $\square$

4 An upper bound on $A_{\textrm{b}}(G)$ analogous to m(G) for $\varphi (G)$

Let c be an acyclic k-coloring of a graph G that is minimal with respect to order $\prec _a.$ Recall that according to the Theorem 3.5 every color class $V_i$ contains an acyclic b-vertex. While for b-vertices, high enough degree is necessary, for acyclic b-vertices we need a high enough degree or sufficient number of even-vertex internally (or EVI for short) disjoint (u, w)-paths of odd order (that is, of even length) between some of its neighbors $u\ne w$ or a combination of both (by even-vertex internally disjoint we mean that two such paths can have odd vertices of such a path in common, but not the even vertices). In particular, if for $u,w\in N_G(v)$ there are k different EVI disjoint (u, w)-paths $P_1,\ldots ,P_k$ of even length, where $P_k=uvw,$ in the worst case these paths can yield k different colors into which v cannot be recolored. Indeed, on every path $P_i,$ $i\in [k-1],$ there can exist $a_i\in V(P_i)$ with $c(a_i)\notin \{c(v),c(u)\}$ and we can have alternating colors $c(u)=c(w)$ and $c(a_i)$ or $P_k\cup P_i$ is c(v)-CC that contains colors c(v), c(u) and $c(a_i)$ and belongs to a CCS(c(v)) that is not recolorable. Hence, in the worst case, $u, a_1,\dots ,a_{k-1}$ are colored differently and v cannot receive any of their colors in an acyclic recoloring step.

This can be generalized to a bigger number of neighbors in the following way. Consider a weak partition $P=\{A^P_0,A^P_1,\ldots ,A^P_k\}$ of $N_G(v)$ into $k+1$ disjoint sets such that $|A^P_0|\ge 0$ and $|A^P_i|\ge 2$ for $i\in [k]$ (the mentioned partition is weak because $A^P_0$ can be empty). Without loss of generality assume that v is colored with color 1,  the vertices of $A^P_0$ with distinct colors from the set $[2,|A^P_0|+1]$ and all the vertices of $A^P_i,$ $i\in [k],$ with color $|A^P_0|+i+1.$ Now, let ${\textrm{elp}}_G(v,P)$ be the maximum number of pairwise EVI disjoint paths disjoint with v having odd number of vertices (i.e., of even length), with both ends in one of the sets $A^P_i,$ $i\in [k].$ Observe that given a partition with color classes defined as above, in the worst case one cannot recolor v to exactly $(|A^P_0|+k+{\textrm{elp}}_G(v,P))$ colors different than c(v): $(|A^P_0|+k)$ colors are blocked by the neighbors and ${\textrm{elp}}_G(v,P)$ by the alternately colored bi-chromatic EVI disjoint paths that could appear in the coloring. This encourages us to define the acyclic degree of v as

$$\begin{aligned} d_G^a(v)=\max _{P\in {\mathcal {P}}(v)}\{(|A^P_0|+(|P|-1)+{\textrm{elp}}_G(v,P))\}, \end{aligned}$$

where ${\mathcal {P}}(v)$ is the family of all the weak partitions P of $N_G(v)$ defined as above.

See Fig.  with the only optimal weak partition of $N_G(y_1^1)$ defined as $P=\{A^P_0,A^P_1\},A^P_0=\{u,z_1^1,y_1^2\},$ $A^P_1=\{x_1^1,x_2^1\}.$ Clearly, $|A^P_0|=3,$ $|P|-1=1$ and ${\textrm{elp}}_G(v,P)=3$ (the paths being $x_1^1y_2^1x_2^1, x_1^1y_3^1x_2^1, x_1^1y_4^1x_2^1$), thus $d_G^a(y_1^1)=7.$

Fig. 3

Graph G with the optimal weak partition $A^P_0=\{u,z_1^1,y_1^2\},$ $A^P_1=\{x_1^1,x_2^1\},$ implying $|A^P_0|=3,$ $|P|-1=1,$ ${\textrm{elp}}_G(v,P)=3$ and $d_G^a(y_1^1)=7$

Since we traverse over all weak partitions in ${\mathcal {P}}(v),$ notice that $d_G^a(v)$ represents the maximum number of colors in $N_G(v)$ and on EVI disjoint paths of even length between vertices of $N_G(v)$ into which v cannot be recolored in a recoloring step. This gives an analogy to the relation between degree $d_G(v)$ and $\varphi (G),$ where we needed a sufficient number of vertices of high degree to expect $\varphi (G)$ to be large. Hence, we are encouraged to define an $m_a$-degree of a graph G denoted by $m_a(G).$ First we order the vertices $v_1,\ldots ,v_{n_G}$ of G by non-increasing acyclic degree. The value of $m_a(G)$ is then the maximum position i in this order such that $d_G^a(v_i)\ge i-1,$ that is

$$\begin{aligned} m_a(G)=\max \{i: i-1\le d_G^a(v_i)\}. \end{aligned}$$

Theorem 4.1

For any graph G we have $A_{\textrm{b}}(G)\le m_a(G).$

Proof

On the way to a contradiction suppose that there exists a graph G for which $k=A_{\textrm{b}}(G)>m_a(G)$ and that $c:V(G)\rightarrow [k]$ is an appropriate acyclic b-coloring of G. We may assume that $v_1,\ldots , v_{n_G}$ are ordered by non-increasing acyclic degree. Clearly, not all colors from [k] are present on the vertices $v_1,\ldots ,v_{k-1}$ and we may assume that $c(v_i)\ne k$ for every $i\in [k-1].$ This means that $d_G^a(v)<k-1$ for every vertex v of color k. Hence, for every vertex v of color k,  (3) does not hold, a contradiction with Theorem 3.5. $\square$

In general case, it seems to be hard to compute $m_a(G)$ because we need to derive acyclic degrees for every vertex v of G. This is further connected with all the weak partitions from ${\mathcal {P}}(v).$ Moreover, for every such weak partition we need to get the maximum number of EVI disjoint paths of even length.

The problem of finding a maximum cardinality set of disjoint paths between two fixed vertices is obviously related to the connectivity of graph and Menger’s Theorem (Menger 1927) and has been studied for many years. It was proved to be polynomially solvable already by Even and Tarjan (1975) with network flow algorithms and no spectacular progress has been made since then, although some papers may be found giving better results in special cases (see e.g. Grossi et al. 2018 or Preißer and Schmidt 2020 for some recent results). Unfortunately, when the path lengths are somehow restricted, the problem was proved to be NP-complete already by Itai et al. (1982). Bley (2003) proved its APX-completeness. Also the version of the problem of finding k disjoint paths between k disjoint pairs of terminals has been studied, see e.g. (Fleszar et al. 2018) for some recent results. We do not know any results about the problem of finding maximum cardinality set of EVI disjoint paths between arbitrary vertices, even if they are members of one fixed set.

Nevertheless, one can expect some success with $m_a(G)$ for certain graph classes, mainly the ones with low connectivity which are not too dense or with low maximum degree. In the next part of this section, we demonstrate this approach on a family of graphs. It will allow us to show that there is no linear relationship between $A_{\textrm{b}}(G)$ and $\Delta (G)$ in general case. This underlines another difference between $A_{\textrm{b}}(G)$ and $\varphi (G).$ Recall that $\varphi (G)\le m(G)\le \Delta (G)+1,$ however, as we are going to show, $A_{\textrm{b}}(G)$ can be arbitrarily larger than $\Delta (G).$

Theorem 4.2

There exists an infinite family of graphs $G_1, G_2, \dots$ such that $(A_{\textrm{b}}(G_n)-\Delta (G_n))\rightarrow \infty$ as $n\rightarrow \infty .$

Proof

For $n\ge 1,$ let $H_n^i,$ $i\in [2n+4],$ be isomorphic graphs with

$$\begin{aligned} V(H_n^i)=\{y_1^i,\ldots ,y_{n+2}^i\}\cup \{x_1^i,x_2^i\}\cup \{z_1^i,\ldots ,z_{n-1}^i\} \end{aligned}$$

and

$$\begin{aligned} E(H_n^i)=\{x_j^iy_{\ell }^i:j\in [2],\ell \in [n+2]\}\cup \{y_1^iz_j^i:j\in [n-1]\}. \end{aligned}$$

Notice that in Fig. 3 a graph $H_2^1$ is presented with two additional leaves u and $y_1^2.$ Using graphs $H_n^i,$ $i\in [2n+4],$ we construct graph $G_n$ with

$$\begin{aligned} V(G_n)=\{u,v\}\cup \bigcup _{i=1}^{2n+4}V(H_n^i) \end{aligned}$$

and

$$\begin{aligned} E(G_n)=\{uy_1^1,vy_1^{2n+4},y_1^iy_1^{i+1}:i\in [2n+3]\}\cup \bigcup _{i=1}^{2n+4}E(H_n^i). \end{aligned}$$

Observe $G_2$ in Fig. , while the first part $H_2^1$ together with the neighbors u and $y_1^2$ of $y_1^1$ in $G_2$ is presented in Fig. 3.

Notice that $d_{G_n}(y_1^i)=n+3,$ $d_{G_n}(x_j^i)=n+2,$ $j\in [2],$ and that the degree of the other vertices of $G_n$ is at most 2. Hence, $\Delta (G_n)=n+3$ and $m(G_n)=n+4$ (actually, we have also $\varphi (G_n)=n+4,$ the appropriate b-coloring is easy to obtain). Next we show that $A_{\textrm{b}}(G_n)=2n+4.$ For given $i\in [2n+4],$ observe the partition $P=\{A_0^i=\{y_1^{i-1}, y_1^{i+1}, z_j^i:j\in [n-1]\},A_1^i=\{x_1^i,x_2^i\}\}$ of $N_{G_n}(y_1^i),$ where $y_1^0=u$ when $i=1$ and $y_1^{2n+5}=v$ when $i=2n+4.$ First notice that ${\textrm{elp}}_{G_n}(y_1^i,P)=n+1$ as $\{x_1^iy_j^ix_2^i:j\in [2,n+2]\}$ are EVI disjoint $(x_1^i,x_2^i)$-paths of even length. Thus, $d_{G_n}^a(y_1^i)=(n+1)+1+(n+1)=2n+3,$ $i\in [2n+4],$ which gives $m_a(G_n)=2n+4,$ as there are exactly $2n+4$ vertices of this acyclic degree. By Theorem 4.1 we have $A_{\textrm{b}}(G_n)\le 2n+4.$

To show the equality we construct an acyclic b-coloring $c:V(G_n)\rightarrow [2n+4]$ with an acyclic b-vertex in every color class. For that purpose, let

$$\begin{aligned} A_i=\{c(x_1^i)=c(x_2^i), c(y_2^i), \dots , c(y_{n+2}^i), c(z_1^i), \dots , c(z_{n-1}^i)\} \end{aligned}$$

and

$$\begin{aligned} B_i=([2n+4]-[i-1,i+1])-\{-2n-4+i+1,2n+4+i-1\} \end{aligned}$$

for $i\in [2n+4].$ Notice that $|A_i|=|B_i|=2n+1.$ If c satisfies $c(y_1^i)=i$ and $c(x_1^i)=c(x_2^i)$ for every $i\in [2n+4],$ $A_i=B_i$ for every $i\in [2n+4],$ $c(u)=2n+4$ and $c(v)=1,$ then every vertex $y_1^i,$ $i\in [2n+4],$ is an acyclic b-vertex. Hence, $A_{\textrm{b}}(G_n)\ge 2n+4.$ One such coloring for $G_2$ is presented in Fig. 4. With this $A_{\textrm{b}}(G_n)=2n+4$ and $A_{\textrm{b}}(G_n)-\Delta (G_n)=n+1$ for every $n\ge 1$ and finally $(A_{\textrm{b}}(G_n)-\Delta (G_n))\rightarrow \infty$ as $n\rightarrow \infty .$ $\square$

Fig. 4

Graph $G_2$ with $\Delta (G_2)=5<8=A_{\textrm{b}}(G_2)$

In the remainder of this section, we will prove that there is a nonlinear bound on $A_{\textrm{b}}(G)$ with respect to $\Delta (G)$ and present an infinite family of extremal graphs for this bound. The following upper bound on $A_{\textrm{b}}(G)$ can be deduced from Theorem 4.1.

Corollary 4.3

For any graph G with $\Delta (G)\ge 2$ we have $A_{\textrm{b}}(G)\le \frac{1}{2}(\Delta (G))^2+1.$

Proof

Observe that for any weak partition $P=\{A^P_0,A^P_1,\ldots ,A^P_k\}$ of $N_G(v)$ there is

$$\begin{aligned} (|P|-1)\le \left\lfloor \frac{d_G(v) - |A_0^p|}{2}\right\rfloor \quad \text {and}\quad {\textrm{elp}}_G(v,P)\le \left\lfloor \frac{d_G(v) - |A_0^p|}{2}\right\rfloor (\Delta (G) -1). \end{aligned}$$

This implies

$$\begin{aligned} d_G^a(v)\le |A^P_0|+\frac{d_G(v) - |A_0^p|}{2}+\frac{d_G(v) - |A_0^p|}{2}(\Delta (G)-1)\le \frac{1}{2}(\Delta (G))^2. \end{aligned}$$

In consequence

$$\begin{aligned} m_a(G)\le \frac{1}{2}(\Delta (G))^2+1. \end{aligned}$$

$\square$

The above bound is tight, as the example of $C_4$ shows. Moreover, it belongs to an infinite family of graphs satisfying the condition with equality.

Theorem 4.4

There exists an infinite family of graphs $G_1, G_2, \dots$ such that $A_{\textrm{b}}(G_n)=m_a(G_n)=\frac{1}{2}(\Delta (G_n))^2+1.$

Proof

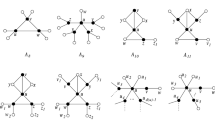
For any positive integer n,  we define a graph $H_n.$ Then, by combining some number of copies $H_{n,i}$ of $H_n,$ we will define graph $G_n$ being a member of the desired family. The vertices and edges of $H_{n,i}$ are defined as follows:

$$\begin{aligned} V(H_{n,i})&=\{v^i\}\cup \{x^i_j:j\in [2n]\}\cup \{y^i_k:k\in [n(2n-1)]\},\\ E(H_{n,i})&=\{v^ix^i_j:j\in [2n]\}\\&\cup \{x^i_jy^i_k:j\in \{2\ell -1,2\ell \}, k\in [(2n-1)(\ell -1)+1,(2n-1)\ell ], \ell \in [n]\}. \end{aligned}$$

Graphs $H_{1,i}=C_4,$ $H_{2,i}$ and $H_{3,i}$ are presented in Fig. .

Now let $G_1=H_{1,1}=C_4.$ Recall that $A_{\textrm{b}}(G_1)=3=\frac{1}{2}(\Delta (G_1))^2+1$ and, since for every $v\in V(G_1)$ we have $d_{G_1}^a(v)=2,$ also $m_a(G_1)=3.$ For $n\ge 2,$ in order to obtain $G_n$ we take $2n^2+1$ graphs $H_{n,i},$ $i\in [0,2n^2],$ and identify $y_{n(2n-1)}^{i-1}$ with $y_1^{i}$ for $i\in [2n^2].$ Note that $G_n$ has $2n^2+1$ vertices $v^i,$ $i\in [0,2n^2]$ of degree 2n,  $(2n^2+1)2n$ vertices $x_j^i,$ $i\in [0,2n^2],$ $j\in [2n]$ of degree 2n,  $2n^2$ vertices $y_{n(2n-1)}^{i-1}=y_1^{i},$ $i\in [2n^2],$ of degree $4\le 2n$ and $n(2n-1)(2n^2+1)-4n^2=(2n^2+1)(n(2n-1)-2)+1$ vertices $y_k^i,$ $(i,k)\in ([0,2n^2]\times [2,n(2n-1)-1])\cup \{(0,1),(2n^2,n(2n-1))\}$ of degree 2. Thus $\Delta (G)=2n.$

For every vertex $v^i,$ $i\in [0,2n^2],$ we have $d_{G_n}^a(v^i)=2n^2.$ Indeed, for the weak partition P of its neighborhood $A_0=\emptyset ,$ $A_{\ell }=\{x_{2\ell -1}^i,x_{2\ell }^i\}$ for $\ell \in [n],$ we have $|A_0^P|=0,$ $|P|-1=n$ and ${\textrm{elp}}_{G_n}(v,P)=n(2n-1)$ is the number of EVI disjoint paths of the form $x_{2\ell -1}^iy_k^ix_{2\ell }^i,$ where $(\ell ,k)\in [n]\times [(2n-1)(\ell -1)+1,(2n-1)\ell ].$ This implies that $d_{G_n}^a(v^i)\ge 0+n+n(2n-1)=2n^2=\frac{1}{2}(\Delta (G_n))^2.$ The inequality $d_{G_n}^a(v^i)\le \frac{1}{2}(\Delta (G_n))^2$ follows from the proof of Corollary 4.3. Obviously, no other vertex can have a higher acyclic degree. Since there are $2n^2+1$ vertices $v^i,$ from Theorem 4.1 we obtain $A_{\textrm{b}}(G_n)\le m_a(G_n)=2n^2+1.$

To finish the proof we define the following coloring c,  using the elements of additive group ${\mathbb {Z}}_{2n^2+1}$ as colors (with addition modulo $(2n^2+1)$ in the formulae):

$$\begin{aligned} c(y^i_1)&=i,\qquad \qquad \qquad \qquad \qquad \qquad i \in [0,2n^2],\\ c(y^i_{n(2n-1})&=i+1,\qquad \quad \qquad \qquad \qquad \quad i\in [0,2n^2],\\ c(y^i_k)&=i+k,\quad \qquad \qquad \qquad \qquad \quad i\in [0,2n^2], k\in [2,n(2n-1)-1],\\ c(x^i_{2\ell -1})=c(x^i_{2\ell })&=i+n(2n-1)-1+\ell ,\quad i\in [0,2n^2], \ell \in [n],\\ c(v^i)&=i+2n^2,\qquad \qquad \qquad \qquad \quad i\in [0,2n^2]. \end{aligned}$$

Note that c is an acyclic coloring of $G_n$ (only the colors of $x_j^i$ are used twice in every part $H_{n,i}$). Moreover, every $v^i$ is an acyclic b-vertex: n colors are blocked by its neighbors $x_j^i$ and $n(2n-1)$ other colors because of the cycles $v^ix_{2\ell -1}^iy_k^ix_{2\ell }^iv^i,$ which makes any of the potential $2n^2$ recolorings impossible. Since there is a vertex $v^i$ in every color class, c is an acyclic b-coloring and $A_{\textrm{b}}(G_n)\ge 2n^2+1.$ $\square$

Fig. 5

Graphs $H_{1,i}=C_4,$ $H_{2,i}$ and $H_{3,i}$

Remark 4.5

Note that the family defined in the proof of Theorem 4.4 is another family proving Theorem 4.2.

5 Acyclic b-chromatic number of joins

For more exact results we recall that the join of graphs G and H is the graph $G\vee H$ obtained from disjoint copies of G and H joined with all the possible edges between V(G) and V(H). More formally, $V(G\vee H)=V(G)\sqcup V(H)$ and $E(G\vee H)=E(G)\sqcup E(H)\sqcup \{uv:u\in V(G)\wedge v\in V(H)\}$ where $\sqcup$ denotes the disjoint union.

Theorem 5.1

For two non-complete graphs G and H we have

$$\begin{aligned} A_{\textrm{b}}(G\vee H)=\max \{A_{\textrm{b}}(G)+n_H,A_{\textrm{b}}(H)+n_G\}. \end{aligned}$$

If $H\cong K_q,$ then $A_{\textrm{b}}(G\vee H)=A_{\textrm{b}}(G)+q.$

Proof

Let G and H be two non-complete graphs. Let $c_G$ be an $A_{\textrm{b}}(G)$-coloring of G and let $V(H)=\{v_1,\ldots , v_{n_H}\}.$ The map

$$\begin{aligned} c(v)=\left\{ \begin{array}{ll} c_G(v) &{} \quad \text {if}\ v\in V(G), \\ A_{\textrm{b}}(G)+i &{} \quad \text {if}\ v=v_{i}\in V(H), \end{array} \right. \end{aligned}$$

(4)

is an acyclic coloring of $G\vee H,$ because $c_G$ is an acyclic coloring and all vertices of H receive different colors. Suppose that we can present a recoloring step for color i of c in $G\vee H$ to obtain coloring $c'.$ If $i>A_{\textrm{b}}(G),$ then vertex $v_{i-A_{\textrm{b}}(G)}\in V(H)$ is the only vertex of color i. Since $v_{i-A_{\textrm{b}}(G)}$ is adjacent to all vertices of G,  i is recolored in $c'$ by some color $j>A_{\textrm{b}}(G)$ where $j\ne i.$ Again, $v_{j-A_{\textrm{b}}(G)}\in V(H)$ is the only vertex from H with color j in coloring c. Since G is not complete, we have $A_{\textrm{b}}(G)<n_G$ by Proposition 3.2 and there exist $x,y\in V(G)$ with $c(x)=c(y).$ But now $xv_{i-A_{\textrm{b}}(G)}yv_{j-A_{\textrm{b}}(G)}x$ is a bi-chromatic 4-cycle under coloring $c',$ a contradiction. So we may assume that $i\le A_{\textrm{b}}(G)$ and that all the vertices of color i are from V(G). Every vertex of color i is adjacent to all vertices of H and they can therefore be recolored only with colors already used in G. But this is not possible because $c_G$ is an $A_{\textrm{b}}(G)$-coloring. Hence $A_{\textrm{b}}(G\vee H)\ge A_{\textrm{b}}(G)+n_H.$ By symmetric arguments we can show that $A_{\textrm{b}}(G\vee H)\ge A_{\textrm{b}}(H)+n_G$ which yields $A_{\textrm{b}}(G\vee H)\ge \max \{A_{\textrm{b}}(G)+n_H,A_{\textrm{b}}(H)+n_G\}.$

We prove the opposite inequality by a contradiction. Indeed, suppose that $A_{\textrm{b}}(G\vee H) > \max \{A_{\textrm{b}}(G)+n_H, A_{\textrm{b}}(H)+n_G\}$ for some graphs G and H that are not complete. Let c be an $A_{\textrm{b}}(G\vee H)$-coloring and let $c_G$ and $c_H$ be colorings of G and H,  respectively, induced by c,  that is $c_G(v)=c(v)$ for every $v\in V(G)$ and $c_H(u)=c(u)$ for every $u\in V(H).$ Clearly colors of $c_G$ are different than colors of $c_H.$ If $c_G$ has less than $n_G$ colors and $c_H$ less than $n_H$ colors, then $c_G(u)=c_G(v)$ and $c_H(x)=c_H(y)$ for some $u,v\in V(G)$ and $x,y\in V(H).$ But then we have a bi-colored four cycle uxvyu,  a contradiction. So, $c_G$ has $n_G$ colors or $c_H$ has $n_H$ colors. Without loss of generality we can assume that $c_G$ has $n_G$ colors. But then $c_H$ has more than $A_{\textrm{b}}(H)$ colors in H and does not yield a minimal element with respect to $\prec _a$ in ${\mathcal{A}\mathcal{F}}(H).$ So, there exists $c'_H$ such that $c'_H\triangleleft _a c_H$ and the coloring

$$\begin{aligned} c'(v)=\left\{ \begin{array}{ll} c(v) &{} \quad \text {if}\ v\in V(G), \\ c'_H(v) &{} \quad \text {if}\ v\in V(H), \end{array} \right. \end{aligned}$$

is obtained from c by an acyclic recoloring step, a contradiction with c being an $A_{\textrm{b}}(G\vee H)$-coloring. This yields the desired equality and we are done with the first part.

If $G\cong K_p$ and $H\cong K_q,$ then $G\vee H\cong K_{p+q}$ and equality holds by Corollary 3.2. If only one of G and H is complete, say $H\cong K_q,$ then we can use the coloring c defined in (4) for an $A_{\textrm{b}}(G)$-coloring $c_G$ of G. Following the same reasoning after (4), this time only for $i\le A_{\textrm{b}}(G),$ we obtain that $A_{\textrm{b}}(G\vee K_q)\ge A_{\textrm{b}}(G)+q$ (notice that $i>A_{\textrm{b}}(G)$ yields a contradiction since $H\cong K_q$ now).

Conversely, suppose that $A_{\textrm{b}}(G\vee K_q)>A_{\textrm{b}}(G)+q$ and let c be an $A_{\textrm{b}}(G\vee H)$-coloring. Again we can follow the above steps and see that $c_G,$ that is the restriction of c to G,  contains more than $A_{\textrm{b}}(G)$ colors and one can perform an acyclic recoloring step in G. This yields an acycling recoloring step in $G\vee K_q$ and c is not a minimal element of $\prec _a,$ a final contradiction. $\square$

Recall that complete bipartite graph $K_{m,n}=\overline{K}_n\vee \overline{K}_m,$ wheel $W_n=K_1\vee C_{n-1},$ fan $F_n=K_1\vee P_{n-1}$ and complete split graph $K_n\vee \overline{K}_m$ are all joins of two graphs. Hence the following corollary follows directly from Theorem 5.1 and Corollaries 3.2 and 3.8.

Corollary 5.2

For every positive integers $k,\ell ,m,n,$ where $k,\ell \ge 5,$ we have

• $A_{\textrm{b}}(K_{n,m})=1+\max \{n,m\};$

• $A_{\textrm{b}}(W_k)=4;$

• $A_{\textrm{b}}(F_k)=4;$

• $A_{\textrm{b}}(K_n\vee \overline{K}_m)=n+1;$

• $A_{\textrm{b}}(P_k\vee P_{\ell })=A_{\textrm{b}}(P_k\vee C_{\ell })=A_{\textrm{b}}(C_k\vee C_{\ell })=3+\max \{k,\ell \}.$

Corollary 5.2 implies in particular that the difference between $A_{\textrm{b}}(G)$ and $\varphi (G)$ can be arbitrarily large.

Corollary 5.3

There exists an infinite family of graphs $G_1, G_2, \dots$ such that $(A_{\textrm{b}}(G_n)-\varphi (G_n))\rightarrow \infty$ as $n\rightarrow \infty .$

Proof

For $n\ge 1,$ let $G_n=K_{n,n}.$ Since the proper 2-coloring of $K_{n,n}$ is its b-coloring, we have $\varphi (K_{n,n})=2,$ while $A_{\textrm{b}}(K_{n,n})=1+n,$ so $A_{\textrm{b}}(K_{n,n})-\varphi (K_{n,n})=n-1$ for $n\ge 1$ and $(A_{\textrm{b}}(G_n)-\varphi (G_n))\rightarrow \infty$ as $n\rightarrow \infty .$ $\square$

Notice also that the family $\{G_n\}$ defined in the proof of Theorem 4.2 is another family of graphs for which $(A_{\textrm{b}}(G_n)-\varphi (G_n))\rightarrow \infty$ when $n\rightarrow \infty .$

6 Final remarks

In the paper, we introduced a new graph invariant, the b-acyclic chromatic number $A_{\textrm{b}}(G)$ and proved some of its properties. Some problems, however, remain still open.

Although the construction of a b-acyclic coloring seems very similar to one of b-colorings (one considers only acyclic colorings instead of all colorings), we observed some interesting differences between them. In particular, $A_{\textrm{b}}(G)$ can be arbitrarily larger than the acyclic chromatic number A(G),  maximum degree $\Delta (G)$ and b-chromatic number $\varphi (G).$ The last result is consistent with the intuition that $A_{\textrm{b}}(G)$ should be not less than $\varphi (G),$ since the strictly partial ordered set of acyclic colorings is obviously a subset of the strictly partial ordered set of all proper colorings. However, we can neither prove nor disprove it.

On the other hand, we proved the theorem allowing to verify whether a coloring is a minimal element of the strictly partial ordered set of acyclic colorings, using the criterion of the existence of a b-acyclic vertex in every color class (where the concept of b-acyclic vertex is a natural generalization of the notion of a b-vertex). We also proved an inequality analogous to $\varphi (G)\le m(G).$ To this end, we introduced a new vertex measure, the acyclic degree $d_G^a(v)\ge d_G(v)$ and resulting graph invariant $m_a(G)\ge m(G)$ allowing to define the upper bound $A_{\textrm{b}}(G)\le m_a(G).$ But these results still do not help to prove any relation between $A_{\textrm{b}}(G)$ and $\varphi (G).$

One of the causes of the difficulties in proving any relationship between these two parameters is the fact that a minimal element of the poset of proper colorings does not need to be an acyclic coloring and vice versa. A simple example is presented in Fig.  (the graph was originally presented in a different context in Tuite et al. 2022).

Fig. 6

Graph G from Tuite et al. (2022) for which $6=\varphi (G)\le A_{\textrm{b}}(G)$ and the minimal colorings are incomparable

Indeed, one can easily check that the coloring c in which $c(x)=6$ is the only (up to obvious rotations) b-coloring of G with b-vertices u and the five ones marked with black circles. However, this coloring is not acyclic, due to the cycle $xx'y'yx.$ On the other hand, in the acyclic coloring $c'$ defined as $c'(x)=3$ and $c'(w)=c(w)$ for $w\in V(G)-\{x\},$ we have five b-vertices (being by definition b-acyclic vertices) marked with black circles and the sixth b-acyclic vertex v,  that cannot be recolored with neither 1,  3,  4 nor 6 because they are the colors of its neighbors, but also color 5 is forbidden because of the 4-cycle vzyxv. On the other hand, there is no b-vertex in color class 2. This means in particular, that $c'$ is minimal in the poset of acyclic colorings, but not in the strictly partial ordered set of proper colorings. Moreover, since c and $c'$ use the same number of colors, there is no sequence of recoloring steps leading from one to the other, so they are incomparable in the poset of proper colorings.

Taking into account the above considerations, we formulate the first open problem.

Problem 6.1

Prove or disprove the inequality $A_{\textrm{b}}(G)\ge \varphi (G).$

If the inequality comes out to be false (i.e., if there is a counterexample), it would be interesting to know, for which graphs it is true. This leads us to a relaxed version of the last problem.

Problem 6.2

Characterize the graphs,  for which $A_{\textrm{b}}(G)\ge \varphi (G).$

Another interesting question refers to the results about $\phi (G)$ presented in Irving and Manlove (1999) and Campos et al. (2009).

Problem 6.3

Characterize the graphs,  for which $A_{\textrm{b}}(G)\ge m_a(G)-c$ for some constant c. In particular,  characterize the graphs,  for which $A_{\textrm{b}}(G)= m_a(G).$

We have seen some examples, see Figs. 1 and 2, of $A_{\textrm{b}}(G)$-colorings that contain not recolorable critical cycle systems or, in other words, some colors have a acyclic b-vertex that is not a weak acyclic b-vertex. However, all such examples also have $A_{\textrm{b}}(G)$-coloring where every color has its weak acyclic b-vertex. So, we ask if weak acyclic vertices are enough to describe acyclic b-chromatic number of a graph in the meaning of Corollary 3.6?

Problem 6.4

Is it true that the acyclic b-chromatic number $A_{\textrm{b}}(G)$ of a graph G is the largest integer k,  such that there exists an acyclic k-coloring,  where every color class $V_i,$ $i\in [k],$ contains a weak acyclic b-vertex?

The next problem refers to the complexity of finding $A_{\textrm{b}}(G),$ which is expected to be at least NP-hard in general.

Problem 6.5

Find the complexity of deriving $A_{\textrm{b}}(G).$

We do expect that there are some special families of graphs, for which polynomial time is enough for solving $A_{\textrm{b}}(G)$ (see Corollary 3.9 for trees).

Problem 6.6

Find polynomial algorithms for finding $d_G^a(v),$ $m_a(G)$ and $A_{\textrm{b}}(G)$ for chosen families of graphs.

In particular some exact values or estimates for $A_{\textrm{b}}(G)$ for families of graphs other than analyzed in this paper would be a valuable contribution.

Problem 6.7

Find explicit formulae or tight lower and upper bounds on $d_G^a(v),$ $m_a(G)$ and $A_{\textrm{b}}(G)$ for chosen families of graphs.