Superconvergence of interpolated collocation solutions for weakly singular Volterra integral equations of the second kind

Abstract

In this paper, we discuss the superconvergence of the “interpolated” collocation solutions for weakly singular Volterra integral equations of the second kind. Based on the collocation solution $u_h$, two different interpolation postprocessing approximations of higher accuracy: $I_{2h}^{2m-1}u_h$ based on the collocation points and $I_{2h}^{m}u_h$ based on the least square scheme are constructed, whose convergence order are the same as that of the iterated collocation solution. Such interpolation postprocessing methods are much simpler in computation. We further apply this interpolation postprocessing technique to hybrid collocation solutions and similar results are obtained. Numerical experiments are shown to demonstrate the efficiency of the interpolation postprocessing methods.

1 Introduction

In this paper, we consider the following weakly singular Volterra integral equation (VIE) of the second kind:

$$\begin{aligned} u(t)=g(t)+\int _0^t (t-s)^{-\alpha }K(t,s)u(s)ds,\ \ \ \ t\in I:=[0,T], \end{aligned}$$

(1)

with $0<\alpha <1$. K(t, s), g(t) are known functions and u(t) is the function to be determined. Let $D:=\{(t,s):0\le s< t \le T\}$. We assume that $K(t,s)\in C(D)$ , with $K(t,t)\ne 0$ for $t\in I$.

(1) arises in many modeling problems in mathematical physics and chemical reactions, such as stereology, heat conduction, crystal growth, electrochemistry, superfluidity, and the radiation of heat from a semi-infinite solid.

The second kind Volterra integral equations with weakly singular kernels typically have solutions whose derivatives are unbounded at the left endpoint of the interval of integration. Due to this singular behavior, the optimal global and local (super-) convergence results of collocation solutions in piecewise polynomial spaces on uniform meshes will no longer be valid (Brunner 1983). The use of suitable graded meshes (Brunner 1985; Tang 1992) is a possible alternative approach for dealing with this order reduction problem. However, as pointed out in (Brunner 1983; Diogo et al. 1994), the initial stepsize becomes very small in the graded mesh and may cause serious round-off errors when the number of elements N is increased or high-order piecewise polynomials are used. Alternatively, some other numerical methods are proposed to get the optimal convergence of the numerical solutions. See, for example, nonpolynomial spline functions reflecting the singularity on uniform meshes (Brunner 1983), $\beta -$polynomial collocation methods under quasi-graded meshes (Hu 1996, 1997), and variable transformations followed by standard methods (Pedas and Vainikko 2004a, b). The hybrid method first proposed by Cao et al. (2003) uses “looser” graded partitions to avoid round-off errors and nonpolynomial interpolation in the first stepsize to preserve the optimal order of convergence.

Superconvergence is a hot topic in solving various differential equations and integral equations. Based on current convergence results of numerical solutions, suitable postprocessing with relative cheap computation can result in global superconvergence of the new “postprocessed” solutions. There are many postprocessing methods to get the superconvergence of the “postprocessed” solutions of partial differential equations and integral equations. See, for instance, iterated postprocessing (Graham et al. 1985; Sloan 1976, 1990), interpolation postprocessing (Lin and Lin 2006; Lin and Yan 1996), and PPR ( Naga and Zhang 2004; Zhang and Naga 2005), etc. For weakly singular Volterra integral equations, generally, the iterated postprocessing method (including the classical iterative and hybrid iterative methods) is used to accelerate the approximation. See, for example, Diogo 2009; Huang and Xu 2006; Rebelo and Diogo 2010. Interpolation postprocessing was proposed by Lin and his group to accelerate the convergence of finite-element solutions for various partial differential equations, integral equations, and integro-differential equations, and the corresponding works are contained in some papers (such as Lin et al. 1998; Zhang et al. 2000; Huang and Zhang 2010; Huang and Xie 2009) and two monographs (Lin and Lin 2006; Lin and Yan 1996). For weakly singular VIEs, the interpolation postprocessing is used to $\beta$-polynomial collocation solutions to get the superconvergence of the new solutions (Hu 1997). Theoretical analysis and numerical results show that this interpolation postprocessing technique is both simple and of higher accuracy.

In this paper, we apply the interpolation postprocessing technique to the collocation solution under graded mesh and the hybrid collocation solution under “looser” graded mesh to get the same superconvergence as the iterated methods. This interpolation postprocessing is simpler in computation than the iterated postprocessing method. Since the former just needs to interpolate $u_h$ at some nearby points, and, however, the latter needs to compute an integral (probably weakly singular) for each t.

Here is the outline of the remaining sections. The collocation method, the hybrid collocation method, and the corresponding iterated methods for weakly singular Volterra equations are presented in Sect. 2 to make the paper self-contained. In Sect. 3, the supercloseness between the (hybrid) collocation solution and the interpolation of the exact solution u is proved, and the main results about the superconvergence of interpolation postprocessing method, instead of the iterated method, are obtained. Finally, numerical experiments are provided in Sect. 4 to show the efficiency of the interpolation postprocessing method and to compare the computational efficiency of these two postprocessing methods.

2 Iterated collocation method for weakly singular Volterra integral equations

In this section, we first introduce the collocation method and the hybrid collocation method for weakly VIEs. The iterated postprocessing is then presented based on these two methods.

2.1 Collocation method for weakly singular VIEs

Define the linear Volterra integral operator ${\mathcal {V}}_\alpha$ as:

$$\begin{aligned} ({\mathcal {V}}_\alpha u)(t):=\int _0^tH_\alpha (t,s)u(s)ds,\ \ \ \ t\in I:=[0,T], \end{aligned}$$

(2)

with

$$\begin{aligned} H_\alpha (t,s):= (t-s)^{-\alpha } K(t,s),\quad 0<\alpha < 1. \end{aligned}$$

(3)

Then, the corresponding operator form of the linear Volterra integral equation (1) is as follows:

$$\begin{aligned} u(t)=g(t)+({\mathcal {V}}_\alpha u)(t),\ \ \ \ t\in I. \end{aligned}$$

(4)

The existence and uniqueness of the solution for (1) (or (4)) are given in the following Theorem (see Brunner (2004) for details).

Theorem 1

Assume that $K\in C(D)$ and $0<\alpha <1$. Then, for any $g\in C(I)$ the linear, weakly singular Volterra integral equation (1) possesses a unique solution $u\in C(I)$. If $g\in C^m(I)$ and $K\in C^m(D)$ with $K(t,t)\ne 0$ on I, then:

$$\begin{aligned} u\in C^m(0,T]\cap C(I),\quad with \quad |u'(t)|\le C_\alpha t^{-\alpha }, \quad for\quad t\in (0, T]. \end{aligned}$$

Typically, VIEs with weakly singular kernels behave like $t^{-\alpha }\ (0<\alpha <1)$ have solutions whose derivatives are unbounded at the left endpoint of the interval of integration. Due to this singular behavior, the optimal global and local (super-) convergence results for collocation solutions in piecewise polynomial spaces on uniform meshes will no longer be valid. The use of appropriately graded meshes is one of the possible alternative approaches for dealing with this order reduction.

We recall that for an interval $I:=[0,T]$, a graded mesh with grading exponent $r>1$ is defined by:

$$\begin{aligned} I_h:=\{t_n=t_n^{(N)}:=(n/N)^rT,\ n=0,1,\ldots ,N\}. \end{aligned}$$

(5)

The sequence $\{h_n=t_{n}-t_{n-1} \ (n=1,2,\ldots , N)\}$ is strictly increasing.

The piecewise polynomial space of degree $\le m-1$ is defined as:

$$\begin{aligned} S_{m-1}^{(-1)}(I_h):=\{v\in L^2(I): v|_{I_n}\in {\mathcal {P}}_{m-1}\ (1\le n\le N)\}, \end{aligned}$$

where ${\mathcal {P}}_{m-1}$ is the space of all polynomials of degree $\le m-1$.

The desired collocation solution $u_h$ for the weakly singular VIE (4) is defined by:

$$\begin{aligned} u_h(t)=g(t)+({\mathcal {V}}_\alpha u_h)(t),\ \ \ \ t\in X_h, \end{aligned}$$

(6)

where the set of collocation points:

$$\begin{aligned} X_h:= & {} \{t_{ni}=t_{n-1}+c_ih_n: 0< c_1< \ldots<c_i< \ldots <c_m\le 1,\nonumber \\&n=1,2,\ldots , N;\ i=1,2,\ldots , m\}. \end{aligned}$$

(7)

is determined by the given mesh $I_h$ and the (distinct) collocation parameters $\{c_i\}$.

Define the corresponding interpolatory projection operator $P_h: C[0,T]\rightarrow S_{m-1}^{(-1)}(I_h)$ satisfying that for $x\in C[0,T]$:

$$\begin{aligned} P_h(x(t_{n,i}))=x(t_{n,i})\ (n=1,2,\ldots , N; i=1,\ldots , m). \end{aligned}$$

(8)

It is easy to verify that $P_h$ is bounded. The collocation equation (6) has the following operator form:

$$\begin{aligned} u_h=P_h g+P_h({\mathcal {V}}_\alpha u_h). \end{aligned}$$

(9)

Theorem 2

(Brunner 2004) Assume:

• 1. The given functions in the Volterra integral equation (1) satisfy $K\in C^m(D)$ and $g\in C^m(I)$.

• 2. $u_h\in S^{(-1)}_{m-1}(I_h)$ is the (unique) collocation solution to (1) defined by (6), with $h:=T/N\in (0,{\bar{h}})$ and corresponding to the collocation points $X_h$, where ${\bar{h}}={\bar{h}}(\alpha )>0$.

• 3. The grading exponent $r=r(\alpha )\ge 1$ determining the mesh $I_h$ is given by:

  $$\begin{aligned} r(\alpha )=\frac{\mu }{1-\alpha },\quad \mu \ge 1-\alpha . \end{aligned}$$

Then, we have:

$$\begin{aligned} \Vert u-u_h\Vert _\infty :=\sup \limits _{t\in I}|u(t)-u_h(t)| \le C(r)\left\{ \begin{array}{ll} h^\mu , &{} \hbox { if } 1-\alpha \le \mu < m, \\ h^m, &{} \hbox { if } \mu \ge m, \end{array} \right. \end{aligned}$$

(10)

holds for any set $X_h$ of collocation points with $0\le c_1<\cdots <c_m\le 1$. The constant C(r) depends on $\{c_i\}$ and on the grading exponent $r=r(\alpha )$, but not on h.

2.2 Hybrid collocation method for weakly singular VIEs

Although the graded mesh can get the desired convergence, its initial stepsize becomes very small and may cause round-off errors for $\alpha \rightarrow 1$ when N is increased or high-order piecewise polynomials are used. A “looser” graded mesh combining nonpolynomials interpolation in the initial stepsize called the hybrid method (Cao et al. 2003) was proposed to optimize the grid while maintaining the same accuracy.

In this subsection, we describe the “looser” graded partition of I. Specifically, for a real number $r \ge 1$, we let $i_{0}$ be an integer, such that:

$$\begin{aligned} \left\lceil \left( \frac{N}{i_{0}}\right) ^{r}\right\rceil = N, \end{aligned}$$

where $\lceil a\rceil$ denotes the smallest integer greater than or equal to a.

It is easy to verify that such an integer $i_{0}$ exists and satisfies:

$$\begin{aligned} N^{1-1/r} \le i_{0} < N(N-1)^{-1/r} \end{aligned}$$

or the equivalent estimate:

$$\begin{aligned} N^{1-1/r} \le i_{0} < N^{1-1/r}+1. \end{aligned}$$

Set $N' :=N - i_{0} +1$. The partition on I is given by:

$$\begin{aligned} t_{0}=0,t_{i}=\left( \frac{i_{0}+i-1}{N}\right) ^{r}T, \ i=1,2,...,N'. \end{aligned}$$

(11)

Note that $t_{N'}=T$ and the stepsize of the first subinterval for this partition is larger than that for the graded mesh and reduces the possibility of round errors.

However, this “looser” partition cannot capture the singularity of the exact solution as well as the graded mesh due to the “bigger” stepsize of the initial subinterval. To preserve the singularity properties of the solution, the nonpolynomial interpolation reflecting the singularities of the exact solution is used in the first subinterval.

For $0<\alpha <1$ and a positive integer, we introduce an index set:

$$\begin{aligned} W_{\alpha ,m}=\{i+j\alpha :i+j\alpha < m,\ i, j\in N^{*}\}, \end{aligned}$$

where $N^{*}$ denotes the set of the nonnegative integers and l is the cardinality of the dimension of the space $W_{\alpha ,m}$ ($l:=\dim W_{\alpha ,m}$).

The nonpolynomial space $V_{m}$ of degree $< m$ is defined by:

$$\begin{aligned} V_{m} :=\mathrm{span}\{t^{\nu _{j}}: j=0,1,...,l-1, \ \nu _j\in W_{\alpha ,m}\}. \end{aligned}$$

The hybrid space $S_{m}^{(-1)}(I_h)$ of degree $< m$ is defined by:

$$\begin{aligned} S_{m}^{(-1)}(I_h):=\{v\in L^2(I): v|_{I_1}\in V_{m}, v|_{I_i}\in {\mathcal {P}}_{m-1}, i=2,3,\cdots ,N' \}. \end{aligned}$$

(12)

Let $0\le c_{1}<c_{2}<...<c_{l}\le 1$, and we choose l collocation points $t_{1j}:=t_{0}+c_{j}h_{1}\ (j=1,2,...,l)$ in $I_1=[t_0, t_1]$ and $t_{ij}=t_{i-1}+c_{j}h_{i}\ (j=1,2,...,m)$ in $I_i=[t_{i-1}, t_i]\ (i=2,...,N')$, and denoted by:

$$\begin{aligned} {\bar{X}}_h=\left\{ \begin{array}{ll} t_{1j}:=t_{0}+c_{j}h_{1}\ (j=1,2,...,l),\ t_{1j}\in I_1\\ t_{ij}=t_{i-1}+c_{j}h_{i}\ (j=1,2,...,m),\ t_{ij}\in I_i,\ i=2,...,N'. \end{array} \right. \end{aligned}$$

(13)

For simplicity of the notations, we introduce the notation:

$$\begin{aligned} m_n:= \left\{ \begin{array}{ll} l, &{} n=1; \\ m, &{} n=2,3,...,N'. \end{array} \right. \end{aligned}$$

The hybrid collocation method for (1) [or the relevant operator form (4)] is to seek $u_h\in S_{m}^{(-1)}(I_h)$, such that:

$$\begin{aligned} u_h(t_{nj})=g(t_{nj})+({\mathcal {V}}_\alpha u_h)(t_{nj}),\ \ n=1,2,\ldots ,N',\ j=1,2,\ldots ,m_n. \end{aligned}$$

(14)

For $f \in C(I)$, we define the relevant hybrid interpolation operator $Q_{h}: C(I)\rightarrow S_{m}^{(-1)}(I_h)$ by:

$$\begin{aligned} (Q_{h}f)(t_{ni})=f(t_{ni}),\ \ n=1,2,\cdots , N', j=1,2,\cdots , m_n. \end{aligned}$$

(15)

We know from the definition of $Q_{h}$ that the singularity preserving (nonpolynomial) interpolation is used in the first subinterval and the standard piecewise polynomial interpolation in the rest of subintervals. We refer (Cao et al. 2003) for more details of $Q_{h}$.

Then, the operator form of the hybrid collocation method for weakly singular VIE (4) or (1) is to seek $u_{h}\in S_{m}^{(-1)}(I_h)$, such that:

$$\begin{aligned} u_h=Q_h g+Q_h({\mathcal {V}}_\alpha u_h), \end{aligned}$$

(16)

where $Q_{h}$ is defined by (15) under the mesh defined by (11).

The following lemma shows the convergence of the hybrid collocation solution.

Lemma 1

(Cao et al. 2003) Let u be the exact solution of (1) and N be a positive integer. Let $Q_{h}$ be the hybrid interpolation operator defined by (15) associated with the graded partition (11). Suppose the forcing function g in (1) has the form $g(t)\ =\sum \limits _{j+i\alpha < m}g_{ij}t^{j+i\alpha }\ +\ g_{m}(t)$. Then, for sufficiently large N, (16) has a unique solution $u_h$ and there exists a positive constant C independent of N, such that:

$$\begin{aligned} \parallel u-u_{h}\parallel _{\infty }\le CN^{-m}. \end{aligned}$$

2.3 Iterated postprocessing for (hybrid) collocation solutions

The iterated collocation solution $u_{h}^{it}$ corresponding to the (hybrid) collocation solution $u_h$ is then defined by:

$$\begin{aligned} u_h^{it}(t):=g(t)+({\mathcal {V}}_\alpha u_h)(t),\quad t\in I. \end{aligned}$$

(17)

It trivially satisfies:

$$\begin{aligned} u_h^{it}(t)= u_h(t),\quad \forall t\in X_h({\bar{X}}_h). \end{aligned}$$

(18)

That is, $P_hu_h^{it}= u_h$ for the traditional collocation method and $Q_hu_h^{it}= u_h$ for the hybrid collocation method.

It is easy to prove that the iterated collocation solution $u_{h}^{it}$ have the following operator form:

$$\begin{aligned} u_h^{it}=g+{\mathcal {V}}_\alpha (R_h u_h^{it}), \end{aligned}$$

(19)

where the operator $R_{h}:=P_{h}$ for the traditional collocation method and $R_{h}:=Q_{h}$ for the hybrid collocation method.

Next, we give the superconvergence results of iterated collocation solutions and iterated hybrid collocation solutions.

Theorem 3

(Brunner 2004) Assume:

• 1. $g\in C^{m+1}(I), K\in C^{m+1}(D)$, with $K(t,t)\ne 0$ on I, and $0<\alpha <1$;

• 2. $u_h\in S^{(-1)}_{m-1}(I_h)$ is the (unique) collocation solution to (1), with corresponding iterated collocation solution $u_h^{it}$;

• 3. the collocation parameters satisfy $J_0:=\int _0^1\prod \limits _{i=1}^m(s-c_i)ds=0$;

• 4. $I_h$ is the graded mesh (5) with grading exponent $r=r(\alpha )\ge 1$ and $h:=T/N$.

Then:

$$\begin{aligned} \Vert u-u_h^{it}\Vert _\infty \le C(r) \left\{ \begin{array}{l@{\quad }l} h^{2(1-\alpha )}, &{} \hbox {if } r=1, \\ h^{m+1-\alpha }, &{} \hbox {if }r\ge \frac{m}{1-\alpha }. \end{array} \right. \end{aligned}$$

(20)

Similarly, the hybrid collocation parameters is supposed to satisfy:

$$\begin{aligned} J_0:=\int _0^1s^j\prod \limits _{i=1}^m(s-c_i)ds=0,\ \ (j=0,...,r_0), \end{aligned}$$

(21)

where $r_0$ is a nonnegative integer less than m. When $r_0=1$, the following result for the iterated hybrid collocation method is obtained.

Theorem 4

(Huang and Xu 2006) Suppose that $K\in C^{m+2}(D)$ and $g\in C^{m+2}(I)$. Let u be the exact solution of (1) and $u_h\in S^{(-1)}_{m}(I_h)$ is the (unique) hybrid collocation solution to (1), with corresponding iterated hybrid collocation solution $u_h^{it}$. Then, there exists a positive constant C and a positive integer $N_{0}$, such that for all $N>N_{0}:$

$$\begin{aligned} \Vert u-u_h^{it}\Vert _\infty \le CN^{-m-1+\alpha }. \end{aligned}$$

(22)

If $r_0=0$ in the orthogonal condition (21), we can get the similar result of iterated hybrid collocation solutions under the same regularity restrictions of K, g as Theorem 3:

Corollary 1

Assume that $g\in C^{m+1}(I)$, $K\in C^{m+1}(D)$, with $K(t,t)\ne 0$, the hybrid collocation parameters satisfy $\int _0^1\prod \nolimits _{i=1}^m(s-c_i)ds=0$. Then, for the iterated hybrid collocation solution, there holds:

$$\begin{aligned} \parallel u-{u_{h}^{it}}\parallel _\infty \le C \left\{ \begin{array}{l@{\quad }l} N^{-(m+1-\alpha )}, &{} \hbox {if}\quad \alpha \ge \frac{1}{m+1}, \\ N^{-(m+1-\frac{1-\alpha }{m})}, &{} \hbox {if } \quad \alpha < \frac{1}{m+1}. \end{array} \right. \end{aligned}$$

In fact, when $r_0=0$, (21) simplifies to $\int _0^1\prod \limits _{i=1}^m(s-c_i)ds=0$.

The kernel $H_{\alpha }(t,s)$ satisfies the following condition on $D=\{(t,s):0\le s\le t\le T\}$:

$$\begin{aligned} \mid \frac{\partial ^{i}}{\partial s^{i}}H_{\alpha }(t,s)\mid \le C(t-s)^{-\alpha -i}, \ \ i=0,1,...,m. \end{aligned}$$

See (3.2) of Huang and Xu (2006) for details, where $l=-1, \beta =0$. The conclusion is valid by Lemma 3.2 and (3.23) of Huang and Xu 2006. We leave the details to the reader.

Remark 1

We see from Lemma 1 and Theorem 4 that the graded parameter r of the hybrid collocation method is not as sensitive to the values of $m, \alpha$ as the traditional collocation method.

3 Global superconvergence of interpolation postprocessing

In this section, some results on supercloseness between the (hybrid) collocation solution $u_h$ and the interpolant defined in (8) [(15) for hybrid collocation] of the exact solution u are given, and then, we use two postprocessing methods based on the supercloseness to accelerate the (hybrid) collocation solutions.

3.1 Supercloseness analysis between $u_h$ and $P_hu\ (Q_hu)$

We begin by citing from (Lin and Lin 2006; Lin and Yan 1996) the following definition of “supercloseness”.

Definition 1

If the error between the numerical solution and some interpolant of the exact solution is much smaller than that between the numerical solution and the exact solution; that is, if:

$$\begin{aligned} \Vert P_hu-u_h\Vert _\infty \ll \Vert u-u_h\Vert _\infty , \end{aligned}$$

then this phenomenon is called “supercloseness”.

We then introduce the following $H\ddot{o}lder$ space:

$$\begin{aligned} C^{(0,\beta )}[a,b]=\{g\in C[a,b]|d_{\beta }(g)\equiv \sup _{a\le t,\tau \le b}\frac{|g(t)-g(\tau )|}{|t-\tau |^{\beta }}<\infty \}, \end{aligned}$$

where $0<\beta <1$, and if $u\in C^{(0,\beta )}[a,b]$, then u is called $\beta -H\ddot{o}lder$ continuous.

Lemma 2

Atkinson 1997 For $N,m>0$ and grading exponent $r\ge 1$, $P_h$ is the interpolation projection operator defined by (8) in Sect. 2. For $0<\alpha <1$, assume $u\in C^{(0,1-\alpha )}[0,1]\cap C^m(0,1]$, with:

$$\begin{aligned} |u^m(t)|\le c_{\alpha ,m}(u)t^{1-\alpha -m},\ \ 0<t\le 1, \end{aligned}$$

where $C^{(0,1-\alpha )}[0,1]$ is the H$\ddot{o}$lder space,

Then, for $r\ge \frac{m}{1-\alpha }$, we have:

$$\begin{aligned} \Vert u-P_hu\Vert _\infty \le \frac{c}{N^m} \end{aligned}$$

with c a constant independent N.

Theorem 5

Under the conditions stated in Theorem 3, the following global supercloseness result holds:

$$\begin{aligned} \Vert u_h-P_hu\Vert _\infty \le C(r) \left\{ \begin{array}{l@{\quad }l} h^{2(1-\alpha )}, &{} \hbox {if}\quad r=1, \\ h^{m+1-\alpha }, &{} \hbox {if }\quad r\ge \frac{m}{1-\alpha }. \end{array} \right. \end{aligned}$$

(23)

Proof

We know from (4) and (9) that:

$$\begin{aligned} u_h-P_h u= & {} P_h g+P_h({\mathcal {V}}_\alpha u_h)-(P_h g+P_h({\mathcal {V}}_\alpha u))\\= & {} P_h{\mathcal {V}}_\alpha (u_h-u)=P_h{\mathcal {V}}_\alpha (u_h-P_hu+P_hu-u); \end{aligned}$$

then:

$$\begin{aligned} u_h-P_h u=(I-P_h{\mathcal {V}}_\alpha )^{-1}P_h{\mathcal {V}}_\alpha (P_hu-u). \end{aligned}$$

(24)

For the first subinterval, i.e., for $n=1$, we combine Lemma 2 and Theorem 1 that:

$$\begin{aligned} \parallel {\mathcal {V}}_\alpha (P_hu-u)\parallel _{I_1,\infty }= & {} \max \limits _{t\in [0,t_{1}]}\left| \int _0^t(t-s)^{-\alpha } K(t,s)(P_hu-u)(s)ds\right| \\\le & {} \max \limits _{t,s\in D}|K(t,s)|\Vert P_hu-u\Vert _{I_1,\infty }\max \limits _{t\in [0,t_{1}]}\left| \int _0^t(t-s)^{-\alpha }ds\right| \\\le & {} C\Vert P_hu-u\Vert _{I_1,\infty }\max \limits _{t\in [0,t_{1}]}\left| \int _0^{t}(t-s)^{-\alpha } ds\right| \\= & {} C\max \limits _{t\in [0,t_{1}])}\left| \frac{t^{1-\alpha }}{1-\alpha }\right| \Vert P_hu-u\Vert _{I_1,\infty }\le C\frac{h_{1}^{1-\alpha }}{1-\alpha }h_1^{1-\alpha }\\\le & {} C h^{1-\alpha } \left( \frac{1}{N}\right) ^{r(1-\alpha )}\le C h^{(1+r)(1-\alpha )}\\\le & {} \left\{ \begin{array}{ll} h^{2(1-\alpha )}, &{} \hbox {if }r=1, \\ h^{m+1-\alpha }, &{} \hbox {if} r\ge \frac{m}{1-\alpha }. \end{array} \right. \end{aligned}$$

For $n\ge 2$, we write $t\in I_n$ as $t=t_{n-1}+vh_n$ with $v\in [0,1]$. Then:

$$\begin{aligned}&{\mathcal {V}}_\alpha (P_hu-u)(t)\nonumber \\= & {} \int _0^{t_{n-1}}(t-s)^{-\alpha } K(t,s)(P_hu-u)(s)ds\nonumber \\&+h_n^{1-\alpha }\int _0^v(v-s)^{-\alpha } K(t_{n-1}+vh_n,t_{n-1}+sh_n)(P_hu-u)(t_{n-1}+sh_n)ds. \end{aligned}$$

(25)

For the second term of the right-hand side of (25), by Lemma 2, we obtain:

$$\begin{aligned}&h_n^{1-\alpha }\left| \int _0^v(v-s)^{-\alpha }K(t_{n-1}+vh_n,t_{n-1}+sh_n)(P_hu-u)(t_{n-1}+sh_n)ds\right| \\\le & {} h_n^{1-\alpha } \max \limits _{t,s\in D}|K(t,s)|\Vert P_hu-u\Vert _\infty \left| \int _0^v(v-s)^{-\alpha }ds\right| \\\le & {} Ch_n^{1-\alpha }\Vert P_hu-u\Vert _\infty \left| \int _0^{v}(v-s)^{-\alpha } ds\right| \\= & {} Ch_{n}^{1-\alpha }\Vert P_hu-u\Vert _\infty \frac{v^{1-\alpha }}{1-\alpha }\\\le & {} Ch^{1-\alpha }\Vert P_hu-u\Vert _\infty \le Ch^{1-\alpha }\cdot h^{m}\\\le & {} Ch^{m+1-\alpha }. \end{aligned}$$

The first term of the right-hand side of (25) can be written as:

$$\begin{aligned}&\left| \int _0^{t_{n-1}}(t-s)^{-\alpha } K(t,s)(P_hu-u)(s)ds\right| \\&\quad =\left| \sum \limits _{l=1}^{n-1}\int _{t_l-1}^{t_{l}}(t-s)^{-\alpha } K(t,s)(P_hu-u)(s)ds\right| \\&\quad =\left| \sum \limits _{l=1}^{n-1}h_l^{1-\alpha }\int _0^1\left( \frac{t_{n-1}+vh_n-t_{l-1}}{h_l}-s\right) ^{-\alpha }K(t_{n-1}+vh_n,t_{l-1}+sh_l)(P_hu-u)(t_{l-1}+sh_l)ds\right| \\&\quad =\left| \sum \limits _{l=1}^{n-1}h_l^{1-\alpha }\left( \sum \limits _{j=1}^{m}\omega _{j}\left( \frac{t_{n-1}+vh_n-t_{l-1}}{h_l}-c_j\right) ^{-\alpha }K(t_{n-1}+vh_n,t_{l-1}+c_jh_l)(P_hu-u)(t_{l-1}+c_jh_l)\right. \right. \\&\qquad +E_l(t))\mid , \end{aligned}$$

where $\omega _{j}$ is the weight function, and we write the integral into the numerical quadrature with the reminder $E_l(t)$, $\left| E_l(t)\right| \le Ch^d (d\ge m+1)$.

From the definition of $P_h$, we know that:

$$\begin{aligned} (P_hu-u)(t_{l-1}+c_jh_l)=0. \end{aligned}$$

Therefore:

$$\begin{aligned}&\left| \int _0^{t_{n-1}}(t-s)^{-\alpha } K(t,s)(P_hu-u)(s)ds\right| =\left| \sum \limits _{l=1}^{n-1}h_l^{1-\alpha }E_l(t)\right| \\\le & {} Ch^{1-\alpha }\sum \limits _{l=1}^{n-1}h_l^{m+1}\le Ch^{m+1-\alpha }\sum \limits _{l=1}^{n-1}h_l\\\le & {} Ch^{m+1-\alpha }, \end{aligned}$$

where it is easy to verify that $h_l\le Ch$.

Hence, for $n\ge 1$, we have:

$$\begin{aligned} \Vert u_h-P_h u\Vert _{\infty }= & {} \Vert (I-P_h{\mathcal {V}}_\alpha )^{-1}P_h{\mathcal {V}}_\alpha (P_hu-u)\Vert _{\infty }\\\le & {} Ch^{m+1-\alpha } \end{aligned}$$

$\square$.

Theorem 6

Under the conditions stated in Corollary 1, we have the following supercloseness between the hybrid collocation $u_h$ and the hybrid interpolation $Q_hu$ of the exact solution u:

$$\begin{aligned} \parallel u_h-Q_hu\parallel _\infty \le C \left\{ \begin{array}{ll} N^{-(m+1-\alpha )}, &{} \hbox {if }\alpha \ge \frac{1}{m+1}, \\ N^{-(m+1-\frac{1-\alpha }{m})}, &{} \hbox {if } \alpha < \frac{1}{m+1}. \end{array} \right. \end{aligned}$$

The proof is similar with the iterated hybrid collocation method in Huang and Xu (2006) (Theorem 3.4), since $u_h-Q_h u=(I-Q_h{\mathcal {V}}_\alpha )^{-1}Q_h{\mathcal {V}}_\alpha (Q_hu-u)$ and $u-u_h^{it}=(I-{\mathcal {V}}_\alpha Q_h)^{-1}{\mathcal {V}}_\alpha (u-Q_hu)$. We omit the details and leave the proof to the reader.

Remark 2

The conclusions in Theorem 5 and Theorem 6 can also be obtained by the results of the iterated collocation and iterated hybrid collocation solutions. In fact, from the relationship between $u_h$ and $u_h^{it}$, we know that:

$$\begin{aligned} u_h-P_hu=P_hu_h^{it}-P_h u=P_h(u_h^{it}-u). \end{aligned}$$

Then:

$$\begin{aligned} \Vert u_h-P_hu\Vert _\infty =\Vert P_h\Vert _\infty \Vert u_h^{it}-u\Vert _\infty \le C\Vert u_h^{it}-u\Vert _\infty . \end{aligned}$$

(20) leads to the supercloseness results. We replace $P_h$ by $Q_h$ and the relevant supercloseness results of the hybrid collocation method can be obtained in the same way.

3.2 Global superconvergence of interpolation collocation solutions

Based on the supercloseness between $u_h$ and $P_hu$, we can obtain the global superconvergence of the new “interpolated collocation solution” by applying the interpolation postprocessing technique to the collocation solution instead of the iterated collocation method.

We assume that $I_h$ is gained from $I_{2h}$ with mesh size 2h by subdividing each element of $I_{2h}$ into two equal elements, so that the number of elements N for $I_h$ is even. Then, we define a higher order interpolation operator $I_{2h}^{2m-1}$ of degree $(2m-1)$ associated with $I_{2h}$ satisfying the following conditions:

$$\begin{aligned} I_{2h}^{2m-1}u|_{I_i\cup I_{i+1}}\in {\mathcal {P}}_{2m-1} \ \ (i=1,3,\cdots ,N-1), \end{aligned}$$

(26)

and

$$\begin{aligned}&I_{2h}^{2m-1}u(t_{ni})=u(t_{ni}),\nonumber \\&I_{2h}^{2m-1}u(t_{(n+1)i})=u(t_{(n+1)i}), \ \ (n=1,3,\ldots ,N-1; i=1,2,\ldots ,m). \end{aligned}$$

(27)

It is easy to check that:

$$\begin{aligned} \Vert v-I_{2h}^{2m-1}v\Vert _\infty\le & {} Ch^{m+1}\Vert v\Vert _{m+1,\infty }, \quad \forall v\in W^{m+1,\infty }(I);\end{aligned}$$

(28)

$$\begin{aligned} I_{2h}^{2m-1}P_h= & {} I_{2h}^{2m-1};\end{aligned}$$

(29)

$$\begin{aligned} \Vert I_{2h}^{2m-1}v\Vert _\infty\le & {} C\Vert v\Vert _\infty ,\ \ \ \ \forall v\in S_{m-1}^{(-1)}(I_h). \end{aligned}$$

(30)

Thus, we can get the global superconvergence of the new “interpolated collocation solution” by the interpolation postprocessing method as follows.

Theorem 7

Under the conditions stated in Theorem 3 and assume that $u\in W^{m+1,\infty }(I)$, the following global superconvergence result holds:

$$\begin{aligned} \Vert I_{2h}^{2m-1}u_h-u\Vert _\infty \le C(r) \left\{ \begin{array}{l@{\quad }l} h^{2(1-\alpha )}, &{} \hbox {if } r=1, \\ h^{m+1-\alpha }, &{} \hbox {if } r\ge \frac{m}{1-\alpha }. \end{array} \right. \end{aligned}$$

(31)

Proof

It follows from (30), the interpolation error estimates, and (23) that:

$$\begin{aligned} \Vert I_{2h}^{2m-1}u_h-u\Vert _\infty\le & {} \Vert I_{2h}^{2m-1}u_h-I_{2h}^{2m-1}P_hu\Vert _\infty +\Vert I_{2h}^{2m-1}P_h u-u\Vert _\infty \\\le & {} C\Vert u_h-P_hu\Vert _\infty +\Vert I_{2h}^{2m-1}u-u\Vert _\infty \\\le & {} C\Vert u_h-P_hu\Vert _\infty +Ch^{m+1 }\\\le & {} C(r) \left\{ \begin{array}{ll} h^{2(1-\alpha )}, &{} \hbox {if } r=1, \\ h^{m+1-\alpha }, &{} \hbox {if } r\ge \frac{m}{1-\alpha }. \end{array} \right. \end{aligned}$$

$\square$

We observe that the degree $(2m-1)$ is not the unique choice for the interpolation postprocessing operator. In fact, the superconvergence result (31) is valid for any interpolation operator $I_{2h}^p$ ($p\ge m$) that satisfies (28)-(30).

In contrast to (26)–(27), the operator $I_{2h}^p$ can also be constructed by the least-squares method (Naga and Zhang 2004; Zhang and Naga 2005).

Polynomial Preserving Recovery (PPR). In this scheme, the higher order interpolation operator $I_{2h}^{m}$ of degree m associated with $I_{2h}$ is:

$$\begin{aligned} I_{2h}^{m}u|_{I_n\cup I_{n+1}} \in {\mathcal {P}}_{m}\ \ \ (n=1,3,\ldots , N-1). \end{aligned}$$

(32)

In each bigger subinterval $I_n\cup I_{n+1}$, $I_{2h}^{m}u$ is the solution of the least-squares problem:

$$\begin{aligned} \sum _{i=1}^{2m}\big |u(t_i^*)-I_{2h}^{m}u(t_i^*)\big |^2=\min _{v\in {\mathcal {P}}_{m} (I_n\cup I_{n+1})}\sum _{i=1}^{2m}\big |u(t_i^*)-v(t_i^*)\big |^2, \end{aligned}$$

(33)

where $t_i^* (i=1, \cdots , 2m)$ are the 2m collocation points in $I_n$ and $I_{n+1}\ (n=1, 3, \dots , N-1)$. It is readily verified that this type of interpolation also satisfies the conditions (28)–(30).

Theorem 8

Let the conditions stated in Theorem 3 hold and assume that $u\in W^{m+1,\infty }(I)$. The interpolation operator $I_{2h}^{m}$ is defined by (32)–(33), and then, the following global superconvergence estimate holds:

$$\begin{aligned} \Vert I_{2h}^{m}u_h-u\Vert _\infty \le C(r) \left\{ \begin{array}{ll} h^{2(1-\alpha )}, &{} \hbox {if} r=1, \\ h^{m+1-\alpha }, &{} \hbox {if } r\ge \frac{m}{1-\alpha }. \end{array} \right. \end{aligned}$$

(34)

The proof is similar with Theorem 7. We omit here and leave it to the reader.

3.3 Global superconvergence for interpolated hybrid collocation solutions

Based on the supercloseness between $u_h$ and $Q_hu$, we can obtain the global superconvergence of the new “interpolated hybrid collocation solution” by applying the interpolation postprocessing to the hybrid collocation solution.

Similar with Sect. 3.2, we assume the number of elements N for $I_h$ is an even number. We define the higher order interpolation operator ${\hat{I}}_{2h}:={\tilde{I}}_{2h}^{m+1}\cup I_{2h}^{2m-1}$, where ${\tilde{I}}_{2h}^{m+1}$ denotes the nonpolynomial interpolation of degree $<m+1$ in $I_1\cup I_2$ and $I_{2h}^{2m-1}$ denotes the normal higher order polynomial interpolation of degree $(2m-1)$ associated with $[t_2,T]$ satisfying the following conditions:

$$\begin{aligned} {\tilde{I}}_{2h}^{m+1}u|_{I_1\cup I_{2}}\in & {} V_{m+1},\\ I_{2h}^{2m-1}u|_{I_i\cup I_{i+1}}\in & {} P_{2m-1} \ \ (i=3,5,\ldots ,N-1), \end{aligned}$$

and

$$\begin{aligned}&{\tilde{I}}_{2h}^{m+1}u(t_{1i})=u(t_{1i}), \ \ ( i=1,2\ldots ,l).\end{aligned}$$

(35)

$$\begin{aligned}&{\tilde{I}}_{2h}^{m+1}u(t_{2i})=u(t_{2i}), \ \ ( i=1,2\ldots ,m).\end{aligned}$$

(36)

$$\begin{aligned}&I_{2h}^{2m-1}u(t_{ni})=u(t_{ni}), \end{aligned}$$

(37)

$$\begin{aligned}&I_{2h}^{2m-1}u(t_{(n+1)i})=u(t_{(n+1)i}), \ \ (n=3, 5,\ldots ,N-1; i=1,2\ldots ,m). \end{aligned}$$

(38)

where $V_{m+1}$ is the nonpolynomial space of degree $<m+1$ defined in the hybrid collocation method.

We note that when we get the “better” approximation based on the hybrid collocation solution, the first “bigger” subinterval ${\tilde{I}}_{1}=I_1\cup I_2$ need to be paid attention. For the “bigger” new subinterval ${\tilde{I}}_{1}$, we compute the interpolated hybrid collocation solution using the singularity preserving (nonpolynomial) interpolation rather than an easy addition of nonpolynomial interpolation and piecewise polynomial interpolation. We use the $l+m$ collocation points to get the nonpolynomial interpolation ${\tilde{I}}_{2h}^{m+1}u$ of degree $<m+1$ in ${\tilde{I}}_{1}$. Let $M:=\dim V_{m+1}$. Normally, $M\ne l+m$. The least-squares method is usually used to get ${\tilde{I}}_{2h}^{m+1}u$ by the interpolation conditions (35) and (36).

It is easy to verify that ${\hat{I}}_{2h}$ of (35)–(38) satisfies (28)–(30), with $P_h$ replaced by $Q_h$.

Thus, we can get the global superconvergence result of the new “interpolated hybrid collocation solution” by applying the interpolation postprocessing to the “hybrid collocation solution”.

Theorem 9

Under the conditions stated in Theorem 3, the following global superconvergence result holds:

$$\begin{aligned} \Vert {\hat{I}}_{2h}u_h-u\Vert _\infty \le C N^{-m-1+\alpha }. \end{aligned}$$

(39)

The proof is similar with the proof of Theorem 7. We omit here and leave it to the reader.

Similarly, the postprocessing operator ${\tilde{I}}_{2h}$ is not the unique choice and the superconvergence result (39) is valid for any interpolation operator $I_{2h}^p\ (p \ge m)$ that satisfies (35)-(38).

3.4 Interpolation postprocessing VS iteration postprocessing

In this subsection, we compare the computational complexities of the two kinds of postprocessings. For simplicity, we only take the interpolation postprocessing $I_{2h}^{2m-1} u_h$ and the iterated postprocessing $u_h^{it}$ on the collocation solution as an example.

Interpolation postprocessing solution $I_{2h}^{2m-1} u_h(t)$.

We get the “better” approximation $I_{2h}^{2m-1} u_h$ of the exact solution u by combining the adjacent subinterval and constructing higher order polynomials in each “bigger” subintervals ${\tilde{I}}_{\frac{n+1}{2}}:=I_n\cup I_{n+1} (n=1,3,\cdots ,N-1)$.

The computing form of the interpolation postprocessing in the bigger subinterval ${\tilde{I}}_{\frac{n+1}{2}} (n=1,3,\cdots ,N-1)$ is as follows.

For $t\in {\tilde{I}}_{\frac{n+1}{2}}:=[t_{n-1},t_{n+1}] \ (n=1,3,\ldots ,N-1)$:

$$\begin{aligned} I_{2h}^{2m-1}u_h(t)=\sum \limits _{j=1}^{2m}{\tilde{u}}_{\frac{n+1}{2}j}{\tilde{L}}_{\frac{n+1}{2}j}(t). \end{aligned}$$

Where the Lagrange basis functions ${\tilde{L}}_{\frac{n+1}{2}j}(t) (j=1,2,\ldots , 2m)$ are constructed by the 2m collocation points. Because of the local property of the basis function, it is very easy to show that:

$$\begin{aligned} I_{2h}^{2m-1}u_h(t)=\sum \limits _{j=1}^{m}u_{n,j}{\tilde{L}}_{\frac{n+1}{2}j}(t)+\sum \limits _{j=m+1}^{2m}u_{n+1,j}{\tilde{L}}_{\frac{n+1}{2}j}(t). \end{aligned}$$

Therefore, the computing time is mainly composed by the computation of the higher order Lagrange polynomials, which greatly simplifies calculation.

Iteration postprocessing solution $u_h^{it}(t)$

For the iteration postprocessing, we compute the new approximation $u_h^{it}(t)$ at $t=t_{n-1}+vh_n\in I_n=[t_{n-1},t_n]$ with $v\in [0,1]$:

$$\begin{aligned} u_{h}^{it}(t)= & {} g(t)+\int _0^t (t-s)^{-\alpha }K(t,s)u_h(s)ds\\= & {} g(t)+\sum \limits _{l=1}^{n-1}\int _{t_{l-1}}^{t_l} (t-s)^{-\alpha }K(t,s)u_h(s)ds+\int _{t_{n-1}}^{t} (t-s)^{-\alpha }K(t,s)u_h(s)ds\\= & {} g(t)+\sum \limits _{l=1}^{n-1}\sum \limits _{j=1}^{m}u_{l,j}\int _{t_{l-1}}^{t_l} (t-s)^{-\alpha }K(t,s)L_{l,j}(s)ds\\&+\sum \limits _{j=1}^{m}u_{n,j}\int _{t_{n-1}}^{t} (t-s)^{-\alpha }K(t,s)L_{n,j}(s)ds\\= & {} g(t)+\sum \limits _{l=1}^{n-1}\sum \limits _{j=1}^{m}u_{l,j}h_l\int _0^1 (t-t_{l-1}-sh_l)^{-\alpha }K(t,t_{l-1}+sh_l)L_j(s)ds\\&+\sum \limits _{j=1}^{m}u_{n,j}h_n^{1-\alpha }\int _0^v (v-s)^{-\alpha }K(t,t_{n-1}-sh_n)L_j(s)ds. \end{aligned}$$

Because of the weak singularity of the kernel, the normal numerical integral is no longer valid. We must divide the interval [0, v] into several subintervals (using graded mesh) and compute numerical integral in each subinterval (omitting the subinterval containing the singular point v).This increases the complexity of the iteration solution $u_{h}^{it}(t)$. (See Kaneko and Xu 1994 for details).

4 Numerical experiments

In this section, we give an example to illustrate the theory established in the previous section.

Example 4.1

We solve the following second kind weakly singular VIE:

$$\begin{aligned} y(t)=f(t)+\int _{0}^t \frac{1}{\sqrt{|t-s|}}y(s)ds, \quad t\in [0,1], \end{aligned}$$

(40)

where f(t) is given to make the exact solution $y(t)=\sqrt{t}$.

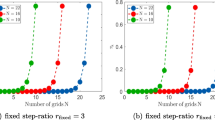
We first compute the piecewise linear ($m=2$) collocation solution $u_h$ under graded mesh, and obtain two different interpolated collocation solutions $I_{2h}^{2m-1}u_h$ (27) and $I_{2h}^{m}u_h$ (33). The numerical results and error figures for the error estimates are given in Table 1 and Fig. 1.

Table 1 Supercloseness and superconvergence results of numerical solutions for $m=2$

Fig. 1

Superclose and superconvergence (left) and least-squares postprocessing (right)

We see from Table 1 and Fig. 1 that:

$$\begin{aligned}&\Vert u-u_h\Vert _\infty ={\mathcal {O}}(h^m),\ \Vert u-I_{2h}^{2m-1}u_h\Vert _\infty ={\mathcal {O}}(h^{m+1-\alpha }),\\&\quad \Vert u_h-P_hu\Vert _\infty ={\mathcal {O}}(h^{m+1-\alpha })\ \Vert u-I_{2h}^{m}u_h\Vert _\infty ={\mathcal {O}}(h^{m+1-\alpha })\ (m=2). \end{aligned}$$

We calculate the interpolated hybrid collocation solution ${\hat{I}}_{2h}u_h$ based on the piecewise quadratic hybrid collocation solution $u_h$ ($m=3$). As mentioned in Sect. 3.3, in practical computation, we just need to calculate the interpolated hybrid collocation solution ${\tilde{I}}_{2h}u_h$ by the least-squares method in the first two subintervals $I_1\cup I_2$. We also make a comparison between the interpolated hybrid collocation solution and the iterated hybrid collocation solution. The relevant numerical results are illustrated in Table 2.

Table 2 Interpolated hybrid collocation solutions vs iterated hybrid collocation solutions ($m=3$)

We see from Table 2 that the convergence order for the interpolated hybrid collocation solution is ${\mathcal {O}}(h^{m+1-\alpha })$ and the CPU time of getting the interpolated hybrid collocation solution is much less than that of getting the iterated hybrid collocation solution which shows the efficiency our proposed method.

5 Concluding remarks

In this paper, we propose two different interpolation postprocessing approximations of higher accuracy based on the collocation solutions and the hybrid collocation solutions. The superconvergence orders of the proposed methods are the same as those of the iterated methods, but are much simpler in computation. The following problem remains to be addressed in future research work:

• 1. The nonpolynomial spectral methods for high-dimensional IEs.

• 2. The new numerical method combining the multistep collocation and the hybrid collocation method and aiming to reduce the computational complexity of the numerical solution for IEs.