N-Step-Ahead Optimal Control of a Compartmental Model of COVID-19

Abstract

This paper uses a compartmental model that accounts for some of the main features of the COVID-19 pandemic. Assuming a control that represents the aggregated intensity of non pharmaceutical interventions, such as lockdown in varying degrees and the use of masks and social distancing, this text proposes an N-step-ahead optimal control (NSAOC) method that is easy to calculate and provides a guideline for implementation. The compartmental model is extended to account for vaccination, and the N-step-ahead optimal control is calculated for this case as well. The proposed control is robust to parameter variation in all model parameters, when they are assumed to be normally distributed about nominal values. In addition, the proposed NSAOC is shown to compare favorably with a recently proposed PID-like controller.

1 Introduction and Literature Review

The COVID-19 pandemic is an ongoing pandemic of coronavirus disease and has emerged as one of this century’s major global health challenges. Insufficient scientific knowledge, the fast pace of its spread, and its capacity to cause deaths in vulnerable groups have generated worldwide discussion and research on the best strategies for confronting the epidemic in different parts of the world.

Governments are struggling to determine the correct course of action as the epidemic goes through its stages. If they decide to do nothing, a lot of deaths, mainly of the most susceptible individuals, will occur. On the other hand, full lockdowns affect the economy and society negatively. Modeling the pandemic also poses several difficulties, among these the rapid variation of several important parameters.

Although several vaccines have been developed, most countries have insufficient supplies to be able to vaccinate at a recommended level. Also, even though vaccines are effective against serious symptoms, they do not guarantee complete immunity so that strategies such as social distancing, washing hands and wearing face masks, known collectively as non-pharmaceutical interventions (NPIs), continue to play an important role in controlling this epidemic.

Predictive mathematical models for epidemics are fundamental to understand the course of the epidemic and to plan effective control strategies. The most simple and commonly used model is the SIR model (first introduced by Kermack & McKendrick, 1927) for human-to-human transmission, which describes the passage of individuals through three mutually exclusive stages of infection: susceptible, infected and recovered (Giordano et al., 2020).

Carcione et al. (2020) implemented an SEIR model to compute the infected population and the number of casualties in the Italian region of Lombardy, one of the regions most severely impacted by the epidemic in the world. The additional feature of this model, with respect to the SIR model, is the exposed state E, which represents individuals who have been exposed to the virus, but still not developed the infection, due to the incubation period of the virus. After this period, the exposed population transitions to the infected state.

A model named SEIHRD was introduced by Ivorra et al. (2020) and studied further by Pazos and Felicioni (2021) and its main novelty is the introduction of the state hospitalized corresponding to individuals who require ICU installations. Inclusion of the hospitalized population in the model is important from a strategic point of view, since it allows public health officials to avoid shortages in hospital beds and supplies. In addition, the hospitalized population is a variable that is easy to monitor and is made available in real time. This model is the one that is used in this work and will be further explained in the next section.

Non-pharmaceutical interventions (NPIs) are crucial to avoid the contagion and to mitigate the spread of the epidemic. Ferguson et al. (2020) exemplify and analyze different NPI policies to control the transmission of the virus.

The approach of designing NPI strategies by applying tools from control theory is not new. One of the first papers (Stewart et al., 2020) used an SEIRD model to show that a simple feedback law can manage the response to the pandemic for maximum survival while containing the damage to the economy.

Pazos and Felicioni (2021) propose the use of a simple feedback controller proportional to a suitable combination of the measurable state variables that ensures that the hospitalized population remains below the healthcare capacity.

Optimal control applied to mitigate the spread of the COVID-19 disease is also addressed in the literature. Tsay et al. (2020) propose an optimal controller applied to a deterministic epidemic model with six groups (denoted as SEIRP) in order to keep the number of infected individuals below a predetermined upper bound. Three scalar control laws are calculated, the social distances between susceptible individuals and infected and exposed individuals, respectively, and the testing rate. The control is calculated over a horizon time of 100 days, but with policies updated after each 25-day period.

Ames et al. (2020) propose the use of optimal control where so-called safety functions are included as constraints to ensure that the infected population (in the SIR model) plus the hospitalized population and the number of deaths (in the SIHRD model) do not exceed certain upper bounds.

An optimal control problem of obtaining, by enforcing social distancing, the largest value for the number of susceptible individuals at infinity is studied by Bliman et al. (2021). They first established that stopping arbitrarily close to the herd immunity threshold through long enough intervention is possible only if the social distancing intensity is sufficiently large. They also show that this problem may be interpreted as equivalent to reaching a given distance to the herd immunity level in minimal intervention time.

Since the report first presented by Alleman et al. (2020), many works have addressed the model predictive control approach (MPC, see Camacho & Bordons, 1999; Maciejowski, 2002) to design NPI policies in order to mitigate the spread of the COVID-19 disease.

Morato et al. (2020a) formulate a model predictive control (MPC) policy to mitigate the COVID-19 contagion in Brazil, designed as an optimal on–off social isolation strategy. The authors consider two different models to determine the optimal time of every lockdown.

Péni et al. (2020) applied a nonlinear MPC to an eight-compartment epidemiological model. The constrained optimization problem includes bounds on the states and on the control signal. The control signal is calculated over a fixed time horizon of 180 days and updated weekly. The authors also consider the use of an observer assuming that only the hospitalized population and the number of deaths are well known.

Köhler et al. (2020) considered the SIDHARTE epidemiological model, first presented by Giordano et al. (2020). The authors propose the use of a model predictive control (MPC) and admit uncertain data and model mismatch. The NPI policies are updated weekly. A robust MPC is also implemented.

Carli et al. (2020) applied a MPC in a multi-region scenario. In each region, a SIRQTHE epidemiological model is considered, admitting a dynamic that represents inter-regional mobility.

Armaou et al. (2022) propose a probabilistic model predictive control (PMPC) to determine different social distancing policies for six different activities. The epidemic model used has ten groups (denoted as SEASQHRD, where R is divided into three subgroups). The design of the PMPC formulates the policy question as an optimization problem that minimizes a cost function subject to the epidemic dynamics, to maximum values for each control law according to the activity and other probabilistic constraints necessary because only two groups are directly measured. The constrained optimization problem is solved for a finite time horizon forward, called the prediction horizon, $T_P$, given the current state of the epidemic.

Some authors considered the influence of vaccination on the epidemic model. Kar and Batabyal (2011) studied a SIR epidemic model with a vaccination program. They used optimal control strategies in the form of vaccination to control the number of susceptible individuals and increase the number of recovered individuals.

An optimal daily vaccination strategy is proposed by Acuña-Zegarra et al. (2021). They established an optimal control problem to design vaccination strategies where vaccination modulates dynamics susceptibility through an imperfect vaccine. The aim was to provide vaccination policies that minimize the lost life years due to disability or premature death by COVID-19. The simulations suggested a better response compared with a constant vaccination rate.

Parino et al. (2021) propose a model predictive control (MPC) to optimally calibrate a two-dose vaccination strategy during the epidemic outbreak. The constrained optimization problem is solved for an unspecified finite time horizon.

In contrast to most papers aiming at reproducing the dynamics of the pandemic observed through various data, a study related to the concepts of epidemic final size and herd immunity in an ample setting is done by Almeida et al. (2021). They considered an epidemic in a heterogeneous population modeled by a SEIR model with a continuous structure variable and a general contact matrix. They derived and studied the final size equation fulfilled by the limit distribution of the population and showed that this limit exists and satisfies the final size equation. The main contribution was to prove the uniqueness of this solution among the distributions smaller than the initial condition.

Other works addressing epidemic control and vaccination are listed in Table 1. They are divided into the following sections:

• Control strategy indicates which control strategy is used in the paper (Optimal Control, MPC or Other).

• Uncertain parameters indicate if the authors used uncertain parameters in the epidemic model.

• $\le 4$ CPs and $\ge 5$ CPs indicate how many compartments (CPs) the epidemic model contains.

• Vaccination indicates if the paper used vaccination as a control variable.

Some of these works do not consider maintaining the number of individuals hospitalized below the maximum capacity of the health care system as an additional constraint, at best including a penalty term in the objective function (an exception is Péni et al., 2020). Most of them do not consider the time horizon as a variable to be optimized, but the optimization problem is solved over a fixed time horizon arbitrarily chosen. Many approaches presented in the references cited also consider fixed parameters, excepting (Armaou et al., 2022) which present a stochastic approach and Péni et al. (2020) which admit uncertainties in the parameters.

In this work, we investigate strategies based on N-steps-ahead optimal control for mitigation of the COVID-19 pandemic. The main goal is to minimize the number of deaths over time without inducing excessive economic costs, while respecting an upper bound on the hospitalization rate. In order to do that, an optimization problem is modeled and solved based on the techniques presented by Canon et al. (1970) and Kirk (1970).

The main contributions of this paper are:

• An MPC-type control approach with low computational effort.

• A normalized aggregate control effort that models the effect of all non-pharmaceutical interventions and therefore takes values between zero and one, rather than being on-off.

• Inclusion of vaccination as a design variable, making the proposed approach a good candidate for use in future outbreaks.

Table 1 shows that the the present paper is the only one, to the best of our knowledge, that treats all the relevant aspects that labels the rows of the table, namely parameter uncertainty, a sufficient number of compartments (for greater model accuracy) and vaccination.

Table 1 Classification of the references used in this work

In Sect. 2, the epidemic model SEIHRD is explained in more detail. In Sect. 3, we detail the optimal algorithm that is used to calculate the best strategy for each moment of the epidemic. In Sect. 4, we develop all simulations and compare our strategy with other strategies already used for the same problem. Additionally, the impact of the vaccination rate is shown in Sect. 4.3. Finally, conclusions and future work are presented in Sect. 5.

2 The SEIHRD Model

In this section, we detail each state of the SEIHRD model and its relevance in the COVID-19 epidemic model. The choice of the model is an important step. In order to be useful for the design of control policies, it should contain the main variables of interest, keeping in mind the difficulty of obtaining reliable data that will permit estimation of the main model parameters. In this study, we opted for a model called the SEIHRD model, explained in the next paragraph, since it allows for a more detailed model of features specific to the COVID-19 epidemic, such as exposed and asymptomatic populations, in addition to modeling occupation of hospitals, which is important from a decision making perspective.

The SEIHRD model contains the following states or populations that each individual can belong to:

• Susceptible (S): Individuals who did not get exposed to the virus and are not infected.

• Exposed (E): Individuals who got exposed to the virus and are in the incubation period. Even though there are no visible clinical signs, the individual could infect other individuals with a lower probability (compared to one in the infected state). Part of this group will present symptoms after an incubation period, moving to group I and another part will remain asymptomatic.

• Infected (I): Individuals who can infect others and may start developing clinical signs. Asymptomatic individuals who have been diagnosed as positive are also considered in this group. After a period, the individual recovers or is hospitalized, if the symptoms are very serious.

• Hospitalized (H): Individuals who need medical assistance and occupy beds in the hospital. After treatment, the individual might recover or die.

• Recovered (R): Individuals who recover from the infection or acquired immunity.

• Dead (D): Individuals who were infected, hospitalized and then died.

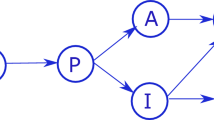
This is a typical compartmental model and Fig. 1 shows the manner in which individuals transit between these states or populations. This model also has a mathematical representation given by the following difference equations.

$$\begin{aligned} S_{k+1}&= S_{k} - ({\alpha }S_{k}E_{k} + {\beta }S_{k}I_{k}) - v_{k-d_{1}} \end{aligned}$$

(1)

$$\begin{aligned} E_{k+1}&= E_{k} + ({\alpha }S_{k}E_{k} + {\beta }S_{k}I_{k}) - ({\gamma }p_{1} \nonumber \\&\quad + {\zeta }(1 - p_{1}))E_{k} \end{aligned}$$

(2)

$$\begin{aligned} I_{k+1}&= I_{k} + {\gamma }p_{1}E_{k} - ({\delta }p_{2} + {\eta }(1 - p_{2}))I_{k} \end{aligned}$$

(3)

$$\begin{aligned} H_{k+1}&= H_{k} + \delta p_{2}I_{k} - ({\epsilon }p_{3} + {\mu }(1 - p_{3}))H_{k} \end{aligned}$$

(4)

$$\begin{aligned} R_{k+1}&= R_{k} + {\zeta }(1 - p_{1})E_{k} + {\eta }(1 - p_{2})I_{k} \nonumber \\&\quad + {\mu }(1 - p_{3})H_{k} + v_{k} \end{aligned}$$

(5)

$$\begin{aligned} D_{k+1}&= D_{k} + {\epsilon }p_{3}H_{k} \end{aligned}$$

(6)

Fig. 1

SEIHRD model diagram

where:

• k $\in$ $\left\{ 1, 2,\ldots , K\right\}$ where $K \in {\mathbb {N}}$ is the maximum time horizon considered in the study.

• $v_{k-d_{1}}$ is the vaccination rate applied on the population at instant k and $d_1$ is the length of the period after which the vaccine takes effect, considering that one shot gives full immunity.

• ${\alpha }S_{k}E_{k}$ is the transmission rate of the virus between susceptible and exposed populations, while ${\beta }S_{k}I_{k}$ is the transmission between susceptible and infected populations. Parameters $\alpha$ and $\beta$ are the probability of disease transmission in a single contact between individuals of the group S and E. Typically, $\alpha$ is greater than $\beta$, since each individual tends to avoid contact with individuals showing symptoms. Also, the viral load is higher in the second case.

• $p_1$ is the probability that exposed individuals develop symptoms.

• ${\gamma }^{-1}$ is the average period to develop symptoms.

• ${\zeta }^{-1}$ is the average time to overcome the disease while remaining asymptomatic.

• $p_2$ is the probability that infected individuals with symptoms require hospitalization.

• ${\delta }^{-1}$ is the average time between infection and the need for hospitalization.

• ${\eta }^{-1}$ is the average time for infected individuals to recover without hospitalization.

• $p_2$ is the probability that infected individuals with symptoms required hospitalization.

• ${\epsilon }^{-1}$ is the average time between hospitalization and death.

• ${\mu }^{-1}$ is the average time to recover after hospitalization.

• $p_3$ is the probability that hospitalized individuals die.

According to the equations, the populations in the compartments R and D are always increasing, while S is always decreasing. This is expected, since the number of recovered and dead individuals may stop increasing but will never decrease (with the assumption that reinfections are not possible). The same idea can be applied to the group S, which will decrease until the epidemic is finished.

This model does not discriminate between detected and undetected cases of infection as this would add an extra complexity which, in addition, is difficult to observe and quantify. Although this assumption ignores the more complex biology, it does allow the inclusion of some important real world issues such as scarcity of hospital beds.

The transference between the model compartments is based on mean rates, indicating that the individuals stay for a certain period in each compartment. This could also be represented by adding delays instead of using mean rates. There are other modeling techniques, which use a conveyor to represent the delays (Isee, 2021). However, in this work we chose to use the mean rates as a simplification. A basic quantity in the analysis of epidemic models is the basic reproduction number $R_0$, which, informally, is the expected number of individuals who will be infected by one person with the disease. If $R_0$ is less than 1, each infected person can transmit the virus to less than one susceptible person. This means the number of infected will decline and the disease will die out. If $R_0$ is greater than 1, the disease will spread into the population and the number of infected individuals will increase, causing an epidemic. A detailed explanation of the basic reproduction number can be found in Kermack and McKendrick (1927).

The parameters used in the model will generally assume different values for different regions in the world. Specially, the parameters $\alpha$ and $\beta$ are related with $R_0$ and they are influenced by different factors, like population density of a community, the general health and average age of its population and medical infrastructure.

In this work, the values of the parameters used in (1)–(6) are based on the studies reported by Pazos and Felicioni (2021) and can be found in Table 2.

Table 2 Values for SEIHRD model parameters (Pazos & Felicioni, 2021)

3 Optimal Control Problem

Optimal control applied to mitigate the spread of diseases was addressed before the Covid-19 outbreak. The book (Lenhart & Workman, 2007) and especially the article (Lin et al., 2010) are references on which many works are based (Armaou et al., 2022; Tsay et al., 2020; Moore & Okyere, 2020; Djidjou-Demasse et al., 2020; Perkins & España, 2020; Mallela, 2020; Gondim & Machado, 2020; Angulo et al., 2020). In this section, we present the theory behind an optimal control problem. We base our studies mainly on Kirk (1970) and Canon et al. (1970). In the subsequent sections, we introduce and explain different types of controller and strategies used to control the COVID-19 epidemic.

3.1 SEIHRD Model with Control Variable

The characteristics of COVID-19 disease make the virus spread incredibly fast into the population. One of the strategies the government can apply is to attack the source, when the disease is not yet disseminated in the population. Isolation of cases and tracking of new cases and individuals that were in contact with someone infected would interrupt the transmission in the source. Of course, this is very difficult in a globalized world, where individuals can easily travel anywhere.

Another strategy is to interrupt (or reduce) the transmission. This is mainly achieved by increasing personal and environmental hygiene (washing hands, etc.), using appropriate masks when in public and restricting population movements. A lockdown strategy and social distancing have been observed in several parts of the world. Middle- and low-income countries do not have sufficient resources and face financial and economic challenges, which may hinder their ability to effectively implement the abovementioned policies.

The strategies described above are the so-called non-pharmaceutical interventions (NPIs). Pharmaceutical intervention is mainly achieved by vaccinating the population since, to date, there is no proven reliable treatment for infected individuals.

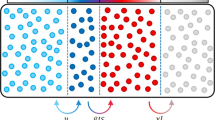
In this paper, an aggregate normalized control effort varying between zero and one will be taken to represent all the NPIs being applied (i.e., lumping together social distancing, use of masks, adoption of hygienic measures, etc.).

Since we can only try to control the transmission between individuals, in the mathematical model introduced in Sect. 2 we may only affect the relations between compartmental groups S, E and I. In other words, we would like to prevent susceptible individuals from getting into contact with individuals that have the virus (exposed and infected). Therefore, the proposed model is the following:

$$\begin{aligned} S_{k+1}&= S_{k} - (1 - u_{k})({\alpha }S_{k}E_{k} + {\beta }S_{k}I_{k}) \nonumber \\&\quad - v_{k-d_{1}} \end{aligned}$$

(7)

$$\begin{aligned} E_{k+1}&= E_{k} + (1 - u_{k})({\alpha }S_{k}E_{k} + {\beta }S_{k}I_{k}) \nonumber \\&\quad - ({\gamma }p_{1} + {\zeta }(1 - p_{1}))E_{k} \end{aligned}$$

(8)

$$\begin{aligned} I_{k+1}&= I_{k} + {\gamma }p_{1}E_{k} - ({\delta }p_{2} + {\eta }(1 - p_{2}))I_{k} \end{aligned}$$

(9)

$$\begin{aligned} H_{k+1}&= H_{k} + \delta p_{2}I_{k} - ({\epsilon }p_{3} + {\mu }(1 - p_{3}))H_{k} \end{aligned}$$

(10)

$$\begin{aligned} R_{k+1}&= R_{k} + {\zeta }(1 - p_{1})E_{k} + {\eta }(1 - p_{2})I_{k} \nonumber \\&\quad + {\mu }(1 - p_{3})H_{k} + v_{k} \end{aligned}$$

(11)

$$\begin{aligned} D_{k+1}&= D_{k} + {\epsilon }p_{3}H_{k} \end{aligned}$$

(12)

The control variable affects directly the parameters $\alpha$ and $\beta$ of the SEIHRD model, as shown in Fig. 2. One important fact is that by increasing the control input, we are decreasing the observed $\alpha$ and $\beta$. In other words, the control prevents susceptible individuals from getting in contact with exposed and infected individuals, respectively.

Fig. 2

SEIHRD model diagram with control variable

The control variable $u_{k}$ can assume any value between 0 and 1 ($u_{k} \in [0,1]$). The lower bound of 0 means that no social distancing strategy is applied and individuals are free to go wherever they want. The upper bound of 1 means that a lockdown is in place and individuals have no contact with each other, meaning that the transmission is interrupted. This is impossible in practice, since basic services for the population require some movement of populations.

It should be observed that states D and R do not affect the dynamics of the rest of the model [i.e., do not occur in the Eqs. (7)–(12)]. In the next sections, we will not include them in the optimization problem as they would only add unnecessary complexity, since they can be calculated using the other state variable values.

Social distancing is the main NPI strategy to interrupt the spread of the virus in the population. When the number of infected and hospitalized individuals is too high, social distancing needs to be implemented. Since complete lockdown has well known adverse effects in the economy, this work postulates a certain level of normalized control effort (between zero and one) that translates into partial lockdown and relaxation of other measures (such as the use of masks). The focus of this paper is on strategies to calculate the value of this aggregate control. It is then the task of decision makers to translate this level of control effort into concrete NPI policies, which is, of course, a nontrivial task. In the next sections, we show different algorithms to calculate the best values of the control variable $u_{k}$ during the time horizon.

3.2 N-Steps-Ahead Optimal Control (NSAOC)

In this work, we introduce a controller that uses model predictive control theory. The main idea is to calculate, at each time instant, a new control value based on the estimation of the evolution of the state vector during the next N time instants. So, at each time step $k=1, 2,\ldots , K$, where k corresponds to days and K is the time horizon applied to the COVID model, we solve an optimization problem over the horizon $k,\ldots , k+N$, where N is the number of days that is used to calculate what are the best values for the control variable u. The optimization result gives the best values for the next N control inputs. However, we only use the control $u_k$, since at instant $k+1$, we assume that information from the real environment (namely the states of day $k+1$ resulting from the application of $u_k$).

It is important to note that the solution of the optimization problem is based on a certain COVID model (SEIHRD in this work). However, the computed optimal control variable is applied to a real COVID environment, where some parameters (if not all) can differ from those of the model. The diagram in Fig. 3 illustrates the flow used in the problem. One can see that the states of the model are estimated at time k, in the computational (controller) block labeled NSAOC, while the ones from the environment (i.e. the output $X_{k+1}$ of the block labeled environment) are real measured states.

The optimization process is responsible for the calculation of the next control inputs taking into consideration an adequate objective function. The mathematical model is described below:

$$\begin{aligned}&\min \quad \quad J = \sum _{k}^{k+N} u_k&\end{aligned}$$

(13)

$$\begin{aligned}&\text {subject to: } \nonumber \\&\quad S_{k+1} = S_{k} - (1 - u_{k})({\alpha }S_{k}E_{k} + {\beta }S_{k}I_{k}) \nonumber \\&\quad \quad \quad \quad \quad - v_{k-d_{1}} \end{aligned}$$

(14)

$$\begin{aligned}&\quad E_{k+1} = E_{k} + (1 - u_{k})({\alpha }S_{k}E_{k} \nonumber \\&\quad \quad \quad \quad \quad + {\beta }S_{k}I_{k}) - ({\gamma }p_{1} + {\zeta }(1 - p_{1}))E_{k}&\end{aligned}$$

(15)

$$\begin{aligned}&\quad I_{k+1} = I_{k} + {\gamma }p_{1}E_{k} - ({\delta }p_{2} + {\eta }(1 - p_{2}))I_{k}&\end{aligned}$$

(16)

$$\begin{aligned}&\quad H_{k+1} = H_{k} + \delta p_{2}I_{k} - ({\epsilon }p_{3}&\nonumber \\&\quad \quad \quad \quad \quad + {\mu }(1 - p_{3}))H_{k} \end{aligned}$$

(17)

$$\begin{aligned}&\quad \quad H_{k} \le H_{\textrm{max}}&\end{aligned}$$

(18)

$$\begin{aligned}&\quad \quad 0 \le u_{k} \le 1&\end{aligned}$$

(19)

$S_{k}$, $E_{k}$, $I_{k}$ and $H_{k}$ are the initial conditions and input of the algorithm. $H_{\textrm{max}}$ is the maximum capacity of the medical resources. If $H_{k}$ assume values higher than the upper bound $H_{\textrm{max}}$, the number of deaths would have a considerable increase, since the medical capacity will be exceeded and, consequently, part of the population will not be covered by medical care. No government wants this to happen, so the constraint (18) is added to make sure the optimization takes this into consideration.

Fig. 3

N-steps-ahead control diagram (the variable X is defined by $X = \left[ S, E, I, H \right]$)

The objective function (13) takes into account only resources available for the implementation of control efforts, while the constraints model available hospital infrastructure. In other words, (13) is an administrator’s ideal objective function. The decision to choose this specific function is explained by the focus on solving one of the main concerns of all governments, which is to exceed the capacity of hospitals with individuals infected by COVID-19. In practice, of course, other humanitarian concerns, such as limiting the number of deaths, are more important and should also be added to the objective function. The formulation presented in this paper is applicable to all such objective functions and can be regarded as a tool to aid decision making by simulating scenarios, with different objective functions, parameters and so on. Thus there are other objective functions that might be tested as well. One can try to maximize the number of susceptible individuals and simultaneously minimize the sum of all control efforts, for example. Also, some weights can be added to each factor term in the objective function, to express its relative importance.

Another important issue is the choice of suitable values for N. We would like to choose values as small as possible to avoid unnecessary computation. On the other hand, N cannot be too small, because, over a prediction horizon that is too short, an exponential rise in hospitalizations would not be foreseen and the situation would get out of control. In the next section, we investigate the issue of the most suitable values for N.

The algorithm used in this paper is shown in Algorithm 1 table:

We note that (13)–(19), following Canon et al. (1970), is treated as an optimization problem. Specifically, this means that the decision variables are $\{u_k\}_{k=1}^N$, and ${\{S_k,E_k,I_k,H_k\}_{k=1}^{N+1}}$, where the latter (S, E, I, H) do not occur in the linear objective function (13), but are subject to the quadratic equality constraints (14) through (17), as well as the box constraints (18), (19). Such an optimization problem is easily handled by many modern solvers and, in our implementation, we used the algebraic modeling language JuMP [Julia for Mathematical Programming, see Dunning et al. (2015)], which itself is written in the scientific computation language Julia (Bezanson et al., 2014), to write the optimization code and used the Coin-OR solver Ipopt Wächter (2009). The reasons for these choices are that Julia and JuMP are fast, modern (JIT compiler) open source languages for scientific computation and optimization, respectively, and Ipopt is a reliable, modern solver, based on interior-point algorithms, for a large range of optimization problems.

3.3 PID-Like Control

This section will briefly present a controller proposed by Pazos and Felicioni (2021) for the purposes of comparison. The authors used control theory to determine public NPIs in order to control the evolution of the pandemic, avoiding the collapse of the healthcare systems while minimizing harmful effects on the population and economy.

Again, the control law is given by the control variable $u_k$ in Eqs. (7)–(12). No intervention is represented by $u_k = 0$ and a full lockdown with no movement allowed translates to $u_k = 1$.

There are several possible choices of the reference signal or set point of the control system. We also must keep in mind that some groups of the SEIHRD model are subjected to large inaccuracies due to unreported or undiagnosed cases. So, ideally the controller should use states for which reliable data are available. The number of hospitalized (H) individuals is very reliable. The number of individuals diagnosed as positive (I) and deaths (D) is also reasonably reliable.

The controller proposed by Pazos and Felicioni (2021) is shown schematically in Fig. 4.

Fig. 4

PID-like controller diagram (Pazos & Felicioni, 2021)

The obvious choice of feedback variable would be the number of hospitalized individuals. However, since NPIs reduce contagion between susceptible and infected or exposed population, when an individual is infected, hospitalization may be required after $\delta ^{-1} = 5.5$ days or after $\delta ^{-1} + \gamma ^{-1} = 10.6$ days on average if the infection was recent. Hence, there exists a delay between the adoption of NPIs and their consequences on hospitalization. If the control action relies only on the number of hospitalized compartment, too many individuals may require hospitalization in the next 10.6 days, exceeding the capacity for medical care.

Therefore, the control action should also take into consideration the number of infected individuals. The addition of this state emulates a type of predictive control, since it is proportional to the number of individuals who would require hospitalization in the next 5 or 6 days.

However, not all infected individuals need hospitalization. It is reported that most symptomatic cases are mild and remain mild. According to Table 2, $p_2 = 19\%$ of infected individuals will need hospitalization in the following 5.5 days ($\delta ^{-1}$). This number plus the number of individuals already hospitalized must remain below the set point. So, the normalized PID-Like control law proposed by Pazos and Felicioni (2021):

$$\begin{aligned} u_k = k_{\textrm{p}} \left( 1 - \frac{H_{\textrm{max}} - H_k - p_{2}I}{SP-H_k} \right) \in [0,1] \end{aligned}$$

(20)

where $k_{\textrm{p}}$ is a scalar gain with values between [0, 1].

3.4 Omniscient Control

Finally, we present a benchmark globally optimal control policy, that is hypothetical, since it assumes that all data for the whole control horizon is known. In this case, of course, it is possible to calculate the open-loop globally optimal control for any given performance index, and we will refer to this as the omniscient control, since the control design can observe all data, without any errors or estimates. The main objective in presenting and calculating this strategy is to have a baseline for comparison of the other practically implementable strategies.

Given a performance index, omniscient control follows the classical recipe of optimal control. At instant $k=1$ we calculate all $u_k$ for k lying in the interval (1, K). The omniscient control is shown schematically in Fig. 5.

Fig. 5

Omniscient control diagram (the variable X is defined by $X = \left[ S, E, I, H \right]$)

The omniscient optimal control problem is described below in Eqs. (21)–(27):

$$\begin{aligned}&\min \quad J = \sum _{k=1}^{K} u_k&\end{aligned}$$

(21)

$$\begin{aligned}&\text {subject to: } \nonumber \\&\quad S_{k+1} = S_{k} - (1 - u_{k})({\alpha }S_{k}E_{k} + {\beta }S_{k}I_{k})&\nonumber \\&\qquad \quad \quad \quad - v_{k-d_{1}} \end{aligned}$$

(22)

$$\begin{aligned}&\quad E_{k+1} = E_{k} + (1 - u_{k})({\alpha }S_{k}E_{k}&\nonumber \\&\qquad \quad \quad \quad + {\beta }S_{k}I_{k}) - ({\gamma }p_{1} + {\zeta }(1 - p_{1}))E_{k}&\end{aligned}$$

(23)

$$\begin{aligned}&\quad I_{k+1} = I_{k} + {\gamma }p_{1}E_{k} - ({\delta }p_{2} + {\eta }(1 - p_{2}))I_{k}&\end{aligned}$$

(24)

$$\begin{aligned}&\quad H_{k+1} = H_{k} + \delta p_{2}I_{k} - ({\epsilon }p_{3}&\nonumber \\&\qquad \quad \quad \quad + {\mu }(1 - p_{3}))H_{k} \end{aligned}$$

(25)

$$\begin{aligned}&\quad H_{k} \le H_{\textrm{max}}&\end{aligned}$$

(26)

$$\begin{aligned}&\qquad 0 \le u_{k} \le 1&\end{aligned}$$

(27)

After all control variable values are calculated, we can use them in a real world environment. If the SEIHRD model parameters are exactly equal to the real world parameters, the omniscient control would have a perfect performance. Of course, given the multiple uncertainties and assumptions made in the model, this will almost never happen. Thus, for each instant k, the respective optimal control $u_k$ calculated from the model is applied to the real system which responds with the actual state variables of the instant $k+1$.

4 Results

In the previous section, we explained the theory behind the strategies we chose to use in this work. In this section we perform numerical experiments based on this theory. The experiments consider two cases. In the first one, the environment parameters are constant and equal to the model used to calculate the control values. Next, parameter uncertainty is introduced in the SEIHRD Environment block (Fig. 3) and, consequently, their values will differ from the ones used in the NSAOC block (Fig. 3). Also, three different objective functions will be used separately to evaluate the NSAOC algorithm:

$$\begin{aligned}{} & {} J_1 = \sum _{k}^{k+N} u_k \end{aligned}$$

(28)

$$\begin{aligned}{} & {} J_2 = \sum _{k}^{k+N} w_k u_k \end{aligned}$$

(29)

$$\begin{aligned}{} & {} J_3 = \sum _{k}^{k+N} w_k u_k + \sum _{i=k}^{k+N-1} \sum _{j=k+1}^{k+N} (u_i-u_j)^2 \end{aligned}$$

(30)

The main goal of (28) is to simply minimize the total control input applied on the population. The second objective function (29) is similar to the first one, except for the inclusion of a weight vector $w = [w_1, \ldots , w_N]$. It is chosen as $w = [N^2, (N-1)^2, (N-2)^2,\ldots , 1^2]$. This modification results in giving more importance to the near future, and reducing the importance of controls far in the future. Last, (30) adds a slew rate penalty to the objective in (29). As we will see in the simulations, the second objective makes the controller vary a lot between high values and low values. The slew rate term penalizes big jumps in the control, smoothening the control signal, which is desirable, because it avoids big changes in policies, which tend to confuse the population (subjects of the control action).

4.1 NSAOC Simulation

Before comparing different strategies, in this section we analyze the results of NSAOC strategy using performance index $J_1$ in a SEIHRD model with constant parameters. The simulation horizon is $K = 600$ days.

In NSAOC strategy, the only parameter we need to adjust is the parameter N and, indeed, this is one of the good features of the proposed NSAOC strategy. As stated earlier, this parameter represents the number of steps ahead of the actual instant the calculation of the optimal solution is carried out. For example, if we use $N=10$ (Fig. 6), the epidemic can be controlled and the number of hospitalized individuals never exceeds the specified limit of $0.8\%$.

The control input is only greater than zero when the number of hospitalized individuals reaches a dangerous level. Then, a severe lockdown is put in place ($u=1$) for a week, approximately. After the contamination starts to decrease, the input control can be relaxed to a lower level. The final percentage of deaths is 3.62%. Also, the peak of infected and exposed individuals are smaller, since the control applied reduces the contact between susceptible and individuals carrying the virus.

Fig. 6

Results of a SEIHRD model with constant parameters using NSAOC algorithm with $N=10$ and $K=600$ (time horizon)

4.1.1 Parameter N: Impact Study

In this section, we vary the parameter N of the NSAOC algorithm and experiment in the SEIHRD model without parameter uncertainty. We consider all three objective functions discussed earlier, defined in Eqs. (28), (29) and (30).

As stated before in this work, COVID-19 is a disease with a relatively high incubation period and the consequences of the actions taken today will most likely only appear in a week or even more. Therefore, parameter N must be chosen wisely in order to predict the hospitalization level early enough, which is critical for good decision making.

First, we investigate the impact of different values of N on the hospitalization level and number of deaths. As shown in Fig. 7, when using the objective function $J_1$ the minimum value we should use for N is 9, while for objective functions $J_2$ and $J_3$ this value changes to 10. This strategy maintains the hospitalization level below the desired limit $H_{\textrm{max}}$.

Fig. 7

Hospitalization level and total number of deaths for different values of parameter N of NSAOC Algorithm using performance indices $J_1$, $J_2$ and $J_3$ in an environment with constant parameters. The vertical black dashed line shows the smallest prediction horizon N that is able to achieve a steady state hospitalization level below the maximum specified capacity $H_{\textrm{max}}$

We also note that for values of N below 9 (using $J_1$) and 10 (using $J_2$ and $J_3$), the optimization problem is infeasible. This occurs because it cannot see enough steps ahead to identify that the individuals exposed and infected at the actual instant will become ill a few days later and the number of hospitalized individuals will exceed the limit $H_{\textrm{max}}$, violating the constraint (and making $N<9$-step-ahead problem infeasible).

As long as N increases (and is larger than 10), the maximum hospitalization level stabilize near the specified limit $H_{\textrm{max}}$ for all performance indexes, even though it takes more time to reach the limit using the objective function $J_1$, as shown in previous simulations. The number of deaths oscillates near the value 3.8%, indicating that increasing the horizon parameter N does not result in better results. So, considering Fig. 7, we conclude that the best choice for N is 10, since it results in the lowest feasible computational effort.

When it comes to total control effort (Fig. 8), a different behavior when using different objective functions can be also noted. Again, for N smaller than 10, the algorithm is not able to find a feasible solution. For higher values of N, the total control effort increases as N also increases when using the objective function $J_1$. However, when using functions $J_2$ and $J_3$, the total control does not vary much as N increases, because the controller only acts when it is really needed.

Fig. 8

Total control input for different values of parameter N of NSAOC Algorithm using performance indices $J_1$, $J_2$ and $J_3$ on an environment with constant parameters

4.2 Comparison of Strategies

This section considers all strategies explained in Sect. 3 and compares the results. When using NSAOC, the parameter N assumes the value 10. Therefore, the following strategies are used:

• 1. NSAOC-J1 ($N=10$)

• 2. NSAOC-J2 ($N=10$)

• 3. NSAOC-J3 ($N=10$)

• 4. Omniscient control

• 5. PID-like control (proposed by Pazos & Felicioni, 2021).

The first simulation applies the above strategies in a SEIHRD environment with constant parameters. The results are shown in Fig. 9. The control input when using NSAOC-J2 and omniscient strategies work approximately as an on-off policy, while the other strategies apply smooth changes from one time instant to another. As a consequence, the exposed, infected populations keep oscillating with a high frequency when using the first two strategies, especially the omniscient strategy. The PID-like strategy tends to choose safer decisions as it starts acting before the others and also tries to respond actively to the number of infected individuals.

Fig. 9

Comparison of results of a SEIHRD model with constant parameters using NSAOC (J1, J2, J3), PID-like and omniscient optimal control algorithms

The aggressiveness of the strategies affect the first peaks of infected and exposed individuals. The omniscient strategy has the highest peak in the infected state I, being followed by strategies NSAOC-J2 and NSAOC-J3. One interesting fact is that the peak of exposed individuals is higher when using NSAOC-J2 whilst the peak of infected individuals is higher when using NSAOC-J3. This is explained by the extra factor present in objective function J3 that smoothens the changes applied in the control input. So, instead of forcing the values to be almost only 0 or 1 (like J2), it tries to choose intermediate values to smooth the lockdown level descent. As a consequence, the interactions are higher after the exposed peak is reached, making the peak of infected individuals higher when using NSAOC-J3.

The number of deaths does not differ between all NSAOC strategies and omniscient strategy, presenting a final value of $3.624\%$ ($3.625\%$ using $J_3$ and $3.623\%$ for omniscient). When using PID-Like strategy, the total control input increases and the number of deaths decreases, which leads to the reasonable conclusion that the final number of deaths decreases if total control input is increased.

The level of hospitalized individuals is below the limit $H_{\textrm{max}}$ for all strategies. The PID-Like strategy keeps the level considerably below the lower bound. This is achieved by applying a stronger total control in the environment, as presented in Table 3. NSAOC-J1 strategy presents a greater slack compared to the specified limit $H_{\textrm{max}}$. The remaining strategies (NSAOC-J2, NSAOC-J3 and omniscient) present curves very close to the limit.

Table 3 Results for each strategy applied in a SEIRHD model with constant parameters

Thus, considering that SEIHRD parameters remain constant during the entire time horizon, strategies NSAOC-J2 and omniscient are impossible to implement due to their high frequency behavior. Even though the PID-Like strategy presents good levels of hospitalization and deaths, the control could be relaxed further to reduce the impact on the economy. Finally, strategies NSAOC-J1 and NSAOC-J3 present the most balanced results.

When parameter variation is allowed in the SEIHRD model, as should be expected, the results will not be as good as when using constant parameters, especially for strategies with more aggressive behavior in the control input. The case of parameter variation is now investigated. Parameters $\alpha$ and $\beta$ are both assumed to be normally distributed, with mean (standard deviation) chosen as 0.1786 (0.05), 0.0825 (0.025), respectively. This situation models the existence of many different COVID-19 variants. 1000 simulations are carried out in order to compute the statistics of each strategy.

In Fig. 10, the continuous lines represent the mean of each instant over all simulations, while the shaded areas represent the variance. The first conclusion is that the variance when using omniscient control is greater than all other strategies due to the absence of feedback structure in its strategy.

Fig. 10

Results of a SEIHRD model with parameter variation using all strategies explained in this work

The control effort graph shows that the mean values resultant from NSAOC strategies after instant $k=60$ tend to decrease together around the same value. However, the variance is different for each objective function and, as we noted when using constant parameters, strategy NSAOC-J1 is smoother than NSAOC-J2 and NSAOC-J3. This is confirmed by the dashed blue area, which is smaller than the green and gray ones.

The most important graph is the one showing Hospitalization. Omniscient strategy is the worst one as expected, since it is open-loop. PID-Like control is the smoothest and safest strategy, securing the greatest hospital capacity margin, at the expense of more severe lockdown controls. The last three strategies use NSAOC algorithm and the hospitalization levels are closer to $H_{\textrm{max}}$ at steady-state.

Figure 11 is a zoom of Fig. 10, close to $H_{\textrm{max}}$ in which the omniscient and PID-like curves have been removed since they are far from the neighborhood of $H_{\textrm{max}}$. First, using strategy NSAOC-J2, the mean value curve exceeds $H_{\textrm{max}}$ with the peak almost reaching 0.009. Strategy NSAOC-J3 has its mean value curve below the specified limit $H_{\textrm{max}}$, however the initial transient hospitalization level exceeds its desired capacity limit, which can be noted by the dashed green area around instant $k=45$. Finally, strategy NSAOC-J1 is always below $H_{\textrm{max}}$, even in the worst case scenario, at the expense of having the third highest total control input, as shown in Table 4.

Fig. 11

Hospitalization level graph amplified with strategies NSAOC-J1, NSAOC-J2 and NSAOC-J3 using a SEIHRD model with constant parameters

Table 4 Results for each strategy applied in a SEIRHD model with parameter variation

Thus, considering that parameters do vary in the real world, the best proposed strategy is NSAOC-J1, as it guarantees the hospitalization level below the specified limit $H_{\textrm{max}}$ with a total control effort slightly superior to other similar strategies.

4.2.1 Comparison of Computational Requirements of the Proposed Control Schemes

The BenchmarkTools suite in Julia (Worldometers, 2020) was used on the code for each control scheme. The command @benchmark from this suite runs the codes being compared several times and produces the following statistics: min, max, median, average and standard deviation of the compute times as well as an estimate of the memory use. It should be noted that only the compute time is measured, not the compilation time. The comparative results are shown in Table 5. The following observations are pertinent. All codes (NSAOC-J1 through J3) which use nonlinear optimization software (Ipopt) obviously have runtimes that are four orders of magnitude larger than the runtime for the PID-like controller (which requires almost no computation). However, given that the time constants of the changes in policy are in days, the change in runtime from a few milliseconds to tens of seconds is not significant. A similar remark holds for memory use: once again, the codes which use nonlinear optimization software use memory which is about three orders of magnitude larger than the memory requirement of the PID-like code, due to the fact that the former need to compute and store all states for N-steps. This is the price to be paid for the advantages of the N-step-ahead controllers, especially NSAOC-J1 which performs better than the PID-like controllers under uncertainty (smaller variance) and with less control effort (meaning fewer and less intense lockdowns), as discussed earlier in this section.

Table 5 Mean execution time and memory usage for strategies NSAOC (J1, J2 and J3), omniscient and PID-like

4.3 Vaccination

In the previous sections, simulations did not consider any kind of vaccination plan. In this section we simulate and quantify the impacts of vaccination on the total control input. We make the following assumptions:

• The vaccine is 100% efficient, meaning that the individuals who take it acquire full immunity to COVID-19 after 21 days.

• The vaccination rate is constant over the specified horizon.

• The immunity is acquired with only one shot.

We use different vaccination rates in order to identify the impacts of each level on the total control input. The strategy used to control the epidemic is NSAOC-J1 ($N=10$). Also, we consider constant parameters in the SEIHRD model, as we want to compare the possible benefits of the vaccination.

From Fig. 12, the total effort to control the epidemic decays when the vaccination rate is increased. When this rate is greater than $1.8\%$, the hospitalization level never reaches $H_{\textrm{max}}$ anymore, eliminating one of the main constraints imposed in the previous sections, namely hospital capacity. This would be equivalent to vaccinating 3.8 million individuals per day in Brazil, for example.

Fig. 12

Total control effort using NSAOC-J1 ($N=10$) versus vaccination rate

The evolution of the control effort and the number of susceptible individuals for each vaccination rate is shown in Fig. 13. In the graph, on the left we note that when the vaccination rate increases, it is possible to start acting ($u_k>0$) with a higher delay, since there are fewer susceptible individuals at the same instant. Also, the peaks around the start of the period have lower values and they last for less time. On the right in Fig. 13, the total number of susceptible individuals decays faster for higher vaccination rates, as expected. In the last case ($v=1.8\%$), the curve decay is constant, since the vaccination rate is constant and no control effort is applied in the population.

Fig. 13

Control effort and susceptible individuals using NSAOC-J1 ($N=10$) with constant parameters for each vaccination rate

5 Conclusion

Different strategies are being used by governments all around the world involving the balance between public health and economic issues. In order to make such decisions, most of them rely on expert advice based on the results of epidemiological mathematical models and on daily case reports.

At the time of writing this paper, the epidemic in Brazil is not at a critical stage in terms of hospital capacity, due to the widespread vaccination campaign, which has reduced death rates as well as severity of the cases. However, there is a significant population of negationists, vaccine deniers and unvaccinated individuals and cases of COVID-19 (variants of omicron) are on the rise again, not only in Brazil, but also in the USA, Japan, Korea and China. This implies that the proposal in the present paper, which constantly reacts to the actual state in its design of vaccination policy, is a suitable candidate for implementation in case of a future outbreak.

In this work, we explored different strategies that governments can use to control the COVID-19 epidemic. The main results from our analysis are the following:

• All strategies worked well when the SEIHRD model parameters are constant. They succeed in controlling the level of hospitalized individuals while minimizing the total control effort.

• The NSAOC-J2 strategy resulted in less total control effort, although it applies too many sequences of full lock down or no restrictions at all (like an on-off policy). This can be difficult to apply in the real world.

• NSAOC-J1 and NSAOC-J3 strategies presented better behavior, since they imply a restricted lockdown at the beginning and start to relax as time goes on.

• PID-like controller is a safer strategy that takes actions before the disease really spreads into the population, while it is easier to control the epidemic. However, it leads to higher total control input, with negative economic impacts.

• When the SEIHRD model parameters are not reliable enough, using any type of open-loop control and, specifically, even the ideal omniscient control could result in not being able to control the level of hospitalized individuals, which can lead to a very high number of deaths.

• Only NSAOC-J1 and PID-Like strategies were able to keep the hospitalization level below the specified limit $H_{\textrm{max}}$ in a SEIHRD model with parameter uncertainty in all simulations. The NSAOC-J3 strategy also succeeds as the mean values are below the limit, but closer to it than the NSAOC-J1 and PID-like strategies.

• The number of deaths is proportional to the total control input applied. Hence, PID-Like strategy had better results in this metric since it uses a larger control effort.

• In a SEIHRD model with parameter uncertainty, the number of deaths in all strategies increased due to the difficulty of predicting the future instants correctly.

• Vaccination results in less total control input, less deaths and smaller pandemic duration. For the initial rate increases, the effects are more significant, leading to higher differences in the main performance indexes.

Ideas for future work include the following:

• In our simulations, we considered daily strategies, which are difficult to apply in practice. Weekly strategies might be investigated corresponding to policies used in practice by several health authorities.

• The vaccination follows a constant rate in this work. However, it is possible to consider variable rates during time as presented by Acuña-Zegarra et al (2021). A different optimization problem could be studied to find an optimal vaccination strategy for SEIHRD model.

• Different performance indexes could be explored.