Abstract
Control moment gyroscope (CMG) is an actuator commonly used in attitude control of satellites and spacecrafts, as well as in stabilization of marine vessels and unmanned vehicles. It is a nonlinear multivariable system and presents considerable coupling depending on the chosen operating point, i.e., the gyroscope gimbals angles. First, the complete modeling of a CMG with four degrees of freedom is shown using the Lagrangian dynamic formulation, resulting in a set of four nonlinear equations. Further, the system is linearized around an equilibrium point, resulting in a coupled two-input two-output system. Next, the application of a linear state feedback decoupling control to this linearized system is developed based on the classical Falb–Wolovich method. Aiming to deal with stationary errors, simple decentralized proportional-integral controllers are designed for each channel. Simulation and practical results with a didactic control moment gyroscope are presented in order to validate the methodology. The resulting system has good decoupling characteristics and presents satisfactory responses in terms of setpoint tracking and disturbance rejection.













Similar content being viewed by others
Notes
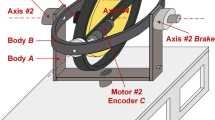
Some gimbal axes in the figure are shifted from their origin to ease visualization.
The plant has only two external torques provided by the two motors \(\tau _{4_{ext}} = T_1\) and \(\tau _{3_{ext}} = T_2\), and therefore \(\tau _{2_{ext}} = \tau _{1_{ext}} =0\).
References
Abbas, H. S., Ali, A., Hashemi, S. M., & Werner, H. (2014). LPV state-feedback control of a control moment gyroscope. Control Engineering Practice, 24, 129–137.
Bhat, S., & Tiwari, P. (2009). Controllability of spacecraft attitude using control moment gyroscopes. IEEE Transactions on Automatic Control, 54(3), 585–590.
Craig, J. J. (1989). Introduction to Robotics: Mechanics and Control (Vol. 2). Boston: Addison-Wesley Publishing.
Durand, S., Boisseau, B., Martinez-Molina, J., Marchand, N., & Raharijaona, T. (2014). Event-based LQR with integral action. In Proceedings of the 2014 IEEE Emerging Technology and Factory Automation (ETFA), Barcelona, pp. 1–7.
Falb, P. L., & Wolovich, W. (1967). Decoupling in the design and synthesis of multivariable control systems. IEEE Transactions on Automatic Control, 12(6), 651–659.
Gagne, J., Piccin, O., Laroche, E., Diana, M., & Gangloff, J. (2012). Gyrolock: Stabilizing the heart with control moment gyroscope (cmg) - from concept to first in vivo assessments. IEEE Transactions on Robotics, 28(4), 942–954.
Ishikawa, K., & Sakamoto, N. (2014). Optimal control for control moment gyros - center-stable manifold approach. In: The 53rd IEEE Conference on Decision and Control 2014, (pp. 5874–5879).
Kurokawa, H. (2007). Survey of theory and steering laws of single-gimbal control moment gyros. Journal of Guidance, Control, and Dynamics, 30(5), 1331–1340.
Parks, T. R. (1999). Manual For Model 750: Control Moment Gyroscope. Bell Canyon: Addison-Wesley Publishing.
Reyhanoglu, M., & van de Loo, J. (2006). State feedback tracking of a nonholonomic control moment gyroscope. In: The 45th IEEE Conference on Decision and Control 2006, (pp. 6156–6161). doi:10.1109/CDC.2006.377590.
Townsend, N., & Shenoi, R. (2014). Control strategies for marine gyrostabilizers. IEEE Journal of Oceanic Engineering, 39(2), 243–255.
Wang, Q. (2002). Decoupling Control. Lecture Notes in Control and Information Sciences. Heidelberg, Berlin: Springer.
Yetkin, H., Kalouche, S., Vernier, M., Colvin, G., Redmill, K., & Ozguner, U. (2014). Gyroscopic stabilization of an unmanned bicycle. In: American Control Conference, (pp. 4549–4554).
Acknowledgments
The authors would like to thank Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for the Grant 2013/25605-2.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The full set of nonlinear equations resulting from the modeling is presented in Sect. 2 and related to Eqs. (3, 4, 5, 6). The inertia parameters are presented in Table 1.
Rights and permissions
About this article
Cite this article
Angélico, B.A., Barbosa, F.S. & Toriumi, F.Y. State Feedback Decoupling Control of a Control Moment Gyroscope. J Control Autom Electr Syst 28, 26–35 (2017). https://doi.org/10.1007/s40313-016-0277-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40313-016-0277-8