Abstract
Bipedal robot control techniques implementing self clocking properties, as presented in Westervelt et al. (Feedback control of dynamic bipedal robot locomotion, Taylor & Francis LLC, Milton Park, 2007) and Novaes et al. (IFAC 19th world congress, 4843–4848, 2014), have desirable properties, like the ability to drive the robot step with respect to its own geometry. In this control technique, one of the possible angular coordinates of the robot is made monotonic during the step execution. The other angular coordinates will track reference functions of the former. One difficulty with this approach is to determine the region around the nominal step for which the stability is assured. In this paper, we propose an algorithm to estimate this stability region by computing numerically an interval matrix related to a Poincaré return map. In conjunction with the algorithm proposed in Ahn and Chen (IEEE Trans Autom Control 52(3):510–514, 2007), we are able to determine the maximum singular value of this interval matrix and so determine a guaranteed stability region.






Similar content being viewed by others
Notes
Exponentially tracked to the planned motion of the step.
As shown in AS7, the absolute orientation \(q_{N}^{+}\) at the beginning of a step is such that \(q_{N}^{+}\in \breve{q}_{N}^{+}\). The “interval dynamics” system will be simulated for a convenient set of initial absolute orientations.
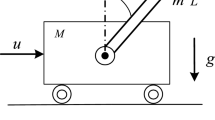
In fact, the inertial wheel is one of these links.
To compute the total angular momentum we use the last line of the Inertia matrix, represented by \({\mathbf {D}}_{N}\left( {\mathbf {q}}\right) \). See Westervelt et al. (2007).
That is, the vertical position of the punctual feet.
This is possible since \(k_{2}\) typically goes from negative to positive through the execution of the step, as shown in Novaes et al. (2014).
Note that (27a) impose poles \(\left\{ -r,\,-r\right\} \) for the dynamics of each component of \({\mathbf {h}}_{r}\).
All the occurrences of the identity matrix on equation (33) has dimension \(N-2\).
This will be true as long as \({\dot{q}}_{n}\ne {\mathbf {0}}\).
Note that \(q_{N}\) acts like a virtual time.
We adopt the \(\breve{\xi }\) notation to represent an interval such that \(\xi \in \breve{\xi }\). This is an unusual notation but allows us more freedom as uppercase, lowercase and other symbols can be related to intervals. The conventional notation is still used for upper and lower boundaries, respectively, \({\overline{\xi }}\) and \({\underline{\xi }}\). See Moore et al. (2009) for more details on interval analysis.
It is desirable to \(\mu \) to be a small value as this will lead to a small value of \({\mathbf {h}}_{r}^{-}\) at the end of the step.
See Westervelt et al. 2007, Appendix C, page 442 for more details on the definition of this implicit functions.
This is shown in Novaes (2016).
Here we use the euclidean norm of a interval matrix, defined as \(\left\| \breve{{\mathbf {x}}}\right\| \triangleq \sup \left\{ \left\| {\mathbf {x}}\right\| :{\mathbf {x}}\in \breve{{\mathbf {x}}}\right\} \).
This could be easily checked with Lyapunov.
There are two other choices. First one is to increase the tunning parameter r for faster convergence to the nominal step geometry. The second one is to choose a higher value for \(\mu \).
By \({\mathbf {y}}_{\left[ k\right] }^{+}\) we mean the value of \({\mathbf {y}}^{+}\)at the k-th step.
Here, \(\left\| {\mathbf {A}}\right\| _{\sigma }\) means the maximum singular value of \({\mathbf {A}}\).
For example, to obtain the faster convergence and/or a greater \({\mathcal {Y}}_\mathrm{{stable}}\) neighborhood.
Note that dependency on the definition of c in Eq. (28b).
This can be easily seen for a scalar system \({\dot{x}}=-ax\) with \(a\in \left[ 1;2\right] \) and with initial condition \(x_{0}=1\). The trivial implementation as an interval system would lead initially to \(\left( \begin{array}{c} \overline{{\dot{x}}}\\ \underline{{\dot{x}}} \end{array}\right) =\left( \begin{array}{cc} 0 &{} -1\\ -2 &{} 0 \end{array}\right) \left( \begin{array}{c} {\overline{x}}\\ {\underline{x}} \end{array}\right) ,\)which is unstable.
Which is itself a function of \({\mathbf {y}}^{+}\).
To be more precise, \({\mathscr {P}}:\hat{{\mathcal {S}}}\longrightarrow \tilde{{\mathcal {S}}}\), as only a subset \(\hat{{\mathcal {S}}}\subset \tilde{{\mathcal {S}}}\) will surely lead to an impact at \({\mathcal {S}}\) and begin another step.
The fgoalattain function of the Matlab optimization toolbox was used.
Some of the elements was smaller than \(10^{-12}\) and were considered to be numerical zeros.
References
Ahn, H.-S., & Chen, Y.-Q. (2007). Exact maximum singular value calculation of an interval matrix. IEEE Transactions on Automatic Control, 52(3), 510–514.
Asano, F., Luo, Z.-W., & Yamakita, M. (2005). Biped gait generation and control based on a unified property of passive dynamic walking. IEEE Transactions on Robotics, 21(4), 754–762.
Goswami, A., Thuilot, B., & Espiau, B. (1998). A study of the passive gait of a compass-like biped robot: symmetry and chaos. International Journal of Robotics Research, 17(12), 1282–1301.
Grizzle, J.W., Chevallereau, C., Ames, A.D., et al. (2010). 3D bipedal robotic walking: Models, feedback control, and open problems. In Proceedings of the IFAC symposium on nonlinear control systems.
Hobbelen, D. G. E., & Wisse, M. (2007). A disturbance rejection measure for limit cycle walkers: The gait sensitivity norm. IEEE Transactions on Robotics, 23(6), 1213–1224.
Isidori, A. (1995). Nonlinear control systems (3rd ed.). Secaucus, NJ: Springer.
Moore, R. E., Kearfott, R. B., & Cloud, M. J. (2009). Introduction to interval analysis. Philadelphia, PA: Society for Industrial and Applied Mathematics.
Novaes, C.E.D.B. (2016). Modelagem e controle de marcha de robô’s bípedes com disco de inercia. Ph.D. thesis, Escola Politécnica da Universidade de São Paulo - USP.
Novaes, C.E., da Silva, P.S.P., & Rouchon, P. (2014). Trajectory control of a bipedal walking robot with inertial disc. In IFAC 19th World Congress (pp. 4843–4848).
Omer, A., Ghorbani, R., Lim, H.O., et al. (2011). Semi-passive dynamic walking approach for bipedal humanoid robot based on dynamic simulation. In Biped robots, chapter 6. InTech.
Schwab, A.L., & Wisse, M. (2001). Basin of attraction of the simplest walking model. In Design engineering technical conferences (p. 9).
Spong, M.W., & Bhatia, G. (2003). Further results on control of the compass gait biped. In Proceedings 2003 IEEE/RSJ international conference on intelligent robots and systems, 2003. (IROS 2003). IEEE (Vol 2, pp. 1933–1938).
Westervelt, E. R., Grizzle, J. W., Chevallereau, C., et al. (2007). Feedback control of dynamic bipedal robot locomotion (1st ed.). Milton Park: Taylor & Francis LLC.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
de Brito Novaes, C.E., da Silva, P.S.P. Numerical Estimation of Stability Region of Self-Clocked Bipedal Robots with Inertial Disk. J Control Autom Electr Syst 27, 634–645 (2016). https://doi.org/10.1007/s40313-016-0266-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40313-016-0266-y