1 Introduction

When questions on sensitive topics, such as cyber bullying, illegal work, sexual behavior, or compulsory vaccination, are directly asked in statistical surveys, the rates of item-nonresponse as well as of untruthful answering might increase far above the usual levels because such questions can be seen as invasion of privacy, or certain answers on these questions can be considered to be socially unacceptable (cf., for instance, Tourangeau and Yan [26]). Such a behavior of the respondents might lead to strongly biased estimators of parameters under study such as the population proportion of people bearing a certain attribute. Therefore, before having to apply the methods of weighting adjustment or data imputation (cf., for instance, Särndal and Lundström [22]), which try to compensate just for the nonresponse that has occurred but not for the untruthful answering, everything should be done to increase the respondents’ willingness to cooperate to make the rates of these two sources of systematic non-sampling errors as small as possible.

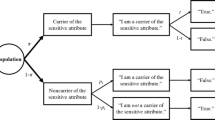
Indirect questioning (IQ) designs intend to ensure respondents’ cooperation by protecting their privacy. To achieve this goal, these techniques “mask” the respondents’ actual status with respect to a variable under study (for an overview of IQ designs see, for instance, Chaudhuri and Christofides [4]). One of these methods is the item count technique (ICT), also known as unmatched count technique or list experiment. Its original version was discussed in detail by Droitcour et al. [9]. Using the ICT, when it comes to the sensitive question, the questionnaire shows a list of different statements, the “items,” describing the membership of different population subgroups. Respondents are asked to report only the number of items that apply to them and not which of them apply. Two independent samples are drawn from the population of interest. In the control sample, the item list consists only of a number of so-called non-key items. In the other sample, the treatment sample, the list does additionally include the “key item” with respect to the sensitive membership of a certain population subgroup under study. The non-key items should be perceived by the respondents as meaningful information in the context of the questionnaire (Chaudhuri and Christofides [3], p. 592). The only task of the control sample is to deliver the information on the non-key items that is needed in the estimation process.

Compared with other privacy protecting IQ designs such as the “randomized response techniques,” the main advantage of the ICT is that the task of the respondents can easily be understood without the need for complex instructions so that it can be implemented very simply even in self-administered questionnaires. Moreover, the interviewees do never have to supply the answer on the sensitive question directly. Various experiments examined the effectiveness of the method (cf., for instance, Droitcour et al. [9], Tsuchiya et al. [27], Coutts and Jann [8], Comsa and Postelnicu [7], Kiewiet de Jonge and Nickerson [16], Wolter and Laier [28], Blair et al. [2], and in particular the meta-analysis by Ehler et al. [10]). Exciting application examples can be found, for instance, in Comsa and Postelnicu [7], Malesky et al. [17], Frye et al. [11], Gibson et al. [12], Rinken et al. [21], or Wolter et al. [29].

Clearly, in order to be recognized as a serious competitor to the common direct questioning approach in empirical research, an IQ technique has to be easy to understand and implement and as accurate as possible. Furthermore, it should be applicable for general probability sampling because in surveys, in which sensitive questions are asked, oftentimes complex sampling methods including stratification and clustering are used. In Sect. 2 of this article, the statistical properties of the basic versions of the ICT with one or two lists of non-key items are discussed. In Sect. 3, modifications of these basic versions are proposed, which make use of available relevant information about at least a part of the used non-key items. These modifications aim to increase the accuracy of the survey results and at the same time reduce the respondents’ burden in the questionnaire. The purpose of the calculations in Sect. 4 is to get a numerical impression of the possible positive effects of the application of the proposed ICT versions on the estimation accuracy. The article is concluded by a summary and an outlook to further research questions.

2 The item count technique

In a generalization of the original version of the ICT, two independent without-replacement probability samples s1 and s2 of sizes n1 and n2, respectively, are drawn from the study population U of size N by probability sampling methods S1 and S2 with first-order inclusion probabilities πk and ρk, respectively, and second-order inclusion probabilities πkl and ρkl. In the control sample s2, the item list consists only of G non-key items. An example with G = 5 non-key items is:

  • I am an only child.

  • I use an electric toothbrush.

  • I have had a reported traffic accident last year.

  • I have been hospitalized last year.

  • I have been abroad in the last year.

The answer x to be reported by a respondent k from the control sample s2 be xk, the number of the G non-key items that apply (xk = 0, 1,…,G). In the treatment sample s1, the short item list consisting of the G non-key items is complemented by the key item under study, which describes the sensitive membership of a certain population subgroup UA \(\subset\) U. An example is:

  • I have been engaged in undeclared work in the last year.

Let variable y indicate this membership of respondent k from the treatment sample s1:

$$ y_{k} = \left\{ {\begin{array}{*{20}c} 1 & {if\;k\; \in \;U_{A} } \\ 0 & {otherwise.} \\ \end{array} } \right. $$

The answer z to be actually reported by such a respondent be zk = xk + yk, the number of all G + 1 items that apply from the long item list (zk = 0, 1,…, G, G + 1) (Table 1).

Table 1 The original ICT
Full size table

Let the proportion p of interest be given by

$$ p = \frac{1}{N} \cdot \sum\nolimits_{U} {y_{k} } $$
(1)

(\(\sum\)U is an abbreviated notation for the sum over all units k ∈ U). Parameter p from Eq. (1) can be expressed by the difference of the population means μz and μx of variables z and x, respectively:

$$ p = \frac{1}{N} \cdot \sum\nolimits_{U} {z_{k} } - \frac{1}{N} \cdot \sum\nolimits_{U} {x_{k} } = \mu_{z} - \mu_{x} $$
(2)

Consequently, the difference

$$ \hat{p} = \frac{1}{N} \cdot \sum\nolimits_{{s_{1} }} {\frac{{z_{k} }}{{\pi_{k} }}} - \frac{1}{N} \cdot \sum\nolimits_{{s_{2} }} {\frac{{x_{k} }}{{\rho_{k} }}} = \overline{z}_{HT} - \overline{x}_{HT} $$
(3)

of the Horvitz–Thompson-based estimators \(\overline{z}_{HT}\) and \(\overline{x}_{HT}\) of the two population means μz and μx calculated from the probability samples s1 and s2, provides an unbiased moment estimator of p under the sampling designs S1 and S2 (cf. Särndal et al. [23], Sect. 2.8). The estimate \(\hat{p}\) could be outside [0; 1]. For such cases, the maximum-likelihood estimator using the EM algorithm is a possible solution (see, for instance, Tian et al. [25]). If non-ignorable nonresponse still occurs, for the application of weighting adjustment techniques, see, for instance, Barabesi et al. [1].

The theoretical variance \(V(\hat{p})\) of the estimator \(\hat{p}\) from Eq. (3) is given by the sum of the usual theoretical variances \(V(\overline{z}_{HT} )\) and \(V(\overline{x}_{HT} )\) of \(\overline{z}_{HT}\) and \(\overline{x}_{HT}\), respectively:

$$ \begin{aligned} V(\hat{p}) &= V(\overline{z}_{HT} ) + V(\overline{x}_{HT} ) \\ &= \frac{1}{{N^{2} }} \cdot \left[ {\sum {\sum\nolimits_{U} {\left( {\pi_{kl} - \pi_{k} \cdot \pi_{l} } \right) \cdot \frac{{z_{k} }}{{\pi_{k} }} \cdot \frac{{z_{l} }}{{\pi_{l} }}} } + \sum {\sum\nolimits_{U} {\left( {\rho_{kl} - \rho_{k} \cdot \rho_{l} } \right) \cdot \frac{{x_{k} }}{{\rho_{k} }} \cdot \frac{{x_{l} }}{{\rho_{l} }}} } } \right] \end{aligned} $$
(4)

(\(\sum \sum\)U is an abbreviated notation for the double sum over all units k,l ∈ U). For the effect of the selection of the non-key items on \(V(\hat{p})\), see, for instance, Glynn [13]. For the variance-optimal allocation of the total sample size n on the two samples, see, for instance, Tian et al. [25]. Perri et al. [19] discuss the idea of optimal allocation extensively for the Item Sum Technique.

The variance from Eq. (4) can be unbiasedly estimated by

$$ \begin{aligned} \hat{V}(\hat{p}) &= \hat{V}(\overline{z}_{HT} ) + \hat{V}(\overline{x}_{HT} ) \\ &= \frac{1}{{N^{2} }} \cdot \left[ {\sum {\sum\nolimits_{{s_{1} }} {\frac{{\pi_{kl} - \pi_{k} \cdot \pi_{l} }}{{\pi_{kl} }} \cdot \frac{{z_{k} }}{{\pi_{k} }} \cdot \frac{{z_{l} }}{{\pi_{l} }}} } + \sum {\sum\nolimits_{{s_{2} }} {\frac{{\rho_{kl} - \rho_{k} \cdot \rho_{l} }}{{\rho_{kl} }} \cdot \frac{{x_{k} }}{{\rho_{k} }} \cdot \frac{{x_{l} }}{{\rho_{l} }}} } } \right] \end{aligned} $$
(5)

For simple random sampling with replacement (SIR) (or also approximately for simple random sampling without replacement from large populations) in both samples, for instance, Eq. (3) results in

$$ \hat{p}_{SIR} = \overline{z} - \overline{x}, $$
(6)

the difference of the simple sample means of z and x in the two SIR samples s1 and s2, respectively. For this sampling design, Eq. (4) results in

$$ V(\hat{p}_{SIR} ) = \frac{{\sigma_{z}^{2} }}{{n_{1} }} + \frac{{\sigma_{x}^{2} }}{{n_{2} }} $$
(7)

with \(\sigma_{z}^{2}\) and \(\sigma_{x}^{2}\), the population variances of z and x. Eventually, Eq. (5) yields

$$ \hat{V}(\hat{p}_{SIR} ) = \frac{{s_{z}^{2} }}{{n_{1} }} + \frac{{s_{x}^{2} }}{{n_{2} }} $$
(8)

with \(s_{z}^{2}\) and \(s_{x}^{2}\), respectively, the sample variances of z and x in s1 and s2.

Besides the previously mentioned advantages of this procedure, also two weaknesses have been discussed in the relevant literature. One is the waste of estimation accuracy because the sensitive information under study is observed only in the treatment sample s1, whereas the control sample s2 only serves as a reference for the calculation of the estimate \(\overline{x}_{HT}\) needed in Eq. (3). The other one is that in s1, the process answers zk = G + 1 and zk = 0, respectively, do reveal a respondent’s true status on the sensitive membership of the group UA (and at the same time also of all non-key items). The probabilities of the occurrence of these “ceiling” or “floor effects,” respectively, can be reduced by a proper choice of the non-key items (see, for instance, Glynn [13], p. 163). The floor effect is less problematic than the ceiling effect unless also the non-membership of UA is sensitive. In s2, the same applies to the response answers xk = G and xk = 0 with respect to the non-key items.

As a consequence of these weaknesses, several modifications of this original ICT have been proposed. The double-list (DL) version by Droitcour et al. [9], for instance, addresses the waste of efficiency by adding to the questionnaires in both samples of the original ICT a second item list, where the non-key items of the first list are replaced by other non-key items. Without loss of generality, let us assume that the number of non-key items equals G in both lists. But, the treatment sample s1 of the original ICT with respect to the first list serves now at the same time as the control sample with respect to the second list and vice versa. Therefore, two answers, z and u, have to be given by a respondent k from sample s1. These are the number zk = xk + yk of applicable items from the long first item list including the key item (as in the original ICT) and the number uk of applicable non-key items from the short second list without the key item (uk = 0, 1,…, G) (Table 2). The answers x and w to be given by a respondent k from sample s2 are the number xk of applicable non-key items from the short first list (as in the original ICT) and the number wk = uk + yk of applicable items from the long second list (wk = 0, 1,…, G, G + 1).

Table 2 The DL version of the ICT
Full size table

By this supplement to the questionnaires, in both samples information on the sensitive variable is observed. This increases the estimation accuracy compared with the original ICT by the price of an only insignificant increase in the respondents’ burden by the usage of a second item list that should hardly negatively affect their willingness to cooperate.

With two different lists of non-key items applied to two samples, from Eq. (3) two separate estimates \(\hat{p}_{1}\) and \(\hat{p}_{2}\), respectively, can be calculated, of which their mean value

$$ \begin{aligned} \overline{\hat{p}} &= \frac{{\hat{p}_{1} + \hat{p}_{2} }}{2} = \frac{1}{2} \cdot \left( {\frac{1}{N} \cdot \sum\nolimits_{{s_{1} }} {\frac{{z_{k} }}{{\pi_{k} }}} - \frac{1}{N} \cdot \sum\nolimits_{{s_{2} }} {\frac{{x_{k} }}{{\rho_{k} }}} + \frac{1}{N} \cdot \sum\nolimits_{{s_{2} }} {\frac{{w_{k} }}{ {\rho_{k} }}} - \frac{1}{N} \cdot \sum\nolimits_{{s_{1} }} {\frac{{u_{k} }}{{\pi_{k}}}} } \right) \\ & = \frac{{\overline{z}_{HT} - \overline{x}_{HT} + \overline{w}_{HT} - \overline{u}_{HT} }}{2} \end{aligned} $$
(9)

is taken as the procedure’s unbiased estimate. In Eq. (9), \(\overline{z}_{HT}\) and \(\overline{u}_{HT}\) calculated from the probability sample s1, and \(\overline{x}_{HT}\) and \(\overline{w}_{HT}\) calculated from the probability sample s2, respectively, are the Horvitz-Thompson-based estimators of the population means μz, μu, μx, and μw. The theoretical variance of \(\overline{\hat{p}}\) is given by

$$ V(\overline{\hat{p}}) = \frac{1}{4} \cdot \left[ {V(\hat{p}_{1} ) + V(\hat{p}_{2} ) + 2 \cdot C(\hat{p}_{1} ,\hat{p}_{2} )} \right] $$
(10)

Equation (10) includes the two variances \(V(\hat{p}_{1} )\) and \(V(\hat{p}_{2} )\), which are calculated applying Eq. (4), and the covariance term \(C(\hat{p}_{1} ,\hat{p}_{2} )\), addressing the levels of dependence of z and u in s1, and x and w in s2, respectively (for the details see Appendix 1). The formula for the estimator of this variance includes the variance estimators that can be generated straightforward from Eq. (5) and an estimator of the covariance term from the sample data. The relevant formulas under the SIR sampling design with the estimator

$$ \overline{\hat{p}}_{SIR} = \frac{{\hat{p}_{1,SIR} + \hat{p}_{2,SIR} }}{2} $$
(11)

can be derived accordingly.

Petróczi et al. [20] and Groenitz [14] proposed the “single sample count technique.” For this ICT approach with only one list, the joint population distribution of the non-key items is assumed to be known so that a control sample is no longer needed. Its theory is developed for the SIR design under practically limiting assumptions about the independence of the individual items. Like the DL version, this technique addresses the efficiency problem of the original ICT. The modifications of the original ICT that will be proposed in Sect. 3 are based on these contributions.

Other modifications of the original ICT concern its ceiling/floor effect. Such methods were presented by Chaudhuri and Christofides [3], Christofides [5], Ibrahim [15], Shaw [24], Christofides and Manoli [6], or Manoli [18].

3 The proposed modifications of the original item count technique

In this section, a modification of the original ICT is proposed that increases the accuracy of the estimation of the proportion p and at the same time reduces the complexity of the questioning design. For this modification, we presume that the population mean value of the number of applicable non-key items among at least a part of these items is available, for instance, from administrative or register data. Non-key items for which this information is available and which do not appear to be completely meaningless, such as asking for the last digit of the phone number, should not be too difficult to find. For this purpose, for example, socio-demographic items with known distribution in the target population such as marital status (e.g. the statement “I am unmarried.”) or education (e.g. “I have a degree of a university of applied sciences.”) might be used. Other examples of such items could be age, gender, place of residence, migration background, nationality, ethnicity, religion, household size, employment, income or working hours. In the following, the effect of the usage of such information on the expressions of the estimator, its theoretical variance, and the variance estimator, respectively, is presented for general probability sampling.

Let the population mean value \(\mu_{{x^{{(F_{1} )}} }}\) of the number \(x^{{(F_{1} )}}\) of applicable items among F1 of the G non-key items be given (0 ≤ F1 ≤ G). Hence, the expression of the parameter p from Eq. (2) can be re-written by

$$ p = \mu_{z} - \left( {\mu_{{x^{{[E_{1} ]}} }} + \mu_{{x^{{(F_{1} )}} }} } \right) $$
(12)

with \(\mu_{{x^{{[E_{1} ]}} }}\), the unknown population mean value of the number \(x^{{[E_{1} ]}}\) of applicable items among the E1 = G – F1 of the G non-key items that are not contained in \(\mu_{{x^{{(F_{1} )}} }}\).

For F1 = 0 (E1 = G), the item list corresponds to that of the original ICT. But for 0 < F1 < G, the item list of the control sample s2 consists only of the E1 non-key items that are not included in \(\mu_{{x^{{(F_{1} )}} }}\), which reduces the respondents’ task in sample s2 compared with the original ICT. The answer to be reported by a respondent k from sample s2 is \(x_{k}^{{[E_{1} ]}}\), the number of the E1 non-key items that apply (\(x_{k}^{{[E_{1} ]}}\) = 0, 1,…, E1). In the treatment sample s1, the answer to be reported by a respondent is the same as in the original ICT (Table 3).

Table 3 The proposed modified version of the original ICT
Full size table

Clearly, the parameter from Eq. (12) is unbiasedly estimated by

$$ \hat{p}^{{(F_{1} )}} = \overline{z}_{HT} - \left( {\overline{x}_{HT}^{{[E_{1} ]}} + \mu_{{x^{{(F_{1} )}} }} } \right) $$
(13)

with \(\overline{z}_{HT}\) from Eq. (3) and the Horvitz–Thompson-based estimator

$$ \overline{x}_{HT}^{{[E_{1} ]}} = \frac{1}{N} \cdot \sum\nolimits_{{s_{2} }} {\frac{{x_{k}^{{[E_{1} ]}} }}{{\rho_{k} }}} $$

of the population mean \(\mu_{{x^{{[E_{1} ]}} }}\) from sample s2. For F1 = 0, \(\hat{p}^{(0)} = \hat{p}\) from Eq. (3) applies.

The theoretical variance V(\(\hat{p}^{{(F_{1} )}}\)) of the estimator \(\hat{p}^{{(F_{1} )}}\) from Eq. (13) is given by the sum of the two theoretical variances \(V(\overline{z}_{HT} )\) and \(V(\overline{x}_{HT}^{{[E_{1} ]}} )\) of \(\overline{z}_{HT}\) and \(\overline{x}_{HT}^{{[E_{1} ]}}\), respectively,

$$ \begin{aligned} V(\hat{p}^{{(F_{1} )}} ) &= V\left(\overline{z}_{HT} \right) + V\left(\overline{x}_{HT}^{{[E_{1} ]}} \right) \\ &= \frac{1}{{N^{2} }} \cdot \left[ {\sum {\sum\nolimits_{U} {\left( {\pi_{kl} - \pi_{k} \cdot \pi_{l} } \right) \cdot \frac{{z_{k} }}{{\pi_{k} }} \cdot \frac{{z_{l} }}{{\pi_{l} }}} } + \sum {\sum\nolimits_{U} {\left( {\rho_{kl} - \rho_{k} \cdot \rho_{l} } \right) \cdot \frac{{x_{k}^{{[E_{1} ]}} }}{{\rho_{k} }} \cdot \frac{{x_{l}^{{[E_{1} ]}} }}{{\rho_{l} }}} } } \right] \end{aligned} $$
(14)

The accuracy of the estimator \(\hat{p}^{{(F_{1} )}}\) increases with F1 → G.

This variance is unbiasedly estimated by

$$ \begin{aligned} \hat{V}(\hat{p}^{{(F_{1} )}} ) &= \hat{V}\left(\overline{z}_{HT} \right) + \hat{V}\left(\overline{x}_{HT}^{{[E_{1} ]}} \right) \\ &= \frac{1}{{N^{2} }} \cdot \left[ {\sum {\sum\nolimits_{{s_{1} }} {\frac{{\pi_{kl} - \pi_{k} \cdot \pi_{l} }}{{\pi_{kl} }} \cdot \frac{{z_{k} }}{{\pi_{k} }} \cdot \frac{{z_{l} }}{{\pi_{l} }}} } + \sum {\sum\nolimits_{{s_{2} }} {\frac{{\rho_{kl} - \rho_{k} \cdot \rho_{l} }}{{\rho_{kl} }} \cdot \frac{{x_{k}^{{[E_{1} ]}} }}{{\rho_{k} }} \cdot \frac{{x_{l}^{{[E_{1} ]}} }}{{\rho_{l} }}} } } \right] \end{aligned} $$
(15)

Under the SIR design in both samples s1 and s2, for instance, Eq. (13) results in

$$ \hat{p}_{SIR}^{{(F_{1} )}} = \overline{z} - (\overline{x}^{{[E_{1} ]}} + \mu_{{x^{{(F_{1} )}} }} ) $$
(16)

with the sample means \(\overline{z}\) and \(\overline{x}^{{[E_{1} ]}}\) of z and \(x_{{}}^{{[E_{1} ]}}\) in s1 and s2, respectively. For this sampling design, Eq. (14) results in

$$ V(\hat{p}_{SIR}^{{(F_{1} )}} ) = \frac{{\sigma_{z}^{2} }}{{n_{1} }} + \frac{{\sigma_{{x^{{[E_{1} ]}} }}^{2} }}{{n_{2} }} $$
(17)

with \(\sigma_{z}^{2}\) and \(\sigma_{{x^{{[E_{1} ]}} }}^{2}\), the population variances of z and \(x_{{}}^{{[E_{1} ]}}\). Eventually, Eq. (15) yields

$$ \hat{V}(\hat{p}_{SIR}^{{(F_{1} )}} ) = \frac{{s_{z}^{2} }}{{n_{1} }} + \frac{{s_{{x^{{[E_{1} ]}} }}^{2} }}{{n_{2} }} $$
(18)

with \(s_{z}^{2}\) and \(s_{{x^{{[E_{1} ]}} }}^{2}\), respectively, the sample variances of z and \(x_{{}}^{{[E_{1} ]}}\) in the SIR samples s1 and s2.

Following the idea of Petróczi et al. [20], in the special case that F1 = G, a control sample is no longer needed because the mean number μx of x from Eq. (2) is known (\(\mu_{{x^{(G)} }} \equiv \mu_{x}\), x(G) ≡ x). This means that the total sample number n = n1 + n2 can be allocated to the treatment sample alone. With only one long list in the whole sample of size n, Eq. (13) reduces to

$$ \hat{p}^{(G)} = \overline{z}_{HT} - \mu_{x} $$
(19)

and Eqs. (14) and (15), respectively, to

$$ V(\hat{p}^{(G)} ) = V(\overline{z}_{HT} ) = \frac{1}{{N^{2} }} \cdot \left[ {\sum {\sum\nolimits_{U} {\left( {\pi_{kl} - \pi_{k} \cdot \pi_{l} } \right) \cdot \frac{{z_{k} }}{{\pi_{k} }} \cdot \frac{{z_{l} }}{{\pi_{l} }}} } } \right] $$
(20)

and

$$ \hat{V}(\hat{p}^{(G)} ) = \hat{V}(\overline{z}_{HT} ) = \frac{1}{{N^{2} }} \cdot \left[ {\sum {\sum\nolimits_{{s_{1} }} {\frac{{\pi_{kl} - \pi_{k} \cdot \pi_{l} }}{{\pi_{kl} }} \cdot \frac{{z_{k} }}{{\pi_{k} }} \cdot \frac{{z_{l} }}{{\pi_{l} }}} } } \right] $$
(21)

For the SIR method, these equations yield

$$ \hat{p}_{SIR}^{(G)} = \overline{z} - \mu_{x} , $$
(22)
$$ V(\hat{p}_{SIR}^{(G)} ) = \frac{{\sigma_{z}^{2} }}{n} $$
(23)

and

$$ \hat{V}(\hat{p}_{SIR}^{(G)} ) = \frac{{s_{z}^{2} }}{n} $$
(24)

For a combination of this modified ICT, which uses relevant prior information on the non-key items, with the DL version of the ICT, which uses two different item lists, let the mean values \(\mu_{{x^{{(F_{1} )}} }}\) of the number \(x_{{}}^{{(F_{1} )}}\) of applicable items of F1 of the G non-key items from the first list (0 ≤ F1 ≤ G) and \(\mu_{{u^{{(F_{2} )}} }}\) of the number \(u^{{(F_{2} )}}\) of applicable items of F2 of the G non-key items from the second list (0 ≤ F2 ≤ G) be known. In this case, the short first item list included in sample s2 consists only of the E1 = G – F1 non-key items that are not included in the known mean value \(\mu_{{x^{{(F_{1} )}} }}\), whereas the short second item list included in sample s1 consists only of the E2 = G – F2 non-key items that are not included in the known mean value \(\mu_{{u^{{(F_{2} )}} }}\). Hence, for F1 > 0 and/or F2 > 0, the use of such prior information does also reduce the respondents’ burden of the original DL design. The numbers to be reported by a respondent k from sample s1 are zk, the number of applicable items from the long first item list including the key item, and \(u_{k}^{{[E_{2} ]}}\), the number of applicable non-key items from the short second item list (\(u_{k}^{{[E_{2} ]}}\) = 0, 1,…, E2). A respondent k from sample s2 has to report \(x_{k}^{{[E_{1} ]}}\), the number of applicable non-key items from the short first item list (\(x_{k}^{{[E_{1} ]}}\) = 0, 1,…, E1), and wk = uk + yk, the number of applicable items from the long second item list (Table 4). For F1 = F2 = 0, the item lists correspond to those of the original DL version.

Table 4 The modified DL version of the ICT
Full size table

This questioning design changes the expression of the estimator (9) to

$$ \overline{\hat{p}}^{{(F_{1} /F_{2} )}} = \frac{{\hat{p}_{1}^{{(F_{1} )}} + \hat{p}_{2}^{{(F_{2} )}} }}{2} $$
(25)

This is the mean value of the two separate estimates \(\hat{p}_{1}^{{(F_{1} )}}\) and \(\hat{p}_{2}^{{(F_{2} )}}\) that can be retrieved from Eq. (13). Its theoretical variance is given by

$$ V(\overline{\hat{p}}^{{(F_{1} /F_{2} )}} ) = \frac{1}{4} \cdot [V(\hat{p}_{1}^{{(F_{1} )}} ) + V(\hat{p}_{2}^{{(F_{2} )}} ) + 2 \cdot C(\hat{p}_{1}^{{(F_{1} )}} ,\hat{p}_{2}^{{(F_{2} )}} )] $$
(26)

with the two variances \(V(\hat{p}_{1}^{{(F_{1} )}} )\) and \(V(\hat{p}_{2}^{{(F_{2} )}} )\), respectively, according to Eq. (14) and a covariance term \(C(\hat{p}_{1}^{{(F_{1} )}} ,\hat{p}_{2}^{{(F_{2} )}} )\) that addresses the levels of dependence of z and \(u^{{[E_{2} ]}}\) in s1, and \(x_{{}}^{{[E_{1} ]}}\) and w in s2, respectively. The variance term (26) can be estimated applying Eq. (21) for the estimation of the variance terms and an estimator of the covariance term using the sample data. For the SIR design, Eq. (25) yields

$$ \overline{\hat{p}}_{SIR}^{{(F_{1} /F_{2} )}} = \frac{{\hat{p}_{1,SIR}^{{(F_{1} )}} + \hat{p}_{2,SIR}^{{(F_{2} )}} }}{2} $$
(27)

If one or both mean values μx and μu are known (F1 = G and/or F2 = G), for the first, the second or both item lists, a control sample would theoretically no longer be needed. But, to apply one of the two or even both long lists to the entire sample of size n could be counter-productive because in such cases, the members of at least one sample would have to respond to two long lists with the same key item. This might have a negative impact on their perceived privacy protection and consequently on their cooperation willingness.

4 A Numerical comparison of the accuracy of different versions of the ICT

In this section, the different ICT versions described in Sects. 2 and 3 are numerically compared under the SIR design to provide an impression of the effect of the proposed techniques on the accuracy of the estimation. For all these methods, the respondents’ task is of similar simplicity, which should ensure a similar effect on the cooperation willingness. For this purpose, from the “imaginary population” provided by Shaw [24], the six-dimensional population distribution of the G = 5 non-key items (there named “1” to “5”) and the key item (named “A”), and their dependence structure is used (see Appendix 2).

On the one hand, for sample sizes n1 and n2, the estimation accuracy of the estimators \(\hat{\theta }_{SIR}\) (\(\hat{p}_{SIR}^{{(F_{1} )}}\) from Eq. (16) and \(\overline{\hat{p}}_{SIR}^{{(F_{1},F_{2} )}}\) from Eq. (27), 0 ≤ F1,F2 ≤ G) of the different ICT methods is compared by the relative variance reduction (RVR) in % of \(V(\hat{p}_{SIR} )\) of the original ICT (Table 5):

$$ RVR = \left( {1 - \frac{{V(\hat{\theta }_{SIR} )}}{{V(\hat{p}_{SIR} )}}} \right) \cdot 100 $$
(28)
Table 5 RVR in % compared with \(V(\hat{p}_{SIR} )\) of the original ICT
Full size table

For \(\hat{\theta }_{SIR} = \hat{p}_{SIR}^{(5)}\) from Eq. (22), for example, for which not only the population mean μx is known, but also the variable z is observed in the whole sample of size n = 1,000, with the variances \(V(\hat{p}_{SIR}^{(5)} )\) and \(V(\hat{p}_{SIR} )\) from Eqs. (20) and (7), the RVR in % is given by

$$ RVR = \left( {1 - \frac{{\frac{{\sigma_{z}^{2} }}{n}}}{{\frac{{\sigma_{z}^{2} }}{{n_{1} }} + \frac{{\sigma_{x}^{2} }}{{n_{2} }}}}} \right) \cdot 100 $$

With the parameters from Shaw’s population (see Appendix 2), this results in an RVR of 72.7% compared to the original ICT approach (Table 5).

On the other hand, the estimation accuracy of the estimators \(\hat{\theta }_{SIR}\) is compared with that of the “direct” estimator

$$ \hat{p}_{SIR}^{D} = \frac{1}{n} \cdot \sum\nolimits_{s} {r_{k} } , $$
(29)

the proportion of the “yes-”responses r = 1 in the SIR sample of size n = n1 + n2 with

$$ r_{k} = \left\{ {\begin{array}{*{20}c} 1 & {if\;respondent\;k\;answers\;{}^{^{\prime\prime}}yes^{^{\prime\prime}} } \\ 0 & {if\;respondent\;k\;answers\;{}^{^{\prime\prime}}no,{}^{^{\prime\prime}}} \\ \end{array} } \right. $$

assuming that with probability q instead of the true status y = 1 the response r = 0 is reported, when the sensitive question is asked directly, and that all other non-sampling error components are equally negligible for the considered questioning designs. For this purpose, the threshold value q0 of the probability q is calculated, the exceeding of which yields a mean square error \(MSE(\hat{p}_{SIR}^{D} )\) larger than the variance \(V(\hat{\theta }_{SIR} )\) of the unbiased estimator \(\hat{\theta }_{SIR}\) (Table 6):

$$ q_{0} = \frac{{\sqrt {V(\hat{\theta }_{SIR} ) - \frac{p(1 - p)}{n}} }}{p} $$
(30)
Table 6 q0 for which \(MSE(\hat{p}_{SIR}^{D} )\) ≤ \(V(\hat{\theta }_{SIR} )\) applies
Full size table

(for the theoretical development, see Appendix 3). For q > q0, the bias of \(\hat{p}_{SIR}^{D}\) will yield \(MSE(\hat{p}_{SIR}^{D} ) > V(\hat{\theta }_{SIR} )\), and the increased privacy protection of the specific ICT design will pay off in terms of accuracy. For \(\hat{\theta }_{SIR} = \hat{p}_{SIR}^{(5)}\) from Eq. (22), for example, Eq. (30) results in

$$ q_{0} = \frac{{\sqrt {\frac{{\sigma_{z}^{2} }}{n} - \frac{p(1 - p)}{n}} }}{p} $$

With the parameters from Shaw’s population (see Appendix 2), this results in q0 = 0.070 (see Table 6). Under the given assumptions, for a probability q larger than only 7.0%, \(V(\hat{p}_{SIR}^{(5)} ) < MSE(\hat{p}_{SIR}^{D} )\) applies and the modification of the original ICT with G = 5 will provide more accurate results than the direct questioning approach.

In the given data set, the proportion p under study is equal to 0.479. The comparison is done with n1 = n2 = 500. The uniform allocation of n to the two samples is a reasonable choice when DL versions of the ICT are included in the investigations. The results presented in Tables 5 and 6 provide a numerical impression of the possible effects of the knowledge of the mean values of at least a part of the G non-key-items in techniques with one or two item lists on the estimation accuracy. For the one list versions of the ICT, n1 > n2 would be a better choice than n1 = n2. Hence, for \(\hat{p}_{SIR}^{{(F_{1} )}}\) (0 ≤ F1 ≤ 5) the results in Table 5 can be interpreted as lower limits of the achievable RVR in % and the results in Table 6 as upper limits of the probability q0.

Clearly, in a one-list design (column \(\hat{p}_{SIR}^{{(F_{1} )}}\) in the Tables 5 and 6), the higher the number F1 of the G non-key items is, for which \(\mu_{{x^{{(F_{1} )}} }}\) is known, the higher is the RVR of \(\hat{p}_{SIR}^{{(F_{1} )}}\) in comparison to \(\hat{p}_{SIR}^{{}}\) of the original ICT. For the given data (see Appendix 2), the DL approach (\(\overline{\hat{p}}_{SIR}^{{(F_{1} /F_{2} )}}\)) with F1 = F2 = 0 (\(\overline{\hat{p}}_{SIR}^{{}}\)) roughly halves the variance of the original ICT (\(\hat{p}_{SIR}\)) by the use of two lists instead of only one. Moreover, Table 5 shows how also the DL version can gain additional accuracy through knowledge of the mean values \(\mu_{{x^{{(F_{1} )}} }}\) and \(\mu_{{u^{{(F_{2} )}} }}\), respectively (0 ≤ F2 ≤ F1 ≤ G). This shows, how the performances of the estimators benefit from both ideas, use of prior knowledge and of two lists. Each additional part of prior information increases the accuracy of the estimator. In the applied setting, only the estimator \(\overline{\hat{p}}_{SIR}^{(5/5)}\) of the DL version with F1 = F2 = 5 provides roughly the same result as \(\hat{p}^{(5)}\), in which no control sample is needed anymore.

When it comes to the comparison with the direct questioning on the sensitive item by q0 from Eq. (30), Table 6 shows that the original ICT would pay off in terms of accuracy if more than only 14.4% of the members of UA would lie to the sensitive question when they were asked directly. As a consequence of the achievable variance reductions of the proposed modified versions of the ICT presented in Table 5, this q0 can accordingly be reduced. For the best case with respect to simplicity and accuracy of the questioning design (Table 5), the estimator \(\hat{p}_{SIR}^{(5)}\) would already be more accurate than the direct estimator (29) (both with n = 1,000) if the absolute bias of \(\hat{p}_{SIR}^{D}\) from Eq. (29) is larger than only 0.070 · 0.479 = 0.033.

5 Summary and outlook

The original ICT is an easy-to-understand and simple-to-implement IQ design to mask sensitive information with the aim to increase respondents’ cooperation willingness. The take-away message of this article is that the usage of certain prior information about at least some of the involved non-key items can substantially decrease the estimators’ additional variance. In addition to contextual non-key items for which such information might be available, for example, socio-demographic items with known distribution in the target population oftentimes could be used for this purpose. In this way, the method has the potential to become an even stronger and more serious competitor of the direct questioning about sensitive characteristics.

For 1 ≤ F1 ≤ G–1, this prior information could additionally be used for regression-type estimators. For this purpose, in the control sample two separate lists with E1 and F1 non-key items would have to be used. For large correlations of \(x^{{[E_{1} ]}}\) and \(x^{{(F_{1} )}}\), such estimators could reduce the second component of the variance \(V(\hat{p}^{{(F_{1} )}} )\) from (14) while the unchanged first component remains responsible for the larger part of the sum. Based on the proposed modifications of the original ICT, it may be of interest to investigate the pros and cons of such estimators in some detail in possible future research.

Moreover, a further combination of the proposed modifications of the ICT with methods that account for the floor/ceiling effect could also address these weaknesses of the original ICT in protecting also the privacy of the few respondents to whom these effects would apply. However, such methods, of course, would have to maintain the simplicity of the original ICT to avoid an increase in the respondents’ task. If this cannot be ensured, it would be preferable to reduce the probability of these two effects by selecting the non-key items appropriately.