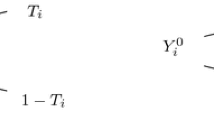1 Introduction

Surveys on highly confidential, stigmatizing or even incriminating issues are prone to produce distorted analyses due to measurement errors mainly ascribable to nonresponse and misreporting. Survey participants, when inquired about sensitive behaviors, attributes or attitudes by means of traditional techniques based on direct questioning (DQ), very often refuse to answer or don’t answer truthfully because of social desirability bias or fear that the released sensitive information will be passed on to third parties, not directly involved in the research, for reasons that have nothing to do with the stated aims of the survey. Although these errors can never be completely eliminated, they can be mitigated to some extent by assuring survey participants that their answers will be used only for scientific purposes and guaranteeing privacy protection.

Over time, many different strategies have been adopted to encourage respondent trust and, thus, enhance cooperation (see, e.g., Tourangeau and Smith 1996; Groves et al. 2004). One possibility is to administer the survey in such a way as to reduce the presence and the impact of the interviewer from the whole response process. Along this line, traditional solutions are represented by self-administered questionnaires with paper and pencil, computer-assisted telephone interviewing, computer-assisted self interviewing, audio computer-assisted self interviewing or computer-assisted Web interviewing. Other factors that play a part in encouraging trust and confidentiality include the questionnaire format, the wording and the placing of the sensitive items, and the setting where data are collected.

Another way to increase confidentiality consists of using alternative questioning methods, different from conventional survey modes, conceived in the sixties for the primary intent to ensure full anonymity of the respondents, cutting down evasive answers of stigmatizing acts and produce reliable estimates of sensitive characteristics. These methods are generally known as indirect questioning (IQ) techniques (IQTs) and are based on the principle that survey participants don’t have to respond to direct questions and, thus, there is no need to openly reveal their true status. In this way, privacy is protected since the information gathered remains confidential and, consequently, the true status of the respondents turns out to be undisclosed to both the interviewer and the researcher. Readers interested in this alternative approach can find a detailed description of various IQTs in Fox and Tracy (1986), Chaudhuri and Mukerjee (1988), Chaudhuri (2011), Chaudhuri and Christofides (2013), Tian and Tang (2014), Chaudhuri et al. (2016) and Fox (2016).

When used in sensitive research, IQTs are very likely to yield more reliable analysis about the investigated issues. Since the data collected by IQTs are assumed to be released truthfully by the respondents, estimates of unknown population parameters, such as the proportion of carriers of a sensitive attribute, are expected to be more reliable than those under DQ which, in general, are threatened by social desirability bias. In other words, since participants tend to provide answers that are in line with social norms or are compliant with laws, DQ data stemming from self-reports may result in an overestimation of socially desirable attributes (e.g., donations to charity, healthy eating, doing voluntary work) and in an underestimation of social undesirable ones (e.g, gender abuse, tax evasion, gambling, drug taking). On the contrary, since the IQ approach basically reduces misreporting, higher [lower] prevalence estimates of undesirable [desirable] behaviors, closer to the real and unknown ones, are more likely to be obtained. Hence, albeit the matter is controversial (see, e.g., Wolter and Preisendörfer 2013; Höglinger and Jann 2018), according to the “more-is-better assumption” [“less-is-better”] the IQTs should be judged more valid than DQ survey modes to elicit sensitive information and produce more reliable estimates (see, e.g., Lensvelt-Mulders et al. 2005; Rosenfeld et al. 2016).

Although the IQTs are oriented to increasing confidentiality, they are affected by a number of drawbacks. First of all, in order to protect respondent privacy, the IQ survey mode missclassifies the responses by perturbing them with a random noise that increases the variance of the estimates and reduces the statistical efficiency of the inferential process, including the statistical power of testing procedures. Furthermore, in spite of the increased confidentiality, some respondents may still be reluctant to disclose sensitive personal information because they don’t trust the approach and believe that there may exist some mathematical trick that permits the researcher to pass from the released perturbed responses to the true sensitive status. Additionally, explaining and understanding the technique to collect information, while protecting privacy, may not be so easy for both the researcher and the survey participants. In the light of the last two remarks, IQ results may be affected by a form of bias which, in a broad sense, includes cheating and self-protective responding, nonadherence to the instructions for the correct implementation of the survey method, carelessness and so on (see, e.g., Clark and Desharnais 1998; Moshagen et al. 2012; Hoffmann and Musch 2016; Heck et al. 2018; Hoffmann et al. 2017; Höglinger and Jann 2018). Finally, we note that implementing IQTs may be more costly and time-demanding than DQ survey modes.

For all the above said considerations, it turns out that the IQ approach may represent a valid alternative to DQ only when the procured advantages outweigh the limits which pertain the practical implementation of indirect data-collection methods. Indeed, ascertaining the effectiveness of the IQTs is a highly complex task since different, albeit conceptually identifiable, aspects that need to be considered are difficult to evaluate in real survey conditions on the basis of unanimously accepted scientific criteria. Such aspects concern, for instance, the degree of sensitivity of the investigated topics and the choice of the IQ method to collect data; the mathematical measure of privacy protection offered by a given method and the protection really perceived by the respondents; the way to asses the extent of nonadherence and cheating; the trade-off between privacy protection and efficiency of the estimates. Considering all these aspects simultaneously is an unfeasible task also because reasonable and accurate comparative validation analyses may be produced only at individual-level by collecting data on the same group of respondents using both direct and indirect survey modes, or assuming that the true population parameters under study are known from external records available for every respondent (Lensvelt-Mulders et al. 2005). However, even assuming that all these aspects could be evaluated, the problem that no general and valid conclusions can be drawn still remains, since the outcomes of the analyses heavily depend on the indirect technique involved in the study.

Given the above considerations, this paper aims to evaluate the effectiveness of certain IQTs over DQ focusing just on one aspect that can be assessed when the same group of respondents is surveyed with both direct and indirect questions. The main idea of the work is to check whether the results obtained using various IQTs are more accurate than DQ results according to the “more-is-better assumption”. In so doing, we propose to test the presence of liars in the surveys. In the case the presence is statistically significant, it will be possible to evaluate the impact of untruthful responses on estimating the proportion of people who possess a stigmatizing attribute.

The remainder of the paper is organized as follows. In Sect. 2, we introduce the notation and the testing procedure. In Sect. 3, it is shown how the testing procedure can be applied in simple random sampling for some discussed IQTs: the Warner model, the unrelated question model (UQM), the item count technique (ICT), the crosswise and triangular models. Section 4 extends the results of the previous section to a general sampling design. In Sect. 5, the procedure is assessed via a simulation study (Sect. 5.1) and two real studies (Sect. 5.2) about racism and workplace mobbing. Finally, Sect. 6 concludes the work with some remarks and suggestions for future research.

2 The method

Let \(U=\left\{ 1,\ldots ,N\right\} \) be a finite population of N distinct and identifiable units who may or may not possess the sensitive attribute A. Let \(Y_k\) be a binary variable, with \(Y_k=1\) if the kth population unit carries A, and \(Y_k=0\) otherwise. Finally, let \(\pi _A\) denote the prevalence in the study population of the attribute A, \(\pi _A=\sum _{k \in U}Y_k/N\).

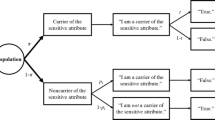
Let us consider the case where units are surveyed to collect information on A, and assume that: (i) only the possession of A is sensitive; (ii) there are no units who refuse to respond at all or are not available. Hence, without loss of generality, we can reasonably assume that the population is divided in three mutually exclusive groups:

\({Group\,\,1\!\!:}\):

Units having A and being honest in declaring to possess the attribute. Let \(\pi _{H}\) denote the proportion of population units belonging to the group;

\({Group\,\,2\!\!:}\):

Units having A and being liars in declaring to possess the attribute. Let \(\pi _{L}\) denote the proportion of population units belonging to the group;

\({Group\,\,3\!\!:}\):

Units who don’t have A.

Hence, under the assumptions (i)–(ii), it immediately follows that:

$$\begin{aligned} \pi _A=\pi _{H}+\pi _{L}. \end{aligned}$$
(1)

Obviously, \(\pi _A\), \(\pi _{H}\) and \(\pi _{L}\) are unknown population parameters and must be estimated. To serve this purpose, we basically assume that a sample s of fixed size n is selected from U according to simple random sampling with replacement (SRSWR). Furthermore, let us assume that each sampled unit is firstly posed the direct question “Do you posses A?”. Accordingly, let \(D_k \) be the binary variable with \(D_k=1\) if the kth unit answers “Yes” and \(D_k=0\) if the response is “No”. Bearing in mind that the respondents may be untruthful when answering to the direct question, let us assume that the sampled units are also asked to provide a response following the rules prescribed by a specific IQT. Hence, let \(I_k=\left\{ 0,1\right\} \) denote the binary missclassified response released by the kth unit under IQ. Therefore, for each unit in the sample, the pair of responses \((D_k, I_k)\) is collected, \(k=1,\ldots ,n\).

The sample proportion of units responding “Yes” under DQ provides the maximum likelihood and unbiased estimator of \(\pi _{H}\), say:

$$\begin{aligned} {\widehat{\pi }}_H=\frac{1}{n}\sum _{k \in s}D_k, \end{aligned}$$

which has variance \(\mathbb {V}({\widehat{\pi }}_H)={\pi _H(1-\pi _H)/n}\).

An estimator of \(\pi _A\), say \({\widehat{\pi }}_A\) is instead obtained using the response \(I_k\) collected under IQ by assuming that respondents release truthful information and no missing responses occur. In the next section we shall show how the estimator can be obtained by means of certain techniques.

To check whether the IQ approach is worth applying, it is sufficient to test the hypotheses:

$$\begin{aligned} H_0 : \pi _{L} = 0 ~~~~\text {vs}~~~~ H_1 : \pi _{L} > 0. \end{aligned}$$

Clearly, if \({\widehat{\pi }}_{L}\) is an estimator of \(\pi _{L}\), the null hypothesis should be rejected for large values of \({\widehat{\pi }}_{L}\). An unbiased estimator of \(\pi _{L}\) can be obtained from Eq. (1) as:

$$\begin{aligned} {\widehat{\pi }}_{L} = {\widehat{\pi }}_A - {\widehat{\pi }}_{H}, \end{aligned}$$
(2)

whose closed expression depends on the IQT used as alternative to DQ. However, whatever the mechanism used to misclassify the response, the Central Limit Theorem (De Moivre-Laplace Theorem) ensures that, for large sample sizes, \({\widehat{\pi }}_{L}\) has limiting normal distribution. Hence, under the null hypothesis \(H_0\),

$$\begin{aligned} Z=\frac{{\widehat{\pi }}_{L}}{\sqrt{\mathbb {V}({\widehat{\pi }}_{L})}} \sim N(0,1), \end{aligned}$$

where \(\mathbb {V}({\widehat{\pi }}_{L})\) is generally unknown and has to be estimated. If \({\widehat{v}}({\widehat{\pi }}_{L})\) is an estimator of \(\mathbb {V}({\widehat{\pi }}_{L})\), such that \({\widehat{v}}({\widehat{\pi }}_{L}) \rightarrow \mathbb {V}({\widehat{\pi }}_{L})\) as n increases, according to the Slutsky Theorem, it follows that:

$$\begin{aligned} Z=\frac{{\widehat{\pi }}_{L}}{\sqrt{{\widehat{v}}({\widehat{\pi }}_{L})}} \sim N(0,1). \end{aligned}$$
(3)

Let us assume that we test \(H_0\) at the \(\alpha \) level of significance. Then, following the standard procedure we reject the null hypothesis at the \(\alpha \) level when:

$$\begin{aligned} \frac{{\widehat{\pi }}_{L}}{\sqrt{{\widehat{v}}({\widehat{\pi }}_{L})}} \ge z_\alpha , \end{aligned}$$

where \(z_\alpha \) denotes the usual upper \(1-\alpha \) quantile of the standard normal distribution.

Construction of Wald \((1-\alpha )\%\) confidence interval (CI) can be carried out in the usual way. The process leads to the approximate CI:

$$\begin{aligned} {\widehat{\pi }}_L\pm z_{\alpha /2} \sqrt{{\widehat{v}}({\widehat{\pi }}_{L})}. \end{aligned}$$

To conclude, it is worth observing that testing hypothesis and confidence intervals rely on the estimation of \(\mathbb {V}({\widehat{\pi }}_{L})\). Hence, it becomes important to express \(\mathbb {V}({\widehat{\pi }}_{L})\) in such a way that it can be estimated using easy to handle results from sampling theory for finite populations. In the next section, therefore, we will show how the problem can be addressed.

3 Some IQTs and \({\pi }_L\) estimation

Here we introduce some IQTs and show how the estimator of \(\pi _A\) can be obtained for each specific technique under SRSWR. Hence, the estimator of \(\pi _L\) and its variance are derived. For the sake of brevity, a detailed discussion is furnished only for the Warner (1965) since it represents the forerunner of the IQTs.

3.1 The Warner method

The technique proposed by Warner (1965) marked the start of a research field known as randomized response (RR) techniques (RRTs). In the Warner procedure the population under study is ideally divided into two mutually exclusive groups, one with and the other without the sensitive attribute A. Accordingly, each respondent is presented with two statements, \(S_A\) and \({\bar{S}}_A\), where \(S_A\) refers to possessing the sensitive attribute, while \({\bar{S}}_A\) acts as the negation of \(S_A\). Consider, for instance, the situation where the researcher is interested in estimating the prevalence of drug users in the population. In this case, each sampled unit is provided with a physical randomization device (randomizer) determining which of the two following statements has to be answered with a “Yes” or “No” response:

\(S_A\)::

I am a drug user

\({\bar{S}}_A\)::

I am not a drug user

The randomizer that drives the response may be a deck containing two different types of cards marked with the statements \(S_A\) and \({\bar{S}}_A\) in the proportion of p and \(1-p\), respectively, with \(p\ne 0.5\). Respondents are asked to shuffle the deck, randomly select a card from it, read in private the statement written on the card, and give a “Yes” or “No” response as to whether their true status does or doesn’t match the statement on the card. Since respondents are instructed not to reveal to anyone the answered statement, and the inquirer is kept blind about the outcome of the randomizer, the RR procedure enables the respondents to reply without openly revealing if they are drug users or not. Thus, the true status remains uncertain and privacy is protected. Consequently, it is expected that respondents will be more truthful when answering.

We observe that the Warner method can also be practically implemented without the use of any physical randomizer. Hence, the method will be applicable not only to face-to-face interview surveys, but also to self-administered, telephone, mail and web surveys. Moreover, the answering process of a cooperative respondent would always be the same and this guarantees the reproducibility of the results. The idea is to replace the physical device with a non-sensitive unrelated question (e.g., the person’s birthdate). In so doing, the Warner method can easily be converted in a nonrandomized response model with the same mathematical properties. This aspect will be further investigated in Sect. 3.4.1.

According to the notation introduced in Sect. 2, let \(I_k=1\) if the kth respondent releases a “Yes” response after the Warner method has been executed, and \(I_k=0\) in the case of a “No” response. In the following, let us indicate with \(\mathbb {E}_r\) and \(\mathbb {V}_r\) the expectation and variance operators with respect to each discussed IQT.

For the Warner RR model, after simple algebra, we obtain:

$$\begin{aligned} \mathbb {E}_r(I_k)=(2p-1)Y_k+(1-p),~~\forall k \in U, \end{aligned}$$

which yields an estimator of the latent value \(Y_k\) as:

$$\begin{aligned} R_k=\frac{I_k-(1-p)}{2p-1}. \end{aligned}$$

By construction, it is straightforward to prove that \(R_k\) is RR-unbiased for \(Y_k\), i.e. \(\mathbb {E}_r(R_k)=Y_k\), and its variance turns out to be:

$$\begin{aligned} \mathbb {V}_r(R_k)=\frac{\mathbb {E}_r(I_k)(1-\mathbb {E}_r(I_k))}{(2p-1)^2}=\phi _r. \end{aligned}$$

According to the elements introduced before, an unbiased estimator of \(\pi _A\) in SRSWR is obtained as the sample mean of the perturbed response \(R_k\):

$$\begin{aligned} {\widehat{\pi }}_A=\frac{1}{n}\sum _{k \in s}R_k=\frac{1}{n}\sum _{k \in s}\frac{I_k-(1-p)}{2p-1}. \end{aligned}$$
(4)

The variance of \({\widehat{\pi }}_A\) is affected by two sources of variability: one is induced by the randomization device and the other is due to sampling the units from the population. Let \(\mathbb {E}_d\) and \(\mathbb {V}_d\) denote, in general, the expectation and variance operators with respect to the sampling design adopted to select the sample s. Hence, we have:

$$\begin{aligned} \mathbb {V}({\widehat{\pi }}_A)=\mathbb {V}_d\left[ \mathbb {E}_r({\widehat{\pi }}_A)\right] +\mathbb {E}_d \left[ \mathbb {V}_r({\widehat{\pi }}_A)\right] . \end{aligned}$$

Assume now that the sampling design and the randomization stage are independent of each other, and that the randomization stage is performed on each sampled units independently. Then, taking into account basic results from SRSWR, the following result holds:

$$\begin{aligned} \mathbb {V}({\widehat{\pi }}_A)=\frac{\pi _A(1-\pi _A)}{n}+\frac{\phi _r}{n}. \end{aligned}$$

It is worth remarking that \(\mathbb {V}({\widehat{\pi }}_A)\) is a symmetric function on \(p=0.5\). Moreover, note that the first addendum in \(\mathbb {V}({\widehat{\pi }}_A)\) is the variance of the sample proportion of units with the attribute A under DQ. Consequently, the second addendum denotes the amount of variance inflation due to randomizing the response in order to protect respondent privacy. Hence, it clearly emerges that the use of the Warner method, but in general of all the IQTs, produces estimates which are less efficient, in terms of variance and for the same sample size, than DQ estimates: this represents the prize to pay for increasing respondent cooperation. However, it is worth observing that the lesser efficiency of the IQT estimators with respect to DQ is found under ideal conditions, i.e. assuming truthful answering and no missing responses for both the types of questioning designs.

From Eq. (2), the unbiased estimator of \(\pi _L\) follows as:

$$\begin{aligned} {\widehat{\pi }}_{L}= \frac{1}{n}\sum _{k \in s} \left( \frac{I_k}{2p-1} - D_k - \frac{1-p}{2p-1} \right) \equiv \frac{1}{n}\sum _{k \in s}L_k, \end{aligned}$$
(5)

which has variance \(\mathbb {V}({\widehat{\pi }}_{L})=\sigma ^2_L/n\), with \(\sigma ^2_L=\sum _{k \in U}(L_k-{\bar{L}})^2/N\) and \({\bar{L}}=\sum _{k \in U}L_k/N\). We observe that \(\sigma ^2_L\) is itself a population parameter which is unknown and that can be unbiasedly estimated with:

$$\begin{aligned} {\widehat{\sigma }}^2_L=\frac{1}{n-1}\sum _{k \in s}(L_k-{\widehat{\pi }}_{L})^2. \end{aligned}$$
(6)

Accordingly, an unbiased estimator of \(\mathbb {V}({\widehat{\pi }}_{L})\) in SRSWR is obtained as \( {\widehat{v}}({\widehat{\pi }}_{L})={\widehat{\sigma }}^2_L/n\), and the Z-statistic given in Eq. (3) for \(H_0: \pi _L=0\) turns out:

$$\begin{aligned} Z=\frac{\sqrt{n}{\widehat{\pi }}_{L}}{{\widehat{\sigma }}_L}. \end{aligned}$$

3.2 The unrelated question model

The UQM is a variant of the Warner device conceived by Greenberg et al. (1969) to enhance respondent cooperation with the use of an innocuous attribute, say W, unrelated to A and possessed by a proportion \(\pi _W\) of the population. For instance, the innocuous trait may be the survey participant’s birth falling between January and April. Under this RR method, as for Warner, a deck of cards with the following two statements may be used to randomize the response:

\(S_A\)::

I am a drug user

\(S_W\)::

I was born between January and April

The cards are present in the proportion of q and \(1-q\), and the procedure to be implemented works exactly as in Warner. If we assume, therefore, that \(\pi _W\) is known, and using the same notation introduced for Warner, it is readily proved that:

$$\begin{aligned} R_k=\frac{I_k-(1-q)\pi _W}{q} \end{aligned}$$

is the RR-unbiased estimator of \(Y_k\). Consequently,

$$\begin{aligned} {\widehat{\pi }}_A= \frac{1}{n}\sum _{k \in s} \left[ \frac{I_k}{q} - \frac{(1-q)\pi _W }{q} \right] \end{aligned}$$
(7)

and

$$\begin{aligned} {\widehat{\pi }}_{L}= \frac{1}{n}\sum _{k \in s} \left[ \frac{I_k}{q} - D_k - \frac{(1-q)\pi _W }{q} \right] \end{aligned}$$
(8)

are the unbiased estimators of \(\pi _A\) and \(\pi _L\), respectively. Finally, under the UQM, the variance estimation for \({\widehat{\pi }}_{L}\) and the Z-statistic are obtained exactly as for Warner by setting:

$$\begin{aligned} L_k=\frac{I_k}{q} - D_k - \frac{(1-q)\pi _W }{q}. \end{aligned}$$

3.3 The item count technique

The ICT (Raghavarao and Federer 1979; Miller 1984; Wolter and Laier 2014) is an IQT that differs from the RR mechanisms discussed above since, at least in its original formulation, two independent samples are required to estimate the prevalence of the sensitive attribute A in the population. However, many variants of the first proposal can be found in the literature. For instance, Hussain and Shabbir (2010), Petróczi et al. (2011) and Nepusz et al. (2014) considered a version of the ICT using only one sample, while Chaudhuri and Christofides (2013) discussed a version based on three samples.

Without loss of generality, let us consider the two-sample version of the ICT where the first sample, say \(s_1\), is considered as a treatment group and the \(n_1\) units belonging to it are provided with a long list of \((G+1)\) dichotomous items, of which G are nonsensitive, while the remaining one refers to the sensitive attribute A. The sampled units are instructed to count and report the number of items (\(X_1\)) that apply to them (i.e., the number of “Yes” responses) without answering each item individually. Consequently, respondent privacy is protected since the true sensitive status of the respondents remains undisclosed unless they report that none (floor effect) or all (ceiling effect) of the items in the list apply to them. To address the floor and the ceiling effects see, among others, Chaudhuri and Christofides (2007), Blair and Imai (2012), Christofides and Manoli (2020). The second sample, say \(s_2\), identifies a control group of size \(n_2\) whose units are asked to release the number of items (\(X_2\)) that apply to them from a list containing the same G innocuous items included in the long list presented to sample \(s_1\).

The answers given in the two samples are pooled together to obtain the unbiased estimator of \(\pi _A\), which is termed as difference-in-means estimator, and defined as the difference between the means of the total counts in sample \(s_1\) and in sample \(s_2\):

$$\begin{aligned} {\widehat{\pi }}_A=\frac{1}{n_1}\sum _{k \in s_1}X_{1k}-\frac{1}{n_2}\sum _{k \in s_2}X_{2k}. \end{aligned}$$

Let us assume that, in addition to the long list of items, the treatment group receives the direct question on the sensitive attribute. Hence, the proportion \(\pi _L\) of liars is estimated as:

$$\begin{aligned} {\widehat{\pi }}_{L} = \frac{1}{n_1}\sum _{k \in s_1}X_{1k}-\frac{1}{n_2}\sum _{k \in s_2}X_{2k} - \frac{1}{n_1}\sum _{k \in s_1} D_k = \frac{1}{n_1}\sum _{k \in s_1}V_{1k} - \frac{1}{n_2}\sum _{k \in s_2}X_{2k}, \end{aligned}$$
(9)

with \(V_{1k}=X_{1k}-D_k\). If both sample sizes are sufficiently large, it is reasonable to assume that \({\widehat{\pi }}_{L}\) is asymptotically normally distributed. Moreover, since the two samples are independently selected, the variance of \({\widehat{\pi }}_{L}\) is readily obtained as:

$$\begin{aligned} \mathbb {V}({\widehat{\pi }}_{L}) = \frac{\sigma ^2_{V_1}}{n_1} + \frac{\sigma ^2_{X_2}}{n_2}, \end{aligned}$$

which is unbiasedly estimated by:

$$\begin{aligned} {\widehat{v}}({\widehat{\pi }}_{L}) = \frac{{\widehat{\sigma }}^2_{V_1}}{n_1} + \frac{{\widehat{\sigma }}^2_{X_2}}{n_2}, \end{aligned}$$
(10)

where \({\widehat{\sigma }}^2_{V_1}\) and \({\widehat{\sigma }}^2_{X_2}\) can be easily computed similarly to Eq. (6). Then, again using the Slutsky Theorem, we conclude that:

$$\begin{aligned} Z=\frac{{\widehat{\pi }}_{L}}{\sqrt{\dfrac{{\widehat{\sigma }}^2_{V_1}}{n_1} + \dfrac{{\widehat{\sigma }}^2_{X_2}}{n_2}}} \sim N(0,1). \end{aligned}$$

3.4 The nonrandomized approach

The Warner method and the UQM discussed above, as well as the other mechanisms grouped under the RRT category, suffer from some inadequacies that can limit their use in real surveys. One major undesirable feature of the RRTs consists in the lack of reproducibility due to the fact that, in principle, the methods can be executed mostly through the use a physical device (deck of cards, spinner, box with numbered/colored balls, etc.) that randomizes the response. Since the responses released by the interviewees depend on the outcome of the randomizer, the same survey participant, if asked to run a second trial and assuming truthful responses, will respond in a different way in the case the outcome produced is different from that in the first trial. Moreover, the use of an external device makes it impossible, in the first place, to use RRTs in data-collection modes other than face-to-face interviews. To overcome problems related to the use of physical devices, nonrandomized response techniques (NRRTs) may be employed (see, e.g., Tian and Tang 2014). The NRRTs offer a simplified assessment of the prevalence of sensitive attributes and guarantee the same confidentiality as RRTs without the need for any external randomizing device.

Without loss of generality, to implement NRR models it is just necessary to introduce a binary variable W associated with a nonsensitive question and independent of the sensitive variable Y, with \(W=1\) denoting the possessing of the innocuous attribute, \(W=0\) otherwise. The nonsensitive attribute should be chosen in such a way that the probability \(\pi _W=\text {Pr}(W=1)\) is either known in advance or can be easily estimated. For instance, as for the UQM, we can define \(W=1\) if a respondent was born between January and April. Hence, it is reasonable to assume \(\pi _W\approx 4/12=0.333\).

In the next two sections we will discuss two NRRTs, the crosswise model and the triangular model.

3.4.1 The crosswise model

Sometimes it is possible to transform a randomized response model into an equivalent NRR one. For instance, the nonrandomized version of the Warner model is the so-called crosswise model (CWM) introduced by Yu et al. (2008). See also, Jann et al. (2012), Korndörfer et al. (2014), Hoffmann et al. (2015), Hoffmann and Musch (2016), Höglinger et al. (2016).

According to the CWM, respondents are presented with the question about the sensitive attribute (Y) and with a question about a nonsensitive matter (W), for example whether their birthday is between January and April. Then, they are asked whether the answer to the two questions is the same (both “Yes” or both “No”) or the answer to the two questions is different. To understand how the method works in practice, assume that a mail questionnaire is used for the survey. Then, information on the sensitive attribute Y can be obtained by including in the questionnaire a tabular form like the one presented in Table 1. According to the CWM, respondents are instructed to release a response by putting a tick in \(\bigcirc \) in the response cell marked R1 if they belong to the subclass of population units with \(\left\{ Y=0, W=0\right\} \cup \left\{ Y=1, W=1\right\} \) (same answer to both the sensitive and nonsensitive questions), or a tick in \(\square \) in the response cell marked R2 if they belong to the subclass \(\left\{ Y=0, W=1\right\} \cup \left\{ Y=1, W=0\right\} \) (different answers).

Under the CWM, since it is mathematically equivalent to the Warner model for \(p=\text {Pr}(W=1)=\pi _W\), the estimators of \(\pi _A\) and \(\pi _L\) are given as in Eqs. (4) and (5) by setting \(I_k=1\) if the kth respondent puts a tick in the response cell R1 (\(\bigcirc \)).

Table 1 Tabular form for the crosswise model
Full size table

3.4.2 The triangular model

Despite the fashion for the NRR approach, the CWM is characterized by the same efficiency as the Warner model. Improvements upon it can be achieved through the triangular model (TM; Yu et al. 2008) which, with the same setting of the CWM, can be described in the tabular form shown in Table 2. Similarly, respondents are instructed to release a response by putting a tick in \(\square \) in the response cell marked R1 if they belong to the subclass of population units with \(\left\{ Y=0, W=0\right\} \), or a tick in \(\bigcirc \) in the response cell marked R2 if they belong to the subclass \(\left\{ Y=0, W=1\right\} \cup \left\{ Y=1, W=0\right\} \cup \left\{ Y=1, W=1\right\} \). Hence, if \(I_k=1\) denotes a tick by the kth respondent in the response cells R2 (\(\bigcirc \)), the estimators of \(\pi _A\) is obtained as:

$$\begin{aligned} {\widehat{\pi }}_A=\frac{1}{n}\sum _{k \in s}\frac{I_k-\pi _W}{1-\pi _W}, \end{aligned}$$
(11)

from which it follows that:

$$\begin{aligned} {\widehat{\pi }}_{L}= \frac{1}{n}\sum _{k \in s} \left( \frac{I_k}{1-\pi _W} - D_k - \frac{\pi _W}{1-\pi _W} \right) . \end{aligned}$$
(12)

Variance estimation for \({\widehat{\pi }}_{L}\) can is easily achieved as in Eq. (6) by setting:

$$\begin{aligned} L_k=\frac{I_k}{1-\pi _W} - D_k - \frac{\pi _W}{1-\pi _W}. \end{aligned}$$
Table 2 Tabular form for the triangular model
Full size table

4 Estimation under a general sampling design

Barabesi (2008) proposed a general sampling design-based approach to RR surveys for the joint estimation of the proportion of individuals in the population bearing a sensitive attribute and the proportion of individuals in the sensitive group divulging truthfully their status. In this section, following a different approach, we extend the results derived in Sect. 3 for SRSWR by setting the theoretical framework for estimating \(\pi _A\), \(\pi _H\) and \(\pi _L\) under a general sampling design. In so doing, with the same notation as in Sect. 2, let us assume that a sample s of n units is selected without replacement from the finite population \(P=\left\{ 1,\dots ,N\right\} \) according to a general sampling design p(s) which admits positive first and second-order inclusion probabilities, say \(\omega _k=\sum _{s \ni k}p(s)\) and \(\omega _{kl}=\sum _{s \ni k,l}p(s)\) with \(k,l \in P\). Under DQ, the estimation of \(\pi _H\) can be achieved through the customary Horvitz-Thompson (HT) estimator (Horvitz and Thompson 1952):

$$\begin{aligned} {\widehat{\pi }}^*_H=\frac{1}{N}\sum _{k \in s} \frac{D_k}{\omega _k}, \end{aligned}$$

which is design-unbiased for \(\pi _H\) and has variance:

$$\begin{aligned} \mathbb {V}({\widehat{\pi }}^*_H)=\frac{1}{N^2} \sum _{k \in U} \sum _{l>k\in U} \left( \frac{D_k}{\omega _k}-\frac{D_l}{\omega _l}\right) ^2(\omega _k \omega _l-\omega _{kl}), \end{aligned}$$

which is itself unknown and can be unbiasedly estimated by:

$$\begin{aligned} {\widehat{v}}({\widehat{\pi }}^*_H)=\frac{1}{N^2} \sum _{k \in s} \sum _{l>k \in s} \left( \frac{D_k}{\omega _k}-\frac{D_l}{\omega _l}\right) ^2\left( \frac{\omega _k \omega _l}{\omega _{kl}}-1\right) . \end{aligned}$$
(13)

Using the HT estimator, it is straightforward to derive the estimators for \(\pi _A\) and \(\pi _L\) under the IQTs discussed in the previous sections. Without loss of generality, and using the notation introduced in Sect. 3, the unbiased HT-type estimators for \(\pi _A\) and \(\pi _L\) turn out, respectively:

$$\begin{aligned} {\widehat{\pi }}^*_A=\frac{1}{N}\sum _{k \in s} \frac{R_k}{\omega _k}\quad \text {and}\quad {\widehat{\pi }}^*_L=\frac{1}{N}\sum _{k \in s} \frac{L_k}{\omega _k}, \end{aligned}$$

where:

$$\begin{aligned} R_k = \left\{ \begin{array}{ll} \dfrac{I_k-(1-p)}{2p-1}, &{} \text {for Warner/CWM} \\ \dfrac{I_k-(1-q)\pi _W}{q}, &{} \text {for UQM } \\ \dfrac{I_k-\pi _W}{1-\pi _W}, &{} \text {for TM }\\ \end{array}\right. , \end{aligned}$$

and

$$\begin{aligned} L_k = \left\{ \begin{array}{ll} \dfrac{I_k}{2p-1}-D_k-\dfrac{1-p}{2p-1}, &{} \text {for Warner/CWM} \\ \dfrac{I_k}{q}-D_k-\dfrac{(1-q)\pi _W}{q}, &{} \text {for UQM }\\ \dfrac{I_k}{1-\pi _W}-D_k-\dfrac{\pi _W}{1-\pi _W}, &{} \text {for TM}. \\ \end{array}\right. . \end{aligned}$$

Finally, similarly to Eq. (13), the variance of \({\widehat{\pi }}^*_L\) can be unbiasedly estimated by:

$$\begin{aligned} {\widehat{v}}({\widehat{\pi }}^*_L)=\frac{1}{N^2} \sum _{k \in s} \sum _{l>k \in s} \left( \frac{L_k}{\omega _k}-\frac{L_l}{\omega _l}\right) ^2 \left( \frac{\omega _k \omega _l}{\omega _{kl}}-1\right) . \end{aligned}$$

Under the ICT, the unbiased HT-type estimator for \(\pi _A\) is given by:

$$\begin{aligned} {\widehat{\pi }}_A^*=\frac{1}{N}\sum _{k \in s_1}\frac{X_{1k}}{\omega _k}-\frac{1}{N}\sum _{k \in s_2}\frac{X_{2k}}{\omega _k}, \end{aligned}$$

while \(\pi _L\) can be estimated with:

$$\begin{aligned} {\widehat{\pi }}^*_L=\frac{1}{N}\sum _{k \in s_1}\frac{V_{1k}}{\omega _k}-\frac{1}{N}\sum _{k \in s_2}\frac{X_{2k}}{\omega _k}. \end{aligned}$$

Since the two samples \(s_1\) and \(s_2\) are independently selected, the variance of \({\widehat{\pi }}^*_L\) is unbiasedly estimated by:

$$\begin{aligned} {\widehat{v}}({\widehat{\pi }}^*_L)= & {} \frac{1}{N^2} \sum _{k \in s_1} \sum _{l>k \in s_1} \left( \frac{V_k}{\omega _k}-\frac{V_l}{\omega _l}\right) ^2 \left( \frac{\omega _k \omega _l}{\omega _{kl}}-1\right) \\+ & {} \frac{1}{N^2} \sum _{k \in s_2} \sum _{l>k \in s_2} \left( \frac{X_{2k}}{\omega _k}-\frac{X_{2l}}{\omega _l}\right) ^2\left( \frac{\omega _k \omega _l}{\omega _{kl}}-1\right) . \end{aligned}$$

5 Numerical assessment

In this section, we evaluate the effectiveness of the proposed method on the basis of a number of some simulation experiments for the Warner method/CWM, the UQM, the TM, the ICT, and two real surveys which produced DQ, CWM and TM data.

5.1 Simulation

In the simulation study, different scenarios are considered to test the presence of liars in a sample where a part of the units possess the sensitive attribute A. The presence and the amount of untruthful answers is ascertained under the Warner method/CWM, the UQM, the TM and the ICT for some fixed values of \(\pi _A\) and \(\pi _H\). The simulation is run separately for each of different IQTs and produces as outcome the estimates \({\widehat{\pi }}_A\), \({\widehat{\pi }}_H\) and \({\widehat{\pi }}_L\), and the confidence interval for \(\pi _L\) computed over a large number of replications.

In the following, we briefly report the description of the algorithm implemented in the R software to get simulation findings (the code is available on request from the authors). It is worth observing that for the Warner method and the UQM the procedure is almost identical, while since the CWM is equivalent to Warner its description will not be reported. For brevity, therefore, we only illustrate in details the steps of the simulation design for the Warner method which reproduces honest DQ and perturbed responses. Hence we proceed with the ICT.

5.1.1 Warner method simulation design

\(\textit{Step 1}\!\!:\) :

Generate a Bernoulli sample of size n, \(s=(Y_1,\ldots ,Y_n)\), with \(Y_k\sim {{\mathcal {B}}}(\pi _A)\) and \(\pi _A\) denoting the prevalence of population units with the sensitive attribute A, \(k=1,\ldots ,n\);

\(\textit{ Step 2}\!\!:\) :

To each unit in s bearing the sensitive attribute, i.e. \(Y_k=1\), randomly assign the status of truthful (\(D_k=1\)) or untruthful respondent (\(D_k=0\)) under DQ. The value of \(D_k\) is obtained as \(D_k=Y_k{{\mathcal {B}}}(\theta )\), where \(\theta =\pi _H/\pi _A\) is the conditional probability of being honest given the sensitive attribute;

\(\textit{Step 3}\!\!:\) :

Obtain the honest DQ estimate of \(\pi _H\) as \({\widehat{\pi }}_H=\sum _{k \in s}D_k/n\);

\(\textit{Step 4}\!\!:\) :

Fix the design parameter p, perturb the values \(Y_k\) according to the Warner method and obtain \(I_k\). Hence, compute the estimates of \(\pi _A\) and \(\pi _L\) according to Eqs. (4) and (5);

\(\textit{Step 5}\!\!:\) :

Compute \({\widehat{\sigma }}^2_L\) according to Eq. (6), and then the \((1-\alpha )\%\) CI for \(\pi _L\);

\(\textit{Step 6}\!\!:\) :

Repeat B times Steps 1-5 and average the outcomes over the B replications.

5.1.2 UQM simulation design

For the UQM, the algorithm is nearly the same as the Warner one with the only difference being in Step 4 where the design parameters q and \(\pi _W\) are settled and the responses \(I_k\) are generated as reported in Sect. 3.2. Furthermore, Eqs. (7) and (8) are used to obtain the estimates of \(\pi _A\) and \(\pi _L\).

5.1.3 TM simulation design

The algorithm mimics the previous ones. In Step 4, the parameter \(\pi _W\) is settled and responses \(I_k\) are generated according to the description reported in Sect. 3.4.2. Further, Eqs. (11) and (12) are used to obtain the estimates of \(\pi _A\) and \(\pi _L\).

5.1.4 ICT simulation design

\(\textit{Step 1}\!\!:\):

Fix \(n_1\) and \(n_2\), with \(n_1>n_2\) to compensate for the extra variability in the responses produced by the presence of the sensitive item in the long list;

\(\textit{Step 2}\!\!:\):

Generate a Bernoulli sample of size \(n_1\), \(s=(Y_1,\ldots ,Y_{n_1})\), with \(Y_k\sim {{\mathcal {B}}}(\pi _A)\) and \(\pi _A\) denoting the prevalence of population units with the sensitive attribute A, \(k=1,\ldots ,n_1\);

\(\textit{Step 3}\!\!:\):

To each unit in \(s_1\) bearing the sensitive attribute, i.e. \(Y_k=1\), apply Steps 2 and 3 of the simulation described for the Warner method.

\(\textit{Step 4}\!\!:\):

Fix G and assign a value for the prevalence \(\pi _g\) of each of the G innocuous and independent traits, \(g=1,\ldots ,G\);

\(\textit{Step 5}\!\!:\):

For the treatment sample \(s_1\), for each \(k \in s_1\), generate \(U_{1k}=(W_{11,k},\ldots ,W_{1G,k}, Y_k)\), where \(W_{1g,k}\sim {{\mathcal {B}}}(\pi _g)\), \(g=1,\ldots ,G\), while \(Y_k\) stems from Step 2. Similarly, for the control sample \(s_2\), for each \(k \in s_2\), generate \(U_{2k}=(W_{21,k},\ldots ,W_{2G,k})\) where \(W_{2g,k}\sim {{\mathcal {B}}}(\pi _g)\);

\(\textit{Step 6}\!\!:\):

Compute \(X_{1k}=\sum _{g=1}^G W_{1g,k}+Y_k\) and \(X_{2k}=\sum _{g=1}^G W_{2g,k}\), then calculate \({\widehat{\pi }}_L\) and \({\widehat{v}}({\widehat{\pi }}_L)\) according to Eqs. (9) and (10). Finally, obtain \((1-\alpha )\%\) CI for \(\pi _L\);

\(\textit{Step 7}\!\!:\):

Repeat B times Steps 2-6 and average the outcomes over the B replications.

All the simulation experiments are performed assuming the following settings: \(\pi _A=\left\{ 0.35, 0.30, 0.25\right\} \); \(\pi _H=0.1\); \(\pi _W=0.30\) for the UQM, CWM and TM; \(q=0.7\) for the UQM; \(n=1000\), \(n_1=800\) and \(n_2=500\); \(G=5\) and prevalence for the five innocuous attribute \(\pi _g=a+(g-1)\times 0.05\) with \(a=\left\{ 0.1, 0.3\right\} \) and \(g=1,\ldots ,5\); \(\alpha =0.05\); \(B=10{,}000\). As mentioned in Sect. 3.4.1, the CWM is equivalent to the Warner method by setting \(p=\pi _W\); moreover due to the symmetry of the variance of the Warner model, the same efficiency is achieved with \(p=1-\pi _W=0.7\). Note, however, that the choice \(p=q=0.7\) doesn’t ensure that the privacy of the respondents is equally protected under the Warner model and the UQM. In general, the evaluation of the efficiency of the estimates (in terms of variance or confidence interval) is not fair because it is done under different levels of privacy protection. It is worth remarking that efficiency and privacy protection are two discordant aspects that characterize the IQTs, meaning that the higher the privacy protection, the lower the efficiency (and vice versa). Finally, we observe that the true values for \(\pi _A\) are not set too close to zero to avoid incurring in negative estimates.

For each of the IQTs considered, Table 3 reports the following outcomes of the simulation: the estimates \({\widehat{\pi }}_A\), \({\widehat{\pi }}_H\) and \({\widehat{\pi }}_L\); the \(95\%\) CI for \(\pi _L\) and its length (L); the p-value of the Jarque-Bera (JB) normality test for the distribution of the estimates over the 10, 000 simulation experiments.

Simulation findings well emphasize the capability of the IQTs to detect the presence of untruthful answers and yield higher (more accurate) estimates than DQ ones. Under all the methods, the estimates of \(\pi _L\) averaged on the 10, 000 trials are statistically significant and nearly identical to the true proportion of liars who are subjected to DQ. The normality of the sampling distribution of the estimates cannot be rejected due to the large p-values for the JB test. The same holds for \({\widehat{\pi }}_A\) and \({\widehat{\pi }}_H\). Therefore, on the basis of the simulated experiments, which underscore a good performance of the estimates, we are confident that the effectiveness of the IQTs to provide accurate estimates of the prevalence of a sensitive trait can also hold in real situations.

Incidentally, the simulation results also appear useful to compare the performance of the Warner method/CWM, the UQM, the TM and the ICT. At least for the setting of design parameters considered in the study, and looking at the length of the CI, it seems that the ICT performs the worst, while the UQM and the TM outperform the other competitive methods.

Table 3 Point, interval and JB normality test for the estimates of \(\pi _A\), \(\pi _H\) and \(\pi _L\) under Warner/CWM, UQM, TM and ICT; \(\pi _H=0.10\)
Full size table

5.2 Real data

Using the CWM and the TM, two distinct sensitive topics have been investigated: racism among students and workplace mobbing. In this section, we discuss the design used to collect the data, show the estimates for the prevalence of the sensitive attributes under study and evaluate the impact of the liars on the reliability of the final results.

5.2.1 Racism

In 2016, data were collected to investigate the problem of racism among students at the University of Calabria, Italy. The problem was raised by some foreign students who, having met difficulties to integrate themselves in the community, felt a climate of marginalization around them. A snowball sample of Italian and foreign students was recruited using personal contacts and social networks (Facebook, Instagram and WhatsApp), and the contacted students were invited to fill in an online questionnaire. At the end of the period scheduled for the data-collection fieldwork, 624 questionnaires were collected of which 55 (\(8.8\%\)) with nonresponse about DQ1 and/or DQ2. The 55 incomplete questionnaires were discarded and only the remaining 569 students who fully completed the survey were considered in the analysis. The questionnaire contained general items on the everyday life of the students, their studies and contacts/collaboration with students of different races or ethnic groups. Beside these, the following two direct questions on racism (DQ1 and DQ2) where placed in the middle and at the end of the questionnaire:

  • \({{\textit{DQ1: }}}\)Usually, do you have any negative attitudes towards other races or ethnic groups?

  • \({{\textit{DQ2: }}}\)Do you feel racist against people other than your race or ethnicity?

We note that the meaning of both the questions is nearly the same, but DQ2 contains the word “racist” which should induce the respondents to feel this question to be more stigmatizing and, thus, procure more underreporting than DQ1. Both the questions were deliberately included in the questionnaire to test the effect of the different level of sensitivity on the response pattern. This aspect is confirmed by the proportions of “Yes” responses for the two questions reported in Table 4: 17.8% for DQ1 vs 12.5% for DQ2.

Table 4 Distribution of the responses about racism by questions DQ1 and DQ2
Full size table

The crosswise and the triangular experiments were placed in a specific section at the end of the questionnaire, and the participant’s month of birth was used as the randomizer. At the beginning of the section the respondents were given the following instruction: “Please, read carefully the four statements indicated below and find the one that reflects your status with respect to your birthday and racism”:

\(\textit{A:}\):

My birthday is between October and December and I am a racist

\(\textit{B:}\):

My birthday is between January and September and I am a racist

\(\textit{C:}\):

My birthday is between October and December and I am not a racist

\(\textit{D:}\):

My birthday is between January and September and I am not a racist

Note that the order of the statements was fixed and didn’t chance across the respondents. After reading the four statements, respondents were asked to run firstly the CWM and then the TM complying with the following rules:

Crosswise model

  • If your status fits statement A or D, please put a tick here \(\bigcirc \)

  • If your status fits statement B or C, please put a tick here \(\square \)

Triangular model

  • If your status fits statement A, B or C, please put a tick here \(\bigcirc \)

  • If your status fits statement D, please put a tick here \(\square \)

With the notation introduced in Sects. 3.4.1 and 3.4.2, a tick in \(\bigcirc \) put by the kth respondent was coded as \(I_k=1\) in the estimation procedure. Moreover, we considered \(W=1\) if the respondent was born between October and December and, hence, we assumed \(\pi _W\approx 3/12=0.25\).

Testing the presence of liars for DQ1 and DQ2 under the CWM and the TM yields the results summarized in Table 5. The two NRRTs provide higher prevalence estimates (\({\widehat{\pi }}_A\)) for racism than under DQ (see Table 4). Across the two methods, and according to the “more-is-better assumption”, not surprisingly the improvement over direct questions is better for DQ2 which, being a more sensitive question, generates much more underreporting of the stigmatizing attribute. For DQ2, the significative presence of liars under DQ is ascertained by both the CWM (\({\widehat{\pi }}_{L_2}=0.092\)) and the TM (\({\widehat{\pi }}_{L_2}=0.144\)). Note that, based only on data collected by DQ, the estimates of \(\pi _A\) is \({\widehat{\pi }}_{H}=0.125\), a value much more lower than CWM and TM estimates. As regards DQ1, the presence of liars doesn’t appear to be significant under the CWM (\({\widehat{\pi }}_{L_1}=0.04\)), but it is under the TM (\({\widehat{\pi }}_{L_1}=0.091\)). The TM appears to be an effective way to collect sensitive data and its benefits are evident.

Table 5 Results for the CWM and the TM
Full size table

5.3 Workplace mobbing

In this second real research, the phenomenon of workplace mobbing has been studied among employees in a call center (68.04%), in two large-scale retail stores (17.53%) and in an agri-food company (14.43%). Survey participants, after the authorization released by the employers, were invited to fill in a paper-and-pencil questionnaire including, among 73 questions, a sensitive question on mobbing and a final section for the TM. More specifically, the employees were asked to answer the following sensitive question:

Have you ever been mobbed in the workplace?

admitting 5 response categories:

$$\begin{aligned} \square \; \textit{never} \qquad \square \; \textit{rarely} \qquad \square \; \textit{sometimes} \qquad \square \;\textit{often} \qquad \square \; \textit{always} \end{aligned}$$

It is worth observing that the question and the number/type of response categories were agreed with the employers who firmily refused to admit the binary responses “Yes” and “No”.

To implement the TM, as for the previous study, the survey participants, after reading the following four statements:

\(\textit{A:}\):

I was born between January and July and I have never been mobbed in the workplace

\(\textit{B:}\):

I was born between August and December and I have never been mobbed in the workplace

\(\textit{C:}\):

I was born between January and July and I have been mobbed at least once in the workplace

\(\textit{D:}\):

I was born between August and December and I have been mobbed at least once in the workplace

released their responses according to the following rule:

  • If your status fits statement B, C or D, please put a tick here \(\bigcirc \)

  • If your status fits statement A, please put a tick here \(\square \)

At the end of the survey, data were collected on a sample of 679 employees of which 8 (1.17%) didn’t answer the direct sensitive question, 3 (0.44%) neither answered the sensitive questions nor performed the TM, and 54 (7.95%) didn’t run the TM at all or failed it in the sense that they didn’t put any tick in \(\bigcirc \) or \(\square \), or put a tick both in \(\bigcirc \) and \(\square \), or marked one or more letters. Missing cases for the two data-collection modes were therefore discarded from the final analysis that is, therefore, based on a sample of 614 respondents. The distribution of the responses to the direct sensitive question is shown in Table 6.

Setting \(I_k=1\) if the kth respondent put a tick in \(\bigcirc \), and assuming \(\pi _W\approx 5/12=0.417\), the percentage prevalence of employees who suffered from mobbing was estimated at \({\widehat{\pi }}_A=11.44\%\) using the TM. We observe that the obtained estimate is always higher than the proportion of the response categories rarely (9.61%), sometimes (7%), often (1.63%) and always (0.98%) under DQ.

Table 6 Distribution of the responses for the frequency of mobbing acts
Full size table
Table 7 Results for three aggregation scenarios of the DQ multichotomous response
Full size table

The evaluation of the effectiveness of the TM through the ascertainment of the significant presence of liars is not so straightforward as in the previous study on racism since the direct question requires a multichotomous response rather than a binary one. Hence, it is somehow necessary to adapt the method introduced in Sect. 2 by merging, for instance, the five response categories in two responses in such a way to symbolize the response of the kth respondent with \(D_k=\left\{ 0,1\right\} \). In so doing, we considered three possibilities:

Case 1::

We set \(D_k=1\) if the response of the kth respondent is \(\left\{ \textit{rarely, sometimes,}\right. \left. { often, always}\right\} \) and \(D_k=0\) if it is \(\left\{ \textit{never}\right\} \);

Case 2::

We set \(D_k=1\) if the response of the kth respondent is \(\left\{ \textit{often, always}\right\} \) and \(D_k=0\) if it is \(\left\{ \textit{never, rarely}\right\} \). Respondents who answered \(\left\{ \textit{sometimes}\right\} \) to the direct question were removed from the sample and the analysis performed on \(n=571\) survey participants;

Case 3::

We set \(D_k=1\) if the response of the kth respondent is \(\left\{ \textit{always}\right\} \) and \(D_k=0\) if it is \(\left\{ \textit{never}\right\} \). Respondents who answered \(\left\{ \textit{rarely, sometimes, often}\right\} \) to the direct question were removed from the sample and the analysis performed on \(n=502\) survey participants.

Results are reported in Table 7. Unsurprisingly, the findings don’t allow us to draw definitive conclusions on the effectiveness of the TM. This is probably because the DQ doesn’t admit a binary response and the response categories have been aggregated differently. In particular, we observe that the estimate of \(\pi _L\) under the aggregation described for the Case 1 is unfeasible since it falls outside the unit interval [0, 1]. For Case 2 and 3, the presence of liars appears significant at the \(5\%\) level of significance. In these two situations, although the empirical evidence is not so striking, we may be confident that the TM is worth applying and can produce estimates of mobbed employees (about \(73\%\)) more realistic than the \(66\%\) from DQ, say the percentage estimate \({\widehat{\pi }}_H\) obtained form Eq. (2) as \({\widehat{\pi }}_A-{\widehat{\pi }}_L\).

6 Conclusions

One of the main concerns for researchers involved in surveys about confidential, stigmatizing or embarrassing topics is the undesirable collection of unreliable data produced by untruthful responses. Limiting the impact of liars, and obtaining accurate estimates of salient characteristics of the population under study, are important issues in survey practice which need to be adequately addressed.

In this paper, we have discussed the use of indirect questioning survey modes as a tool to enhance respondent confidentiality and detect the presence of liars among survey participants when direct questions about sensitive topics are posed. In particular, we have introduced a general framework to estimate the proportion of liars and the prevalence of a sensitive attribute in the surveyed population, thereby deriving operational results for a number of indirect questioning techniques, say the Warner randomized response method, the UQM, the crosswise model, the triangular model and the ICT. Through a number of simulation experiments, we have assessed the effectiveness of these techniques for obtaining reliable and accurate estimates of the proportion of carriers of a sensitive attribute. Furthermore, when combined with truthful responses to direct questions, the techniques allow the researchers to efficiently estimate the amount of liars present in sensitive surveys administered with traditional direct questioning data-collection modes. Finally, the procedure to test the presence of liars has been applied in two real surveys with data collected with both direct and indirect questions. In particular, the crosswise and triangular models have been practically implemented to investigate racism among university students, and the triangular model to survey workplace mobbing among employees.

Results for racism study confirm our expectations. First, the higher the degree of sensitivity of the question, the greater the tendency of respondents to lie by providing responses which comply with social desirability. Second, the proposed testing procedure seems to be able to detect a significant proportion of liars.

Results and conclusions for the mobbing study need to be handled with care. In fact, the questionnaire administered to the employees includes a direct sensitive question on mobbing with five response categories, while our procedure is conceived for a binary response (“Yes” or “No”). Therefore, in order to apply the procedure, we have forced the responses by differently aggregating the five response categories in two categories referable to having suffered or not mobbing. Not surprisingly, the conclusions about the estimates for the proportion of mobbed employees and liars depend on the aggregation of the response categories. In two of the three aggregations, there is sufficient empirical evidence that supports a significant presence of liars.

Stimulated by the encouraging results in this work, we hope that researchers working in different fields can consider the possibility of adopting indirect questioning techniques when doing sensitive research. Methodological advances are also desirable since some points remain beyond the reach of our analysis. For instance, for future research, it would be worth exploiting the effectiveness of the discussed methods under a wide variety of complex sampling designs. Furthermore, it would also be of interest to extend the approach to situations where multicategorical sensitive variables are surveyed and auxiliary information may be available (see, e.g., Rueda et al. 2021).