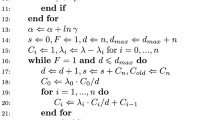Abstract
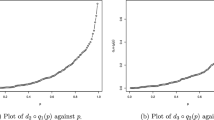
Recurrent competing risks data are common in survival studies. In such contexts the effects of competing risks on lifetime outcomes are important problem of study. In this work we introduce recurrent cumulative incidence function and then propose a non-parametric test for comparing recurrent cumulative incidence functions. Asymptotic distribution of the test statistic is derived. A simulation study is carried out to assess the performance of the proposed test statistic. The proposed method is applied to an auto-mobile warranty data.


Similar content being viewed by others
References
Andersen, P.K., Gill, R.D.: Cox’s regression model for counting processes: a large sample study. Ann. Stat. 10(4), 1100–1120 (1982)
Cook, R.J., Lawless, J.F., Nadeau, C.: Robust tests for treatment comparisons based on recurrent event responses. Biometrics 52(2), 557–571 (1996)
Dauxois, J.Y., Sencey, S.: Non-parametric tests for recurrent events under competing risks. Scand. J. Stat. 36(4), 649–670 (2009)
Dong, H., Robison, L.L., Leisenring, W.M., Martin, L.J., Armstrong, G.T., Yasui, Y.: Estimating the burden of recurrent events in the presence of competing risks: the method of mean cumulative count. Am. J. Epidemiol. 181(7), 532–540 (2015)
Ghosh, D.: Accelerated rates regression models for recurrent failure time data. Lifetime Data Anal. 10(3), 247–261 (2004)
Gouskova, N.A., Lin, F.C., Fine, J.P.: Nonparametric analysis of competing risks data with event category missing at random. Biometrics 73(1), 104–113 (2017)
Hyun, S., Sun, Y., Sundaram, R.: Assessing cumulative incidence functions under the semiparametric additive risk model. Stat. Med. 28(22), 2748–2768 (2009)
Lawless, J.F., Nadeau, C.: Some simple robust methods for the analysis of recurrent events. Technometrics 37(2), 158–168 (1995)
Lin, D.: Non-parametric inference for cumulative incidence functions in competing risks studies. Stat. Med. 16(8), 901–910 (1997)
Lin, D., Wei, L., Ying, Z.: Accelerated failure time models for counting processes. Biometrika 85(3), 605–618 (1998)
Lin, D.Y., Wei, L.J., Yang, I., Ying, Z.: Semiparametric regression for the mean and rate functions of recurrent events. J. R. Stat. Soc. Ser. B 62(4), 711–730 (2000)
Pepe, M.S., Cai, J.: Some graphical displays and marginal regression analyses for recurrent failure times and time dependent covariates. J. Am. Stat. Assoc. 88(423), 811–820 (1993)
Sankaran, P., Anisha, P.: Shared frailty model for recurrent event data with multiple causes. J. Appl. Stat. 38(12), 2859–2868 (2011)
Sankaran, P., Anisha, P.: Additive hazards models for gap time data with multiple causes. Stat. Prob. Lett. 82(7), 1454–1462 (2012)
Somboonsavatdee, A., Sen, A.: Parametric inference for multiple repairable systems under dependent competing risks. Appl. Stochastic Models Bus. Ind. 31(5), 706–720 (2015)
Taylor, L.L., Pena, E.A.: Parametric estimation in a recurrent competing risks model. J. Iran. Stat. Soc. 12(1), 153 (2013)
Taylor, L.L., Pena, E.A.: Nonparametric estimation with recurrent competing risks data. Lifetime Data Anal. 20(4), 514–537 (2014)
Wang, M.C., Chang, S.H.: Nonparametric estimation of a recurrent survival function. J. Am. Stat. Assoc. 94(445), 146–153 (1999)
Acknowledgements
The authors are grateful to the referees and editor for their constructive comments. The first author thanks INSPIRE, Department of Science and Technology, Government of India for providing financial support. The second author thanks KSCSTE, Government of Kerala for providing financial support.
Author information
Authors and Affiliations
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Theorem 2.1
To find the asymptotic distribution of the test statistic \(Z(\tau )\), first consider the quantity
After adding and subtracting \(\int _{0}^{t} w(u)dF_{l}(u)+ \int _{0}^{t} w(u)\frac{dF(u)}{k}\), (A-1) can be modified as,
under \(H_0\), \(F_l(t)=\frac{F(t)}{k}\). Then second term in the (A-2) becomes zero. Then
It can be shown that the difference between \({\hat{F}}_l(t)\) and \(F_{l}(t)\) can be approximated by the sum of independent and identically distributed random variables. For this we need to prove that
This can be shown by the similar method used in the Wang and Chang [18]. Note that
We can shown that \({\hat{F}}_{l}(t)-F_{l}(t)\) is sum of inedependent and identically distributed random varibles by applying (A-4) in (A-5) and following the techniques used in Hyun et al. [7]. Then,
where \(\epsilon _{li}(t)=\int _{0}^{t}[\sum _{l=1}^{k}F^{c}_{l}(t,u)+S(u)]\psi _{il}(u)\) and \(F^{c}_{l}(t,u)=F_{l}(t)-F_{l}(u)\). For fixed t, \(\epsilon _{li}(t)\) are independent and identically distributed mean zero random variables and \(\sqrt{n}({\hat{F}}_l(t)-F_l(t))\) follows a mean zero Gaussian process with variance \(\sigma ^{2}_{l}(t)=E(\epsilon _{li}(t))^{2}\) and variance-covariance function \(\sigma _l(t_1,t_2)=E[\epsilon _{li}(t_1)\epsilon _{li}(t_2)],l=1,2,...,k.\)
From Wang and Chang [18], we can shown that the \({\hat{F}}(t)-F(t)\) is a sum of independent and identically distributed random variables.
where \(\phi _i(t)=\int _{0}^{t}\{H_a(u)\}^{-2}\{\frac{a_i}{m^{*}_{i}}\sum _{j=1}^{m^{*}_{i}} I(y_{ij}\ge u )\}dG_a(u)-\frac{a_iI(m_i\ge 2)}{m^{*}_{i}}\sum _{j=1}^{m^{*}_{i}}\frac{1}{H_a(y_{ij})}I(y_{ij} <t)\).
The random variables \(S(t)\phi _{i}(t)\) are uniformly bounded in \(0 \le t \le t^{*}\) when \(a_{i}\) is bounded by a constant, where \(t^{*}\) is a non negative constant satisfying \(t^{*} < sup \{ t: S(t)G(t) >0\}\). Then by the multivariate central limit theorem, the finite dimensional distributions of the random process \(\sqrt{n}\{{\hat{F}}(t)-F(t)\}\) follows mean zero Gaussian process with variance covariance function \(\sigma (t_1,t_2)\).
Then
\(\square \)
Rights and permissions
About this article
Cite this article
Sisuma, M.S., Sankaran, P.G. Non-parametric test of recurrent cumulative incidence functions for competing risks models. METRON 80, 331–342 (2022). https://doi.org/10.1007/s40300-022-00228-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40300-022-00228-x