Attitude Constrained Robust Explicit Guidance for Terminal Phase of Autonomous Lunar Soft-Landing

Abstract

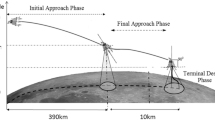
An attitude-constrained jerk-minimizing optimal explicit terminal guidance is presented in this paper for the terminal phase of a multi-phase lunar soft-landing. An analytic expression for the acceleration vector serves as the guidance command that can be computed by low-speed onboard processors in real-time. High terminal accuracy in each phase is achieved by enforcing ‘hard terminal constraints’ on the position, velocity, and acceleration (hence attitude) of the spacecraft. The initial conditions on position, velocity and acceleration are also enforced as hard constraints to ensure a smooth handover between consecutive phases. The required time-to-go is computed to minimize the deviation of the acceleration from the average of initial and final values. This results in a very smooth variation of the acceleration vector (hence attitude as well, owing to the strap-down nature of the thruster), starting from the applicable initial value to the desired final value in the segment. Along the trajectory, compatibility of the recomputed time-to-go in the absence of additional perturbation is maintained by auto-adjusting a tuning parameter. Moreover, if necessary, the time-to-go is adjusted once again to prevent altitude excursion beyond a pre-selected safety margin. This process of careful online auto-adjustment of the time-to-go, followed by using it to recompute the guidance command, makes the guidance operate in closed-loop with significant robustness. Consequently, it enables a larger capture region and introduces the capability to recover from partial failures, which are critical requirements for such challenging missions.

Appendices

Appendix 1: Third-Order Polynomial Guidance and Its Equivalence to Minimum-Jerk Guidance

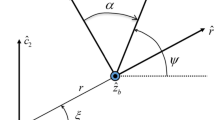
In this guidance, following the Apollo guidance paradigm [20], to account for the boundary conditions on position, velocity, and acceleration at both initial and final times, the acceleration vector is first parameterized as a third-order polynomial function of time-to-go (as against the second-order polynomial proposed in Apollo guidance [20]). Next, by imposing boundary conditions, the coefficients are determined. Note that imposing the hard boundary condition on the acceleration at the initial time helps ensure attitude continuity at the initial time during the transition to a new phase from the previous phase.

In this guidance design, the acceleration vector $\varvec{a}(t_{go}) \in {\mathbb {R}}^3$ is written as

$$\begin{aligned} \varvec{a}(t_{go}) = \varvec{k}_3 t_{go}^3+\varvec{k}_2t_{go}^2+\varvec{k}_1 t_{go}+\varvec{k}_0 \end{aligned}$$

(59)

where, the initial conditions are

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} \varvec{r}(t_{go_0})\\ \varvec{v}(t_{go_0})\\ \varvec{a}(t_{go_0}) \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \varvec{r}_0\\ \varvec{v}_0\\ \varvec{a}_0 \end{array}} \right] \end{aligned} \end{aligned}$$

(60)

and the final conditions are

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} \varvec{r}(0)\\ \varvec{v}(0)\\ \varvec{a}(0) \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \varvec{r}_f\\ \varvec{v}_f\\ \varvec{a}_f \end{array}} \right] \end{aligned} \end{aligned}$$

(61)

where, $\varvec{k}_0,\ \varvec{k}_1,\ \varvec{k}_2,\ \varvec{k}_3 \in {\mathbb {R}}^3$ are the coefficients of the polynomial. Utilizing the system dynamics in Eq. (8) and successively integrating the acceleration expression with respect to $t_{go}$, the spacecraft velocity and position are obtained as follows

$$\begin{aligned} \varvec{v}(t_{go})&= -\frac{\varvec{k}_3}{4} t_{go}^4 - \frac{\varvec{k}_2}{3} t_{go}^3 - \frac{\varvec{k}_1}{2} t_{go}^2 - \varvec{k}_0 t_{go} + \varvec{k}_4 \end{aligned}$$

(62)

$$\begin{aligned} \varvec{r}(t_{go})&= \frac{\varvec{k}_3}{20} t_{go}^5 + \frac{\varvec{k}_2}{12} t_{go}^4 + \frac{\varvec{k}_1}{6} t_{go}^3 + \frac{\varvec{k}_0}{2} t_{go}^2 - \varvec{k}_4 t_{go} + \varvec{k}_5 \end{aligned}$$

(63)

where $\varvec{k}_4,\ \varvec{k}_5 \in {\mathbb {R}}^3$ are integration constants. Applying the boundary conditions at $t_{go} = 0$ and $t_{go} = t_{{go}_0}$, as given in Eqs. (60) and (61), the coefficients of the polynomial are obtained as follows

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} \varvec{k}_5 \\ \varvec{k}_4 \\ \varvec{k}_0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \varvec{r}_f \\ \varvec{v}_f \\ \varvec{a}_f \end{array}} \right] \end{aligned} \end{aligned}$$

(64)

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} \varvec{k}_{\varvec{1}}\\ \varvec{k}_{\varvec{2}}\\ \varvec{k}_{\varvec{3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 6 \left( \dfrac{10}{t_{g{{o}_{0}}}^{3}}{{\varvec{Z}}_{{{\varvec{r}}_{\varvec{0}}}}}+\dfrac{4}{t_{g{{o}_{0}}}^{2}}{{\varvec{Z}}_{{{\varvec{v}}_{\varvec{0}}}}}+\dfrac{1}{2{{t}_{g{{o}_{0}}}}}{{\varvec{Z}}_{{{\varvec{a}}_{\varvec{0}}}}}\right) \\ -12 \left( \dfrac{15}{t_{g{{o}_{0}}}^{4}}{{\varvec{Z}}_{{{\varvec{r}}_{\varvec{0}}}}}+\dfrac{7}{t_{g{{o}_{0}}}^{3}}{{\varvec{Z}}_{{{\varvec{v}}_{\varvec{0}}}}}+\dfrac{1}{t_{g{{o}_{0}}}^{2}}{{\varvec{Z}}_{{{\varvec{a}}_{\varvec{0}}}}}\right) \\ 20 \left( \dfrac{6}{t_{g{{o}_{0}}}^{5}}{{\varvec{Z}}_{{{\varvec{r}}_{\varvec{0}}}}}+\dfrac{3}{t_{g{{o}_{0}}}^{4}}{{\varvec{Z}}_{{{\varvec{v}}_{\varvec{0}}}}}+\dfrac{1}{2t_{g{{o}_{0}}}^{3}}{{\varvec{Z}}_{{{\varvec{a}}_{\varvec{0}}}}}\right) \end{array}} \right] \end{aligned} \end{aligned}$$

(65)

where,

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} {{\varvec{Z}}_{\varvec{r}_{\varvec{0}}}}\\ {{\varvec{Z}}_{\varvec{v}_{\varvec{0}}}}\\ {{\varvec{Z}}_{\varvec{a}_{\varvec{0}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} \varvec{r}_{\varvec{0}}-{{\varvec{r}}_{f}}+{{\varvec{v}}_{f} }{{t}_{go}}-{{\varvec{a}}_{f}}\dfrac{t_{go}^{2}}{2}\\ \varvec{v}_{\varvec{0}}-{{\varvec{v}}_{f}}+{{\varvec{a}}_{f}}{{t}_{go}} \\ \varvec{a}_{\varvec{0}}-{{\varvec{a}}_{f}} \end{array}} \right] \end{aligned} \end{aligned}$$

(66)

Finally, substituting the coefficients from Eqs. (64) and (65) into Eq. (59) the third-order polynomial guidance command is generated.

On the other hand, one can observe from Eq. (23) in Sect. 3, that the minimum jerk guidance law is given by

$$\begin{aligned} \begin{aligned}&{\varvec{a}}({{t}_{go}})=20{{\varvec{c}}_{\varvec{3}}}t_{go}^{3}+12{{\varvec{c}}_{\varvec{2}}}t_{go}^{2} +6{{\varvec{c}}_{\varvec{1}}}{{t}_{go}}+\varvec{a}_f \end{aligned} \end{aligned}$$

(67)

where $\varvec{c}_{\varvec{1}},\varvec{c}_{\varvec{2}}$ and $\varvec{c}_{\varvec{3}}$ are given as

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} \varvec{c}_{\varvec{1}}\\ \varvec{c}_{\varvec{2}}\\ \varvec{c}_{\varvec{3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \dfrac{10}{t_{g{{o}_{0}}}^{3}}{{\varvec{Z}}_{{{\varvec{r}}_{\varvec{0}}}}}+\dfrac{4}{t_{g{{o}_{0}}}^{2}}{{\varvec{Z}}_{{{\varvec{v}}_{\varvec{0}}}}}+\dfrac{1}{2{{t}_{g{{o}_{0}}}}}{{\varvec{Z}}_{{{\varvec{a}}_{\varvec{0}}}}}\\ -\dfrac{15}{t_{g{{o}_{0}}}^{4}}{{\varvec{Z}}_{{{\varvec{r}}_{\varvec{0}}}}}-\dfrac{7}{t_{g{{o}_{0}}}^{3}}{{\varvec{Z}}_{{{\varvec{v}}_{\varvec{0}}}}}-\dfrac{1}{t_{g{{o}_{0}}}^{2}}{{\varvec{Z}}_{{{\varvec{a}}_{\varvec{0}}}}}\\ \dfrac{6}{t_{g{{o}_{0}}}^{5}}{{\varvec{Z}}_{{{\varvec{r}}_{\varvec{0}}}}}+\dfrac{3}{t_{g{{o}_{0}}}^{4}}{{\varvec{Z}}_{{{\varvec{v}}_{\varvec{0}}}}}+\dfrac{1}{2t_{g{{o}_{0}}}^{3}}{{\varvec{Z}}_{{{\varvec{a}}_{\varvec{0}}}}} \end{array}} \right] \end{aligned} \end{aligned}$$

(68)

By comparing the third-order polynomial guidance in Eq. (59) and the minimum jerk guidance in Eq. (67), one can easily see that

$$\begin{aligned} 20{{\varvec{c}}_{\varvec{3}}}&= \varvec{k}_3 \end{aligned}$$

(69)

$$\begin{aligned} 12{{\varvec{c}}_{\varvec{2}}}&= \varvec{k}_2 \end{aligned}$$

(70)

$$\begin{aligned} 6{{\varvec{c}}_{\varvec{1}}}&= \varvec{k}_1 \end{aligned}$$

(71)

Hence, the expression for ${\varvec{a}}({{t}_{go}})$ in Eqs. (59) and (67) are identical as long as the initial time-to-go $t_{{go}_0}$ remains the same. In other words, subject to identical boundary conditions on the initial and final position, velocity, and acceleration along with the reduced case of identical time-to-go, the minimum jerk guidance and modified Apollo guidance with third-order polynomial turn out to be the same.

Note that the major difference here is the fact that the Apollo guidance does not provide any specific instructions to choose $t_{{go}_0}$. It simply designates it as a “tuning parameter”. In the minimum jerk guidance proposed in this paper, it is systematically computed by solving a fourth-order algebraic equation, as discussed in Sect. 4. The advantages of adopting this approach include (i) deriving time-to-go from a meaningful process (i.e. minimizing the deviation of acceleration from the average of the initial and final values), (ii) minimal tuning requirements, (iii) the ability to re-compute time-to-go, allowing for recovery from path perturbations. In addition to this, this paper also proposes a method for auto-adjusting time-to-go to prevent altitude excursion.

Appendix 2: Analytic Solution of a Quartic Equation

It is clear from the discussion in this paper that the roots of a quartic equation is of frequent interest. Section 4 describes a process for finding the $t_{go_0}$, which is nothing but the smallest real positive root of a quartic polynomial given in Eq. (34). Also, the roots of another quartic polynomial given in Eq. (46) are used to determine the time at which the minimum of an altitude profile occurs. Furthermore, a quartic polynomial in Eq. (53) is used to find the modified time-to-go $t^*_{go_0}$ for preventing altitude excursion. Therefore, for all the above scenarios, an analytical solution for finding the roots of a quartic polynomial is necessary for real-time computation. An interested reader can refer to [32] for the solution of this quartic polynomial. For completeness, however, the relevant steps with appropriate explanation for analytically finding the roots of a quartic polynomial is summarized here. Note that this procedure demands the solution of a cubic expression in an intermediate step. Hence, an approach for finding the roots of a cubic polynomial is also included.

1.1 Analytic Solution to a Quartic Expression

Consider a quartic polynomial with constant coefficients $p_4, p_3, p_2, p_1$ and $p_0$ of the following form

$$\begin{aligned} \begin{aligned} p_{4} x^{4}+p_{3} x^{3}+p_{2} x^{2}+p_{1} x+p_{0}=0 \end{aligned} \end{aligned}$$

(72)

The first step is to eliminate the cubic term in the Eq. (72). In order to do that, the equation is divided by $p_{4}$ ($p_{4}\ne 0$) and is rewritten in the terms of new coefficients as follows

$$\begin{aligned} \begin{aligned} x^{4}+a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0}=0 \end{aligned} \end{aligned}$$

(73)

where, $a_3 = {p_3}/{p_4}, \ a_2 = {p_2}/{p_4}, \ a_1 = {p_1}/{p_4}, \ a_0 = {p_0}/{p_4}$. Then the Eq. (73) is transformed using $x=z-{a_{3}}/{4}$. The equation then takes the form of the following depressed quartic polynomial.

$$\begin{aligned} \begin{aligned} z^{4}+p z^{2}+q z+r=0 \end{aligned} \end{aligned}$$

(74)

where,

$$\begin{aligned} p&=a_{2}-\frac{3 a_{3}^{2}}{8} \end{aligned}$$

(75)

$$\begin{aligned} q&=a_{1}-\frac{a_{2} a_{3}}{2}+\frac{a_{3}^{3}}{8} \end{aligned}$$

(76)

$$\begin{aligned} r&=a_{0}-\frac{a_{1} a_{3}}{4}+\frac{a_{2} a_{3}^{2}}{16}-\frac{3 a_{3}^{4}}{256} \end{aligned}$$

(77)

The next step is to write the Eq. (74) in an algebraically factorable form, such as the difference of two squared terms. To achieve this, the terms $u z^{2}$ and ${u^{2}}/{4}$ are added and subtracted respectively, followed by carrying out the relevant algebra as follows

$$\begin{aligned}&\left( z^{4}+u z^{2}+\frac{u^{2}}{4}\right) -u z^{2}-\frac{u^{2}}{4}+p z^{2}+q z+r=0 \end{aligned}$$

(78)

$$\begin{aligned}&\left( z^{4}+u z^{2}+\frac{u^{2}}{4}\right) -(u-p) z^{2}-\frac{u^{2}}{4}+q z+r=0 \end{aligned}$$

(79)

$$\begin{aligned}&\left( z^{2}+\frac{u}{2}\right) ^2-(u-p)\left[ z^{2}-\frac{q z}{(u-p)}+\frac{{u^{2}}/{4}-r}{(u-p)}\right] =0 \end{aligned}$$

(80)

which can be written as

$$\begin{aligned} {P}^{2}-{Q}^{2}=0 \end{aligned}$$

(81)

where,

$$\begin{aligned} {P}&=z^{2}+\frac{u}{2} \end{aligned}$$

(82)

$$\begin{aligned} {Q}&=\sqrt{(u-p)\left[ z^{2}-\frac{q z}{(u-p)}+\frac{{u^{2}}/{4}-r}{(u-p)}\right] } \end{aligned}$$

(83)

Here, the first term $P^2$ is a perfect square, and u can be chosen such that the second term $Q^2$ is a perfect square too. With this in mind, the second term can be rewritten as

$$\begin{aligned} z^{2}-2{B}{z}+B^{2}=0 \end{aligned}$$

(84)

               where,

$$\begin{aligned} 2 B&= \frac{q}{(u-p)} \end{aligned}$$

(85)

$$\begin{aligned} B^{2}&=\frac{{u^{2}}/{4}-r}{(u-p)} \end{aligned}$$

(86)

Comparing the expression for $B^2$ in Eqs. (85) and (86), we obtain the following relation for u

$$\begin{aligned} \frac{{u^{2}}/{4}-r}{(u-p)}=\frac{q^{2}}{4(u-p)^{2}} \end{aligned}$$

(87)

which, after the necessary simplification, leads to

$$\begin{aligned} u^{3}-p u^{2}-4 r u+\left( 4 p r-{q^{2}}\right) =0 \end{aligned}$$

(88)

It is obvious now that the solution of u is obtained as the roots of the cubic expression in Eq. (88). The analytic solution for finding the roots of a cubic expression can be found by following the procedure discussed separately later in this appendix. Since there is a chance of obtaining multiple roots, a detailed procedure for choosing the best possible root is also discussed.

One can also notice that Q can be written as

$$\begin{aligned} \begin{aligned} {Q}&=\sqrt{(u-p)}\left( z-\frac{q}{2(u-p)}\right) \end{aligned} \end{aligned}$$

(89)

Next, using $\left( {P}^{2}-{Q}^{2}\right) = ({P}+{Q})({P}-{Q})$, and assuming that the value of u is available, the quartic polynomial in Eq. (80) can be factorized into two quadratic expressions

$$\begin{aligned} \begin{aligned}&\left( z^{2}+\frac{u}{2}+\sqrt{(u-p)}\left[ z-\frac{q}{2(u-p)}\right] \right) \times \\&\left( z^{2}+\frac{u}{2}-\sqrt{(u-p)}\left[ z-\frac{q}{2(u-p)}\right] \right) =0 \end{aligned} \end{aligned}$$

(90)

Solving the two quadratic expressions given in Eq. (90), four solutions for z are obtained. Subsequently, using the relation $x=z-{a_{3}}/{4}$, and carrying out the necessary algebra [32], the four solutions of the quartic polynomial given in Eq. (72) are obtained, as follows

$$\begin{aligned} x_1&=\frac{-p_{3}}{4p_{4}}+\frac{l}{2}+\frac{m}{2} \end{aligned}$$

(91)

$$\begin{aligned} x_2&=\frac{-p_{3}}{4p_{4}}+\frac{l}{2}-\frac{m}{2} \end{aligned}$$

(92)

$$\begin{aligned} x_3&=\frac{-p_{3}}{4p_{4}}-\frac{l}{2}+\frac{n}{2} \end{aligned}$$

(93)

$$\begin{aligned} x_4&=\frac{-p_{3}}{4p_{4}}-\frac{l}{2}-\frac{n}{2} \end{aligned}$$

(94)

where,

$$\begin{aligned} l&=\sqrt{\frac{3}{8}\left( \frac{p_{3}}{p_{4}}\right) ^{2}-\frac{p_{2}}{p_{4}}+u} \end{aligned}$$

(95)

$$\begin{aligned} m&={\left\{ \begin{array}{ll} \sqrt{\dfrac{3}{8} \left( \dfrac{p_{3}}{p_{4}}\right) ^{2}- \dfrac{p_{2}}{p_{4}}-u+\left( \dfrac{p_{2}p_{3}}{p_{4}^2}-\dfrac{2p_{1}}{p_{4}}-\dfrac{1}{4}\left( \dfrac{p_{3}}{p_{4}}\right) ^{3}\right) l^{-1}}, &{} \text {if } l \ne 0 \\ \sqrt{\dfrac{3}{4} \left( \dfrac{p_{3}}{p_{4}}\right) ^{2}- \dfrac{2p_{2}}{p_{4}}+2 \sqrt{\left( u+\dfrac{1}{8}\left( \dfrac{p_{3}}{p_{4}}\right) ^{2}\right) ^{2}-\dfrac{4p_{0}}{p_{4}}}}, &{} \text {if } l = 0 \end{array}\right. } \end{aligned}$$

(96)

$$\begin{aligned} n&= {\left\{ \begin{array}{ll} \sqrt{\dfrac{3}{8} \left( \dfrac{p_{3}}{p_{4}}\right) ^{2}- \dfrac{p_{2}}{p_{4}}-u-\left( \dfrac{p_{2}p_{3}}{p_{4}^2}-\dfrac{2p_{1}}{p_{4}}-\dfrac{1}{4}\left( \dfrac{p_{3}}{p_{4}}\right) ^{3}\right) l^{-1}}, &{} \text {if } l \ne 0 \\ \sqrt{\dfrac{3}{4} \left( \dfrac{p_{3}}{p_{4}}\right) ^{2}- \dfrac{2p_{2}}{p_{4}}-2 \sqrt{\left( u+\dfrac{1}{8}\left( \dfrac{p_{3}}{p_{4}}\right) ^{2}\right) ^{2}-\dfrac{4p_{0}}{p_{4}}}}, &{} \text {if } l = 0 \end{array}\right. } \end{aligned}$$

(97)

1.2 Analytic Solution of a Cubic Equation

As discussed in the previous section, the solution of the quartic polynomial assumes the solution of a cubic polynomial in Eq. (88). Hence, the solution process of a cubic polynomial is described in this section.

Consider the following cubic polynomial with constant coefficients $q_3, q_2, q_1$ and $q_0$

$$\begin{aligned} q_{3} x^{3}+q_{2} x^{2}+q_{1} x+q_{0}=0 \end{aligned}$$

(98)

Similar to the procedure followed in a solution of the quartic expression given in Appendix section “Analytic Solution to a Quartic Expression”, the quadratic term in Eq. (98) is eliminated first. For this, Eq. (98) is divided by $q_{3}$ ($q_{3}\ne 0$) and rewritten in terms of the new coefficients as follows

$$\begin{aligned} x^{3}+b_2 x^{2}+b_1 x+b_0=0 \end{aligned}$$

(99)

where, $b_2 = {q_2}/{q_3}, b_1 = {q_1}/{q_3}, b_0 = {q_0}/{q_3}$. Next, the transformation, $x=y-{b_2}/{3}$ is used to transform the Eq. (99) to a depressed cubic form as shown in Eq. (100).

$$\begin{aligned} y^{3}+c y+d=0 \end{aligned}$$

(100)

               where,

$$\begin{aligned} c&=b_1-\frac{b_2^{2}}{3} \end{aligned}$$

(101)

$$\begin{aligned} d&=\frac{2 b_2^{3}}{27}-\frac{b_2 b_1}{3}+c \end{aligned}$$

(102)

This depressed cubic expression is written in an algebraically factorable form. To achieve this $y=w-v$ (where, $w \ne v$) is substituted in Eq. (100) to rewrite it as

$$\begin{aligned}&(w-v)^{3}+c(w-v)+d=0 \end{aligned}$$

(103)

$$\begin{aligned}&\left\{ d-\left( v^{3}-u^{3}\right) \right\} +(w-v)(c-3 w v)=0 \end{aligned}$$

(104)

The solution for the Eq. (104) can be obtained by taking $d=v^{3}-w^{3}$ and $c=3 w v$. Solving these two expressions, one gets a quadratic polynomial in $w^3$, as follows

$$\begin{aligned} \left( w^{3}\right) ^{2}+d \left( w^{3}\right) -\frac{c^{3}}{27}=0 \end{aligned}$$

(105)

This quadratic equation is solved to obtain the values for w and v as shown in Eq. (106)

$$\begin{aligned} \begin{aligned} w^{3}&=\frac{-9 d+\sqrt{\left( 12 c^{3}+81 d^{2}\right) }}{18} = \frac{-d}{2}+\sqrt{\Delta }\\ v^{3}&=\frac{9 d+\sqrt{\left( 12 c^{3}+81 d^{2}\right) }}{18} = \frac{d}{2}+\sqrt{\Delta } \end{aligned} \end{aligned}$$

(106)

where, $\Delta ={d^{2}}/{4}+{c^{3}}/{27}$ is the discriminant. Using the relations used earlier, i.e. $y = (w-v)$ and $x=y-{b_2}/{3}$, the solution for the cubic polynomial is obtained. Note that, since the complex roots of a polynomial always occur in pairs, the cubic polynomial will have either one real root or three real roots.

If $\Delta >0$, only one real solution for the cubic expression exists, which then leads to the following solution

$$\begin{aligned} \begin{aligned} x_1=\left( \frac{-d}{2}+\sqrt{\Delta }\right) ^{1 / 3}+\left( \frac{-d}{2}-\sqrt{\Delta }\right) ^{1 / 3}-\frac{b_2}{3} \end{aligned} \end{aligned}$$

(107)

If $\Delta \le 0$, three roots exist for the cubic expression exists, which is given as follows

$$\begin{aligned}&x_1=\frac{2}{\sqrt{3}} \sqrt{-c} \sin \left[ \frac{1}{3} \sin ^{-1} \frac{3 \sqrt{3} d}{2 \sqrt{-c}^{3}}\right] -\frac{b_2}{3} \end{aligned}$$

(108)

$$\begin{aligned}&x_2=\frac{-2}{\sqrt{3}} \sqrt{-c} \sin \left[ \frac{1}{3} \sin ^{-1} \frac{3 \sqrt{3} d}{2 \sqrt{-c}^{3}}+\frac{\pi }{3}\right] -\frac{b_2}{3} \end{aligned}$$

(109)

$$\begin{aligned}&x_3=\frac{2}{\sqrt{3}} \sqrt{-c} \cos \left[ \frac{1}{3} \sin ^{-1} \frac{3 \sqrt{3} d}{2 \sqrt{-c}^{3}}+\frac{\pi }{6}\right] -\frac{b_2}{3} \end{aligned}$$

(110)

For details of this analysis and the associated solution, one can refer to [34].

1.3 Selection of Root of Cubic Expression for Evaluating the Quartic Expression

The solution of the quartic polynomial presented in Appendix 2.1 requires the computation of the cubic polynomial described in Eq. (88). If the cubic polynomial has multiple real roots, then a systematic methodology for selecting the most suitable root is provided here.

Let ${\bar{u}}$ denote a root of the polynomial in Eq. (88). By substituting this root into Eq. (90), we effectively reconstruct the quartic equation as follows

$$\begin{aligned} z^{4}+p z^{2}+q z+\dfrac{1}{4}\left( {\bar{u}}^2-\dfrac{q^2}{{\bar{u}}-p}\right) = 0 \end{aligned}$$

(111)

This equation is compared to the original quartic equation presented in Eq. (74). It is observed that all the coefficients are the same except for the constant term. The purpose here is to identify the root that, when utilized to reconstruct a quartic polynomial, provides an expression that closely resembles the original polynomial. To achieve this, the residue is calculated, which represents the absolute difference in the constant term of both polynomials which is described as follows

$$\begin{aligned} R_0=\dfrac{1}{4}\left( {\bar{u}}^2-\dfrac{q^2}{{\bar{u}}-p}\right) -r \end{aligned}$$

(112)

This residue is found for all three roots. The root corresponding to the smallest residue is chosen as the potential solution. This choice is made because the reconstructed quartic polynomial, as defined in Eq. (111), is closer to the original quartic polynomial stated in Eq. (74). Furthermore, as a final quality check, the cubic root is selected only if its corresponding residue is close to zero, specifically, if it is less than $10^{-3}$ for computational purposes.