Abstract
The most appropriate next step in depression treatment after the initial treatment fails is unclear. This study explores the suitability of the Markov decision process for optimizing sequential treatment decisions for depression. We conducted a formal comparison of a Markov decision process approach and mainstream state-transition models as used in health economic decision analysis to clarify differences in the model structure. We performed two reviews: the first to identify existing applications of the Markov decision process in the field of healthcare and the second to identify existing health economic models for depression. We then illustrated the application of a Markov decision process by reformulating an existing health economic model. This provided input for discussing the suitability of a Markov decision process for solving sequential treatment decisions in depression. The Markov decision process and state-transition models differed in terms of flexibility in modeling actions and rewards. In all, 23 applications of a Markov decision process within the context of somatic disease were included, 16 of which concerned sequential treatment decisions. Most existing health economic models relating to depression have a state-transition structure. The example application replicated the health economic model and enabled additional capacity to make dynamic comparisons of more interventions over time than was possible with traditional state-transition models. Markov decision processes have been successfully applied to address sequential treatment-decision problems, although the results have been published mostly in economics journals that are not related to healthcare. One advantage of a Markov decision process compared with state-transition models is that it allows extended action space: the possibility of making dynamic comparisons of different treatments over time. Within the context of depression, although existing state-transition models are too basic to evaluate sequential treatment decisions, the assumptions of a Markov decision process could be satisfied. The Markov decision process could therefore serve as a powerful model for optimizing sequential treatment in depression. This would require a sufficiently elaborate state-transition model at the cohort or patient level.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
This article demonstrates that the Markov decision process (MDP) has the potential to steer the optimization of sequential treatment to facilitate personalized treatment decisions. |
This article specifically identifies applications of the MDP that have been used to address sequential decision problems in somatic diseases. The results indicate that the MDP could potentially be useful for addressing sequential decision making in depression. |
Our study reveals that, although the structure of the state-transition model could potentially be suitable for extension into the MDP model, doing so would require a sufficiently extensive model. |
1 Introduction
Depression is one of the most burdensome and costly of all mental health disorders, with a worldwide average lifetime and 12-month prevalence of 14.6% and 5.5%, respectively [1]. People with depression experience impairment in daily life, resulting in a quality of life that is lower than in the general population [2]. According to WHO projections, depression will rank first in terms of disability-adjusted life-years lost by 2030 [3]. The economic burden of depression is also high, having been estimated at US$326.2 billion for the United States in 2018 (price level 2020) [4]. Depression thus imposes a high burden on society, the healthcare system, and individuals [5]. To reduce this burden and support appropriate treatment selection, increasing attention is being directed to studies comparing different treatments regarding health outcomes and cost effectiveness. Most previous studies have examined only limited numbers of different treatments (e.g., psychotherapies, pharmacotherapy, brain stimulation therapy [6,7,8], genetic testing) to support targeted therapy [9], using different health economic (HE) models. While such studies have supported choices between different treatments, they have yielded little insight into treatment duration or sequential treatment choices.
To date, no consensus has been reached concerning how long (e.g., days, weeks, months, years) a patient should be treated with a specific treatment for depression [10]. Furthermore, it is unclear how consecutive treatments should be selected when initial treatment is not successful. One widespread approach is stepped care: a gradual increase in the intensity of treatments [11]. More recently, however, scholars have been directing greater attention to matched care [12], which implies that initial and sequential treatment steps are carefully adjusted to the personal characteristics and treatment history of the individual. Such adjustments are usually pragmatic and based on general guidelines, although they might also be informed by data-driven optimization.
The Markov decision process (MDP) is a mathematical model for sequential decisions and dynamic optimization [13], which generalizes standard Markov models by embedding a sequential decision process into the model and allowing multiple decisions in multiple time periods [14]. To support optimization, MDP models have been applied to address a variety of industrial operation problems, including cost-effective maintenance [15,16,17,18], electricity supply [19], and dynamic pricing [20]. Recent studies have demonstrated that MDP has potential to support clinical decision making [14]. Steimle and Denton [21] argue that the MDP model is essential for guiding decision makers in treatment decisions for chronic diseases, as it provides an analytical framework for studying sequential decisions. The framework is very general, however, and not geared toward specific diseases, nor does it contain actual input data. The feasibility of its actual application is therefore unclear. For this reason, two questions are worth exploring. The first concerns the identification of any actual applications of MDP within the field of healthcare, and the second concerns whether MDP could be fruitfully applied to address treatment decision issues in depression.
Given the state of knowledge as described above, the primary aim of this article was to examine how MDP has been implemented by reviewing all existing applications of MDP to medical decision making for diseases. It also provides a review of existing HE models of depression and an analysis of the potential of MDP to support sequential treatment decisions in depression, based on the reformulation of an existing HE model of depression and an assessment of the suitability of MDP.
2 Background
State-transition models (STMs) are structured around a set of mutually exclusive and collectively exhaustive health states, transitions, initial-state vectors, transition probabilities, cycle lengths, and state values (‘rewards’), which conceptualize a decision problem in terms of a set of health (or other) states and transitions among these states [22]. In this background section, the elements of an MDP are defined, starting with and compared with their analogues in STMs. The basic definition of an MDP comprises five elements (\(\mathrm{T},\mathrm{ S},{A}_{s},\) P(.│s, a),\({r}_{t}\left(s,a\right)\)), described using a standard notation [23]. To build an MDP model, the decision epochs (\(\mathrm{T}=\mathrm{1,2},\cdots \mathrm{N}\)), state space (\(\mathrm{S}\)), action space (\({A}_{s}\)), transition probabilities \((\mathrm{P}\left(.|s,a\right)\)), and rewards (\({r}_{t}\left(s,a\right))\) should be defined. All elements of an MDP are listed in Table 1, in comparison with the corresponding elements in a cohort-level STM.
As demonstrated by this comparison, an MDP can be regarded as an extension of an STM. The difference is the addition of actions (e.g., stop treatment, remain on current treatment, change treatment) and rewards, which may depend on these actions, with transition probabilities being conditional on both current state and current action. Conversely, if each state has only one action and if all rewards depend only on the state, the MDP reduces to an STM. Note that most STMs that have been applied to actual HE evaluations deviate in some way from the pure Markov property (e.g., because mortality depends on age or because some pay-offs vary according to both state and model run-time).
It stands to reason that no specific corresponding analogy exists for the MDP actions and decision rules, given that STMs are applied in HE evaluations primarily to compare two or more pre-specified strategies or scenarios. In contrast, states (as applied in STMs) are very similar to the states distinguished in MDPs. The decision epochs of an MDP are a set of points at which decisions are made, and they are analogous to the cycle time in standard Markov models.
While cohort-level Markov models can thus be extended into an MDP at the aggregate level, it is also possible to define an MDP with parameters that depend on individual characteristics and to define optimal strategies that vary by individual. Such patient-level MDPs could be regarded as an extension of patient-level STMs, sometimes also called microsimulation models, or patient-level Markov models. Finally, MDPs can be defined in continuous rather than discrete time, and with a finite or infinite time horizon [24].
3 Methods
We performed two reviews, the first to identify existing applications of the MDP in treatment of disease and the second to identify existing HE models in depression. Data were extracted from MDP applications to articulate assumptions and requirements for the MDP. We then illustrated the elements of an MDP by reformulating an existing HE model and examining its added value. This served as input for discussing the suitability of an MDP for solving sequential treatment decisions in depression. The methodological framework of the present study is displayed in Fig. 1. The protocols for the two reviews were registered in the Open Science Framework.
3.1 Review of Markov Decision Process (MDP) and Health Economic (HE) Models
The two reviews followed the guidelines for Preferred Reporting Items for Systematic reviews and Meta-Analyses extension for Scoping Reviews (PRISMA ScR) (see Appendix Part 1 in the electronic supplementary material [ESM] for the checklist).
The search strings for existing applications of MDP and HE decision models were designed to identify relevant literature (see Appendix Part 2 in the ESM). Web of Science and PubMed were searched in September 2021. An article was eligible for inclusion only if it addressed the treatment of diseases rather than the optimization of hospital operations, surgical techniques, or the application of healthcare devices using MDP. In the review of HE models for depression, publications were eligible for inclusion only if they concerned the economic evaluation of treatments for depression. Both reviews excluded papers published in languages other than English, meeting abstracts, reviews, and publications that were not available in full text.
After eliminating duplicates, two reviewers (F.L, X.L) independently screened titles and abstracts. Disagreements were initially addressed through discussion and consensus. Any remaining disputes between the two reviewers were solved by appealing to a third author (T.F). Two authors (F.L, X.L) abstracted data on general study characteristics using a data extraction form.
For the MDP review, data extraction focused on the structure of the MDP in each of the applications to evaluate the assumptions and requirements of MDP. The following elements were extracted: time horizon, disease, state space, action space, reward function, and main perspective. The authors also attempted to extract the requirements and assumptions of MDP when applied in healthcare settings based on the studies identified. Both general and specific assumptions related to specific applications were included.
The review of HE models for depression started with the categorization of model structures. Given our interest in the structure of STMs and whether this structure could be used as a starting point for MDPs, we retained only models that are structured as a set of health (or other) states and transitions among these states. For these studies, further information on each model was collected. General study characteristics were authors and year, treatment types, and their comparators. Model characteristics were health states, time horizon, cycle length, and aim.
3.2 Illustration of Elements of an MDP Using a Reformulation of an Existing HE Model into an MDP
We use a case study to illustrate how a real-world HE decision problem can be reformulated as an MDP. The required model elements (e.g., states, transition probabilities, costs, quality-of-life weights) were first extracted from an existing HE model. We then translated the HE model to an MDP formulation based on the information collected. To investigate the consistency of conclusions between the existing HE model and the MDP approach, we compared the results from the existing HE model to those of the MDP model. Finally, we discussed the potential added value of MDP after reformulation.
3.3 Assessment of the Suitability of MDP for Optimizing Sequential Treatment in Depression
After comparing the findings of the two reviews to clarify the assumptions about the use of MDP in depression, we examined whether they might be satisfied. We then discussed how to define MDP structure when used in depression. In this step, we also discussed challenges associated with using MDP to optimize sequential treatment decisions for depression.
4 Results
4.1 Overview of Existing Applications of MDP in Treatment of Disease
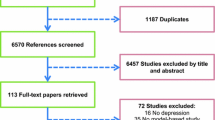
All existing applications of MDP to optimize treatment concern somatic disease. As shown in Fig. 2, we selected a total of 23 applications of MDP for inclusion in the review. An overview of the characteristics of these applications is provided in Table 2.
Researchers have applied MDP models to optimize initial treatment selection [25, 26] and the timing of transplantation [27, 28], to compare the effectiveness of different combinations of treatment [29], to optimize screening policy [30], and to prevent disease-related complications [31]. However, 16 studies concern the optimization of treatment decisions [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. Five studies use the MDP to optimize treatment decisions for cancer [30, 35, 39, 42, 43], five focus on optimizing the treatment of diabetes mellitus [31,32,33,34, 41], and the remaining (N = 13) studies are concerned with liver diseases [27, 28], high blood pressure/hypertension [37, 40], hepatitis C [44], atherosclerotic cardiovascular disease [45], ischemic heart disease [29, 36], atrial fibrillation [38], anemia [47], tuberculosis [46], aneurysms [25], and stroke [26].
The MDP approach has been used to determine the optimal sequence of chemotherapy and radiation therapy [35, 39, 42, 43] and to select the appropriate drugs for anemia [47], tuberculosis [46], atherosclerotic cardiovascular disease [45], and hepatitis C [44]. In studies by Meng et al. [32], Mason et al. [33], and Shifrin and Siegelmann [41], MDP is applied to optimize the management of diabetes medication for glycemic control. An MDP-based treatment recommendation system for diabetes medication steps has also been proposed by Oh et al. [34]. In studies by Choi et al. [37] and Schell et al. [40], MDP is used to develop an automated strategy to select suitable anti-hypertensive medications and dosages for patients, thus accounting for their heterogeneity. In contrast, the articles by Ibrahim et al. [38] and Hauskrecht and Fraser [36] are primarily theoretical and do not apply MDP to any actual clinical settings.
Of the studies identified, 11 address treatment decisions at the individual level, especially in applications for diabetes and ischemic heart disease [32, 33, 35,36,37,38, 40, 41, 44, 45, 47]. They apply risk engines using individual-level covariates (e.g., the Framingham model [48] and the UKPDS risk engine [49]) to calculate transition probabilities between states with different treatments. In the gastro-esophageal cancer treatment application, the transition probability is calculated individually using the expected toxicity level and demographic variables [35]. In contrast, for the hypertension application, the authors examined several individual-level covariates, including 11 variables used as treatment effect modifiers to modify baseline risks [37, 40]. Ibrahim et al. [38] include different transition probabilities when analyzing/optimizing the length of the initiation period of anticoagulation therapy.
In all, 20 studies concern MDPs with a finite time horizon, while another three articles involve MDPs with an infinite time horizon [27, 28, 36]. Infinite-horizon MPDs do not require a pre-defined time horizon. For most algorithms to work and result in a well-defined optimal solution, however, these models do require a boundedness condition on the value function.
Most studies define states according to clinically relevant variables and discretely, with numbers ranging widely from 4 to 8492 states (see Table 1), except for one study [36] that reports 11 state variables rather than listing all the states. Nine studies consider three actions [25, 28, 30, 34, 37, 39, 43, 45, 46], while six consider two actions [27, 31,32,33, 41, 44], four use five actions [29, 35, 38, 40], three use four actions [26, 36, 47], and one does not specify the number of actions [42]. In most cases, larger numbers of actions distinguished are associated with greater complexity in the process of finding an optimal solution. Rewards most frequently consist exclusively of health benefits, with more than half of the studies having optimal treatment outcomes as their objective [25,26,27,28,29, 31, 32, 34, 37, 38, 40,41,42,43,44,45, 47]. Only three studies focus on minimizing costs [30, 35, 36], and three other studies use the combination of treatment outcomes and costs (or net benefits) as the reward function [33, 39, 46].
4.1.1 Assumptions and Requirements of MDP
An MDP model explicates a stochastic control process and formally consists of four essential elements: states, actions, transition probabilities, and rewards. Three common assumptions of all studies in clinical settings are as follows: (i) both states and action space are a finite set; (ii) an absorbing state is included in the Markov process, either death or severe functional impairment, which is essential for any finite-horizon MDP to obtain an optimal solution; (iii) MDP states are observable and mutually exclusive. Several authors make additional assumptions based on the characteristics of specific research questions. For example, Alagoz et al. [28] assume that the reward function is positive and non-increasing in a particular state after a cadaveric liver transplant action. This implies that the intermediate reward does not increase as the patient deteriorates. For diabetes, Eghbali-Zarch et al. [31] assume that the treatment decision of insulin is irreversible (implying that, once patients initiate insulin, they remain on it until the end of the time horizon), thus avoiding optimal strategies that would not correspond to clinical practice. Similarly, to mimic current clinical practice, Choi et al. [37] exclude a dosage decrease in the action space. In the study by Kim et al. [42], a non-zero dose is assumed in each treatment. In this sense, additional assumptions could be added to the model to accommodate current treatment practice or to avoid clinically unrealistic or unacceptable solutions.
4.2 Overview of Existing HE Decision Models for Depression
In all, we identified 63 existing HE decision models in the review of existing HE models, more than half of which are STMs (Appendix Fig. S1 in ESM). The number of model states distinguished varies from three to eight (Appendix Table S1 in ESM). In 21 studies, states are defined by disease severity in terms of clinically relevant criteria (e.g., symptom scores for depression). Only five studies have a lifetime time horizon [50,51,52,53,54]. In the remaining studies, except for one study with a very short time horizon (3 months) [55] and one with a relatively long time horizon (11 years) [56], the time horizon varies between 1 and 5 years [6,7,8,9, 57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77].
The models focus predominantly on five categories of interventions (Appendix Fig. S2 in ESM). In all, 16 studies use a healthcare perspective [7, 8, 50,51,52, 63, 65,66,67,68, 70,71,72,73, 75, 76], while nine adopt a societal perspective [6, 9, 53, 55, 56, 59, 60, 64, 77]. Only two studies use the payer perspective [57, 62], and the rest present results for both the healthcare and societal perspectives [54, 58, 61, 69, 74].
4.3 Illustration of Elements of an MDP Using a Reformulation of an Existing HE Model into an MDP
We applied the MDP to reproduce the research carried out by Ssegonja et al. [74]. This study was chosen for three reasons. First, it involves a relatively small number of states, such that it is easy for readers to understand and suitable for use as an example. Second, the study reports all model parameters clearly, providing a basis for reformulating it into MDP. Finally, the model structure of a pure STM (rather than a combination of Markov and decision tree) facilitates reformulation.
The study by Ssegonja et al. [74] uses a cost-effectiveness analysis at the cohort level to compare a group-based cognitive behavior therapy (GB-CBT) preventive intervention for depression with a non-intervention option in Sweden for adolescents, using an STM. The transition from subthreshold depression to depression and from subthreshold to healthy was affected by GB-CBT, as illustrated in Fig. 3.
Simplification of model structure in the original paper [74]
Translating this decision problem to an MDP formulation, Fig. 4 displays the process of reformulating an existing study into an MDP model, designed to explore the best decision between treating adolescents with GB-CBT and leaving them untreated. The possible decisions are represented by the actions (treating with GB-CBT or leaving untreated).
Process of the Markov decision process (MDP) model based on the original model by Ssegonja et al. [74]. Note: s denotes the current state; \({s}^{^{\prime}}\) denotes the next state; \({R}_{t}\) denotes the reward at time t. The variable \(\upgamma\) is a discount factor. \(\mathrm{Q}({s}_{t,}{a}_{t})\) indicates the monetary value of quality-adjusted life-years in the state \(s\) at time t, taking the decision \(\mathrm{a}\); \(\mathrm{C}({s}_{t,}{a}_{t})\) indicates the total cost in the state \(s\) at time t, taking the decision \(\mathrm{a}\); \(v(s)\) denotes state value function, which is the expected monetary return starting from state s; \(q({s}_{t} ,a)\) indicates the expected monetary return starting from state s, taking action a at time t; \({v}^{*}(s)\) indicates the optimal value function over all decisions in the state \(s\); \({q}^{*}({s}_{t},a)\) is the optimal value function for action a in the state \(s\); t is measured in years
According to the original study, the \(\upgamma\) value was 0.97. The Bellman optimality equation was used to find the solution [78]. Based on the optimal state value function \({v}^{*}(s)\) at the following decision epoch, the optimal action-value function \({q}^{*}\left({s}_{t},a\right)\) was calculated, as shown in Fig. 4. The model was coded in Python software 3.3.8 using the MDP toolbox [79]. In keeping with the uncertainty analysis in the original study, we also considered different willingness-to-pay (WTP) thresholds. The values for each state are presented in Table 3, along with different WTP thresholds. Note that, for this simple example, the optimization could be simplified to decide whether GB-CBT should be implemented in the first epoch, given that the action space for each decision epoch except the first is confined to a single action.
At the WTP threshold value of US$20,000/QALY, the \({q}^{*}\left(subthreshold,intervention\right)\) was US$134,000 at t = 1, and the \({q}^{*}\left(subthreshold,no intervention\right)\) was US$131,000. The optimized value function when choosing to implement GB-CBT is therefore higher than for the alternative strategy, and the former is thus optimal. This means that choosing the intervention brings a net profit. We therefore conclude that adolescents can benefit from the GB-CBT preventive interventions and that it can also generate good value for money, as compared with leaving adolescents with subthreshold depression untreated. This conclusion is consistent with Ssegonja et al.
In contrast to the original HE model, the MDP structure allows for more flexibility. We could now extend the action space and consider other strategies (e.g., starting the preventive treatment after a person has been in the subthreshold space for one period). This could be achieved by separating more minor decision epochs that would allow interventions to be performed at more appropriate times, as well as by increasing the number of actions, making it possible to compare multiple preventive treatments simultaneously. In addition, the comparison between different strategies is based on the reward function, and it might therefore be relatively easy to vary the weight assigned to health outcomes or costs to investigate impact on the optimal decision.
4.4 Assessment of the Suitability of MDP for Solving Sequential Treatment Decisions in Depression
The Markov property is a precondition for any MDP. To assess the suitability of MDP for depression, it is important to recognize two important assumptions of an MDP. First, the state space and the action space are finite. A state explosion might occur, especially in a state-transition system with many processes or a complex data structure. This means that an infinite number of states could trap the model in an endless loop, causing it to fail in finding the optimal solution. All existing HE models for depression consist of a finite number of states (varying from three to eight), indicating that the application of MDP to optimizing sequential treatment decisions for depression would probably not result in a state explosion problem. The second assumption is that MDP states are observable, which essentially corresponds to the situation in which we know with certainty the disease from which the patient is suffering at all epochs.
As for other diseases, the five core elements of MDP for depression are decision epoch, state space, action space, reward, and transition probabilities. The decision epoch of the MDP structure could be the beginning of each treatment cycle, with a decision made at every clinical visit. In practice, this would depend on the frequency of visits. The MDP states could be defined by depression severity. Depression differs from many somatic illnesses, in which states are distinguished according to clinical parameters (e.g., blood glucose level in diabetes mellitus). Such clinical parameters are not easily defined for depression. As illustrated by the review of HE models, the states in most studies concerning depression are defined by disease severity in terms of clinically relevant criteria (e.g., symptom scores for depression).
Regarding the action space, depression interventions can largely be divided into two categories: psychotherapies and medications. The action/treatment choice for a patient at a specific point in time could thus be simplified to no intervention, psychotherapy, medication use, or both. In reality, however, many different medications and psychotherapies might be distinguished, and different intensities (dosages and hours of therapy per unit of time) and combinations could be considered. Finally, QALYs, costs, or their combination could serve as a reward, depending on the objective of the decision maker.
The heterogeneity of patients with depression could also be integrated into the MDP, allowing for individuals experiencing different trajectories. In theory, therefore, it would be feasible to use MDP to optimize the sequential treatment decision at the individual level. For depression, individual-level covariates (including age, gender, baseline symptomatology, educational level, or socio-economic position) could be used to calculate different transition probabilities between states with specific treatment. This would nevertheless require sufficient data on how these covariates affect transition probabilities.
Although MDP proved to be suitable for supporting sequential treatment decisions for depression, several issues continue to require careful consideration. For example, (i) how many states to distinguish and how to define them based on severity; (ii) how to decide on the proper granularity of the treatment choices and decision epochs considered; (iii) which individual characteristics are important to include when optimizing at the individual level; (iv) how to achieve a balance between the level of detail in treatment specification and the feasibility of optimization.
5 Discussion
Markov decision processes can be regarded as an extension of a state-transition model, which is the most frequently applied model structure in health economic evaluations. The STM model structure is based on the Markov chain, which is also the underlying structure in MDPs. In contrast to STMs, however, MDPs include actions and rewards, thereby allowing greater flexibility in defining treatment strategies and enhancing the optimization of these strategies. To optimize sequential treatment decisions in depression, the MDP structure is relevant and interesting for further pursuit. The current study identifies 23 applications of MDP in healthcare, 16 of which use MDP to solve sequential treatment decisions in somatic disease. This demonstrates how MDP has been used to address treatment issues related to somatic disease. In addition, the reformulation of the existing HE model provides insight into how MDP can be applied to depression, and the added value of MDP demonstrates that it has the capacity to make dynamic comparisons of more interventions over time than would a traditional STM.
Our study is subject to several limitations. First, we merely analyze the potential use of MDP for depression in theory. In real-world practical settings, the sequential treatment decision problem might be more complex. Second, we do not assess the quality of each paper, as our main aim is to explore a model of optimizing decision treatment for depression, rather than to analyze the existing publications systematically. Moreover, our search was limited to publications written in English. While we are relatively confident that we identified most existing HE models for depression, we are less certain about our coverage of MDP applications in healthcare, as there is a long list of journals in which such applications could potentially be published. Furthermore, the MDP structure is difficult to identify when it is not adequately described or when it is included as a component of a hybrid model. Third, our review of HE decision models is relatively brief and focused only on aspects that are relevant to the aims of our study. For a complete overview of existing models and their characteristics, other more extensive reviews are available [80, 81].
Sequential decision making in depression treatment is a difficult problem that has given rise to a large volume of research. While some trials have investigated the appropriate type of treatment for patients with depression [82, 83], optimization through a formal simulation modeling approach for depression has yet to be conducted. The repeated choice of optimal sequential treatment decisions (e.g., remain with the current intervention, change to another intervention, or stop treatment) could also help to identify the best treatment duration, based on individual characteristics and a predefined objective.
Recently, a new methodological framework known as whole disease modeling (WDM) has attracted attention. This framework is characterized by its ability to reflect decisions occurring at multiple points within the entire clinical trajectory of a disease. As with MDP, it aims to support decision making throughout the clinical trajectory. In contrast, however, WDM emphasizes macro-level HE evaluation considering all relevant aspects of the disease and its treatment from the preclinical phase until death at the system level (e.g., of a national healthcare system). Like MDP, its decision node is transferable across the entire process, as opposed to the single decision node in conventional HE models. At the same time, however, MDP is suitable for supporting decisions concerning a sequence of treatment decisions that support optimal clinical treatment at the individual level, whereas WDM would not usually allow treatment decisions to be changed based on patient characteristics within a short period. More specifically, the scope of a WDM is usually wider, while its depth is lower.
The current study provides a review of MDP applications within the field of healthcare and demonstrates that the MDP has the potential to steer the optimization of sequential treatment to aid personalized treatment decisions in the treatment of depression. This could potentially inspire healthcare decision makers, modelers, and the research community with regard to optimizing the allocation of healthcare resources.
6 Conclusion
The MDP has been successfully used to address healthcare decision-making problems, especially for those involving sequential treatment decisions. For depression, existing STMs have potential for fitting into the MDP approach, thereby laying a solid foundation for developing an MDP for depression. This approach might be better than STM at depicting continuous treatment decision making. In addition to supporting clinicians by offering an optimal sequential treatment plan over time, this model also provides information about the best timing for starting and ending treatment for heterogeneous patient groups. As in current practice, clinicians lack decision rules on what to do for each patient, when, and in which order. We conclude that the MDP is a potentially powerful model for optimizing sequential treatment in depression and for finding the optimal treatment duration for individuals.
References
Lim GY, Tam WW, Lu Y, Ho CS, Zhang MW, Ho RC. Prevalence of depression in the community from 30 countries between 1994 and 2014. Sci Rep. 2018;8(1):1–10. https://doi.org/10.1038/s41598-018-21243-x.
Stewart AL, Greenfield S, Hays RD, Wells K, Rogers WH, Berry SD, et al. Functional status and well-being of patients with chronic conditions: results from the Medical Outcomes Study. JAMA. 1989;262(7):907–13. https://doi.org/10.1001/jama.1989.03430070055030.
Olesen J, Gustavsson A, Svensson M, Wittchen HU, Jönsson B, Group CS, et al. The economic cost of brain disorders in Europe. Eur J Neurol. 2012;19(1):155–62. https://doi.org/10.1111/j.1468-1331.2011.03590.x.
Greenberg PE, Fournier A-A, Sisitsky T, Simes M, Berman R, Koenigsberg SH, et al. The economic burden of adults with major depressive disorder in the United States (2010 and 2018). Pharmacoeconomics. 2021;39(6):653–65. https://doi.org/10.1007/s40273-021-01019-4.
Mathers CD, Loncar D. Projections of global mortality and burden of disease from 2002 to 2030. PLoS Med. 2006;3(11): e442. https://doi.org/10.1371/journal.pmed.0030442.
Baumann M, Stargardt T, Frey S. Cost-utility of internet-based cognitive behavioral therapy in unipolar depression: a Markov model simulation. Appl Health Econ Health Policy. 2020;18(4):567–78. https://doi.org/10.1007/s40258-019-00551-x.
Solomon D, Adams J, Graves N. Economic evaluation of St. John's wort (Hypericum perforatum) for the treatment of mild to moderate depression. J Affect Disord. 2013;148(2–3):228–34. https://doi.org/10.1016/j.jad.2012.11.064.
Vallejo-Torres L, Castilla I, Gonzalez N, Hunter R, Serrano-Perez P, Perestelo-Perez L. Cost-effectiveness of electroconvulsive therapy compared to repetitive transcranial magnetic stimulation for treatment-resistant severe depression: a decision model. Psychol Med. 2015;45(7):1459–70. https://doi.org/10.1017/S0033291714002554.
Groessl EJ, Tally SR, Hillery N, Maciel A, Garces JA. Cost-effectiveness of a pharmacogenetic test to guide treatment for major depressive disorder. J Manag Care Spec Pharm. 2018;24(8):726–34. https://doi.org/10.18553/jmcp.2018.24.8.726.
Seffinger MA, Hruby RJ. Evidence-based manual medicine: a problem-oriented approach. Elsevier Health Sci; 2007.
Van Straten A, Seekles W, Van ‘t Veer‐Tazelaar NJ, Beekman AT, Cuijpers P. Stepped care for depression in primary care: what should be offered and how? Med J Aust. 2010;192:S36–S9. https://doi.org/10.5694/j.1326-5377.2010.tb03691.x.
Mehltretter J, Rollins C, Benrimoh D, Fratila R, Perlman K, Israel S, et al. Analysis of features selected by a deep learning model for differential treatment selection in depression. Front Artif Intell. 2020;2:31. https://doi.org/10.3389/frai.2019.00031.
Garcia F, Rachelson EJMDPiAI. Markov decision processes. 2013:1–38.
Alagoz O, Hsu H, Schaefer AJ, Roberts MS. Markov decision processes: a tool for sequential decision making under uncertainty. Med Decis Mak. 2010;30(4):474–83. https://doi.org/10.1177/0272989X09353194.
Amari SV, McLaughlin L, Pham H. Cost-effective condition-based maintenance using Markov decision processes. In: Annual reliability and maintainability symposium, 2006; 2006: IEEE. pp. 464–9.
Borrero JS, Akhavan-Tabatabaei R. Time and inventory dependent optimal maintenance policies for single machine workstations: an MDP approach. Eur J Oper Res. 2013;228(3):545–55. https://doi.org/10.1016/j.ejor.2013.02.011.
Abeygunawardane SK, Jirutitijaroen P, Xu H. Adaptive maintenance policies for aging devices using a Markov decision process. IEEE Trans Power Syst. 2013;28(3):3194–203. https://doi.org/10.1109/TPWRS.2012.2237042.
Wei S, Bao Y, Li H. Optimal policy for structure maintenance: a deep reinforcement learning framework. Struct Saf. 2020;83: 101906. https://doi.org/10.1016/j.strusafe.2019.101906.
Song H, Liu C-C, Lawarrée J, Dahlgren RW. Optimal electricity supply bidding by Markov decision process. IEEE Trans Power Syst. 2000;15(2):618–24. https://doi.org/10.1109/59.867150.
Aviv Y, Pazgal A. A partially observed Markov decision process for dynamic pricing. Manag Sci. 2005;51(9):1400–16. https://doi.org/10.1287/mnsc.1050.0393.
Steimle LN, Denton BT. Markov decision processes for screening and treatment of chronic diseases. Markov Decis Process Pract. 2017;189–222.
Siebert U, Alagoz O, Bayoumi AM, Jahn B, Owens DK, Cohen DJ, et al. State-transition modeling: a report of the ISPOR-SMDM modeling good research practices task force-3. Med Decis Mak. 2012;32(5):690–700.
Beck JR, Pauker SG. The Markov process in medical prognosis. Med Decis Mak. 1983;3(4):419–58. https://doi.org/10.1177/0272989X8300300403.
Guo X, Hernández-Lerma O. Continuous-time Markov decision processes. Continuous-Time Markov Decision Processes. Berlin: Springer; 2009. p. 9–18.
Tilson V, Tilson DA. Use of a Markov decision process model for treatment selection in an asymptomatic disease with consideration of risk sensitivity. Socio-Econ Plan Sci. 2013;47(3):172–82. https://doi.org/10.1016/j.seps.2012.09.003.
Shen YJ, Hu MY, Chen QL, Zhang YY, Liang JY, Lu TT, et al. Comparative effectiveness of different combinations of treatment interventions in patients with stroke at the convalescence stage based on the Markov decision process. Evid Based Complement Altern Med. 2020;2020:9. https://doi.org/10.1155/2020/8961341.
Alagoz O, Maillart LM, Schaefer AJ, Roberts MS. The optimal timing of living-donor liver transplantation. Manag Sci. 2004;50(10):1420–30. https://doi.org/10.1287/mnsc.1040.0287.
Alagoz O, Maillart LM, Schaefer AJ, Roberts MS. Choosing among living-donor and cadaveric livers. Manag Sci. 2007;53(11):1702–15. https://doi.org/10.1287/mnsc.1070.0726.
Wu D, Cai Y, Cai J, Liu Q, Zhao Y, Cai J, et al. Comparative effectiveness research on patients with acute ischemic stroke using Markov decision processes. BMC Med Res Methodol. 2012;12(1):1–10.
Akhavan-Tabatabaei R, Sánchez DM, Yeung TG. A Markov decision process model for cervical cancer screening policies in Colombia. Med Decis Mak. 2017;37(2):196–211. https://doi.org/10.1177/0272989X16670622.
Eghbali-Zarch M, Tavakkoli-Moghaddam R, Esfahanian F, Azaron A, Sepehri MM. A Markov decision process for modeling adverse drug reactions in medication treatment of type 2 diabetes. Proc Inst Mech Eng [H]. 2019;233(8):793–811. https://doi.org/10.1177/0954411919853394.
Meng F, Sun Y, Heng BH, Leow MKS. Analysis via Markov decision process to evaluate glycemic control strategies of a large retrospective cohort with type 2 diabetes: the ameliorate study. Acta Diabetol. 2020;57(7):827–34. https://doi.org/10.1007/s00592-020-01492-x.
Mason JE, England DA, Denton BT, Smith SA, Kurt M, Shah ND. Optimizing statin treatment decisions for diabetes patients in the presence of uncertain future adherence. Med Decis Mak. 2012;32(1):154–66. https://doi.org/10.1177/0272989X11404076.
Oh SH, Lee SJ, Noh J, Mo J. Optimal treatment recommendations for diabetes patients using the Markov decision process along with the South Korean electronic health records. Sci Rep. 2021;11(1):10. https://doi.org/10.1038/s41598-021-86419-4.
Bazrafshan N, Lotfi MM. A finite-horizon Markov decision process model for cancer chemotherapy treatment planning: an application to sequential treatment decision making in clinical trials. Ann Oper Res. 2020;295(1):483–502. https://doi.org/10.1007/s10479-020-03706-5.
Hauskrecht M, Fraser H. Planning treatment of ischemic heart disease with partially observable Markov decision processes. Artif Intell Med. 2000;18(3):221–44.
Choi SE, Brandeau ML, Basu S. Dynamic treatment selection and modification for personalised blood pressure therapy using a Markov decision process model: a cost-effectiveness analysis. BMJ Open. 2017;7(11):10. https://doi.org/10.1136/bmjopen-2017-018374.
Ibrahim R, Kucukyazici B, Verter V, Gendreau M, Blostein M. Designing personalized treatment: an application to anticoagulation therapy. Prod Oper Manag. 2016;25(5):902–18.
Abdollahian M, Das TK. A MDP model for breast and ovarian cancer intervention strategies for BRCA1/2 mutation carriers. J Biomed Health Inform. 2015;19(2):720–7. https://doi.org/10.1109/JBHI.2014.2319246.
Schell GJ, Marrero WJ, Lavieri MS, Sussman JB, Hayward RA. Data-driven Markov decision process approximations for personalized hypertension treatment planning. MDM Policy Pract. 2016;1(1):2381468316674214. https://doi.org/10.1177/2381468316674214.
Shifrin M, Siegelmann H. Near-optimal insulin treatment for diabetes patients: a machine learning approach. Artif Intell Med. 2020;107: 101917. https://doi.org/10.1016/j.artmed.2020.101917.
Kim M, Ghate A, Phillips MH. A Markov decision process approach to temporal modulation of dose fractions in radiation therapy planning. Phys Med Biol. 2009;54(14):4455. https://doi.org/10.1088/0031-9155/54/14/007/meta.
Maass K, Kim M. A Markov decision process approach to optimizing cancer therapy using multiple modalities. Math Med Biol. 2020;37(1):22–39. https://doi.org/10.1093/imammb/dqz004.
Liu S, Brandeau ML, Goldhaber-Fiebert JD. Optimizing patient treatment decisions in an era of rapid technological advances: the case of hepatitis C treatment. Health Care Manag Sci. 2017;20(1):16–32. https://doi.org/10.1007/s10729-015-9330-6.
Marrero WJ, Lavieri MS, Sussman JB. Optimal cholesterol treatment plans and genetic testing strategies for cardiovascular diseases. Health Care Manag Sci. 2021;24(1):1–25. https://doi.org/10.1007/s10729-020-09537-x.
Suen S-C, Brandeau ML, Goldhaber-Fiebert JD. Optimal timing of drug sensitivity testing for patients on first-line tuberculosis treatment. Health Care Manag Sci. 2018;21(4):632–46. https://doi.org/10.1007/s10729-017-9416-4.
Escandell-Montero P, Chermisi M, Martinez-Martinez JM, Gomez-Sanchis J, Barbieri C, Soria-Olivas E, et al. Optimization of anemia treatment in hemodialysis patients via reinforcement learning. Artif Intell Med. 2014;62(1):47–60. https://doi.org/10.1016/j.artmed.2014.07.004.
Brown JB, Russell A, Chan W, Pedula K, Aickin M. The global diabetes model: user friendly version 3.0. Diabetes Res Clin Pract. 2000;50:S15–46. https://doi.org/10.1016/S0168-8227(00)00215-1.
Chen J, Alemao E, Yin D, Cook J. Development of a diabetes treatment simulation model: with application to assessing alternative treatment intensification strategies on survival and diabetes-related complications. Diabetes Obes Metab. 2008;10:33–42. https://doi.org/10.1111/j.1463-1326.2008.00885.x.
Serretti A, Olgiati P, Bajo E, Bigelli M, De Ronchi D. A model to incorporate genetic testing (5-HTTLPR) in pharmacological treatment of major depressive disorders. World J Biol Psychiatry. 2011;12(7):501–15. https://doi.org/10.3109/15622975.2011.572998.
Siskind D, Araya R, Kim J. Cost-effectiveness of improved primary care treatment of depression in women in Chile. Br J Psychiatry. 2010;197(4):291–6. https://doi.org/10.1192/bjp.bp.109.068957.
Voigt J, Carpenter L, Leuchter A. Cost effectiveness analysis comparing repetitive transcranial magnetic stimulation to antidepressant medications after a first treatment failure for major depressive disorder in newly diagnosed patients - A lifetime analysis. PLoS ONE. 2017;12(10):15. https://doi.org/10.1371/journal.pone.0186950.
Fitzgibbon KP, Plett D, Chan BCF, Hancock-Howard R, Coyte PC, Blumberger DM. Cost-utility analysis of electroconvulsive therapy and repetitive transcranial magnetic stimulation for treatment-resistant depression in Ontario. Can J Psychiat Rev Can Psychiatry. 2020;65(3):164–73. https://doi.org/10.1177/0706743719890167.
Piera-Jiménez J, Etzelmueller A, Kolovos S, Folkvord F, Lupiáñez-Villanueva F. Guided internet-based cognitive behavioral therapy for depression: implementation cost-effectiveness study. J Med Internet Res. 2021;23(5): e27410.
Sluiter RL, Janzing JG, van der Wilt GJ, Kievit W, Teichert M. An economic model of the cost-utility of pre-emptive genetic testing to support pharmacotherapy in patients with major depression in primary care. Pharmacogenom J. 2019;19(5):480–9. https://doi.org/10.1038/s41397-019-0070-8.
Le LK-D, Lee YY, Engel L, Lal A, Mihalopoulos C. Psychological workplace interventions to prevent major depression: a model-based economic evaluation. Ment Health Prev. 2021;24:200209. https://doi.org/10.1016/j.mhp.2021.200209.
Beil H, Beeber LS, Schwartz TA, Lewis G. Cost-effectiveness of alternative treatments for depression in low-income women. J Ment Health Policy Econ. 2013;16(2):55–65.
van den Berg M, Smit F, Vos T, van Baal PHM. Cost-effectiveness of opportunistic screening and minimal contact psychotherapy to prevent depression in primary care patients. PLoS ONE. 2011;6(8):7. https://doi.org/10.1371/journal.pone.0022884.
Lee Y, Barendregt J, Stockings E, Ferrari A, Whiteford H, Patton G, et al. The population cost-effectiveness of delivering universal and indicated school-based interventions to prevent the onset of major depression among youth in Australia. Epidemiol Psychiatr Sci. 2017;26(5):545–64.
Maniadakis N, Kourlaba G, Mougiakos T, Chatzimanolis I, Jonsson L. Economic evaluation of agomelatine relative to other antidepressants for treatment of major depressive disorders in Greece. BMC Health Serv Res. 2013;13(1):1–10. https://doi.org/10.1186/1472-6963-13-173.
Sawyer L, Azorin J-M, Chang S, Rinciog C, Guiraud-Diawara A, Marre C, et al. Cost-effectiveness of asenapine in the treatment of bipolar I disorder patients with mixed episodes. J Med Econ. 2014;17(7):508–19.
Cheema N, Frangou S, McCrone P. Cost-effectiveness of ethyl-eicosapentaenoic acid in the treatment of bipolar disorder. Ther Adv Psychopharmacol. 2013;3(2):73–81.
Olgiati P, Bajo E, Bigelli M, De Ronchi D, Serretti A. Should pharmacogenetics be incorporated in major depression treatment? Economic evaluation in high-and middle-income European countries. Prog Neuropsychopharmacol Biol Psychiatry. 2012;36(1):147–54. https://doi.org/10.1016/j.pnpbp.2011.08.013.
Zhao YJ, Tor PC, Khoo AL, Teng M, Lim BP, Mok YM. Cost-effectiveness modeling of repetitive transcranial magnetic stimulation compared to electroconvulsive therapy for treatment-resistant depression in Singapore. Neuromodulation. 2018;21(4):376–82. https://doi.org/10.1111/ner.12723.
Nguyen KH, Gordon LG. Cost-effectiveness of repetitive transcranial magnetic stimulation versus antidepressant therapy for treatment-resistant depression. Value Health. 2015;18(5):597–604. https://doi.org/10.1016/j.jval.2015.04.004.
Choi S-E, Brignone M, Cho SJ, Jeon HJ, Jung R, Campbell R, et al. Cost-effectiveness of vortioxetine versus venlafaxine (extended release) in the treatment of major depressive disorder in South Korea. Expert Rev Pharmacoecon Outcomes Res. 2016;16(5):629–38. https://doi.org/10.1586/14737167.2016.1128830.
Soini E, Hallinen T, Brignone M, Campbell R, Diamand F, Cure S, et al. Cost-utility analysis of vortioxetine versus agomelatine, bupropion SR, sertraline and venlafaxine XR after treatment switch in major depressive disorder in Finland. Expert Rev Pharmacoecon Outcomes Res. 2017;17(3):293–302. https://doi.org/10.1080/14737167.2017.1240617.
Young AH, Evitt L, Brignone M, Diamand F, Atsou K, Campbell R, et al. Cost-utility evaluation of vortioxetine in patients with Major Depressive Disorder experiencing inadequate response to alternative antidepressants in the United Kingdom. J Affect Disord. 2017;218:291–8. https://doi.org/10.1016/j.jad.2017.04.019.
Ross EL, Vijan S, Miller EM, Valenstein M, Zivin K. The cost-effectiveness of cognitive behavioral therapy versus second-generation antidepressants for initial treatment of major depressive disorder in the United States a decision analytic model. Ann Intern Med. 2019;171(11):785. https://doi.org/10.7326/M18-1480.
Sado M, Wada M, Ninomiya A, Nohara H, Kosugi T, Arai M, et al. Does the rapid response of an antidepressant contribute to better cost-effectiveness? Comparison between mirtazapine and SSRIs for first-line treatment of depression in Japan. Psychiatry Clin Neurosci. 2019;73(7):400–8. https://doi.org/10.1111/pcn.12851.
Lokkerbol J, Wijnen B, Ruhe HG, Spijker J, Morad A, Schoevers R, et al. Design of a health-economic Markov model to assess cost-effectiveness and budget impact of the prevention and treatment of depressive disorder. Expert Rev Pharmacoecon Outcomes Res. 2020;21(5):1–12. https://doi.org/10.1080/14737167.2021.1844566.
Yamada Y, Miyahara R, Wada M, Ninomiya A, Kosugi T, Mimura M, et al. A comparison of cost-effectiveness between offering antidepressant-CBT combinations first or second, for moderate to severe depression in Japan. J Affect Disord. 2021;292:574–82. https://doi.org/10.1016/j.jad.2021.05.095.
Ross EL, Zivin K, Maixner DF. Cost-effectiveness of electroconvulsive therapy vs pharmacotherapy/psychotherapy for treatment-resistant depression in the United States. JAMA Psychiat. 2018;75(7):713–22.
Ssegonja R, Sampaio F, Alaie I, Philipson A, Hagberg L, Murray K, et al. Cost-effectiveness of an indicated preventive intervention for depression in adolescents: a model to support decision making. J Affect Disord. 2020;277:789–99. https://doi.org/10.1016/j.jad.2020.08.076.
Fabbri C, Kasper S, Zohar J, Souery D, Montgomery S, Albani D, et al. Cost-effectiveness of genetic and clinical predictors for choosing combined psychotherapy and pharmacotherapy in major depression. J Affect Disord. 2021;279:722–9.
Meeuwissen JAC, Feenstra TL, Smit F, Blankers M, Spijker J, Bockting CLH, et al. The cost-utility of stepped-care algorithms according to depression guideline recommendations - Results of a state-transition model analysis. J Affect Disord. 2019;242:244–54. https://doi.org/10.1016/j.jad.2018.08.024.
Cocker F, Nicholson JM, Graves N, Oldenburg B, Palmer AJ, Martin A, et al. Depression in working adults: comparing the costs and health outcomes of working when ill. PLoS ONE. 2014;9(9):9. https://doi.org/10.1371/journal.pone.0105430.
Zhan Z, Wei W, Xu H. Hamilton–Jacobi–Bellman equations on time scales. Math Comput Model. 2009;49(9–10):2019–28.
Chadès I, Chapron G, Cros MJ, Garcia F, Sabbadin R. MDPtoolbox: a multi-platform toolbox to solve stochastic dynamic programming problems. Ecography. 2014;37(9):916–20.
Afzali HHA, Karnon J, Gray J. A critical review of model-based economic studies of depression. Pharmacoeconomics. 2012;30(6):461–82. https://doi.org/10.2165/11590500-000000000-00000.
Kolovos S, Bosmans JE, Riper H, Chevreul K, Coupé VM, van Tulder MW. Model-based economic evaluation of treatments for depression: a systematic literature review. PharmacoEconom Open. 2017;1(3):149–65. https://doi.org/10.1007/s41669-017-0014-7.
von Helversen B, Wilke A, Johnson T, Schmid G, Klapp B. Performance benefits of depression: Sequential decision making in a healthy sample and a clinically depressed sample. J Abnorm Psychol. 2011;120(4):962. https://doi.org/10.1037/a0023238.
DeRubeis RJ, Cohen ZD, Forand NR, Fournier JC, Gelfand LA, Lorenzo-Luaces L. The Personalized Advantage Index: translating research on prediction into individualized treatment recommendations. A demonstration. PLoS ONE. 2014;9(1): e83875. https://doi.org/10.1371/journal.pone.0083875.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
The authors received no financial support for the research, authorship, or publication of this article.
Conflict of interest
All authors declare that they have no conflict of interest.
Ethics approval
This article does not contain any studies involving human participants and, as such, no ethical approval was required.
Consent to participate
Not applicable.
Consent for publication
Not applicable
Availability of data and material
Data for the illustrative application of the Markov decision process were taken from published works. These data are also provided in the supplementary material.
Code availability
The code is available upon request.
Author contributions
Concept and design: FL, FJ, TF. Acquisition of data: FL, XL. Analysis and interpretation of data: FL. Drafting of the manuscript: FL, FJ, TF. Critical revision of the paper for important intellectual content: FL, FJ, XL, TF. Statistical analysis: FL. Supervision: TF.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
Li, F., Jörg, F., Li, X. et al. A Promising Approach to Optimizing Sequential Treatment Decisions for Depression: Markov Decision Process. PharmacoEconomics 40, 1015–1032 (2022). https://doi.org/10.1007/s40273-022-01185-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40273-022-01185-z