Abstract
Background and Objective
Mechanistic static and dynamic physiologically based pharmacokinetic models are used in clinical drug development to assess the risk of drug–drug interactions (DDIs). Currently, the use of mechanistic static models is restricted to screening DDI risk for an investigational drug, while dynamic physiologically based pharmacokinetic models are used for quantitative predictions of DDIs to support regulatory filing. As physiologically based pharmacokinetic model development by sponsors as well as a review of models by regulators require considerable resources, we explored the possibility of using mechanistic static models to support regulatory filing, using representative cases of successful physiologically based pharmacokinetic submissions to the US Food and Drug Administration under different classes of applications.
Methods
Drug–drug interaction predictions with mechanistic static models were done for representative cases in the different classes of applications using the same data and modelling workflow as described in the Food and Drug Administration clinical pharmacology reviews. We investigated the hypothesis that the use of unbound average steady-state concentrations of modulators as driver concentrations in the mechanistic static models should lead to the same conclusions as those from physiologically based pharmacokinetic modelling for non-dynamic measures of DDI risk assessment such as the area under the plasma concentration–time curve ratio, provided the same input data are employed for the interacting drugs.
Results
Drug–drug interaction predictions of area under the plasma concentration–time curve ratios using mechanistic static models were mostly comparable to those reported in the Food and Drug Administration reviews using physiologically based pharmacokinetic models for all representative cases in the different classes of applications.
Conclusions
The results reported in this study should encourage the use of models that best fit an intended purpose, limiting the use of physiologically based pharmacokinetic models to those applications that leverage its unique strengths, such as what-if scenario testing to understand the effect of dose staggering, evaluating the role of uptake and efflux transporters, extrapolating DDI effects from studied to unstudied populations, or assessing the impact of DDIs on the exposure of a victim drug with concurrent mechanisms. With this first step, we hope to trigger a scientific discussion on the value of a routine comparison of the two methods for regulatory submissions to potentially create a best practice that could help identify examples where the use of dynamic changes in modulator concentrations could make a difference to DDI risk assessment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Dynamic physiologically based pharmacokinetic models are typically considered superior to mechanistic static models for quantitative predictions regarding drug–drug interaction risk assessment. |
The case studies presented in this article demonstrate mostly comparable performance of static and dynamic models for high-impact applications of drug–drug interaction risk assessment supporting study waivers and label recommendations. |
We propose that fit-for-purpose simpler approaches can be used to support regulatory filing, reserving the use of physiologically based pharmacokinetic models to those applications that cannot be served by static models. |
1 Introduction
Drug–drug interactions (DDIs) are a major concern in drug development. Drug interaction studies that are designed to maximise the possibility of detecting an interaction are therefore conducted to evaluate the effect of concomitant medications on the pharmacokinetics of the investigational drug, as well as to evaluate the effect of the investigational drug on the pharmacokinetics of concomitant medications. The clinical significance of the observed interaction is assessed based on the therapeutic window and the steepness of the exposure–response curve in the target population to guide risk management in subsequent trials and to guide dosage recommendations in various sections of drug labels. Regulatory DDI guidelines for in vitro [1] and clinical studies [2, 3] are currently being harmonised by an ICH working group.
Mechanistic static models (MSMs) [4] and dynamic physiologically based pharmacokinetic (PBPK) models employing in vitro data to estimate the ratio of the area under the plasma concentration–time curve (AUCR) of a victim drug in the presence and absence of a perpetrator have been used to assess potential clinical DDIs, eliminate DDI risk, guide decisions and support study design (Fig. 1). When an investigational drug is a victim of a DDI, models can be used to predict DDI effects with a less potent modulator after the model has been confirmed with an index modulator as well as to predict clinically relevant DDI effects following multiple-dose administration of a substrate that has time-dependent changes in clearance (e.g. the investigational drug is a victim as well as a time-dependent inhibitor and/or inducer of same enzyme). When the investigational drug is a perpetrator of DDIs, models can be used to support the lack of clinical DDI potential or to predict DDI effects under different dosing regimes, after the model has been confirmed with an index substrate.
Unlike MSMs, PBPK models can consider dynamically varying perpetrator concentrations. By incorporating population differences in physiology and enzyme/transporter expression, they allow simulations of virtual populations and explain pharmacokinetic differences due to genetic polymorphisms. Physiologically based pharmacokinetic models facilitate DDI study design to maximise interactions via what-if scenario testing. Model simulations can be helpful to understand the impact of dose staggering on drug interactions, the impact of a time-dependent inhibitor on the inactivation of an enzyme or explore enzyme-transporter interplay. Dynamic models allow the estimation of maximum concentration ratios in addition to AUCRs. Unlike MSMs, PBPK models allow the evaluation of complex interactions involving transporters and enzymes in multiple sites. However, this would require that underlying mechanisms are captured well, and model parameters are quantitatively reliable. This requirement is often challenged by parameter non-identifiability (especially for an orally administered victim drug) and poor in vitro to in vivo extrapolation. Another unique strength of PBPK modelling is its ability to extrapolate DDI effects in a healthy population to an unstudied population, which could be a target population or organ impaired population. Leveraging this strength requires that population-related changes in physiology and enzyme/transporter expression are well understood. Knowledge gaps in these may limit the accuracy of model extrapolations [5,6,7,8].
Several studies have demonstrated that MSMs can also make quantitative predictions of DDIs [9,10,11,12] with the use of appropriate driver concentrations in the gut and liver. For high-clearance victim drugs with large first-pass extraction, the gut contribution to the overall DDI is likely to be high, but the choice of an appropriate gut concentration for use in MSMs is difficult. Even though gut concentrations are easily determined in dynamic models, the in vivo relevance cannot be validated. For low-clearance victim drugs for which the role of the gut in determining DDIs could be considered negligible, MSM predictions using the average unbound systemic concentration of a modulator as the driver concentration should not be different to predictions from dynamic PBPK models. However, regulatory guidelines for DDIs from the US Food and Drug Administration (FDA) recommend the use of an MSM for screening and warrants further investigations with either PBPK modelling or a clinical study when an MSM predicts an interaction (0.8 > AUCR > 1.25) [1]. This recommendation has led to several PBPK submissions to the FDA both for Investigational New Drugs and New Drug Applications. The FDA’s Office of Clinical Pharmacology published articles summarising the impact of PBPK modelling on prescribing information in the submissions received since 2008 [6, 13]. These articles provide a comprehensive list of all submissions that resulted in a study waiver and label recommendations and those that were not accepted.
Given the uncertainty over regulatory acceptance of PBPK models to support labelling recommendations and the considerable resources in terms of time and cost needed for model development, we asked if it would make sense to reserve PBPK modelling to applications where it brings unique value and where the probability of regulatory acceptance is high; and can MSMs measure up to dynamic models to support regulatory filing for study waivers and label recommendations? As a first step to answering these pertinent questions, we used representative cases of successful PBPK submissions to the FDA where PBPK modelling resulted in averting a clinical DDI study or informed drug labels (dose adjustments, avoid concomitant use, or no warnings) and explore the possibility of employing MSMs to support regulatory filing. We investigated the hypothesis that the use of unbound average steady-state concentrations of modulators as driver concentrations in MSMs should lead to the same conclusions as those from PBPK modelling for non-dynamic measures of DDI risk assessment such as the AUCR, provided the same input data are employed for the interacting drugs. With this first step, we hope to stimulate further discussion within the scientific community, regulatory authorities as well as with academic and industry partners.
2 Methods
Representative cases in the different classes of high-impact applications of PBPK models for investigational drugs as victims or perpetrators of DDIs, submitted to the FDA [6, 13] were chosen for the study. High-impact applications are defined as those regulatory filings that resulted in averting a clinical DDI study or contributed to labelling recommendations. Employing the same data and modelling workflow as described in the FDA clinical pharmacology reviews [6, 13], we compared the results of MSMs with those from PBPK models for representative cases in each class of application. Workflows for all case studies are provided in the Electronic Supplementary Material (ESM). Apart from ibrutinib, representative cases were selected from recent submissions to the FDA, for which a detailed description of the PBPK modelling approach and data were available in the FDA’s clinical pharmacology reviews. Ibrutinib was chosen as an example of a cytochrome P450 (CYP) 3A substrate with high clearance, undergoing considerable first-pass metabolism in the gut and liver.
The mechanistic static equations used in this study are reported elsewhere [4, 14, 15] and provided in the ESM accompanying this article. Average steady-state concentrations were used as the driver concentrations. They were obtained from clinical pharmacokinetic studies, by dividing the steady-state area under the curve (AUC) over one dosing interval by the time of the dosing interval. The overall AUCR of an interaction resulting from two affected enzymes is calculated by multiplying the AUCR of individual interactions.
As the gut contribution to DDIs for CYP3A-metabolised, low-clearance victim drugs is likely to be low because of negligible intestinal metabolism, the induction potency of rifampin (rifampin concentration supporting half-maximal induction, IndC50) relevant for interaction with low-clearance drugs (voxelotor, siponimod, apalutamide and ivosidenib) is only IndC50 of rifampin at the hepatic level. This is estimated to be 1.9 µM from a clinical DDI study of oral rifampin 600 mg and intravenous midazolam 0.5 mg [16] (see ESM). However, for the high-clearance drug, ibrutinib, the gut contribution to overall induction is high and an IndC50 of rifampin used was 0.32 µM. Compound-related parameters for investigational drugs were obtained from FDA reviews [6, 13]. To be consistent between the investigated cases, all interaction parameters for index drugs were taken from Simcyp V19 [17] (Table S1 of the ESM). In this work, inhibitors that increase the AUC of sensitive index substrates of a given metabolic pathway ≥ 5-fold, between 2-fold and 5-fold, and ≥ 1.25 to < 2-fold are defined as strong, moderate and weak inhibitors, respectively. Inducers that decrease the AUC of sensitive index substrates of a given metabolic pathway by ≥ 80%, ≥ 50% to < 80%, and ≥ 20% to < 50% are referred to as strong moderate and weak inducers respectively [18].
3 Results
Table 1 shows the major application areas of successful PBPK submissions to the FDA that resulted in a study waiver or labelling recommendations, both for the investigational drug as a perpetrator of DDIs and as a victim of DDIs. These cases cover drug interactions mediated by CYP2C8, CYP2C9, CYP3A and organic anion transporter 3 (OAT3). The first application under “investigational drug as perpetrator of reversible inhibition and/or induction of CYPs and/or transporter inhibition” is the prediction of a lack of clinical DDI potential, if the model-predicted AUCR with an index substrate under ‘worst-case’ conditions has been confirmed to be within the range of 0.8–1.25. To account for the uncertainty in the key model parameters, fraction unbound in the in vitro incubation (fu,inc) and inhibition constant (Ki), a sensitivity analysis is carried out, by varying these parameters over a reasonable range. A ten-fold range is generally recommended for Ki, reflecting the large inter-laboratory variations in the in vitro assays. No difference in outcome is anticipated between MSM and PBPK for this category, as this is only a screening exercise and both methods are expected to predict a lack of relevant interaction. Therefore, no specific case is chosen for this category. Similarly, no specific case is chosen for the prediction of effect of CYP modulators on sensitive substrates under “investigational drug as victim of CYP inhibition, CYP induction, or transporter inhibition”. Here, a drug is considered a sensitive substrate based on absorption, distribution, metabolism and elimination (ADME)/mass balance studies. A prediction to support conservative labelling to avoid concomitant use of strong inhibitors and inducers cannot be different between MSMs and PBPK models for this class, as this is dependent on the fm,CYP derived from a mass balance study combined with either in vitro recombinant CYP kinetics or an in vitro chemical inhibition study. For all other categories of major applications of PBPK models for an investigational drug as a victim or perpetrator of DDIs, we use representative examples to compare the performance of MSMs and PBPK models. The results from MSMs are presented alongside those reported for PBPK modelling in Sects. 3.1–3.7. The IndC50 for rifampin at a hepatic level derived from its interaction with midazolam administered intravenously [16] is 1.9 µM.
3.1 Voxelotor (CYP3A4 Inhibitor)
To evaluate the effect of voxelotor, a CYP3A modulator on the pharmacokinetics of midazolam, a sensitive CYP3A substrate at the higher registrational dose of voxelotor, after the model confirms the clinical DDI effect observed at a different dosing regime.
3.1.1 Background
In an in vivo cocktail DDI study [19], voxelotor was administered at a dose of 900 mg on days 1 and 2, and at a dose of 600 mg on day 3 through day 7. The cocktail was administered on day 4. In this study, voxelotor altered the exposure of only midazolam (a CYP3A substrate) by 63% (AUCR = 1.63), but not the exposure of other sensitive CYP substrates [19].
3.1.2 PBPK Model Predictions
Physiologically based pharmacokinetic model predictions of DDI effects at the registrational dose of 1500 mg once daily (QD) were performed by the sponsor, following optimisation of voxelotor Ki using the midazolam interaction in a cocktail study. The predictions led to a conservative label recommendation in Sect. 7.2 to avoid coadministration of voxelotor with sensitive CYP3A4 substrates with a narrow therapeutic index or if concomitant use is unavoidable, to consider a dose reduction of the sensitive CYP3A4 substrate(s) [19].
3.1.3 MSM
Mechanistic static models were used in this study to evaluate the effect of voxelotor as a perpetrator at the registrational dose level of 1500 mg QD, after the model confirmed the results of the cocktail study. The input data used in the model are shown in Table 2.
3.1.4 Parameter Optimisation
As in the PBPK analysis, the DDI effect of the voxelotor–midazolam interaction observed in the cocktail study was used to optimise voxelotor Ki for CYP3A inhibition. While voxelotor Ki is the only model parameter requiring optimisation in PBPK modelling, the fraction of midazolam escaping gut metabolism (fgut,i) following inhibition by voxelotor is also unknown in MSMs. To overcome this challenge, all possible combinations of voxelotor Ki and midazolam fgut,i were explored that could recover the observed AUCR of 1.63 for the voxelotor–midazolam interaction.
All possible parameter combinations in two extreme scenarios have been considered to predict DDIs at the clinically tested dosing regime of 900 mg on days 1 and 2, and at a dose of 600 mg on day 3 through day 7. One, where only gut interaction and no systemic interaction occurs (scenario 1) and another, where only a systemic interaction and no gut interaction occurs (scenario 2). To consider scenario 1, fgut,i of midazolam had to be reduced to at least 0.87 (if there was complete inhibition of gut enzymes by voxelotor, fgut,i for midazolam would be 1). In addition, Ki must be 0.5 µM or more to ensure the absence of a systemic interaction to match the predicted DDI to the clinically observed value of 1.63 (see Table 3). To consider scenario 2, fgut,i for midazolam is set to its fgut (0.57) [21], so that the fraction escaping gut metabolism with and without voxelotor is the same. The voxelotor Ki that recovers the observed AUCR of 1.63 for voxelotor-midazolam interaction is then 0.06 µM (see Table 3). In both scenarios, the inhibitor (voxelotor) concentration was set to the average plasma concentration on day 4 in the cocktail study at 900/600 mg (see Table 2).
The MSM was then used to estimate the AUCR of midazolam at the registrational dose of voxelotor (1500 mg). The steady-state concentration of voxelotor at 1500 mg was used in the model (see Table 2) using both sets of parameters. The results are shown in Table 3. The MSM predicted AUCR at 1500 mg of voxelotor compares reasonably well with PBPK predictions (see Table 4).
Thus, the MSM could only predict a range of plausible values for a midazolam interaction with voxelotor 1500 mg QD. However, given the very low fup of voxelotor (see Table 2), scenario 1 (AUCR = 1.78) is more likely.
3.2 Ivosidenib (CYP3A Inducer)
To predict the effect of CYP3A induction on midazolam by using an autoinduction effect of ivosidenib (a sensitive CYP3A substrate), in lieu of a DDI study with midazolam and to evaluate the effects of rifampin (CYP3A) on the steady-state exposure of ivosidenib.
3.2.1 Background
Ivosidenib, an isocitrate dehydrogenase-1 inhibitor to treat acute myeloid leukaemia (AML) in patients with a susceptible isocitrate dehydrogenase-1 mutation, is a substrate of P-glycoproteein (P-gp) and primarily metabolised by CYP3A (98%). It is also an inducer of CYP3A4, CYP2B6, CYP2C8 and CYP2C9 [22]. As a substrate and inducer of CYP3A, auto-induction effects of ivosidenib observed in repeated-dose clinical pharmacokinetic profiles at various doses could be used to characterise the induction potential in lieu of DDI study with a sensitive CYP3A substrate such as midazolam. In the PBPK model, IndC50 was derived through a sensitivity analysis to compare the simulated ratios of maximum concentration and AUC0–24 of ivosidenib at steady state versus a single dose over a range of CYP3A4 induction parameters. The value of IndC50 that led to a prediction of accumulation that best matched with the clinically observed accumulation was identified as the IndC50 [22].
3.2.2 PBPK Model Predictions
The PBPK model predictions of the effect of co-administration of ivosidenib (500 mg QD for 19 days) on midazolam (5 mg on day 15) led to the label recommendation to avoid concomitant use of ivosidenib with sensitive CYP3A substrates [22]. Model predictions of the effect of concomitant rifampin (600 mg QD for 15 days) on the steady-state exposure of ivosidenib (500 mg QD for 30 days) led to the conservative label recommendation to avoid coadministration of strong CYP3A inducers.
The inputs used in the MSM to evaluate the effect of CYP3A induction by ivosidenib at 500 mg QD on midazolam and to evaluate the effects of CYP3A inducer rifampin on steady-state exposure of ivosidenib are shown in Table 5. To evaluate the effect of CYP3A induction by rifampin alone on the steady-state exposure of ivosidenib, the combined effect of rifampin and ivosidenib on the steady-state exposure of ivosidenib is first determined by additive and multiplicative models (see ESM) and the average calculated. The fold induction due to rifampin alone is calculated as the ratio of reduction in the exposure of ivosidenib due to the combined effect to the reduction in exposure of ivosidenib due to the autoinduction effect.
3.2.3 IndC50 Optimisation
As in the PBPK analysis, IndC50 was optimised in MSM, by identifying the value of the parameter needed to recover the observed AUCR of ivosidenib autoinduction, by using ivosidenib victim and perpetrator parameters (Table 5) in the MSM for induction. The AUCR of ivosidenib autoinduction is simply the inverse of the steady-state fold change in the apparent clearance of ivosidenib due to the autoinduction effect of ivosidenib in patients with AML, which was estimated by population pharmacokinetic analyses to be 1.66 [22]. By systematically varying IndC50 value used in the MSM equation for induction, the value leading to a predicted AUCR that matches the observed AUCR of autoinduction is identified as the optimised IndC50. This approach is equivalent to the sensitivity analysis in PBPK modelling described in Sect. 3.2.1.
3.2.4 Results
The MSM predictions of the effect of co-administration of ivosidenib (500 mg QD for 19 days) and midazolam (5 mg on day 15) as well as predictions of the effect of concomitant rifampin (600 mg QD for 15 days) on the steady-state exposure of ivosidenib (500 mg QD for 30 days) are somewhat comparable to those from PBPK modelling (Table 6).
Fold change in ivosidenib clearance due to rifampin alone = fold change in ivosidenib clearance due to combined effect/fold change in ivosidenib clearance due to autoinduction effect (see Table 7)
-
Multiplicative: (1/0.25) / (1/0.6) = (4/1.67) = 2.4;
-
AUCR predicted (MSM) =1/2.4 = 0.42.
3.3 Ibrutinib (CYP3A Substrate)
To predict the effect of moderate (erythromycin, diltiazem) and weak (fluvoxamine) CYP3A inhibitors and moderate CYP3A inducer (efavirenz) on ibrutinib exposure, after the model has been confirmed with a strong CYP3A inhibitor (ketoconazole) and an inducer (rifampin).
3.3.1 Background
Ibrutinib is a potent covalent inhibitor of Bruton’s tyrosine kinase developed for treating B-lymphocyte cell malignancies and is approved for relapsed chronic lymphocytic leukemia and mantle cell lymphoma [23]. The primary route of elimination of ibrutinib is through CYP3A4-mediated metabolism [24]. Co-administration of ibrutinib 40 mg with ketoconazole (400 mg QD) increased ibrutinib AUC by 24-fold, while 560 mg co-administration of ibrutinib with rifampin (600 mg QD) decreased ibrutinib AUC by ten-fold [25].
3.3.2 PBPK Analysis
A PBPK model was developed for ibrutinib by the sponsor based on available physicochemical properties, in vitro experiments and clinical pharmacokinetic parameters [26]. Models for all modulators were from the Simcyp compound library. The DDI of ketoconazole 400 mg QD with ibrutinib was simulated assuming complete inhibition of intestinal CYP3A4 by setting the fraction unbound escaping the intestine (fu,gut) for ibrutinib to 1. The Ki of ketoconazole was optimised (to 2.43 µM) to recover the clinical interaction with ibrutinib (AUCR = 24). Fluvoxamine inhibition potency towards CYP2C19 in vivo is reported to be ∼40 times greater than in vitro [24]. To cover a potential underprediction of the in vitro CYP3A Ki in the fluvoxamine model, the fluvoxamine in vivo CYP3A4 Ki specific for ibrutinib inhibition was determined by adjusting the in vitro Ki of fluvoxamine with ibrutinib by the same factor that was needed to recover the in vivo DDIs with midazolam (Ki = 2.6 μM) or alprazolam (Ki = 0.52 μM), This was possible, although fluvoxamine is known to extensively bind to protein in in vitro models, as the in vitro conditions for all three compounds (midazolam, alprazolam and ibrutinib) were maintained at similar protein concentrations. This strategy has been used and discussed in PBPK models using other Software platforms [27]. The fluvoxamine Simcyp file with the optimised ibrutinib specific Ki (3 μM) was used to predict the fluvoxamine–ibrutinib interaction. For all other modulators, the models in Simcyp V14 were adopted as such. Based on the PBPK predictions, the label for ibrutinib recommends that co-administration of ibrutinib with strong inhibitors or inducers should be avoided. Ibrutinib dose should be reduced to 140 mg (quarter of maximal prescribed dose) when co-administered with moderate CYP3A4 inhibitors so that its exposures remain within observed ranges at therapeutic doses. The label does not specify any recommendation for concomitant moderate inducers.
3.3.3 MSMs
Mechanistic static models were used in this study to evaluate the DDI effects of modulators on ibrutinib with fm = 1, fm,CYP3A =1 and assuming complete inhibition of intestinal CYP3A by ketoconazole (fgut,i = 1). Unlike PBPK simulations, Ki of ketoconazole was not optimised using the ketoconazole-ibrutinib clinical DDI study. Instead, this DDI study was used to optimise the only unknown victim-related parameter in the model, which is fgut of ibrutinib. Optimisation of ibrutinib fgut was achieved by systematically varying its value, until model prediction of ibrutinib AUCR matched the observed ibrutinib AUCR. The optimised value of fgut is 0.345. In a further deviation from the PBPK analysis, the fgut was validated using the clinical DDI study of ibrutinib with itraconazole [42]. Ibrutinib is the only drug in this study, for which a deviation from the PBPK workflow was necessary.
3.3.4 Results
The mechanistic model predictions are not very comparable to those obtained from PBPK models (see Table 8) for induction, possibly owing to the different approaches used in the two models to optimise model parameters based on a clinical DDI study where ketoconazole Ki was optimised in PBPK while fgut was optimised in the MSM). Another reason could be that the interaction parameters for modulators were from Simcyp V19 in the MSM, whereas the submission to the FDA was done with an older version of Simcyp. However, in the absence of a clinical study with efavirenz, it is difficult to understand the differences between the two approaches.
3.4 Voxelotor (CYP3A Substrate)
Evaluate the effects of CYP3A inhibitors (ketoconazole, fluconazole) and inducers (efavirenz, rifampin) on the pharmacokinetics of voxelotor using an estimated contribution of CYP3A4 to the total drug metabolism (fmCYP3A4) of 0.36 or 0.56, derived from mass balance [19] with either in vitro recombinant CYP kinetics or the in vitro chemical inhibition study, respectively. Evaluate the DDI effects considering a worst-case scenario attributing all oxidative metabolism of voxelotor to CYP3A (fmCYP3A4 = 0.74) [19].
3.4.1 Background
Voxelotor undergoes oxidative metabolism mediated by multiple CYPs (3A4, 3A5, 2C9, 2C19 and 2B6) (73.78%), direct conjugation by UGT1A1 and UGT1A9 (18.7%) as well as reduction (7.52%) [19]. Cytochrome P450 3A accounts for 36–56% of metabolism while the fraction metabolised by other individual CYPs is less than 10%. Given its very low metabolic clearance 3.35 L/h [19], it is unlikely to be affected by intestinal CYP3A-mediated metabolism or drug interactions in the gut [19].
3.4.2 PBPK Analysis
Even in the absence of a dedicated DDI study to evaluate the effect of a CYP3A modulator on the pharmacokinetics of voxelotor, the results of the PBPK evaluation [19] and pharmacokinetic/pharmacodynamic analysis were considered sufficient to recommend a dose adjustment in the US prescribing information Sects. 2, 7, 12.3 for voxelotor when it is co-administered with CYP3A modulators.
3.4.3 MSM Calculations
Mechanistic static model calculations were performed using the models shown in the ESM, using the same data that were employed in the PBPK analysis reported [19]. The DDI effects of CYP3A inhibitors (ketoconazole, fluconazole) and inducers (efavirenz, rifampin) on voxelotor exposure were done using an estimated contribution of CYP3A4 to the total drug metabolism (fmCYP3A4) of 0.36 or 0.56 and for the worst-case scenario, attributing all oxidative metabolism of voxelotor to CYP3A. To consider the low likelihood of intestinal CYP3A-mediated drug interactions, fgut,i and fgut were set to 1 (assuming that the fraction of voxelotor escaping intestinal metabolism in the presence and absence of inhibitor is the same). In the case of fluconazole and fluvoxamine that inhibit both CYP3A4 and CYP2C9, MSM predictions were done using Ki for each enzyme separately. The two resulting AUCRs are multiplied to get the overall AUCR, which is then compared to the PBPK model. As with the PBPK analysis, no parameter optimisation was done.
3.4.4 Results
The MSM predictions are comparable to those obtained from PBPK modelling for the modulators evaluated (see Table 9). It is worth noting that a clinical DDI study of voxelotor with itraconazole conducted later showed only a modest 11% increase of voxelotor AUC in healthy subjects according to US product labelling [45]. This modest effect may be explained based on the multiple metabolic pathways and the absence of a gut interaction for voxelotor.
3.5 Siponimod (Substrate of CYP3A4 and CYP2C9)
To predict DDI effects of CYP modulators (CYP3A4/CYP2C9 inhibitors or inducers) on the exposures of siponimod in sub-populations carrying polymorphic CYP2C9 variants.
3.5.1 Background
Siponimod is a sphingosine 1-phosphate receptor modulator indicated for the treatment of relapsing forms of multiple sclerosis. [28, 29] The absolute bioavailability of siponimod is approximately 84%, and the mean elimination half-life is 30 hours, respectively. The oral clearance of siponimod is very low. Siponimod is a substrate of both CYP2C9 and CYP3A4 with fm,CYP of 80% and 18%, respectively, by each enzyme. It is not a modulator of CYP enzymes and is not a substrate of uptake or efflux transporters.
3.5.2 PBPK Analyses [28, 29]
The PBPK analyses [28, 29] were performed by the sponsor to evaluate the effects of CYP3A4/CYP2C9 modulators on siponimod pharmacokinetics in subjects with various CYP2C9 genotypes. The model was initially validated by comparing PBPK predictions with observed pharmacokinetic data in subjects carrying CYP2C9 *1/*1, *2/*3 and *3/*3. The PBPK model was also able to recover the DDI when siponimod was co-administered with fluconazole (a CYP2C9 and CYP3A inhibitor), itraconazole (a CYP3A inhibitor) and rifampin (a CYP2C9 and CYP3A inducer) in subjects carrying CYP2C9 genotypes *1/*1, *1/*2 or 1/*3. It was then used to predict the DDI effects of CYP2C9 and CYP3A modulators (fluconazole, ketoconazole, erythromycin, fluvoxamine, and efavirenz) on the pharmacokinetics of siponimod in subjects carrying CYP2C9 *1/*1, *1/*2, *2/*2, *1/*3 and *2/*3 genotypes.
The PBPK predictions along with genomic and DDI studies led to recommendations to avoid concomitant administration of a moderate CYP2C9/3A4 dual inhibitor or a moderate CYP2C9 inhibitor with a strong or moderate CYP3A4 inhibitor for all patients; avoid concomitant use of strong CYP3A4/moderate CYP2C9 inducers (e.g. rifampicin or carbamazepine) in all patients; and avoid concomitant use of moderate CYP3A4 inducer with siponimod in patients with CYP2C9 *1/*3 or *2/*3 genotypes.
3.5.3 MSM
Mechanistic static models were used in this study to evaluate the effects of CYP2C9 and CYP3A modulators (fluconazole, ketoconazole, erythromycin, fluvoxamine, rifampin and efavirenz) on the pharmacokinetics of siponimod in subjects carrying CYP2C9 *1/*1, *1/*2, *2/*2, *1/*3, and *2/*3 genotypes. First, fm,CYP2C9 and fm,CYP3A4 are estimated for each of the genotypes as shown in Table 10. Clearance driven by CYP2C9 in each genotype is calculated by subtracting the fractional clearance due to all other enzymes (assumed constant in all genotypes) from total clearance in that genotype. Contribution of CYP3A4 and all other enzymes is calculated as 20% of total clearance in *1/*1. To consider the low likelihood of intestinal CYP3A-mediated drug interactions for siponimod because of its low clearance, fgut,i and fgut were set to 1 (fraction of siponimod escaping intestinal metabolism in the presence and absence of inhibitor is the same). Fluconazole and fluvoxamine inhibit both CYP3A and CYP2C9. In MSMs, the Ki of each enzyme is separately used in MSMs to arrive at an AUCR for each enzyme. The individual AUCR values are then multiplied to give the overall AUCR to consider the inhibition of both enzymes.
3.5.4 Results
Table 11 summarises AUCRs predicted by an MSM. Mechanistic static model predictions of siponimod interactions with inhibitors and efavirenz were comparable to those from the PBPK model. However, MSM predictions of siponimod interactions with rifampin showed a higher risk relative to predictions from PBPK modeling. In a dedicated DDI study with rifampin 600 mg once daily, the AUC of siponimod was reduced by 57% (AUCR ~0.43) [29]. Thus, PBPK predictions are closer to the observation. Deviations were also higher for the *2/*2 genotype. For this genotype, the interaction risk predicted by PBPK modeling appears to be higher than in the *1/*1 genotype, which is difficult to understand considering fm,CYP2C9 in the two genotypes.
3.6 Apalutamide (Substrate of CYP3A and CYP2C8)
To predict the effects of CYP3A and CYP2C8 modulators on the steady-state pharmacokinetics of apalutamide and its active metabolite, N-desmethyl apalutamide (NAPA).
3.6.1 Background
Apalutamide is a selective androgen receptor inhibitor for the treatment of prostate cancer. It is metabolised by CYP2C8 and CYP3A4 to form an active metabolite, NAPA. In vitro, it is a CYP2C8 inhibitor, CYP3A inducer, and an inhibitor of other enzymes and transporters (CYP2C19 and OCT2, multidrug and toxin extrusion proteins, and OAT3). In vivo, apalutamide showed dose-proportional increases in exposure across the dose range of 30–480 mg following both single and repeated doses [30]. Itraconazole did not change the AUC of apalutamide and NAPA; gemfibrozil increased the AUC0–672 and AUCinf of apalutamide by 53% and 68%, respectively, and decreased the area AUC0–672 and AUCinf of NAPA by 43% and 15%, respectively, following a single-dose administration of apalutamide. In vivo, multiple daily doses of apalutamide decreased the AUC of the CYP3A substrate midazolam and CYP2C8 substrate pioglitazone (a) by 92% and 18%, respectively [31, 32]. As a substrate and inducer of both CYP3A and CYP2C8, apalutamide has a higher clearance at steady state. The apparent clearance of apalutamide was estimated by population pharmacokinetics to be 1.31 L/h after single dosing and increased to 2.04 L/h at steady state after QD dosing, resulting in an AUCR of 0.64 due to autoinduction [30]. As the clinical DDI studies were done with single-dose apalutamide, the goal of the PBPK analysis was to assess the impact of CYP inhibition and induction on the steady-state exposure of apalutamide.
3.6.2 PBPK Models
The PBPK models of apalutamide and NAPA were developed by sponsor using data from in vitro, human mass balance, pharmacokinetic, and multiple clinical DDI studies. The model was used to simulate untested DDI scenarios of a CYP2C8 inhibition by gemfibrozil, CYP3A inhibition by ketoconazole and CYP induction by rifampin on the pharmacokinetics of apalutamide and its active metabolite, NAPA, at steady state, after the model confirmed the clinical interactions following a single dose of apalutamide. As the exposure of ketoconazole was significantly decreased by rifampin, it is likely to be affected by multiple-dose administration of apalutamide (also, a strong CYP3A inducer) [31]. The PBPK model therefore simulated two different scenarios of an apalutamide–ketoconazole interaction, depending on whether ketoconazole exposure was affected (real-world scenario) or unaffected (worst-case scenario mimicking a strong CYP3A inhibitor that is not a CYP3A substrate) by apalutamide [30,31,32]. The untested combined induction effect of rifampin and apalutamide on the steady-state pharmacokinetics of apalutamide, evaluated with multiplicative and additive induction models, showed that the combined induction effect is not very different to the autoinduction of apalutamide. Based on the modelling results, the FDA label does not recommend any dose adjustments with concomitant administration of apalutamide and strong CYP3A or CYP2C8 inhibitors or with CYP3A/CYP2C8 inducers as the combined exposure of apalutamide and NAPA may not significantly change.
3.6.3 MSM
Mechanistic static models were used to (1) evaluate the effects of gemfibrozil and ketoconazole (in both real-world and worst-case conditions) on the pharmacokinetics of apalutamide and NAPA at steady state, after model-confirmed clinical interactions of apalutamide single dose with gemfibrozil and itraconazole; and (2) to evaluate the combined CYP3A inducer effects of apalutamide and rifampin on the steady-state exposure of apalutamide and NAPA by multiplicative and additive models. The input data used in the model are presented in Table 12.
3.6.4 Other Input Parameters
The induction parameters (maximum induction, Indmax and IndC50) of CYP2C8 by rifampin were obtained from Simcyp V19 (6.7 and 0.3 µM, respectively).
3.6.5 Methods
3.6.5.1 Calculation of Altered fm,CYP3A and fm,CYP2C8 at Steady State of Apalutamide Due to CYP3A Induction and CYP2C8 Net Induction by Apalutamide
The fm,CYP2C8 of CYP2C8 substrate pioglitazone, derived from clinical DDI studies with trimethoprim and gemfibrozil, are 0.6 and 0.73 respectively (average = 0.67). Apalutamide has a net induction effect on CYP2C8 at steady state and decreases the AUC of pioglitazone by 18%. This 18% decrease in exposure corresponds to a fold increase in the total clearance of pioglitazone of 1/(1–0.18) = 1.22-fold, due to CYP2C8 induction by apalutamide. Assuming this fold increase in total clearance is all due to CYP2C8 induction, the fractional CYP2C8 clearance of pioglitazone following induction by apalutamide = CLpio × 1.22 − CLpio × (1–0.67) = CLpio × 0.89, where CLpio is the clearance of pioglitazone in the absence of apalutamide. Thus, the fold induction of CYP2C8 is (CLpio × 0.89)/(CLpio × 0.67) = 1.33. The fractional CYP2C8 clearance of apalutamide at SS = 1.33 × fractional CYP2C8 clearance after single dose = 1.33 × 0.56 = 0.74 L/h. Subtracting the increase in CYP2C8 clearance from the total increase in clearance stemming from autoinduction of both CYP3A and CYP2C8 (0.73 L/h), the increase in apalutamide clearance at steady state due to CYP3A4 induction alone can be estimated. fm,CYP2C8,SS and fm,CYP3A,SS are calculated by dividing the fractional clearance of CYP2C8 and CYP3A at steady state (fCL2C8,SS and fCL3A4,SS) by the total clearance at steady state. Thus,
Instead of using the pioglitazone–apalutamide DDI for the calculation of fm,CYP2C8,SS and fm,CYP3A4,SS as above, the midazolam–apalutamide DDI could have been used. This requires deconvolution of the gut contribution of apalutamide induction from the systemic contribution (because apalutamide will only have the systemic interaction), which would add to the uncertainty. Results are shown in Table 13.
3.6.5.2 Estimation of Impact of Modulators on the Exposure of Apalutamide
Use perpetrator and victim parameters of apalutamide (Table 12) and interaction parameters of modulators (Table S1 of the ESM) in MSMs to estimate the AUCRs of apalutamide. Detailed workflow and calculations are available in the ESM. Results are shown in Tables 14 and 15.
3.6.5.3 Estimation Impact of Modulators on the Exposure of the Active Metabolite, NAPA
The NAPA levels are is proportional to the sum of CYP3A- and CYP2C8-mediated clearances as they are formed by the action of both enzymes on apalutamide. The effect of CYP3A4 and CYP2C8 modulators on NAPA levels is estimated by considering the changes in the fractional clearances by the two enzymes brought about by the modulators. The AUCR of NAPA at steady state due to inhibition of CYP3A4-mediated clearance of apalutamide by ketoconazole without incorporating induction of ketoconazole by apalutamide is estimated by recognising that NAPA levels are proportional to the sum of CYP3A- and CYP2C8-mediated clearances (CL2C83A4). Therefore, the AUCR of NAPA due to CYP3A inhibition by ketoconazole is calculated as follows:
Similarly, the AUCR of NAPA at steady state due to inhibition of the CYP3A4-mediated clearance of apalutamide by ketoconazole incorporating induction of ketoconazole is estimated. The AUCR of NAPA at steady state due to inhibition of CYP2C8-mediated clearance of apalutamide by gemfibrozil is also estimated by suitably adapting the above equation to CYP2C8. Results are presented in Table 16.
3.7 Baricitinib (Substrate of OAT3)
To predict the effect of OAT3 inhibition by the moderate-to-weak OAT3 inhibitors ibuprofen and diclofenac on baricitinib exposure after model confirmation of a clinical DDI study with a strong OAT3 inhibitor (probenecid).
3.7.1 Background
Baricitinib is a JAK1/2 inhibitor that reversibly inhibits JAK1/2’s JH1 tyrosine kinase domain in the active conformation by acting as an ATP-competitive inhibitor. It is currently approved for the treatment of rheumatoid arthritis [33]. Baricitinib is a substrate for OAT3, multidrug and toxin extrusion protein 2‐K, P‐gp, and breast cancer resistance protein in vitro. Probenecid, a strong OAT3 inhibitor, increased the AUC of baricitinib by two-fold [34].
3.7.2 PBPK Analysis
Full PBPK models for baricitinib, probenecid, ibuprofen, and diclofenac were developed using measured and predicted physicochemical and biological data [35]. The active secretion of baricitinib was modeled using the in vitro measured Vmax and Km values for OAT3 and MATE2‐K, and intrinsic clearances of P‐gp and breast cancer resistance protein. Simulations with ibuprofen and diclofenac were performed setting the in vitro Ki of the modulators to either half-maximal inhibitory concentration (IC50) or IC50/2. The AUCRs of their interactions with baricitinib were predicted using ibuprofen and diclofenac in vitro IC50 values of 4.4 and 3.8 μM toward OAT3, respectively. These predictions suggest clinically relevant DDIs with ibuprofen and diclofenac are unlikely. Therefore, the reviewer recommended a dose adjustment in the label for co-administration with strong OAT3 inhibitors but not for moderate.
3.7.3 MSM
The estimation of the AUCR of baricitinib for OAT3 inhibition can be performed using mechanistic static equation for reversible inhibition (see ESM), substituting fm.fm,CYP with the fraction of drug transported via OAT3 (ft) and taking figut and fgut as 1 (as no gut interactions are expected). As OAT3 is a basolateral transporter, the average systemic inhibitor concentration can be considered as the driver concentration.
Two approaches were used to calculate the fraction of baricitinib transported (ft) by OAT3.
In the first method, ft is calculated by extracting the calculated renal clearance due to filtration from the total renal clearance and estimating the fractional clearance mediated by the OAT3 uptake transporter:
Systemic clearance of baricitinib = 17 L/h
Total renal clearance of baricitinib = 11 L/h
Renal clearance of baricitinib due to filtration = fup *GFR = 0.5*7 L/h = 3.5 L/h
Renal clearance of baricitinib due to transporter activity = 11–3.5 = 7.5 L/h
ft = 7.5/17 = 0.44
All input values relating to baricitinib were taken from the literature [34].
In the second method, the probenecid clinical DDI with baricitinib was used to derive the ft (ft = 0.55). By systematically varying ft in MSM, the value of ft that leads to a predicted AUCR matching the observed AUCR is identified.
The baricitinib ft was then used in the mechanistic static equation for reversible inhibition to predict the interaction with ibuprofen and diclofenac considered as moderate-to-weak inhibitors of OAT3. The inhibitor data used in the model are the same as those reported for the PBPK analysis [35]. The AUCR values for these predictions are shown in Table 16.
3.7.4 Results
The mechanistic model predictions are comparable to those obtained from PBPK modeling (see Table 17).
4 Discussion
Application of modelling workflows to MSMs that are similar to those used for dynamic models required the recognition of a common language for the mechanistic static and dynamic models. The workflow for PBPK modelling often comprises model building, model verification of drug exposure, model validation to demonstrate a model fit for an intended purpose and model application to simulate unstudied scenarios. Inconsistent terminologies in the literature have led to considerable confusion. The terms validation, verification, model confirmation and qualification are used interchangeably. In general, the purpose of validation would be to determine model accuracy to predict observed data and evaluate model assumptions. In practice, however, in several of the examples presented in this study, model ‘validation’ in PBPK modelling is often done to optimise/refine parameters to fit/recover observed data. In other words, parameter values are derived from observed data. For example, the FDA review for apalutamide [30] states that “the CYP3A and CYP2C8 contributions to the apalutamide metabolism were validated with the itraconazole and gemfibrozil DDI studies” and “the effects of apalutamide on CYP3A, CYP2C8, and CYP2C19 substrates were validated with DDI studies with midazolam, pioglitazone, and omeprazole, respectively”. This statement could easily be misinterpreted to mean that model predictions are confirmed by clinical observations. In reality, model parameters were derived/optimised/refined with observed clinical DDI. The Open System Pharmacology community has recently proposed a more formal framework for the qualification and validation of DDI networks that actually fulfil the requirements of proper model qualification and validation [36]. In our study, we have used the term ‘parameter optimisation’ to allow for a generic workflow for both static and dynamic models. This workflow includes (1) model development or integration of all relevant data into the model; (2) optimisation of key model parameters from clinical pharmacokinetic and DDI data; and (3) model application for DDI prediction for the intended purpose.
The use of maximum concentration in static models to exclude DDI liability under worst-case settings has led to the misconception that static model predictions are generally conservative. However, the use of average steady-state concentrations as driver concentrations in MSMs should lead to mostly comparable results as those from PBPK modelling for non-dynamic measures of DDI risk assessment, such as AUCR, provided the same input data as are employed for the interacting drugs [37].
Optimisation of Ki against clinical DDI studies with sensitive substrates is challenged by the unknown role of the gut in contributing to the magnitude of observed DDIs. In MSMs, the estimation of interaction in the gut requires the fraction of substrate escaping gut metabolism in the presence of the inhibitor, fgut,i, which is not easy to estimate. In the case of voxelotor-midazolam interaction, this challenge was handled by demonstrating poor sensitivity of AUCR when varying fgut,i of midazolam over its entire plausible range of values (no inhibition to complete inhibition of intestinal CYP3A by voxelotor). It is worth noting that the optimisation of Ki against clinical DDIs using PBPK models is challenged by the uncertainty associated with the relevant perpetrator concentrations in the gut, interaction parameters, as well as mechanisms relevant for the absorption, metabolism and elimination of the victim drug.
For an investigational drug as an inducer, there are two parameters to be optimised, Indmax and IndC50. Indmax is estimated by calibrating in vitro Indmax against rifampin (control) as well as in vivo rifampin Indmax, while IndC50 may be derived from the autoinduction effects observed in repeat-dosing studies at multiple doses, if the inducer is a moderately sensitive or sensitive substrate of the affected enzyme. Rifampin is widely recognised as a pleiotropic inducer of both P-gp and CYP3A. Therefore, induction potency parameter IndC50 for rifampin calibrated against clinical DDI studies of orally administered sensitive CYP3A or dual substrates is likely to be different to IndC50 calibrated using clinical DDI studies with CYP3A substrates administered intravenously. For low-clearance victim drugs, with a low risk for intestinal metabolism-mediated DDI effects (voxelotor, siponimod, apalutamide and ivosidenib), it is reasonable to apply the IndC50 calibrated using rifampin clinical DDI studies with intravenously administered midazolam, a sensitive CYP3A substrate. In this study, except for ibrutinib, all victim drugs with CYP-mediated metabolism have low clearance, for which the contribution of the gut to intestinal metabolism and therefore to drug interactions is expected to be negligible. As a good practice, DDI predictions for a new investigational drug may be done with and without gut interactions when the clearance of the drug is not known to be low.
In the case of ivosidenib, a sensitivity analysis to identify optimal IndC50 by comparing the simulated ratios of steady-state to single-dose exposure over a range of CYP3A4 induction parameters with those observed in clinical pharmacokinetic data in the PBPK model led to a value of 2.5µM, which is very different to the one used in the MSM (8.6 µM). This is perhaps owing to differences in the driver concentrations in the two models. In the PBPK model, a fu,gut of 0.057 has been used [22]. The impact of this on the perpetrator concentrations is difficult to say. Irrespective of the absolute values of potency and driver concentration, it is the ratio of perpetrator concentration to potency that matters. Therefore, the impact of differences in IndC50 on the predictions of DDI effects is minimal, provided the perpetrator concentration to potency values from the two models are similar. As exemplified by ivosidenib and apalutamide, the magnitude of interactions for concurrent inductions (autoinduction and induction due to rifampin) estimated by MSMs and PBPK models are different, even though the overall conclusions would remain the same. In the absence of clinical DDI studies, it is difficult to say anything about the performance of either method. In general, confidence in the prediction of induction-mediated interactions is limited by the quality of interaction parameters generated in vitro for investigational drug or derived from clinical DDIs for pleiotropic index inducers such as rifampin. In addition, the contribution of the gut to the overall magnitude of the CYP3A4-mediated interaction is associated with uncertainty for orally administered victim and perpetrator drugs. There is also considerable uncertainty in predicting CYP2C-driven induction effects because of fewer in vivo data and limitations with in vitro data (the ranges of induction effects on messenger or activity are limited).
The higher levels of toxicity and generally narrow therapeutic window often seen in oncology warrant precise optimisation of drug exposure for drugs that are victims of DDI. However, clinical DDI studies are difficult to conduct because of the shortage of appropriate patient populations and ethical/safety concerns of over-exposing healthy volunteers to oncology medications. Thus, there is a wider regulatory acceptance of PBPK models supporting accelerated timelines for breakthrough therapies in oncology or rare diseases, provided any uncertainty in the quantitative prediction from a model could be covered by the relatively wide therapeutic window of the drug or by a conservative labelling language to avoid concomitant use with strong/moderate inhibitors or inducers. Ibrutinib is one of the early examples of oncology drugs, where PBPK model predictions of DDI effects with weak and moderate inhibitors and inducers informed key safety and dosing issues, after the model was validated with clinical DDI studies with strong modulators. Ibrutinib is a high-clearance drug with considerable first-pass gut metabolism. While PBPK models can, in principle, account for the contribution of gut metabolism to the overall DDI of ibrutinib with CYP3A inhibitors, it is difficult to validate the quantitative prediction because of model non-identifiability issues. For example, when the model-predicted DDI effect of ketoconazole on ibrutinib did not match the clinical observation, the inhibition constant of ketoconazole was altered in the PBPK model, to cover for uncertainty in the in vitro data. Similarly, Ki of fluvoxamine was adjusted to an ibrutinib-specific value. However, optimising the interaction parameter of an index drug using a clinical DDI study with an investigational drug is not a good practice, as the interaction parameter of an index drug in a PBPK platform is expected to be validated using all known DDI studies involving that drug. In fact, a good fit to the observed data would have been possible by adjusting many other model parameters related to ibrutinib (e.g. fu,gut, P-gp efflux parameters in the gut). When different model parameter combinations can describe observed data equally well, they are said to be non-identifiable. Because of parameter non-identifiability, models lack the mechanistic credibility for reliable extrapolation to an unstudied scenario. In the MSM, the workflow employed by the sponsor could not be used, as the model parameter fgut (the fraction of drug escaping intestinal metabolism in the absence of a CYP3A inhibitor) for ibrutinib would then not have a value. Therefore, the ketoconazole-ibrutinib clinical DDI study was used to optimise fgut, which is the only unknown parameter. The fgut value of ibrutinib was then validated with the clinical interaction study with itraconazole. The difference in approach is reflected in some differences in model predictions between MSMs and PBPK models for ibrutinib interactions, although they are unlikely to alter the overall conclusions. In recent PBPK submissions that were accepted by the FDA, victim drugs that are CYP3A substrates tend to be low-clearance drugs for which the role of gut metabolism in determining DDI is likely to be negligible.
The tendency of MSM to underpredict the impact of modulators affecting multiple enzymes (e.g., fluconazole, fluvoxamine and rifampin affecting both CYP3A and CYP2C9) on victim drugs that are substrates of the affected enzymes is illustrated by both voxelotor and siponimod. For both compounds, the worst-case scenario attributing all oxidative metabolism of the drug to CYP3A leads to similar results as PBPK modeling. When a drug is metabolised by multiple enzymes including CYPs, UGTs, and SULTs, the uncertainty in the fraction metabolised by each of those enzymes and the lack of experience and knowledge with induction of uridine diphosphate-glucuronyltransferases (UGTs) and sulfotransferases (SULTs) make it difficult to predict the overall effects of inducers on their substrates. This uncertainty in the quantitative prediction is reflected in the conservative label for voxelotor, which recommends avoiding coadministration with strong or moderate CYP3A4 inducers and to increase its dosage when coadministration with a strong or moderate CYP3A4 inducer is unavoidable.
The application of an MSM to apalutamide, a substrate and inducer of CYP3A and CYP2C8, for predicting the effects of CYP3A and CYP2C8 inhibitors and inducers on the steady-state pharmacokinetics of apalutamide and its active metabolite, NAPA, demonstrates that an MSM can be applied even for these complex scenarios, but with some assumptions. Both apalutamide and NAPA induce CYP3A and CYP2C8, and it is not possible to deconvolute their individual contributions to CYP3A and CYP2C8 induction. Therefore, in this study, the IndC50 derived from the clinical DDI study of apalutamide with midazolam as well as from its autoinduction effect is a bundle into the parent apalutamide IndC50, which is the more potent inducer of the two. In the absence of clinical DDI data, it is difficult to assess the validity of these assumptions.
In the case of baricitinib, a substrate of OAT3, the relative activity factor/relative expression factor for OAT3 uptake was assumed to be 1 to simulate the effects of the OAT3 inhibitors probenecid, ibuprofen or diclofenac on the pharmacokinetics of baricitinib in healthy subjects. Additionally, the in vitro IC50 values were used as the inhibitory constant (Ki) in MSM. The observed effect of probenecid on baricitinib pharmacokinetics was assumed to occur on the basolateral side, where OAT3 is located. These were also the assumptions for the PBPK modelling. The MSM predictions using calculated ft as well as the optimised ft using the probenecid-baricitinib clinical DDI study resulted in AUCR values that were close to results from PBPK modeling. This example shows that a basolateral transporter such as OAT3 can be treated similar to a hepatic enzyme, by substituting in MSM, fm x fm,CYP with ft.
It is clear from the case studies described in this article that successful PBPK submissions to the FDA for an investigational drug that is a victim of DDI require its metabolic and elimination pathways to be well characterised by human mass balance. When the investigational drug is a substrate of an enzyme encoded by a polymorphic gene, its fractional clearance by this enzyme in the different genotypes can be derived from population pharmacokinetic modelling. Adequacy of PBPK models for investigational drugs as modulators requires clearance derived from clinical pharmacokinetics and a sensitivity analysis to cover for any uncertainty in interaction parameters (Ki, KI, kinact, Indmax, IndC50) and binding parameters (fu,inc and fu,p). Indmax of a CYP3A4 inducer is required to be calibrated against in vitro and in vivo rifampin data. IndC50 of a sensitive CYP3A4 substrate may be derived from autoinduction observed in pharmacokinetic profiles following repeated dosing of multiple doses. Extrapolation of DDI effects of an investigational drug as a modulator to dosing regimes that are different to the one clinically tested requires an understanding of how modulator exposure changes with dose in the dose range of interest. Publications from the FDA provide a comprehensive list of New Drug Approvals by the FDA [6, 13] as well as the agency’s assessment of adequacy or inadequacy of the PBPK models for an intended purpose [13] (Table 18).
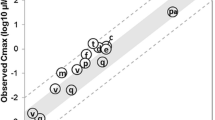
The performance of MSMs and PBPK models in the case studies discussed in this paper confirms earlier reports of good predictive performance of MSMs [4, 9, 11, 12, 38] and shows that neither the complexity (e.g. gut model) nor the dynamic variation in perpetrator concentrations makes a big difference for the investigated scenarios. Table 19 shows an overall comparison of the two approaches for the 90 predictions done with the two methodologies (see also Fig. S1 of the ESM). Sixty-eight percent of the MSM/PBPK prediction ratios are between 0.8-fold and 1.25-fold interval and 90% within the 0.5-fold to 2-fold interval. The biggest differences were found for siponimod. A recent systematic evaluation of time-dependent inhibition of CYP3A showed reliable predictions for 23 inhibitors using dynamic or static models using unbound average modulator concentrations and interaction parameters from human liver microsomes or hepatocytes [37]. The Innovation and Quality Induction Working Group showed that the quantitative prediction accuracy was highest with the R3 method [1] using an unbound average concentration at steady state (31% within bioequivalence and 94% within two-fold when using the median in vitro donor data) [39]. These results are not surprising because the average concentrations can be the best alternative to using a dynamically varying modulator concentration. The quantitative prediction accuracy of both static and dynamic models is limited by poor in vitro to in vivo extrapolation, knowledge gaps in system parameters, non-identifiability issues challenging model parameterisation and validation, and a lack of mass balance data to characterise metabolic and elimination pathways for the victim drug. In addition, the in vivo relevance of transporters for their substrates is difficult to know and the intracellular driving concentrations for modulators of efflux transporters cannot be measured. These limitations are common to both MSMs and PBPK models, as are the requirements to establish confidence in model predictions [5, 40]. Limitations discussed here are likely to have far greater consequences on regulatory acceptance of model predictions than the modelling approach.
In the future, a routine comparison of MSMs and PBPK models for all regulatory submissions could create a best practice that would allow an understanding of potential differences between the predictive performances of the two. A routine comparison is currently challenged by the availability and access to reliable harmonised data for interaction parameters, binding parameters and driver concentrations for index modulators, and parameters related to pathway characterisation for index substrates such as fraction absorbed, fraction escaping gut metabolism, fraction metabolised in the liver, fraction transported via transporters of interest and fractions eliminated in bile and urine. Some of these are obtainable from the University of Washington database [41], but inter-laboratory differences in the measurement of interaction parameters make it difficult to determine the best value to use in MSM. A single repository of all relevant data for index substrates and modulators that is acceptable for regulatory agencies is highly desirable. In addition, it is desirable to harmonise and publish physiological parameters such as blood flow rates and turnover rates of proteins to enable an easy comparison of methods. A comparison of methods would allow the future application of one or the other methods based on the ability to leverage its individual strengths to answer the specific questions that are relevant for an investigational drug. While the strength of an MSM is its simplicity, the unique strengths of a PBPK model include its ability to perform what-if scenario testing to understand the effect of dose staggering, evaluate the role of uptake and efflux transporters and assess the impact of DDIs on the exposure of a victim drug with concurrent mechanisms. In addition, a PBPK model allows the extrapolation of DDI effects from a healthy population to unstudied populations such as a target population (e.g. patients with cancer) or organ-impaired populations. A recent publication evaluating the predictive performance of PBPK models in renal impairment and hepatic impairment populations concluded that although predictions can be made, real causes for the correlations are not always clear [44]. Some molecules show significant changes with severity, and others not. Thus, confidence in the magnitude of the predictions may not be high enough to allow impactful regulatory recommendations. A systematic evaluation for PBPK predictions of DDI effects in patients with cancer is not available.
5 Conclusions
It is widely accepted that when a risk for DDIs is identified by static models, PBPK models are used for quantitative predictions of DDIs. However, the case studies presented in this article demonstrate mostly comparable performance of static and dynamic models when the same input data are used, and model parameters are optimised in the same way. The predictions from the two approaches were not very comparable for interactions mediated by enzyme induction. However, given the uncertainties associated with the predictions of induction-mediated interactions, the differences in the two approaches are not too large to alter high-impact applications supporting study waivers and label recommendations. This evaluation has thus served to enhance confidence in the use of MSMs to inform enrolment for DDI clinical studies, support DDI study design and enable label recommendations (dose adjustment, avoid concomitant use, or no warnings). The simpler computations needed for MSMs make them easier to use, review, understand and interpret [43]. In the interest of saving valuable resources for both sponsors and regulators, fit-for-purpose approaches may be preferred, reserving the use of PBPK models to those applications that cannot be served by static models. When a case is made for a preference for a PBPK model over an MSM for a particular application, a comparison of results from a PBPK model with that from an MSM by adopting the same modelling workflow and data could promote an understanding of any differences seen between the two approaches, which in turn could prove valuable for guiding future changes to DDI guidelines. With this first step, we hope to trigger a scientific discussion between scientists in industry, regulatory agencies and academia to pave the way for industry to employ the modelling approach that best fits an intended purpose and for regulatory agencies to view both MSMs and PBPK models through the same lens.
References
US Food and Drug Administration. Guidance for industry: in vitro drug interaction studies: cytochrome P450 enzyme- and transporter-mediated drug interactions. 2020. Available from: https://www.fda.gov/media/134582/download. [Accessed 30 Mar 2022].
US Food and Drug Administration. Guidance for industry: clinical drug interaction studies: cytochrome P450 enzyme- and transporter-mediated drug interactions. 2020. Available from: https://www.fda.gov/media/134581/download. [Accessed 30 Mar 2022].
European Medicines Agency. Guideline on the investigation of drug interactions. 2012. Available from: https://www.ema.europa.eu/en/documents/scientific-guideline/guideline-investigation-drug-interactions-revision-1_en.pdf. [Accessed 30 Mar 2022].
Fahmi OA, Maurer TS, Kish M, Cardenas E, Boldt S, Nettleton D. A combined model for predicting CYP3A4 clinical net drug-drug interaction based on CYP3A4 inhibition, inactivation, and induction determined in vitro. Drug Metab Dispos. 2008;36(8):1698–708.
Peters SA, Dolgos H. Requirements to establishing confidence in physiologically based pharmacokinetic (PBPK) models and overcoming some of the challenges to meeting them. Clin Pharmacokinet. 2019;58(11):1355–71.
Grimstein M, Yang Y, Zhang X, Grillo J, Huang SM, Zineh I, et al. Physiologically based pharmacokinetic modeling in regulatory science: an update from the US food and drug Administration’s office of clinical pharmacology. J Pharm Sci. 2019;108(1):21–5.
Jean D, Naik K, Milligan L, Hall S, Mei Huang S, Isoherranen N, et al. Development of best practices in physiologically based pharmacokinetic modeling to support clinical pharmacology regulatory decision-making: a workshop summary. CPT Pharmacometr Syst Pharmacol. 2021;10(11):1271–5.
Perry C, Davis G, Conner TM, Zhang T. Utilization of physiologically based pharmacokinetic modeling in clinical pharmacology and therapeutics: an overview. Curr Pharmacol Rep. 2020;6(3):71–84.
Peters SA, Schroeder PE, Giri N, Dolgos H. Evaluation of the use of static and dynamic models to predict drug–drug interaction and its associated variability: impact on drug discovery and early development. Drug Metab Dispos. 2012;40(8):1495–507.
Fahmi OA, Hurst S, Plowchalk D, Cook J, Guo F, Youdim K, et al. Comparison of different algorithms for predicting clinical drug-drug interactions, based on the use of CYP3A4 in vitro data: predictions of compounds as precipitants of interaction. Drug Metab Dispos. 2009;37(8):1658–66.
Einolf HJ. Comparison of different approaches to predict metabolic drug–drug interactions. Xenobiotica. 2007;37(10–11):1257–94.
Boulenc X, Barberan O. Metabolic-based drug-drug interactions prediction, recent approaches for risk assessment along drug development. Drug Metabol Drug Interact. 2011;26(4):147–68.
Zhang X, Yang Y, Grimstein M, Fan J, Grillo JA, Huang SM, et al. Application of PBPK modeling and simulation for regulatory decision making and its impact on US prescribing information: an update on the 2018–2019 submissions to the US FDA’s Office of Clinical Pharmacology. J Clin Pharmacol. 2020;60(Suppl 1):S160–78.
Almond LM, Yang J, Jamei M, Tucker GT, Rostami-Hodjegan A. Towards a quantitative framework for the prediction of DDIs arising from cytochrome P450 induction. Curr Drug Metab. 2009;10(4):420–32.
Obach RS. Predicting drug-drug interactions from in vitro drug metabolism data: challenges and recent advances. Curr Opin Drug Discov Devel. 2009;12(1):81–9.
Asaumi R, Toshimoto K, Tobe Y, Hashizume K, Nunoya KI, Imawaka H, et al. Comprehensive PBPK model of rifampicin for quantitative prediction of complex drug-drug interactions: CYP3A/2C9 induction and OATP inhibition effects. CPT Pharmacometr Syst Pharmacol. 2018;7(3):186–96.
Jamei M, Marciniak S, Edwards D, Wragg K, Feng K, Barnett A, et al. The simcyp population based simulator: architecture, implementation, and quality assurance. In Silico Pharmacol. 2013;1:9.
US Food and Drug Administration. Drug development and drug interactions. Available from: http://www.fda.gov/Drugs/DevelopmentApprovalProcess/DevelopmentResources/DrugInteractionsLabeling/ucm080499.htm. [Accessed 30 Mar 2022].
US Food and Drug Administration. NDA213137 voxelotor multi-discipline review. 2019. Available from: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2019/213137Orig1s000Multidiscipline.pdf. [Accessed 30 Mar 2022].
Hutchaleelaha A, Patel M, Washington C, Siu V, Allen E, Oksenberg D, et al. Pharmacokinetics and pharmacodynamics of voxelotor (GBT440) in healthy adults and patients with sickle cell disease. Br J Clin Pharmacol. 2019;85(6):1290–302.
Galetin A, Burt H, Gibbons L, Houston JB. Prediction of time-dependent CYP3A4 drug-drug interactions: impact of enzyme degradation, parallel elimination pathways, and intestinal inhibition. Drug Metab Dispos. 2006;34(1):166–75.
US Food and Drug Administration. NDA211192 ivosidenib multi-discipline review. 2018. Available from: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2018/211192Orig1s000MultidisciplineR.pdf. [Accessed 30 Mar 2022].
Davids MS, Brown JR. Ibrutinib: a first in class covalent inhibitor of Bruton’s tyrosine kinase. Future Oncol. 2014;10(6):957–67.
de Zwart L, Snoeys J, De Jong J, Sukbuntherng J, Mannaert E, Monshouwer M. Ibrutinib dosing strategies based on interaction potential of CYP3A4 perpetrators using physiologically based pharmacokinetic modeling. Clin Pharmacol Ther. 2016;100(5):548–57.
de Jong J, Skee D, Murphy J, Sukbuntherng J, Hellemans P, Smit J, et al. Effect of CYP3A perpetrators on ibrutinib exposure in healthy participants. Pharmacol Res Perspect. 2015;3(4): e00156.
US Food and Drug Administration. NDA205552 ibrutinib clinical pharm review. 2013. Available from: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2013/205552orig1s000clinpharmr.pdf [Accessed 30 Mar 2022].
Christmann R, Ho DK, Wilzopolski J, Lee S, Koch M, Loretz B, et al. Tofacitinib loaded squalenyl nanoparticles for targeted follicular delivery in inflammatory skin diseases. Pharmaceutics. 2020;12(12):2.
Jin Y, Borell H, Gardin A, Ufer M, Huth F, Camenisch G. In vitro studies and in silico predictions of fluconazole and CYP2C9 genetic polymorphism impact on siponimod metabolism and pharmacokinetics. Eur J Clin Pharmacol. 2018;74(4):455–64.
US Food and Drug Administration. NDA 209884 siponimod clinical pharmacology and biopharmaceutics review(s). 2019. Available from: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2019/209884Orig1s000ClinPharmR.pdf. [Accessed 30 Mar 2022].
Us Food and Drug Administration. NDA 210951 apalutamide multi-discipline review. 2018. Available from: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2018/210951Orig1s000MultidisciplineR.pdf. [Accessed 30 Mar 2022].
Duran I, Carles J, Bulat I, Hellemans P, Mitselos A, Ward P, et al. Pharmacokinetic drug-drug interaction of apalutamide, part 1: clinical studies in healthy men and patients with castration-resistant prostate cancer. Clin Pharmacokinet. 2020;59(9):1135–48.
Van den Bergh A, Snoeys J, De Zwart L, Ward P, Lopez-Gitlitz A, Ouellet D, et al. Pharmacokinetic drug-drug interaction of apalutamide, Part 2: investigating interaction potential using a physiologically based pharmacokinetic model. Clin Pharmacokinet. 2020;59(9):1149–60.
Alexander M, Luo Y, Raimondi G, O’Shea JJ, Gadina M. Jakinibs of all trades: inhibiting cytokine signaling in immune-mediated pathologies. Pharmaceuticals. 2021;15(1):2.
Posada MM, Cannady EA, Payne CD, Zhang X, Bacon JA, Pak YA, et al. Prediction of transporter-mediated drug-drug interactions for baricitinib. Clin Transl Sci. 2017;10(6):509–19.
US Food and Drug Administration. NDA207924 baricitinib clinical pharm review. Available from: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2018/207924Orig1s000ClinPharmR.pdf . Published 2017. [Accessed 30 Mar 2022].
Frechen S, Solodenko J, Wendl T, Dallmann A, Ince I, Lehr T, et al. A generic framework for the physiologically-based pharmacokinetic platform qualification of PK-Sim and its application to predicting cytochrome P450 3A4-mediated drug-drug interactions. CPT Pharmacometrics Syst Pharmacol. 2021;10(6):633–44.
Tseng E, Eng H, Lin J, Cerny MA, Tess DA, Goosen TC, et al. Static and dynamic projections of drug-drug interactions caused by cytochrome P450 3A time-dependent inhibitors measured in human liver microsomes and hepatocytes. Drug Metab Dispos. 2021;49(10):947–60.
Ramsden D, Perloff ES, Whitcher-Johnstone A, Ho T, Patel R, Kozminski KD, et al. Predictive in vitro-in vivo extrapolation for time dependent inhibition of CYP1A2, CYP2C8, CYP2C9, CYP2C19, and CYP2D6 using pooled human hepatocytes, human liver microsomes, and a simple mechanistic static model. Drug Metab Dispos. 2022;50(2):114–27.
Kenny JR, Ramsden D, Buckley DB, Dallas S, Fung C, Mohutsky M, et al. Considerations from the Innovation and Quality Induction Working Group in response to drug-drug interaction guidances from regulatory agencies: focus on CYP3A4 mRNA in vitro response thresholds, variability, and clinical relevance. Drug Metab Dispos. 2018;46(9):1285–303.
Kuemmel C, Yang Y, Zhang X, Florian J, Zhu H, Tegenge M, et al. Consideration of a credibility assessment framework in model-informed drug development: potential application to physiologically-based pharmacokinetic modeling and simulation. CPT Pharmacometrics Syst Pharmacol. 2020;9(1):21–8.
Hachad H, Ragueneau-Majlessi I, Levy RH. A useful tool for drug interaction evaluation: the University of Washington Metabolism and Transport Drug Interaction Database. Hum Genomics. 2010;5(1):61–72.
Tapaninen T, Olkkola AM, Tornio A, Neuvonen M, Elonen E, Neuvonen PJ, et al. Itraconazole increases ibrutinib exposure 10-fold and reduces interindividual variation: a potentially beneficial drug-drug interaction. Clin Transl Sci. 2020;13(2):345–51.
Sugano K. Lost in modelling and simulation? ADMET DMPK. 2021;9(2):75–109.
Heimbach T, Chen Y, Chen J, Dixit V, Parrott N, Peters SA, et al. Physiologically-based pharmacokinetic modeling in renal and hepatic impairment populations: a pharmaceutical industry perspective. Clin Pharmacol Ther. 2021;110(2):297–310.
Oxbryta® (voxelotor): prescribing information. 2021. Available from: https://www.accessdata.fda.gov/drugsatfda_docs/label/2021/213137s006lbl.pdf. [Accessed 28 Nov 2022].
Acknowledgements
The authors gratefully acknowledge the contributions of Eva Sherbetjian and Ping Hu, Merck KGaA, Germany, Venkatesh Reddy from AstraZeneca, Alexander Staab, Valerie Nock, Nina Hanke, Sabrina Wiebe, Ghazal Montaseri, Angèle Fleury, Doreen Lüdtke, Maria Franz and Tobias Kanacher from Boehringer Ingelheim, and Rafael Leal Monteiro Paraiso for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
This study was funded by Boehringer Ingelheim Pharma GmbH & Co. KG.
Conflicts of Interest
Jose David Gomez-Mantilla, Fenglei Huang, and Sheila Annie Peters (employees of Boehringer Ingelheim Pharma GmbH & Co. KG) have no conflicts of interest that are directly relevant to the content of this article.
Availability of Data and Material
All data generated or analyzed during this study are included in this published article (and its supplementary information files).
Authors’ Contributions
JDG-M: data curation, analysis, writing, reviewing and editing. FH: data curation, analysis, writing, reviewing and editing. SAP: conceptualisation, methodology, supervision, writing, reviewing and editing.
Ethics approval, Consent to participate, Consent for publication, Code availability
Not applicable.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
Gomez-Mantilla, J.D., Huang, F. & Peters, S.A. Can Mechanistic Static Models for Drug-Drug Interactions Support Regulatory Filing for Study Waivers and Label Recommendations?. Clin Pharmacokinet 62, 457–480 (2023). https://doi.org/10.1007/s40262-022-01204-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40262-022-01204-4