Abstract
Background and Objectives
The interplay between liver metabolising enzymes and transporters is a complex process involving system-related parameters such as liver blood perfusion as well as drug attributes including protein and lipid binding, ionisation, relative magnitude of passive and active permeation. Metabolism- and/or transporter-mediated drug–drug interactions (mDDIs and tDDIs) add to the complexity of this interplay. Thus, gaining meaningful insight into the impact of each element on the disposition of a drug and accurately predicting drug–drug interactions becomes very challenging. To address this, an in vitro–in vivo extrapolation (IVIVE)-linked mechanistic physiologically based pharmacokinetic (PBPK) framework for modelling liver transporters and their interplay with liver metabolising enzymes has been developed and implemented within the Simcyp Simulator®.
Methods
In this article an IVIVE technique for liver transporters is described and a full-body PBPK model is developed. Passive and active (saturable) transport at both liver sinusoidal and canalicular membranes are accounted for and the impact of binding and ionisation processes is considered. The model also accommodates tDDIs involving inhibition of multiple transporters. Integrating prior in vitro information on the metabolism and transporter kinetics of rosuvastatin (organic-anion transporting polypeptides OATP1B1, OAT1B3 and OATP2B1, sodium-dependent taurocholate co-transporting polypeptide [NTCP] and breast cancer resistance protein [BCRP]) with one clinical dataset, the PBPK model was used to simulate the drug disposition of rosuvastatin for 11 reported studies that had not been used for development of the rosuvastatin model.
Results
The simulated area under the plasma concentration–time curve (AUC), maximum concentration (C max) and the time to reach C max (t max) values of rosuvastatin over the dose range of 10–80 mg, were within 2-fold of the observed data. Subsequently, the validated model was used to investigate the impact of coadministration of cyclosporine (ciclosporin), an inhibitor of OATPs, BCRP and NTCP, on the exposure of rosuvastatin in healthy volunteers.
Conclusion
The results show the utility of the model to integrate a wide range of in vitro and in vivo data and simulate the outcome of clinical studies, with implications for their design.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As the proportion of candidate drugs within the Biopharmaceutical Drug Disposition Classification System (BDDCS) class 2–4 entering development increases, it is becoming evident that transporter-mediated drug–drug interactions (tDDIs) may pose challenges for regulatory approval and clinical practice [1, 2]. So it is not surprising that many regulatory agencies are now requesting investigation of transporter effects in vivo whenever they are likely to be clinically relevant [3, 4]. Considering the number of transporters in the body, including the gut, liver, kidney, heart and brain, investigation of tDDIs can be complicated, difficult to interpret and costly.
The contribution of the organic anion-transporting peptide (OATP) family of solute carriers (SLCs) to the hepatic elimination of many drugs and associated drug–drug interactions (DDIs) is significant [5, 6]. This may lead to an increase in the susceptibility of a drug to a tDDI. This is particularly the case for statins (HMG-CoA reductase inhibitors), as many patients taking these drugs for lipid lowering have co-morbidities and are co-prescribed a number of other medications [7]. Rosuvastatin is a relatively hydrophilic statin (Class 3 according to the BDDCS) with a low oral bioavailability of ~20 % [8]. With limited metabolism (~10 %) occurring mainly via cytochrome P450 (CYP) 2C9 and uridine diphosphate glucuronosyltransferase (UGT) 1A1 [9–12], the main excretion pathways of rosuvastatin are mediated via the biliary and renal routes [8, 13]. Despite a low passive diffusion into hepatocytes [14], rosuvastatin is extensively distributed into the liver, its site of action [15, 16]. This is mainly due to active uptake of rosuvastatin by OATP1B1, OATP1B3 and OATP2B1, as well as the sodium-dependent taurocholate co-transporting polypeptide (NTCP) [17, 18]. On the canalicular side, rosuvastatin is excreted into the bile via the breast cancer resistance protein (BCRP) [17, 19]. An increase in the plasma area under the concentration–time curve (AUC) of rosuvastatin was observed in patients pre-treated with gemfibrozil, an inhibitor of OATPs [20]. Similarly, rosuvastatin AUC and the maximum plasma concentration (C max) were increased by 7- and 10-fold, respectively, in heart transplant recipients (compared with healthy volunteers [HVs]) on an anti-rejection regimen including the immunosuppressant cyclosporine (ciclosporin), which is an inhibitor of OATPs and NTCP [21].
Application of in vitro–in vivo extrapolation (IVIVE), a “bottom-up” approach, in conjunction with physiologically based pharmacokinetic (PBPK) modelling under a mechanistic systems biology approach can help to predict complex DDIs and also inform the design of clinical studies in HVs or patient populations [22, 23]. The model that is incorporated within the Simcyp Population Based Simulator [24] allows investigation of metabolism and transport interplay within the liver and can also be used for quantitative prediction of metabolism-mediated drug–drug interactions (mDDIs) and tDDIs. In this study, we present an IVIVE framework for scaling in vitro liver transporter kinetic data to in vivo. We account for the impact of drug ionisation on extra- and intracellular water (EW and IW) concentrations within the permeability-limited liver (PerL) model and present equations to estimate the unbound concentration fractions in EW and IW compartments based on tissue composition and drug physicochemical data. We demonstrate application of the approach by describing the development of a PBPK model for rosuvastatin, incorporating active uptake into the liver via OATP1B1, OATP1B3, OATP2B1 and NTCP, in addition to excretion of the drug into the bile by BCRP. The impact of co-administration of cyclosporine is also investigated.
2 Methods
2.1 Model Theory and Development
2.1.1 Physiologically Based Pharmacokinetic Models
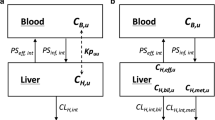
A schematic structure of the PBPK model is shown in Fig. 1. It comprises 15 compartments, where all compartments apart from the liver and gut are well-stirred models. The gastrointestinal tract is modelled using the Advanced Dissolution, Absorption and Metabolism (ADAM) model [25]. The model accounts for interplay of gut metabolism and transport and also the heterogeneity of distribution of enzymes and transporters along the gastrointestinal tract [26, 27]. The typical tissue volumes, tissue density values and tissue blood flows are provided in the Electronic Supplementary Materials.
PBPK model showing both the ADAM and PerL model. The ADAM module represents the gastrointestinal tract as compartments based upon their physiological and anatomical attributes, hence the relationship between permeability, metabolism and dissolution, amongst other factors, can be assessed quantitatively. Once the drug has passed into the portal vein the drug’s kinetics are described by a full PBPK model using the PerL model along with the rest of the well-stirred compartments. ADAM Advanced Dissolution, Absorption and Metabolism, BCRP breast cancer resistance protein, EHC extrahepatic circulation, fu IW unbound fraction in intracellular water, IV intravenous, K tEW-in and K tIW-out overall transport rate in and out of the intracellular water, respectively, NP, NL and AP neutral phospholipids, neutral lipids and acidic phospholipids, respectively, P plasma protein, PBPK physiologically based pharmacokinetic, Perl permeability-limited liver, PO oral, +ve and −ve represent the drug in ionised form, i.e. with and without a valence electron
2.1.2 Perfusion Versus Permeability-Limited Models
In PBPK models tissues/organs are generally represented as perfusion-limited models, where it is assumed that drugs passively diffuse into tissue water and reach equilibrium instantaneously and distribute homogeneously into the available space [28]. Therefore, for a non-eliminating tissue, a single-compartment well-stirred model can be used to describe the distribution process using the following mass balance differential equation (Eq. 1):
where V T, Q T and C T are the tissue volume, blood flow and concentration, respectively. C AR is the arterial blood concentration, K p is the tissue-to-plasma partition coefficient and B:P is the blood-to-plasma ratio. For modelling transporter functionality or scenarios where the tissue plasma membranes limit the drug distribution from the extracellular water (EW) into cells these models cannot be used. Instead multi-compartment permeability-limited models are used to describe the distribution process. Figure 1 shows a schematic of this model for the liver where two membrane sides (sinusoidal and canalicular) are considered. The proposed PerL model is divided into three compartments: vascular space (VS), EW and IW. Many processes are considered simultaneously, including protein and lipid binding and ionisation, all of which are assumed to be instantaneous, and active and passive transport in and out of the compartments.
The following assumptions apply to the PerL model:
-
The vascular and extracellular compartments are in instantaneous equilibrium, although the total concentration in these compartments can be different [29].
-
Only un-ionised and unbound species can passively permeate through the plasma membrane [30] and transporters act only on unbound drug.
-
The movement of the unbound un-ionised species from the VS to the EW is not a rate-limiting process.
-
Passive permeability at the canalicular side of the liver plays a negligible role in biliary secretion.
These assumptions underpin the need to determine unbound extracellular and intracellular concentrations. Unbound fractions in these milieus are usually unknown or challenging to measure in vitro. Thence, having models to predict these fractions based on the physicochemical properties of the compound and tissue compositions is desirable. The development of mechanistic equations incorporating compound lipophilicity, binding of compound to plasma and tissue macromolecules, and levels of phospholipids and neutral lipids in plasma and tissues has improved prediction of the tissue distribution of many compounds [31, 32]. These in silico models have been further developed to account for both protein binding in the EW and binding of strong bases (drug acid-ionisation constant [pKa] >7.0) to acidic phospholipids [30, 33, 34]. Steady-state conditions and instantaneous equilibrium of the unbound drug at membranes are assumed. Using the same approach [30, 33, 34], and based on the aforementioned assumptions, equations have been developed to estimate unbound concentrations of drug in IW and EW and to predict transporter functionality in the liver (see the Electronic Supplementary Materials for the derivations).
2.1.3 Liver Compartmental Concentrations
The differential equations for the liver compartments are developed in a general form and can consider any number of efflux and/or update transporters at each of the liver membranes. Assuming the transporter functionality can be described using a Michaelis–Menten equation, J max (in vivo maximum rate of transporter-mediated efflux or uptake) and K m (Michaelis–Menten constant) are the required parameters to determine the transport rate of the drug across membranes. The drug passive permeation is determined by the passive diffusion parameter, CLint,PD, which is equal to the permeability surface product.
Berezhkovskiy [29] proposed using the effective organ volume rather than actual volume. This can be particularly important for drugs with high blood-to-plasma ratio and in tissues with a high proportion of VS. Therefore, the effective extracellular tissue volume (V EW-eff), which is a combination of the extracellular volume and the VS, is considered, as shown in Eq. 2:
where V EW is the EW volume and K EW:B is the quotient of total EW concentration and the total blood concentration in the tissue VS (see Electronic Supplementary Materials). Volume of the VS (V VS) represents 15 % of the liver volume [35]. As a result, the unbound extracellular concentration is (Eq. 3):
where Q PV and Q AR are the portal vein and arterial blood flows, respectively, C AR and C PV are the arterial and portal vein concentrations, respectively, “Sin” represents the sinusoidal membrane, n and m represent the total number of uptake and efflux transporters involved in the drug transport, and “uptake” and “efflux” represent the transport functionality. CuEW and CuIW represent the unbound EW and IW concentrations, respectively, and fu EW is the extracellular unbound fraction. W and α for a monoprotic base are \( 1 + 10^{{{\text{p}}K{\text{a}} - {\text{pH}}_{\text{EW}} }} \) and \( 10^{{{\text{p}}K{\text{a}} - {\text{pH}}_{\text{IW}} }} \) where pKa is the drug acid-ionisation constant, and pHEW and pHIW are the EW and IW pH values, respectively. For other drug charge types these equations can be defined similarly based on the compound charge type using the Henderson–Hasselbalch equation (see Electronic Supplementary Materials). Similarly, the intracellular unbound concentration is (Eq. 4):
where ‘Can’ refers to the canalicular side and I represents the total number of efflux transporters pumping the drug into bile ducts. fu IW is the intracellular unbound fraction, f IW is the intracellular volume fraction, V Liv is the liver volume V max is the in vivo maximum metabolism rate and K m is the metabolism Michaelis–Menten constant for each of the enzymes that metabolise the drug. As uptake transporters on the canalicular membrane have not been reported for drugs, this is not considered.
2.1.4 In Vitro–In Vivo Extrapolation of Transporter Kinetic Parameters
Assuming that a Michaelis–Menten equation can describe uptake or efflux of drugs in and out of cells then J max (in pmol/min/million hepatocyte) and K m (in μmol/L) are needed to determine CLint,T (transport clearance in μL/min/million hepatocyte) as follows (Eq. 5):
where Cu is the unbound concentration at the transporter site. Hence, for the liver uptake transporters Cu is the unbound concentration in the EW and for efflux transporters it is the unbound concentration in the IW. In the differential equations described in the previous section, J max represents the in vivo value for maximum flux rate of the whole liver and thus this in vitro value needs to be scaled by the following scaling factor (SF) [Eq. 6]:
where HPGL is the hepatocellularity, i.e. the hepatocytes per gram of liver [36], LiverWt is the liver weight [37] and REF is the relative expression factor, which can also be replaced by a relative activity factor (RAF), and 60 × 10−6 is the unit change to convert the CLint,T to L/h. The liver REF or RAF values are determined as the ratio of the transporter expression and/or functionality in vivo relative to the corresponding value in the relevant in vitro system (e.g. hepatocyte or expression systems such as HEK [human embryonic kidney] cells) according to the following equation (Eq. 7):
The same approach is applied to scale up the CLint,PD (mL/min/millions of hepatocyte) value; therefore, the SF for passive permeability (SFPD) across the hepatocyte is defined by Eq. 8:
2.1.5 Transporter-Mediated Drug–Drug Interactions
Drug–drug interactions can occur for both metabolising enzymes and transporters. For cytochrome P450 (CYP) enzymes, competitive and/or time-dependent inhibition and induction are accounted for as previously explained [38–40]. Here, we describe equations relating to tDDIs, assuming that the mechanism of inhibition is competitive. Equation 9 can be used to modify transporter-mediated intrinsic clearance values:
where CLint,T-inh is the transporter-mediated intrinsic clearance in the presence of an inhibitor, the “inh” suffix refers to the inhibited value, Iu is the unbound concentration at the binding site of a transporter and Ku i is the unbound concentration of the inhibitor that supports half-maximal inhibition (corrected for non-specific binding). In the case of multiple inhibitors, it is assumed that all inhibitors are acting via the same mechanism (or the overall effect is similar) on each transporter. Therefore, the overall effect can be modelled using the same approach reported for metabolism interaction [41], as shown in Eq. 10:
where j represents the inhibitor index of either the parent drug, its metabolites or both, and C is the victim drug concentration at the transporter site. There are literature reports that support such assumptions [42]. Further, the developed model handles metabolism- and transporter-mediated DDIs for both victim and perpetrator drugs; hence, drugs can mutually affect each other.
2.2 Development of the Rosuvastatin Model
The sub-models and differential equations described in the previous sections were used to develop a full PBPK model, including permeability-limited diffusion into the liver to describe the disposition of rosuvastatin. The absorption of rosuvastatin from solution was defined using the ADAM model.
2.2.1 Data Used for Simulations of Rosuvastatin Pharmacokinetics
In vitro and pharmacokinetic parameters for rosuvastatin were collated from data in the literature (Table 1). Where data from more than one source were available for the same parameter, weighted means were calculated based on the number of observations reported. Details relating to some of the key input parameters are given in the following sections.
2.2.2 Whole-Organ Metabolic Clearance
Rosuvastatin undergoes only minor metabolism and thus these enzyme kinetics have not been characterised quantitatively in vitro. Therefore, a global value of net intrinsic hepatic clearance (CLuint,H) was back-calculated from in vivo clearance (CLiv,B) using Eq. 11:
where fu B = fu/(B:P) (values were 0.107 and 0.625 for fu and B:P, respectively), Q H is hepatic blood flow (90 L/h) and CLH,B is the hepatic metabolic clearance in blood (50.9 L/h) derived from CLiv,B (78.1 L/h) after subtraction of CLR,B (renal clearance with respect to blood, 27.2 L/h). The estimated net CLuint,H of 648.2 L/h was divided by an average liver weight of 1,648 g [37], a microsomal protein per gram of liver (MPPGL) value of 39.8 mg of microsomal protein/g liver [52] to obtain a value of 174 μL/min/mg protein. As the derived value is a composite of transport and metabolism, 10 % (17.4 μL/min/mg protein) was assigned as the metabolism component for human liver microsomes (HLM) based on previously published data [8, 13, 53].
2.2.3 Permeability Data
Permeability data obtained using Caco-2 cells (P app) for rosuvastatin (3.395 × 10−6 cm/s) was calibrated using propranolol (20 × 10−6 cm/s) and then extrapolated to an effective permeability in human (P eff,man) of 0.855 × 10−4 cm/s using the default regression equation within the Simcyp Simulator. It was assumed that P eff,man was consistent across all segments of the intestine including the duodenum, jejunum, ileum and colon.
2.2.4 Kinetic Data for Rosuvastatin Transport
Active and passive kinetic transport data for the hepatic sinusoidal uptake (OATP1B1, OATP1B3 and NTCP) and canalicular efflux (BCRP) of rosuvastatin were available. It is not always possible to recover observed drug plasma concentration–time profiles accurately purely from the ‘bottom-up’ using physicochemical, in vitro permeability and metabolism/transport data. To accommodate inherent uncertainty, the parameter estimation (PE) module within the Simcyp Simulator may be used to optimise key parameter values. This provides a link between the ‘bottom-up’ and ‘top-down’ pharmacokinetic modelling paradigms by utilising available in vivo data to modify parameters based purely on in vitro studies. The simulations then move forward more effectively to predict the impact of specific perturbations of drug kinetics as a consequence of a DDI.
Preliminary simulations indicated that the experimental transporter kinetic data were not able to recover the observed profiles of rosuvastatin. Thus, a global intrinsic clearance for the active hepatic uptake (global CLint,T) of rosuvastatin was obtained using the PE module within the Simcyp Simulator and the observed plasma concentration–time data from Martin and co-workers [8] following intravenous administration of rosuvastatin in HVs. Other parameters were fixed to the in vitro values (Table 1), and optimisation was done using the Nelder–Mead minimisation method and weighted least squares algorithm. A global CLint,T of 222 μL/min/million cells was obtained for hepatic uptake of rosuvastatin. This was apportioned to OATP1B1, OATP1B3 and NTCP, based on the relative contributions of each of the transporters to the active uptake of rosuvastatin in vitro. According to the study of Kitamura and co-workers [17], the contribution of OATP1B1 to the active hepatic uptake of rosuvastatin in human hepatocytes is on average about 49 %. Using sandwich culture human hepatocyte (SCHH), Ho and co-workers [18] estimated that the percentage contribution of NTCP is about 35 %. It was assumed that the remaining 16 % represented the transporter-mediated uptake of rosuvastatin into the liver via OATP1B3. Thus, CLint,T values of 109, 36 and 78 μL/min/million cells were assigned to hepatic uptake of rosuvastatin by OATP1B1, OATP1B3 and NTCP, respectively (Table 1). It has been reported that OATP2B1 also contributes to the uptake of rosuvastatin. However, since modelling this transporter requires more sophisticated models that account for ion gradients and multiple binding sites, its contribution was combined with that of OATP1B3. As the data were derived from in vivo data, no REFs were applied (the REFs/RAFs were set to 1). The hepatic canalicular efflux contribution was recalculated from in vitro data in SCHH (CLint biliary 3.39 mL/min/kg [49]) using 107 × 106 HPGL and 25.7 g of liver per kg bodyweight and assigned to BCRP. A value of 1.23 ((3.39/25.7)/107) × 1,000) μL/min/million hepatocytes was obtained.
Although rosuvastatin has been shown to be a substrate of intestinal BCRP in vitro [19], no quantitative data were available. Therefore, a sensitivity analysis was performed to obtain estimates of the intestinal CLint,T of BCRP using observed rosuvastatin time to C max (t max) and C max for a given dose of 40 mg [21, 54]. A value of 35 μL/min/cm2 was able to recover observed t max and C max values and was thus applied in further simulations.
2.2.5 Data Used for Simulations of Cyclosporine Pharmacokinetics
In vitro and pharmacokinetic parameters for cyclosporine were taken from data in the literature (Table 2). Cyclosporine is an inhibitor of OATP1B1, OATP1B3, NTCP and BCRP; IC50 (the concentration that inhibits 50 % of the transporter activity) values of 0.1, 0.05, 4.5 and 2.0 μmol/L, respectively, have been generated in the same laboratory and reported by Clarke and co-workers [55, 56]. The OATP1B1 inhibition constant (K i) is approximately 10-fold higher than that reported previously by Amundsen and co-workers [57]. It has been demonstrated that the value derived in the latter study (0.014 μmol/L) can be applied successfully for prediction of tDDIs involving OATP1B1 [58, 59]. Thus, all of the IC50 values reported by Clarke and co-workers [55, 56] were converted to K i values and calibrated using the 10-fold factor derived for OATP1B1 to retain the same relative inhibitory potencies; final values of 0.014, 0.007, 0.28 and 0.07 μmol/L were used for OATP1B1, OATP1B3, NTCP and BCRP, respectively. In the full PBPK model of cyclosporine a well-stirred liver model was used; therefore, the surrogate inhibitory concentrations according to Table 3 were applied.
2.2.6 Simulations
All simulations were performed using the Simcyp Simulator (version 12, release 2). The program allows facile extrapolation of in vitro enzyme kinetic data in both liver and intestine, to predict pharmacokinetic changes in vivo in virtual populations. Genetic, physiological and demographic variables relevant to the prediction of DDIs are generated for each individual using correlated Monte-Carlo methods and equations derived from population databases obtained from literature sources. To ensure that the characteristics of the virtual subjects were matched closely to those of the subjects studied in vivo, numbers, age range and sex ratios were replicated. The following simulations were performed:
-
Ten virtual trials of HVs (subject number, age range, % female according to Table 4) receiving a single oral dose of rosuvastatin 10, 20, 40 or 80 mg were generated. The simulated profiles for rosuvastatin were compared with observed data from 11 independent pharmacokinetic studies (Table 4).
Table 4 Details on the single-dose clinical studies used for rosuvastatin performance verification -
Ten virtual trials of ten HVs aged 30–65 years (0.11 % female; one female subject) receiving multiple oral doses of rosuvastatin 10 mg co-administered with oral cyclosporine (200 mg twice daily) for 10 days were generated. The simulated profiles for rosuvastatin were compared with observed data [21, 54].
3 Results
Simulated rosuvastatin plasma concentration–time profiles following oral doses (10–80 mg) were reasonably consistent with observed data from 11 independent clinical studies in HVs (Fig. 2). The individually simulated profiles matching each study and the comparison to observed data are shown in the Electronic Supplementary Material. It should be noted that over the dose range 10–80 mg, the observed data were highly variable; however, apparent total oral clearance (CL/F), C max and t max ratios for predicted versus observed data were generally within 2-fold. Following oral administration, the median predicted AUC from time zero to time t (AUC t ) values of rosuvastatin at 10 mg ranged from 23.95 to 39.70 ng/mL·h for the ten simulated trials (mean 35.16, median 32.06, geometric mean 31.82) using 50 % male subjects between 20 and 50 years of age; the observed geometric mean values were 31.6 [54] and 45.9 ng/mL·h [68]. Median predicted AUC t values of rosuvastatin at 20 mg ranged from 47.79 to 79.37 ng/mL·h for the ten simulated trials (mean 70.06, median 63.99, geometric mean 63.45); the observed geometric mean value was 56.8 ng/mL·h [54]. Median predicted AUC t values of rosuvastatin at 40 mg ranged from 95.58 to 158.74 ng/mL·h for the ten simulated trials (mean 140.12, median 127.97, geometric mean 126.91); the observed geometric mean values were 98.2 [54], 165 [8] and 216 ng/mL·h [14]. Mean predicted AUC t values of rosuvastatin at 80 mg ranged from 198.03 to 342.74 ng/mL·h for the ten simulated trials (mean 284.57, median 252.29, geometric mean 255.76); the observed geometric mean values were 253 [69], 268 [54], 325 [70], 397 [68] and 410 ng/mL·h [20].
Simulated and observed plasma concentration–time profiles of rosuvastatin in healthy volunteers following the oral administration of a 10 mg, b 20 mg, c 40 mg and d 80 mg. The black line represents the mean concentration for the simulated population (n = 100, 20–50 years, health volunteers, 50 % female). The light and dark grey lines represent the upper (95 %) and lower (5 %) percentile concentrations of the simulated populations, respectively. The markers denote mean values from the clinical studies [8, 14, 20, 54, 68–70]
Simulated rosuvastatin plasma concentration–time profiles in the absence and presence of cyclosporine (200 mg twice daily) following 10 days of rosuvastatin administration (10 mg multiple dose) in HVs are shown in Fig. 3. Predicted median AUC t and C max ratios for the ten virtual trials ranged from 1.45 to 1.68 and 2.73 to 3.62, respectively (Fig. 3). Although HV data weren’t available for direct comparison, clinical data indicated that the AUC from time zero to 24 h (AUC24) and C max values were increased 7.1- and 10.6-fold, respectively, in stable heart transplant recipients (>6 months after transplant) on an anti-rejection regimen including cyclosporine compared to HV [21]. Sensitivity analysis of different elimination pathways suggests the hepatic uptake transporter is the most sensitive factor in rosuvastatin elimination (data not shown). Figure 4 shows the rosuvastatin unbound concentrations in the liver extracellular (CuEW) and intracellular (CuIW) compartments in absence and presence of cyclosporine for the simulated population. The figure shows that there is significant difference between CuEW and CuIW and the differential impact of transporter-mediated inhibition in the extracellular and intracellular compartments.
a Simulated plasma concentration–time profiles of rosuvastatin on day 10 in the absence and presence of cyclosporine (200 mg twice daily) in healthy volunteers following the oral administration of rosuvastatin 10 mg (multiple dose). b Simulated versus observed plasma concentration–time profile of cyclosporine (200 mg twice daily) on day 10. The thin grey lines represent simulated individual trials (ten trials of ten subjects) and the thick black lines are the simulated mean of the healthy volunteer population (n = 100) without (solid lines) and with interaction (dashed lines). The circles denote mean values from the clinical studies for rosuvastatin [21] and for cyclosporine [86]
Simulated unbound liver concentrations in a extracellular (CuEW) and b intracellular (CuIW) compartments of rosuvastatin on day 10 in the absence and presence of cyclosporine (200 mg twice daily) in healthy volunteers following the oral administration of rosuvastatin 10 mg (multiple dose). The grey and black lines represent the mean concentrations for the simulated population in the absence and presence of cyclosporine, respectively
4 Discussion
4.1 Model Development and Unbound Fractions
To model pravastatin pharmacokinetics in humans, Watanabe and co-workers used a PBPK model where the liver was divided into five units consisting of the extracellular and subcellular compartments [71, 72]. The units were connected in tandem by blood flow rate to mimic the liver dispersion model. They argued that, especially for high extraction drugs, the well-stirred model underestimates the hepatic clearance compared with the parallel tube and dispersion models, and the difference becomes greater when active uptake increases. The unbound fraction in the extracellular compartment and subcellular compartments was assumed to be the same as the unbound fraction in blood and the tissue unbound fraction (measured in rats), respectively.
Jones and co-workers [43] also used PBPK models with a liver permeability model to predict the pharmacokinetics of seven OATP substrates using in vitro data generated from SCHH. As per Watanabe et al. [71], they divided the liver into five units and used measured unbound fractions from in vitro experiments. Measuring unbound extracellular and intracellular fractions is a laborious and complex process and, thus, it is highly desirable to predict these values at early stage of drug development. Recently, the advent of more mechanistic approaches to assess drug distribution into tissues has led to the development of methods for prediction of unbound fractions using physicochemical properties [30–32, 34]. The Rodgers and Rowland equations improved K p predictions largely due to the incorporation of distribution processes related to drug ionisation, an issue that was not addressed in earlier equations [34]. These methods were mainly developed assuming steady-state conditions and instantaneous equilibrium of the unbound drug at membranes. However, researchers have tried modifying these equations to account for non-equilibrium conditions to develop models that describe transporter functionality in different organs such as the liver, brain and heart [73, 74]. Fenneteau and co-workers [73] proposed mechanistic transport-based models to investigate the impact of P-glycoprotein-meditated efflux in mouse brain and heart. Their model assumed that transport occurs at the capillary membrane. They developed an equation for estimating the tissue unbound fraction where they assumed CuEW and Cup (unbound concentration in plasma) are equal and CuIW and Cup only differ by an ionisation factors. Nevertheless, these assumptions are only valid for passive permeability and instantaneous equilibrium, which are not applicable in this case. Poirier and co-workers [74] used a similar approach to simulate the plasma concentration of napsagatran and fexofenadine in rats and that of valsartan in humans [75]. They predicted fu IW using the method by Poulin and Theil [31, 32] and fu EW using the method by Rodgers and Rowland [30, 34]. However, their fu IW equation for the permeability-limited model was independent of f IW.
Our proposed liver model (PerL) and the unbound fraction prediction equations account for the processes involved in drug transport at the liver membranes. Obviously, their validity should be assessed for a range of compounds. It should be noted that these equations are mainly developed to provide predictions during the discovery and early stages of drug development when measured values are not available. Generally, to increase confidence in pharmacokinetic predictions it is recommended these values be obtained from in vitro experiments whenever possible [76].
4.2 Development of the Rosuvastatin Model
In this study, we have presented a PBPK model for rosuvastatin, incorporating gut efflux by BCRP and active uptake into the liver via OATP1B1, OATP1B3 (OATP2B1) and NTCP, in addition to excretion of the drug into the bile by BCRP. Although the model was able to recover the observed data in most cases, for some studies the absorption delay was not captured. The delay may be a result of increasing solubility along the intestine due to pH changes or, alternatively, rosuvastatin may be a substrate of other efflux transporters that have higher expression in the proximal part of the intestine, e.g. MRP2 (multi-drug resistance protein 2). However, as there was considerable variability in clinical data across doses and the rosuvastatin model was able to recover observed data in most cases, the model was considered to be reasonably robust for assessment of the magnitude of interaction with cyclosporine, an inhibitor of OATPs and NTCP.
Predicted median AUC and C max ratios of rosuvastatin (10 mg multiple dose) following co-administration of cyclosporine (200 mg twice daily) for 10 days ranged from 1.45 to 1.68 and 2.73 to 3.62, respectively, for the ten trials. Although clinical data from a crossover study design in HVs were not available for direct comparison, rosuvastatin pharmacokinetic parameters had been assessed in an open-label trial involving stable heart transplant recipients (>6 months after transplant) on an anti-rejection regimen including cyclosporine [21]. In these patients taking rosuvastatin 10 mg for 10 days, geometric mean values and percentage coefficient of variation for steady-state AUC24 and C max were 284 ng·h/mL (31.3 %) and 48.7 ng/mL (47.2 %), respectively. In controls (historical data AUC24 and C max from 21 HVs taking rosuvastatin 10 mg), these values were 40.1 ng·h/mL (39.4 %) and 4.58 ng/mL (46.9 %), respectively [21]. Thus, compared with control values, AUC24 and C max values were increased 7.1- and 10.6-fold, respectively, in transplant recipients. The predicted increase in exposure of rosuvastatin following co-administration of cyclosporine in virtual HV subjects is lower than observed in vivo.
Recently, Gertz and co-workers [77] developed a PBPK model to predict the inhibitory effects of cyclosporine and its mono-hydroxylated metabolite on intestinal CYP3A4 metabolism and uptake and efflux transporters. Their model indicated that cyclosporine had the highest impact on the liver uptake transporters and minimal impact on hepatic efflux and metabolism. Inclusion of the cyclosporine metabolite had little impact on the predicted interaction with liver uptake transporters. Thus, the fact that we did not consider the impact of the cyclosporine metabolite does not account for the under-prediction of the tDDIs with rosuvastatin seen in our study. However, it should be noted that other disease-related factors may contribute to increased exposure of rosuvastatin in patients. In addition, the exposure of cyclosporine itself may differ between heart transplant patients and the virtual HV subjects. Despite the limitations and lack of clinical data for direct comparison, the PBPK model presented here for rosuvastatin is sensitive to inhibition of the transporters OATP1B1, OATP1B3, OATP2B1, NTCP and BCRP by cyclosporine. The developed PBPK model also predicts the intracellular liver concentration of rosuvastatin in the presence and absence of the inhibitor. As Fig. 4 shows, the predicted magnitude of interaction within the tissue can be different to that obtained in the plasma. Depending on the drug characteristics, the difference can be significant. Such knowledge can be valuable, especially when liver toxicity is an issue for some drugs or when the site of drug action is within the liver, in the case of statins. Indeed, it can only increase our understanding of the drug response and its variability [23].
Given the complexity of processes involved in the transport of drugs into cells, obtaining accurate kinetic parameters from in vitro assays is very challenging. Recently, model-based data analysis of in vitro assays has attracted more attention and new methods and data analysis techniques are proposed; for more detail see previous publications [76, 78–80]. The functional translation of some SLC effects using IVIVE approaches is challenging due to the existence of several binding sites [81], the possible time-dependent inhibition for some SLCs [57, 77] and the limitations of apparent in vitro kinetic parameter measurements [82]. Adding to this complexity, in order to have a robust PBPK model, the relative contributions of both active and passive components need to be assigned correctly. In addition, the active component itself can be a sum of different uptake and efflux transporters working in parallel or against each other on the same membrane. Thus, the fractional contribution of each transporter (ft) to the global transport is as important as the ‘fm’ (the fraction of a drug metabolized by an enzyme) for CYP enzymes in the prediction of interactions involving metabolism. For our PBPK model of rosuvastatin, a global hepatic uptake was fitted using intravenous clinical data and the relative contributions of OATP1B1, OATP1B3 (OATP2B1), NTCP and BCRP were assigned based on in vitro data. Our model has also successfully been applied to predict the disposition and DDIs of other drugs such as repaglinide and pravastatin [40, 58, 83, 84].
Transporters’ ‘ft’ values are used to predict tDDIs in a manner similar to that used for CYP enzymes. These fraction values have been used in static equations with different degrees of success depending on the applied assumptions [84, 85]. In some cases it is assumed that the transport process occurs exclusively via a particular uptake transporter, ignoring the potential contribution of passive diffusion or other transporters or involvement of metabolism. The static equations cannot account for the time-varying nature of the substrate and inhibitor concentrations and assume constant values. Further, since these models cannot estimate the relevant concentrations at the transport site, surrogate concentrations such as plasma or average gut concentration (highest oral dose diluted in 250 mL) are used. These assumptions often increase the possibility of encountering false positive predictions and may lead to unnecessary clinical studies being conducted. Given the complexity of the processes involved in metabolism and transport interplay, dynamic models for determining DDIs are preferable. However, in some cases during the early stages of drug development, static equations, if applied with correct assumptions, may provide a reasonable estimate of tDDIs.
5 Conclusions
Incorporation of transporters within PBPK models can provide some insight into their role in drug disposition and lead to improved understanding of the drug response and its variability. In particular, when these models account for mDDIs and tDDIs simultaneously for multiple moieties they become very powerful tools for investigating complex cases that can occur in clinical practice. Although there are still gaps in our knowledge regarding physiological data such as reliable absolute abundance/activity data for transporters, observed clinical data can be used to estimate the unknown model parameters and, once validated, the model can then be applied prospectively, to predict tDDIs.
Application of these models can aid in making informed decisions on the design of clinical studies and give an indication of whether such studies are needed. Indeed, successful application of these models (e.g. Varma et al. [58, 83]) demonstrates the value and impact of model-based drug development in the pharmaceutical industry.
References
Giacomini KM, Huang SM, Tweedie DJ, Benet LZ, Brouwer KL, Chu X, et al. Membrane transporters in drug development. Nat Rev Drug Discov. 2010;9(3):215–36.
Huang SM, Zhang L, Giacomini KM. The International Transporter Consortium: a collaborative group of scientists from academia, industry, and the FDA. Clin Pharmacol Ther. 2010;87(1):32–6.
Committee for Human Medicinal Products. Guideline on the investigation of drug interactions. European Medicines Agency; 2012. http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2012/07/WC500129606.pdf. Accessed 1 Apr 2013.
Food and Drug Administration. Drug interaction studies—study design, data analysis, implications for dosing, and labeling recommendations (draft). U.S. Department of Health and Human Services; 2012. http://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/ucm292362.pdf. Accessed 1 Apr 2013.
Niemi M. Role of OATP transporters in the disposition of drugs. Pharmacogenomics. 2007;8(7):787–802.
Shitara Y. Clinical importance of OATP1B1 and OATP1B3 in drug–drug interactions. Drug Metab Pharmacokinet. 2011;26(3):220–7.
Elsby R, Hilgendorf C, Fenner K. Understanding the critical disposition pathways of statins to assess drug–drug interaction risk during drug development: it’s not just about OATP1B1. Clin Pharmacol Ther. 2012;92(5):584–98.
Martin PD, Warwick MJ, Dane AL, Brindley C, Short T. Absolute oral bioavailability of rosuvastatin in healthy white adult male volunteers. Clin Ther. 2003;25(10):2553–63.
White CM. A review of the pharmacologic and pharmacokinetic aspects of rosuvastatin. J Clin Pharmacol. 2002;42(9):963–70.
Garcia MJ, Reinoso RF, Sanchez Navarro A, Prous JR. Clinical pharmacokinetics of statins. Methods Find Exp Clin Pharmacol. 2003;25(6):457–81.
Prueksaritanont T, Tang C, Qiu Y, Mu L, Subramanian R, Lin JH. Effects of fibrates on metabolism of statins in human hepatocytes. Drug Metab Dispos. 2002;30(11):1280–7.
McCormick A, McKillop D, Butters C. ZD4522—an HMG-CoA reductase inhibitor free of metabolically mediated drug interactions: metabolic studies in human in vitro systems. Twenty Ninth Annual Meeting, American College of Clinical Pharmacology, September 17–19 Chicago, A46. J Clin Pharmacol. 2000;40:1055.
Martin PD, Mitchell PD, Schneck DW. Pharmacodynamic effects and pharmacokinetics of a new HMG-CoA reductase inhibitor, rosuvastatin, after morning or evening administration in healthy volunteers. Br J Clin Pharmacol. 2002;54(5):472–7.
Lee E, Ryan S, Birmingham B, Zalikowski J, March R, Ambrose H, et al. Rosuvastatin pharmacokinetics and pharmacogenetics in white and Asian subjects residing in the same environment. Clin Pharmacol Ther. 2005;78(4):330–41.
Bergman E, Forsell P, Tevell A, Persson EM, Hedeland M, Bondesson U, et al. Biliary secretion of rosuvastatin and bile acids in humans during the absorption phase. Eur J Pharm Sci. 2006;29(3–4):205–14.
Bergman E, Lundahl A, Fridblom P, Hedeland M, Bondesson U, Knutson L, et al. Enterohepatic disposition of rosuvastatin in pigs and the impact of concomitant dosing with cyclosporine and gemfibrozil. Drug Metab Dispos. 2009;37(12):2349–58.
Kitamura S, Maeda K, Wang Y, Sugiyama Y. Involvement of multiple transporters in the hepatobiliary transport of rosuvastatin. Drug Metab Dispos. 2008;36(10):2014–23.
Ho RH, Tirona RG, Leake BF, Glaeser H, Lee W, Lemke CJ, et al. Drug and bile acid transporters in rosuvastatin hepatic uptake: function, expression, and pharmacogenetics. Gastroenterology. 2006;130(6):1793–806.
Huang L, Wang Y, Grimm S. ATP-dependent transport of rosuvastatin in membrane vesicles expressing breast cancer resistance protein. Drug Metab Dispos. 2006;34(5):738–42.
Schneck DW, Birmingham BK, Zalikowski JA, Mitchell PD, Wang Y, Martin PD, et al. The effect of gemfibrozil on the pharmacokinetics of rosuvastatin. Clin Pharmacol Ther. 2004;75(5):455–63.
Simonson SG, Raza A, Martin PD, Mitchell PD, Jarcho JA, Brown CD, et al. Rosuvastatin pharmacokinetics in heart transplant recipients administered an antirejection regimen including cyclosporine. Clin Pharmacol Ther. 2004;76(2):167–77.
Gibson GG, Rostami-Hodjegan A. Modelling and simulation in prediction of human xenobiotic absorption, distribution, metabolism and excretion (ADME): in vitro–in vivo extrapolations (IVIVE). Xenobiotica. 2007;37(10–11):1013–4.
Rostami-Hodjegan A. Physiologically based pharmacokinetics joined with in vitro–in vivo extrapolation of ADME: a marriage under the arch of systems pharmacology. Clin Pharmacol Ther. 2012;92(1):50–61.
Jamei M, Marciniak S, Feng K, Barnett A, Tucker G, Rostami-Hodjegan A. The Simcyp® population-based ADME simulator. Expert Opin Drug Metab Toxicol. 2009;5(2):211–23.
Jamei M, Turner D, Yang J, Neuhoff S, Polak S, Rostami-Hodjegan A, et al. Population-based mechanistic prediction of oral drug absorption. AAPS J. 2009;11(2):225–37.
Darwich AS, Neuhoff S, Jamei M, Rostami-Hodjegan A. Interplay of metabolism and transport in determining oral drug absorption and gut wall metabolism: a simulation assessment using the “Advanced Dissolution, Absorption, Metabolism (ADAM)” model. Curr Drug Metab. 2010;11(9):716–29.
Harwood MD, Neuhoff S, Carlson GL, Warhurst G, Rostami-Hodjegan A. Absolute abundance and function of intestinal drug transporters: a prerequisite for fully mechanistic in vitro–in vivo extrapolation of oral drug absorption. Biopharm Drug Dispos. 2012;34(1):2–28.
Gibaldi M. Pharmacokinetic aspects of drug metabolism. Ann N Y Acad Sci. 1971;179(1):19–31.
Berezhkovskiy LM. A valid equation for the well-stirred perfusion limited physiologically based pharmacokinetic model that consistently accounts for the blood-tissue drug distribution in the organ and the corresponding valid equation for the steady state volume of distribution. J Pharm Sci. 2009;99(1):475–85.
Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94(6):1259–76.
Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies 1. Mechanism-based prediction of volume of distribution. J Pharm Sci. 2002;91(1):129–56.
Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. J Pharm Sci. 2002;91(5):1358–70.
Rodgers T, Leahy D, Rowland M. Tissue distribution of basic drugs: accounting for enantiomeric, compound and regional differences amongst beta-blocking drugs in rat. J Pharm Sci. 2005;94(6):1237–48.
Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95(6):1238–57.
Brauer RW. Liver circulation and function. Physiol Rev. 1963;43:115–213.
Barter ZE, Bayliss MK, Beaune PH, Boobis AR, Carlile DJ, Edwards RJ, et al. Scaling factors for the extrapolation of in vivo metabolic drug clearance from in vitro data: reaching a consensus on values of human microsomal protein and hepatocellularity per gram of liver. Curr Drug Metab. 2007;8(1):33–45.
Johnson TN, Tucker GT, Tanner MS, Rostami-Hodjegan A. Changes in liver volume from birth to adulthood: a meta-analysis. Liver Transpl. 2005;11(12):1481–93.
Almond LM, Yang J, Jamei M, Tucker GT, Rostami-Hodjegan A. Towards a quantitative framework for the prediction of DDIs arising from cytochrome P450 induction. Curr Drug Metab. 2009;10(4):420–32.
Rowland Yeo K, Jamei M, Yang J, Tucker GT, Rostami-Hodjegan A. Physiologically-based mechanistic modelling to predict complex drug–drug interactions involving simultaneous competitive and time-dependent enzyme inhibition by parent compound and its metabolite in both liver and gut-the effect of diltiazem on the time-course of exposure to triazolam. Eur J Pharm Sci. 2010;39(5):298–309.
Rowland Yeo K, Jamei M, Rostami-Hodjegan A. Predicting drug–drug interactions: application of physiologically based pharmacokinetic models under a systems biology approach. Expert Rev Clin Pharmacol. 2013;6(2):143–57.
Rostami-Hodjegan A, Tucker GT. ‘In silico’ simulations to assess the ‘in vivo’ consequences of ‘in vitro’ metabolic drug–drug interactions. Drug Discov Today Technol. 2004;1(4):441–8.
Englund G, Hallberg P, Artursson P, Michaelsson K, Melhus H. Association between the number of coadministered P-glycoprotein inhibitors and serum digoxin levels in patients on therapeutic drug monitoring. BMC Med. 2004;2:8.
Jones HM, Barton HA, Lai Y, Bi YA, Kimoto E, Kempshall S, et al. Mechanistic pharmacokinetic modelling for the prediction of transporter-mediated disposition in human from sandwich culture human hepatocyte data. Drug Metab Dispos. 2012;40(5):1007–17.
Ahmad S, Madsen CS, Stein PD, Janovitz E, Huang C, Ngu K, et al. (3R,5S,E)-7-(4-(4-fluorophenyl)-6-isopropyl-2-(methyl(1-methyl-1h-1,2,4-triazol-5-yl)amino)pyrimidin-5-yl)-3,5-dihydroxyhept-6-enoic acid (BMS-644950): a rationally designed orally efficacious 3-hydroxy-3-methylglutaryl coenzyme-a reductase inhibitor with reduced myotoxicity potential. J Med Chem. 2008;51(9):2722–33.
Avdeef A. Absorption and drug development. 2nd ed. Hoboken: Wiley-Interscience; 2012.
Li J, Volpe DA, Wang Y, Zhang W, Bode C, Owen A, et al. Use of transporter knockdown Caco-2 cells to investigate the in vitro efflux of statin drugs. Drug Metab Dispos. 2011;39(7):1196–202.
Pasanen MK, Fredrikson H, Neuvonen PJ, Niemi M. Different effects of SLCO1B1 polymorphism on the pharmacokinetics of atorvastatin and rosuvastatin. Clin Pharmacol Ther. 2007;82(6):726–33.
Keskitalo JE, Kurkinen KJ, Neuvonen M, Backman JT, Neuvonen PJ, Niemi M. No significant effect of ABCB1 haplotypes on the pharmacokinetics of fluvastatin, pravastatin, lovastatin, and rosuvastatin. Br J Clin Pharmacol. 2009;68(2):207–13.
Abe K, Bridges AS, Brouwer KL. Use of sandwich-cultured human hepatocytes to predict biliary clearance of angiotensin II receptor blockers and HMG-CoA reductase inhibitors. Drug Metab Dispos. 2009;37(3):447–52.
Bergman E, Matsson EM, Hedeland M, Bondesson U, Knutson L, Lennernas H. Effect of a single gemfibrozil dose on the pharmacokinetics of rosuvastatin in bile and plasma in healthy volunteers. J Clin Pharmacol. 2010;50(9):1039–49.
Kotani N, Maeda K, Watanabe T, Hiramatsu M, Gong LK, Bi YA, et al. Culture period-dependent changes in the uptake of transporter substrates in sandwich-cultured rat and human hepatocytes. Drug Metab Dispos. 2011;39(9):1503–10.
Barter ZE, Chowdry JE, Harlow JR, Snawder JE, Lipscomb JC, Rostami-Hodjegan A. Covariation of human microsomal protein per gram of liver with age: absence of influence of operator and sample storage may justify interlaboratory data pooling. Drug Metab Dispos. 2008;36(12):2405–9.
Martin PD, Warwick MJ, Dane AL, Hill SJ, Giles PB, Phillips PJ, et al. Metabolism, excretion, and pharmacokinetics of rosuvastatin in healthy adult male volunteers. Clin Ther. 2003;25(11):2822–35.
Martin PD, Warwick MJ, Dane AL, Cantarini MV. A double-blind, randomized, incomplete crossover trial to assess the dose proportionality of rosuvastatin in healthy volunteers. Clin Ther. 2003;25(8):2215–24.
Clarke J, Generaux G, Harmon K, Kenworthy KE, Polli JW. Predicting clinical rosuvastatin interactions using in-vitro OATP inhibition data. Drug Transporters in ADME: From Bench to Bedside, AAPS Transporters Workshop, 14–16 Mar 2011, Bethesda.
Clarke J. The use of in-vitro BCRP/OATP data to predict rosuvastatin DDI: a static modelling approach. 3rd International clinically relevant drug transporters, 28–29 Feb 2012, Berlin.
Amundsen R, Christensen H, Zabihyan B, Asberg A. Cyclosporine A, but not tacrolimus, shows relevant inhibition of organic anion-transporting protein 1B1-mediated transport of atorvastatin. Drug Metab Dispos. 2010;38(9):1499–504.
Varma M, Lai Y, Feng B, Litchfield J, Goosen T, Bergman A. Physiologically based modeling of pravastatin transporter-mediated hepatobiliary disposition and drug–drug interactions. Pharm Res. 2012;29(10):2860–73.
Barton HA, Lai Y, Goosen TC, Jones HM, El-Kattan AF, Gosset JR, et al. Model-based approaches to predict drug–drug interactions associated with hepatic uptake transporters: preclinical, clinical and beyond. Expert Opin Drug Metab Toxicol. 2013;9(4):459–72.
Legg B, Rowland M. Cyclosporin: measurement of fraction unbound in plasma. J Pharm Pharmacol. 1987;39(8):599–603.
el Tayar N, Mark AE, Vallat P, Brunne RM, Testa B, van Gunsteren WF. Solvent-dependent conformation and hydrogen-bonding capacity of cyclosporin A: evidence from partition coefficients and molecular dynamics simulations. J Med Chem. 1993;36(24):3757–64.
Cefalu WT, Pardridge WM. Restrictive transport of a lipid-soluble peptide (cyclosporin) through the blood–brain barrier. J Neurochem. 1985;45(6):1954–6.
Chiu YY, Higaki K, Neudeck BL, Barnett JL, Welage LS, Amidon GL. Human jejunal permeability of cyclosporin A: influence of surfactants on P-glycoprotein efflux in Caco-2 cells. Pharm Res. 2003;20(5):749–56.
Ducharme MP, Warbasse LH, Edwards DJ. Disposition of intravenous and oral cyclosporine after administration with grapefruit juice. Clin Pharmacol Ther. 1995;57(5):485–91.
Tsunoda SM, Harris RZ, Christians U, Velez RL, Freeman RB, Benet LZ, et al. Red wine decreases cyclosporine bioavailability. Clin Pharmacol Ther. 2001;70(5):462–7.
Min DI, Lee M, Ku YM, Flanigan M. Gender-dependent racial difference in disposition of cyclosporine among healthy African American and white volunteers. Clin Pharmacol Ther. 2000;68(5):478–86.
Kawai R, Mathew D, Tanaka C, Rowland M. Physiologically based pharmacokinetics of cyclosporine A: extension to tissue distribution kinetics in rats and scale-up to human. J Pharmacol Exp Ther. 1998;287(2):457–68.
Cooper KJ, Martin PD, Dane AL, Warwick MJ, Schneck DW, Cantarini MV. Effect of itraconazole on the pharmacokinetics of rosuvastatin. Clin Pharmacol Ther. 2003;73(4):322–9.
Cooper KJ, Martin PD, Dane AL, Warwick MJ, Raza A, Schneck DW. The effect of erythromycin on the pharmacokinetics of rosuvastatin. Eur J Clin Pharmacol. 2003;59(1):51–6.
Cooper KJ, Martin PD, Dane AL, Warwick MJ, Schneck DW, Cantarini MV. The effect of fluconazole on the pharmacokinetics of rosuvastatin. Eur J Clin Pharmacol. 2002;58(8):527–31.
Watanabe T, Kusuhara H, Maeda K, Shitara Y, Sugiyama Y. Physiologically based pharmacokinetic modeling to predict transporter-mediated clearance and distribution of pravastatin in humans. J Pharmacol Exp Ther. 2009;328(2):652–62.
Watanabe T, Kusuhara H, Sugiyama Y. Application of physiologically based pharmacokinetic modeling and clearance concept to drugs showing transporter-mediated distribution and clearance in humans. J Pharmacokinet Pharmacodyn. 2010;37(6):575–90.
Fenneteau F, Turgeon J, Couture L, Michaud V, Li J, Nekka F. Assessing drug distribution in tissues expressing P-glycoprotein through physiologically based pharmacokinetic modeling: model structure and parameters determination. Theor Biol Med Model. 2009;6:2.
Poirier A, Funk C, Scherrmann J-M, Lave T. Mechanistic modeling of hepatic transport from cells to whole body: application to napsagatran and fexofenadine. Mol Pharma. 2009;6(6):1716–33.
Poirier A, Cascais A-C, Funk C, Lavé T. Prediction of pharmacokinetic profile of valsartan in human based on in vitro uptake transport data. J Pharmacokinet Pharmacodyn. 2009;36(6):585–611.
Menochet K, Kenworthy KE, Houston JB, Galetin A. Simultaneous assessment of uptake and metabolism in rat hepatocytes: a comprehensive mechanistic model. J Pharmacol Exp Ther. 2012;341(1):2–15.
Gertz M, Cartwright CM, Hobbs MJ, Kenworthy KE, Rowland M, Houston JB, et al. Cyclosporine inhibition of hepatic and intestinal CYP3A4, uptake and efflux transporters: application of PBPK modeling in the assessment of drug–drug interaction potential. Pharm Res. 2013;30(3):761–80.
Baker M, Parton T. Kinetic determinants of hepatic clearance: plasma protein binding and hepatic uptake. Xenobiotica. 2007;37(10–11):1110–34.
Poirier A, Lave T, Portmann R, Brun M-E, Senner F, Kansy M, et al. Design, data analysis and simulation of in vitro drug transport kinetic experiments using a mechanistic in vitro model. Drug Metab Dispos. 2008;36(12):2434–44.
Paine SW, Parker AJ, Gardiner P, Webborn PJ, Riley RJ. Prediction of the pharmacokinetics of atorvastatin, cerivastatin, and indomethacin using kinetic models applied to isolated rat hepatocytes. Drug Metab Dispos. 2008;36(7):1365–74.
Shirasaka Y, Mori T, Shichiri M, Nakanishi T, Tamai I. Functional pleiotropy of organic anion transporting polypeptide OATP2B1 due to multiple binding sites. Drug Metab Pharmacokinet. 2012;27(3):360–4.
Zamek-Gliszczynski MJ, Lee CA, Poirier A, Bentz J, Chu X, Ellens H, et al. ITC recommendations on transporter kinetic parameter estimation and translational modeling of transport-mediated PK and DDIs in humans. Clin Pharmacol Ther. 2013;94:64–79.
Varma MS, Lai Y, Kimoto E, Goosen T, El-Kattan A, Kumar V. Mechanistic modeling to predict the transporter- and enzyme-mediated drug–drug interactions of repaglinide. Pharm Res. 2013;30(4):1188–99.
Varma MVS, Lin J, Bi YA, Rotter CJ, Fahmi OA, Lam J, et al. Quantitative prediction of repaglinide–rifampicin complex drug interactions using dynamic and static mechanistic models: delineating differential CYP3A4 induction and OATP1B1 inhibition potential of rifampicin. Drug Metab Dispos. 2013;41(5):966–74.
Yoshida K, Maeda K, Sugiyama Y. Hepatic and intestinal drug transporters: prediction of pharmacokinetic effects caused by drug–drug interactions and genetic polymorphisms. Annu Rev Pharmacol Toxicol. 2013;53(1):581–612.
Oliveira-Freitas VL, Dalla Costa T, Manfro RC, Cruz LB, Schwartsmann G. Influence of purple grape juice in cyclosporine bioavailability. J Ren Nutr. 2010;20(5):309–13.
Acknowledgments
This work was funded by Simcyp Limited (A Certara Company). The Simcyp Simulator is freely available, following completion of the training workshop, to approved members of academic institutions and other not-for-profit organisations, for research and teaching purposes. Parts of this work have been published as posters at ASCPT (American Society for Clinical Pharmacology and Therapeutics) in 2011 and AAPS (American Association of Pharmaceutical Scientists) in 2012. The help of James Kay and Eleanor Savill in preparing the manuscript is appreciated.
Conflicts of interest
Masoud Jamei, Sibylle Neuhoff, Zoe Barter and Karen Rowland-Yeo are employees of Simcyp Limited (A Certara Company). Amin Rostami-Hodjegan is an employee of the University of Manchester and part-time secondee to Simcyp Limited (A Certara Company). Jiansong Yang is an employee of GSK, China. Fania Bajot is an employee of British American Tobacco.
Author contributions
MJ, YJ, SN, KR-Y and AR-H designed the research, developed the PBPK model and algorithms and wrote the manuscript. MJ, FB, SN, ZB and KR-Y designed the research, developed the compound files, ran simulations, analysed the data and wrote the manuscript. All authors read and approved the final manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Jamei, M., Bajot, F., Neuhoff, S. et al. A Mechanistic Framework for In Vitro–In Vivo Extrapolation of Liver Membrane Transporters: Prediction of Drug–Drug Interaction Between Rosuvastatin and Cyclosporine. Clin Pharmacokinet 53, 73–87 (2014). https://doi.org/10.1007/s40262-013-0097-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40262-013-0097-y