FormalPara Key Points for Decision Makers

There is emerging interest in the use of risk-stratification in the national breast cancer screening programme (risk-stratified NBSP) in the UK.

There is a key role for the use of decision-analytic-model-based analysis of healthcare interventions that are difficult to evaluate in trials, such as cancer screening programmes.

This study follows structured frameworks to assess the internal and external validity of a decision-analytic model to assess the cost-effectiveness of exemplar approaches to risk-stratified NBSP.

The decision-analytic model is shown to perform to a satisfactory level, with possible limitations described clearly, to inform resource allocation decisions from the perspective of the UK healthcare system.

1 Introduction

A suite of recommendations have been developed in the healthcare context which are designed to enable decision analysts to have a structured approach to developing, building and appraising the quality of decision-analytic models [1,2,3,4,5,6]. A crucial element in these recommendations is the need for validation [7]. Enabling decision-makers’ trust and confidence, by conducting a systematic and transparent process of validation, is a vital component that decision analysts should take seriously so the decision-analytic model has sufficient credibility [6]. A fundamental component supporting the process of validation is the need for transparency in the decision-analytic model structure and use of data. Simplistically, transparency can be achieved by using open-source programming languages, such as R, and making the code public [8,9,10]. This level of transparency is necessary, but not sufficient, to enable the informed use of decision-analytic models to guide resource allocation decisions. The process of validation for a published decision-analytic model should also be transparent.

There are numerous recommendations and guidelines suggesting the need for, and approaches to, decision-analytic model validation. Such recommendations and guidelines, for example, the Technical Verification (TECH-VER) and Assessment of the Validation Status of Health-Economic Decision Models (AdViSHe) checklists, have been produced by small groups of individual researchers (of note, for example, McCabe and Dixon) or groups of researchers, reaching consensus or making task forces as part of international societies such as the International Society for Pharmacoeconomics and Outcomes Research [6, 11,12,13]. There are, however, correspondingly few publications that explicitly report the steps to completing model validation [14].

A particular clinical area where model validation may be valuable is in the evaluation of cancer screening models. Such models can be very complex, incorporating natural history models, which explain how cancers grow and spread over time. Changes to cancer screening programmes can have implications for large numbers of individuals, so ensuring that the assumptions and predictions of cancer screening models are correct is particularly important for decision-makers. In the UK, in 2023, the current national breast cancer screening programme (NBSP) invites women, via a letter sent to their home address, to have a mammogram that is then repeated every 3 years. The current eligible age-range for the UK-NBSP starts within 3 years of a woman reaching their 50th birthday up to the age of 70 years (inclusive) [16]. This means that in the UK over 2 million women attend breast cancer screening annually.

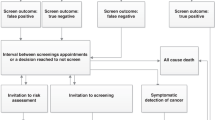
The aim of breasts cancer screening is to identify cancers at an earlier stage, making them more treatable [15]. However, there are harms to screening, including the risk of false-positive results and overdiagnosis of cancers which would never have grown to a size which would have caused harm to the woman. Risk-stratified national breast screening programmes (NBSP) are being suggested as a potential adaptation to existing programmes that offer a mammogram (X-ray of the breast) to all women in a selected age group. The approach to a NBSP can vary in terms of the age at which screening is first offered to women in the population (NBSP starting age), interval between screenings (NBSP screening interval), age at which screening is stopped (NBSP stopping age), number of X-rays used (one- or two-view mammography), supplementary screening technologies used (ultrasound and/or magnetic resonance imaging) and interpretation of the X-ray (manual or digital).

Factors known to influence a women’s 10-year risk of developing breast cancer have been used to develop risk prediction models developed in various formats and with criteria to categorise woman into specified risk groups [17,18,19,20,21,22,23,24,25]. For example, the Tyrer–Cuzick risk calculator asks women to record their age, weight and height (to calculate body mass index), age at menarche, obstetric history, age at menopause (if applicable), history of a benign breast condition that increases breast cancer risk, history of ovarian cancer, use of hormone replacement therapy and family history (including breast and ovarian cancer, Ashkenazi inheritance, BRCA 1 and 2 genetic testing) [26, 27]. The ‘score’ from this risk-calculator may then be used to categorise a women into pre-defined risk categories, such as population-average-level risk (10-year risk of 2 to < 3%); low (below average) risk (10-year risk of < 2%); above-average risk (10-year risk of 3 to < 5%); moderate risk (10-year risk of 5 to <8%); high risk (10-year risk of ≥ 8%) [28]. When a woman’s risk of breast cancer has been estimated, the intensity of screening can be altered for women in different risk categories. The frequency of screening can be increased for those at higher risk to find more cancers at an earlier stage, improving treatment outcomes. For women at low risk of cancer, the frequency of screening can potentially be reduced to decrease the degree of overdiagnosis and false-positive results in this group while also saving healthcare resources. A risk-stratified breast cancer screening programme may therefore be able to improve the balance of the benefits and harms of screening while not requiring a significant increase in the number of screens. To date, there are no examples of a risk-stratified NBSP used in practice, but there is consensus about the need for different types of evidence to support their introduction [29].

Generating trial-based clinical evidence of the effectiveness of a risk-stratified NBSP compared with existing approaches to NBSP is neither feasible nor perhaps desirable due to the inherent limitations of the necessary follow-up and the challenges of including women from different risk groups. Within this context, and in keeping with the predominant view, economic evidence needed to understand the potential value of risk-stratified NBSP should come from decision-analytic-model-based analyses using appropriate methods that answer the specified decision problem [30,31,32,33]. Tappenden and Chillcott suggest the need to include a process involving cycles of model checking and validation [34] mirroring the recommendations for an iterative approach towards a definitive evidence base made by Sculpher and colleagues [35].

This study aimed to design a structured process to update and then assess the internal and external validity of a decision-analytic model. This structured approach to model validation was then applied to update and validate a case study model structured to estimate the incremental healthcare costs and health consequences of exemplar risk-stratified national breast screening programmes (NBSP) in the UK [36]. The resulting outputs of the validated model (called MANC-RISK-SCREEN) reporting the healthcare costs and health consequences of a risk-stratified NBSP compared with universal triyearly screening, universal biyearly screening or no screening in the UK setting will be published separately in a follow-up paper.

2 Methods

A pre-defined set of steps were used to conduct the process of validation of a published decision-analytic-model-based cost-effectiveness analysis [36]. This early economic evaluation sought to estimate the cost-effectiveness of different breast cancer screening strategies in the UK, including risk-based approaches. This study was reported in detail in the original paper, but the model code was not made publicly available, and the predictions of the model were not explored. There is growing interest in risk-based breast cancer screening in the UK, and as such, a full update and validation of this model was conducted to provide decision-makers with transparent information about the strengths and weaknesses of the model.

There are numerous, and inconsistent, definitions of the process of decision-analytic model validation [13]. This study therefore took a pragmatic approach to describe the required steps of validation that are needed (in a normative sense) to enable a transparent description of the process. The contribution of individual recommendations, identified in the extant literature, used to inform the discrete steps of the process of decision-analytic model validation are cited where relevant in the sections that follow.

2.1 Description of the original decision-analytic model

The original decision-analytic model reported in Gray et al. (2015) [36], the focus for this validation process, was developed to address the decision problem: “What are the key drivers of the incremental costs and benefits of example stratified breast screening programs compared with the current National Breast Cancer Screening Program?” Gray and colleagues conducted an early economic analysis. The key characteristics of the ‘Gray’ decision-analytic model, a discrete event simulation, are outlined in Table 1. Further details regarding the Gray model can be found in Appendix 1.

Table 1 Key characteristics of the original Graya decision-analytic model
Full size table

2.2 The components of the model validation process

The validation process aimed to explore the degree of internal and external validity. Internal validation has been described in terms of three criteria [6, 37]: descriptive validity, to assess whether the degree of simplification used in the decision-analytic model structure still adequately represents the natural history of the specified disease and/or pathways of care; technical validity, to assess whether the decision-analytic model was appropriately programmed to produce the intended outputs from the specified inputs; and face validity, to assess whether the decision-analytic model produces outputs consistent with theoretical basis of disease and the intervention [12]. External validation can be described in terms of three criteria: operational validation, to assess whether the outputs produced by the decision-analytic model are sufficiently accurate; convergent validity (or corroboration), to compare the decision-analytic model with other published approaches addressing a similar decision problem; and predictive validity, to assess whether the outputs produced by the model sufficiently represent outputs from alternative sources. For the purpose of validation, the following six steps, broken down by criterion, were carried out.

2.2.1 Face Validity

Face validity refers to whether the decision-analytic model is measuring what is intended—in this case whether the model structure and parameter values produce outputs that are clinically credible. Face validity is a type of internal validity that captures first-order validation as defined by Haji Ali Afzali and colleagues [38]. The process of assessing face validity is often intuitive and subjective in that it requires value judgements to be made by the decision analyst. These value judgements require the decision analyst to be explicit about the criteria used when assessing face validity. There are no available published criteria to assess the face validity of a decision-analytic model. Assessing face validity was, therefore, reliant on the team of decision analysts, with input from relevant clinical expertise, producing an adequate explicit description of whether, and how, the outputs are consistent pre-defined elements (description of the intervention and comparators, assignment to risk categories, natural history of cancer, treatment of cancer by disease stage) for a decision-maker to assess the credibility of the decision-analytic model in this regard. We assessed whether sufficient face validity had been achieved by presenting the results to a group of experts in breast screening [39]. The threshold for face validity of the model was the agreement by a consensus group of stakeholders involved in the implementation of breast cancer screening that the model represented a close approximation of reality.

2.2.2 Descriptive Validity

Descriptive validity has been viewed as being synonymous with the model conceptualisation process [2] and ensuring the model structure and pathways being represented are adequate while recognising that all models are a simplification of reality. The process of understanding the degree of descriptive validity has also been referred to as conceptual validation as part of published criteria ‘Assessment of the Validation Status of Health-Economic decision models (AdViSHE)’ for assessing model validation to assess: ‘whether the theories and assumptions underlying the conceptual model … are correct and the models representation of the problem entity and the models’ structure, logic and mathematical and causal relationships are ‘reasonable’ for the intended purpose of the model’ [11]. Assessing descriptive validity was a subjective process and required ‘expert’ input from people with relevant knowledge of the disease and intervention being represented by the decision-analytic model and supported by people with relevant technical expertise in decision-analytic modelling. Similar to the application of survey-based consensus methods, such as Delphi [40], it is also necessary to have a clear threshold of what is a ‘sufficient’ level of ‘descriptive validity’, which required taking account of the purpose of the decision-analytic model (the decision problem). We assessed whether sufficient descriptive validity had been achieved when all experts in risk-stratified breast screening involved in providing input agreed the model structure was appropriate.

2.2.3 Technical Verification

Technical verification is a type of internal validity that captures second-order validation [38] and involves a debugging process and assessment of the accuracy of the decision-analytic model in terms of inputs creating ‘valid’ outputs. Technical verification essentially answers the question: does the decision-analytic model do the calculations correctly? The process of completing technical verification was supported by following a published verification checklist designed to ‘reduce errors in models and improve their credibility’ called Technical Verification (TECH-VER) [12]. The TECH-VER checklist is a highly detailed list of steps to be used by decision analysts to reduce the chance of errors in coding the model structure and calculating data inputs from external data sources (e.g. generating measures of overall survival). The TECH-VER checklist does not generate an overall score of technical validity but relies on a decision analyst describing which criteria are relevant and have been met with a description of how. A decision analyst external to the core research team was employed to complete technical verification and produce a TECH-VER report. We assessed whether sufficient technical verification had been achieved using the TECH-VER report from this independent expert. The model was deemed to meet the threshold for technical validity if, following technical verification, there were no remaining issues which would affect the potential ordering of strategies in terms of their cost-effectiveness.

2.2.4 Operational Validation

The process of assessing operational validation is, perhaps, the one most readily interpreted, using lay terms, as assessing ‘external’ validity. Haji Ali Afzali and colleagues [38] call this third-order validation. Operational validation involves comparing decision-analytic model outputs using different sources inputs that may come from (i) data that were used in the original model (dependent operational validation) or (ii) data identified from alternative sources (independent operational validation) [11]. The operational validation of MANC-RISK-SCREEN involved determining whether the clinical outputs of the model aligned with an external data source (independent operational validation). Intuitively, independent operational validation is more robust, in terms of assessing operational validation, than dependent operational validation. However, both independent and dependent validation have key roles when assessing external validity. The threshold for external validity would be deemed to have been met if it was not possible to change the input parameters to improve the fit of given outputs (for example, cancer incidence by age or distribution of cancer stages) to external data without worsening the fit of other output categories.

2.2.5 Predictive Validity

In the context of decision-analytic models, predictive validation is about understanding how well the analysis has predicted future events [38]. We employed the interpretation of predictive validity offered by Gray and colleagues as a process to test the impact on outputs when more data have become available. In this way it was possible to see whether the decision-analytic model had predicted future events [41]. The degree of congruence between predicted and ‘actual’ (future) events was assessed qualitatively.

2.2.6 Cross-Validation

Cross-validation (our preferred term) is also referred to as assessing convergent validity. Cross-validation is used to assess whether two different decision-analytic models designed to address the same decision problem produce similar results. This process requires an alternative decision-analytic model that addresses a similar decision problem to be available. It is most commonly applied for decision-analytic models that have multiplicative purposes rather than in instances when a bespoke structure has been created for a single decision problem. A well-established process of assessing convergent validity has been set up by the Mount Hood challenge for decision-analytic models in the area of diabetes [7]. Convergent validity is also a descriptive process in which the decision analyst should outline the ways in which different decision-analytic models are the same. We conducted a rapid review of the PubMed database up to the year 2022 to identify relevant alternative models looking at risk-based breast screening in the UK. Models were selected based on the similarity of their participants, interventions, comparators, and outcomes (PICO). Differences between different decision-analytic models in terms of the outputs produced were identified. Where the degree of convergent validity could not be directly compared due to variations in the PICO, the results were assessed qualitatively.

2.3 Completing the Model Validation Process

A team of six health economists, supported by an external expert in building decision-analytic models for national decision-making bodies, conducted the model validation process. The first meeting between the six health economists set the thresholds for when the model validation process was sufficient. There were discrete thresholds for each component of model validation, which are described in each relevant section. This team of health economists worked closely with a national group of experts in breast screening as part of the process assessing, in particular, face and descriptive validity [39]. The process of model validation involved going through each component part of validation in a stepwise manner. The external expert completed the TECH-VER process. At the end of the model validation process, two published checklists were completed: TECH-VER and AdViSHE.

3 Results

This section describes the results from the validation of the Gray model. Following model updates and validation, the Gray model was named ‘MANC-RISK-SCREEN’. The TECH-VER

checklists and AdViSHE checklists are reported in Supplementary Appendices 2 and 3, respectively. All code and documentation relating to MANC-RISK-SCREEN are located on GitHub (see https://github.com/stuwrighthealthecon/MANC-RISK-SCREEN). GitHub is an online site designed to share software and model code [42].

3.1 Validation of MANC-RISK-SCREEN

The development and validation, together with the independent assessment process, of the original model by Gray started in February 2021. The version of the decision-analytic model called MANC-RISK-SCREEN was produced in June 2022. The process of updating and validating the decision-analytic model took place in discrete steps:

  1. 1.

    Independently reproducing the original Gray decision-analytic model to check for errors and identify areas for improvement;

  2. 2.

    Updating the decision-analytic model to finalise the structure of the decision-analytic model;

  3. 3.

    Updating input parameters from the Gray decision-analytic model to produce MANC-RISK-SCREEN;

  4. 4.

    Checking the face validity of MANC-RISK-SCREEN with experts in breast screening;

  5. 5.

    Checking the descriptive validity MANC-RISK-SCREEN with experts in breast screening;

  6. 6.

    Conducting independent technical verification of MANC-RISK-SCREEN;

  7. 7.

    Operational validation of MANC-RISK-SCREEN;

  8. 8.

    Assessing the predictive validity of MANC-RISK-SCREEN for specified targets;

  9. 9.

    Cross-validation of MANC-RISK-SCREEN.

These steps were performed in sequence. The steps addressed each of the components of the model validation process.

3.2 Reproducing the Original Model

The decision-analytic model was re-built by a health economist (Stuart Wright) not involved in the design and conduct of the original decision-analytic model built by Gray and colleagues. The health economist (SW) first read the original R code, including accompanying functions, and wrote a text-based algorithm (see the documentation folder of the GitHub repository) in Microsoft Word explaining the steps taken in each stage of the model to conduct the analysis. This text-based algorithm was then checked by the lead modeller in the early economic evaluation (EG), who clarified any areas of confusion.

The health economist (SW) then used the text-based algorithm to reconstruct the model in a new R script, and this script was then compared with the original to detect potential errors in both model versions. Only two significant errors (that could influence the estimated cost-effectiveness) were identified in the original Gray model during this process. To determine whether a cancer was screen detected, a random number was drawn and compared with the value of a variable representing the proportion of cancers that are screen detected in the health system. In the original code, the cancer was assigned to be a screen-detected cancer if the random number was greater than the value of the variable. However, this should only have occurred if the random number was lower than the value of the variable and was changed in the updated model. As the value of this variable was set to 0.5 and not varied in the probabilistic sensitivity analysis, this error had not had an impact on the published early economic analysis results [36]. In addition, the original Gray model did not include a cost of follow-up testing for false-positive screening results, thereby potentially overestimating the cost-effectiveness of strategies with more frequent screening. Therefore, the cost of follow-up testing for false-positive screening was added to the R code for MANC-RISK-SCREEN.

During the recoding process, other changes to the original Gray model were made for improvements in the speed of execution, for example, defining variables before loops rather than in them, or, cosmetically, in making the code more readable. An example of the latter was the inclusion of four required R functions in a single accompanying script rather than four individual ones.

3.3 Structural Update

When MANC-RISK-SCREEN was built in R, structural changes and additional features were included. A key change was that the categorisation of breast tumours was changed from Nottingham Prognostic Indicator (NPI)-based classification to a stage-based classification, as this significantly increased the availability of relevant data for key input parameters. The start age of the screening was changed to a fixed age of 50 years rather than uniformly varying between 47 and 51 years. This change was made because the varying start age had only been applied to some of the strategies in the early model and was deemed to potentially bias the results.

The original Gray model was populated with individual-level data for a population of women aged between 50 and 70 years (n = 53,596) recruited to a cohort study in England called Predicting Risk of Cancer at Screening (PROCAS) 1 to provide estimates of the distribution of estimated 10-year risk of breast cancer [24]. The MANC-RISK-SCREEN model was populated with updated data from a second cohort study in England called PROCAS 2 that recruited 15,613 women aged between 50 and 70 years [25]. These estimates were calculated in the original cohort studies using an adaptation of the Tyrer–Cuzick risk assessment tool. The Tyrer–Cuzick risk calculator was modified into a two-page survey to collect the information required to calculate individual 10-year breast cancer risk: family history information (including number and ages of sisters, current age or age at death of mother and details of any relatives affected by breast or ovarian cancer), hormonal risk factors (age at menarche, menopausal status and hormone replacement therapy use and parity) and lifestyle information [current body mass index (BMI), BMI at age of 20 years, clothing size, alcohol consumption and exercise habits) [24]. The calculated risk scores in the cohort study sample were, for the purpose of the intervention arm in the decision-analytic model, divided into three risk categories: 10-year risk < 3.5%, directed to triyearly screening; 10-year risk between ≥ 3.5 and < 8%, directed to biyearly screening; and 10-year risk ≥ 8%, directed to annual screening. Changes in the risk groups used in recently published clinical research meant that in the updated model the risk thresholds used to define the different risk groups have changed [25]. In the MANC-RISK-SCREEN model, moderate risk is defined as 5–8%, rather than 3.5–8% as in the PROCAS-based strategies. This also means that normal risk is defined as less than 5% in the first PROCAS strategy. In the second risk-based strategy with less frequent screening for women at lower risk, normal risk is now defined as a 10-year risk between 1.5 and 5%.

Parameters relating to three types of imperfect uptake for risk-stratified screening were added: uptake for risk prediction (do the clinicians use the risk-prediction tool?), uptake for receipt of risk prediction (do women get their individual risk level?) and uptake for changed screening intervals (do women decide to change their screening interval?). A number of additional screening strategies were added to the model, including reduced (every five or six years) screening for women at low (below-average) 10-year risk of breast cancer, and a fully stratified screening programme with more frequent screening for those at higher risk and less frequent screening for those at lower risk.

3.4 Update Input Parameters

The original early analysis was published by Gray in 2017, and the decision-analytic model validation process was started in early 2021. This time period meant it was likely that values of the parameters used in the Gray decision-analytic model were likely to be out of date. A comprehensive update of decision-analytic model inputs for MANC-RISK-SCREEN was conducted. The process of updating the input parameters is provided in detail in the documentation folder in the model GitHub repository. Systematic reviews were conducted (by AD and RH) to identify more recent health utility and cost estimates by breast cancer stage. The cost of stratification was updated to incorporate estimates from a published micro-costing study [43]. New values for screening-related parameters were identified from published audits and reports on the status of the National Health Service (NHS) breast cancer screening programme [15]. Studies citing the sources of clinical parameters, including the tumour growth model, were searched to determine whether any newer appropriate values were available.

Following the search for new parameter values, the following parameters were updated in the final MANC-RISK-SCREEN model: the proportion of cancers detected by screening, all-cause mortality, cancer-stage-specific mortality, breast cancer incidence by age, breast cancer risk, the proportion of cancers that are ductal carcinoma in situ, the proportion of cancers diagnosed at different stages based on their size, mammographic sensitivity by Volpara breast density group, screening recall rate, all costs in the model and utility values for stage I–III and IV breast cancer.

3.5 Face Validity

Following the reconstruction and parameter update, preliminary results from MANC-RISK-SCREEN were presented at a close-out meeting of the research programme (called PROCAS 2) funding the validation process [25, 39]. This meeting was attended by 58 individuals (38 face-to-face and 20 virtual) with relevant expertise in breast screening from academic, clinical and/or policy-making perspectives.

Two suggestions from this meeting were to include uptake for risk stratification and screening attendance. These two parameters were subsequently added to the original Gray decision-analytic model. Data on screening uptake, reflecting the correlation between an individual’s previous and future attendance, were sourced from the annual UK breast cancer screening report [15]. Parameters relating to an individual’s uptake of risk prediction, the feedback of their risk information and the changing of their screening intervals were added to the MANC-RISK-SCREEN model. In the current model iteration, it is assumed that uptake for risk prediction is perfect, but the impact of imperfect uptake for risk prediction on the cost-effectiveness of a risk-stratified NBSP will be explored in future work. Further suggestions to extend the decision-analytic model to estimate the cost-effectiveness of adding single-nucleotide polymorphisms (SNPs) to the risk stratification strategy and of adding in the impact of starting women at high risk of breast cancer on preventive medicines are topics for further development of MANC-RISK-SCREEN.

3.6 Descriptive Validity

The descriptive validity of the model was assessed on a continual basis by monthly meetings between the six health economists involved in the validation of MANC-RISK-SCREEN. Two of these health economists (SW and KP) directly interacted with two clinical experts in risk-based breast screening, a statistician involved in generating the risk-prediction model underpinning the Tyrer–Cuzick algorithm and a health psychologist involved in assessing uptake as part of the PROCAS 2 programme.

These supporting researchers were consulted on key changes to the assumptions of the model. These were the change of the treatment aspect of the model from Nottingham Prognostic Indicator to stage-based treatment and the inclusion of uptake which depended on participants’ previous attendance at screening. The switch to stage-based treatment was deemed to be acceptable, although it was identified that there are more granular stages of breast cancer than simply stages 1,II,III and IV. As data for treatment costs and utilities were not available at this level of detail, it was assumed that cancer only fell into these stages. In future versions of the model, data will be sought for more granular staging of breast cancer.

The researchers approved of the move to using different uptake parameters to reflect women’s history of participation in screening. It was deemed that this more closely represented the reality of non-attendance and attendance being correlated.

3.7 Technical Verification

To complete technical verification of MANC-RISK-SCREEN involving an assessment of an error check, an independent experienced R user with expertise in producing decision-analytic models for national decision-making body was employed to follow the TECH-VER checklist. This analyst also made suggestions about improving analysis time and documentation for the model. A number of errors were identified in MANC-RISK-SCREEN in this process. The duration of quality-adjusted life-years (QALYs) experienced was forced to be an integer year, and so sometimes patients had higher QALYs than life-years. This problem was solved by allowing a fraction of a year to be lived in the last year of the vector collecting quality of life values for each year. A problem in one of the functions meant that patients diagnosed with cancer sometimes lived longer than they would have done without the cancer. This was addressed by setting the age of death to the minimum of the age of cancer death or the age of all-cause mortality. A problem with two of the screening strategies was identified whereby a variable was being called by an out-of-date name, meaning the model would not run. In the updated MANC-RISK-SCREEN model, all references to the out-of-date parameter name were updated to the current name. In addition, an error was identified with the use of supplemental screening, whereby in some iterations of an ‘if’ statement, no value was assigned to a variable, causing problems further on in the model. This problem was solved by setting a baseline value for the parameter to take in the absence of supplemental screening being used. Following these updates, technical verification was performed again by a member of the research team, and no further problems were found.

3.8 Operational Validation

Results used in the operational validation were generated from the model output using the scenario of the current (3-year interval) screening programme targeted at women aged between 50 and 70 years. The independent operational validation of MANC-RISK-SCREEN involved determining whether the clinical outputs of the model aligned with epidemiological data on breast cancer observed in the UK [15, 44,45,46].

  • Operational validation targets were selected based on our belief that close correspondence of these model outputs to targets may increase confidence in model primary cost-effectiveness results (see https://cisnet.cancer.gov/). Target selection was also limited by the availability of target data or summary statistics. Selected targets were related to incidence and detection rates. Survival by cancer stage was also considered as a target, but the authors are not aware of any sources of these data for the UK other than those used to generate the input parameters for the model. During operational validation it was observed that estimated age-specific cancer incidence under the current screening scenario was close to that reported in national cancer incidence statistics [source: Office for National Statistics (ONS) cancer incidence UK 2017 [44]].

  • The estimated proportion of breast cancers detected by screening matched the proportion reported in national breast cancer screening audits [source: NHS Digital Official Statistics [45]].

  • The estimated stage/size distribution of cancers detected at screening and through all diagnostic routes matched that reported in available registry data [Source: Cancer Research UK (CRUK) compiled from registries in each nation [46] and NHS Digital Official Statistics [45]].

3.9 Predictive Validity

The observed and predicted age-specific breast cancer incidence rates are reported in Table 2 and displayed in Fig. 1. The cancer rates were visually similar for women before screening age. After the age of 50 years, MANC-RISK-SCREEN appears to underestimate cancer rates compared with the UK registry data from the years 2016–2018. There was a larger underestimation for the ≥ 80-year-old age groups. A potential explanation for this divergence is the use of all-cause mortality data from the years 2018–2020, which may incorporate higher mortality as age increased due to the beginning of the coronavirus pandemic. The ONS mortality data used to derive life expectancy due to all-cause mortality were subsequently changed to the data from the years 2016–2018. However, when the root mean squared error was calculated to compare the cancer incidence predictions of the model with those observed in the health system, using the earlier all-cause mortality data marginally reduced the fit of the model (90.103 versus 86.212 deviation in incidence per 100,000 per year).

Table 2 Predicted and observed age-specific incidence rates
Full size table
Fig. 1
figure 1

Predicted and observed age-specific incidence rate. Data source: [46]

Full size image

An alternative explanation for the difference in cancer incidence observed is that there is a difference in the probability a woman will be diagnosed with breast cancer in reality (1 in 7 or 14.3%) compared with the value used in the model (11.8%). The latter lower figure is driven by the average lifetime breast cancer risk for the women who participated in the study used to populate the model (PROCAS 2), which is lower than the population average. To determine whether the difference in lifetime breast cancer risk was likely to be the cause of differences in incidence by age, the predicted incidence rates by MANC-RISK-SCREEN were inflated by the proportional difference in lifetime risk (Fig. 2). In this case the model-predicted rate appears to track the actual rate more closely, if at a little higher rate. The predicted and observed rates diverge at the age of 70 years, although to a lesser degree than with the unadjusted rates. When comparing the root mean squared error, using an inflated rate of lifetime cancer risk improves the fit of the model (54.882 versus 86.212 deviation in incidence per 100,000 per year). This suggests that the differences in the lifetime cancer risk between the sample from the BC-PREDICT sample and the general population explain a large part, but not all, of the deviation in the cancer incidence by age.

Fig. 2
figure 2

Inflation of predicted incidence rates estimated by MANC-RISK-SCREEN by the proportional difference in lifetime risk. Data source: [46]

Full size image

It was not possible to assess whether the risk-prediction tool used to assign a risk score in PROCAS 2 had sufficient predictive value in the general population. MANC-RISK-SCREEN was populated using an observed distribution of 10-year risk in the women recruited to PROCAS 2. There is evidence that the data sources used to develop these risk-prediction models mean they may perform poorly in ethnically diverse populations [47]. An alternative data source would be needed to assess whether the predicted assignment to risk categories would be observed in a UK population. It was, therefore, not possible to assess the predictive ability of the Tyrer–Cuzick risk-prediction tool.

The original Gray model overestimated the proportion of cancer identified by screening, producing a value of 50.2% compared with 43% published by NHS England [45]. A potential explanation for the higher proportion of cancers identified by screening in the Gray model was due to the approach taken to code imperfect screening uptake. In the Gray model, individuals were assigned a probability of 60.5% of attending their first screen. Individuals that had attended at least one screen were assigned an 85.2% probability of attending further screens. In the UK-NBSP it has been observed that women who do not attend their first screen have a reduced likelihood of attending subsequent screens [45]. As such, MANC-RISK-SCREEN was recoded such that women had a 60.5% of attending their first screen and, if they did not attend this screen, only a 19.1% chance of attending subsequent screens. When a woman had attended at least one screen, the probability that she would attend subsequently was increased to 85.2% in MANC-RISK-SCREEN. Following this change, MANC-RISK-SCREEN predicted that 43% of cancers in the age group eligible for screening would be detected by screening, and this estimate exactly matched the proportion observed in the UK-NBSP.

Table 3 shows the proportions of cancers observed and predicted to be of different stages at diagnosis for cancers diagnosed clinically or by screening. The observed rates are taken form women diagnosed with breast cancer in England [46]. Cancers of unknown size have been excluded from MANC-RISK-SCREEN. The proportion of cancers have been adjusted to incorporate ductal carcinoma in situ that are reported separately. Across all cancers, the Gray model generated too many cancers at stage III (18.9% versus 8% in UK-NBSP) and too few at stage I (28.6% versus 39.4% in UK-NBSP). In addition, the Gray model predicted too few ductal carcinoma in situs (DCIS; 5.5% versus 12.9% in UK-NBSP) [48].

Table 3 Predicted proportion of clinical and screen-detected cancers of different stages
Full size table

In the Gray model, it was assumed the DCIS were only diagnosed as part of a UK-NBSP and assigned an occurrence in 21% of the available cancers regardless of the tumour size. This assumption is likely to be why the proportion of tumours diagnosed as DCIS were considerably lower in the Gray model when compared with the observed data, as in reality DCIS can also be diagnosed clinically. In addition, the approach of allocating any-sized cancer as DCIS regardless of size in MANC-RISK-SCREEN may have affected the stage distribution; DCIS are likely to be smaller than cancers of other stages. In the Gray model the matrix used to determine the probability that a cancer of a given size was of stage I, II or III, an assumption had been made using data from source studies [49, 50]. One of the source studies (Kollias et al., 1999 [49]) included estimates in which there was lymph node involvement in a cancer, and this was equally likely to involve one or more than one node [49]. Cancers with more than one lymph node involved are disproportionately likely to be at a higher stage compared with one or fewer lymph nodes, and this may have biased cancers estimated in the Gray model towards a higher stage of diagnosis. To address these issues, MANC-RISK-SCREEN was recoded such that cancers were allocated to a stage or as DCIS based on their size. Data from a study of DCIS were incorporated into the input matrix of the probability of a cancer of a given size being diagnosed at different stages [51]. In addition, the proportion of cancers with lymph node involvement in the study where these data were available (Wen et al., 2015 [50]) was used to adjust the distribution of cancer from the study where lymph node involvement was not available (Kollias et al, 1999) [49].

The predicted proportion of cancers of different stages generated by MANC-RISK-SCREEN is shown in Table 4. The estimated proportion of cancers diagnosed as DCIS are similar to the values observed in data from Cancer Research UK, with a maximum deviation of two percentage points [52]. The observed values were derived by using the size of cancers diagnosed through the UK-NBSP applying the cancer stage by size matrix (see the parameter update document in the GitHub repository). In some cases, the band of cancer size reported in the UK-NBSP data spanned two bands of cancer size used in the matrix. In these situations, it was assumed that cancer size was evenly distributed across the two bands. Tumours greater than 5cm were assumed to be stage IV at diagnosis. The proportion of DCIS were added from separate data available from Cancer Research UK [52]. To compare the closeness of the predicted distribution of cancer stages to those observed in England, the root mean squared error of the predictions were calculated. These values represent the average percentage point deviation of the model predictions from those observed in the health service.

Table 4 Predicted proportion of screen-detected cancers of different stages
Full size table

The distribution of stages for screen-detected cancers estimated in MANC-RISK-SCREEN had low deviation (2.706 percentage points) from the values observed in the UK-NBSP. However, adjustments subsequently made to the cancer stage by size matrix to improve the fit for the distribution of stages of cancer for all diagnosis routes (6.903 versus 8.616 percentage point deviation) resulted in greater deviations from the observed data for screen-detected cancer (5.023 versus 2.706 percentage point deviation). Therefore, the stage by size matrix in the final MANC-RISK-SCREEN model uses a combination of the Wen et al. data, which has details of lymph node involvement, and the Kollias et al. data with the likelihood of lymph node involvement for different sizes of cancer taken from the Wen et al. data [49, 50]. This choice of data sacrifices improved fit in the distribution of screen-detected cancers at the expense of a smaller loss of fit in the distribution of the stages of all diagnosed cancers.

3.10 Cross-Validation

There is one alternative decision-analytic-model-based economic evaluation of a risk-stratified NBSP published relevant to the UK setting [53]. Pashayan et al. investigated the cost-effectiveness of alternative risk-stratified NBSP conceptualised as the addition of a risk threshold to the existing age threshold used to determine who is offered screening. On face value, the Pashayan model appears to be directly comparable to the Gray model and MANC-RISK-SCREEN. However, it was not possible to conduct a formal cross-validation of the Pashayan model and MANC-RISK-SCREEN in terms of model outputs because the stated decision problems, intervention under evaluation, decision-analytic model types and structures were not comparable (Table 5). Although the original model was shared with two further academic groups, the results of the additional models created as part of this work were not available for comparison at the time of the validation exercise.

Table 5 Comparison of the Pashayan model and MANC-RISK-SCREEN
Full size table

4 Discussion

This study reports the development and use of a validation process which was then applied to a case study early decision-analytic-model-based cost-effectiveness analysis (CEA) of a risk-stratified NBSP [36]. Existing validation concepts were consolidated into a single step-by-step process resulting in the transparent presentation of the assumptions, strengths and weaknesses of a decision-analytic model.

The application of this validation process aimed to assess an existing decision-analytic model structure and understand whether it adequately captures the relevant pathways representing the risk stratification process, using a version of the Tyrer–Cuzick risk assessment tool with defined risk categories and assigned screening intervals, and subsequent interventions, the current breast screening programme, the natural history of breast cancer and treatment of breast cancer. Input parameters were updated as part of this validation process, but this is likely to be an ongoing process, as recommended by Sculpher and colleagues [30], as and when new data become available. This study has illustrated how the development and use of the validation process is a resource-intensive exercise involving the combined skills of health economists and experts relevant to the specific decision problem (evaluation of risk-stratified breast screening programmes).

Through the process of model validation, the strengths and weaknesses of the MANC-RISK-SCREEN have been discussed transparently, allowing decision-makers to gauge the quality of the model when using it to inform decisions as to the potential introduction of risk-stratified breast cancer screening. MANC-RISK-SCREEN is now available as an open-source model published on GitHub. A structured and transparent validation process was followed to produce MANC-RISK-SCREEN, which is now proposed to be a decision-analytic model with the potential to inform whether, and how, healthcare resources should be diverted towards risk-stratified NBSP implemented using different components. The component parts of a risk-stratified NBSP can be varied in terms of the age at which screening is first offered to women in the population (NBSP starting age), interval between screenings (NBSP screening interval), age at which screening is stopped (NBSP stopping age), number of X-rays used (one- or two-view mammography), supplementary screening technologies used (ultrasound and/or magnetic resonance imaging), interpretation of the X-ray (manual or digital), approach used to calculate a women’s risk of breast cancer, whether supplementary breast density measurements are taken, classification of the risk categories, approach taken to feedback risk to the women and strategies recommended as a result of identifying a women to be at high risk.

The operational validation, together with the assessment of predictive validity, were the main components assessing the external validity of MANC-RISK-SCREEN. It was planned to supplement external validation with cross-validation with a published model. The cross-validation was not successful, because the only decision-analytic model available for comparison did not match in terms of the interventions used for comparison or model structure. The external validity of MANC-RISK-SCREEN is not perfect. We suggest that decision analysts or decision-makers wanting to use MANC-RISK-SCREEN are aware that it overpredicts clinically diagnosed stage III cancers and underpredicts clinically diagnosed stage I. This overprediction is likely to affect the results of comparisons of screening programmes compared with no screening.

4.1 Limitations

The main limitation as part of this validation process was the need to rely on estimating intermediate outcomes generated by the decision-analytic model against data available from a limited range of sources reporting outcomes. These data sources only report outcomes from a single scenario: the current screening programme. There is, therefore, limited ability to discriminate between a decision-analytic model that performs well or poorly at the task of predicting comparative cost-effectiveness of alternative screening programmes. The specific targets that were selected for assessing predictive ability were based on the available data sources, rather than choosing targets that would be most informative for decision-making.

When comparing the predicted distribution of cancer stages detected at screening, cancers of unknown size were omitted from the observed data, as the MANC-RISK-SCREEN model does not currently produce such cancers. Such cancers may be those that occur in individuals who die between the detection of the cancer and receiving a full diagnosis. This may predominantly include those of lower socio-economic status or those who face barriers to accessing health system services, such as those from ethnic minorities. Omitting such cancers may therefore mean that the results of the model are biased. Including unstaged cancers in a future version of the model is therefore a priority alongside updates identified by the expert group, such as imperfect uptake for risk prediction and the addition of preventative medicine for those at higher risk of cancer.

Due to the large number of parameters in the decision-analytic model and paucity of data with which to fit the model to, calibration of most of the model was not conducted in the Gray model or MANC-RISK-SCREEN. The tumour growth model was calibrated. For the remaining parameters in the model, a key focus was to avoid overfitting the model to the UK national screening context that is the source of the available data for use as input parameters.

A related issue to validation of MANC-RISK-SCREEN that needs consideration is the limitations of the risk-prediction models used to allocate a women’s individual risk. The data sources used to develop these risk-prediction models mean they perform poorly in ethnically diverse populations [47]. The impact of this limitation will be most apparent if risk-based NBSP are rolled out into practice. In the absence of datasets to assess the predictive value of the risk-prediction models, it is impossible to know the extent of the impact of poorly performing risk prediction on the cost-effectiveness of risk-stratified NBSP.

5 Conclusion

This study has reported a structured and transparent validation process of an early decision-analytic model built to assess the potential cost-effectiveness of exemplar risk-stratified NBSP compared with current NBSP or no screening. The validation has suggested MANC-RISK-SCREEN has sufficient internal validity. There are some concerns regarding external validity, but these can only be rectified as and when new data sources become available to populate MANC-RISK-SCREEN.