Abstract
The correct determination of the phase transition behaviour of phase change materials (PCMs) is paramount for assessing their application potential. In this work, the merits of a novel calorimetric technique, Peltier-element-based adiabatic scanning calorimetry (pASC), for PCM characterisation are investigated, especially in comparison with the commonly-used differential scanning calorimeter (DSC). A comparative study of two alkane-based PCMs, the commercial mixture RT42 and the pure alkane tricosane (C23) with these two techniques shows that pASC provides data at much higher resolution than DSC, due to its operation in thermodynamic equilibrium. Specifically the rate-dependence and deformation that is inherent to DSC experiments is absent in pASC. In addition, the enthalpy of the PCM is directly obtained. pASC results easily conform to the accuracy limits that are proposed in literature for the transition temperature and storage capacity of PCMs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The increasing concern about the finiteness of the planet’s resources stimulates research in very diverse fields. In the case of energy, two major angles can be distinguished: the development or improvement of sustainable energy sources and increasing the effectiveness of energy use. One approach for the latter is the temporary storage of heat (or cold) for later use, or to dampen or delay undesired temperature variations. The research into the so-called phase change materials (PCMs) aims to provide us with materials with suitable properties for these tasks. It is evident that apart from such aspects as environmental safety, economic feasibility and ease of application, correct knowledge of the physical properties of the candidate materials is required, in particular the thermal properties [1].
PCMs as available and studied today rely on the presence of a temperature-driven phase transition to achieve their energy storage or release. The conversion from one phase to another requires that the material acquires or releases energy to its environment, and this can be used, for example, to maintain a constant temperature of a room in a building, to name one of the prototypical applications for PCMs.
But science knows a multitude of different phase transitions, and the involved transition heats vary widely. For example, in liquid crystals, the transition from the nematic phase (a fluid state with one-dimensional orientational order) to the isotropic liquid phase has a heat of a few J g\(^{-1}\) associated with it [2], about 100 times smaller than the transition from ice to water (333 J g\(^{-1}\)). Thus, a careful choice of the transition is important. In general, the larger the difference in order between the two phases, the larger the transition heat will be, although the intermolecular interactions will also play an important role. As a consequence, transitions from solid to liquid and from liquid to vapour have high transition heats involved, but for practical applications, the large difference in volume between liquid and vapour is a problem (a short discussion and further references can be found in Reference [1]). Therefore, attention has been focussed at the solid–liquid transition [1, 3, 4], and to a lesser extent at solid–solid transitions [5–8].
In terms of material properties and application feasibility, alkanes and salt hydrates are generally considered the most promising candidates for PCMs, although a lot of different materials have also been studied, such as eutectic mixtures, fatty acids, polymers, metals, and specific high-temperature materials. All of these categories have their specific advantages and disadvantages, and books and reviews give systematic overviews of these [1, 3, 4, 9–13]. The use of ice as a material for cold storage is an age-old and common example of PCM use [14].
In this paper, we draw attention to another aspect of PCM research, namely the characterisation of the thermal properties. The application potential of a PCM is determined by a limited number of thermal parameters, corresponding to some evident questions: (1) at which temperature will it store/release heat? (2) How much heat will it store/release? (3) How efficiently will it exchange heat with its environment? The latter can be quantified in different ways, but most commonly, thermal conductivity is taken as the measure.Footnote 1 In this paper, we will only be concerned with questions (1) and (2). Question (1) asks for the determination of the phase transition temperature, whereas (2) relates to the transition heat, and the heat capacity over the temperature range of application.
Commonly, the transition temperature \(T_\mathrm{tr}\), the transition heat \(\Delta h\) and the specific heat capacity \(c_p\) of materials are determined by means of differential scanning calorimetry (DSC). This technique allows for a fast and relatively easy determination of these thermal properties, but it has a fundamental flaw for the characterisation of PCMs: it is fundamentally unable to provide correct data for transitions with large heats involved. This deficiency of DSC is caused by its very measurement principle. In a simplified picture of a heating run on the common heat-flux DSC, the furnace of the DSC is heated up at a fixed scanning rate. The sample cell, in thermal contact with this furnace by means of a heat-flux sensor, follows the temperature evolution of the furnace with a small delay, as the heat needs some time to flow into the sample. When a transition is reached, the sample will need the transition heat at once, in order to keep up with the furnace, but this is not possible due to the limited thermal conductance of the heat-flux sensor. Thus, the registered heat flow does not correctly relate to the properties of the sample, but rather to the properties of the heat-flux sensor, a situation which persists until all transition heat has been delivered. Even in power-compensated DSCs, which actively provide heat to the sample, this cannot be avoided, as the instantaneous demand for heat during the transition may exceed the power of the heater system.
As a consequence, a DSC can only provide a deformed effective heat capacity curve in the vicinity of a phase transition, leading to incorrect values of the transition temperature and of the spread of transition heat over the temperature region of the phase transition. In general, a DSC heating experiment will broaden the transition region, overestimate the transition temperature and associate more heat with the high-temperature part of the transition region. In our view, while a DSC gives a useful first picture of a phase transition, high-quality data cannot be obtained with it. This is realised by researchers in the field of PCMs [15, 16], and careful DSC use [17] and improved analysis of DSC data [18, 19] have been proposed.
But also a number of alternative methods have been put forward. Among the examples, we first note the possibility of running a DSC in an isothermal (step) mode [1, 16], operating much like a relaxation calorimeter [20–23]. A common method is the so-called T-history method [1, 16, 24–26], in which a PCM sample is studied in conditions that mimic the operational use of PCMs: its response to a changing environment is recorded. A relatively large PCM sample (for example 20 ml [16] as compared to a DSC sample of few \(\upmu \mathrm{l}\)) is placed inside a temperature-controlled chamber together with a reference sample. The temperature of the chamber is then suddenly changed, and the temperature response of sample and reference is recorded. A comparison of the two curves allows the extraction of information about \(T_\mathrm{tr}\), \(\Delta h\) and \(c_p\). Closely related to this method is the three-layer-calorimeter [27, 28], in which even larger samples (typically 100 g) in hermetically sealed bags are studied.
In this paper, we present a calorimetric method that provides another alternative to DSC, in the particular case of PCMs as well as in general. The adiabatic scanning calorimeter allows the determination of the same parameters as a DSC, combined with a direct measurement of the enthalpy curve h(T), but it does not suffer from the phase transition deformation because of a fundamentally different measurement principle [29–32]. In adiabatic scanning calorimetry (ASC), the sample is heated by a controlled, constant amount of power. The sample uses this power, either to heat itself up, or, at the appropriate temperature, to undergo phase conversion. In the latter case, the sample remains at the same temperature until the conversion is complete. As such, the sample remains in equilibrium all the time, and the results do thus not suffer from deformation like in a DSC. We will provide a more detailed description of the technique below.
For PCMs, we highlight two main advantages of ASC, especially when comparing with DSC. First, ASC provides the researcher with a correct, undeformed, equilibrium heat capacity, and also with direct enthalpy data. Second, the use of a constant power mimics much better the actual thermal behaviour of a PCM in operational conditions than the forced temperature evolutions in a DSC. In addition, ASC can readily be performed at lower temperature rates, for example at 1 K h\(^{-1}\), which is a more realistic rate in many real-life situations than the 1 or 10 K min\(^{-1}\) typically used in DSC. In this paper, we investigate the difference between ASC and DSC for the measurement of a commercial alkane-based PCM, as well as of a pure alkane with a comparable melting point.
Experimental details
RT42 Samples
The PCM RT42 was obtained from Rubitherm Technologies GmbH, Berlin, Germany. Although not specified on the current data sheet [33], older versions mention that this material is a mixture of alkanes. It is described as a solid–liquid PCM with a melting region of 38–43 \(\,^{\circ }\)C, and it stores 174 kJ kg\(^{-1}\) between 35 and 50 °C.
Three samples were prepared. For the ASC measurements, a sample of 80.0 mg was placed inside a Mettler–Toledo 120 \(\upmu \mathrm{l}\) stainless steel Medium Pressure Crucible. Two samples, of 8.41 and 8.95 mg, in TA Standard Aluminum Hermetic cells were used for the DSC measurement.
C23 Samples
C23 is a shorthand notation for the linear alkane tricosane, C\(_{23}\)H\(_{48}\). The high-purity C23 used in this work was obtained from Sigma-Aldrich: tricosane analytical standard (product number 91,447), and the CoA mentioned a purity of 99.8 % as obtained from gas chromatography. Literature data indicate that this compound has multiple phase transitions, the two most important ones are the crystal to rotator phase transition at about 42.5\(\,^{\circ }\)C and the rotator to liquid transition at 47.3\(\,^{\circ }\)C; these transitions involve 66.9 and 163.7 J g\(^{-1}\) of transition enthalpy, respectively [34].
Three samples were prepared, using the same types of DSC cells as for RT42. The ASC sample mass was 59.8 mg. The first DSC sample mass was 7.03 mg, the second one 7.15 mg.
DSC
A Q1000 DSC (TA Instruments, New Castle DE, USA) was used for the DSC measurements. This instrument is a heat-flux DSC using the so-called Tzero technique, which allows for a separate calibration of the heat capacity and thermal resistance of the sample and reference platforms of the DSC, leading to an improved baseline stability and better heat capacity determination [35]. The samples were measured under nitrogen flow.
For this work, the calibrations were performed as recommended by the instrument’s manuals. First, the temperature scale was corrected on the basis of the melting points of cyclopentane (\(-\)93.43\(\,^{\circ }\)C), diphenyl ether (26.86\(\,^{\circ }\)C) and indium (156.60\(\,^{\circ }\)C) as determined at 10 K min\(^{-1}\). Diphenyl ether was specifically used for these experiments to have a calibration point inside the temperature region of interest in this work, \(-\)20 to 70\(\,^{\circ }\)C. The Tzero calibration (involving measurement of the empty DSC and of (nearly) identical sapphire disks) was made at 20 K min\(^{-1}\), determining the heat capacity and thermal resistance of the sample and reference platforms. The thermal resistance of the sample pans was calibrated based on the melting curve of indium. For the calibration of the heat capacity, a 12 mg piece of sapphire was placed in a sample pan and measured at 10 K min\(^{-1}\). The ratio between the obtained and literature value was used to calculate \(c_p\).
We found that obtaining a correct value for \(c_p\) from the DSC measurements is a far from trivial task. These calibrations are in principle sufficient for runs at 10 K min\(^{-1}\). Accurate determination of \(c_p\) at different rates would require these to be redone at each of these rates, a procedure which is very time-consuming, particularly for slow rates. Therefore, instead of performing the calibration extensively at all rates, a carefully conducted heating run at 10 K min\(^{-1}\) was taken as a reference run, and the \(c_p\) values at other rates away from the transitions were additively shifted until they matched with these reference data away from the transitions. Since a DSC uses the ratio of the heat flow and the temperature rate for the calculation of \(c_p\), this additive shift corresponds to correcting the level of zero heat flow during the experiment (an experimental correction in the DSC software that was performed for the reference runs, but not for the other ones). Since the detected heat flow (as calibrated by the Tzero method) is not altered in this calculation, transition enthalpy values as calculated directly from integration of the heat flow or from integration of \(c_p\) are identical. Effectively, this procedure corresponds to a correction of the DSC baseline.
ASC
Adiabatic scanning calorimetry [30] obtains the heat capacity \(C_p\) and enthalpy H of the sampleFootnote 2 by applying a constant power P to the sample, and continuously registering the temperature evolution with time T(t). Then, \(C_p\) and H are calculated on the basis of the following equations, where the temperature rate \(\dot{T}\equiv \mathrm{d}T/\mathrm{d}t\) is introduced:
\(H_0\) denotes the enthalpy of the sample at the starting temperature \(T_0\) of the experiment. One can see that the constant power allows for a straightforward determination of the enthalpy of the system: a continuous curve with the same temperature resolution as for the direct T(t) data and as for the heat capacity is obtained.
An illustration of the data and data processing in an ASC experiment on a sample with a phase transition with a small latent heat and substantial pre-transtional contributions to the heat capacity. A constant power P is applied to the sample at starting time \(t_0\), this leads to a variable temperature evolution T(t) of the sample; during the phase transition at \(T_\mathrm{tr}\) the temperature stays constant between \(t_\mathrm{i}\) and \(t_\mathrm{f}\). These two quantities P and T can be used to calculate directly the enthalpy H(T), or with the rate \(\dot{T}\) as intermediate, the heat capacity \(C_p(T)\)
The data processing during the course of a typical experiment is illustrated in Fig. 1, for the case of a weakly first-order transition, a transition with a small latent heat and considerable pre-transitional contributions, as commonly observed in liquid crystals [2]. Starting at a time \(t_0\), a constant power P is applied to the sample, leading to an evolution of its temperature T(t). In the low-temperature phase, the temperature increases, but gradually slower when approaching the transition. During the phase transition between \(t_\mathrm{i}\) and \(t_\mathrm{f}\), all added power is used for the phase conversion and the temperature does not change. Once the conversion is complete and the high-temperature phase is reached, the temperature increases again. Via numerical differentiation, the rate \(\dot{T}\) is calculated from T(t), displaying the decreasing value close to the transition; the rate becomes zero at the transition. Division of P and \(\dot{T}\) leads to \(C_p\), showing the increase in the pre-transitional wings. In the enthalpy, the phase transition is visible as the jump, of which the height corresponds to the latent heat. In order to arrive at the specific values, the pre-calibrated contribution from the sample addenda needs to be subtracted and the sample mass taken into account.
pASC
The challenge of ASC resides in the implementation. Currently, there are two possibilities. The “classical” ASC implementation will not be discussed here, as these instruments are difficult to operate and require rather large samples (typically 0.5 g or more), but they were very successful in high-resolution studies of phase transitions [29, 30, 36]. The successor of the classical ASC is the novel Peltier-element-based adiabatic scanning calorimeter (pASC), which provides greater user-friendliness and also allows smaller samples [31, 32, 37, 38].
A sketch of the core part of a pASC. The sample cell is placed on top of a platform with a thermometer and heater. The Peltier element acts as a differential thermometer between the sample and the sourronding adiabatic shield. While a constant power is applied to the sample, the temperature of the cell is recorded; the output of the Peltier element is used to control the temperature difference between sample and shield
At the core of the pASC, as can be seen in the schematic depiction in Fig. 2, there is a sample platform equipped with an electrical heater and a thermistor (NTC resistance thermometer). This sample platform accommodates an sample cell, which is airtight to allow for operation under vacuum. The platform itself is mounted on top of a Peltier element, which acts as a differential thermometer for the temperature difference between the sample and the surrounding adiabatic shield. If this difference is maintained at zero, then all heat provided by the heater goes only to the sample (and its addenda), and hence the power required for Eqs. (1) and (5) is exactly known. This is achieved by feeding the Peltier output into a PID control system for the adiabatic shield, resulting in a temperature stability better than 50 \(\upmu\)K. This performance can only be attained because the adiabatic shield is itself surrounded by an additional thermal shield and a heat bath, each maintained at a slightly lower temperature; the details of these additional elements depend on the specific model of pASC.
The description above is valid for heating runs: all power to the sample is provided electrically, and due to the zero temperature gradient over the Peltier element, this is exactly the power used to heat the sample. Cooling runs are performed by imposing (by the PID control loop) a fixed temperature gradient over the Peltier element: this leads to a constant power drawn from the sample, which is measured by the Peltier, now also acting as a heat-flux sensor.
For this work, two pASC instruments were used. RT42 was measured by a pASC with a water thermostat as the base heat bath, allowing an operational temperature range from 5 to 90\(\,^{\circ }\)C. C23 was measured by a pASC using a temperature-controlled air chamber as the base heat bath, providing a temperature range from \(-30\) to 120 °C . For improved adiabatic conditions, the internal volume of both calorimeters was kept vacuum.
Comparison with other methods
pASC versus DSC
Both (p)ASC and DSC implement Eq. (1) for the determination of the heat capacity. The key difference between the two is that in ASC, P is kept constant and the varying \(\dot{T}\) is measured, exactly opposite to DSC where \(\dot{T}\) is constant and P is measured. The consequences for the sample are enormous: in a DSC, the sample is forced to follow \(\dot{T}\), even if its own thermodynamics dictate that it should remain at the same temperature to undergo phase conversion. Thus at a phase transition, the sample is driven out of thermal and thermodynamic equilibrium, and the instrument output is a mixture of the sample properties and the instrument characteristics. In contrast, ASC only provides the sample with an amount of power that it can freely use, and the calorimeter follows the behaviour of the sample. The sample is in no way forced and remains in thermodynamic equilibrium. One can state that in an ASC, the sample is in control of the calorimeter. pASC allows to perform such equilibrium experiments on samples of the order of 10 mg up to several g.
Another important consequence of the constant-power approach is that rate-dependence, an intrinsic feature of DSC, does not exist in ASC. Provided that the experiment takes place at an applied power such that there are no thermal gradients in the sample, the result is independent of the rate: upon approaching a phase transition, the increasing \(c_p\) of the sample will lead to a decreasing rate, and regardless of the applied power, the sample will “slowly” pass the transition.
A fundamental difference between ASC and DSC is the opposite relation between measurement speed and sensitivity. In a DSC, a lower rate leads to a lower heat flux to the sample, and thus a decreasing sensitivity [1, 39]. In an ASC, even a small power (for example 50 \(\upmu\)W) remains always easy to apply, so that this does not influence the data quality. For the two techniques, slower runs generate more data points for the same temperature range, achieving a higher resolution.
An apparent disadvantage of ASC in comparison with DSC is the longer time needed for the experiments. Whereas DSC experiments typically are performed at 10 K min\(^{-1}\) (although lower rates are recommended for experiments with PCMs [1, 16, 17, 40]), ASC experiments are typically performed at a few K h\(^{-1}\) away from the transitions. But this disadvantage is offset by the higher resolution of the ASC data and the fact that a complete understanding of a sample from DSC experiments requires in principle runs at several rates. Additionally, the required calibration efforts for ASC are negligible compared to those of a DSC: once constructed and after an initial calibration, an ASC does not require periodical recalibration.
Finally, we note the ability of ASC to directly measure the enthalpy of the sample, independent of the heat capacity. In DSC, enthalpy must be calculated as the temperature integral of the heat capacity, itself calculated from the measured power and the applied (or measured) rate. Alternatively, the measured heat flow can be integrated with respect to time. In ASC the integration is absent: as the applied power is constant, the enthalpy depends only on P and t, Eq. (5). The difference between ASC and DSC was discussed in Reference [41]. An extensive illustrated discussion of this issue is made in Reference [31], where thermal data for the melting of gallium as obtained by ASC and DSC are compared.
pASC versus T-history method
The T-history method [1, 16, 24] and the largely equivalent three-layer-calorimeter [27, 28] use rather large samples, arguing that for inhomogeneous systems typical DSC-sized samples are not representative. These methods derive from a more general approach for determining transition temperatures. In its simplest form, the material in a container is heated up above its phase change, and allowed to cool down while its temperature is monitored. When the latent heat is released, the temperature stays constant. The innovation of Zhang et al. was the introduction of a second container with a reference material of known thermal properties [24]. Comparison of the temperature evolution of the sample and the reference allows to estimate the heat that leaks out of the sample. Combined with the duration of the transition plateau, this allows the calculation of the transition heat.
From a conceptual point of view, these methods are rather close to ASC. The difference is that instead of a controlled and predefined power like in ASC, an unknown variable power is used: the heat leak with the environment, which depends on the changing temperature difference between sample/reference and the environment. The power itself is obtained from the simultaneous calibration experiment with the reference. As such, the main advantage of ASC, the sample controlling the experiment, is also present here: the heat leak provided by the temperature difference between sample and environment is used by the sample according to its own thermodynamics. The difference with ASC is the variable power. In this respect, the methods can be seen as the differential equivalent of the nonadiabatic scanning calorimeter [21]. While obviously much larger temperature steps are used for the T-history method and the power is determined by a differential approach, the essence of the methods is the same. A notable difference between ASC and the T-history methods is the requirement of a known reference material in the latter. This means that a determination of the properties of an unknown PCM depends on the quality of the set-up and literature data, but for ASC only on the set-up.
Requirements for thermal storage data
Although from a fundamental perspective, experimental data cannot be “too good”, the cost of experiments in terms of time, manpower or money puts practical limits on data quality. Therefore, it is good to ask the question what the required data quality would be for PCMs, particularly in view of the typical applications of these data. For the PCMs, these questions have been considered explicitly, and have, for Germany, resulted in a quality assurance standard published by RAL [40]. Several papers communicating aspects of the research underlying this document are available, of which we draw attention to some papers pertaining to the determination of heat storage capacity [16, 42], as well as to the description of this subject in Reference [1].
When we look at some of the sources for the standard, we find that, for the purpose of using these values in practical applications, the accuracy of the stored heat as a function of temperature should be better than 10 % for the specific enthalpy and better than 0.5 K for the temperature [42]; in another source also 1 K is indicated for the latter [16]. Most of the standard was created to assure that this accuracy can be achieved, mainly with, sometimes elaborate, procedure descriptions to overcome the intrinsic problems a DSC has in measuring a PCM.
With respect to the phase transition temperature the RAL document implies that the temperature interval over which the stored heat is specified should be given, both for melting and crystallisation, rather than a single temperature; if present, the extent of supercooling should be specified. The main document does not specify the required accuracy for the values of the temperature and stored heat (in contrast to the values of the thermal conductivity). However, an accompanying document on the website of RAL (only available in German), gives more details on these requirements. For constant-rate dynamic measurements (such as DSC), a “sufficiently low” heating and cooling rate should be used. This rate is the slower one of the following two possibilities: either the rate at which the temperatures of the inflection point in the enthalpy for repeated heating runs at this rate coincide with each other within 0.2 K and idem for repeated cooling runs, or the rate where the difference between the inflection point for a heating and cooling run is less than 0.5 K. Thus, an accuracy of 0.5 K is recommended for the transition temperature. Further in the document, a rate of 1 K min\(^{-1}\) is recommended. Similar definitions are formulated for the T-history method. For the accuracy of the enthalpy, no value is specified.
Results
pASC
RT42
For RT42, several heating and cooling runs were performed. Because the rate in an ASC run is variable, the speed of the runs is quantified by the average rate in the liquid phase, this was of the order of 1.3 K h\(^{-1}\) (0.022 K min\(^{-1}\)) for heating runs and −1.2 K h\(^{-1}\) (0.020 K min\(^{-1}\)) for cooling runs. A selection of representative runs is shown in Fig 3.
ASC runs on RT42. a Specific heat capacity \(c_p(T)\), showing the presence of two smaller transitions in addition to the large one at 42\(\,^{\circ }\)C. b Specific enthalpy h(T), normalised at 300 J g\(^{-1}\) at 45\(\,^{\circ }\)C, indicating that most energy is associated with the main transition. Inset: enlarged view on the enthalpy during the supercooling of the main transition. The data for the two heating or cooling runs nearly coincide, showing the reproducibility, while the difference between heating and cooling behaviour is small
The first observation is that this PCM not only has the transition at 42\(\,^{\circ }\)C after which it is named, but also two other ones, at 27\(\,^{\circ }\)C and at 14\(\,^{\circ }\)C. Both of these extra transitions are relatively broad, stretching over several K. They are much less prominent than the main transition, but the low-temperature one contains enough enthalpy to make it clearly visible in the h(T) plots in Fig. 3b, and the middle transition can be discerned.
The reproducibility of the data can easily be asserted: the two cooling runs essentially coincide over the entire temperature range, whereas the heating runs do so everywhere except at the lowest transition. The latter difference is a consequence of the deviating thermal history of the runs combined with the transition being close to the lower temperature limit of the calorimeter. Because the transition cannot be entirely completed within the instrument’s range, the initial states of the heating runs are not the same. Similar effects were also observed for other heating runs with different starting points and thermal histories.
Comparison of the heating and cooling runs shows that RT42, while having a strongly first-order main transition (large latent heat), does not exhibit strong supercooling of this 42\(\,^{\circ }\)C transition. However, the manufacturer’s claim that there is no supercooling [33] is not entirely valid. It is very clear that there is a difference in the high-temperature edge of the \(c_p(T)\) curves. This is further supported by the sharp peak in the cooling \(c_p(T)\) at that side of the transition. This peak indicates the temperature at which the supercooled liquid suddenly starts to crystallise; at this moment, it immediately releases the latent heat associated with that part of the transition it has already passed, and the temperature of the sample increases for a short time. But, while the supercooling is clearly asserted, the less than 0.1 K effect will have hardly any repercussions for practical applications.
For the two smaller transitions, we note that there is no hysteresis evident for the mid-temperature transition. For the low-temperature transition, on the other hand, hysteresis is evident, even with the different shape of the two heating runs taken into consideration. The peak maxima differ about 0.5 K, the high-temperature edges about 2–3 K.
Figure 3b shows the h(T) curves. Like the \(c_p(T)\) data, they also show the reproducibility of the experiments. For the interpretation of h(T) for practical applications, one must select two temperatures \(T_1\) and \(T_2\), the difference \(\delta h= h(T_2)-h(T_1)\) is the energy that the PCM can store this temperature interval. The PCM has a good stability over the range from 10 to 50\(\,^{\circ }\)C: there is no difference in \(\delta h\) for the four displayed runs over this total temperature range. However, the main transition at 42 \(^{\circ }\)C shows some difference in the heating and cooling h(T): while having the same \(\delta h\) between 30 and 45\(\,^{\circ }\)C, the distribution over the temperature range is different.
Comparison of the specific heat capacity \(c_p\) of RT42 obtained in a normal (\(\dot{T}_\mathrm{liq} \approx\) 1.3 K h\(^{-1}\) = 0.022 K min\(^{-1}\)) and a fast (\(\dot{T}_\mathrm{liq} \approx\) 32 K h\(^{-1}\) = 0.53 K min\(^{-1}\)) ASC heating run. The transitions in the fast run as slightly shifted and broadened due to the thermal gradient in the sample
In addition to these slow runs, also a fast ASC heating run was made at 32 K h\(^{-1}\) \(\approx\) 0.5 K min\(^{-1}\) in the liquid phase, to allow for a comparison with a slow DSC run (see Sect. 4.3). Figure 4 shows \(c_p(T)\) in comparison with a normal-speed ASC heating run. While all the features are retained, the three transition peaks are shifted to higher temperature. This is not a consequence of a failure of the measurement method, like in DSC, but an indication that a substantial temperature gradient is generated inside the sample.
C23
Figure 5 shows that C23 has no less than five transitions between 35 and 50\(\,^{\circ }\)C. We refer the reader to References [34, 43–45] for a detailed description of the different phases of this compound. The exact nature of the phases is not relevant for the discussion here, but we introduce the names of the phases for easy referral to the different transitions. In the heating run, below about 39\(\,^{\circ }\)C, the sample is a crystalline phase (Cry\(_\mathrm{I}\)), which is followed by a narrow Cry\(_\mathrm{II}\) phase. At 41\(\,^{\circ }\)C, the alkane undergoes its first major transition, from the crystalline region to the rotator region. In the rotator phases, the positional order of the crystal is retained, while the orientational is lost (the elongated molecules can rotate around their long molecular axis). Different rotator phases are observed: between 41 and 42\(\,^{\circ }\)C, the sample is in the R\(_\mathrm{V}\) phase, followed by the R\(_\mathrm{I}\) phase up to 45\(\,^{\circ }\)C. The next one is the R\(_\mathrm{II}\) phase, and finally the liquid is reached at 47\(\,^{\circ }\)C, after passing through the most prominent transition in C23.
ASC runs on C23. a Specific heat capacity \(c_p\). b Specific enthalpy h, normalised to 300 J g\(^{-1}\) at 49\(\,^{\circ }\)C. The data show the presence of six phases; the transitions all show hysteresis or supercooling. Most of the energy is associated with the Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\) and R\(_\mathrm{II}\)–Liq transitions
Comparison of heating and cooling data reveals hysteresis for all transitions. This is clearly visible for all of them, but there is some dependence on thermal history (in the first heat/cool cycle, depicted in Fig. 5, the hysteresis is nearly absent (except for Cry\(_\mathrm{I}\)–Cry\(_\mathrm{II}\)), so we refer here to subsequent runs). Typical values for the hysteresis, expressed as the difference between the high-temperature edges, are 1 K for Cry\(_\mathrm{I}\)–Cry\(_\mathrm{II}\), 3 K for Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\), 0.3 K for R\(_\mathrm{V}\)–R\(_\mathrm{I}\), 0.4 K for R\(_\mathrm{I}\)–R\(_\mathrm{II}\) and 0.15 K for R\(_\mathrm{II}\)–Liq.
Like RT42, C23 shows a minute supercooling of its Liq–R\(_\mathrm{II}\) transition. The effect is a bit larger here. Earlier ASC measurements on a series of alkanes showed that the Liq–Rot transition hardly supercools, the authors gave an upper limit of 0.03 K [44]. Our value here is a bit higher, but this may be a consequence of samples of different size, geometry and purity used here, as well as a difference in measuring speed. For the Rot–Cry transition, the situation is different for odd and even alkanes. While both are susceptible to supercooling, the effect is limited for odd ones, but much larger for the even ones [44], an observation that we already earlier made from ASC data for C24 [46].
The transition from R\(_\mathrm{V}\) to Cry\(_\mathrm{II}\) in the cooling run displays a large supercooling, terminating at 39\(\,^{\circ }\)C with a sudden end-of-supercooling heat release. Due to the large amount of enthalpy in this transition, this heat drives the sample back to more than 40\(\,^{\circ }\)C, a temperature well within the two-phase region of this transition, as can be seen from the substantial effective \(c_p\) values in the continuation of this curve. In fact, while suddenly crystallising, the sample releases so much heat that it nearly converts itself back to the rotator state.
The h(T) curves in Fig. 5b clearly show that most of the enthalpy in C23 is associated with the Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\) and R\(_\mathrm{II}\)–Liq transitions, in a ratio of about 1:2. The other transitions are hardly visible on the scale of this figure, and are thus of minimal importance for the application of C23 as a PCM.
The supercooling of the R\(_\mathrm{V}\)–Cry\(_\mathrm{II}\) transition is also clearly visible in h(T): a marked discontinuous step in the T axis is displayed. It is notable that after the transition is completed at about 38\(\,^{\circ }\)C, the values of h(T) for heating and cooling coincide again. This means that no heat has gone undetected in the run, and it is a feature of ASC that this is possible: the suddenly released heat at the end of the supercooling remains inside the sample cell due to the adiabatic conditions, and is afterwards gradually extracted under the normal experimental conditions.
DSC
DSC experiments were performed at rates of 10, 2 and 0.5 K min\(^{-1}\) in all cases. Before starting the scans, the samples were heated to 60 or 70\(\,^{\circ }\)C, in the liquid phase, to make sure that the contact between the sample and the cell was optimal. Several cooling–heating combinations with the different rates were then made. For clarity of presentation, only runs at 10 and 0.5 K min\(^{-1}\) are given in the figures. The results of the 2 K min\(^{-1}\) runs generally show the expected intermediate behaviour between the 10 and 0.5 K min\(^{-1}\) ones. To verify the reproducibility, two nearly identical samples of each material were prepared, and both for RT42 and for C23 the results were essentially identical; hence, only data for one sample are presented.
RT42
Figure 6 shows three phase transitions over temperature range between 5 and 45\(\,^{\circ }\)C. A small transition can be found in the region from 8 to 18 \(^{\circ }\)C, visible as a broad largely symmetric peak. There is a clear hysteresis between heating and cooling. The second transition is a small feature between 24 and 27 \(^{\circ }\)C, more of a broad bump than a clear peak. The main transition is a large peak between 30 and 45 \(^{\circ }\)C.
The data show all the typical features expected from a comparison of DSC runs at different rates: higher rates lead to a broadening of transition (if the results are presented with T on the x axis), an effect which becomes especially pronounced for transitions with large heats involved. For the 10 K min\(^{-1}\) heating run, this is obvious: the transition seems to continue up to 46 \(^{\circ }\)C, 4 K above the nominal value for RT42. In fact, the transition peak at 10 K min\(^{-1}\) reaches its maximum when the 0.5 K min\(^{-1}\) transition peak is completely subsided. This clearly learns that PCMs should be not be measured at the conventional high rates, a conclusion shared with the authors of Reference [17].
The main transition shows a distinct shape in the cooling curves. One would expect some onset behaviour, and a gradual increase of \(c_p\), instead, a rather sudden increase is found in this case. This is combined with a double-peak feature, minute for the fast run, pronounced for the slow runs. Similar to the ASC data, this is the signature of supercooling the sample: the sudden heat release results also in DSC in an anomalous temperature evolution (\(\dot{T}\) is not a constant value). Due to the closeness of the temperature sensor to the sample cell in the design of the Q1000 as well as the strong thermal coupling [35], this evolution is registered in T(t).
C23
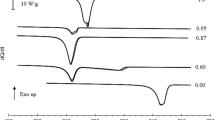
Two samples of C23 have been studied, and the results were essentially identical. Figure 7 shows the results for scans at their full scale, indicating the notable difference in height of the transition peaks in comparison with RT42. The figure shows that much higher \(c_p\) values are reached with the transition peaks than for RT42, indicating that the transition enthalpy is concentrated in a smaller temperature region in C23. The other common observations about DSC measurements, rate dependence and transition broadening, are also clearly present, to a larger extent than in RT42. Due to the large heats involved and the closeness of the transitions, there is considerable overlap between the broadened transition peaks for the 10 K min\(^{-1}\) data.
Figure 8 displays several selections from the DSC data for C23. As a first observation, the smaller transitions are not very well visible in the DSC data. In general, the Cry\(_\mathrm{I}\)–Cry\(_\mathrm{II}\) transition becomes a small shoulder on the low-temperature side of the Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\) transition, while it is more pronounced and much more clearly separated in ASC. The transition from R\(_\mathrm{V}\) to R\(_\mathrm{I}\) is difficult to assess. The R\(_\mathrm{I}\) to R\(_\mathrm{II}\) transition is present in all runs, although the exact characteristics differ from run to run.
The two main transitions, Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\) and R\(_\mathrm{II}\)–Liq, are clearly visible. In contrast to the sharp transitions in ASC, the smearing out due to the measurement concept is particularly clear. In this case, even reducing the rate does not help very much. The DSC data for the cooling runs show supercooling for both transitions and the strong end-of-supercooling jump that was already seen in the ASC data for the Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\) transition. Even in the DSC, where the thermal contact between sample and environment is supposed to be very efficient, so much heat is released that the temperature of the sample rises substantially. The R\(_\mathrm{II}\)–Liq transition does not display a strong jump at the end of supercooling, although all the runs do show the spike at the high-temperature side of the transition that we saw earlier in RT42 and found to be indicative of a small supercooling effect.
Discussion
Stored heat
Generally the transition heat \(\Delta h\) of a phase transition is reported, which is the heat needed for the phase conversion only. In terms of DSC analysis, it is the integral of the heat flux above the transition’s baseline. We have compared \(\Delta h\) values from our experiments with those available in the literature for RT42 [47] and C23 [34, 44] and obtained always good agreement with these values, both for ASC and DSC.
However, in PCM applications, the transition heat is not the most relevant way of describing the properties: it only takes into account the heat that is associated with the phase conversion, and not the heat that is needed for the heating of the sample itself. For PCMs both of these contribute to the storage capacity, and therefore the total energy content over a temperature interval, the stored heat \(Q_\mathrm{stored}\), is the relevant quantity. This is the change in enthalpy over the temperature interval.
The stored heat was calculated in two different ways, depending on the measurement technique. The enthalpy h(T) is a direct result of an ASC experiment, see Eq. (5), and the calculation of the stored heat is trivial: the difference in enthalpy at two temperatures is the stored heat for that temperature interval. For DSC, separate experiments (also used for the absolute value determination of \(c_p\)) were performed in which the instrument was allowed to stabilise extensively before starting the run, the same was done afterwards so that the zero-level of the heat flow was accurately known. In order to further reduce potential errors, only data from 10 K min\(^{-1}\) heating runs will be discussed, as higher rates result in larger heat flows. For these runs, the measured contribution from the spurious heat flow was less than 1 % compared to the heat flow away from the transitions, and evidently much less than that during the transitions. We have not integrated \(c_p(T)\) to obtain h(T), because calculating \(c_p(T)\) requires an extra calibration step and thus introduces an extra error; instead, the heat flow was directly integrated. It should be noted that DSC is here at a double disadvantage compared to ASC: there is not only the deformation of the heat flow/heat capacity, but also, accurate measurements of the absolute value of the heat flow must be made at high rates, where the deformation is worse. The results are summarised in Table 1.
For RT42, DSC seems to overestimate \(Q_\mathrm{stored}\) a bit with respect to ASC. On the other hand, the value given by the supplier for the Rot–Liq transition is almost the same as the ASC value. As this value is obtained by a three-layer-calorimeter and not a DSC, it acts as an independent result here. Likely, the heat-flux calibration during the DSC runs was slightly off. The correspondence for the stored heat of C23 for the large transitions between ASC and DSC is quite good, provided one compares the same temperature regions. When only the region directly surrounding the transition peak is taken into account, ASC gives smaller values, because of the smaller contribution of the sensible heat over such smaller interval. Thus, even though most of the stored heat is contained in the transitions, a considerable amount is still present in the form of sensible heat, a consequence of the rather high heat capacity in the rotator phases (see Sect. 4.2).
Mehling and Cabeza have proposed the stored heat over a series of small temperature intervals (as opposed to a single \(Q_\mathrm{stored}\) value for the entire transition region) as a convenient representation of the storage capacity of a PCM in a given temperature region [1]. In terms of ASC data, this is equivalent to reporting the difference of the enthalpy at the end and the beginning of each such interval. For DSC, the same calculation is made on the basis of the integrated heat flow. The results of these calculations are presented in Figs. 9 and 10.
For RT42, we limit the view to the main transition, but the observations for the two other transitions are exactly the same. Away from the transitions, the values for the stored heat are more or less the same for both techniques. There is an important difference for the phase transition: where ASC shows all heat concentrated between 37 and 43 \(^{\circ }\)C, the DSC makes the transition double as wide, with most of the heat present in the upper half of the transition. In fact, the DSC data indicate that most of the storage capacity is present in a temperature region where the ASC data say that there is no phase-change-enhanced storage any more.
For C23, all transitions except the Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\) and R\(_\mathrm{II}\)–Liq are invisible, as they are overshadowed by these two main transitions. In comparison with RT42, the separation between the ASC and DSC is even worse: there is no overlap between the transitions. Apart from the disparity in the position of the transitions, a second observation is that the DSC width of the transition is seriously increased. Where the effect is reasonably limited for the lower transition, the higher transition is substantially widened: in ASC, the transition is limited to a single 0.5 K interval, whereas it takes six or seven of these in DSC.
These data sets illustrate clearly that if a transition is sharp in reality (as observed by ASC), DSC fails to correctly obtain the transition temperature and profile. This is a consequence of the fact that in the DSC more heat should be provided at the same time interval for a sharp peak, which is made impossible by its construction, while for ASC, the transition takes just more time, but the temperature of the sample does not change.
Solid heat capacity
As mentioned by Charvat et al., several sources disagree on the value of the heat capacity of RT42 at either side of the main transition [48]. Our earlier ASC work gave 3.5 J g\(^{-1}\) K\(^{-1}\) for the low-temperature phase and 2.3 J g\(^{-1}\) K\(^{-1}\) for the liquid phase [47]; these values are confirmed by the present results. The data sheet that Rubitherm currently provides [33] mentions 2 J g\(^{-1}\) K\(^{-1}\) for both liquid and solid phase, but an earlier version of it mentioned 1.8 and 2.4 J g\(^{-1}\) K\(^{-1}\) for solid and liquid respectively; these are the literature values that appear in Reference [47] and probably also in Reference [10].
Before discussing this issue in RT42, we will first discuss the situation for C23: RT42 is a mixture of alkanes, and therefore one should first review the situation in a pure compound. As seen above, C23 has additional phases between the crystal and the liquid. The presence of these so-called rotator phases is a common phenomenon for alkanes of intermediate chain length n [34, 45, 49]. In particular the region between \(n=20\) and \(n=30\) has received considerable attention, and detailed x-ray and calorimetric data have clarified the nature of the five rotator phases [43, 44]. Although most attention has been paid to the properties of the phase transitions, the thermal data from different calorimetric techniques show that the heat capacity in the rotator phases is higher than that of the (normal) solid and liquid phases [44, 46, 50, 51]. This can be understood from the additional degrees of freedom present in the rotator crystals. The present results for C23 fall in line with the earlier observations: instead of values around 2 J g\(^{-1}\) K\(^{-1}\) commonly seen for crystals and liquids, values above 5 J g\(^{-1}\) K\(^{-1}\) are observed for most of the rotator region. A value of about 2.3 J g\(^{-1}\) K\(^{-1}\) is found in the crystal phase.
Our current measurements and the fact that RT42 is an alkane mixture now sheds some light on the differing \(c_p\) values. The rotator phases of the pure alkanes persist in mixtures of alkanes, at least provided the differences in chain length of the components are not too different; also, the temperature range in which the rotator phases exist is broadened [34, 52, 53]. Combining this information with our measurements, we conclude that RT42 displays a normal crystalline phase below 10 \(^{\circ }\)C, a first rotator phase between 16 and 26 \(^{\circ }\)C, and a second rotator phase between 29 and 36 \(^{\circ }\)C, finally followed by the liquid phase above 42 \(^{\circ }\)C. Calorimetric data do not allow the identification of the phases, but a best guess based on the phase diagram of the pure alkanes with similar melting points suggests that the lower rotator is the R\(_\mathrm{I}\) phase and the upper one the R\(_\mathrm{II}\) phase. It is likely that similar conclusions can be drawn for many other Rubitherm RT PCMs, and more generally for any alkane-based PCM.
The assertion that the phase below the main transition in RT42 is not a “normal” crystal, in combination with the relative proximity of the phase transition, explains the high value of \(c_p\) that we observed earlier [47], a value that is essentially confirmed in the present work. The values reported in the other sources should be treated as more approximate values, suitable for approximate PCM application calculations, but, in fact, outside the uncertainty limits that have been put forward, which demand an uncertainty of less than 10 % [16].
ASC versus DSC
Figures 11 and 12 make a comparison between ASC and DSC data for the two PCMs. As already noted in the discussion of the measurement results, the shapes of the \(c_p\) curves are quite different, illustrating the opposite measurement principles.
For the RT42 heating runs, the two ASC runs differ by a factor 20 in nominal rate, and so do the DSC runs. The ASC data undergo some marginal broadening, whereas the shape and width of the transition remain unaffected. For the same change of rate, the DSC data show a peak that is more than double as wide and completely deformed. This illustrates the advantage of the constant power/variable rate approach in ASC: irrespective of the amount of power applied, the calorimeter will slow down for a transition, allowing the phase conversion to take place in equilibrium. The same broadening is also apparent in Fig. 12 for the C23 DSC data, but, due to the intrinsically sharper transitions, the effects are even worse. Where for RT42 the 0.5 K min\(^{-1}\) DSC data are comparable to the ASC data, in C23 this is not the case. The R\(_\mathrm{II}\)-Liq transition is in heating more than two times as broad in the 0.5 K min\(^{-1}\) run than in the ASC data, while it does not fit within the chosen temperature axis for the 10 K min\(^{-1}\) run. The effect is more pronounced for the Cry\(_\mathrm{II}\)–R\(_\mathrm{V}\) transition, because it is even sharper in the ASC runs.
Another important issue is the sensitivity trade-off that is inherent to DSC. High rates are required for large heat flows, however, they enhance the broadening and shift of the transitions. For the wide and separated transitions in RT42, this is not too problematic, but for C23, with its five phase transitions over a 10 K range, including two with a large transition heat, it becomes dramatic. In the 10 K min\(^{-1}\) experiments, only the two large transitions can be considered unambiguously present. Even in the 0.5 K min\(^{-1}\) runs, the detection of the small transitions remains problematic, with Cry\(_\mathrm{I}\)–Cry\(_\mathrm{II}\) and R\(_\mathrm{I}\)–R\(_\mathrm{II}\) clearly present, but with noticeably different features than in the ASC experiments. R\(_\mathrm{V}\)–R\(_\mathrm{I}\) is not detected.
The dynamic range of ASC does not overlap much with that of a DSC. Current implementations of pASC cover rates (away from transitions) from 0.1 to 60 K h\(^{-1}\) (0.001 K min\(^{-1}\) to 1 K min\(^{-1}\)), while commercial DSCs usually indicate such ranges as 0.1–100 K min\(^{-1}\). For the particular case of PCMs, where the interest lies with large transitions, the higher rates of DSCs, combined with the measurement principle, cause problems because the results do not correctly represent the h(T) behaviour that a PCM will exhibit in typical applications. As an example, we point to a study where DSC data at different rates were inserted in a model for an application and compared with actual measurements, it was found that the data from the slowest runs (0.1 K min\(^{-1}\)) gave the best correspondence [54]. The authors also note that better data are necessary, which can be provided by ASC, not by using lower rates as in DSC, but by a measurement principle that is closer to the actual application conditions.
Typical PCM applications consist of placing the PCM in an environment from which they need to extract heat (or give to). In a DSC, due to the forced temperature rate, the temperature gradient between the sample and the furnace will increase while passing the transition, a situation which is more or less the opposite of, for example, a solid PCM in a wall board of a warm room: the PCM melting will extract heat from the room, reducing the temperature gradient. In that respect, an ASC (with constant power) or the T-history method (with variable power) provide experimental circumstances much closer to real-life situations.
We also recorded approximately the time that was needed for the experiments. When referring to the pure measurement time, the time that the sample of interest is inside the instrument, DSC is clearly the faster method. A measurement cycle over 60 K, with heating and cooling runs at the three rates (0.5, 2 and 10 K min\(^{-1}\)) takes about 6 h, including temperature stabilisations, thus amounting to a single working day. However, this turns out to be far from the complete picture: the execution of this study has shown that the careful operation of a DSC, with the attention needed to the calibration of the heat flow and heat capacity at low scanning rates consumes an enormous amount of manpower and time. Due to the rate dependence of the DSC, these calibrations need to be performed at all measurement rates, and as there is a need for periodic recalibration, this is a serious burden on the DSC operator. The full supplier-suggested calibration at 10 K min\(^{-1}\) requires about one working day, and this time needs to be multiplied with the number of rates needed (and more time is needed for lower rates). And ideally, such calibration should be regularly repeated. Alternatively, in case \(c_p\) is determined with an approach in which three curves (empty pans, reference material, sample) are measured [39], then (supposing a 60 K range, heating and cooling runs + 30 min for mounting, stabilisation,...) about three times 45 min, 2.25 h is needed for 10 K min\(^{-1}\) and three times 2.5 h, about a day for 0.5 K min\(^{-1}\) (and because the operator may need to be present to exchange the samples, this may need to be done over multiple working days). Thus, although the direct measurement time is short, the full measurement time including calibrations becomes substantial.
From our experience in this work, a “pre-calibrated pASC” (factory-calibrated as would be the case if the instrument was commercially available) gives a finalised result like presented in Fig. 3 in about 1 h of operator time for the sample mounting, about 100 h of measuring time (requiring no user intervention) and about 15 min for analysis.
While a DSC may objectively still be the faster instrument, the difference is not that large once the complete picture is taken into account. In addition, this work shows, in agreement with literature, that correct thermal data on PCMs should be obtained in equilibrium, which can only be achieved at the lower rates at which a pASC naturally operates. The quality of these results further motivates the use of a somewhat slower method.
Conclusion
We believe that for accurate determination of heat capacity profiles, and the derived enthalpy profiles and stored heat per temperature interval tables, DSCs will need to be operated at rates below 0.5 K min\(^{-1}\). This is a regime where DSCs are generally not readily used, and due to their construction, also do not perform particularly well. The effort needed in terms of calibration, combined with the longer measurement times make it worthwhile to look at other measurement techniques. While the virtues of the T-history method (and comparable techniques) are well-established for the study of PCMs, we believe that this paper has also made clear that pASC is a suitable technique for this type of research.
The pASC instrument resembles in several aspects a DSC, while it allows to incorporate an important improvement in PCM research that has been added by the T-history method: experimental circumstances that mimic the operational use of PCMs, and which are close to thermal and thermodynamic equilibrium, at least much closer than can be achieved in a DSC. As such, one can regard pASC as a T-history-like method, but operating in a much tighter controlled environment. As a consequence, smaller samples can be used, although the technique also allows them to be sufficiently large to correctly represent the large bulky application quantities.
Although ASC requires longer measurements than DSC, the difference is not that large due to the time needed for the required DSC calibration work (absent for pASC). In addition, the determination of thermal parameters in thermodynamic equilibrium requires the use of slow scanning rates, for which DSC is intrinsically unsuitable, in contrast to ASC which is made for it. This makes the advantage of ASC with respect to DSC clear for any thermal measurement with higher demands than fast screening.
Notes
In fact, it is the thermal effusivity e that is the correct measure here, since \(e = \sqrt{\kappa \rho c_p}\), with \(\kappa\) the thermal conductivity, \(\rho\) the density and \(c_p\) the specific heat capacity.
In the text, capital letters for \(C_p\) and H will refer to a total heat capacity and enthalpy, expressed in J K\(^{-1}\) and J, and lower case letters \(c_p\) and h to specific values, expressed in J g\(^{-1}\) K\(^{-1}\) and J g\(^{-1}\).
References
Mehling, H., Cabeza, L.F.: Heat and cold storage with PCM—an up to date introduction into basics and applications. Springer, Berlin, Heidelberg (2008). doi:10.1007/978-3-540-68557-9
Van Roie, B., Leys, J., Denolf, K., Glorieux, C., Pitsi, G., Thoen, J.: Phys. Rev. E 72(4), 041702 (2005). doi:10.1103/PhysRevE.72.041702
Zhou, D., Zhao, C.Y., Tian, Y.: Appl. Energy 92, 593 (2012). doi:10.1016/j.apenergy.2011.08.025
Hyun, D.C., Levinson, N.S., Jeong, U., Xia, Y.: Angew. Chem. Int. Ed. 53(15), 3780 (2014). doi:10.1002/anie.201305201
Busico, V., Carfagna, C., Salerno, V., Vacatello, M., Fittipaldi, F.: Solar Energy 24(6), 575 (1980). doi:10.1016/0038-092X(80)90356-4
Li, W., Zhang, D., Zhang, T., Wang, T., Ruan, D., Xing, D., Li, H.: Thermochim. Acta 326(1–2), 183 (1999). doi:10.1016/S0040-6031(98)00497-3
Pielichowska, K., Pielichowski, K.: Polym. Adv. Technol. 22(12), 1633 (2010). doi:10.1002/pat.1651
Alkan, C., Günther, E., Hiebler, S., Ensari, Ö.F., Kahraman, D.: Solar Energy 86(6), 1761 (2012). doi:10.1016/j.solener.2012.03.012
Zalba, B., Marín, J.M., Cabeza, L.F., Mehling, H.: Appl. Therm. Eng. 23(3), 251 (2003). doi:10.1016/S1359-4311(02)00192-8
Kenisarin, M., Mahkamov, K.: Renew. Sustain. Energy Rev. 11(9), 1913 (2007). doi:10.1016/j.rser.2006.05.005
Kenisarin, M.M.: Renew. Sustain. Energy Rev. 14(3), 955 (2010). doi:10.1016/j.rser.2009.11.011
Cabeza, L.F., Castell, A., Barreneche, C., de Gracia, A., Fernéndez, A.I.: Renew. Sustain. Energy Rev. 15(3), 1675 (2011). doi:10.1016/j.rser.2010.11.018
Oró, E., de Gracia, A., Castell, A., Farid, M.M., Cabeza, L.F.: Appl. Energy 99, 513 (2012). doi:10.1016/j.apenergy.2012.03.058
Morofsky, E.: Energy efficient building design and thermal energy storage. In: Paksoy, H.Ö. (ed.) Thermal energy storage for sustainable energy consumption. NATO science series, vol. 234, pp 103–132. Springer, Dordrecht (2007). doi:10.1007/978-1-4020-5290-3_6
He, B., Martin, V., Setterwall, F.: Energy 29(11), 1785 (2004). doi:10.1016/j.energy.2004.03.002
Günther, E., Mehling, H., Hiebler, S., Redlich, R.: Int. J. Thermophys. 30(4), 1257 (2009). doi:10.1007/s10765-009-0641-z
Lazaro, A., Peñalosa, C., Solé, A., Diarce, G., Haussmann, T., Fois, M., Zalba, B., Gshwander, S., Cabeza, L.F.: Appl. Energy 109, 415 (2013). doi:10.1016/j.apenergy.2012.11.045
Albright, G., Farid, M., Al-Hallaj, S.: J. Therm. Anal. Calorim. 101(3), 1155 (2010). doi:10.1007/s10973-010-0805-x
Gibout, S., Franquet, E., Maréchal, W., Dumas, J.P.: Thermochim. Acta 566, 118 (2013). doi:10.1016/j.tca.2013.04.023
Ema, K., Uematsu, T., Sugata, A., Yao, H.: Jap. J. Appl. Phys. 32(4R), 1846 (1993). doi:10.1143/JJAP.32.1846
Yao, H., Ema, K., Garland, C.W.: Rev. Sci. Instrum. 69(1), 172 (1998). doi:10.1063/1.1148492
Lashley, J.C., Hundley, M., Migliori, A., Sarrao, J.L., Pagliuso, P.G., Darling, T.W., Jaime, M., Cooley, J.C., Hults, W.L., Morales, L., Thoma, D.J., Smith, J.L., Boerio-Goates, J., Woodfield, B.F., Stewart, G.R., Fisher, R.A., Phillips, N.E.: Cryogenics 43(6), 369 (2003). doi:10.1016/S0011-2275(03)00092-4
Quantum Design PPMS with heat capacity option. http://www.qdusa.com/products/ppms.html (2016). Accessed 7 Feb 2016
Zhang, Y., Jiang, Y., Jiang, Y.: Meas. Sci. Technol. 10(3), 201 (1999). doi:10.1088/0957-0233/10/3/015
Marín, J.M., Zalba, B., Cabeza, L.F., Mehling, H.: Meas. Sci. Technol. 14(2), 184 (2003). doi:10.1088/0957-0233/14/2/305
Kravvaritis, E.D., Antonopoulos, K.A., Tzivanidis, C.: Meas. Sci. Technol. 21(4), 045103 (2010). doi:10.1088/0957-0233/21/4/045103
Laube, A.: Das 3-Schicht-Kalorimeter—Ein einfaches, aber präzises Verfahren zur Bestimmung der Speicherkapazität von Latentwärmespeichermaterial. http://www.waermepruefung.de (2016). Accessed 7 Feb 2016
Kenfack, F., Bauer, M.: Energy Procedia 46, 310 (2014). doi:10.1016/j.egypro.2014.01.187
Thoen, J., Marynissen, H., Van Dael, W.: Phys. Rev. A 26(5), 2886 (1982). doi:10.1103/PhysRevA.26.2886
Thoen, J.: High Resolution adiabatic scanning calorimetry and heat capacities. In: Wilhelm, E., Letcher, T.M. (eds.) Heat capacities: liquids, solutions and vapours, pp. 287–306. The Royal Society of Chemistry, London (2010). doi:10.1039/9781847559791-00287
Leys, J., Losada-Pérez, P., Glorieux, C., Thoen, J.: J. Therm. Anal. Calorim. 177(1), 173 (2014). doi:10.1007/s10973-014-3654-1
Leys, J., Losada-Pérez, P., Slenders, E., Glorieux, C., Thoen, J.: Thermochim. Acta 582, 68 (2014). doi:10.1016/j.tca.2014.02.023
Rubitherm Technologies GmbH. Data sheet RT42 (2013)
Dirand, M., Bouroukba, M., Chevallier, V., Petitjean, D., Behar, E., Ruffier-Meray, V.: J. Chem. Eng. Data 47(2), 115 (2002). doi:10.1021/je0100084
Danley, R.L.: Thermochim. Acta 395(1–2), 201 (2003). doi:10.1016/S0040-6031(02)00212-5
Thoen, J., Cordoyiannis, G., Glorieux, C.: Liq. Cryst. 36(6–7), 669 (2009). doi:10.1080/02678290902755564
Thoen, J., Leys, J., Glorieux, C.: Adiabatic scanning calorimeter. Int. Appl. PCT/BE2011/000042, patent pending (2010)
Losada-Pérez, P., Mertens, N., de Medio-Vasconcelos, B., Slenders, E., Leys, J., Peeters, M., van Grinsven, B., Gruber, J., Glorieux, C., Pfeiffer, H., Wagner, P., Thoen, J.: Adv. Condens. Matter Phys. 2015(4), 1 (2015). doi:10.1155/2015/479318
Höhne, G.W.H., Hemminger, W.F., Flammersheim, H.J.: Differential scanning calorimetry—an introduction for practitioners. Springer, Berlin, Heidelberg (1996). doi:10.1007/978-3-662-03302-9
Gütegemeinschaft PCM e.V. RAL-GZ 896: Phase change material. RAL Deutsches Institut für Gütesicherung und Kennzeichnung e.V. (2013)
Thoen, J.: Int. J. Mod. Phys. B 9(18–19), 2157 (1995). doi:10.1142/S0217979295000860
Mehling, H., Ebert, H.P., Schossig, P. In: Proceedings of the 7th IIR Conference on phase change materials and slurries. Dinan (2006)
Sirota, E.B., King Jr, H.E., Singer, D.M., Shao, H.H.: J. Chem. Phys. 98(7), 5809 (1993). doi:10.1063/1.464874
Sirota, E.B., Singer, D.M.: J. Chem. Phys. 101(12), 10873 (1994). doi:10.1063/1.467837
Dirand, M., Bouroukba, M., Briard, A.J., Chevallier, V., Petitjean, D., Corriou, J.P.: J. Chem. Thermodyn. 34(8), 1255 (2002). doi:10.1006/jcht.2002.0978
Leys, J., Glorieux, C., Thoen, J.: High-resolution adiabatic scanning calorimetry applied to the phase transitions in the n-alkanes tetradecane and tetracosane. In: Kiss, L., St.-Georges, L. (eds.) Proceedings of the 31th International Thermal Conductivity Conference and 19th International Thermal Expansion Symposium, pp. 57–66. DEStech Publications Inc., Lancaster (2013)
Losada-Pérez, P., Tripathi, C.S.P., Leys, J., Cordoyiannis, G., Glorieux, C., Thoen, J.: Int. J. Thermophys. 32(5), 913 (2011). doi:10.1007/s10765-011-0984-0
Charvát, P., Klimeš, L., Ostrý, M.: Energy Build. 68(part A), 488 (2014). doi:10.1016/j.enbuild.2013.10.011
Broadhurst, M.G.: J. Res. Natl. Inst. Stand. Technol. 66A(3), 241 (1962). doi:10.6028/jres.066A.024
Roblès, L., Mondieig, D., Haget, Y., Cuevas-Diarte, M.A.: J. Chim. Phys. 95(1), 92 (1998). doi:10.1051/jcp:1998111
Zammit, U., Marinelli, M., Mercuri, F., Paoloni, S.: J. Phys. Chem. B 114(24), 8134 (2010). doi:10.1021/jp102609y
Ungar, G., Mašić, N.: J. Phys. Chem. 89(6), 1036 (1985). doi:10.1021/j100252a030
Sirota, E.B., King Jr, H.E., Shao, H.H., Singer, D.M.: J. Chem. Phys. 99(2), 798 (1995). doi:10.1021/j100002a050
Arkar, C., Medved, S.: Thermochim. Acta 438(1–2), 192 (2005). doi:10.1016/j.tca.2005.08.032
Acknowledgments
The authors thank Patricia Losada-Pérez for her assistance with the C23 pASC measurements. This research was supported by the Research Council of KU Leuven through IOF Leverage Project IOF-HB/11/022 and Research Project OT/11/064. J.L. thanks ULCO for a post-doctoral fellowship.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Leys, J., Duponchel, B., Longuemart, S. et al. A new calorimetric technique for phase change materials and its application to alkane-based PCMs. Mater Renew Sustain Energy 5, 4 (2016). https://doi.org/10.1007/s40243-016-0068-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40243-016-0068-y