1 Introduction

High-strength fine-grained structural steels are increasingly used today for economic and design reasons in modern steel construction, e.g., in building construction, plant engineering, and crane construction. By using fine-grain structural steels with higher yield strengths (≥ 690 MPa), significant weight reductions and lower processing costs can be achieved by reducing wall thickness. For example, replacing S235J2 with S960QL can reduce weight by up to 78% [1, 2]. Current light weighting efforts stem from the German government’s goal of reducing greenhouse gas emissions by up to 65% from 1990 levels by 2030. These requirements imply a significant reduction of process emissions in industry by increasing energy, raw material, and material efficiency [3]. This often leads to more complex components and structures. Today, additive manufacturing for the modification or production of high-strength components offers many economic advantages over conventional processes and a significant gain in design freedom, for example, to realize bionic designs [4]. In addition, expensive machining steps can be saved by direct manufacturing of near-net-shape components [5]. In particular, the use of high-strength fine-grain structural steels has great potential for weight-optimized, efficient structures with high mechanical strength for many areas of steel construction [6]. Based on gas metal arc welding (GMAW), the wire arc additive manufacturing (WAAM) process has been developed in recent years. In addition, special welding wires for the manufacture of high-strength components using WAAM, which were developed on the basis of high-strength filler metals for joint welding, are already available on the market [7] and safe to use [8].

WAAM is particularly suitable for the generation of complex structures due to its high deposition rates, process reliability, and good automation capability [4, 5]. The fundamental applicability for large-format components with welding robots has already been demonstrated in several studies [4, 9]. However, a broad economic industrial application is still hindered by the lack of quantitative statements on the manufacturing-related stresses and the component safety during production and operation. This applies in particular to process- and material-related influences, the constructive shrinkage restraints associated with the formation of high tensile residual stresses, and the associated risk of delamination between the component and substrate. This requires comprehensive knowledge of the complex interactions between the welding process and heat control during production and the metallurgical processes in order to reliably avoid a high production-related stress level and the formation of cracks during production that can be traced back to it, or premature component failure. For high-strength welded joints, stress optimization by means of adapted heat conduction concepts has already been the subject of research. Studies on their transferability to generative manufacturing steps for high-strength steels are still lacking [10]. Although, manufacturing-related stresses in generative manufacturing have already been the subject of research [11,12,13,14], these, however, have not yet been considered in the context of the special microstructures and low strain reserves of high-strength steels in GMAW-based additive welding. Depending on the component dimensions, commercial ready-to-use WAAM welding systems are now available in various sizes, which can be used to generate components by multi-axis gantries or robots [15]. Modified GMAW short arc processes are particularly suitable for large volume components (e.g., cold metal transfer, CMT, or ColdArc) due to their high deposition rate with low heat input [16]. Welding experiments and accompanying numerical simulations demonstrated the high dependence of the temperature distribution and the resulting component geometry on the manufacturing parameters [17, 18]. These investigations confirmed that sufficient heat dissipation in the WAAM process poses great challenges for the special microstructure of high-strength steels. The necessary cooling rates to achieve the required microstructures, low manufacturing-related stresses, and mechanical properties (e.g., ∆t8/5 time for S690: about 5 s to 20 s) can only be achieved by limiting component temperatures and heat input. For this purpose, the build-up strategy and heat control (energy per unit length or heat input and preheating or interlayer temperature) must be adapted so that as little heat as possible is introduced during production [18, 19].

In this respect, systematic investigations are currently being carried out in a research project of the TU Chemnitz and BAM. The present work deals with the fundamental relationships between the welding parameters, the resulting cooling time, and the generated layer geometry. Furthermore, the resulting residual stresses are quantified and compared with respect to the application of different welding or heat input values.

2 Materials and method

2.1 WAAM welding system

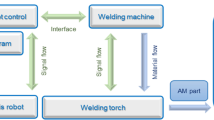
The robot-assisted welding system at Chemnitz Technical University consists of a 6-axis robot (KUKA KR 6) and the welding system (Fronius TransPuls Synergic, TPS 5000). Figure 1 shows the block diagram of the complete welding system. The robot controller, the central processing unit of the robot system, interprets the robot programs and moves the manipulator along the programmed paths. A robot interface serves as a link between the robot controller and the welding system.

Fig. 1
figure 1

Signal and material flow of the robot-based WAAM welding system; welding parameters (welding speed vT, volume per time V/t), which determine the layer width bS and height hS

Full size image

The commands for the welding system and the movement of the robot are located in the corresponding program line of the robot program, which are interpreted by the controller and sent to the robot (movement) and the welding system (welding commands). The modified short arc welding process CMT used for these investigations is adjusted not only by the welding speed (traverse speed of the robot) but also by the parameters wire feeding speed, arc correction, and dynamic factors. The path coordinates for additive manufacturing are basically derived from a CAD model using slicers and translated into executable welding programs using a specially developed compiler. The workflow for the manufacturer-independent generation of executable robot programs as well as the required software is developed at the TU Chemnitz.

2.2 Materials

In the project, a high-strength filler metal with a strength class of 790 MPa and a diameter of 1.2 mm specially developed for WAAM is used. Compared to conventional high-strength solid wire filler materials with a yield strength of at least 790 MPa, e.g., G 79 5 M21 Mn4Ni1.5CrMo (EN ISO 16834-A), the modification of the alloy composition for WAAM welding enables optimized deposition conditions. With regard to welding heat control, this ensures an extended processing window while at the same time the required mechanical properties are ensured. A 30-mm-thick plate of high-strength S690QL steel with a minimum yield strength of 690 MPa serves as substrate plate. In accordance with the recommendations of the steel manufacturers, this allows welding in a species-similar working range with regard to heat control for substrate and filler metal, and thus adequate bonding of the AM component. In this way, sufficient ductility in the transition area and, at the same time, sufficiently high strength of the substrate in conjunction with high stiffness ratios close to the application are realized when welding the components. Table 1 shows the chemical composition and mechanical properties of all test materials.

Table 1 Chemical composition (in wt.%, Fe balanced) and mechanical properties of the filler metal and the base metals investigated in the recommended ∆t8/5 range from 5 to 20 s [7]
Full size table

2.3 Welding experiment

The experiment was carried out with a robot-assisted welding unit consisting of a 6-axis KUKA KR 6 robot and a Fronius TransPuls Synergic TPS 5000 CMT welding system. In additive manufacturing, the robot moves the welding torch at a constant speed along a programmed path. The welding system feeds the wire-shaped filler material at a defined wire feed rate, cf. Figure 1. Wire feed and welding speed influence the cross-section of the applied weld bead [4]. In addition, these parameters are direct influencing variables on the heat input and also determine the flow and solidification behavior of the metallic melt due to the amount of heat introduced. In order to meet the requirements of process control, a systematic knowledge of these relationships in the intended parameter range is necessary. The focus of this paper is therefore on the systematic investigation of additive welding parameters in terms of heat control and their influence on cooling times and residual stresses. For this purpose, a total of nine geometrically identical open hollow cuboids were fabricated and investigated under systematic (full factorial) variation of interlayer temperature (100 °C, 200 °C, and 300 °C) and energy per unit length (200 kJ/m, 425 kJ/m, and 650 kJ/m) just by varying the welding speed (≈ 60 m/min, ≈ 40 m/min, and ≈ 20 m/min), cf. Figure 2a. Moreover, the influence of the component dimension was investigated by varying the length (120 mm and 190 mm), the height (35 mm and 50 mm), and the wall thickness (9 mm and 12 mm) of the hollow cuboid, cf. Figure 2b. The cooling times were determined during welding by means of temperature measurements with thermocouples (type-K). Because the focus of the investigation is on the effect of heat control, the other welding parameters were left as constant as possible, cf. Figure 2c, and only minimally adjusted to ensure a constant layer width. In order to ensure an unbiased measurement and analysis of the induced residual stresses, the additive manufacturing of the samples was carried out on unclamped substrate plates, which were only held in position by an appropriate fixture.

Fig. 2
figure 2

a Parameter matrix and build-up sequence for 9-mm-wide layer for WAAM experiments, b specification of the reference geometry (open hollow cuboid); CAD model (left), weld result (right), c welding parameters

Full size image

2.4 Thermo-physical welding and strength simulation with dilatometer, ultimate tensile strength, and hardness

For this investigation, the novel WAAM wire was comparatively analyzed. In order to be able to make detailed findings about the ultimate tensile strength as a function of the ∆t8/5 cooling time, tests were carried out to thermo-physically simulate a welding process. In the test series, the water jet cut and milled to size sheet specimens of the seamless long wall of the hollow cuboid (cf. Figure 3, right) were subjected to time–temperature cycles (free of clamping) obtained during the WAAM process using a dilatometer (Baehr Dilatometer DIL805), cf. Figure 3, left. After cooling to room temperature (RT) defined by the ∆t8/5 cooling time, the flat specimens were subjected to a tensile test (test speed 10 mm/min) in the same setup. These outcomes were correlated with WAAM process thermal cycles so that resulting mechanical-technological properties as well as thermophysical effects of the AM components can be analyzed and defined.

Fig. 3
figure 3

Schematic of the test sequence of the thermomechanical simulation (left) and specimen geometry of the sheet specimens used (right)

Full size image

During additive manufacturing, each layer is subjected to a complex heat treatment due to multiple cyclic heating and cooling similar to multilayer welding. In the process, the peak temperature of the considered layer gradually decreases due to layer wise build-up. Both single heat treatment and cyclic heating and cooling were performed in three test series, cf. Tables 3, 4, and 5. This analysis aims on determination of the effect of peak temperature (640–1200 °C), cooling time (∆t8/5 = 5 s to 45 s), and heat cycle (up to seven cycles) on the ultimate tensile strength of the materials.

In addition to the weld simulations with the dilatometer, real welded specimens were examined with respect to ultimate tensile strength and hardness. To investigate the influence of heat input on the ultimate tensile strength, microtensile specimens with a test cross-section of 2 × 2 mm2 were taken from the real WAAM specimens by water jet cutting (transverse and perpendicular to the welding direction) and subjected to a standard tensile test. Hardness measurement was performed in the prepared cross-section of the specimen geometries using the UCI method (HV1) with a spacing of 0.3 mm between indentations.

2.5 Residual stress analysis

The analysis of local residual stresses is performed by X-ray diffraction (XRD [20, 21]) longitudinal to the welding direction, since it is assumed that this is the direction with the maximum restraint condition and, thus, highest residual stresses. The sin2ψ method (Stresstech Xstress G3) is used for stress analysis at defined positions on the surface of the side wall of the hollow blocks (cf. Figures 6 and 7) to determine the influence of heat control and design. Table 2 shows the parameters used for residual stress analysis.

Table 2 Parameters for residual stress analysis using XRD (sin2ψ method)
Full size table

3 Results and discussion

3.1 Thermo-physical welding and strength simulation with dilatometer

The entire experiment consisted of three test series (S1–3), which differed in the number of temperature cycles, the set peak temperatures, and cooling rates. The interpass temperature Ti was 200 °C each time. In series S1, cf. Table 3, the weld metal was subjected to a single heat treatment consisting of heating to 1200 °C (heating rate: ≈ 200 K/s, holding time: 1 s) and cooling with different ∆t8/5 times between 5 and 45 s. Between 5 and 20 s (S1.1–1.3) the ultimate tensile strength of the test materials decreases with increasing cooling time ∆t8/5. From ∆t8/5 = 20 s, the strength of the material remains more or less constant up to 45 s. From that a wide ∆t8/5-time range without significant loss of ultimate tensile strength of such WAAM wires for additive manufacturing can be observed.

Table 3 Ultimate tensile strength of WAAM wire (G79) after single heating to 1200 °C and cooling with selected ∆t8/5 times in MPa, average of three experiments per value
Full size table

In the second test series (S2) of the thermo-physical strength simulation, the component was cyclically heated and cooled three, five, and seven times with continuously decreasing peak temperatures. From the point of view of additive manufacturing, the ultimate tensile strengths of the third, fifth, and seventh (last) layers were determined in this test series. The cooling time ∆t8/5 was kept constant at 20 s, see Table 4.

Table 4 Ultimate tensile strength of WAAM wire (G79) after repeated heating and cooling with constant ∆t8/5 time of 20 s, average of three experiments per value
Full size table

This second test series exhibits a decrease of the ultimate tensile strength with increasing number of temperature cycles. After seven cycles, the ultimate tensile strength was reduced by approx. 200 MPa, which is due to the heat treatment in connection with recrystallization and/or annealing processes of the microstructure, which contains a considerable share of martensite.

Finally, different ∆t8/5 cooling times were considered for the same number of heat treatments and peak temperatures. For this purpose, the cooling time of the second or third temperature cycle was varied, cf. Table 5. In the first and second experiments of this third series, the specimen was cooled in the last cycle with higher and lower ∆t8/5 times of 25 s and 12 s, respectively. In comparison to the first experiment of the second series (∆t8/5 = 20 s for the third cycle), a trend can be observed that the increase of the cooling time during the last cycle with a peak temperature of 850 °C reduces the ultimate tensile strength from 1277 MPa for ∆t8/5 = 12 s to 1185 MPa for ∆t8/5 = 25 s. Hence, it can be concluded that the properties of AM microstructure are significantly influenced by the heat control parameter or ∆t8/5 times of the last cycle or welded layer. In test no. S3.3, a slower cooling was performed for the second cycle (∆t8/5 = 25 s) and ∆t8/5 = 20 s for the third (last) cycle. As a result, a higher ultimate tensile strength of 1234 MPa exhibits compared to test S3.1, in which the slower cooling was performed for the last cycle and, also compared to test S1.3 (cf. Table 3), in which a single heating to 1200 °C with cooling time ∆t8/5 = 20 s led to an ultimate tensile strength of only 1160 MPa. In comparison to test no. S2.1 (three cycles of repeated heating and cooling with constant ∆t8/5 = 20 s), cf. Table 4, the ultimate tensile strength is at the same level. Thus, it can be assumed that the softening caused by welding with a higher ∆t8/5 time can be inhibited or restored by the additional application of a tempering layer.

Table 5 Ultimate tensile strength of WAAM wire (G79) after repeated heating and different ∆t8/5 cooling times in the second and third temperature cycles, average of three experiments per value
Full size table

3.2 Correlation between welding parameters, cooling time, hardness and tensile strength

In additive manufacturing, each layer undergoes a complex heat treatment consisting of multiple cyclic heating and cooling. In this paper, the last effective cooling time ∆t8/5 between 800 and 500 °C was chosen as a benchmark for the cooling rate. Particularly in the case of high-strength structural steels, this significantly influences the microstructural properties and, thus, the mechanical-technological properties of the generated component. Figure 4a shows the quadratic regression model of the determined ∆t8/5 times as a function of the factors heat input and interlayer temperature. The model quality is high with R2 = 98.6%. In the regression model, the effects of interlayer temperature and heat input are significant. The ∆t8/5 cooling time increases approximately linear with increasing heat input. Due to the low interaction between heat input and interlayer temperature, this linear increase can be observed at all interlayer temperatures. The effect of the interlayer temperature on the ∆t8/5 cooling time is smaller than that of the heat input. Thus, the energy per unit length has a major influence on the cooling behavior of the component and ∆t8/5 cooling time. Furthermore, due to the nearly constant heat dissipation in the relevant temperature range, the ∆t8/5 cooling time is only adjustable to a rather small extent by varying the interlayer temperature at constant heat input. Microstructural analyses and hardness measurements were carried out on microsections of the welded WAAM specimens, showing a fine-grained martensitic microstructure particularly in the area of the two to three top weld layers and a fine ferritic microstructure in the remaining cross-section, cf. Figure 4b.

Fig. 4
figure 4

a Contour plot of cooling time ∆t8/5 as a function of heat input E and interlayer temperature Ti (quadratic regression model, model quality R.2 = 98.6%); b SEM images of the microstructures for two regions of the wall cross section of WAAM specimen V5

Full size image

Figure 5a shows the distribution of hardness on the cross-section of a weld with central point parameters of the DoE (V5). In the area of the two to three top layers, the hardness is significantly higher than in the rest of the cross-section due to the high heat dissipation and the lack of annealing of overlying weld beads. The evaluation of the influence of the heat input, cf. Figure 5b, and interlayer temperature, cf. Figure 5c, on the average hardness is therefore carried out for two different zones in the AM specimen cross section: zone 1 at the top and zone 2 in the following center to bottom position. As heat input increases, the average hardness in zones 1 and 2 decreases, as does the difference between the two zones. The interlayer temperature shows no significant influence on the hardness, cf. Figure 5c. An average hardness of > 380 HV1 in the area of the top layers indicates a microstructure with critical behavior in terms of cold cracking. This behavior is in good agreement with the observations considering the correlation between welding parameters, cooling time ∆t8/5, hardness, and ultimate tensile strength as well as the results of the thermo-physical welding and forming simulation via dilatometer.

Fig. 5
figure 5

a Distribution of the hardness in a wall cross-section (V5, E = 425 kJ/m, Ti = 200 °C); effect diagrams on average hardness of both zones 1 and 2 for b heat input E (standard deviation due to all corresponding interpass temperatures) and c interpass temperature Ti (standard deviation due to all corresponding heat inputs)

Full size image

In addition to the thermo-physical simulation of the welding process with the dilatometer, tensile tests were carried out using micro-tensile specimens with a (2 × 2) mm2 test cross-section extracted from the actual WAAM specimens (transverse and perpendicular to the welding direction), welded with the parameters V4–6 at constant interpass temperature Ti = 200 °C, and varied heat input. Table 6 shows the ultimate tensile strengths determined in accordance with standard specifications and manufacturer’s data for the three WAAM specimens and heat input values, respectively. The data exhibits no significant influence of the heat input on the ultimate tensile strength of the AM specimens. However, it is noticeable that the ultimate tensile strength values of the actual WAAM specimens are lower than the values determined via dilatometer experiments, cf. Tables 3, 4, and 5. The best agreement exhibits for the dilatometer test S2.3, cf. Table 4, in which a sevenfold heating and cooling was applied with continuously decreasing peak temperatures from 1200 to 640 °C. Nevertheless, the difference is still over approx. 100 MPa. Based on these deviations, it can be assumed that there are certain deviations between the thermo-physical simulation and the actual layer-by-layer built-up material due to the rather anisotropic and heterogeneous microstructure. In contrast to the simulation, the real weld specimens underwent at least 5 further temperature cycles between 640 and 400 °C which contributed to the annealing, relaxation, and softening of the specimens. However, by using a close-to-reality heat treatment or by imposing the actual welding heat cycle, it is possible to achieve values that are quite comparable. It remains to be tested how this can also be transferred to other mechanical properties, such as yield strength or ductility.

Table 6 Ultimate tensile strength of actual WAAM specimens taken from taken from straight walls vs. heat input at interlayer temperature of Ti = 200 °C (average of seven tensile tests per value)
Full size table

3.3 Residual stress analysis

Figure 6 shows the analyzed longitudinal residual stress distribution σrsx(x,y) of the surface depicted by the marked area exemplarily for the side wall of a WAAM specimen, which was welded with the center point parameters (test no. V5), cf. Figure 2. The contour plot includes 110 analyzed points. The maximum value of the residual stresses in the welding direction is in the range of approx. 65% of the nominal yield strength of the applied filler metal, which may be critical in terms cracking, component performance, for instance, considering fatigue behavior. The residual stress maxima are located in the upper half in the direction of the center of the hollow cubic walls in each case of all WAAM specimens. Remarkably, the maximum residual stresses in welding direction do not occur at the top of side wall but two to three layers below This is assumably the result of high transformation residual stresses due to martensitic transformation, located at the top layers that were not heated and tempered several times like the layers underneath.

Fig. 6
figure 6

Longitudinal residual stress distribution σrsx(x,y) of the surface of the WAAM specimen side wall (test no. V5)

Full size image

For the statistical evaluation of the influence of the heat control on the welding-induced stresses, average values were determined from the longitudinal residual stresses of the upper left quadrant, in which the highest stresses occurred at all specimens. Thus, Fig. 7 shows a contour plot of the regression model derived from these average values as a function of heat input and interlayer temperature. The linear regression model has a rather high model quality of R2 = 93% with a significant effect of the heat input. It can be observed that the residual stress level decreases with increasing energy per unit length. The effect of interlayer temperature is not significant in the model within this parameter matrix. Also, no significant interaction could be observed. In comparison with the analysis of the ∆ t8/5 cooling times, a correlation between the cooling times and residual stress level is observable. It remains to be investigated in the future to which extent these observations regarding the residual stress levels are also applicable to the specimen volume and other specimen geometries, in particular, in connection with different heat dissipation conditions and the associated interaction with interlayer temperature and layer structure.

Fig. 7
figure 7

Contour plot of the linear regression model of average longitudinal residual stresses σrsx,avg of the area with max. residual stresses of the WAAM specimen side wall as function of heat input E and interpass temperature Ti (R.2 = 0.93%)

Full size image

As a first test considering the aforementioned design effects, the specimen dimensions were varied by means of increasing the specimen length (190 mm), height (50 mm), and the wall thickness (12 mm). All other welding parameters and the welding regime were left constant according to V5. To generate the 3 mm wider wall, only the distance between the 2 parallel tool paths was increased and the number of layers was adjusted. Figure 8 shows the analyzed longitudinal residual stress distribution σrsx(x,y) of the larger-sized WAAM specimen. It is observable that the different heat dissipation and restraint conditions considerably influence the level and the distribution of the residual stresses. For instance, the effect of transformation-induced residual stresses as seen in Fig. 6, including somewhat lower stresses at the top layer, seems to not occur here, which may be the result of higher number of weld beads per layer and larger cross section area of the wall. However, it is also conceivable that the higher shrinkage force due to the larger specimen dimensions can no longer be compensated to the same extent by this local effect of the transformation residual stress as was still the case with the smaller specimen dimension. Furthermore, the maximum residual stresses of approx. 350 MPa are somewhat lower than those of the smaller specimen. These are also more in the direction of the center of the sample. It is evident that almost the entire lower third of the sample exhibits longitudinal residual stresses in the compression range and somewhat higher stress gradients. This is not the case with the smaller WAAM specimen. It can be assumed that the larger dimensions as a whole are more capable of deforming the substrate plate, which has not been changed in thickness, due to the higher shrinkage forces, whereby bending stresses build up in the longitudinal direction of the entire sample and the neutral axis regarding the bending moment is considerably higher, i.e., within the WAAM specimen walls. In the smaller WAAM specimen, on the other hand, the neutral axis is apparently still in the height of the substrate plate. A final evaluation in this regard can therefore only be made by further variations of the heat control and WAAM component dimensions, which will be reserved for future experimental investigations and residual stress analyses, also in the component bulk and substrate plate.

Fig. 8
figure 8

Longitudinal residual stress distribution σrsx(x,y) of the surface of the side wall of the WAAM specimen design variation with increased dimensions (welding parameters and heat control according to test no. V5)

Full size image

4 Conclusion

This study deals with the influence of WAAM thermal cycles in thermo-physical simulations of test samples from special high-strength steel WAAM wire on the ultimate tensile strength and, in comparison, the effect of interpass temperature and heat input as well as specimen design on the cooling time, hardness, and residual stresses of WAAM processed component specimens. The following conclusions can be drawn from the results:

  1. 1.

    The investigated high-strength solid wire, especially designed for WAAM, can be processed over a wide range of ∆t8/5 cooling time without pronounced decrease in ultimate tensile strength.

  2. 2.

    The welding thermal cyclic due to layer-wise AM component build-up affects the strength properties of already-deposited material of the layers below. Especially, reduced mechanical-technological properties, e.g., as a result of improper welding parameters or to low cooling rates, within the last layers, may be compensated by additional welding layers and the resulting tempering effects.

  3. 3.

    Thermophysical simulation can reproduce such phenomena and make them analyzable as well as tensile strength comparable to actual WAAM specimens when realistic thermal cycling is applied.

  4. 4.

    WAAM components with similar design are producible using different heat control parameters by adapting the layer-wise build-up strategy. Increased heat input causes significantly higher cooling times. However, no significant effect of heat input on ultimate tensile strength was found for actual WAAM specimens. Interpass temperature exhibits a less significant, smaller effect on cooling time within the test setup and parameter range of this study and, thus, should be suitable for optimizing process time and welding stresses.

  5. 5.

    Microstructural and hardness analyses exhibited different microstructure for the 2–3 top layers and the rest of the WAAM specimen cross sections, with a fine-grained martensitic and harder microstructure (top) and a fine ferritic microstructure (rest), respectively. The hardness and the difference (between top and rest of the specimen) decrease significantly with lower heat input.

  6. 6.

    Longitudinal residual stresses of all welded WAAM specimens have a maximum at the side wall in the upper third area toward the specimen center up to over 400 MPa, which is 65% of the nominal material strength. Residual stress levels are reduced significantly for higher heat input values applied during WAAM. Interpass temperature exhibits no significant effect within the analyzed parameter matrix.

  7. 7.

    First tests with variation of the specimen design by magnification of height, length, and wall thickness showed considerable effects on the distribution of the longitudinal residual stresses on the side wall, e.g., compressive stresses in almost the entire lower third of the side wall.

A final clarification of the effects and interactions of heat control and design require further investigations and more intense analysis of local effects due to shrinkage and transformation caused by high local temperature gradients during cooling and investigations of residual stress state in the bulk. Further investigations to determine the influence of heat input and component design on mechanical-technological properties such as yield strength, toughness, as well as dynamic behavior are still pending. The findings are to be used to derive recommendations for processing of stress-optimized production and to develop a practicable cold cracking test for industrial users, especially SMEs, in processing of high-strength steels using WAAM.