1 Introduction

Additive manufacturing (AM) has gained tremendous momentum over the last decade and is emerging as a key technology of the future. At present, conventional manufacturing processes are being replaced with AM for its various applications producing high-strength components [1]. AM has the potential to reduce carbon footprint by optimizing design and reducing the material waste. Furthermore, several processing steps can be avoided by direct manufacturing of near-net-shape components [2]. Today, lightweight design is key to energy and resource efficiency [3]. To meet the growing demand in lightweight requirements, the high-strength steels are increasingly used in the modern steel construction, e.g., in building, plant engineering, and crane construction. Reducing thickness allows for significant weight reductions and low processing costs when employing fine-grain structural steels with yield strengths higher than 690 MPa. For example, about 78% of the weight can be reduced by replacing S235J2 with S960QL [4, 5]. This often results in intricate components and structures. Thus, in numerous areas of steel construction, the use of high-strength, fine-grained structural steels has a significant potential for weight optimization. In recent years, there has been a substantial development in wire arc additive manufacturing (WAAM) based on gas metal arc welding (GMAW). WAAM is characterized by high deposition rates, capacity to manufacture larger geometries, low equipment cost, high material utilization, and resource efficiency [6, 7]. Multiple studies show fundamental applicability for large, structured components with welding robots [8]. In 2020, the largest propeller was built using WAAM technology and was successfully tested under real conditions [9].

A wide-ranging overview of the research status is given in [8, 10, 11]. Essential attributes for an AM component are the resulting mechanical properties of the final product. These properties depend substantially on the thermal history of the material and relate with the microstructure, toughness, and the material [1, 12, 13]. For additive manufacturing, the knowledge of multilayer welding can be adapted with a few modifications. WAAM and joint welding differ mainly in heat dissipation and the associated microstructural phenomena [8]. Plangger et al. and Yildiz et al. have shown that the mechanical properties of high-strength steels are related to the heat input [1, 14]. In addition to the heat input, the path planning and buildup strategy have a significant influence on the heat control and thus on the residual stresses and distortion [15]. Furthermore, the tensile residual stresses in WAAM components can reach the yield strength [16]. Welding experiments and accompanying numerical simulations demonstrated the high dependence of the temperature distribution and the resulting component geometry on the manufacturing parameters [17, 18]. These investigations confirmed that sufficient heat dissipation in the WAAM process poses great challenges for the special microstructure of high-strength steels. The requisite cooling rates to achieve the required microstructures, low production-related stresses, and mechanical properties (e.g., ∆t8/5 time for S690: roughly 5 s to 20 s) can only be attained by restraining component temperatures and heat input. To achieve this, the build-up strategy and heat control (energy per unit length or heat input, preheating, and interpass temperature) must be adjusted to introduce the least amount of heat throughout production [18, 19]. Residual stresses in WAAM components are the subject of research; however, there is limited knowledge on residual stress development during processing of high-strength steels. Furthermore, the residual stress level of components is influenced locally and globally by the degree of restraint of the structure [20] and solid phase transformations of the material [21] during cooling. For high-strength welded joints, stress optimization by means of adapted heat control concepts has already been the subject of research. Studies on their transferability to generative manufacturing steps for high-strength steels are still lacking [22]. A wide industrial application is limited by the lack of quantitative data on manufacturing-related stresses and component safety. This applies in particular to the process- and material-related influences, the constructive shrinkage restraints associated with the formation of high tensile residual stresses, and the corresponding risk of cold cracking. This requires profound knowledge of the complex interactions between the welding process, cooling conditions, heat input during production, and the consequent metallurgical processes in order to avoid excessive production-related stresses and the development of cracks during production or premature component failure [22].

Therefore, systematic investigations are carried out in a research project of TU Chemnitz and BAM (FOSTA P1380/IGF 21,162 BG). The focus of this study is the analysis of the influences of interpass temperature and heat input on cooling time, macrostructure, hardness, residual stresses, and the influence of the component design on the residual stresses.

2 Materials and method

2.1 WAAM welding system

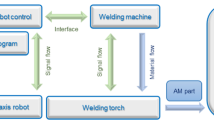
The 6-axis robot (KUKA KR 6) and weld system (Fronius TPS 5000) form the robot-assisted welding system at TU Chemnitz. The block diagram of the entire welding system is shown in Fig. 1. For AM, the path coordinates are essentially derived from a CAD model using slicers and interpreted into executable welding programs. The robot controller interprets the programmed lines and controls the traversing movement and the welding machine. In addition to the welding speed (robot traverse speed), parameters such as wire feeding speed, arc correction, and dynamic influences are employed to regulate the modified short-arc welding process CMT for these investigations.

Fig. 1
figure 1

Block diagram for the signal and material flow of the robot-based WAAM welding system; welding parameters (welding speed vT, volume flow per time V/t), which determine the layer width bS and height hS [23]

Full size image

2.2 Materials

In this investigation, a high-strength filler metal with a diameter of 1.2 mm specially developed for WAAM is used. Compared to conventional high-strength solid wire filler materials with a yield strength of at least 790 MPa, e.g., G 79 5 M21 Mn4Ni1.5CrMo (EN ISO 16834-A), the modification of the alloy composition for WAAM welding enables optimized deposition conditions. With regard to welding heat control, an extended processing window is achieved while at the same time ensuring the required mechanical properties. As substrate, a 30 mm-thick S690QL high-strength steel plate with a minimum yield strength of 690 MPa is used. This permits welding in a similar operating range with respect to heat control of the substrate and filler metal and hence appropriate bonding of the AM component. When the components are welded together, sufficient ductility in the transition area and, at the same time, appropriate substrate strength in conjunction with high stiffness ratios near to the application are realized. The mechanical properties and chemical composition of each test material are shown in Table 1.

Table 1  Chemical composition (in wt.%, Fe balanced) and mechanical properties of the filler metal and the base metals investigated in the recommended ∆t8/5 range from 5 to 20 s [9]
Full size table

2.3 Welding experiment

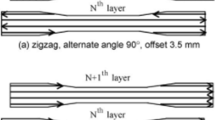
The robot moves the welding torch along a programmed path at a constant speed. The filler metal is fed through the welding system at a defined wire feed speed or a defined volume flow, cf. Fig. 1. The cross-section of the applied weld bead is significantly influenced by the wire feed and welding speed [1]. These parameters have a direct influence on the heat input and also determine the flow and solidification behavior of the weld pool through the amount of heat introduced. The systematic knowledge of these interrelationships in the intended parameter range is of particular importance for the design of the process control. In addition to knowledge about the influence of the welding parameters, knowledge about the influences of the design and the build-up strategy on the manufacturing-related stresses is of major importance. Therefore, the focus of this study is on the systematic investigation of welding parameters and geometric dimensions of component specimens and their influence on cooling times, hardness, and residual stresses. For this purpose, nine geometrically similar open hollow cuboids were fabricated and investigated under systematic (full factorial) variation of interpass temperature (100 °C, 200 °C, and 300 °C) and energy per unit length (200 kJ/m, 425 kJ/m, and 650 kJ/m), cf. Fig. 2a. In addition, the influence of the component design was investigated by varying the length (50 mm, 120 mm, and 190 mm), the height (20 mm, 35 mm, and 50 mm), and the thickness (6 mm, 9 mm, and 12 mm) on eight open hollow cuboids, cf. Fig. 3. The cooling times were determined during welding by temperature measurements with thermocouples (type-K). The other welding parameters were kept constant as far as possible and only minimally adjusted to ensure a constant layer width, cf. Fig. 2c.

Fig. 2
figure 2

a Welding parameters and build-up strategy for a 9 mm thick wall for WAAM experiments, b specification of the reference geometry (open hollow cuboid); CAD model and weld result, c welding parameters [23]

Full size image
Fig. 3
figure 3

a Parameter matrix of the design variation and b CAD model of the different geometries

Full size image

2.4 Component design

In order to investigate the influence of the component design on the residual stresses, the geometric dimensions of the open hollow cuboid were systematically varied equidistantly, as it is shown in Fig. 3a, starting from the central point test V5 of the welding experiments (cf. Fig. 2a). The specimen length was reduced by 70 to 50 mm (square) and increased by 70 to 190 mm. Starting from the central point V5 with 9 mm and two weld beads, the width of 6 mm was realized with one weld bead and 12 mm with 3 weld beads. The height was set to 20 mm and 50 mm. In all experiments, the welding parameters of the central point V5 (energy per unit length E = 425 kJ/m and interpass temperature Ti = 200 °C) were used. Fig. 3b shows the renderings of the component geometries.

2.5 Residual stress analysis

X-ray diffraction (XRD) was used to analyze the local residual stresses [24, 25] along the welding direction, as this is the direction with the maximum degree of restraint. The sin2ψ method is used for stress analysis at defined positions on the surface of the sidewall of the hollow cuboids (cf. Figs. 6–9) to determine the influence of heat control and design. Table 2 shows the parameters used for the residual stress analysis.

Table 2 Parameters for residual stress analysis using XRD (sin2ψ method)
Full size table

2.6 Preparation of the macrosections

Samples for the metallographic investigations were cut from the manufactured AM wall structures. These were embedded, ground, and polished to 1 μm and etched for 10 to 15 s with 2% Nital for the optical macrographs and hardness measurements.

2.7 Hardness measurements

The analyses of the hardness distribution in the AM structures were carried out by means of surface hardness measurements on cross-section specimens with the UCI (ultrasonic contact impedance) method (ISO 50159–1 [26]). The hardness indents were performed out on ground, polished, and etched samples. The hardness was determined with a hardness scanner UT-200 from BAQ GmbH. The loading force was 9.807 N (HV 1), whereby the indentations were set with a distance to each other of Δs = 0.3 mm and with a duration time of 0.5 s.

3 Results and discussion

3.1 Macrostructure and hardness

All investigations were performed on defect-free specimens without defects, which may influence the integrity or residual stress state of the components, e.g., cracks or lack of fusion. As a first result, Fig. 4a shows the interaction diagram of the ∆t8/5 cooling time and the interpass temperature as a function of the heat input E, as also shown as a result in [23, 27]. For the cooling time measurement, the last effective ∆t8/5 cooling time with a peak temperature above 800 °C was considered during WAAM of the specimen, cf. Fig. 2b. The peak temperature significantly influences the microstructural properties and thus the mechanical-technological properties of the manufactured component, especially in the case of the special microstructure high-strength structural steels. The interpass temperature significantly influences the cooling times. As the interpass temperature increases and the temperature gradient decreases, the cooling times increase. The heat input E shows a significant effect on the cooling time. Increasing heat input increases the cooling time significant [23].

Fig. 4
figure 4

a Interaction diagram of Δt8/5 cooling time as a function of the interpass temperature Ti and b macrographs of the cross-sections of WAAM wall (Nital echting) with heat input E of 200 kJ/m and 650 kJ/m from different areas

Full size image

Figure 4b shows macrographs of the cross sections with heat input E = 200 kJ/m and E = 650 kJ/m, in the area of the top layer and in the center of the wall. The different build-up strategies and the heat-affected zones as well as the influence of the different heat inputs can be observed. A low heat input with a short cooling time provides a narrow heat-affected zone and a columnar dendritic solidification. A high heat input provides a wide heat-affected zone and a coarse columnar structure.

Hardness maps for the analysis of the hardness in the cross sections were made on macrosections. The hardness measurement was performed according to the UCI method and Vickers HV1. The distance between indentations corresponded to Δs = 0.3 mm. The hardness maps in Fig. 5 show the effect of build-up strategy and heat input on the hardness in the cross-section. Specimen V1, with an interpass temperature Ti = 100 °C and a heat input E = 200 kJ/m, shows an inhomogeneous but structured topology of the hardness. In accordance with the build-up strategy, low heat input, and the associated short cooling time, the areas of the heat-affected zone with reduced hardness are narrow. The heat input was low enough that the layers are only partially tempered by the subsequent layers, and the hardness is lower (fine-ferritic microstructure) than in the area of the top layer. Here, a high hardness can be analyzed due to the high cooling rate and the lack of tempering (fine-grained martensitic microstructure). Likewise, there is a clear gradient between the top layer and the rest of the cross-section. Specimen V5 shows a similar hardness map. Corresponding to the buildup strategy, the hardness in the heat-affected zones is formed and reduced. The hardness in the cross section is lower due to the increased heat input and cooling time (cf. Fig. 4a). In the area of the top layer, the hardness is significantly higher, but lower than V1. The hardness map of V9 indicates even lower hardness values than V5 and V1 due to the higher heat input and the associated higher cooling time. Similarly, the gradient between the top layer and the cross section is also reduced. However, the area of increased hardness in cross section V9 is significantly larger compared to V5 and V1 due to the cooling conditions.

Fig. 5
figure 5

Vickers hardness (UCI) in a wall cross-section (V1, V5, and V9)

Full size image

3.2 Influence of the process parameter on the residual stresses

The residual stresses in AM components can be significantly affected by the solid phase transformation of the material as a result of high cooling rates. This phenomenon is known from joint welding, where solid phase transformations can lead to a reduction of the local [21] or even global [28] residual stress level as a result of locally or globally restraint volume expansion during phase transformation. Comparing with [27], Fig. 6 shows the distribution of the analyzed longitudinal residual stresses σrsx(x,z) (110 measurement points) on the sidewall of the marked surface on a central point specimen. Note that due to a number of repeating central point test almost identical topology of residual stress maps were observed, as can be seen compared to specimens with same test parameter/conditions in [27], indicating a high level of reproducibility of the manufacturing process. The longitudinal residual stresses reach a maximum value of 65% of the nominal yield strength of the filler metal used, which can be critical for crack formation and component behavior. As in the previous specimen, a reduction of residual stresses in the area of the top layer is shown due to a solid phase transformation and the associated volume expansion.

Fig. 6
figure 6

Distribution of the longitudinal residual stress σrsx(x,z) on the surface of the WAAM specimen wall (test no. V5)

Full size image

Figure 7a-d show the influence of heat input and interpass temperature on the residual stresses. The longitudinal residual stress σrsx(x,z) on the sidewall of the marked area of the WAAM specimens was analyzed. A minimum of 99 measurement points were analyzed per specimen. In the white area of the diagrams of specimens V1, V3, and V7, the measured values could not be evaluated due to geometric inaccessibility or coarse-grained microstructure. The heat input E1 causes higher longitudinal residual stresses than E3. Low cooling times cause the layers to be partially tempered, and the residual stresses cannot be relieved. The interlayer temperature Ti = 300 °C results in a lower gradient of residual stresses in the component due to the lower cooling rates, compared to Ti = 100 °C. The residual stresses are more homogeneous over the component height. However, this effect is not significant. The lowest residual stresses could be achieved with the high heat input and high interpass temperature. The analysis of the measured values of all specimens shows that the effect of the interpass temperature is not significant, while the heat input has a significant effect on the longitudinal residual stress. This offers the possibility to optimize the manufacturing process via the interpass temperature with regard to residual stresses [27].

Fig. 7
figure 7

Distribution of the longitudinal residual stress σrsx(x,z) on the surface of the WAAM specimen wall (test no. V1, V3, V7, and V9) with different heat input E and interpass temperature Ti

Full size image

3.3 Influence of the design on the residual stresses

In order to analyze the influence of the design on the residual stresses, the geometric dimensions of length, height, and thickness were systematically varied. Figure 8 shows the analyzed longitudinal residual stress distribution σrsx(x,y) of the WAAM specimen with increased dimensions in all 3 design factors. The distribution and level of residual stresses are clearly influenced by the changed heat dissipation and restraint conditions. The effect of the lower residual stress of the upper weld layers due to the solid phase transformation shown in Fig. 6 does not present up here, which could be due to the changed number of weld beads per layer and thus the changed heat dissipation. Likewise, the larger specimen dimensions could cause higher shrinkage forces, which can no longer be compensated to the same extent by the local effect of the transformation residual stress as was still the case with the smaller specimen dimensions. In addition, the maximum residual stresses of approx. 350 MPa are somewhat lower than with the smaller structure, which may be due to the higher wall thickness. In the lower third of the specimens, almost the entire specimen has a longitudinal compressive residual stress. This is not the case for WAAM specimens with smaller dimensions, cf. Fig. 6. Therefore, it can be assumed that the substrate plate is subjected to higher shrinkage forces due to the larger dimensions, which causes higher bending stresses to build up in the specimen.

Fig. 8
figure 8

Distribution of the longitudinal residual stress σrsx(x,z) on the surface of the WAAM specimen wall; design variation with increased dimensions (welding parameters and heat control according to test no. V5) [27]

Full size image

Figure 9 shows, analogous to Fig. 8, the longitudinal residual stresses σrsx(x,z) of the WAAM specimens with the smallest geometric dimensions. In the middle area of the wall, near the substrate plate, higher residual stresses are observed than in the central point specimen. The residual stress level is influenced to higher residual stresses due to the smaller geometric dimensions by the shrinkage restraint of the substrate plate. In the area of the top layer, the residual stresses are influenced analogously to the central point by the martensitic transformation due to high cooling rates to lower residual stresses, cf. Fig. 6.

Fig. 9
figure 9

Longitudinal residual stress distribution σrsx(x,z) of the surface of the side wall of the WAAM specimen design variation with reduced dimensions (welding parameters and heat control according to test no. V5)

Full size image

For the statistical evaluation of the influence of the component design on the residual stresses, average values were determined from the longitudinal residual stresses of the analyzed surfaces. Figure 10 shows the contour plots of the linear regression model derived from the average values as a function of height h and length l (Fig. 10a, t = 12 mm) as well as height h and thickness t (Fig. 10b, l = 190 mm). The model quality of the linear regression model is R2 = 85%. It can be observed that the residual stress level in the investigated parameter range is not significantly influenced by the length and the thickness, likewise no interaction between the parameters can be identified. A variation of the thickness influences the cooling times and causes a solid phase transformation at a low thickness (cf. Fig. 6), which locally influences the residual stress in the area of the top layer (cf. Fig. 9). The height of the specimen significantly influences the residual stress level, cf. Fig. 10. A low height is associated with a high residual stress. The stiffness of the substrate plate restraints shrinkage in the area of the bonding and causes an increase in residual stresses. With increasing height, the additional welded layers cause tempering of the subjacent layers and cause a decrease in residual stress due to the shrinkage forces. Further tests should analyze the influence of the component design on the residual stresses. The complexity of the components will be increased by means of transverse and longitudinal stiffeners. Furthermore, the influence of the thickness of the substrate plate on the residual stresses will be investigated.

Fig. 10
figure 10

Contour plot of the linear regression model of the average longitudinal residual stresses σrsx,avg of the WAAM specimen sidewall as function of a height h and length l and b height h and thickness t

Full size image

4 Conclusion

This study focuses on the influence of interpass temperature and heat input on cooling time, hardness, and residual stresses, as well as the influence of the component design on the residual stresses of component specimens which have been produced using WAAM. The following conclusions can be drawn from the results:

  1. 1.

    Adaptation of the build-up strategy enables the production of WAAM components with similar design. The cooling times are significantly influenced by the heat input. A high heat input leads to low cooling rates. The interpass temperature shows a significant but rather small influence on the cooling time in the parameter range investigated in this study and should therefore be used to optimize process time and welding stresses.

  2. 2.

    The heat input has a significant influence on the hardness. The top 2–3 layers show a different microstructure in the analysis of microstructure and hardness compared to the rest of the WAAM cross-sections, with a fine-grained martensitic and harder microstructure (top) or a fine-ferritic microstructure (rest). The hardness and gradient (between the top and the rest of the specimen) decrease significantly with high heat input.

  3. 3.

    The heat input has a significant influence on the residual stresses. High heat input leads to lower longitudinal residual stresses within the investigated parameter range. The interpass temperature shows a non-significant effect on the longitudinal residual stresses.

  4. 4.

    The variation of height, length, and thickness of the specimen design showed significant effects on the distribution and magnitude of the longitudinal residual stresses of the sidewall. The effect of length and thickness is not significant, while height has a significant effect. With increasing height, the average residual stresses decrease. This is due to the local restraint intensity of the substrate plate. Therefore, the local and global degree of restraint of the structure should be considered during design and manufacturing.

The findings are to be used to derive recommendations for processing of stress-optimized production and to develop a practicable cold cracking test for industrial users, especially SMEs, in processing of high-strength steels using WAAM. It should be intended in further investigations to clarify the effects and interactions of heat control and design in more detailed analysis by means of focusing local effects due to shrinkage and transformation caused by high local temperature gradients during cooling and due to additional residual stress analyses in the bulk.