1 Introduction

Increasingly, civil engineering, mechanical engineering and the offshore industry are seeking to optimize structural design in order to reduce material consumption and construction costs. The operationally safe and economical design of steel structures subject to cyclic loading is a central challenge in this context. For the fatigue strength of welded steel structures, the local loading of the fatigue-critical locations is of decisive importance. The fatigue strength and thus the durability can be increased by post-treatment methods. As confirmed by numerous studies [1,2,3,4,5,6,7,8,9,10], high-frequency mechanical impact (HFMI) post-treatment in particular has proven to be a user-friendly and effective method for increasing the fatigue strength of welded details. The strength-increasing influence of HFMI treatment on welded joints was derived by comparing test data of as-welded (AW) and HFMI-treated welds. Results of these studies have been commonly accepted and incorporated into recommendations and guidelines [11, 12]. However, the effectiveness of HFMI treatment under real service loading is currently still questioned. Investigations [13,14,15] confirm that residual compressive stresses induced by the HFMI can relax due to cyclic loading and high peak stresses as part of the service load and thus lose their initially beneficial influence on the fatigue behaviour of welded steel structures. Recent studies show that high peak stresses of a variable amplitude loading (VAL) reduce the induced compressive residual stresses and thus might decrease the effectiveness of the HFMI treatment [16,17,18,19,20]. However, the beneficial effect of the strain-hardened surface layer, as well as the reduction of notch stresses due to the HFMI treatment, is not affected. These studies focus mostly on the influence of high mean stresses, high peak stresses as single incidents or the influence of randomly distributed VAL on the fatigue strength of HFMI-treated notch details. For untreated welded joints, first studies on the sequence effect were carried out in [21]. From the comparative fatigue tests carried out in [21], it became clear that there were differences in fatigue life when the same tests were performed once with blocked and once with random loading sequence. These results are in accordance with the literature study [22], showing that due to random loading, lower fatigue life is to be expected compared to blocked loading sequence. However, there are no studies available for HFMI-treated welds that focus on sequence effects for discrete load spectra. Previous studies have focused on the sequence effect of individual overloads within a constant amplitude load or the influence of random service loading on the fatigue strength of HFMI-treated welds. For this purpose, investigations on welded and HFMI-treated specimens under service load were performed. The aim of this study was to determine the sequence effect of as-welded (AW) and HFMI-treated transverse attachments under randomly distributed and blocked VAL with linear spectrum. In order to analyse the influence of local stresses on the residual stress condition and strain hardening, extensive X-ray diffraction measurements and macro-hardness analyses are carried out in addition to fatigue tests. The presented results are part of a more comprehensive research project in which the sequence effect of different load spectra on HFMI-treated and welded transverse attachments of different steel grades has been analysed [23]. First results were published in [24].

1.1 Fatigue strength of HFMI-treated welded joints under CA and VA loading

The potential for increasing the fatigue strength of welded joints through HFMI has already been demonstrated in numerous studies [1,2,3,4,5, 25]. As already mentioned in [24], design proposals [11, 12] and quality assurance guidelines [26] for HFMI-treated welded steel structures have been developed on the basis of these studies. One of the central issues of the HFMI recommendations [12] is the increase of the fatigue strength as a function of the base material yield strength. According to [12] the fatigue class (FAT) of welded steel joints with a minimum yield strength of 355 MPa can be raised by five classes, when HFMI-treatment is applied. In addition, the FAT can be further increased in case the yield strength of the base material is raised by 200 MPa. The slope of the S/N-curves given in [12] is defined to be m = 5. The influence of the stress ratio on the fatigue strength of HFMI-treated welds is considered by a further modification of the FAT-class. The strength-reducing influence of stress ratios greater than R > 0.15 is defined as reduction in terms of fatigue strength improvement. For the fatigue assessment of HFMI-treated welded steel joints under service loading with variable amplitudes, the IIW recommendation [12] refers to the equivalent stress range formula known for AW joints. The formula for calculating Δσeq is related to the rainflow counting method and the modified Palmgren–Miner’s rule:

$$\Delta {\sigma }_{eq}={\left(\frac{1}{D}\cdot \frac{\sum {\Delta \sigma }_{i}^{m}\cdot {N}_{i}+{\Delta \sigma }_{k}^{\left(m-{m}^{^{\prime}}\right)}\cdot \sum {\Delta \sigma }_{j}^{{m}^{^{\prime}}}\cdot {N}_{j}}{\sum {N}_{i}+\sum {N}_{j}}\right)}^{{~}^{1}\!\left/ \!{~}_{m}\right.}$$
(1)

According to [27] the slopes m and m′ of the corresponding S–N curves are set to m = 5 and m’ = 9 instead of m = 3 and m’ = 5 for the AW state. The fact that the allowable damage sum Dal = 0.5 is currently still under discussion was already mentioned in [24].

A good approximation to the test data was achieved considering an allowable damage sum of Dal = 0.5 in [18] whereas the fatigue test data in [16] yielded to damage sums ranging from D = 0.3 to D = 0.5. The assumption of an allowable damage sum of D = 0.5 to D = 1.0 respecting the FAT class for HFMI, however, may lead to a conservative estimation of the fatigue strength of HFMI-treated notch details [17]. Since the fatigue strength of welded details depends on a wide range of variables, the results of the studies under VAL should be considered in a more differentiated way.

To verify the positive effect of HFMI treatment on the fatigue strength of welded structures, a reliable and realistic estimation of the influences from service loads, notch geometry and surface condition is necessary. Currently, the number of studies on the influence of VAL on the fatigue strength of HFMI-treated steel joints is continuously increasing, and more and more information is being obtained on the influence of individual parameters such as mean stress, high peak stresses and notch effects. In this paper, another parameter is analysed — the influence of load sequence on the fatigue behaviour of as-welded and HFMI-treated transverse joints under variable loading with linear spectrum.

2 Experimental work

2.1 Load sequences and testing procedure

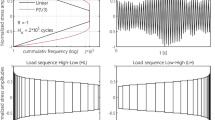
The influence of service loads on the fatigue strength of AW and HFMI-treated joints was studied by performing uniaxial fatigue tests with constant and variable amplitude loading on transverse attachments in the AW and HFMI-treated condition. The VAL tests were performed with different load sequences — random, high-low and low–high — of a linear spectrum. The different sequences as well as the spectrum type are qualitatively explained in Fig. 1. The spectrum length used for the VAL fatigue test is H0,exp = 200,000 load-cycles with an irregularity factor of I = 0.99 and a stress range of R =  − 1. This shortened spectrum length is obtained by applying a 13% omission to the cumulative frequency distribution of a standardised linear spectrum with an original length of H0 = 1.23∙106 load-cycles. The generation of the random and block loading sequences is based on a similar approach outlined in [24]. The applied sequence of the high-low and low–high block loading spectra should have the same length and the same amplitudes as a fictitious performed fatigue test of random loading on this load level. For more details, see [24]. The cumulative distribution of the linear spectrum is described by Eq. (2) with a shape parameter ν = 1.

$$H=H_o\cdot\exp\left(-\ln\left(H_0\right)\cdot\left(\frac{\sigma_a}{{\widetilde\sigma}_a}\right)^\nu\right)$$
(2)
Fig. 1
figure 1

Studied sequences and stress spectrum [23]

Full size image

The fatigue tests were performed under alternating uniaxial loading at the Institute of Joining and Welding of the University of Braunschweig and at the Laboratory for Steel and Lightweight Structures of the University of Applied Sciences Munich. Constant amplitude loading (CAL) fatigue tests were performed on both servo-hydraulic and resonance testing machines. VAL tests were solely done on servo-hydraulic machines. Specimen failure for all fatigue tests is defined by a displacement increase of Δs =  ± 2 mm of the global displacement extrema measured in the uncracked state. For CAL tests, a second failure criterion was defined by a frequency change of Δf =  ± 1 Hz. X-ray diffraction measurements and macro-hardness analyses were carried out. To evaluate the influence of service loading and, in particular, the loading sequence on the condition of the HFMI-treated boundary layer, X-ray residual stress measurements and microhardness profile measurements were performed.

2.2 Specimens

The investigations were carried out on welded specimens containing transverse attachments as shown in Fig. 2. The specimen type was chosen because extensive test results under CA loading are available and because the notch effect is relatively high. The investigations were conducted on as-welded and HFMI-treated specimens. The joints were fabricated out of mild (S355J2 + N) and high-strength steel (S700M). The chemical composition and the corresponding material properties are outlined in Tables 1 and 2. The welding process parameters are given in Table 3.

Fig. 2
figure 2

T-joint specimen dimensions [23]

Full size image
Table 1 Chemical composition of S355 mild steel and S700 high strength steel
Full size table
Table 2 Mechanical properties of S355 mild steel and S700 high strength steel
Full size table
Table 3 Welding process parameters of T-Joint of S355 mild steel and S700 high strength steel
Full size table

After welding, the samples were cut by water jet. In the areas near the weld toe, the cuts were made as a fine cut (Q5) according to [28]. The remaining areas were sectioned out with a standard cut (Q3). Due to the weldment, an angular distortion of the specimens occurred, which was minimised by using a three-point bending fixture as seen in Fig. 3. The specimens were straightened at the clamping surface so that the angular distortion between the clamping surfaces after straightening was approx. 0.05°. The straightening process maintained the initial residual stress state and minimised the influence of distortion on the local stress ratio. Water jet cutting resulted in additional notches on the cut surface before the actual weld toe. These notches were machined with a flap disc and then sandblasted to prevent a crack initiation at the edge (Fig. 4). The HFMI treatment of specimens made of mild steel S355 was done by using a HiFIT device and a pin radius of 1.5 mm. For specimens made of S700, a PITEC device with a pin radius of 2.0 mm was applied for the HFMI treatment. The HFMI treatment was carried out by a single pass at the weld toe according to the manufacturer’s recommendations. Figure 5 shows an example of the weld toe of a specimen in the as-welded state and one of a specimen in the HFMI-treated state. The treatment parameters can be found in Table 4. The series were termed according to the applied load spectrum (N = Linear spectrum), the load sequence (R = random, HL = high-low, LH = low–high), the post-treatment condition (H/P = HFMI treated, AW = as welded) and the used material (S355 or S700).

Fig. 3
figure 3

Straightening of the clamping surfaces

Full size image
Fig. 4
figure 4

Test specimen, HFMI-treatment with and without finishing of the edges

Full size image
Fig. 5
figure 5

Weld toe before (top) and after (bottom) HFMI-treatment

Full size image
Table 4 Process parameters of the HFMI treatment
Full size table

2.3 Results

2.3.1 Statistical evaluation of fatigue test data

The S–N curves and Gaßner-lines shown in the following figures were computed according to the approach outlined in [29] using a prediction interval. S–N curves with a survival probability of Ps = 50% are calculated by linear regression. The characteristic S–N curves represent the lower limit of prediction for a single future test with 95% confidence (Ps = 95%). The values for the fatigue strength were determined with free slope. The reference value of the calculated fatigue strength Δσc is given for N = 2∙106 load cycles. The results of the VAL fatigue test are given in Table 5. The table also shows the value Ts which is the stress range ratio between the lower and the upper bound of the logarithmic standard normal distribution for specific values of survival probability. Typically, these survival probabilities are between Ps = 90% and Ps = 10%. As described in [24], the statistical evaluation was done with the lower prediction bound for a single future test with 95% confidence. Therefore, a conversion into equivalent values of probability of survivals for the equal stress range ratio Ts was made.

Table 5 Fatigue test series of AW and HFMI-treated specimens, axial loading, variable amplitude, R =  − 1
Full size table

2.3.2 CAL fatigue test

Constant amplitude fatigue tests were carried out using five as-welded and five HFMI-treated specimens of S355 mild steel, while for CAL test on specimens of S700 high-strength steel, a number of seven specimens were tested. This small number of data is based on the small surplus of samples that were kept in stock for the VAL tests and were not needed for this purpose. The results of the CAL fatigue tests are shown in Figs. 6 and 7. The S–N curves derived from evaluation of the test data were used for the damage accumulation of the data obtained from the VAL tests. Data points with more than N = 5∙106 load cycles were defined as run outs and tested again at a higher stress level. Outliers and run outs were not considered in the statistical evaluation. To classify the results, the corresponding S–N curves for as welded according to [27] and HFMI-treated non-load carrying transverse attachments according to [12] are shown as well. As the results of the specimens, tested again with an increased stress range, are within the corresponding scatter range of the test series, they were taken into account for the evaluation of the fatigue strength.

Fig. 6
figure 6

CAL-AW and CAL-HFMI series (S355)

Full size image
Fig. 7
figure 7

CAL-AW and CAL-HFMI series (S700)

Full size image

Respecting the limited specimen number, the series CAL-AW-S355 confirmed with a characteristic fatigue strength of Δσc,AW,CAL = 100 MPa and with a slope of mAW,CAL = 3.0 detail category of FAT 80 quite well. The series of HFMI-treated transverse attachments (CAL-H-S355) has a significantly flatter slope of mHFMI,CAL = 9.9. The computed characteristic value of the fatigue strength is Δσc,HFMI,CAL = 304 MPa. Compared to the FAT 140 for transverse attachments (TS) and a recommended slope of m = 5, the S–N data of the series CAL-H-355 show a significant increase for the finite life region of HCF. By using the higher-strength steel S700, the fatigue strength was significantly increased compared to the test series containing specimens of mild steel S355.

For the CAL-AW-S700 series, the characteristic value of the fatigue strength was calculated as Δσc,AW,CAL = 200 MPa with a slope of mAW,CAL = 4.6. The slope due to HFMI-treatment resulted in mHFMI,CAL = 5.8, and the fatigue strength of the series CAL-P-S700 was raised to Δσc,HFMI,CAL = 333 MPa.

Analysing the results of the CAL fatigue tests shown in Figs. 6 and 7, it is important to mention that the cracks of the HFMI-treated specimens initiated exclusively in the base material (BM). That is why in Figs. 6 and 7, the FAT class FAT 160 for base material is given.

The results of these investigations suggest that the HFMI treatment increases the local fatigue strength to such an extent that a failure in the base material becomes decisive for the fatigue life consideration. To make a final statement, further detailed analyses and evaluations regarding the local stress state and the surface layer condition have to be carried out. This topic will be part of further studies.

2.3.3 VAL fatigue test, random

As already mentioned, the fatigue tests under random VAL followed the approximated linear spectra with a spectrum length of H0 = 200,000 cycles and an irregularity factor of I = 0.99. The stress ratio was set to R =  − 1. The results of fatigue tests with random load sequence are shown in Figs. 8 and 9. To categorise the results, the characteristic S–N curves for the CAL series are shown in addition to the Gaßner lines of the VAL series.

Fig. 8
figure 8

VAL-Random-AW and VAL-Random-HFMI series (S355)

Full size image
Fig. 9
figure 9

VAL-Random-AW and VAL-Random-HFMI series (S700)

Full size image

In order to roughly assess sequence effects of service loads on the fatigue behaviour of HFMI-treated and as-welded transverse attachments, values of fatigue strength at N = 2∙106 cycles are given. A fatigue strength of ΔσC,AW,VAL,R = 322 MPa for the series N-R-AW–S355 and a value of ΔσC,HFMI,VAL,R = 563 MPa for the series N-R-HFMI-S355 were determined. The strength-increasing effect of the HFMI treatment is thus of similar significance to that of CAL.

As expected from the CAL test results, the fatigue strength was also increased for the VAL tests due to the use of the high-strength steel. This is shown by the Gaßner lines lying at higher stress levels compared to the VAL-S355 series. For both series N-R-AW-S700 and N-R-P-S700, the Gassner-lines are flatter than for the corresponding series of material S355. Based on the resulting slope of the N-R-AW-S700 series with a value mAW,VAL,R = 4.9, the characteristic fatigue strength leads to approx. ΔσC,AW,VAL,R = 738 MPa. The slope value of the series N-R-P-S700 results in mHFMI,VAL,R = 11.1, which is significantly flatter than the slope of the series N-R-AW-S355. The computed value for the fatigue strength of the N-R-P-S700 series is ΔσC,HFMI,VAL,R = 930 MPa.

In accordance with the CAL series, the failure locations of the AW specimens were at the weld toe (WT). The cracks of the HFMI-treated welds made of S355 initiated exclusively in the base material (BM). For three out of eight HFMI-treated specimens of the N-R-P-S700 series, failure occurred initiating by a crack at the weld toe (WT). The data points lie within the scatter band of the test series and therefore were considered in the evaluation. Figure 10 shows typical failure locations of AW and HFMI-treated specimens under CA and VA loading.

Fig. 10
figure 10

Failure locations of the AW series (WT) and the HFMI series (BM) as well as typical fracture pattern of the one-sided TS

Full size image

2.3.4 VAL fatigue test, high-low and low–high

To determine a possible load sequence effect, fatigue tests with a high-low and low–high ordered VAL of the linear spectrum were carried out. The results of the VAL fatigue tests with blocked VAL of linear spectra are shown in Figs. 11 and 12. No significant sequence effect was observed between the high-low and low–high ordered VAL when evaluating the S–N data. Following, these series were evaluated commonly. The slope and fatigue strength values of the obtained Gaßner lines with ordered blocked High-Low and Low–High VAL are given in Table 5. Comparing the CAL series of the AW and HFMI-treated condition, the change in slopes and the benefit of HFMI treatment in the ordered high-low and low–high VAL series can be observed, as already determined in the random VAL series.

Fig. 11
figure 11

VAL-Blocked-AW and VAL-Blocked-HFMI series (S355)

Full size image
Fig. 12
figure 12

VAL-Blocked-AW and VAL-Blocked-HFMI series (S700)

Full size image

Transverse attachments of S355

Three of the HFMI-treated specimens of the N-HL/LH-H-S355 series were declared as outliers or run outs and are marked in Fig. 11. They were not considered in the evaluation of the Gaßner lines. The two outliers buckled due to the high compressive stresses. For the third specimen, no failure was detected at N = 2.3 × 107 cycles. This specimen was defined as a run out. Two specimens failed at the weld toe (WT). The remaining specimens failed starting from the base material (BM), similar to the CAL and Random series. The specimens in the AW state failed initiating from a crack at the weld toe. The data of the N-HL/LH-S355 series show a lower scatter in comparison to the VAL Random series. The slope is slightly flatter. The Gaßner lines of both series in the AW and HFMI-treated state show an offset to the series under random loading. This offset can be seen by comparing Figs. 8 and 11. In the AW state, the characteristic value of the fatigue strength increased by 157% compared to random VAL. For the series in the HFMI-treated state, the characteristic value of the fatigue strength increased by 125% due to high-low and low–high–ordered VAL.

Transverse attachments of S700

For the N-LH/HL-P-S700 series of HFMI-treated specimens, the Gaßner line is steeper with a value m = 8.8 compared to the random VAL series. However, the fatigue strength was significantly increased due to blocked VA loading. The slope of Gaßner lines as well as the characteristic fatigue strength of the series in the AW condition is similar to the series with the random VAL series (N-R-AW-S700). Two test data of the N-HL-AW-S700 series were marked as outlier or run out in Fig. 12. The tests of these two data were performed with the same maximum nominal stress amplitude σn,a,max = 500 MPa. At one of these specimens, no crack could be detected after N = 13 × 106 cycles. It was defined as a run out. The second specimen marked as an outlier failed at load cycle N = 377,198 cycles. It can be assumed that this specimen has internal defects in the weld, which led to early crack initiation. Considering this result in the statistical evaluation would lead to a disproportionate shift of the lower scatter band. The specimens in the HFMI state mainly failed initiating by a crack at the base material (BM). However, failure occurred initiating from a crack at the weld toe (WT) as well. This was the case in four of the 14 samples. The data points were nevertheless taken into account for the evaluation of the Gaßner line.

2.4 Evaluation and discussion about sequence effect

2.4.1 Evaluation of the damage accumulation

The test results were analysed and evaluated using the “Miner”-modified linear damage accumulation hypothesis. The results were compared, and the analysis was classified with respect to the reference S–N curve on which the calculation was based. The reference S–N curve on which the calculation was based is decisive for the fatigue assessment and for the determination of damage sums. The recommendations of the IIW [27] specify the knee point of the S–N curve at Nk = 1∙107 cycles. The second slope of the S–N curves changes under the knee-point of the constant amplitude fatigue limit (CAFL) at Nk = 1 × 107 cycles and follows a value of m′ = 2 m − 1. The calculations of damage sums were based on the experimentally determined S–N-curves with a second slope as recommended in [27]. The rainflow counting method was used on the measured load signal of the test rig to determine the real stress spectra for each test specimen. The resulting real spectra, the nominal stress range and their corresponding frequencies were used as input parameters for the damage accumulation.

To assess the quality of the calculated fatigue life estimation, the calculated and experimental fatigue life values Ncalc. and Nexp. were compared. In Figs. 13 and 14, dashed lines are also drawn, which show the ratio of the service life values in relation to each other. The calculated damage sum Dcal was derived from the ratio Nexp/Ncalc. For data points below the D = 1 line, the estimation of calculated fatigue lifetime was on the safe side. If the data points were above the D = 1 line, the calculated fatigue lifetime estimation predicted a longer lifetime than the experiments indicate.

Fig. 13
figure 13

Comparison of the experimental fatigue life Nexp and the calculated fatigue life Ncalc of the steel grade S355 in the as-welded (left) and HFMI-treated (right) states, for the linear spectra

Full size image
Fig. 14
figure 14

Comparison of the experimental fatigue life Nexp and the calculated fatigue life Ncalc of the steel grade S700 in the as-welded (left) and HFMI-treated (right) states, for the linear spectra

Full size image

Due to VAL, the HFMI-treated specimens failed mainly in the base material. A few of them failed at the weld toe. As mentioned above, the test data were within the same scatter. Therefore, the statistical evaluation of the damage accumulation was done regardless of the failure location.

The calculated fatigue life of transverse attachments of steel grade S355 in the AW state showed a good agreement with the experimental fatigue life. The sequence effect of the linear spectra can be seen in a slight shift towards higher damage sums. The computed fatigue life of transverse attachments of steel grade S355 in the HFMI state with a damage sum of D < 1 overestimated the actual fatigue life gained by experimental studies. The sequence effect of the fatigue life of HFMI-treated specimens of S355 can also be seen in a slight shift towards a higher damage sum.

A differentiated result can be seen for the steel grade S700. For specimens in the AW state, damage sums of D < 1 were determined in most cases, regardless of the loading sequence. The estimation of fatigue life using the modified Miner rule fitted better for specimens made of S355 than for specimen of S700. As the evaluation was based on the nominal stress method, possible material-related local effects could not be considered. The sequence effect on samples made of S700 in the AW and HFMI-treated state was less significant compared to the tests with specimens made of S355.

2.4.2 Results and discussion about the sequence effect

Based on the statistical evaluation of the S–N data shown in Figs. 8, 9, 11 and 12, a sequence effect of the fatigue life of AW and HFMI-treated transverse attachments can be seen. This effect becomes significant especially by comparing the values of fatigue strength, determined by linear regression (Ps = 50%). Figure 15 shows the ratio Δσn,VAL/Δσn,CAL of the allowable maximum stress range at N = 2 × 106 cycles between CA and VA loading. The ratio between VAL versus CAL was reported separately according to random and ordered blocked loading sequence. Higher fatigue strengths tended to be achieved by the ordered blocked VA loading, and thus, an increased fatigue life can be expected. As mentioned before, no significant sequence effect was observed between the high-low and low–high ordered VAL when evaluating the S–N data. However, sequence effect between the high-low and low–high ordered VAL was apparent in the evaluation of damage sums by the slight shift towards higher damage values in Figs. 13 and 14. As shown in Figs. 8, 9, 11 and 12, a predominant portion of HFMI-treated transverse attachments failed due to cracks at the base material. Compared to other studies, crack initiation in the base material is rather atypical for this type of HFMI-treated weld. Nevertheless, results from [7] show that at a stress ratio of R =  − 1, crack initiation in the base material may be expected especially for higher strength steels. This conclusion was further validated by analysing existing literature data in [2]. Therefore it is possible that the shifting of the crack initiation into the base material may reduce the sequence effect between the high-low and low–high–ordered VAL.

Fig. 15
figure 15

VAL-Blocked-AW and VAL-Blocked-HFMI series (S355)

Full size image

For the transferability of the results to other notch details, deviating stress ratios and loading types, further studies must be carried out. Especially due to a deviating loading type such as bending load, the crack initiation of the one-sided HFMI-treated transverse attachments of this study could shift into the weld toe. As shown by Ahola et al. in [30], the effect of different loading types on the fatigue behaviour of a welded joint is affected by the attached joint arrangement, which can be either symmetrical (X-joint) or asymmetrical (T-joint). It was observed that bending in asymmetric T-joints leads to a higher notch stresses in the weld toe compared to axial loading. This is caused by the secondary effects in the former case. In further investigations [31] on AW and HFMI-treated T-joints, the notch stresses at the weld toe were also generally higher under bending load than under axial tensile load. Applying a bending load on the HFMI-treated specimens of this study could therefore lead to a failure at the weld toe instead of a failing in the base material due to the expected higher stress concentration at the weld toe. To verify this effect, further experimental and numerical studies are necessary.

3 Conclusions

Fatigue tests under CAL, random VAL, high-low VAL and low–high VAL with linear spectrum on transverse attachments in the AW and HFMI state were performed and evaluated. The failure mechanisms of the performed fatigue tests of CAL, VAL random and VAL high-low/low–high series were similar within the respective AW or HFMI state. While for the AW state all specimens showed a typical fracture pattern in the weld toe, most of the HFMI series specimens failed in the base material. This indicates that the fatigue strength was locally increased by the HFMI treatment to such an extent that the strength of the base material becomes decisive for the service life of the component.

The results of the experimental work confirm the strength-increasing effect of the HFMI treatment on the fatigue strength regardless of the loading sequence. The evaluation of the S–N curves showed a significant sequence effect of as-welded and HFMI-treated transverse attachments under variable loading with linear spectrum. In addition to the experimental studies, fatigue life was calculated by using a linear damage accumulation hypothesis of the modified “Miner” rule according to [32]. Based on the damage accumulation, a slight sequence effect between the high-low and low–high–ordered VAL has been revealed. Anyhow, the sequence effect for the HFMI-treated transverse attachments could not be related to a change of the beneficial effects of the HFMI treatment because all cracks occurred predominately in the base material.

In further research, local analyses based on the present results can provide an answer for the typical failure location of HFMI-treated specimens. Thereby, the effect of strain hardening and the effect of the improved weld geometry the fatigue behaviour should be considered.

To further validate the strength-increasing effect of HFMI treatment under VAL, further experimental studies are recommended. For this purpose, it must be evaluated if and how the results obtained in this study can be applied to varying parameters such as notch geometry, stress ratio or spectrum shape.